Attenuation of Rayleigh waves by a combined periodic open trench-wave impeding block vibration isolating barrier considering tunnel influence

Traditional open trench and wave-impeding block barriers often suffer from narrow vibration isolation bandwidths, and their performance is further affected by tunnel scattering. To overcome these limitations, this study proposes a periodic open trench-impeding block joint barrier that combines Bragg scattering and local resonance to achieve broadband attenuation of Rayleigh waves. A plane strain tunnel-barrier coupling model incorporating Floquet periodic boundary conditions and the finite element method was developed to reveal the mechanisms of bandgap formation and parameter regulation under multi-physical field coupling. Dispersion analysis demonstrates that the proposed barrier produces three bandgaps within 11.3∼67.3 Hz, covering the dominant frequencies of seismic and environmental vibrations. The trench depth-to-width ratio is identified as the primary factor governing low-frequency expansion and mid-to-high-frequency stability through its effects on unit stiffness and Bragg scattering efficiency, while the material properties of the wave-impeding block play only a minor role, thereby supporting a design strategy centered on geometry optimization. Furthermore, tunnel scattering is shown to enhance isolation performance in the mid- and high-frequency ranges, where secondary reflections and phase cancellation lead to a 46% increase in peak transmission attenuation. These findings highlight the synergistic effect of geometric design and tunnel scattering in broadening vibration isolation bandwidth, providing a theoretical foundation for the development of efficient broadband vibration isolation barriers in complex underground environments.

1 Introduction

Surface waves, particularly Rayleigh waves, serve as primary carriers for energy transmission during seismic events and in urban environmental vibrations, such as those induced by rail transit and industrial machinery. As Rayleigh waves propagate along the ground surface, their energy is concentrated within shallow soil layers, with amplitude attenuating exponentially with depth. This behavior poses significant threats to the stability and safety of underground structures (e.g., tunnels, subways, and pipelines) as well as nearby buildings [1–3]. For example, in seismic scenarios, Rayleigh waves can induce severe surface shaking, leading to tunnel lining cracks and foundation liquefaction. In urban contexts, high-frequency vibrations generated by metro operations are transmitted to building foundations via Rayleigh waves, potentially triggering structural resonance and noise pollution. Global estimates suggest that vibration-induced tunnel maintenance costs amount to several billion USD annually, while secondary hazards such as ground subsidence exert a more profound and lasting impact on infrastructure stability [4, 5]. Consequently, the development of efficient and cost-effective vibration isolation technologies aimed at mitigating Rayleigh wave propagation has emerged as a pressing challenge in the field of underground engineering.

Among conventional isolation strategies, open trenches and wave impeding block represent two principal approaches. Open trenches reflect elastic wave energy through geometric scattering and impedance mismatch; however, their effectiveness at low frequencies is constrained by geometric limitations [6–8]. This limitation arises from the fact that Rayleigh wavelengths at low frequencies may span several tens of meters, while practical trench depths are typically less than 5 m-failing to meet the theoretical depth requirement of one-quarter the wavelength. Moreover, deep excavation incurs substantial financial and operational risks, including potential damage to underground utilities, exacerbation of ground settlement, and the induction of seepage issues in groundwater-rich regions [9, 10]. In contrast, wave impeding block relies on impedance contrast between their material stiffness and the surrounding soil to reflect high-frequency vibrations [11–14]; however, their performance is markedly reduced for mid-to low-frequency waves, particularly in soft soils where the impedance mismatch is insufficient to ensure effective energy reflection. These two traditional methods, when used independently, suffer from narrow frequency response bandwidths, rendering them inadequate for comprehensive isolation across the full spectrum-from low-frequency seismic waves (<20 Hz) to high-frequency environmental vibrations (30–80 Hz).

In recent years, researchers have explored the integration of trenches and wave impeding block to extend the isolation bandwidth. For instance, Zhou et al. [15], Cao et al. [16] and Cai et al. [17], Cai et al. [18] have demonstrated, through both theoretical and experimental approaches, the enhanced performance of open trench–wave impeding block combined systems. Nonetheless, these composite systems remain limited by key constraints: the low-frequency bandgap is still reliant on trench depth, necessitating extensive excavation; the high-frequency bandgap is governed by the impedance matching between the wave impeding block and the soil; and frequency blind zones persist between bandgaps, hindering full-spectrum isolation. More critically, the majority of existing studies assume idealized homogeneous ground conditions, neglecting the scattering effects introduced by realistic geological heterogeneities such as depressions [19, 20], elevations [21, 22], and tunnels [23–25]. Tunnels, as typical subsurface structures, can significantly alter the wavefield distribution through reflection and diffraction, particularly when their burial depth is comparable to the vibration wavelength. Failure to account for such scattering effects may result in isolation designs that are misaligned with the actual wavefield behavior, thereby compromising performance.

To address these limitations, this study proposes a periodic open trench–wave impeding block combined isolation system that leverages the synergistic effects of Bragg scattering and local resonance to achieve broadband vibration attenuation. The key innovations of this work are as follows: (1) the adoption of periodically arranged unit cells that integrate the “soft” properties of trenches with the “stiff” characteristics of wave impeding block, thereby overcoming the frequency constraints associated with single-mechanism designs; and (2) the incorporation of a tunnel–barrier interaction model to quantitatively assess the enhancement in bandgap behavior due to tunnel-induced scattering, offering a theoretical foundation for adaptive design in complex geological settings. A coupled plane-strain model featuring the tunnel and isolation barrier is developed, and, by employing Floquet periodic boundary conditions alongside finite element simulations, the mechanisms of bandgap formation and the parameter-dependent tunability under multiphysics interactions are comprehensively investigated.

The remainder of this paper is structured as follows: Section 2 details the formulation of the mathematical model for the periodic open trench–wave impeding block system. Section 3.1 presents the dispersion analysis of the periodic structure. Section 3.2 investigates the influence of material and geometric parameters on bandgap characteristics. Section 3.3 explores the impact of tunnel–barrier interaction on isolation performance. Finally, Section 4 summarizes the principal findings of the study.

2 Mathematical model and eigenvalue calculation of periodic wave barrier

2.1 Mathematical model of the problem

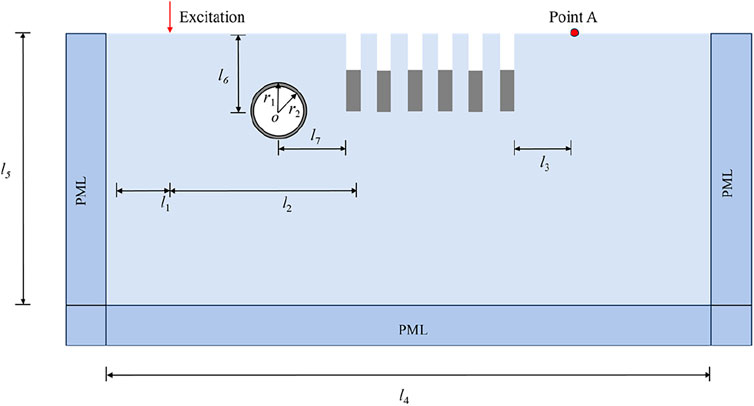
To achieve broadband vibration isolation by leveraging the respective advantages of wave barriers and open trenches, a novel type of periodic trench–wave impeding combined isolation system is designed. Furthermore, to account for the scattering effects of existing tunnels on vibration waves, a mathematical model of a tunnel–periodic wave barrier system is established, as illustrated in Figure 1a. It is assumed that the trench–wave impeding block structure extends infinitely along the z-direction, allowing the three-dimensional problem to be reduced to a plane strain problem. By applying periodic boundary conditions, the two-dimensional model can be further simplified to a unit cell model for computational efficiency. In the simplified model, the upper surface is treated as traction-free, while the bottom boundary is fixed. These conditions are standard for modeling wave propagation in a semi-infinite elastic domain: a fixed base approximates motionless bedrock at great depth, and a free surface mimics the ground-air interface. The resulting unit cell model is shown in Figure 1b, where the white region at the top represents the trench, and the gray region at the bottom denotes the wave barrier. It is noted that a represents the lattice constant of the periodic structure, and the combined height of the trench and wave barrier within a unit cell is h₁+h₂ = 2 m. The trench width is denoted as a_t. The right side of Figure 1b presents the irreducible Brillouin zone that will be scanned during the band structure analysis.

Figure 1

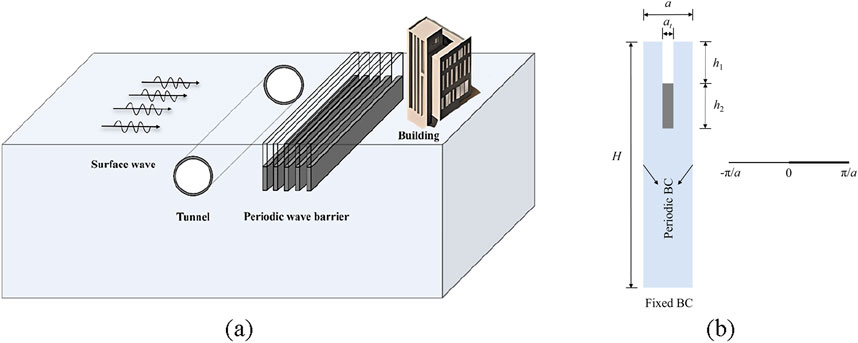
Figure 1. Periodic open trench-wave impeding block combined vibration isolation barrier and unit cell diagram. (a) Schematic diagram of open trench-wave impeding block combined periodic wave barrier (b) Unit cell diagram.

2.2 Eigenvalue calculation

The wave impeding block and the foundation are simulated by homogeneous isotropic completely elastic medium, ignoring the influence of volume force. For the semi-infinite foundation, the wave equation of the medium is as follows:

$\left(\lambda +\mu \right)\nabla \left(\nabla ·\mathit{u}\right)+\mu {\nabla }^2\mathit{u}=\rho \frac{{\mathrm{\partial }}^2\mathit{u}}{\mathrm{\partial }{t}^2}(1)$

where ρ denotes elastic medium density; λ and μ are lamb constants for the elastic medium; u denotes the displacement vector of elastic medium.

In order to calculate the dispersion relation of infinite periodic lattices, Floquet periodic boundary conditions are applied on the left and right sides of the unit. According to Bloch-Flock theory, the solution of Equation 1 can be written as follows:

$\mathit{u}\left(\mathit{r},t\right)={\mathrm{e}}^{\mathrm{i}\left(\mathit{k}·\mathit{r}-\omega t\right)}{\mathit{u}}_k\left(\mathit{r}\right)(2)$

where r denotes the position vector; t denotes time; k =(k_x, k_y) is the Bloch-Floquet wave vector; ${\mathit{u}}_k\left(\mathit{r}\right)$ is the displacement function relative to the position vector, and ω denotes the angular frequency.

In Equation 2 ${\mathit{u}}_k\left(\mathit{r}\right)$, is defined as follows:

${\mathit{u}}_k\left(\mathit{r}\right)={\mathit{u}}_k\left(\mathit{r}+\mathit{a}\right)(3)$

where a denotes the unit constant vector.

Substituting Equation 3 into the periodic displacement boundary conditions in Equation 2 can be expressed as follows:

$\mathit{u}\left(\mathit{r}+\mathit{a},t\right)={\mathrm{e}}^{\mathrm{i}\left(\mathit{k}·\mathit{a}\right)}\mathit{u}\left(\mathit{r},t\right)(4)$

By applying periodic boundary conditions, the infinite propagation problem is transformed into the eigenvalue problem of the unit cell. Combining the Equations 1, 4, the eigenvalue equation of the unit cell can be obtained as follows:

$\left(\mathit{K}-{\omega }^2\mathit{M}\right)\mathit{u}=0(5)$

where K and M represent the stiffness matrix and mass matrix respectively. By solving the eigenvalues and eigenvectors in Equation 5, the dispersion relationship between the wave vector k and the angular frequency ω can be obtained.

3 Solving the dynamic response problem of unsaturated ground

The typical unit of the periodic open trench-wave imped block composite vibration isolation barrier used in this paper is shown in Figure 1b, in which the wave impeding block and the existing tunnel structure are made of concrete. Based on the existing research results, the main geometric parameters of the barrier system are shown in Table 1. The physical and mechanical parameters of the site soil are listed in Table 2, and the parameter settings meet the simulation requirements of the semi-infinite uniform foundation. Aiming at the study of vibration propagation characteristics of periodic barrier, the dispersion relation calculation and vibration transmission analysis are carried out by COMSOL multi-physics simulation platform. In order to improve the calculation accuracy of the numerical model, the maximum size of the unit is strictly controlled within 1/5 of the minimum wavelength in the process of free triangular mesh generation. The research focuses on the interaction mechanism between periodic barrier and Rayleigh wave. The sound cone method is used to extract the Rayleigh wave field. The boundary condition of the sound cone is determined according to the shear wave velocity of the soil, and the effective decoupling of surface wave and body wave is realized by the sound cone separation technology. The surface wave mode is distributed in the area below the sound cone. This processing method fully considers the fluctuation characteristics that the Rayleigh wave velocity is less than the body wave velocity.

Table 1

Table 1. Dimensional parameters of periodic barriers.

Table 2

Table 2. Physical and mechanical parameters of periodic barriers and soils.

3.1 Dispersion curve analysis

Figure 2a illustrates the dispersion curve of the periodic open trench-wave-impeding block combined vibration isolation barrier, with the normalized Bloch wave vector on the horizontal axis and the frequency on the vertical axis. Three bandgaps (blue shaded areas) clearly exist in the curves in the following ranges: first bandgap: 11.3 Hz–14.6 Hz, second bandgap: 33.5–36.8 Hz, and third bandgap: 40.9 Hz∼67.3 Hz. Since the frequency of the seismic wave is mainly located below 20 Hz, the ambient vibration Since the frequency of seismic wave is mainly located below 20 Hz, and the frequency of environmental vibration is around 30 Hz∼80 Hz, from the above bandgap analysis, it can be seen that the periodic air-gap-wave impeding block joint vibration isolation barrier covers the main bands of seismic wave and environmental vibration frequency respectively, and the superposition of the three bandgaps realizes a wide-frequency isolation from the low-frequency seismic wave to the high-frequency environmental vibration, which breaks through the band limitations of the traditional vibration isolation barriers. Figure 2b labels the vibration modes of three special points (A, B, C) on the dispersion curve, which reveal the formation mechanisms of different bandgaps. For the point A mode the displacement amplitude in the characteristic air-gap region is the largest, and the wave impeding block has almost no deformation. The low-frequency band gap is dominated by the local resonance effect. The trench acts as a “soft” unit and forms a mass-spring system with the surrounding foundation, which resonates at a specific frequency. For point B, the displacement at the junction of the wave impeding block and the trench fluctuates violently, forming a standing wave mode. For point C, the air-gap exhibits high-frequency bending vibration with a complex displacement distribution in the air-gap region. The high-frequency bandgap is formed by impedance mismatch and mode coupling, and the high stiffness of the wave impeding block and the flexibility of the foundation form a strong impedance contrast, reflecting high-frequency waves. Meanwhile, the geometric scattering of the air gap further dissipates the energy. By analyzing the vibration modes and bandgap mechanisms at points A, B, and C, the multiscale modulation capability of the periodic open trench-wave impeding block joint barrier is revealed: the low-frequency relies on the local resonance, and the medium- and high-frequency relies on the impedance mismatch and Bragg scattering. The synergistic effect of the three bandgaps realizes the full-frequency coverage from seismic waves to environmental vibrations, providing an efficient broadband vibration damping solution for complex underground projects.

Figure 2

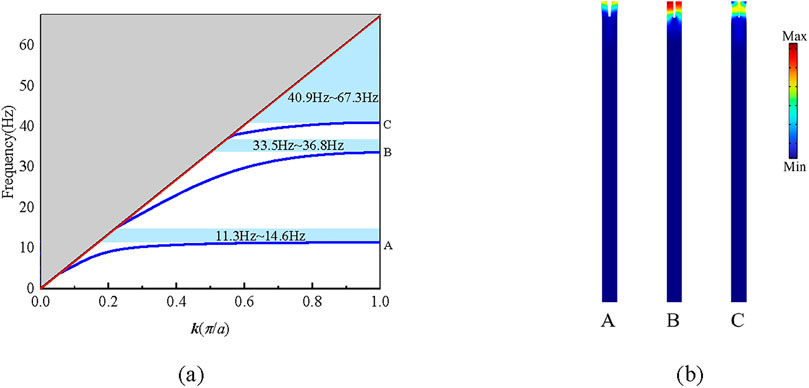
Figure 2. Dispersion relations and vibration modes at special points. (a) Dispersion relation (b) Vibration modes.

3.2 Influence of material parameters and geometrical parameters on the band gap

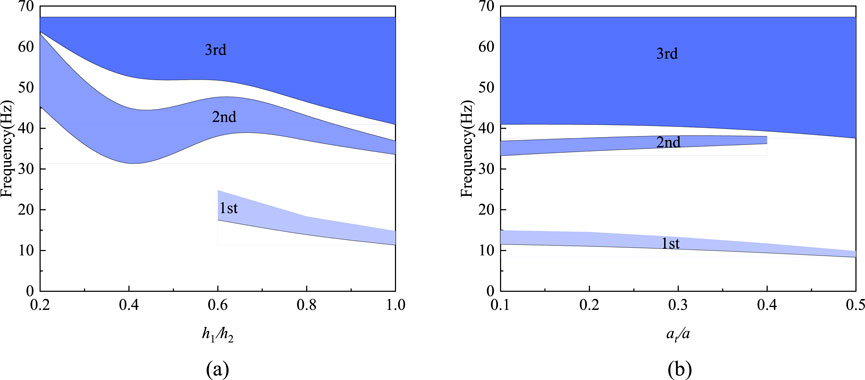
Figure 3 shows that the bandgap range of the combined periodic open trench wave impeding block vibration isolation barrier is significantly affected by the geometrical parameters. The ratio of the depth of the open trench to the depth of the wave impeding block(h₁/h₂) significantly affects the low-frequency bandgap by regulating the balance between local resonance and Bragg scattering. From Figure 3a, it can be seen that the first bandgap starts to appear when h₁/h₂ increases from 0.2 to 0.6, and the increase in the depth of the open trench reduces the overall stiffness of the single cell, which shifts the local resonance frequency to lower frequencies and significantly increases the bandgap width. From Figure 3b, it can be seen that the open trench width ratio (a_t/a), on the other hand, controls the Bragg scattering efficiency of the mid- and high-frequency bandgap, and when the ratio a_t/a increases from 0.1 to 0.4, the second-order bandgap disappears, and the first-order bandgap and the third-order bandgap show a decreasing trend. When the period constant a is fixed, its value directly determines the critical wavelength of Bragg scattering, thus locking the center frequency range of the bandgap, while the adjustment of the null channel width a_t (i.e., the variation of the null channel width ratio a_t/a) enhances the phase-cancelling interference efficiency by expanding the range of the scattering interface, but if a_t/a is too large, the open trench occupies the main volume of the single cell will weaken the mass inertia effect of the wave impeding block, leading to the narrowing of the low-frequency bandgap width.

Figure 3

Figure 3. Influence law of geometrical parameters on band gap. (a) h₁/h₂ (b) a_t/a.

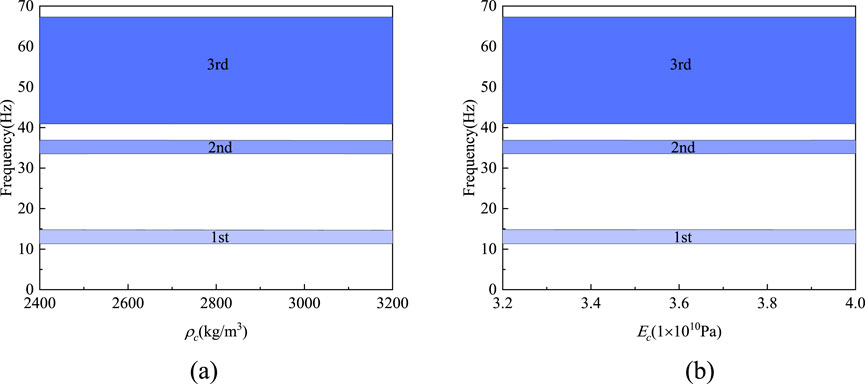
Although the geometrical parameters are the core tuning variables, the material parameters of the wave impeding block (density ρ, elastic modulus E) play synergistic roles under specific conditions. For example, the wave impeding block density enhances the low-frequency impedance mismatch and compensates for the local resonance efficiency of the shallow trench, while the modulus of elasticity optimizes the phase-matching conditions for the high-frequency Bragg scattering by adjusting the wave impeding block stiffness. However, Figure 4 shows that the variation of the elastic modulus and density of the wave impeding block does not have a significant effect on the bandgap. This is due to the limited space for tuning the material parameters under the existing design framework, and when the impedance difference between the wave impeding block and the foundation is significant enough, further adjustment of the material parameters has a weak effect on the bandgap broadening. Therefore, geometrical optimization should be the main focus of the actual project, supplemented by the adaptability of material parameters, to achieve efficient vibration isolation in a wide band under the premise of cost control.

Figure 4

Figure 4. Influence law of material parameters on band gap. (a) ρ_c (b) E_c.

3.3 Transmission analysis of a finite number of periodic barriers considering the effect of tunneling

In order to verify the accuracy of the dispersion relationship and the vibration isolation performance of the periodic combined vibration isolation barrier, and considering the scattering effect of the existing tunnel on the vibration wave, a two-dimensional finite element model is established as shown in Figure 5, and six rows of barriers are set up. A vertical harmonic load with an amplitude of 1000 N is applied to the input end on the left side of the model, and the output end point A is set on the right side of the model to detect the surface displacement amplitude. A PML matching layer is added to the boundary around the model to prevent the reflection of the vibration wave from the boundary. The specific dimensions of the model are as follows: l₁ = 5 m, l₂ = 20 m, l₃ = 3 m, l₄ = 4 m, l₅ = 15 m, l₆ = 8, l₇ = 10 m, r₁ = 3 m, r₂ = 2.7 m. In order to evaluate the vibration isolation performance of the periodic wave barrier considering tunnel scattering, the transmission attenuation (TA) coefficient (Equation 6) defined by Gao et al. [26] is used to measure the vibration isolation effect of the periodic combined vibration isolation barrier:

$TA=20{\log }_{10}\frac{{\stackrel{\sim }{u}}_y}{u_y}(6)$

where ${\stackrel{\sim }{u}}_y$ is the average vertical displacement of the output end of the foundation surface after setting the barrier; $u_y$ is the average vertical displacement of the output end of the foundation surface without barrier.

Figure 5

Figure 5. Two-dimensional analysis model of finite number of periodic wave barriers.

Figure 6 verifies the correctness of the 3.2-section dispersion curve by the transmission attenuation coefficient, and reveals the enhancement mechanism of the tunnel on the vibration isolation performance. Without considering the influence of the tunnel, the TA curve is consistent with the predicted band gap range of the dispersion curve. The peak attenuation value in the low frequency band is 16 dB, and the peak attenuation in the middle and high frequency band can reach 45 dB, which corresponds to the band gap generated by local resonance and Bragg scattering, respectively. The accuracy of the theoretical model is verified. When considering the influence of the tunnel, the band gap range predicted by the dispersion curve is roughly consistent. As the frequency increases, it can be seen that in the low frequency band, the transmission curve considering the existence of the tunnel is roughly the same as that without considering the existence of the tunnel, and there is a significant difference in the middle and high frequency bands. In the middle frequency range of f = 36 Hz ∼ 40 Hz, the transmission curve considering the influence of the tunnel has a significant attenuation. Compared with the peak attenuation difference of the transmission curve without considering the influence of the tunnel, the difference can reach 46%. This is because the buried depth of the tunnel is shallow, and the wave field in the intermediate frequency band is just equal to the buried depth of the tunnel. Most of the elastic waves are reflected by the tunnel and scattered into the interior of the foundation, which results in the difference of vibration isolation effect before and after considering the influence of the tunnel. When the vibration frequency increases to a higher range, it can also be seen from the figure that in the high frequency band, the transmission curves in the two cases are roughly the same. This is because the wavelength of the high frequency band is small, and only a part of the elastic wave will be reflected and scattered by the tunnel.

Figure 6

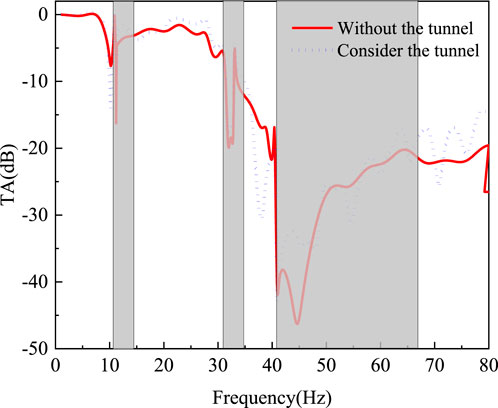
Figure 6. The transmission attenuation coefficient of the periodic barrier considering the influence of the tunnel.

In order to further analyze the causes of the difference in vibration isolation effect caused by the existence of the tunnel, Figure 7 shows the variation curve of the vertical displacement of the ground surface with and without the vibration isolation barrier with frequency. From Figure 7a, it can be seen that when there is no barrier, the vertical displacement of the surface in the tunnel is obviously different in the range of 15 Hz–40 Hz. When the frequency increases to the high frequency band, the difference of surface displacement in the two cases decreases. It can be seen from Figure 7b that the vertical displacement of the ground surface has obvious attenuation in some local frequency bands after the vibration isolation barrier is set, which corresponds to the band gap range of the periodic vibration isolation barrier. In addition, Figure 7b also shows the joint action mechanism of the tunnel and the periodic vibration isolation barrier, that is, after considering the existence of the tunnel, the elastic wave reflected by the periodic vibration isolation barrier in the band gap range will be affected by the tunnel, and the secondary reflection and scattering will occur, which will cause significant differences in the vibration isolation effect.

Figure 7

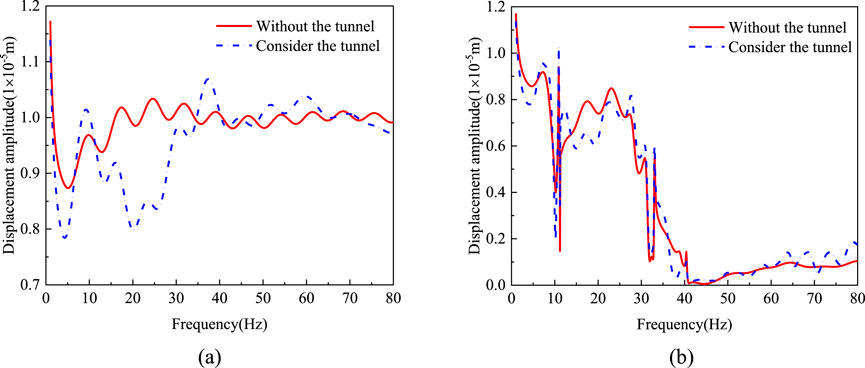
Figure 7. Variation of surface displacement with frequency for unbarred and barred surfaces. (a) Without periodic wave barrier (b) With periodic wave barrier.

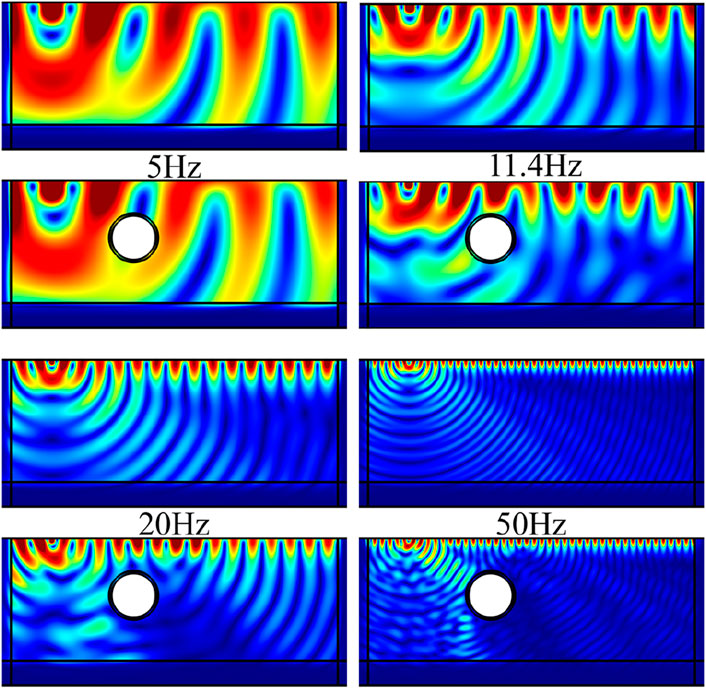
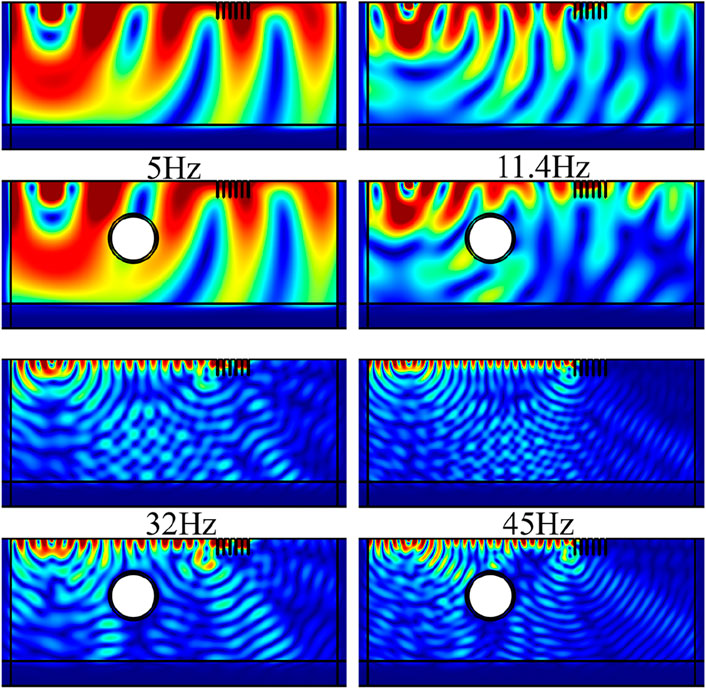
In order to demonstrate the above mentioned mechanism of joint action of tunnel and periodic vibration isolation barrier on elastic waves, the foundation displacement clouds at different frequencies before and after considering the effect of tunnel without barrier and after setting up the barrier are given in Figures 8, 9, respectively. The comparison between Figure 8 (without barrier) and Figure 9 (with barrier) reveals the mechanism of joint vibration isolation by tunnel and periodic barrier at different frequencies. Low frequency band (5 Hz): without barrier, the tunnel has limited reflection efficiency for long wavelength seismic waves and the low frequency vibration at 5 Hz is not within the band gap, the corresponding displacement maps with or without tunnel are roughly the same. When the frequency is increased to 11.4 Hz, the tunnel reflects the elastic wave without barrier as can be seen from Figure 8, and the local displacement of the surface becomes larger. When the barrier is set up, part of the surface wave energy is localized and another part is reflected by the barrier to the interior of the foundation, while part of the elastic wave is reflected by the tunnel. When the frequency is increased to 20 Hz and 32 Hz, the bypassing of the 20 Hz wave by the tunnel without barrier leads to the concentration of lateral displacement. After the barrier is set up, the barrier scatters through Bragg, and the tunnel reflected wave and the barrier scattered wave form a phase cancellation interference, which significantly optimizes the isolation efficiency of the main frequency of rail traffic vibration. When the frequency is increased to 45 Hz and 50 Hz, without the barrier, the tunnel has a weak effect on the short wavelengths generated at 50 Hz, and the displacement distribution is similar to that of the free field. After setting up the barrier, the barrier suppresses the 45 Hz displacement by high-frequency Bragg scattering, and the displacement in the region behind the barrier is affected due to the standing wave modes of the tunnel-barrier gap, resulting in oscillatory variations of the transmission curves in Figure 6 under the consideration of the tunnel effect.

Figure 8

Figure 8. Ground displacement clouds before and after considering tunnel without barrier.

Figure 9

Figure 9. Ground displacement clouds before and after considering tunnel with barrier.

4 Conclusion

In this study, by constructing a tunnel coupling model of periodic open trench-wave impeding block combined vibration isolation barrier, combined with Floquet periodic boundary conditions and finite element simulation, the band gap formation mechanism is revealed from the aspects of dispersion relationship and vibration mode. The influence of the depth ratio, width ratio and material parameters of the wave impeding block on the band gap range is discussed. By comparing the transmission attenuation coefficient with the displacement cloud diagram, the enhancement effect of tunnel scattering on the vibration isolation performance is quantified, and the interaction mechanism between elastic wave and tunnel-barrier composite structure is analyzed. The results show that:

1. Through the synergistic effect of low-frequency local resonance and medium-high frequency Bragg scattering, a triple band gap is formed in the range of 11.3–67.3 Hz, covering the main frequency bands of seismic waves and environmental vibrations, breaking through the narrow-band vibration isolation limit of traditional barriers.

2. The trench depth ratio and the width ratio are the key variables to control the band gap range. When h₁/h₂ increases to 0.6, the low-frequency band gap width is expanded. When a_t/a is more than 0.4, the inertia effect of the wave impeding block is weakened due to the excessive proportion of the open trench volume. The material parameters of the wave impeding block have a synergistic effect on the band gap under certain conditions. However, when the impedance difference between the wave impeding block and the foundation is significant, the further adjustment has a weak effect on the band gap widening, and the actual project should be based on geometric optimization.

3. The existence of the tunnel has a significant effect on the vibration isolation performance of the periodic vibration isolation barrier. In the middle frequency band, the peak attenuation difference of the transmission attenuation coefficient reaches 46% after considering the influence of the tunnel. In the low frequency band, the elastic wave is blocked by the barrier and is emitted to the tunnel area. The reflection efficiency of the tunnel to the long-wavelength seismic wave is limited. However, in the high frequency band, the wavelength is shorter, and only part of the elastic wave is reflected and scattered by the tunnel. This promotes the secondary reflection of the elastic wave energy into the foundation and forms a destructive interference with the barrier scattering wave, which reveals the synergistic vibration isolation mechanism of the tunnel and the periodic wave barrier at different frequencies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BH: Validation, Formal Analysis, Methodology, Conceptualization, Investigation, Writing – original draft, Visualization, Resources, Writing – review and editing. WL: Writing – review and editing, Visualization, Validation, Conceptualization, Data curation, Supervision. JP: Writing – original draft, Formal Analysis, Supervision, Data curation, Resources, Conceptualization, Visualization, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors gratefully acknowledge the financial support of the Gansu Provincial University Teachers Innovation Fund Project (Grant No. 2025A-333) and Tianshui Science and Technology Support Plan Project (TS-STK-2024A-265).

Acknowledgments

The authors are grateful to the reviewers for their helpful advice and comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang Z, Tang A, Huang D, Wu C, Huang Z. A novel environmental vibration analysis system and its application in isolation of environmental vibration induced by high-speed train in Harbin frozen soil site. Appl Acoust (2022) 193:108781. doi:10.1016/j.apacoust.2022.108781

CrossRef Full Text | Google Scholar

2. Çelebi E, Kırtel O, İstegün B, Navdar MB, Subaşı A, Göktepe F, et al. High-speed train induced environmental vibrations: Experimental study on Isolation efficiency of recyclable in-filling materials for thin-walled hollow wave barrier. Eng Structures (2024) 312:118207. doi:10.1016/j.engstruct.2024.118207

CrossRef Full Text | Google Scholar

3. Mazumdar A, Bhowmik D. A Numerical Study of the Behavior of Sand–Crumb Rubber Mixture–Filled Trench for Active Vibration Isolation. Int J Geomechanics (2025) 25(4):04025023. doi:10.1061/ijgnai.gmeng-10408

CrossRef Full Text | Google Scholar

4. Xia J, Wang B, Guo X, Xie Z. Vibration response and safety control for blasting vibration of the existing tunnel with defects. Underground Space (2024) 15:76–89. doi:10.1016/j.undsp.2023.08.011

CrossRef Full Text | Google Scholar

5. Hou R, Li T, Zhang Z, Li L, Liu B, Ren D. Experimental study on modal analysis and vibration response of tunnel structures under different damage conditions due to subway train loads. Scientific Rep (2025) 15(1):3022. doi:10.1038/s41598-025-87004-9

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Bazoobandi S, Shamekhi Amiri M, Keramati M. Laboratory Evaluation of Vibration Isolation of Dynamic Loads Caused by Machine Foundations by Surface Trenches. Shock and Vibration, (2024) (1): 9215081, doi:10.1155/2024/9215081

CrossRef Full Text | Google Scholar

7. Liang Y, Zhou F, Cao X, Wang L, Zhu S, Zhou Z. Time-domain analysis for the scattering of plane elastic waves in half-space with an open trench. J Vibration Control (2024) 30(1-2):354–65. doi:10.1177/10775463221147155

CrossRef Full Text | Google Scholar

8. Liang Y, Zhou F, Qu Y. Semi-analytical solution for seismic response of circular lined tunnel in alpine valley composite site. Comput Geotechnics (2024) 172:106475. doi:10.1016/j.compgeo.2024.106475

CrossRef Full Text | Google Scholar

9. Ghorbanzadeh A, Shiri H, Dong X. Subsea pipeline design against ice gouging: Influence of trenching techniques and trench geometry. Cold Regions Sci Technology (2025) 237:104535. doi:10.1016/j.coldregions.2025.104535

CrossRef Full Text | Google Scholar

10. Zou X, Xie B, Bai X, Guo Y, Yuan Q, Zang Z. Investigations on free span rectification for a submarine pipeline on sand wave seabeds. J Mar Sci Eng (2025) 13(1):107. doi:10.3390/jmse13010107

CrossRef Full Text | Google Scholar

11. Takemiya H, Fujiwara AJSD. Wave propagation/impediment in a stratum and wave impeding block (WIB) measured for SSI response reduction. Soil Dyn Earthquake Eng (1994) 13(1):49–61. doi:10.1016/0267-7261(94)90041-8

CrossRef Full Text | Google Scholar

12. Zhang M, Ma Q, Zhou F. Analysis of the vibration isolation performance of layered periodic wave impeding blocks in unsaturated soil. J Eng Mech (2025) 151(6):04025020. doi:10.1061/JENMDT.EMENG-7987

CrossRef Full Text | Google Scholar

13. Ma Q, Shu J, Zhou F. Theoretical study of S wave passing through a double-layer wave impeding block in the unsaturated soil. Comput Geotechnics (2022) 152:105018. doi:10.1016/j.compgeo.2022.105018

CrossRef Full Text | Google Scholar

14. Gao G, Shi W, Zhang Y, Zhong W, Bi J. Vibration isolation performance of WIB on nearly saturated layered soil caused by high-speed trains. Soil Dyn Earthquake Eng (2025) 190:109126. doi:10.1016/j.soildyn.2024.109126

CrossRef Full Text | Google Scholar

15. Zhou F, Zhou Z, Ma Q. Study on the vibration isolation performance of an open trench–wave impedance block barrier using perfectly matched layer boundaries. J Vibration Control (2022) 28(3-4):329–38. doi:10.1177/1077546320976962

CrossRef Full Text | Google Scholar

16. Cao X, Zhou F, Liu J, Ma Q. Experimental study and numerical analysis for vibration isolation performance on open trench and wave impeding block combined vibration isolation barrier. Soil Dyn Earthquake Eng (2024) 177:108418. doi:10.1016/j.soildyn.2023.108418

CrossRef Full Text | Google Scholar

17. Cai C, Xiong Q, Gao L, Xu Y, Wu D. Periodic WIB-trench wave barriers for seismic surface waves. Mech Adv Mater Structures (2024) 31(29):11379–92. doi:10.1080/15376494.2024.2304153

CrossRef Full Text | Google Scholar

18. Cai C, Xu Y, Gao L, Deng S, Wu D. Surface wave isolation by variable depth infilled trenches. Sci The Total Environ (2024) 953:176071. doi:10.1016/j.scitotenv.2024.176071

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ma Q, Zhou F, Shao S, Shao S, Zhang M. Diffraction of plane P waves by a circular-arc canyon in an unsaturated poroelastic half-space. Soil Dyn Earthquake Eng (2023) 174:108163. doi:10.1016/j.soildyn.2023.108163

CrossRef Full Text | Google Scholar

20. Ma Q, Zhang M, Zhou F, Shao S. Analytical analysis of the scattering problem of plane SV waves caused by a circular arc canyon in an unsaturated half-space. Int J Geomechanics (2025) 25(5):04025058. doi:10.1061/ijgnai.gmeng-9986

CrossRef Full Text | Google Scholar

21. Von Rütte F, Kahl A, Rohrer J, Lehning M. How forward-scattering snow and terrain change the alpine radiation balance with application to solar panels. J Geophys Res Atmospheres (2021) 126(15):e2020JD034333. doi:10.1029/2020jd034333

CrossRef Full Text | Google Scholar

22. Awasthi S, Varade D. Recent advances in the remote sensing of alpine snow: A review. GIScience and Remote Sensing (2021) 58(6):852–88. doi:10.1080/15481603.2021.1946938

CrossRef Full Text | Google Scholar

23. Zhao S, Ma Q. Diffraction of plane P waves by a circular unlined tunnel in an unsaturated poroelastic half-space. J Vibration Eng & Tech (2024) 12:1501–19. doi:10.1007/s42417-024-01487-w

CrossRef Full Text | Google Scholar

24. Liu G, Li X, Zhu H. Plane SV-waves scattering by seawater convex surface topography and underlying lined tunnel in a saturated half-space. Soil Dyn Earthquake Eng (2024) 184:108847. doi:10.1016/j.soildyn.2024.108847

CrossRef Full Text | Google Scholar

25. He B, Lai Y, Wu L, Zhu S, Xu C. Scattering of SH Waves Induced by Interaction between a Truncated Semicircular Canyon and a Lined Tunnel. Int J Geomechanics (2025) 25(4):04025033. doi:10.1061/ijgnai.gmeng-10627

CrossRef Full Text | Google Scholar

26. Gao L, Cai C, Mak CM, He X, Zou Y, Wu D. Surface wave attenuation by periodic hollow steel trenches with Bragg band gap and local resonance band gap. Construction Building Mater (2022) 356:129289. doi:10.1016/j.conbuildmat.2022.129289

CrossRef Full Text | Google Scholar