The pn interaction and isospin symmetry

Abstract

A possible correlation between isospin symmetry/breaking and the average proton-neutron interaction of the last particles, , is discussed. This correlation is tested for = 1/2 mirror nuclei in terms of a differential of , , and their low-lying excited levels. Some nuclei, whose mass measurements will be useful for future studies, are suggested.

1 Introduction

The strong nuclear force is considered charge-independent and has charge symmetry. The latter means that the interaction strength between protons and neutrons is the same, and being independent of charge means that the sum of proton-proton and neutron-neutron interaction strengths is two times proton-neutron interaction strength. If the Coulomb interaction is ignored, charge independence and charge symmetry will have the same meaning for isobaric nuclei which have the same mass number with different proton and neutron numbers.

Mirror nuclei are pairs of atomic nuclei in which the number of protons in one nucleus equals the number of neutrons in the other, and vice versa (e.g., ²⁵Mg and ²⁵Al). In such mirror isobaric nucleus pairs, we expect similar nuclear structures [1]. We can easily see this from similar level schemes.

To understand this, it is useful to define the concept of isospin, . Both protons and neutrons are assigned the same isospin value of = 1/2, but differ in their isospin z-projection. Protons have = -1/2, while neutrons have = 1/2. Isospin symmetry is related to similar behavior of nucleons (protons and neutrons). Since some configurations such as and with = 0 are forbidden, the Pauli principle should not be forgotten at this point. That is, the isospin symmetry only connects to = 1 in the and interactions. For a given nucleus, the isospin projection is given by = (-)/2 where and are, respectively, the number of protons and neutrons. While the low-lying states of a nucleus with given , which we focus on here, generally have = , higher states can have higher values, being part of more extended multi-isobar isospin multiplets.

Mirror nuclei have different . The similar nuclear structure in such nuclei means that their excited states are (almost) identical, in terms of both their energies and spin-parity values. For example, the low-lying states of the = 23 isobaric nuclei, ²³Na with = 1/2 and ²³Mg with = -1/2, are shown in Figure 1. As can be seen from the figure, the level schemes of the two nuclei are almost identical, so their nuclear structures are expected to be very similar. For these states, these nuclei exhibit good isospin symmetry. The assumption of perfect isospin symmetry implies that the difference between the binding energies of the mirror nuclei is zero if the differences in the Coulomb interaction in the two nuclei are ignored. Isospin symmetry breaking can occur due to increases in parts of the Coulomb interaction, especially as the mass number increases. Isospin breaking can also occur for other reasons beside the Coulomb interaction (e.g. [3, 4]). By taking these isospin symmetry breaking effects into account, the isospin concept can provide a tool for understanding the excitation energies and binding energies of exotic nuclei that are difficult to reach experimentally. In addition, the study of isospin symmetry breaking plays an important role not only in nuclear physics but also in particle physics, especially in testing the unitarity of the Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix [5–9].

FIGURE 1

Many isobaric nuclei with different isospin projections, such as = 1, = 2 have been investigated by experimental charge-exchange reactions [10, 11] and -decay studies (e.g. [12]). In such studies, the () values from isobaric = 1 nuclei to a = 0 nucleus can be compared using both experimental techniques. If the experimental values of () are similar, isospin symmetry between mirror, = 1, nuclei can be confirmed. If the values are different, the isospin symmetry may be broken.

2 Approach and methods

In this paper, we explore another observable as a possible indicator or signature of isospin symmetry or its breaking. Since the valence proton-neutron interaction plays an important role in the evolution of nuclear structure [13–15], we will investigate whether an empirical measure of those strengths correlates with isospin symmetry or its breaking. This measure is called [16; 17; 18] and is the average interaction strength of the last proton(s) and neutron(s). It reflects the spatial overlap of their respective wave functions. We will examine values of for nuclei near = and will also discuss a related quantity obtained from adjacent values. We can extract the strengths of these interactions for the last valence proton(s) and neutron(s) from the following expressions in terms of binding energies [16, 17]:where is the nuclear binding energyand in Equation 3 is the nuclear mass. Equations 1, 2 are given for odd-. More detailed information can be found in Ref. [18]. Here we look at other applications of to understand nuclear structure and its trends.

3 Results and discussion

In recent years, many light nuclei have been studied especially in such contexts as of the island of inversion, appearance, and disappearance of closed shells, etc. [19]. In addition, such nuclei have been studied in terms of , in particular for the case where the values of have obvious spikes at = . This has been explained by Wigner’s SU(4) symmetry [20, 21]. In these = nuclei, since protons and neutrons fill the same nuclear shell model orbitals, there can be a large spatial overlap between the proton and neutron wave functions and therefore we expect a large interaction between protons and neutrons, . As the mass number increases, the values of decrease presumably due to the Coulomb and spin-orbit interactions, and perhaps due to the greater average spacing of the last protons and neutrons.

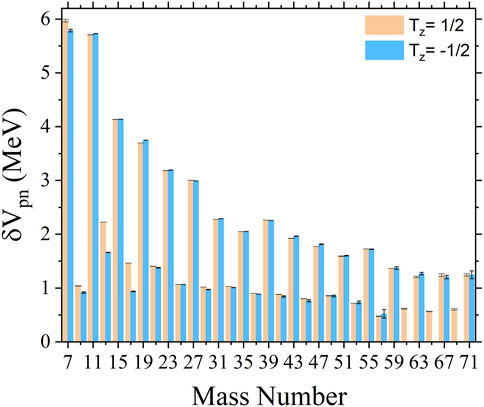
Turning now to isobaric mirror nuclei, Figure 2 shows the experimental values of odd- = 1/2 mirror nuclei versus their mass numbers. There are two values in each mass number shown with vertical bars for = 1/2 (orange) and = -1/2 (blue). The = 61, 65, and 69 nuclei have only = 1/2 data due to missing experimental values for the masses of the involved nuclei.

FIGURE 2

Perhaps a simple way of stating the systematics in Figure 2 is that is large for nuclei with = 4 - 1 and small for nuclei with = 4 + 1. Interestingly, large and small values involve different sets of values (see Equations 1, 2), the large bars contain equals 0, 1/2 and 1; small bars contain values 0, 1/2, 1 and 3/2.

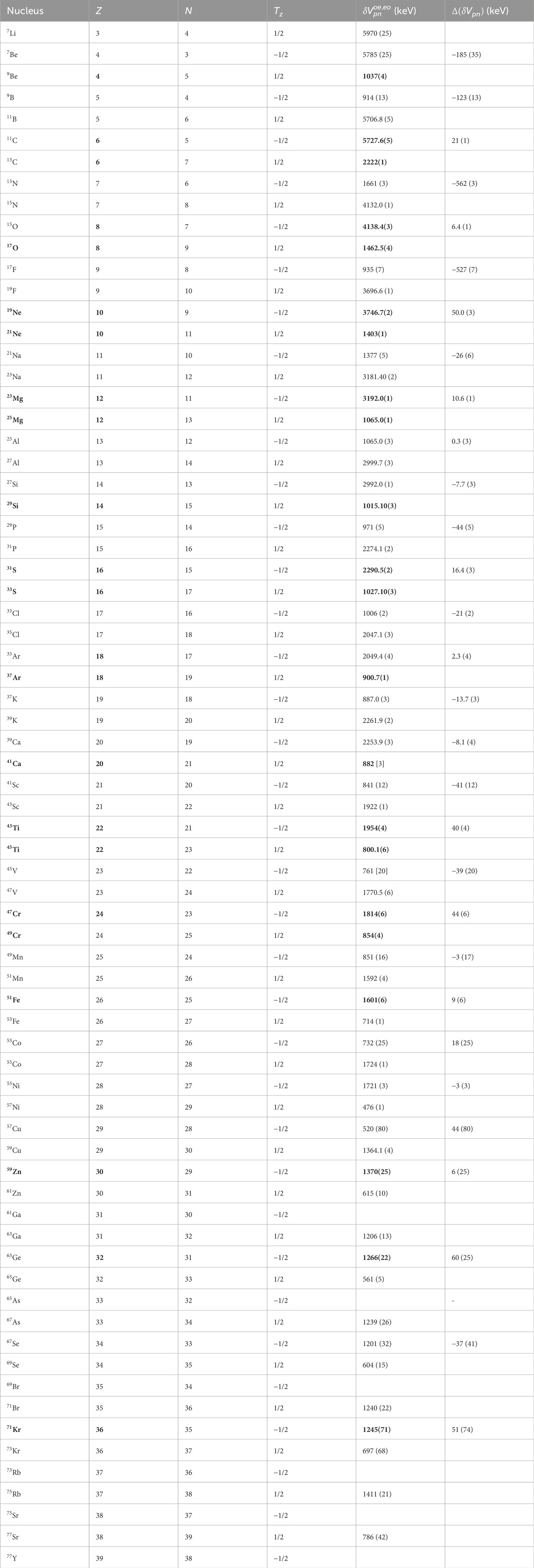
There is another systematic effect in Figure 2. For mass numbers where is large (e.g., = 7, 11, 15, 19, etc.), is always higher for = -1/2 for even- and odd- except for = 7, 27, 39, 55, 57, 59 and 67. For mass numbers where is small (e.g., = 9, 13, 17, 21, etc.), is again always higher for cases of even- and odd- but now for = 1/2. That is, except for a few mass numbers and regardless of what is, is always higher in the case of even- and odd- compared to odd- and even-. This effect is even more visible in Table 1 which shows the data on which Figures 2, 3 are based on. Bold face is used for the cases of even- and high values for each mirror pair.

FIGURE 3

When we look at the trends of the large values of in Figure 2, we see a smooth decrease except at = 39 and 55 in which increases a little compared to the general downward trend. For = 39, the values of = (19, 20) and (20, 19) are very close to each other within their error bars. A small increase is seen because both and contain the magic number 20. Similarly, in = 55, the effect of the magic number 28 is observed in = (27, 28) and (28, 27). For the smaller pairs of bars, in the case of = 17, the effect of the magic number eight should also be considered for = (8, 9) and (9, 8). After the decrease in = 9, there is an increase in = 13. The question here is whether = 9 is exceptionally low or = 13 high.

At this point, it is useful to introduce an empirical quantity related to , but which is more sensitive to details of the p-n interactions. It is basically a differential of . If we expect the nuclear structures of the mirror isobaric nuclei to be nearly identical, then we expect the values of these nuclei to be quite close to each other. Although the values of these mirror isobaric nuclei appear to be close to each other in Figure 2, the difference between two experimental values of = -1/2 and = 1/2 is quite interesting. This quantity, , is defined as follows:

Equation 4 and a similar approach as presented here have recently been discussed in Refs. [24–26]. Here, however, we investigate which nuclei have isospin symmetry by looking at both the values and some of the lowest excited states in mirror pairs.

The results are shown in Figure 3. There are some clear trends in the results. Except for = 7, which seems highly anomalous, the pink bars (for odd-, = 1/2) are always positive (in some cases the values are very close to zero where uncertainties generally overlap with zero). The blue bars (for even- = -1/2) are always negative, except in a few cases above = 50 where the data has large uncertainties that again overlap with zero. There are also some other interesting features. As can be seen in the figure, there are quite high negative values for a few mass numbers such as -600 keV for . The largest differences are seen at = 7, 9, 13 and 17. A 50 keV band around zero is shaded as a reference to guide the eye. Most of the bars are within this 50 keV band. Note that the largest errors are at = 7, 57, 63, 67 and 71. We see results for closest to zero in many cases such as = 15, 25, 37, 59, etc. Due to the lack of experimental mass values, there are no values at = 61, 65 and 69 (see also Figure 2).

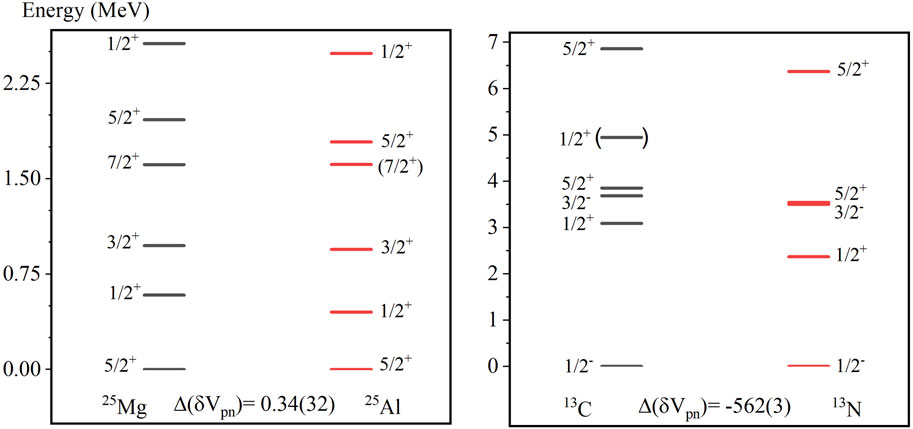
What can we learn about the nuclear structure of mirror nuclei from these values? Does a small value hint to a similar structure between mirror pairs? In other words, can be used as a measure of isospin symmetry and/or its breaking? For example, in Figure 3, the value of the mirror nuclei , ²⁵Mg and ²⁵Al, is approximately zero, while the value of mirror nuclei = 13, ¹³C and ¹³N, is approximately −600 keV. In this case, is the nuclear structure of = 25 = 1/2 mirror nuclei more similar to each other compared to the nuclear structure of = 13 = 1/2 mirror nuclei? The rest of this paper looks at this possibility in greater detail.

Each panel of Figure 4 shows some low-lying excited levels of a pair of mirror nuclei (left) and = 13 (right). As can be clearly seen, there is almost perfect similarity between the level schemes of ²⁵Mg and ²⁵Al, while there is very little similarity between ¹³C and ¹³N. In fact, the isospin symmetry between ²⁵Mg and ²⁵Al has been experimentally demonstrated [27]. This correlates very well with the result. On the other hand, Ref. [3] shows isospin breaking in ¹³C using pion inelastic scattering. The = 13 spectra are very dissimilar and is large. This pair of examples suggests that may be useful as a filter or signature for the goodness of isospin, or its breaking. To study if this approach is accidental or not, one should look at each example of shown above in Figure 3. Of course, the absolute binding energies of the two mirror nuclei are different because of the Coulomb interaction. But, this does not play a role in the figure since we normalize the ground state energies to zero.

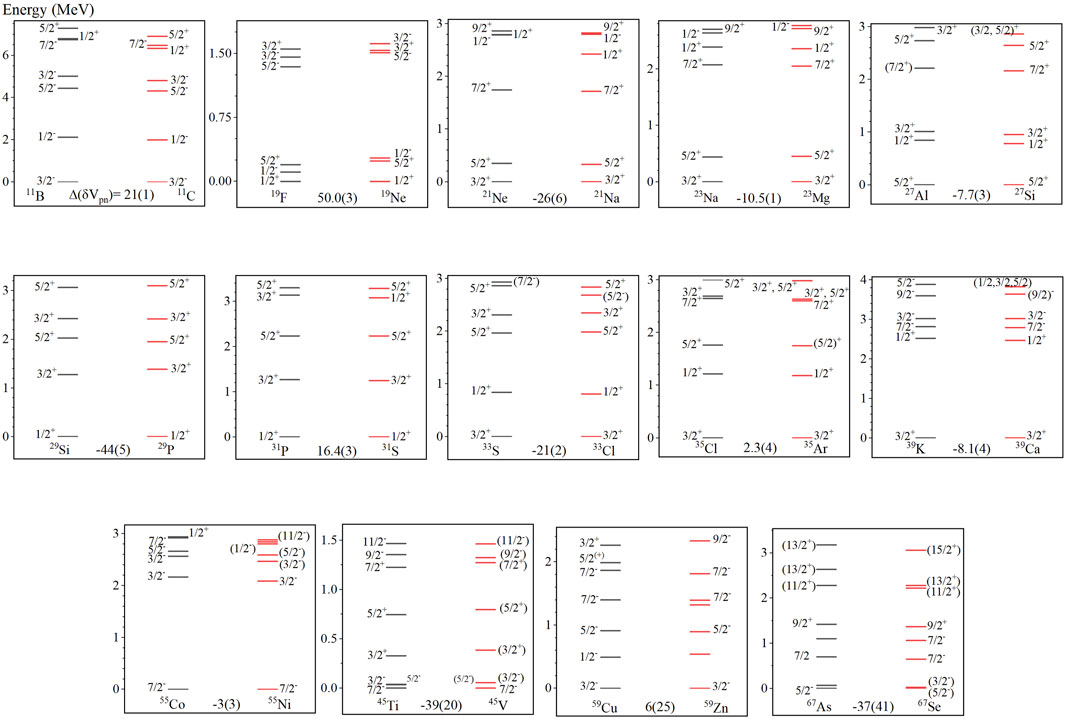
Figure 5 shows all pairs of mirror nuclei with level schemes that are very similar, including = 23 from Figure 1 but not = 25 just shown in Figure 4. Here, similarity in the level schemes, the energy difference between the excited states (level spacing) and the fact that these similar states have the same spin-parity are used as criteria. Besides the fact that the level schemes of these nuclei are very similar, their values are quite small. The nuclei with the largest in Figure 5 are the = 19 mirror nuclei with 50.0 (3) keV and the = 29 mirror nuclei with 44 (5) keV. The others have maximum values of 25 keV.

FIGURE 4

FIGURE 5

These results confirm that small values might be a useful filter for mirror nuclei with small isospin symmetry breaking. We will see below that there are some exceptions to this that need to be studied further. In some cases, like = 55 and 59, further study of experimental spectra would be useful.

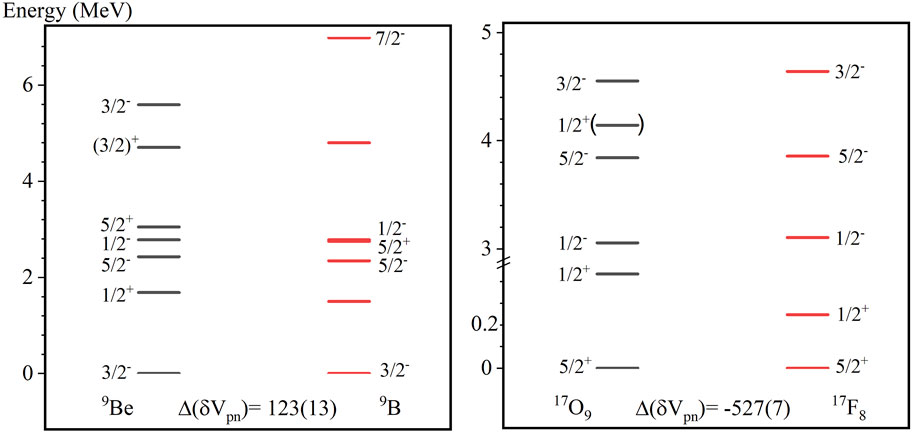
This idea can be tested in an inverse way. The = 9 and 17 cases are shown in Figure 6 and have both incompatible level schemes and values that are rather large. At first glance, there seems to be no serious difference between the two level schemes in each pair but, for example, if we look at the level spacing in ¹⁷O and ¹⁷F carefully, there is about a factor of two difference in the energies of their first excited levels. The large , -500 keV, also points to this disagreement. Indeed, in Ref. [4] isospin breaking has been discussed on the basis of quark-meson coupling. Thus, we again see the use of values as a signature, in this case of symmetry breaking. Note that ⁹B has an unbound proton, therefore a large may be expected. However, the mass ⁹B is used not only for (⁹B) but also for (¹¹B). In Figure 5, a small value is given together with nice agreement on the level schemes of ¹¹B and ¹¹C. Clearly, the effects of extended proton radial distributions in proton unbound nuclei need further study.

FIGURE 6

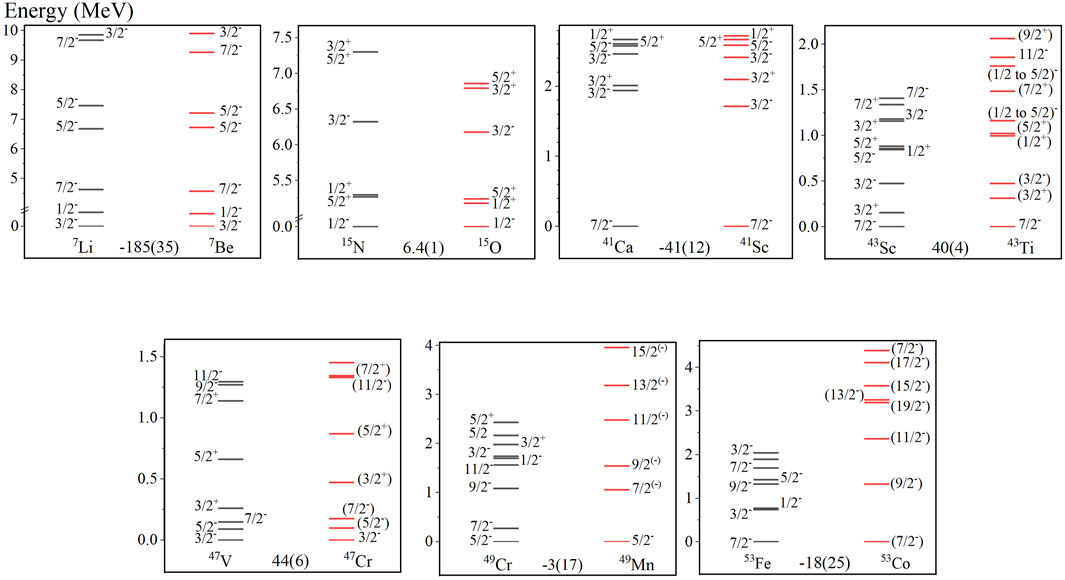
While this correlation of and the degree of similarity in mirror pair level schemes is suggestive of a new tool to assess isospin symmetry, however, there are also a few counter examples that may hint to its limitations. Figure 7 shows one case of similar level schemes but a large for = 7, −185 (35) keV, and a number of = 1/2 mirror nuclei with dissimilar level schemes but low values. There is no noticeable anomaly in the results for the ⁷Li and ⁷Be nuclei, except for mass error of about 50 keV for both ⁵Li and ⁵He. If is a reliable filter for isospin breaking, one would expect more consistency of spectra and values. This needs further investigation.

FIGURE 7

The rest of Figure 7 shows cases of dissimilar level schemes. Most of these are in heavier nuclei compared to the nuclei in Figure 5. As the mass number increases, the filter may simply break down. As mentioned in the beginning of this paper, isospin breaking occurs when the mass number increases due to Coulomb force among protons. Also, especially in heavier nuclei, there can be states of higher (1/2) at higher energies, which are part of extended isospin multiplets, and there can also be isospin mixing in complex states. This could lead to some differences in spectra.

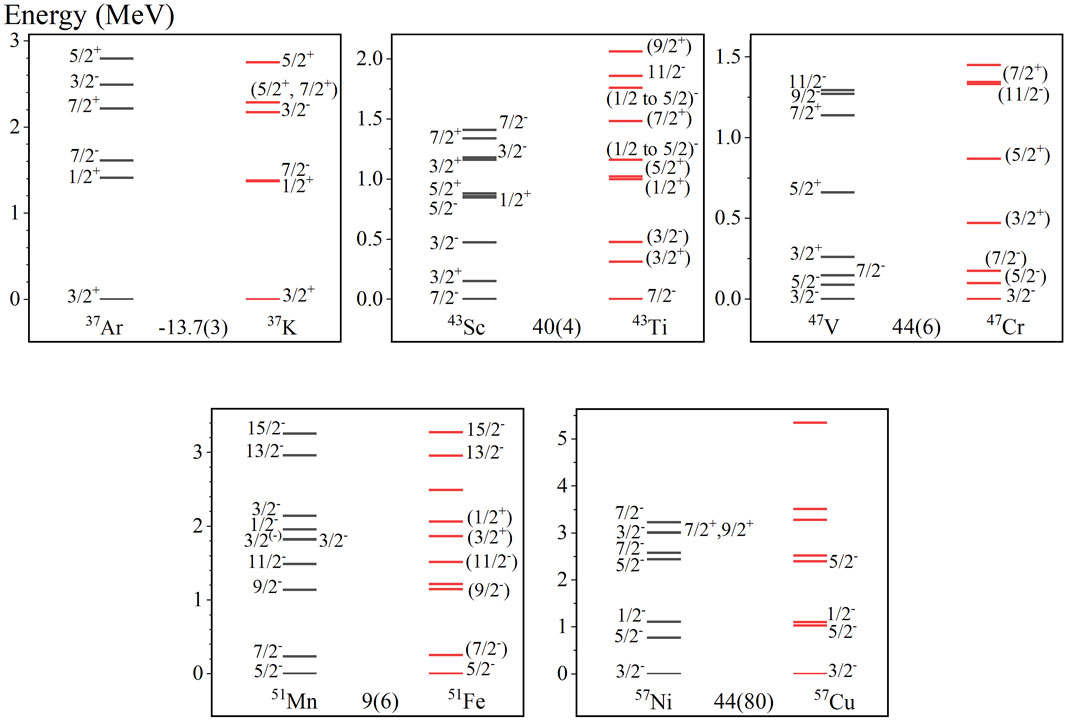
Finally, there are a number of nuclei with insufficient data to assess the correlations. In these cases, either further spectroscopic or mass data would be highly useful. We first consider cases of insufficient level scheme information. In some nuclei, spin-parity of the excited levels is unknown or not fully known, and their values are small. Such nuclei are shown in Figure 8. These nuclei should be studied by -ray spectroscopy. If the experimental data of these nuclei are clarified, further tests of the usefulness of as a signature of isospin symmetry may emerge.

FIGURE 8

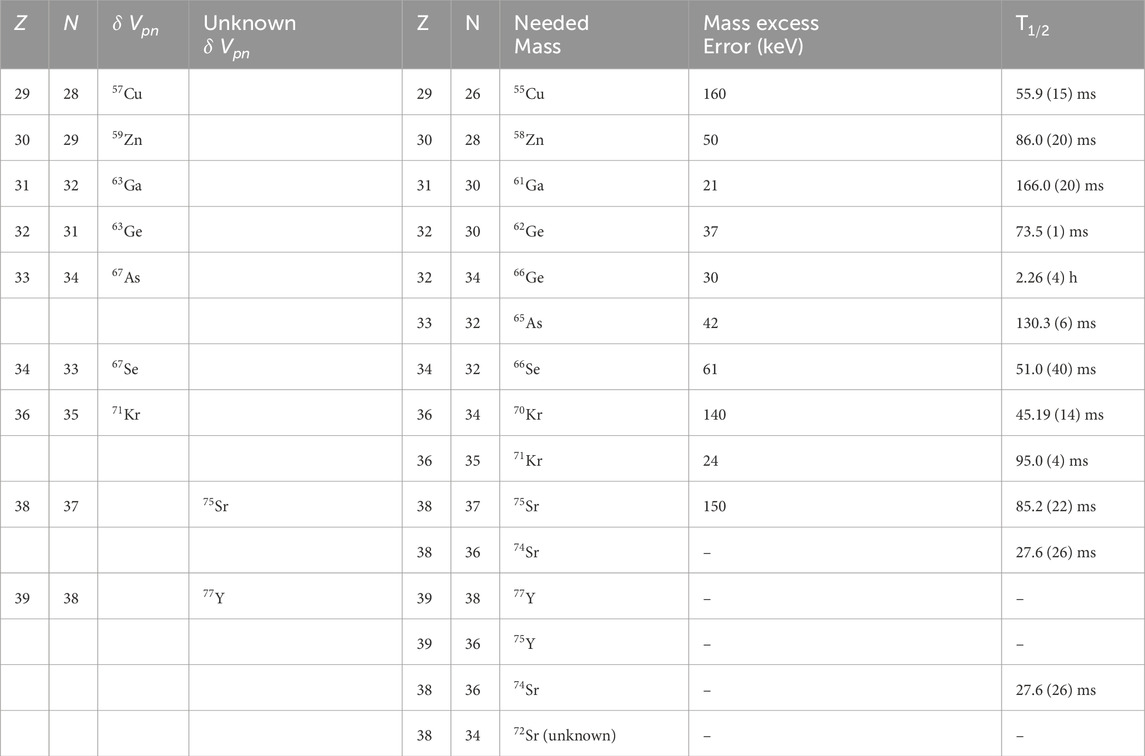
A recent -ray spectroscopic study focusing on isospin symmetry breaking is Ref. [28]. The study finds evidence for the breaking of isospin symmetry in the mirror system ⁷¹Kr and ⁷¹Br by -decay. As seen in Figure 3, of = 71 has a large error. Therefore, in order to test our approach here with , ⁷⁰Kr and even maybe ⁷¹Kr mass excess values should be improved. There are a number of other cases where additional mass measurements would be helpful to further study the use of to assess the degree of isospin symmetry breaking. These are listed in Table 2 and provide motivation for further experimental mass measurements.

As seen in Figure 2, there are no values at A = 61 = -1/2, ⁶¹Ga, = 65 = -1/2, ⁶⁵As, and = 69 = -1/2, ⁶⁹Br. Since the half-lives of ⁵⁹Ga, ⁶³As and ⁶⁷Br are in the order of nanoseconds, it is impossible to measure the masses of these nuclei today. Finally, the values for ⁷⁵Sr and ⁷⁷Y are experimentally not known due to missing masses, as seen in Table 2. They are the heaviest nuclei suggested here where we can possibly test isospin symmetry/breaking with . The other nuclei in the table have values but their errors can be improved. The masses needed for this purpose are also listed. The = 79 = 1/2 mirror nuclei do not have any value for either = 1/2 or = -1/2 nuclei.

4 Conclusion

We have discussed a possible correlation between isospin symmetry in mirror nuclei and its breaking and empirical measures of the average proton-neutron interaction. The correlation is suggestive but not perfect, and breakdowns in it need to be further investigated by both -ray spectroscopy and mass spectrometry. For the latter, possible nuclides of interest are listed in Table 2.

References

• 1.

  DeShalitAFeshbachH. Theoretical nuclear physics. Vol 1, nuclear structure. New York: Wiley (1974).

  • Google Scholar

• 2.

  National Nuclear Data Center. NNDC. Available online at: https://www.nndc.bnl.gov/ (Accessed June 12, 2025).

  • Google Scholar

• 3.

  PetersonRJ. Simple isospin relations for transitions in A=13. Physica Scripta (1983) T5:190–2. 10.1088/0031-8949/1983/t5/037

  • CrossRef
  • Google Scholar

• 4.

  SaitoK. Isospin symmetry breaking in nuclei—Ons anomaly. AIP Conf Proc (2000) 539:245–54. 10.1063/1.1330925

  • CrossRef
  • Google Scholar

• 5.

  CiriglianoVCrivellinAHoferichterMMoulsonM. Scrutinizing CKM unitarity with a new measurement of the K_μ3/K_μ2 branching fraction. Phys Lett B (2023) 838:137748. 10.1016/j.physletb.2023.137748

  • CrossRef
  • Google Scholar

• 6.

  MillerGASchwenkA. Isospin-symmetry-breaking corrections to superallowed Fermi β-decay: formalism and schematic models. Phys Rev C (2008) 78(3):035501. 10.1103/physrevc.78.035501

  • CrossRef
  • Google Scholar

• 7.

  MillerGASchwenkA. Isospin-symmetry-breaking corrections to superallowed Fermi β-decay: radial excitations. Phys Rev C (2009) 80(6):064319. 10.1103/physrevc.80.064319

  • CrossRef
  • Google Scholar

• 8.

  SengC-YGorchteinM. Electroweak nuclear radii constrain the isospin breaking correction to V_ud. Phys Lett B (2023) 838:137654. 10.1016/j.physletb.2022.137654

  • CrossRef
  • Google Scholar

• 9.

  MaierFMBollenGBrownBACampbellSEChenXEringtonHet alExploring isospin symmetry breaking in exotic nuclei: High-Precision mass measurement of ²³Si and shell-model calculations of T=5/2 nuclei. arXiv:2503 (2025). 10.48550/arXiv.2503.03034

  • CrossRef
  • Google Scholar

• 10.

  FujitaYRubioBGelletlyW. Spin–isospin excitations probed by strong, weak and electro-magnetic interactions. Prog Part Nucl Phys (2011) 66(3):549–606. 10.1016/j.ppnp.2011.01.056

  • CrossRef
  • Google Scholar

• 11.

  FujitaYFujitaHAdachiTSusoyGAlgoraABaiCLet al (2015) ‘High-resolution study of Gamow-Teller excitations in the ⁴²Ca. 42Sc reaction and the observation of a “low-energy super-Gamow-Teller state, Phys Rev C, 91, 064316(6). 10.1103/physrevc.91.064316

  • CrossRef
  • Google Scholar

• 12.

  OrrigoSEARubioBGelletlyWAguileraPAlgoraAMoralesAIet alβ-decay of the very neutron-deficient ⁶⁰Ge and ⁶⁰Ge nuclei. Phys Rev C (2021) 103(1):014324. 10.1103/physrevc.103.014324

  • CrossRef
  • Google Scholar

• 13.

  DeShalitAGoldhaberM. Mixed configurations in nuclei. Phys Rev (1953) 92(5):1211–8. 10.1103/physrev.92.1211

  • CrossRef
  • Google Scholar

• 14.

  TalmiI. Effective interactions and coupling schemes in nuclei. Rev Mod Phys (1962) 34(4):704–22. 10.1103/revmodphys.34.704

  • CrossRef
  • Google Scholar

• 15.

  FedermanPPittelS. Towards a unified microscopic description of nuclear deformation. Phys Lett B (1977) 69(4):385–8. 10.1016/0370-2693(77)90825-5

  • CrossRef
  • Google Scholar

• 16.

  ZhangJ-YCastenRFBrennerDS. Empirical proton-neutron interaction energies. Linearity and saturation phenomena. Phys Lett B (1989) 227(1):1–5. 10.1016/0370-2693(89)91273-2

  • CrossRef
  • Google Scholar

• 17.

  CakirliRBBrennerDSCastenRFMillmanEA. Proton-neutron interactions and the new atomic masses. Phys Rev Lett (2005) 94(9):092501. 10.1103/physrevlett.94.092501

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 18.

  BrennerDSCakirliRBCastenRF. Valence proton-neutron interactions throughout the mass surface. Phys Rev C (2006) 73(3):034315. 10.1103/physrevc.73.034315

  • CrossRef
  • Google Scholar

• 19.

  OtsukaTGadeASorlinOSuzukiTUtsunoY. Evolution of shell structure in exotic nuclei. Rev Mod Phys (2020) 92(1):015002. 10.1103/revmodphys.92.015002

  • CrossRef
  • Google Scholar

• 20.

  Van IsackerPWarnerDDBrennerDS. Test of Wigner’s spin-isospin symmetry from double binding energy differences. Phys Rev Lett (1995) 74(23):4607–10. 10.1103/physrevlett.74.4607

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 21.

  WignerE. On the consequences of the symmetry of the nuclear hamiltonian on the spectroscopy of nuclei. Phys Rev (1937) 51(2):106–19. 10.1103/physrev.51.106

  • CrossRef
  • Google Scholar

• 22.

  HuangWJWangMKondevFAudiGNaimiS. The AME 2020 atomic mass evaluation (I). evaluation of input data, and adjustment procedures. Chin Phys C (2021) 45(3):030002. 10.1088/1674-1137/abddb0

  • CrossRef
  • Google Scholar

• 23.

  WangMZhangYHZhouXHZhouXSXuHSLiuMLet alMass Measurement of Upper f p-Shell N=Z − 2 and N=Z − 1 Nuclei and the Importance of Three-Nucleon Force along the N=Z line. Phys Rev Lett (2023) 130(19):192501. 10.1103/physrevlett.130.192501

  • Pubmed Abstract
  • CrossRef
  • Google Scholar

• 24.

  XingYMLuoYFLiKHZhangYHLiJGWangMet alEffective proton-neutron interaction in mirror nuclei. Phys Rev C (2025) 111(2):024313. 10.1103/physrevc.111.024313

  • CrossRef
  • Google Scholar

• 25.

  ZhangMZhouXWangMZhangYHLitvinovYAXuHSet alB ρ-defined isochronous mass spectrometry and mass measurements of ⁵⁸Ni fragments. The Eur Phys J A (2023) 59(2):27. 10.1140/epja/s10050-023-00928-6

  • CrossRef
  • Google Scholar

• 26.

  ZhangYHZhangPZhouXHWangMLitvinovYAXuHSet alIsochronous mass measurements of T_z=-1 f − p-shell nuclei from projectile fragmentation of ⁵⁸Ni. Phys Rev C (2018) 98(1):014319. 10.1103/physrevc.98.014319

  • CrossRef
  • Google Scholar

• 27.

  ShimbaraY. Isospin identification for A=25 mirror nuclei by high resolution experiments. AIP Conf Proc (2001) 570:886. 10.1063/1.1384200

  • CrossRef
  • Google Scholar

• 28.

  AlgoraAVitéz-SveiczerAPovesAKissGRubioBde AngelisGet alIsospin symmetry breaking in the ⁷¹Kr and ⁷¹Br mirror System. Phys Rev Lett (2025) 134(16):162502. 10.1103/physrevlett.134.162502

  • Pubmed Abstract
  • CrossRef
  • Google Scholar