A flexible finite-state birth–death model for the number of active users in a cognitive network environment

Introduction: Reliable handover mechanisms are vital for ensuring seamless connectivity in cognitive radio networks (CRNs). The challenge becomes more complex when the upper limit of allowable users fluctuates randomly and when arrival and service rates vary over time. To address these uncertainties, this study develops a dynamic modeling framework that captures the time-varying behavior of active users in CRNs.

Method: The system is formulated as a generalized birth–death queuing model with non-stationary transition rates and a flexible upper bound on the number of users. Arrival and service rates are modeled as functions of traffic intensity, reflecting peak and off-peak conditions. Transitions are restricted to adjacent states, and global balance equations are employed to establish the theoretical foundations of the model. Extensive simulations are conducted under multiple traffic scenarios to validate the model.

Results: The proposed flexible finite-state stochastic model effectively represents the temporal variations in user activity within CRNs. Simulation results confirm that the model accurately adapts to changing arrival and service rates and handles stochastic fluctuations in the system’s capacity limit. These findings demonstrate that the model can reliably predict system behavior under diverse network conditions.

Discussions: By capturing dynamic system variations and operational uncertainties, the developed model provides valuable insights for designing robust handover strategies in CRNs. Its ability to characterize real-world traffic patterns makes it a useful analytical tool for future cognitive communication systems. The work lays a foundation for optimizing device-level handover decisions and enhancing network reliability in environments with unpredictable user behavior.

1 Introduction

Future communication systems, such as 5G, which is predicated on cooperative spectrum usage, are actively researching cognitive radios (CRs) [1–3]. For dependable and effective performance, researchers are incorporating the concept of cognitive radio into nearly every communication system currently in use, including 4G and the most recent smart grid projects for future energy needs [4–6]. Channel sensing, access to spectrum holes or channels, and resource optimization are the three main areas of research on cognitive radios used to make the most use of the existing channels. Channel sensing techniques provide dynamic spectrum access to unlicensed cognitive users for efficient utilization of available network resources and throughput enhancement [7, 8]. Spectrum holes can be considered multidimensional regions within frequency, time, and space that are suitable for cognitive users, guaranteeing non-interfering communication. Spectrum hole access schemes enable cognitive radios to access spectrum holes for interference-free safe use of the spectrum [9, 10]. Optimization of resources in cognitive radio can be considered a multi-objective optimization problem in terms of channel capacity, transmitted power, and QoS. Researchers have addressed these issues as individual and hybrid problems [11, 12].

Compared to the above-mentioned three areas, little research is available on the reliable channel model for active users in cognitive radio [1], which is necessary to evaluate resources available to cognitive radio networks (CRNs) operating in parallel with the primary networks. The level of reliability that a cognitive radio network offers to its clients depends on these resources. Channel availability is the probability of a licensed channel being available for communications of unlicensed cognitive users. After estimating the spectrum holes through suitable algorithms [13, 14], the next step is the evaluation of the capability of CR to accommodate the users, i.e., the probability of active users in the cognitive radio network environment. Recently, a flexible quieting model has been presented in [1] to evaluate the probability of active cognitive users under certain available resources.

This research work presents a more realistic approach to finding the probability of the number of active users in a cognitive radio environment. Since changes in the number of users occur when a single user appears or leaves the network, forward and backward transitions are taken adjacent to the current state. Moreover, the forward and backward transition probabilities are not considered stationary; instead, they are higher at peak hours. The global balance equation has been used to solve the problem.

This article’s remaining sections are arranged as follows: the mathematical framework is the focus of Section 2. Section 3 discusses a flexible queuing model that has been proposed for cognitive radio networks. The entire system model is shown in Section 4. Section 5 presents the findings of the simulation, and Section 6 contains the conclusion.

1.1 Research significance

The main obstacle in the way of a cognitive radio network is handoff. This problem could be handled sophistically if a clear picture of the network and the number of channels available at any particular time instant were known. The significance of this research is that it will give the probability of having any number of cognitive users in the network at any given time instant. Therefore, this Probability Mass Function (PMF) is very important for estimating the number of cognitive users at any given time interval and provides a solid basis for devising an applicable and successful handoff scheme.

1.2 Research questions

• The normal cognitive user population within a Global System for Mobile Communications (GSM) cell is stochastic. What will be the PMF for these cognitive users?

• How to obtain a global balance equation for incoming and outgoing cognitive users in the GSM cell?

• How to calculate a joint PMF by using the total probability theorem?

1.3 Research beneficiary

The most important beneficiaries of this research are cognitive service providers working in GSM. The arrival and departure of primary and secondary users in a cell are random processes, so with the help of this research work, an efficient and reliable handoff strategy could be devised for cognitive users. However, GSM and other cellular operators could also gain benefits with some alteration to this probabilistic model, according to their practical scenario.

2 Literature review

The proposed approach introduces a two-stage, dual-threshold random early detection (TD-RED) control mechanism, as outlined in [15]. It uses a three-stage Markov-modulated Poisson process to effectively analyze and manage the bursty traffic patterns in cognitive radio networks.

In [16], the focus is on optimizing the queuing process in software-defined radio (SDR) to boost performance and address key challenges. Queuing theory is vital in SDR, helping manage tasks such as receiving Radio Frequency (RF) signals, performing digital down-conversion, and handling higher-level protocol processes effectively. In [17], a new single-server queuing model with service retrials has been introduced specifically for cognitive radio networks. This model allows cognitive users to temporarily join an orbit queue when the server is busy, ensuring that they do not lose their chance for service. In [18], the authors explored important performance metrics, such as the expected queue length for primary users and the likelihood of the system being busy. The paper begins by deriving expressions for generating functions using balance equations, making it easier to calculate these key indicators. In [19], the study addressed the challenges faced by secondary users due to the increasing spectrum shortage caused by a high influx of licensed users. It is analyzed [20] that the increase in mobile traffic will be five times more within the next few years. It would seem very difficult that with the available spectrum, it would satisfy the requirements of telecom users. There are many challenges in cognitive radio, and one of the most important challenges is to assign the available spectrum among various candidates in cognitive radio users. In this paper, the channel assignment techniques are discussed with taking into view the phenomenon of the wireless regional area network. This paper provides a brief overview of the different challenges of the cognitive radio network and, in particular, focuses on channel assignment.

A combination of queening and game theory with rigorous mathematics is provided in [21]. This reduces the blocking probability and improves other performance parameters, especially related to channel assignment, in a cognitive radio network. The most challenging fact in dynamic spectrum access/cognitive radio is that the number of users is more than the available spectrum chunks. Therefore, every user wants to gain access to the spectrum, and this leads to an increase in the blocking probability. In [22], a cooperative spectrum-sharing environment is proposed for cognitive radio users. Cooperative spectrum sharing is the most common technique and has taken priority over non-cooperative schemes. In this paper, the cooperative spectrum-sharing scheme is modified, and a hybrid approach (both cooperative and non-cooperative) is proposed. A game theory (Stackelberg) is applied to cognitive radio, and each user of cognitive radio is a player of that game. Moreover, this hybrid technique with game theory is applied, and for spectrum sharing, the famous queuing model M/D/I is allowed to work. The most important challenge for cognitive radio is to get an exact overview of the secondary users in the presence of primary users. For efficient media access control schemes, queuing is one of the best approaches as it allows better observation and control of important parameters of secondary users, including delay and throughput. In this survey paper [23], different queuing models and their classification, on the basis of their performances, are presented. Moreover, this important feature of queuing models, including open problems and potential applications, is also discussed. It has been claimed [24] that due to the potential increase in wireless traffic and tremendous development in wireless devices, it is obvious that wireless users will have a scarcity of the spectra. In this paper, the factors related to spectrum sharing for multiple users are addressed. Therefore, to achieve better analysis of the cognitive radio network and, in particular, for spectrum sharing, the number of active users present at a given time is obtained analytically. Two types of systems, queued and non-queued, are investigated.

It has been claimed [25] that the priority of Primary Users (PUs) is much higher in CRNs than that of Secondary Users (SUs). Considering the tremendous increase in IoTs, it is very difficult to predict an accurate traffic pattern. Therefore, a dynamic cognitive channel allocation (DCCA) algorithm is proposed. The main aim of this algorithm is to provide a balance between PUs and SUs. The structure of this algorithm is based on a continuous time Markov chain. A queuing model is applied to achieve optimization in CRN, particularly in terms of spectrum utilization. It has been reported [26, 27] that no such work has been done previously for secondary users’ access control. The scenario for the proposed scheme is based on the assumption that only two secondary users are active simultaneously in a network. The queuing theory, along with the weighted process, is applied. The two-queue model has been proposed in [28]. These queues are structured for efficient spectrum and resource allocation in a maritime cognitive radio network. The architecture of this proposed model is centralized, along with a two-dimensional Markov chain. In [29], a three-layer system with SUs is depicted. This detection of SUs is performed to categorize them, based on priority, into two classes. The channel aggregation CR is the actual backbone of such a system, which overcomes the problems of spectrum availability. It is necessary to assign different priorities to different applications, and different applications are given different priorities. This paper presents a novel approach to categorizing SUs based on priority, compared to previous research, which focused only on assigning priority between PUs and SUs. All possible approaches to address bandwidth utilization, multilevel reservation, and aggregation are presented. To achieve successful handoff, a priority-based non-preemptive M/G/I queuing model has been proposed [30]. To get coherence among the channels, a scheme with the help of starvation and mitigation is applied. In the queuing model with prioritization, the main threat is starvation; to get rid of starvation problems, the aging phenomenon has been introduced. In this scheme, the priority of a packet is increased when an SU sits in a queue for three successive time frames. The reactive and proactive schemes are used for channel bonding based on whether the size of the packet is larger than the given time interval or not. When the handoff process is initiated, the prior information about the two subsequent time slots is necessary.

A prioritized proactive spectrum handoff decision has been presented [31] to minimize the latency of handoff and improve the total service time. This scheme is based on making an M/G/I queue, and preemptive resume priority (PRP) is given to all SUs in this queue. On the basis of this priority, the decision for handoff and allocating another available spectrum is made. A learning base spectrum handoff scheme has been proposed [32]. This scheme is analyzed using Universal Software Radio Peripheral and GNU. This scheme depends upon learning as well as transfer learning for spectrum handoff. This scheme also takes into account whether the channels occupied are free and what the channel conditions are. A unique spectrum handoff scheme, spectrum admission control (SAC), has been proposed [33]. This scheme is based on a group formed by SUs, and there is cooperative spectrum sensing within this group to defeat the arrival of PUs. A Markov model is also used in this scheme. It has been suggested [34] that cognitive radio networks, along with non-orthogonal multiple access (NOMA), are better choices to address the problem of spectrum scarcity. It is further proposed that to take more advantage of the above-mentioned schemes, it is necessary to create a link between them. A unique mathematical model for resource allocation, especially for tele-traffic, has been introduced. This mathematical model is based on a birth–death model for tele-traffic. In this model, the arrival and the departure of PUs and SUs are assumed to be a die and birth and show these data as a two-dimensional Markovian process. A priority scheduling strategy with a reserved queue is presented [35], and it has been reported that by using a scheduling algorithm and a dynamic spectrum access protocol, the performance of the network could be maximized. To estimate an idle channel for SU in CRN, an 8-state-based discrete-time Markov chain model has been proposed [36]. This scheme estimates the busy and idle channels in the network. In [37], the MAC protocol, along with the joint allocation scheme, has been proposed. It has been reported that the throughput is maximized and delay is reduced. A tree of available channels is constructed using the central node [38], suggesting that this tree approach will not only provide an efficient management scheme but also enhance the authenticity mechanism and reduce the interference between users.

2.1 Research gap

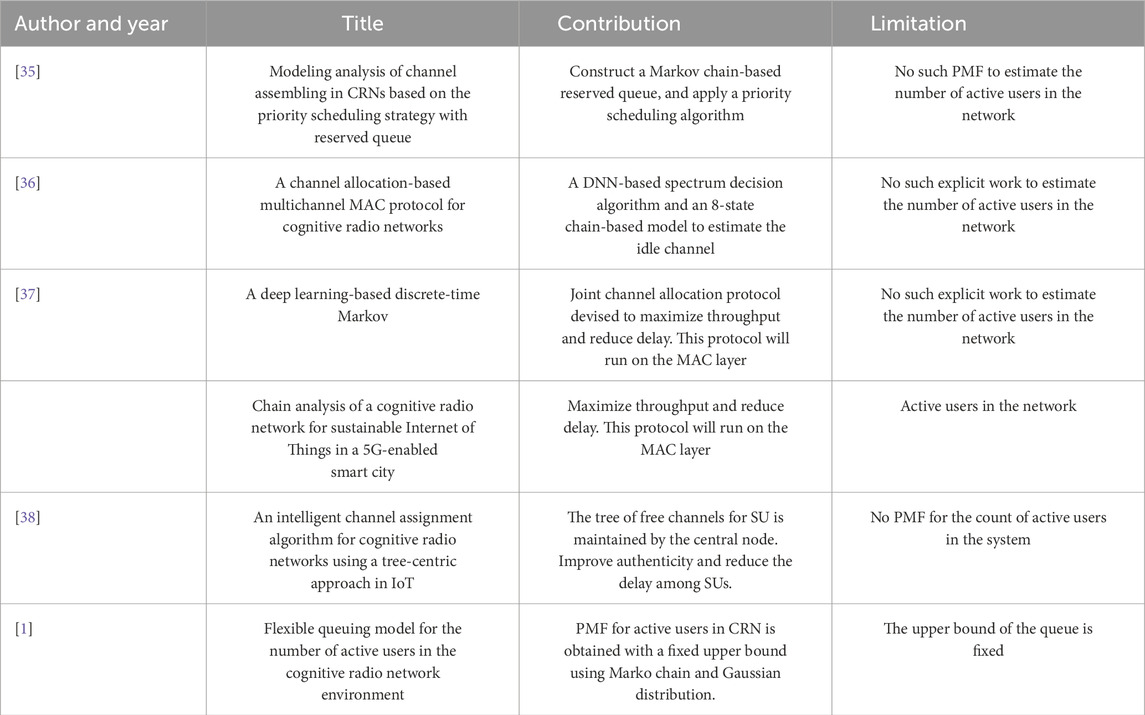
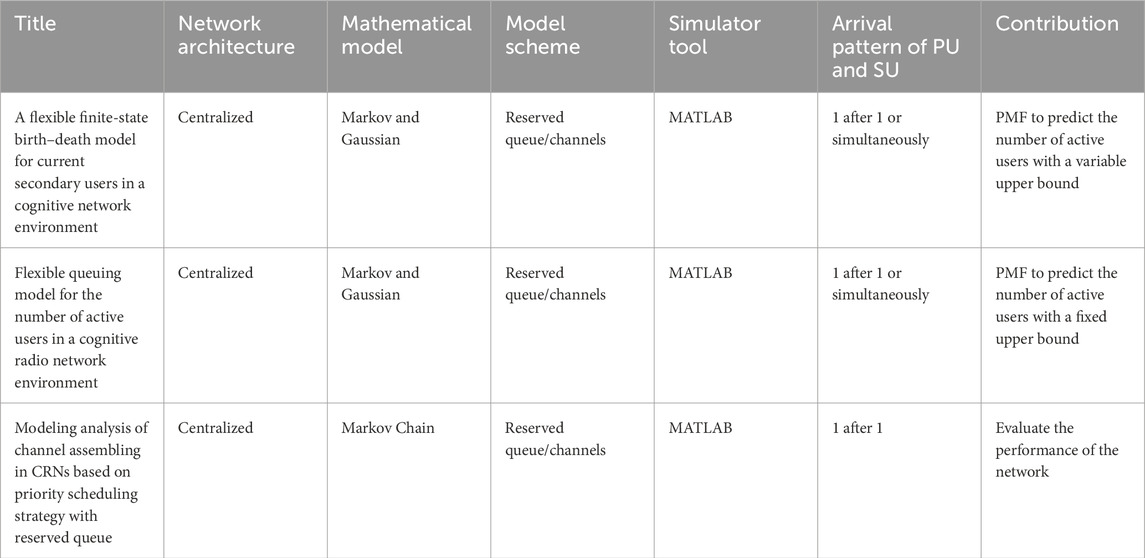
All the related work concerns the efficient channel assignment schemes and maximizing the performance of the network, but there is a lack of potential work to compute the number of active users in CRN. This valuable data yields a solid base for an efficient handoff scheme. A summary of the reviewed Markov chain-based research articles is presented in Table 1, highlighting their contributions and limitations. A comparison of the features of these research articles, including their network architecture, mathematical models, and contributions, is summarized in Table 2.

Table 1

Table 1. Literature review of Markov chain-based research articles.

Table 2

Table 2. Comparison of features of research articles.

3 Mathematical framework for the proposed model

The number of active users in the cognitive/existing cellular network with a fixed upper bound is provided as follows:

$p_j={\xi }^j\frac{1-\xi }{1-{\xi }^{K+1}}.$

However, the upper bound, i.e., K is fixed in this case, which indicates the maximum allowable users in the network. The situation becomes complicated while dealing with CRN. In other words, the upper bound should logically be a random variable. Accordingly, a model for the active number of users has been proposed. The probability for j-active users in that case is given as

$p_j={\lambda }^j\left(1-\lambda \right){\displaystyle \sum _{k=0}^K}\frac{P\left(K=k\right)}{1-{\lambda }^{k+1}}.$

This equation provides the probability of having j users in the system, where j is any random number from 0 to K and K is a finite number. This is the probabilistic model to compute the number of cognitive users in the system with a finite upper bound.

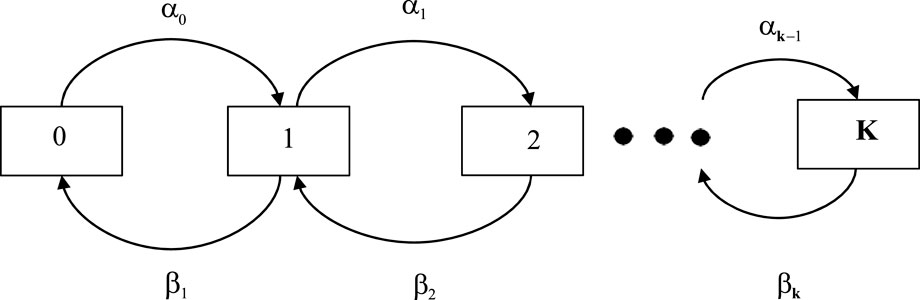
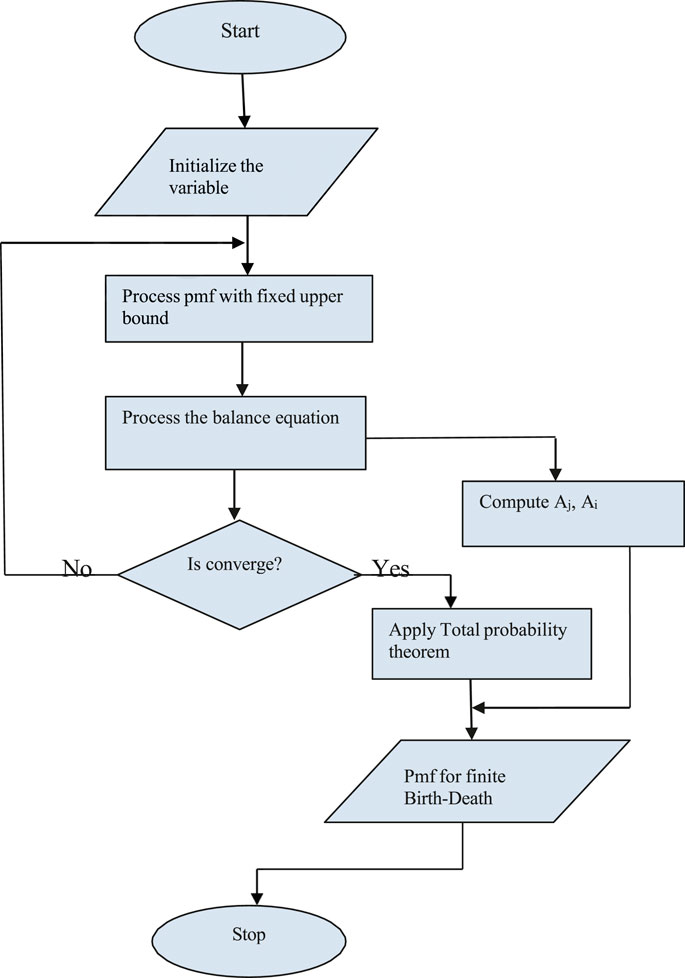
Although the proposed model was a value-added contribution in the sense that there was no such model available in the literature, The model is applicable in a setup where statistics of occupying and releasing states do not change with time, i.e., the stochastic process was assumed to be stationary. Now, we consider a more realistic setup for cognitive radio networks, where forward and backward transition states are not stationary and they change with the number of occupied states. It may be noted that due to the cognitive setup, the upper limit, i.e., the maximum allowable users, would not be fixed. The upper limit could be the maximum resources available with the primary network; however, the probability would be almost negligible due to the primary users and the presence of other cognitive networks appearing in the same region. Figure 1 indicates the proposed queuing model with k-maximum allowable users.

Figure 1

Figure 1. Flexible death–birth queuing model with variable states.

The value of the random variable k will lie between 1 to K i.e. k $\in$ {1, 2,…, K}, however, the probability decreases by increasing the number increases. The PMF for the active number of users for the proposed birth-death process may be found by using the global balance equation, which is being reproduced here for convenience.

$p_j\left({\displaystyle \sum _i}{\gamma }_{ji}\right)={\displaystyle \sum _i}{\gamma }_{ji}pi.$

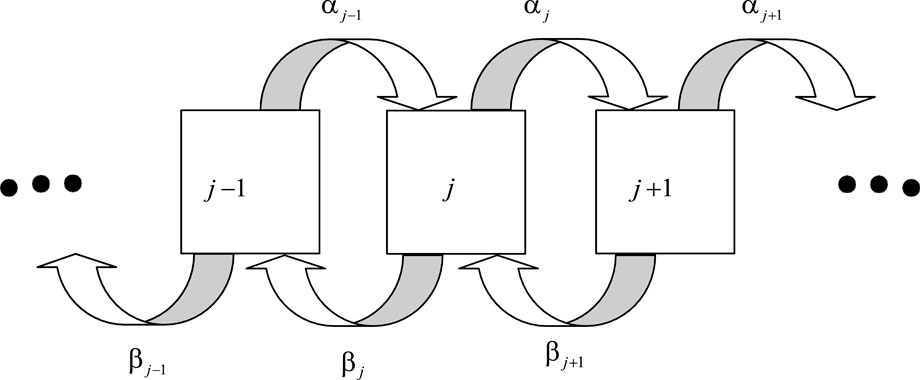
The output of this balance equation is a steady state, which is achieved when this equation converges. As the possible transitions are only for the adjacent states in the proposed setup, the problem becomes relatively simple. Considering the process in the jth state, as indicated in Figure 2, then the following equations are obtained.

${\gamma }_{j,j+1}={\alpha }_j,{\gamma }_{j,j-1}={\beta }_j,$

${\gamma }_{j-1, j}={\alpha }_{j-1},{\gamma }_{j+1,j}={\beta }_{j+1.}$

Figure 2

Figure 2. Birth–death process in the jth state.

Hence, the global balance equation yields

$p_j{\alpha }_j+p_j{\beta }_j=p_{j-1}{\alpha }_{j-1}+p_{j+1}{\beta }_{j+1.}$

By re-arranging it, the following equation is obtained:

${\alpha }_j{p}_j-{\beta }_{j+1}{p}_{j+1}=p_{j-1}{\alpha }_{j-1}-p_j{\beta }_j.$

This is the demonstration of a balance state, where α_j and β_j are the current states and α_j−1 and β_j−1 are the previous states. It may be observed that we have shifted one state forward on the right-hand side, yet the difference in the terms is equal to the left-hand side, which was the previous state. Thus,

$p_{j-1}{\alpha }_{j-1}-p_j{\beta }_j=Constant.$

The value of the constant may be evaluated from state 0, which yields

${\alpha }_0{p}_0-{\beta }_1{p}_1=0.$

This implies that constant = 0. Ultimately,

$p_j=\frac{{\alpha }_{j-1}}{{\beta }_j}{p}_{j-1},\text{put\hspace{0.17em}}{\alpha }_j=\frac{{\alpha }_{j-1}}{{\beta }_j}.$

Hence, p_j = α _j p_{j −1}. This is the recursive formula to generate the following equations.

$p_j={\alpha }_j{\alpha }_{j-1}{p}_{j-2},\dots ,$

$p_j={\alpha }_j{\alpha }_{j-1}\dots {\alpha }_1{p}_0.$

Let $A_j={\alpha }_j{\alpha }_{j-1}\dots {\alpha }_1,$ then $p_j=A_j{p}_0.$ The value of $p_0$ can be obtained by normalization, i.e., ${\displaystyle \sum _i}{p}_i=1$, where the summation is over the total number of possible states. Hence,

$p_0+A_1{p}_0+A_2{p}_0+···+A_K{p}_0=1$

$\Rightarrow p_0=\frac{1}{{\displaystyle {\sum }_{i=0}^K}{A}_j}$

$\Rightarrow p_{j,K}=\frac{A_i}{{\displaystyle {\sum }_{i=0}^K}{A}_i},$

where Aj is the parameter, and these equations are used to derive the PMF for simplicity. This completes the PMF for the process under consideration for a fixed K number of maximum states.

4 Proposal of a finite-state birth–death process

4.1 Flexible queuing model for a generalized birth–death process

The situation becomes more complicated while dealing with the CRN, where the maximum number of states is a random variable. The PMF in the scenario can be estimated as indicated in the theorem below.

4.2 Theorem

Consider a generalized birth–death process indicating the active number of users in a CRN at a given instant. Then, according to the total probability, the PMF for active users can be computed as follows:

$\sum p_j|k,P\left(\mathit{k}=k\right)=p_j.$

The output of this equation is that it gives the overall probability of different finite states in the system, where p _j ⎢k is the conditional probability indicating the probability of finding the process in the jth state, where there are a total of k states. Similarly, P (k = k) indicates the probability of having k, the maximum number of states in the cognitive network. Now, p j ⎢k has been derived in the previous section, i.e.,

$p_{j|k}=A_j{p}_0=A_j\frac{1}{{\displaystyle {\sum }_{i=1}^k}{A}_i}.$

This equation provides the probability of having j users in the system, and this equation could be achieved by putting different forms of A_j. Utilizing this expression in the above equation, we get

$p_j={\displaystyle \sum _{k=1}^{N_i}}{p}_{j|k}P\left(\mathit{k}=k\right),$

$p_j={\displaystyle \sum _k}\frac{A_j}{{\displaystyle {\sum }_{i=1}^{\mathit{k}}}{A}_i}P\left(\mathit{k}=k\right).$

This is the PMF for having jth users in the system, with the upper boundary also dynamic, and cognitive users arrive and depart in the network randomly, where N_T is the total number of channels available to the primary cellular network. N_T is used in summation because there might be some probability that all of these channels may be unoccupied, and the cognitive network under consideration may be able to win all of the available channels. Logically, the probability of occupying a larger number of channels decreases and becomes negligible beyond a certain value of k. The PMF given in the above equation is generalized and may be used to compute the probabilities for active users in a cognitive radio network. However, it is necessary to know the values of A_j, j = 1, 2,…, K and p_k P (k = k), where k $\in$ {1, 2,… NT }, that is, the PMF of p_k must be available, representing the probability of occupying k maximum channels for the CRN under consideration.

4.3 Different cases for A_js

By definition, Aj = α1α2…α j, j = 1, 2,…, K, where α j is the ratio of the arrival rate and the departure rate of a cognitive user in CRN. In the case of the birth–death process under consideration, these rates are different for each state. Logically, these rates cannot be independent. In other words, a correlation may be assumed to be there. The value of A_j = α₁α₂ …α _j, j = 1, 2,…, K depends on the type of correlation and also on the ratio $\frac{{\alpha }_{j-1}}{{\beta }_j}$; in particular, the product of these ratios may be increasing or decreasing by increasing the value of j. As K increases NT, the probability pk, i.e., P (k = K), becomes negligible. Hence, α j decreases in accordance with increasing j. β _j may be taken as constant, or it may increase by increasing j. Hence, logically, α _j and β _j for the birth–death process under consideration is inversely proportional to each other.

4.4 Hump state

There is a hump point, that is, the point at which α _j = β _j. When we move toward the right to this point, i.e., toward j +1,…, K, the ratios α _j+1,…,α_K become less than unity, and similarly, if we move toward the left, i.e., j −1, j − 2,…,1, then the ratio α _j11,…,α₁ becomes greater than unity. The jth state is a hump state. The hump point directly depends on the number of channels available to CRN, which, in turn, depends on ^NT, β _j, and also on the total number of active CRNs in the same zone. A variety of scenarios regarding the forward rates, i.e., birth-rates, αi, and death rates, βi, have been discussed in the subsequent section, specifically in simulations to demonstrate the results with the shifting of the hump point.

$p_j={\displaystyle \sum _{k=1}^{N_T}}\left(\frac{A_j}{{\displaystyle {\sum }_{i=1}^k}{A}_i}\right)P\left(\mathit{k}=k\right),$

$p_j=A_j{\displaystyle \sum _{k=1}^{N_T}}\left(\frac{1}{{\displaystyle {\sum }_{i=1}^k}{A}_i}\right)P\left(\mathit{k}=k\right).$

As the arrival and departure of cognitive users are a random process and these rates are independent of each other, the hump state is a situation where the arrival of cognitive user α = departure of cognitive user β at a given time instant. This hump state yields the maximum value of probability, and in the case of a Gaussian distribution, it is the peak of the bell. The probability increases until this peak and then decreases, so except for the value at the peak or hump, all probabilities are minimum, where the parameter p_j is the probability of finding the process in

jth a state. ^NT=total number of states (channels) available in the primary cellular network.

k = number of channels occupied by the cognitive network. It may take some value between 1 and ^NT depending on the number of primary users and other CRNs operating in the same region. Since it is a random variable, P (k = k) is the probability of occupying k −states.

5 Simulations

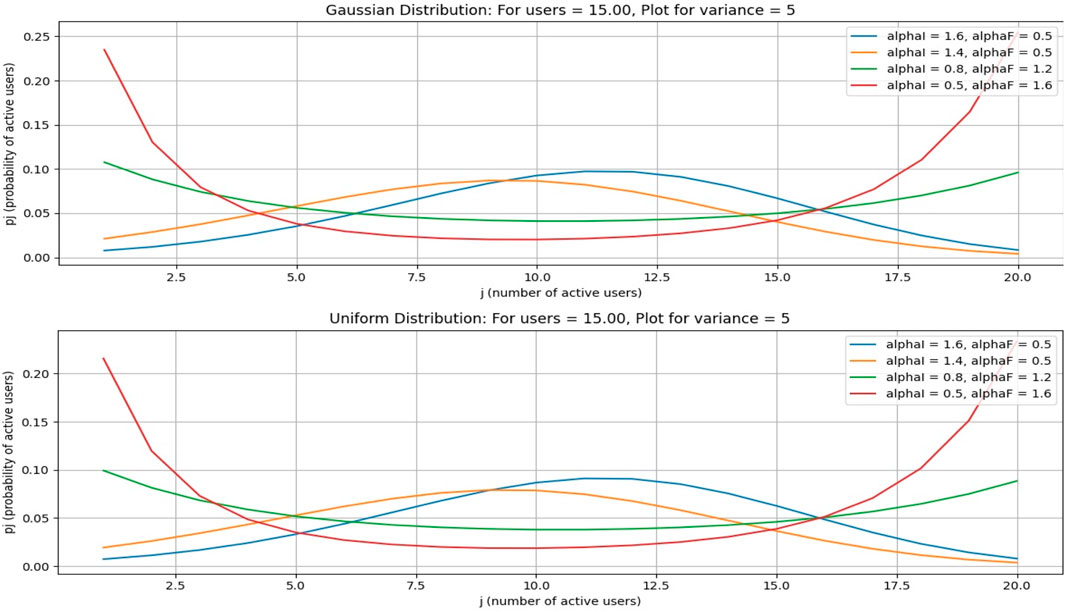
To evaluate the performance of the proposed model, the simulations are performed in MATLAB. The simulation results validate the performance of the algorithm. To show the probability of active users in the cognitive radio network, we have considered N_t = 100 number of channels for the primary base station. Out of these 100 channels, 40 are occupied by primary users. Therefore, the number of free channels for cognitive users is 60. Suppose that there are five active cognitive users (networks) in the region, and the average number of channels for each network is 60/5 = 12. All the simulation results are calculated by using the Gaussian and uniform probability distribution functions.

5.1 Case 1

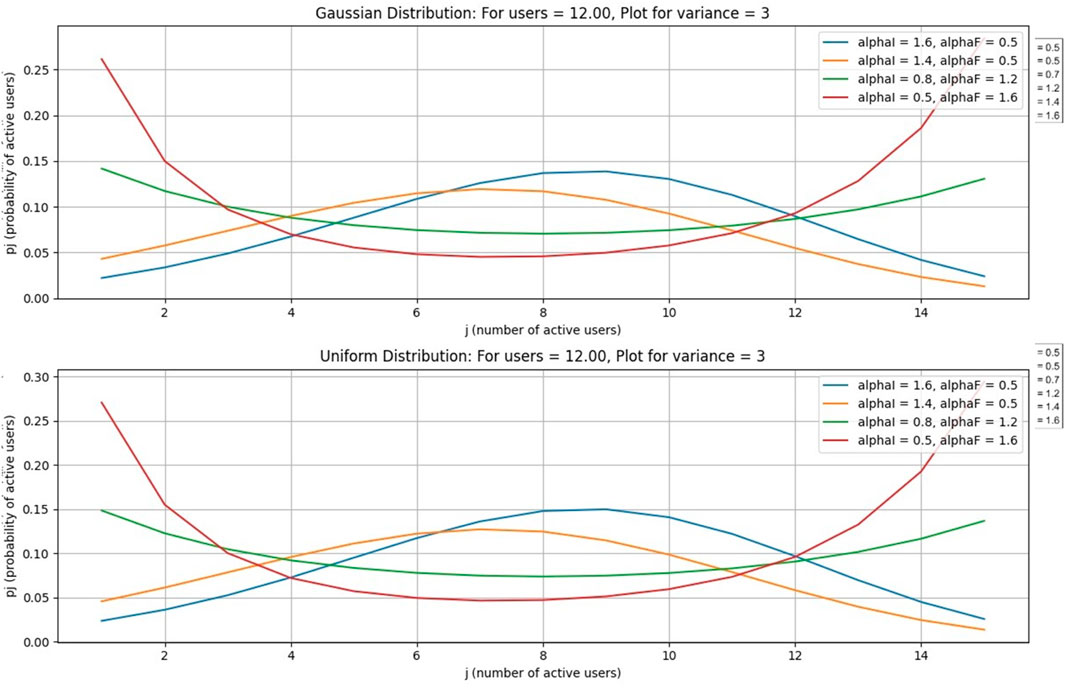
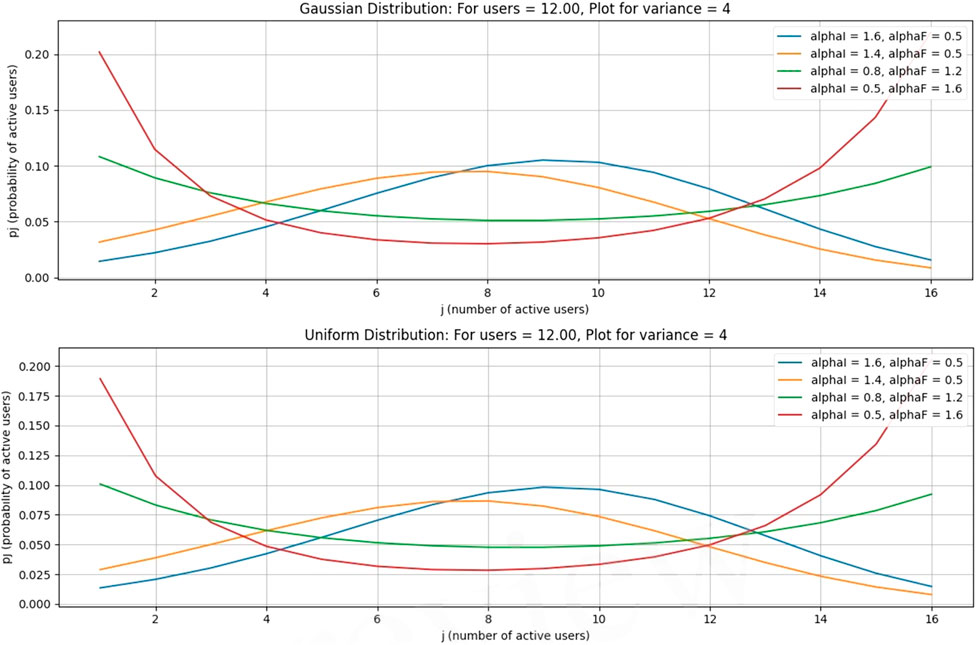
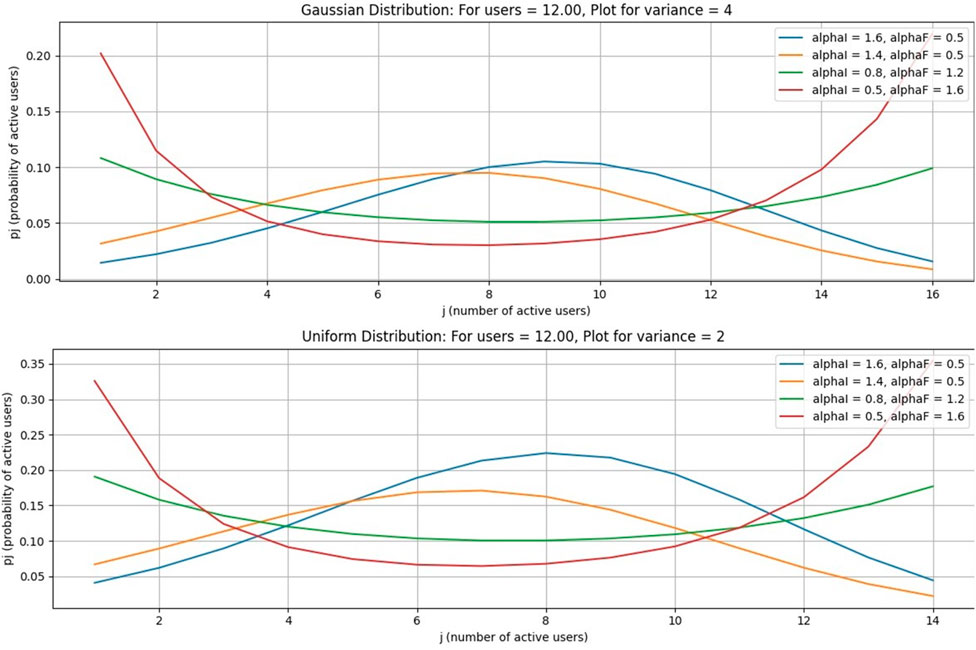
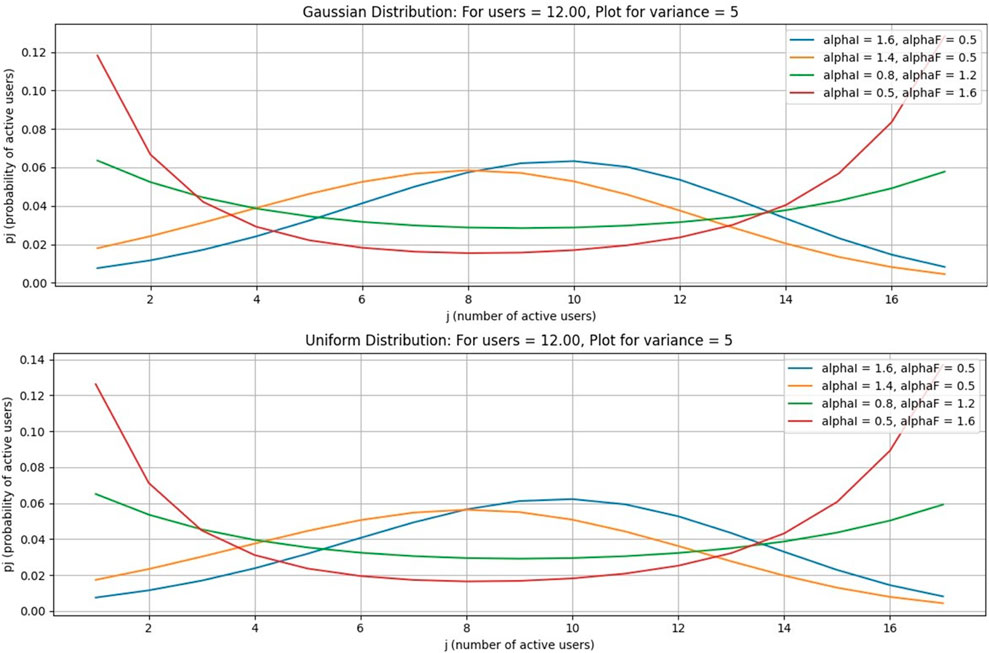
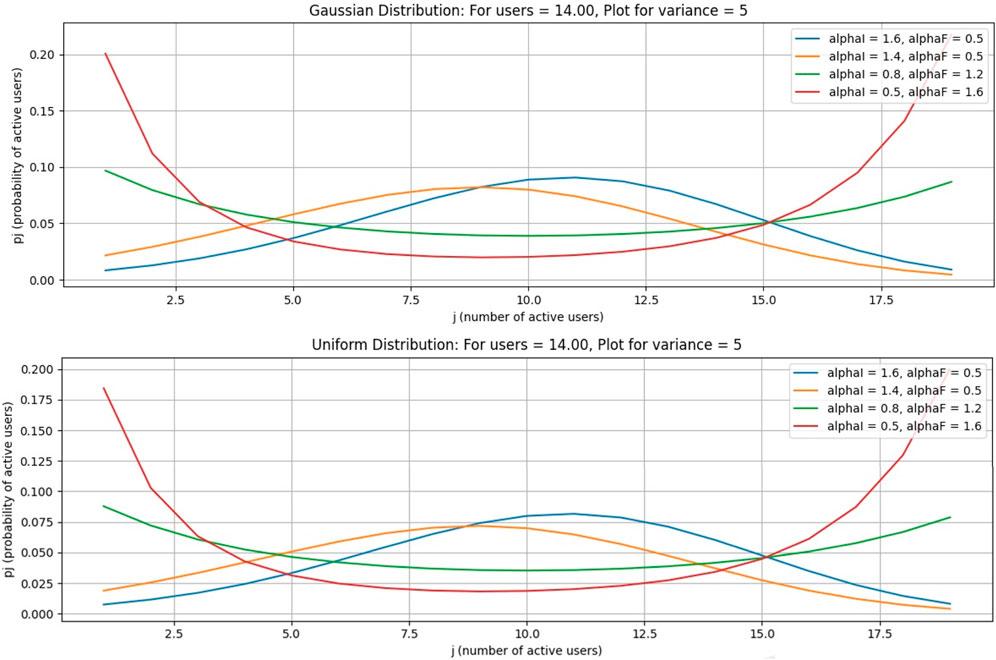
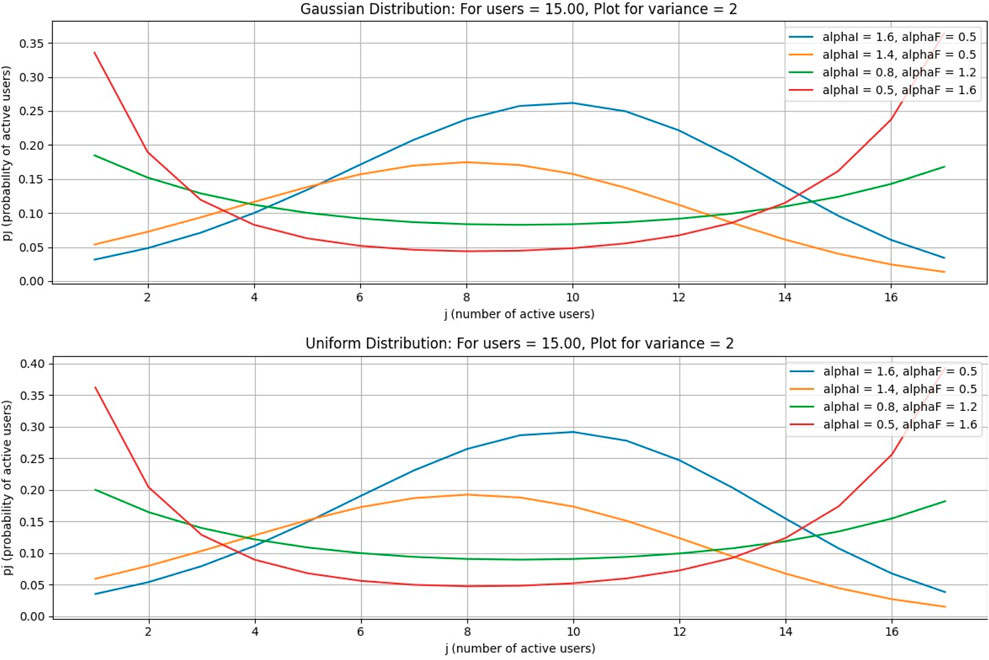
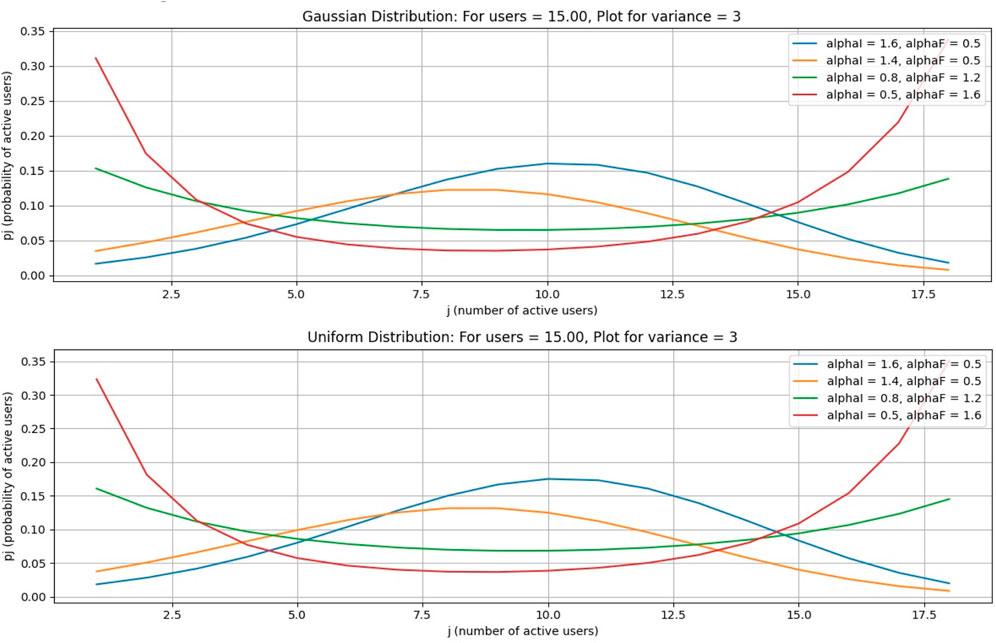
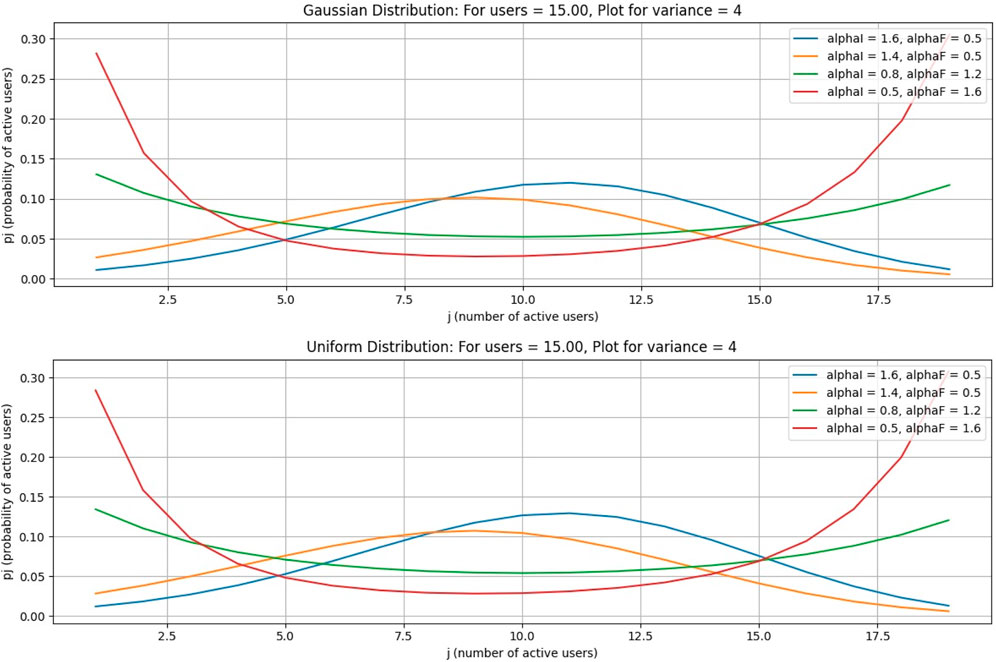
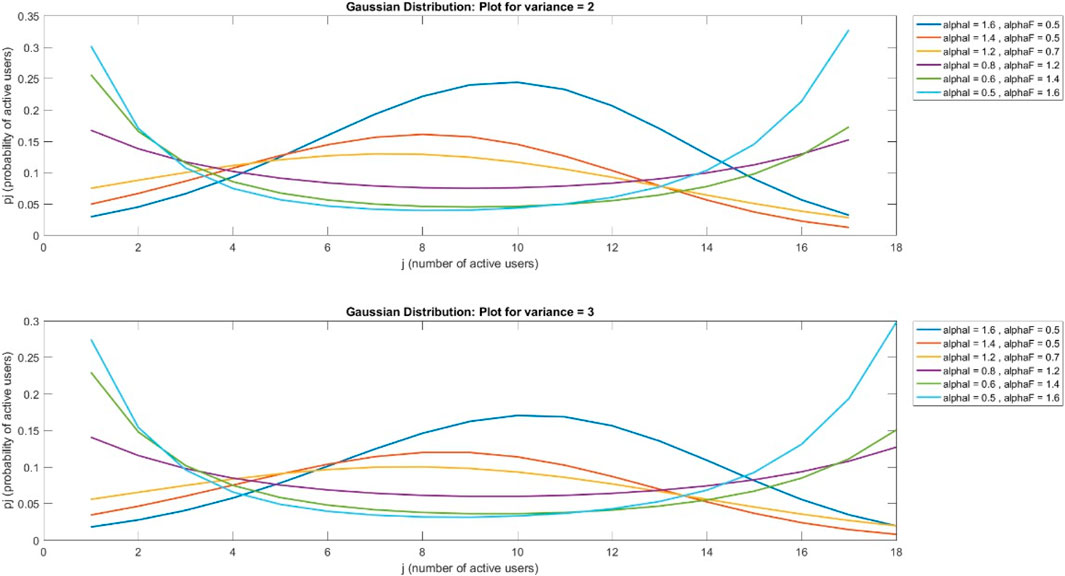
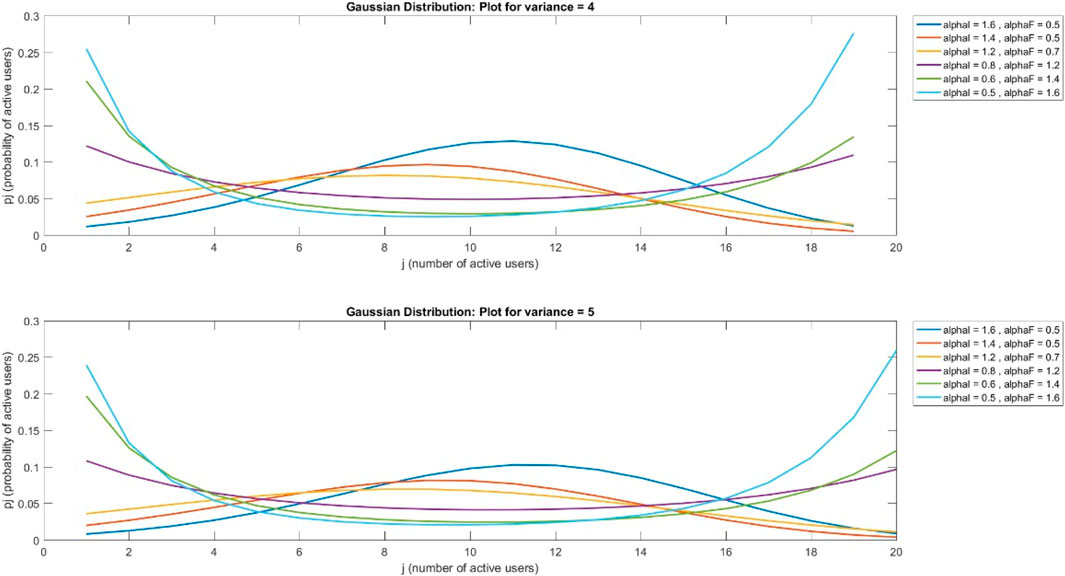
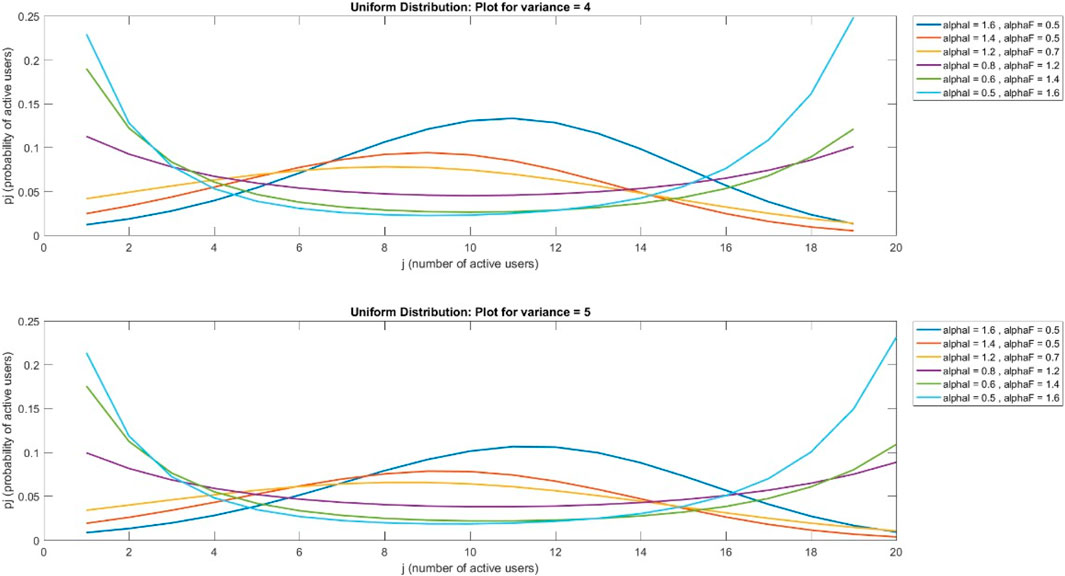
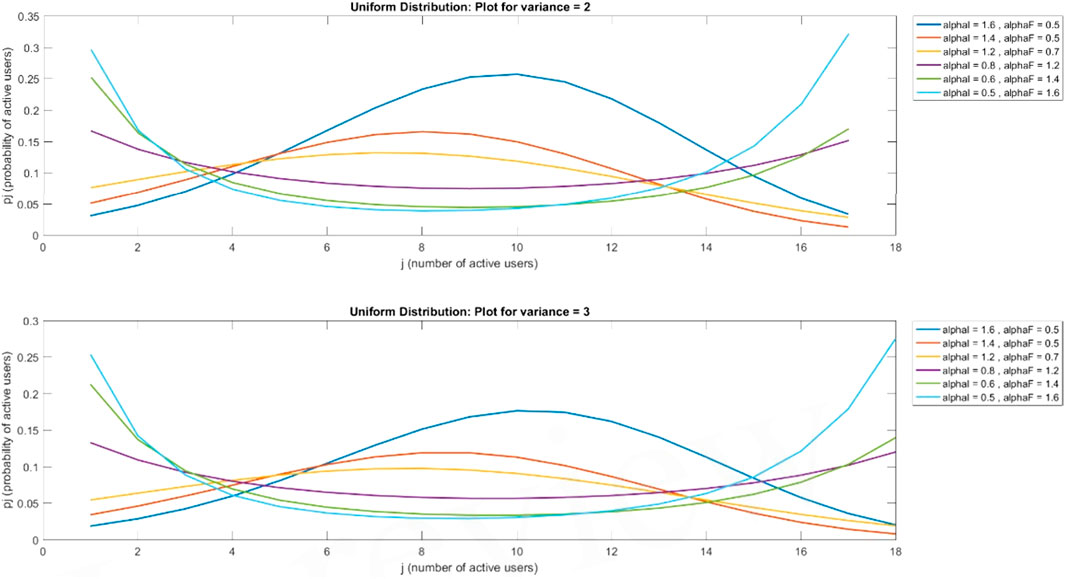
This case is for a Gaussian distribution. In this paper, from Figures 3–6, Figure 7 is drawn using subplot (211), (212), alphI_vect = [2, 1.6, 1.2, 0.5, 0.5, 0.5], and alphF_vect = [0.5, 0.5, 0.5, 1.2, 1.6, 2]. For Figure 5, var = 2. Similarly, Figure 3 is drawn using var = 3, and for Figures 4, 6, variance = 4 and 5, respectively, and all other values are the same as shown in the previous figures. The upper part of these figures shows the Gaussian distribution, and the lower part reflects the uniform distribution for the same parameters.

Figure 3

Figure 3. Gaussian distribution and normal distribution with var = 3.

Figure 4

Figure 4. Gaussian distribution and normal distribution with var = 4.

Figure 5

Figure 5. Gaussian distribution and normal distribution with var = 2.

Figure 6

Figure 6. Gaussian distribution and normal distribution with var = 5.

Figure 7

Figure 7. Flowchart.

The Gaussian distribution with VAR = 2, 3, 4, 5, and arrival rate alphaI decreases, and departure rate alphaF increases. It is obvious in Figure 7 that the maximum probability of having a particular number of cognitive users could be achieved by setting alphaI = 1.6 and alphaF = 0.6. Reducing the alphaI and increasing alphaF shifts the peak of the distribution toward smaller values of users. In the next figure, a 4–6 increase in VAR values causes a decrease in the probabilities.

5.2 Case 2

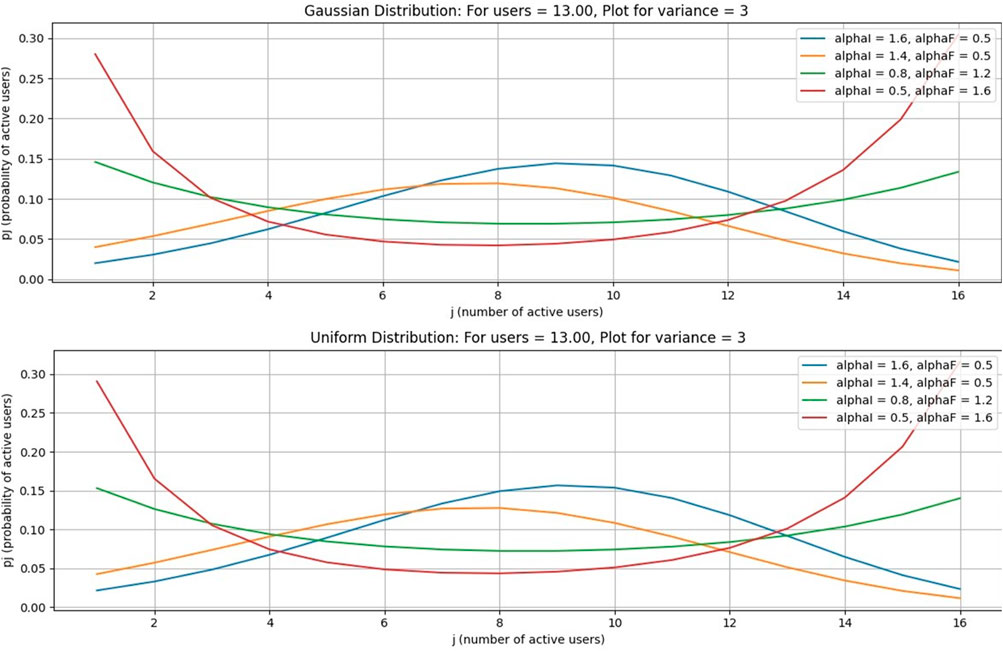
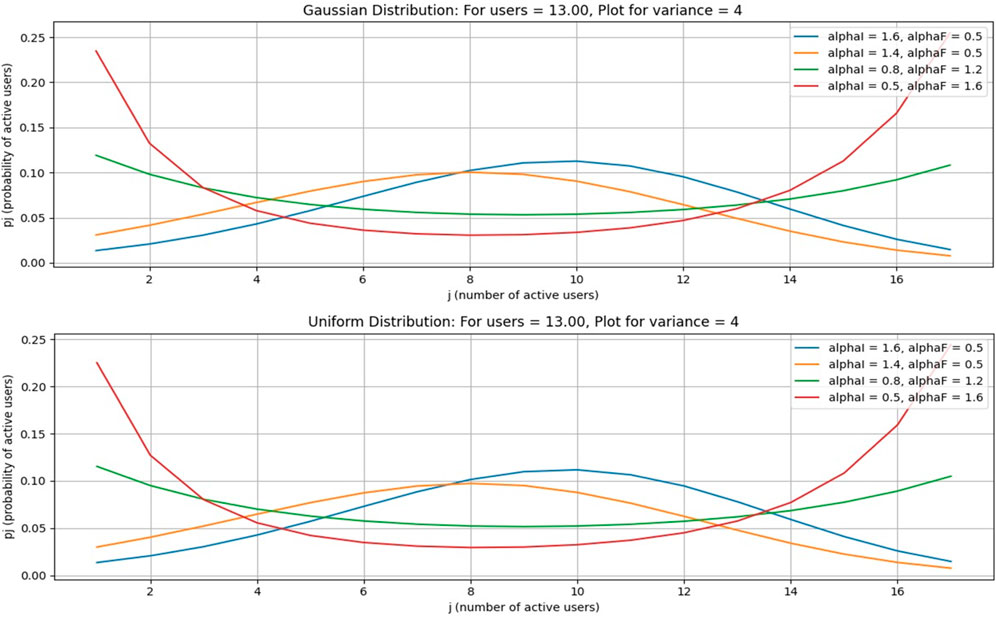
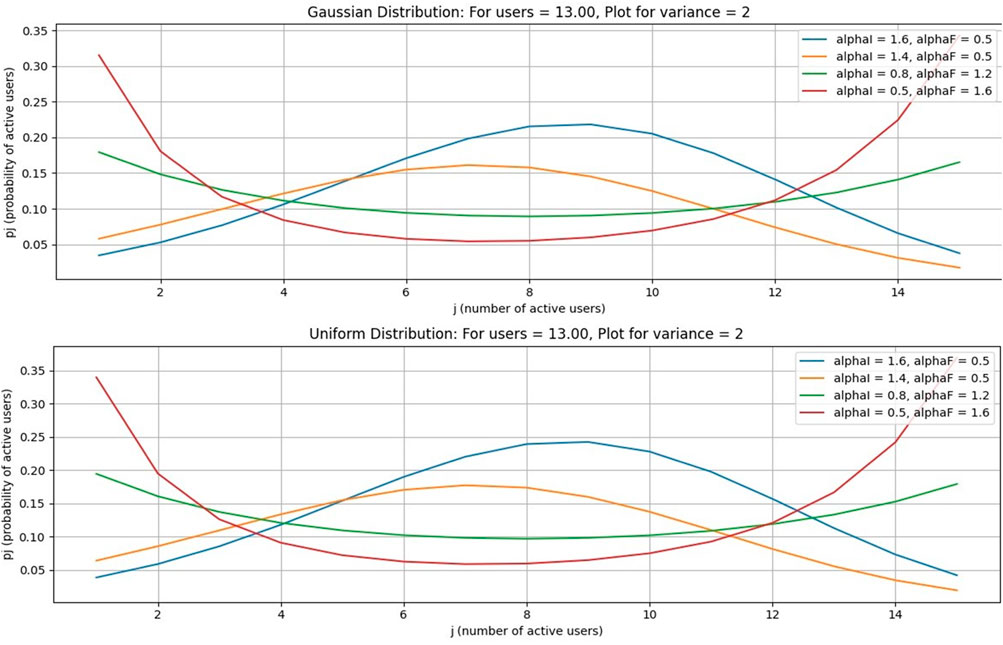
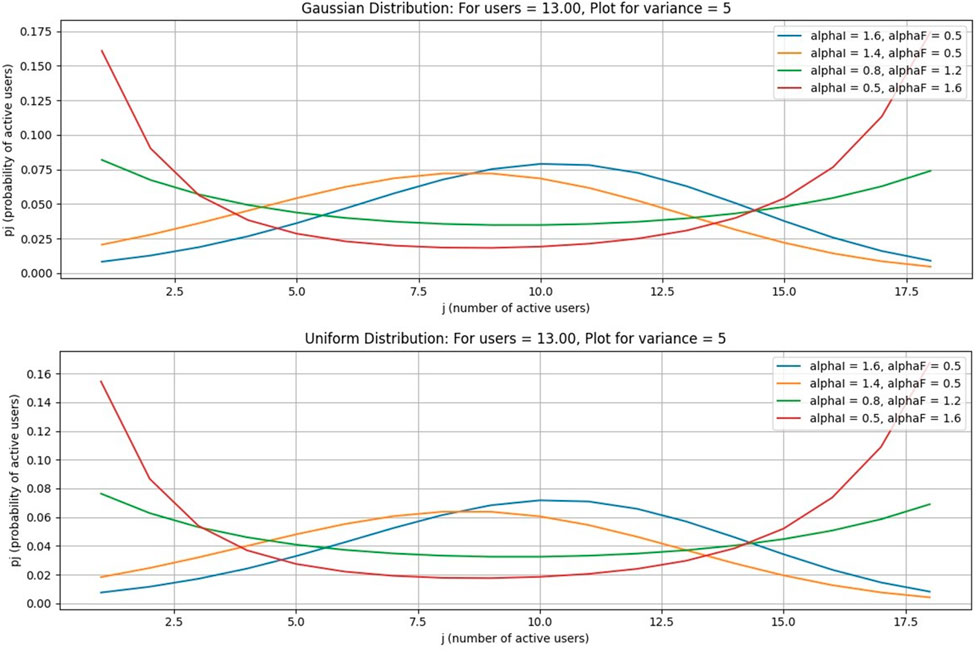
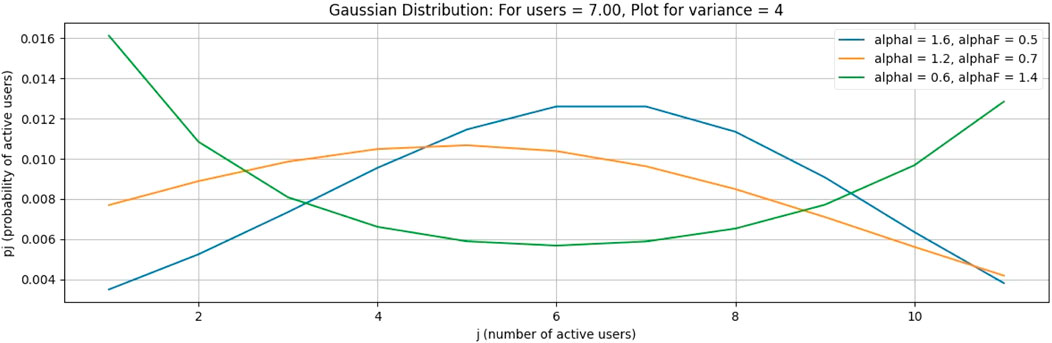
This case is for a Gaussian distribution for the number of average free channels = 13, as shown in Figures 8–11. Figure 8 is drawn using subplot (211), (212), alphI_vect = [2, 1.6, 1.2, 0.5, 0.5, 0.5], and alphF_vect = [0.5, 0.5, 0.5, 1.2, 1.6, 2]. For Figure 10, var = 2. Similarly, Figure 8 is drawn using var = 3, and for Figures 9, 11, variance = 4 and 5, respectively, and all other values are the same as in previous figures. The upper part of these figures shows the Gaussian distribution, and the lower part reflects the uniform distribution for the same parameters.

Figure 8

Figure 8. Gaussian distribution and normal distribution with var = 3.

Figure 9

Figure 9. Gaussian distribution and normal distribution with var = 4.

Figure 10

Figure 10. Gaussian distribution and normal distribution with var = 2.

Figure 11

Figure 11. Gaussian distribution and normal distribution with var = 5.

When free channels for cognitive users are increased from 60 to 65, each cognitive service provider obtains 13 channels. As the number of channels increases, the probability decreases. However, the number of channels increases at the peak of the curve.

5.3 Case 3

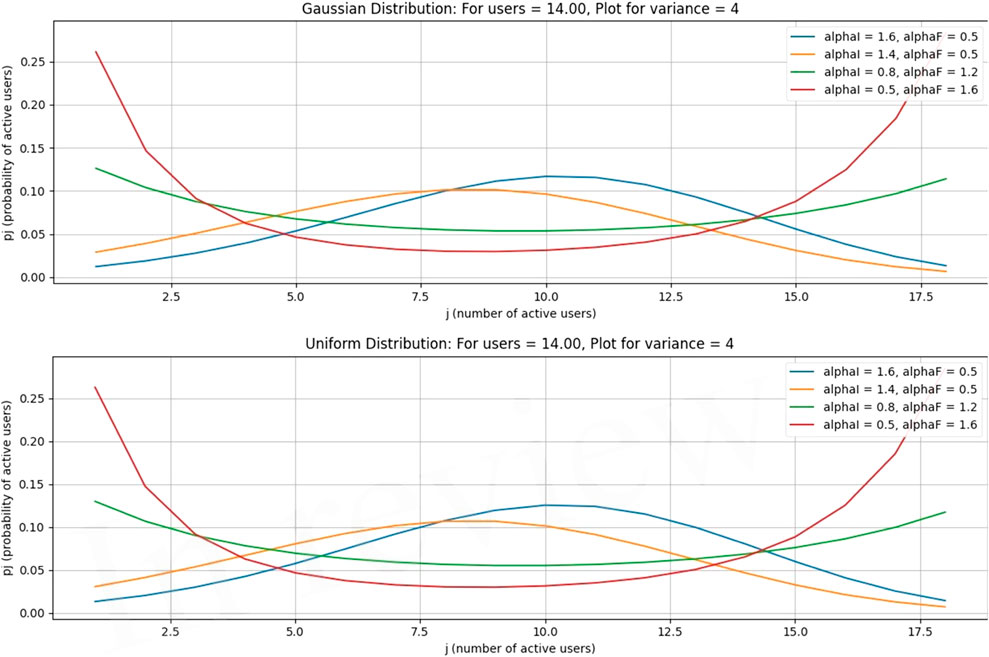
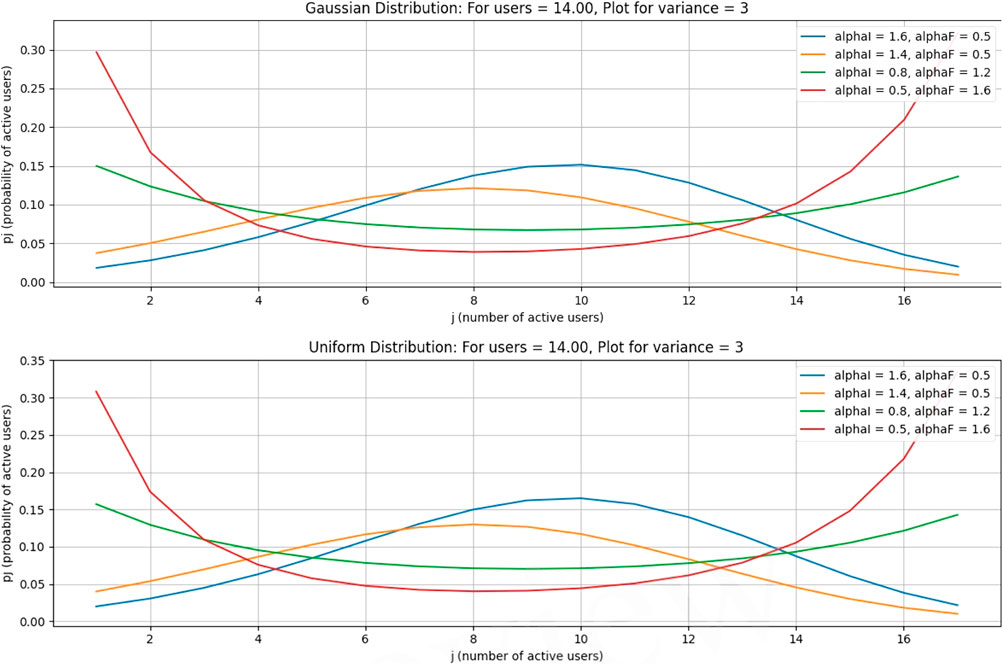
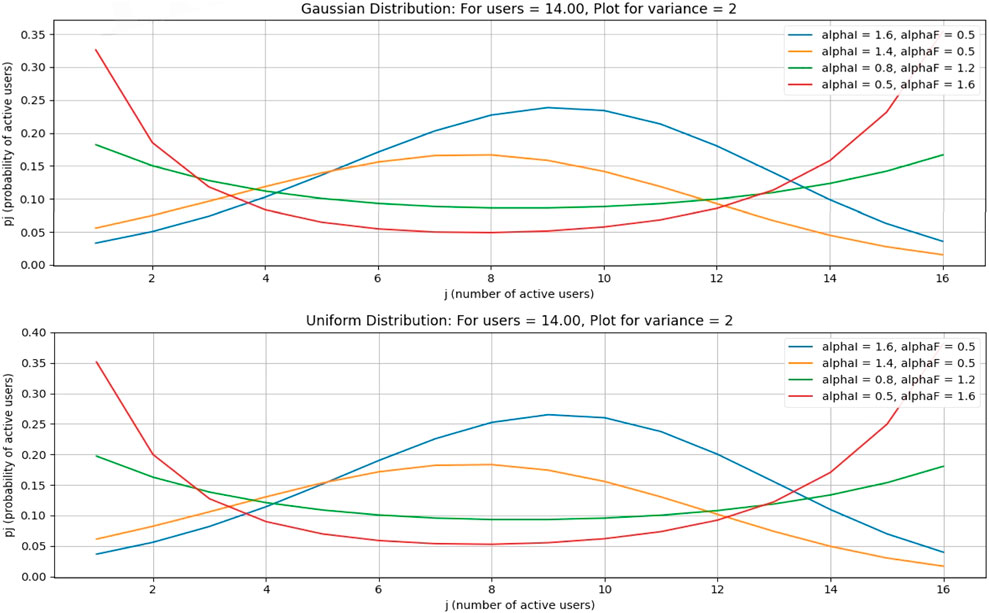
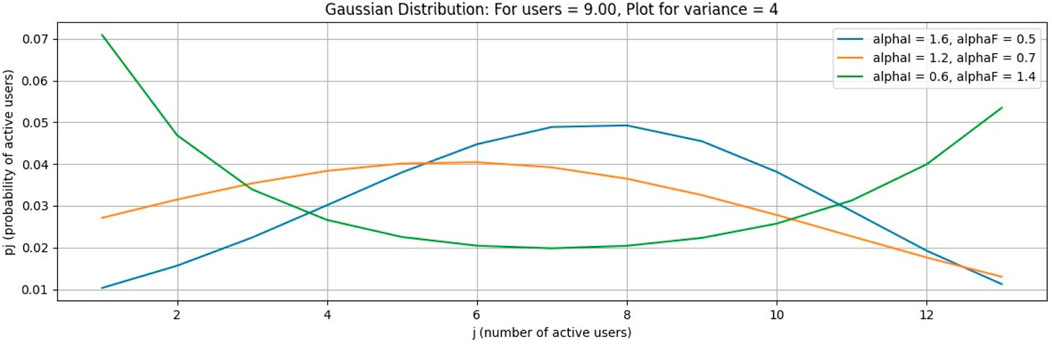
In this case, the number of free channels is 70, and the average number of free channels per user is 14. All other parameters are the same as in previous cases.

In Figures 12–15, it is obvious that, by increasing the number of channels for users, the probability will decrease as the curve will become flat, but the peak of the curve will shift to a larger number of users. Figures 16–19, show that as the number of channels increases, the curve becomes flatter. The overall probability decreases, but the peak shifts upward because the maximum probability occurs at a higher number of users. Figures 20–23, show that as the variance increases, the Gaussian curve becomes flatter. The probability decreases, but the peak shifts to a higher value because the mean (or the most likely number of users) increases.

Figure 12

Figure 12. Gaussian distribution and normal distribution with var = 4.

Figure 13

Figure 13. Gaussian distribution and normal distribution with var = 3.

Figure 14

Figure 14. Gaussian distribution and normal distribution with var = 2.

Figure 15

Figure 15. Gaussian distribution and normal distribution with var = 5.

Figure 16

Figure 16. Gaussian distribution and normal distribution with var = 2.

Figure 17

Figure 17. Gaussian distribution and normal distribution with var = 3.

Figure 18

Figure 18. Gaussian distribution and normal distribution with var = 4.

Figure 19

Figure 19. Gaussian distribution and normal distribution with var = 5.

Figure 20

Figure 20. Gaussian distribution with different values of variance.

Figure 21

Figure 21. Gaussian distribution with different values of variance.

Figure 22

Figure 22. Normal distribution with different values of variance.

Figure 23

Figure 23. Normal distribution with different values of variance.

5.4 Case 4

In this case, the number of free channels is 75, and the average number of free channels per user = 15. All other parameters are the same as in previous cases.

5.5 Case 5

In this case, a comparison of different values of variance is carried out; details are shown in Figure 20.

A comparison of different values of variance shows that variance increases in a Gaussian distribution, while probability decreases as the curve becomes flat, but the mean value or peak of the curve increases.

5.6 Comparison with existing models

The schemes that are very close to our research are presented for comparison.

1. In the research article “Q. Xu, S. Li, J. Gaber, and Y. Han, “Modeling Analysis of Channel Assembling in CRNs Based on Priority Scheduling Strategy with Reserved Queue,” Electronics, vol. 13, no. 15, p. 3051 Aug. 2024,” a priority scheduling algorithm has been proposed using reserved channel queues. In this paper, there is some work that computes the number of active users in the system. The work presented in this research article is based on elastic services and not on the overall number of SU. However, a comparison could be generated. The parameters for comparison are taken almost the same, i.e., Nt (total number of channels), number of users, and number of free channels. Results are generated, and a comparison is drawn.

In the existing model, as shown in Figure 24, on the y-axis, there is the spectrum utilization by SUs, which is the same as the probability of having the same number of SUs as shown in the Figure 25. Because spectrum sharing implies that the available channels are occupied, the number of occupied channels represents the number of active users in the system. However, on the x-axis in the existing model, instead of the actual number of secondary users, it is based on the nature of services required by these users. It is obvious from the figures that the curves in the proposed scheme are very close to a Gaussian distribution compared to the existing model.

2. The second comparison is drawn with “A.Tanveer, Z. U. Khan, A. N. Malik, and I. M. Qureshi, “Flexible Queuing Model for Number of Active Users in Cognitive Radio Network Environment,” Wireless Communications and Mobile Computing, vol. 2018, Article ID 8349486, 2018. doi: [10.1155/2018/8349486]”. In this study, the PMF is computed from the number of active users but with a fixed upper bound of the queue, such that the arrival rate and the random departure rate are fixed.

In the existing model as shown in Figure 26 due to a fixed upper bound, that is arrival rate of the user is random, but the departure is fixed, the probability will decrease by increasing the number of users. On the other hand, in the proposed work shown in Figure 27, arrival and departure are random, so the probability will rise until the hump state occurs, where the arrival and departure rates are the same, and then the probability reduced after that hump state.

Figure 24

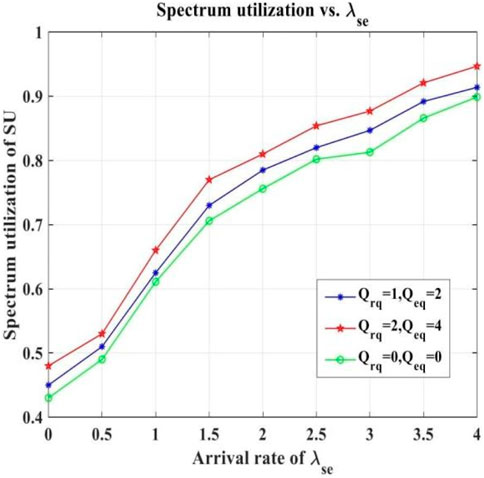
Figure 24. Spectrum utilization of SUs [35].

Figure 25

Figure 25. PMF with a Gaussian distribution with seven users.

Figure 26

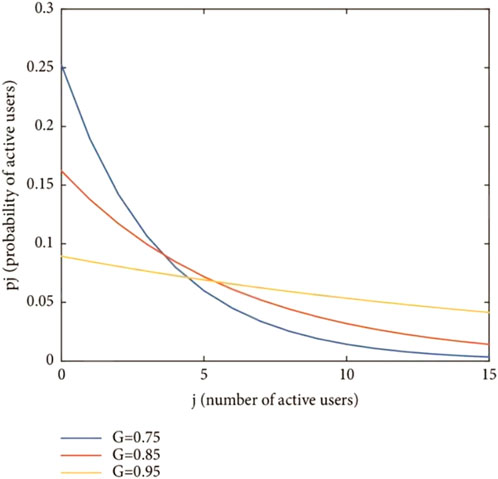
Figure 26. Probabilities of different numbers of active users for ς = 0.75, 0.85, and 0.95 [1].

Figure 27

Figure 27. PMF with a Gaussian distribution with nine users.

6 Conclusion

The suggested paradigm has been put into practice and examined in a variety of situations. The results are quite close to the expectations, as discussed in the theoretical framework. At present, the forward transition rates have been varied in flexible generalized queuing, whereas the backward transition rate has been kept constant, yet the problem is generalized because of their difference, which is not stationary. In existing work, the variation in forward transition rates has been taken linear; however, the derivations are generalized and may be applicable for any type of nonlinear rates. Similarly, in simulations, the upper limit for available channels to the cognitive network has been derived with uniform and Gaussian distributions; again, the derivations are generalized and are assumed to be equally applicable for other random variables. This work may be used as an effective basis to plan handover schemes in a cognitive environment.

7 Limitations and future work

• This work was carried out in a stationary environment, and it could be applied in a dynamic environment.

• All cognitive service providers have the same capability, i.e., a homogeneous environment. The study can be extended to a heterogeneous environment.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

AhM: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review and editing. AsM: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Supervision, Validation, Visualization, Writing – review and editing. ZM: Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing – original draft, Writing – review and editing. AqM: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing. AA: Conceptualization, Data curation, Formal Analysis, Resources, Validation, Writing – review and editing. MH: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Resources, Validation, Writing – review and editing. JS: Conceptualization, Formal Analysis, Funding acquisition, Resources, Visualization, Writing – review and editing.

Funding

The authors declare that financial support was received for the research and/or publication of this article. This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2503).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tanveer A, Khan MZU, Malik AN, Qureshi IM. Flexible queuing model for number of active users in cognitive radio network environment. Wireless Commun Mobile Comput (2018) 2018:8349486. doi:10.1155/2018/8349486

CrossRef Full Text | Google Scholar

2. Zenalden F, Hassan S, Habbal A. Vertical handover in wireless heterogeneous networks. J Telecom Elec and Comp Eng (2017) 9(1-2):81–5.

Google Scholar

3. Esenogho E, Mambou EN, Ferreira HC. On the evaluation of handover exchange schemes between two cognitive radio base stations with and without buffers. Int J Electronics Telecom. (2018) 64(4):513–8. doi:10.24425/123553

CrossRef Full Text | Google Scholar

4. Malathy EM, Muthuswamy V. State of art: vertical handover decision schemes in next-generation wireless network. J Comm Info Networks (2018) 3(1):43–52. doi:10.1007/s41650-018-0009-2

CrossRef Full Text | Google Scholar

5. Alam S, Sohail MF, Ghauri SA, Qureshi IM, Aqdas N. Cognitive Radio-based smart grid communication network. Renew and Sustainable Energ Rev (2017) 72:535–48. doi:10.1016/j.rser.2017.01.086

CrossRef Full Text | Google Scholar

6. Alam S, Malik AN, Qureshi IM, Ghauri SA, Sarfraz M. Clustering-Based channel allocation scheme for neighborhood area network in a cognitive radio-based Smart Grid communication. IEEE Access (2018) 6:25773–84. doi:10.1109/access.2018.2832246

CrossRef Full Text | Google Scholar

7. Cheng H, Zhuang W. Simple channel sensing order in cognitive radio networks. IEEE J Selected Areas Commun (2011) 29(4):676–88.

Google Scholar

8. Jaishanthi B, Ganesh EN, Sheela D. Priority-based reserved spectrum allocation by multi-agent through reinforcement learning in cognitive radio network. Automatika (2019) 60(5):564–9. doi:10.1080/00051144.2019.1674512

CrossRef Full Text | Google Scholar

9. Choi KW, Hossain E. Opportunistic access to spectrum holes between packet bursts: a learning-based approach. IEEE Trans Wir Comm (2011) 10(8):2497–509.

Google Scholar

10. Zhao H, Wang S, Li L. A directly seeking spectrum holes algorithm by compressive sampling. Int J Comm Syst (2019) 32:e4107. doi:10.1002/dac.4107

CrossRef Full Text | Google Scholar

11. Xu H, Li B. Resource allocation with flexible channel cooperation in cognitive radio networks. IEEE Trans Mob Comput (2013) 12(5):957–70. doi:10.1109/tmc.2012.62

CrossRef Full Text | Google Scholar

12. Bharathi GP, Jeyanthi KMA. An optimization algorithm-based resource allocation for cooperative cognitive radio networks. J Supercomp (2018) 76:1180–200.

Google Scholar

13. Cacciapuotu A, Caleffi M, Paul L, Rahman M. Channel availability for mobile cognitive radio networks. J Netw Comp. Appl. (2015) 47:131–6.

Google Scholar

14. Tarek D, Benslimane A, Darwish M, Kotb AM. Cognitive radio networks channel State estimation using machine learning techniques 15^thinternational wireless comm. In: Mobile computing conf. IWCMC (2019).

Google Scholar

15. Yan J, Zhang B, Wang S, Lan H, Wang X. Burst traffic: congestion management and performance optimization strategies in heterogeneous cognitive radio networks. IET Commun (2024) 18(8):523–33. doi:10.1049/cmu2.12753

CrossRef Full Text | Google Scholar

16. Maragathasundari S, Sudhakar V, Vignesh S, Balamurugan B, Swedheetha C, Vanalakshmi R. Queuing process optimization in software-defined radio: enhancing System performance and adaptability. Ain Shams Eng J (2024) 15:102976–432. doi:10.1016/j.asej.2024.102976

CrossRef Full Text | Google Scholar

17. Sun K, Liu Y, Li K. Energy harvesting cognitive radio networks with strategic users: a two-class queueing model with retrials. Comput Commun (2023) 199:98–112. doi:10.1016/j.comcom.2022.12.017

CrossRef Full Text | Google Scholar

18. Cao YY, Zhao Y, Li H. A spectrum occupancy model for primary users in cognitive radio systems. J Comput Commun (2023) 11(11):78–86. doi:10.4236/jcc.2023.1111005

CrossRef Full Text | Google Scholar

19. Behera JR, Imoize AL, Singh SS, Tripathy SS, Bebortta S. Optimizing priority queuing systems with server reservation and temporal blocking for cognitive radio networks. Telecom (2024) 5(2):416–32. doi:10.3390/telecom5020021

CrossRef Full Text | Google Scholar

20. Gupta N, Kumar Dhurandher S. Cross-layer perspective for channel assignment in cognitive radio networks: a survey. Int J Commun Syst (2020) 33(5):e4261. doi:10.1002/dac.4261

CrossRef Full Text | Google Scholar

21. Alberto L, Borja-Benítez B, Marcelin-Jiménez R, Rodríguez-Colina E, Tirado-Mendez JA. Mathematical analysis of highly scalable cognitive radio systems using hybrid game and queuing theory. AEU-International J Electronics Commun (2020) 127:153406. doi:10.1016/j.aeue.2020.153406

CrossRef Full Text | Google Scholar

22. Kotobi K, Bilén SG. Spectrum sharing via hybrid cognitive players evaluated by an M/D/1 queuing model. EURASIP J Wireless Commun Networking (2017) 1:85.

CrossRef Full Text | Google Scholar

23. Palunčić F, et al. Queueing models for cognitive radio networks: a survey. IEEE Access (2018) 6:50801–23.

CrossRef Full Text | Google Scholar

24. Afzal H, Mufti MR, Ahmed KT, Ajmal S, Yousaf M. Performance analysis of hybrid spectrum sharing in Cognitive Radio- based wireless regional area network. The Nucleus (2020) 57(1):27–32. doi:10.71330/nucleus.57.01.1082

CrossRef Full Text | Google Scholar

25. Barman S, Biswas A, Kundu A. Analysis of a dynamic queuing model for secondary users in cognitive radio networks. In: 2020 IEEE calcutta conference CALCON. IEEE (2020).

Google Scholar

26. Tsimba H, Maharaj BT, Alfa A. Optimal spectrum utilisation in cognitive radio networks based on processor sharing techniques. Int J Commun Syst (2020) 33(4):e4242. doi:10.1002/dac.4242

CrossRef Full Text | Google Scholar

27. Tsimba HM. Queueing-Based Resource Allocation in Cognitive Radio Networks. South Africa: University of Pretoria (2017).

Google Scholar

28. Zhang J, Yang J, Zhang Y, Zhang S. A dynamic spectrum allocation algorithm for a maritime cognitive radio communication system based on a queuing model. Information (2017) 8.4:119. doi:10.3390/info8040119

CrossRef Full Text | Google Scholar

29. Bayrakdar ME, Calhan A. Improving spectrum handoff utilization for prioritized cognitive radio users by exploiting channel bonding with starvation mitigation. AEU- Int J Electronics Commun (2017) 71:181–91. doi:10.1016/j.aeue.2016.10.022

CrossRef Full Text | Google Scholar

30. Zahed S, Awan I, Cullen A. Analytical modeling for spectrum handoff decision in cognitive radio networks. Simulation Model Pract Theor (2013) 38:98–114. doi:10.1016/j.simpat.2013.07.003

CrossRef Full Text | Google Scholar

31. Koushik AM, Bentley E, Hu F, Kumar S. A hardware testbed for learning-based spectrum handoff in cognitive radio networks. J Netw Comput Appl (2018) 106:68–77. doi:10.1016/j.jnca.2017.11.003

CrossRef Full Text | Google Scholar

32. Wu C, He C, Jiang L, Chen Y. A novel spectrum handoff scheme with spectrum admission control in cognitive radio networks. Proc IEEE Glob Telecommunications Conf. (Globecom) (2011) 1–5. doi:10.1109/glocom.2011.6133715

CrossRef Full Text | Google Scholar

33. Mir U, Bhatti ZA. Time triggered handoff schemes in Cognitive Radio Networks: a Survey. J Netw Comput Appl (2018) 102:71–85. doi:10.1016/J.JNCA.2017.11.008

CrossRef Full Text | Google Scholar

34. Briones-Reyes A, Vásquez-Toledo LA, Prieto-Guerrero A, Aguilar-Gonzalez R. Mathematical evaluation of spectrum sharing in cognitive radio networks for 5G systems using Markov processes. Computer Networks (2020) 182:107521. doi:10.1016/j.comnet.2020.107521

CrossRef Full Text | Google Scholar

35. Xu Q, Li S, Gaber J, Han Y. Modelling analysis of channel assembling in CRNs based on priority scheduling strategy with reserved queue. Electronics (2024) 13(15):3051. doi:10.3390/electronics13153051

CrossRef Full Text | Google Scholar

36. Cheng P, Yang X, Zhang Z, Wang L. A channel allocation-based multichannel MAC protocol for cognitive radio networks. IEEE Sensors J (2024) 24(16):26788–801. doi:10.1109/jsen.2024.3424778

CrossRef Full Text | Google Scholar

37. Sethi SK, Mahapatro A. A deep learning-based discrete-time Markov chain analysis of cognitive radio network for sustainable internet of things in 5G-enabled smart city. Iranian J Sci Technol Trans Electr Eng (2024) 48:37–64. doi:10.1007/s40998-023-00665-y

CrossRef Full Text | Google Scholar

38. Mughal MA, Ullah A, Cheema MAZ, Yu X, Jhanjhi NZ. An intelligent channel assignment algorithm for cognitive radio networks using a tree-centric approach in IoT. Alexandria Eng J (2024) 91:152–60. doi:10.1016/j.aej.2024.01.071

CrossRef Full Text | Google Scholar