Robust GNSS/INS hybrid integration based on multi-state validation of GNSS measurements

The Global Navigation Satellite System (GNSS) is generally combined with the Inertial Navigation System (INS) to deliver reliable and high-performance navigation, particularly in scenarios where GNSS signals may be compromised. This integration leverages the inherent strengths of both systems to ensure continuous and accurate positioning. To enhance the robustness and accuracy of navigation systems in challenging environments, this paper proposes a novel hybrid integration (HI) approach for GNSS/INS fusion. The system incorporates a Multiple State Inspection of GNSS Observations (MSI-GO) mechanism, which dynamically selects the optimal integration mode based on the number of visible satellites (NoS) and position dilution of precision (PDoP), thereby achieving a balance between positioning performance and computational efficiency. Simulation results using an open dataset demonstrate that, compared to traditional loosely coupled (LC) and tightly coupled (TC) methods, the HI scheme improves positioning accuracy by approximately $5\%$ while reducing computational complexity by around $25\%$. This validates the proposed approach as both stable and resource-efficient, with strong applicability in real-world navigation scenarios.

1 Introduction

To achieve globally available, accurate, and dependable navigation services, integration of the Global Navigation Satellite System (GNSS) [1] and the Inertial Navigation System (INS) is essential [2]. Together, they ensure seamless coverage with enhanced positioning performance [3, 4]. The INS is capable of continuously delivering information on a vehicle’s position, velocity, and orientation, thereby effectively supporting and improving the accuracy of GPS-based navigation and positioning [5]. When GNSS signals become weak or unavailable, the integrated GNSS/INS system can rely on INS-derived position data to maintain continuous navigation support [6, 7]. Moreover, the high-precision positioning output from GPS can be used to update the INS through filtering techniques, effectively mitigating the accumulated drift in INS navigation parameters and enhancing the overall accuracy of the system [8, 9]. Therefore, the strengths and weaknesses of GNSS and INS effectively offset each other, making their integration one of the most efficient and reliable approaches to achieve robust navigation [10, 11].

Based on the degree of data integration and fusion complexity, GNSS/INS coupled navigation systems can be classified into loosely coupled (LC), tightly coupled (TC), and deeply coupled (DC) types [12–14]. Developing a deeply coupled GNSS/INS system requires utilizing specific variables from the GNSS receiver’s signal tracking loop, which differentiates it from LC/TC GNSS/INS systems [15, 16]. Since the GPS receiver typically provides the user’s position, velocity, and associated mean square error estimates, LC integration can be achieved when the outputs from the GNSS receiver and the INS subsystem are synchronized and match in value [17]. This makes it feasible for virtually anyone to implement GNSS/INS integration. Furthermore, if the receiver offers detailed GPS observations along with their associated mean square errors, the essential requirements for TC GNSS/INS integration are fulfilled [18, 19]. Given their low implementation complexity and strong robustness, research on LC/TC GNSS/INS systems remains highly valuable and relevant in practical applications [20–23]. Currently, the research directions can be classified into four categories: (1) Data Processing Software and Algorithms; (2) Navigation Algorithm; (3) Performance Evaluation and Optimization; (4) Fusion with Other Sensors.

(1) Data Processing Software and Algorithms: fundamental research [15]. Places strong emphasis on the precision and dependability of the software’s performance, recognizing them as essential for achieving consistent and trustworthy results. Additionally, the article rigorously tests the software under diverse operational conditions–including dynamic, obstructed, and GNSS-denied environments–and benchmarks its performance against comparable systems, highlighting its competitive advantages in accuracy, stability, and resilience [24]. Introduces GINav, a MATLAB-based software specifically developed for processing and analyzing data from GNSS/INS integrated navigation systems. The software supports a range of functions, including data visualization and error analysis, making it a valuable resource for research and practical implementation. These efforts underscore the crucial role of GNSS/INS data processing platforms in diverse application fields and demonstrate how targeted software development and validation can significantly enhance navigational accuracy and system reliability. (2) Navigation Algorithm: traditional research [25]. Proposes an algorithm to further low-end GNSS/INS systems used for land vehicle navigation [26]. Introduces using of “signals of opportunity” to enhance the performance of an INS [27]. Explores the application of a cubature Kalman filter with enhanced adaptability and robustness in TC GNSS/INS systems. (3) Performance Evaluation and Optimization: engineering research [28]. Suggests employing Allan variance to assess the relative accuracy of GNSS/INS on different time scales [29]. Also evaluates the performance of TC GPS/BDS/INS integration based on carrier phase measurements under GNSS-degraded and GNSS-denied conditions [30]. Assesses the accuracy and reliability of LC/TC GNSS/INS systems in practical urban environments [31]. Suggests a multi-receiver strategy to improve the performance of TC GNSS/MEMS-IMU systems. Moreover [32], Investigates how adaptive and fading factors influence the performance of filtering algorithms in GNSS/INS systems, and [33] proposes a low-cost GNSS/INS combination method for developed land vehicle performance [34]. Proposes a robust vehicular navigation solution by integrating multi-antenna GNSS with inertial sensors/odometer measurements [35]. Presents a motion-constrained GNSS/INS integration approach utilizing a backpropagation (BP) neural network for enhanced navigation accuracy. Collectively, these investigations promote the progressive optimization of GNSS/INS fusion strategies, emphasizing higher accuracy, improved system resilience, and broader environmental adaptability. (4) Fusion with Other Sensors: frontier research [36]. Improves GNSS/INS navigation performance in harsh environments through the application of adaptive information fusion techniques [37]. Introduces a real-time kinematic (RTK) solution supported by an inertial navigation algorithm tailored for smartphone-based pedestrian tracking, which significantly enhances positioning accuracy in challenging urban environments [27]. Introduces a novel fuzzy strong tracking cubature Kalman filter (KF) tailored for GNSS/INS integration, demonstrating superior navigation accuracy and robustness compared to conventional algorithms [38]. Proposes a MEMS-IMU-based autonomous navigation algorithm designed to enhance the positioning accuracy of UAV platforms. Navigation accuracy and robustness under various flight scenarios have been successfully verified. Additionally, studies by other researchers demonstrate that integrating an RTK receiver into GNSS/INS systems improves positioning precision in both railway measurement [39] and hydrographic survey [40] tasks, with analyses revealing performance gains and influencing parameters. A novel selective integration framework using weighted DOP is proposed by [41] to combine GNSS, visual sensing, and inertial measurements for robust navigation in GNSS-denied or degraded environments. Collectively, this body of work contributes valuable knowledge and innovative solutions to bolster the performance and robustness of GNSS/INS integration in land and air vehicles, which is essential for the development of autonomous vehicles and unmanned systems.

Based on the literature review, achieving both high accuracy and low computational complexity is critical for real-time positioning applications Tang et al. [42]; Li et al. [43]; Tang et al. [44]. Tightly Coupled (TC) GNSS/INS systems provide superior positional accuracy compared to Loosely Coupled (LC) GNSS/INS, especially in environments where GNSS signals are degraded. However, LC GNSS/INS systems are simpler to implement and deliver reliable positioning results when GNSS signals are strong, making them advantageous in such conditions. Given this existing gap, it is both necessary and timely to develop a novel method that reduces computational demands without compromising accuracy [45]. To address this, we propose the HI GNSS/INS system, which integrates the strengths of both LC and TC modes and employs Multiple State Inspection of GNSS Observations (MSI-GO) for data processing. Our approach effectively lowers computational complexity while ensuring the required positioning accuracy.

2 Fundamental theory

An overview of the commonly used LC and TC GNSS/INS integration architectures is presented in this section [17]. Conventional GNSS/INS integration commonly relies on the Kalman Filter [46, 47]. This section aims to provide readers with a comprehensive and clear explanation of the mathematical principles and architectural designs behind LC and TC methods.

2.1 GNSS/INS basic mechanisation

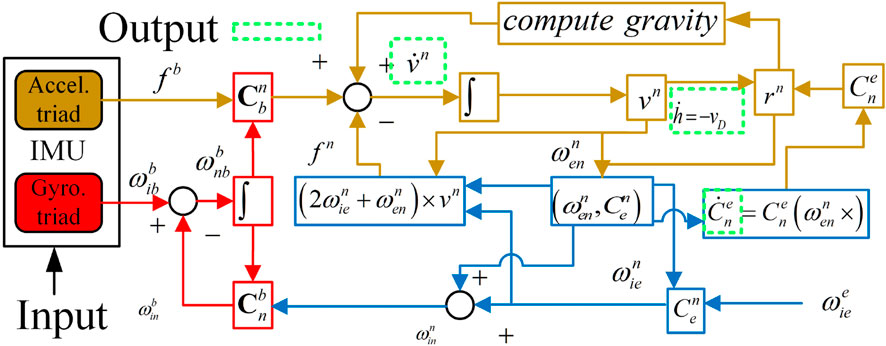
Practically, GNSS receivers obtain pseudorange and its rate by tracking the carrier and code phase of the signals received. These data are then used to estimate the receiver’s absolute location, accounting for errors such as atmospheric interference and noise, thereby improving positional accuracy. Currently, most GNSS/INS systems utilize Strapdown INS (SINS). The overall framework of the standard SINS algorithm is shown in Figure 1.

Figure 1

Figure 1. Strap-down Inertial Navigation System (SINS) schematic diagram.

The horizontal position estimation here is virtually accomplished through the update of ${\mathit{C}}_e^n$, which involves data regarding the latitude and longitude [15]; [48]. Table 1 indicates the definitions which apply to all symbols depicted in Figure 1.

Table 1

Table 1. Definitions of symbol in SINS algorithm.

The INS works discretely, and the IMU typically provides results for delta-angle $\mathrm{\Delta }{\tilde{\mathit{\theta }}}_{ib}^b$ and delta-velocity $\mathrm{\Delta }{\tilde{\mathit{v}}}_f^b$. Accordingly, we utilize discrete integration algorithms to convert these measurements into navigation quantities. The digital algorithm for velocity update can be written in a general format as Equation 1.

${\mathit{v}}_k^n={\mathit{v}}_{k-1}^n+\mathrm{\Delta }{\mathit{v}}_{f,k}^n+\mathrm{\Delta }{\mathit{v}}_{g/cor,k}^n(1)$

$\mathrm{\Delta }{\mathit{v}}_{g/cor,k}^n$ is the velocity increment due to the gravity and Coriolis force. $\mathrm{\Delta }{\mathit{v}}_{f,k}^n$ represents the velocity increment due to the specific force. They can be written respectively as Equation 2 and Equation 3.

$\mathrm{\Delta }{\mathit{v}}_{\mathit{g}/cor,k}^n\approx {\left[{\mathit{g}}^n-\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times {\mathit{v}}^n\right]}_{k-0.5}\mathrm{\Delta }{t}_k(2)$

$\mathrm{\Delta }{\mathit{v}}_{f,k}^n=\frac{1}{2}\left[{\mathit{C}}_{n\left(k-1\right)}^{n\left(k\right)}+\mathit{I}\right]{\mathit{C}}_{b\left(k-1\right)}^{n\left(k-1\right)}\mathrm{\Delta }{\mathit{v}}_{f,k}^{b\left(k-1\right)}(3)$

$\mathrm{\Delta }{\mathit{v}}_{f,k}^{b\left(k-1\right)}\approx \mathrm{\Delta }{\mathit{v}}_{f,k}^b+\frac{1}{2}\mathrm{\Delta }{\mathit{\theta }}_k\times \mathrm{\Delta }{\mathit{v}}_{f,k}^b+\frac{1}{12}\left(\mathrm{\Delta }{\mathit{\theta }}_{k-1}\times \mathrm{\Delta }{\mathit{v}}_{f,k}^b+\mathrm{\Delta }{\mathit{v}}_{f,k-1}^b\times \mathrm{\Delta }{\mathit{\theta }}_k\right)(4)$

where $\mathit{I}$ is an identity matrix. $b\left(k\right)$ and $n\left(k\right)$ denote the b-frame and n-frame at time $t_k$ in Equation 3. In Equation 4, $\frac{1}{2}\mathrm{\Delta }{\mathit{\theta }}_k\times \mathrm{\Delta }{\mathit{v}}_{f,k}^b$ is the rotation correction. $\frac{1}{12}\left(\mathrm{\Delta }{\mathit{\theta }}_{k-1}\times \mathrm{\Delta }{\mathit{v}}_{f,k}^b+\mathrm{\Delta }{\mathit{v}}_{f,k-1}^b\times \mathrm{\Delta }{\mathit{\theta }}_k\right)$ is sculling correction. These two parts are necessary, as concurrent integration of angular rate and linear acceleration is unattainable in a digital implementation.

The quaternion form is utilized to update the position, as shown in Equation 5, for the horizontal position (latitude and longitude) to prevent numerical integration errors. The height can be updated independently using Equation 6.

$\left\{\begin{array}{c}{\mathit{q}}_{n\left(k\right)}^{e\left(k-1\right)}={\mathit{q}}_{n\left(k-1\right)}^{e\left(k-1\right)}\ast {\mathit{q}}_{n\left(k\right)}^{n\left(k-1\right)}\hfill \\ {\mathit{q}}_{n\left(k\right)}^{e\left(k\right)}={\mathit{q}}_{e\left(k-1\right)}^{e\left(k\right)}\ast {\mathit{q}}_{n\left(k\right)}^{e\left(k-1\right)}\hfill \end{array}\right.(5)$

$h_k=h_{k-1}-v_{D,k-1/2}\mathrm{\Delta }{t}_k(6)$

The attitude quaternion update algorithm can be written as Equation 7.

$\left\{\begin{array}{c}{\mathit{q}}_{b\left(k\right)}^{n\left(k-1\right)}={\mathit{q}}_{b\left(k-1\right)}^{n\left(k-1\right)}\ast {\mathit{q}}_{b\left(k\right)}^{b\left(k-1\right)}\hfill \\ {\mathit{q}}_{b\left(k\right)}^{n\left(k\right)}={\mathit{q}}_{n\left(k-1\right)}^{n\left(k\right)}\ast {\mathit{q}}_{b\left(k\right)}^{n\left(k-1\right)}\hfill \end{array}\right.(7)$

where ${\mathit{q}}_{b\left(k\right)}^{b\left(k-1\right)}=\left[\begin{array}{c}\hfill \cos ‖0\cdot 5{\mathit{\varphi }}_k‖\hfill \\ \hfill \frac{\sin ‖0\cdot 5{\mathit{\varphi }}_k‖}{‖0\cdot 5{\mathit{\varphi }}_k‖}0\cdot 5{\mathit{\varphi }}_k\hfill \end{array}\right]$ and ${\mathit{\varphi }}_k$ is the b-frame rotation vector. ${\mathit{\varphi }}_k$ can be obtained by Equation 8, where $\frac{1}{12}\left(\mathrm{\Delta }{\mathit{\theta }}_{k-1}\times \mathrm{\Delta }{\mathit{\theta }}_k\right)$ is the second order coning correction term.

${\mathit{\varphi }}_k=\mathrm{\Delta }{\mathit{\theta }}_k+\frac{1}{12}\left(\mathrm{\Delta }{\mathit{\theta }}_{k-1}\times \mathrm{\Delta }{\mathit{\theta }}_k\right)(8)$

2.2 Common loosely coupled GNSS/INS architecture

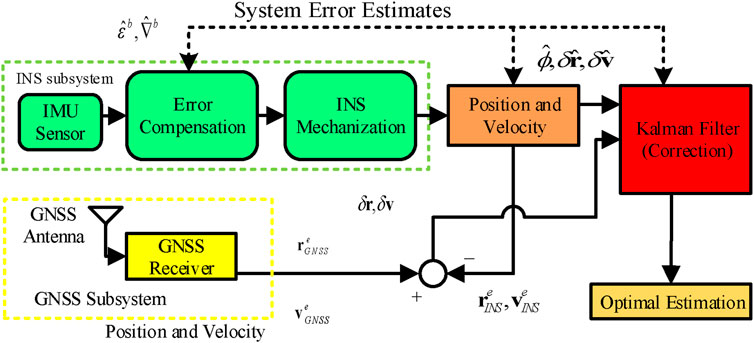
Figure 2 illustrates the architecture of the LC GNSS/INS system, where position and velocity outputs from the GNSS are fed into the Kalman filter to be fused with the inertial navigation data. In this system, the KF estimates error states (i.e., $\delta \mathit{x}$) rather than the states themselves (i.e., $\mathit{x}$), due to the nonlinear relationship between the system states and the measurements. The estimated states include both navigation variables (i.e., position, velocity, and attitude) and inertial sensor errors (i.e., bias and scale factor). To handle this nonlinearity, the centralized Kalman filter adopts a linearization technique, which corresponds to the Extended Kalman Filter (EKF).

Figure 2

Figure 2. The schematic of the LC GNSS/INS diagram.

2.2.1 System dynamics analysis model

A typical error state vector used in case of LC GNSS/INS architecture is shown in Equation 9.

$\mathit{\delta }{\mathit{x}}_{LC}={\left[\mathit{\varphi },\mathit{\delta }{\mathit{r}}^n,\mathit{\delta }{\mathit{v}}^n,{\mathit{\epsilon }}^b,{\mathbf{\nabla }}^b\right]}^{\text{T}}(9)$

where misalignment vector is denoted as $\mathit{\varphi }={\left[{\varphi }_N,{\varphi }_E,{\varphi }_D\right]}^{\text{T}}$. The position error vector and velocity error vector along the east, north and up directions are denoted as $\delta {\mathit{r}}^n={\left[\delta r_N,\delta r_E,\delta r_D\right]}^{\text{T}}$ and $\delta {\mathit{v}}^n={\left[\delta v_N,\delta v_E,\delta v_D\right]}^{\text{T}}$, respectively. Moreover, the gyro and accelerometer measurement biases along each sensing axis in the b-frame are represented by ${\mathit{\epsilon }}^b={\left[{\epsilon }_X,{\epsilon }_Y,{\epsilon }_Z\right]}^{\text{T}}$ and ${\mathbf{\nabla }}^b={\left[{\nabla }_X,{\nabla }_Y,{\nabla }_Z\right]}^{\text{T}}$, correspondingly. The error state dynamic model (i.e., INS error model) can be derived as Equation 10.

$\left\{\begin{array}{c}\delta {\dot{\mathit{r}}}^n=\delta {\mathit{r}}^n\times \left(-{\mathit{\omega }}_{en}^n\right)+\delta {\mathit{v}}^n\hfill \\ \delta {\dot{\mathit{v}}}^n={\mathit{C}}_b^n{\mathit{f}}^b\times \mathit{\varphi }-\left(2{\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n\right)\times \delta {\mathit{v}}^n-\left(2\delta {\mathit{\omega }}_{ie}^n+\delta {\mathit{\omega }}_{in}^n\right)\hfill \\ \times {\mathit{v}}^n+\delta {\mathit{g}}^n+{\mathit{C}}_b^n\mathbf{\nabla }b\hfill \\ \dot{\mathit{\varphi }}=-{\mathit{\omega }}_{in}^n\times \mathit{\varphi }+\delta {\mathit{\omega }}_{in}^n-{\mathit{C}}_b^n{\mathit{\epsilon }}^b\hfill \\ {\dot{\mathit{\epsilon }}}^b=-\frac{1}{T_{\epsilon }}{\mathit{\epsilon }}^b+{\mathit{\zeta }}_{\epsilon }\hfill \\ {\dot{\mathbf{\nabla }}}^b=-\frac{1}{T_{\nabla }}{\mathbf{\nabla }}^b+{\mathit{\zeta }}_{\nabla }\hfill \end{array}\right.(10)$

where ${\mathit{\omega }}_{ie}^n$ denotes the turn rate of the Earth resolved in n-frame. The transport rate ${\mathit{\omega }}_{en}^n$ represents the turn rate of n-frame with respect to e-frame and ${\mathit{\omega }}_{in}^n={\mathit{\omega }}_{ie}^n+{\mathit{\omega }}_{en}^n$. The e-frame is a geocentric coordinate system whose origin is at the Earth’s center of mass. Its axes are defined as follows: Z-axis: aligned with the Earth’s mean rotation axis, pointing toward the conventional terrestrial North Pole. X-axis: points from the Earth’s center to the intersection of the equator and the prime meridian (0°longitude, Greenwich). Y-axis: completes the right-handed system, pointing to 90°East longitude along the equator. Unlike the inertial frame, the Earth-Centered, Earth-Fixed (ECEF) frame rotates with the Earth, so it is fixed relative to positions on the Earth’s surface. ${\mathit{C}}_b^n$ is the transformation matrix from b-frame to n-frame. The error vectors are $\delta {\mathit{\omega }}_{ie}^n$ and $\delta {\mathit{\omega }}_{en}^n$. The gravity error $\delta {\mathit{g}}^n$, can be expressed as the function of the position error $\delta {\mathit{r}}^n$, velocity error $\delta {\mathit{v}}^n$, and misalignment $\mathit{\varphi }$; ${\mathit{\omega }}_{ib}^b$ and ${\mathit{f}}^b$ represent the angular rate and specific force measured by gyros and accelerometers; $T_{\epsilon }$ and $T_{\nabla }$ are the correlation time of gyros and accelerometers, while ${\mathit{\zeta }}_{\epsilon }$ and ${\mathit{\zeta }}_{\nabla }$ are the driven noises, whose parameters can be determined by the Allan variance analysis or simply found in the IMU technical specifications. The system dynamic model, as represented by Equation 10, can be expressed in matrix form as Equation 11.

$\delta {\dot{\mathit{x}}}_k={\mathit{F}}_{SINS}\cdot \delta {\mathit{x}}_k+{\mathit{G}}_{SINS}\cdot {\mathit{\zeta }}_k(11)$

where $\delta {\mathit{x}}_k$ is the INS error state vector at the $k$th discrete time instant; ${\mathit{\zeta }}_k={\left[{\mathit{\zeta }}_{\epsilon }^T,{\mathit{\zeta }}_{\epsilon }^{\nabla }\right]}^{\text{T}}$ is the process noise, which assumes ${\mathit{\zeta }}_k\sim \mathit{N}\left(\mathit{0},{\mathit{Q}}_k\right)$; ${\mathit{F}}_{SINS}$ is the system dynamics matrix, which can be used to obtain the state transition matrix ${\mathbf{\Phi }}_{k,k-1}$ for small time interval $\left[t_{k-1},t_k\right]$ which can be expressed as ${\mathbf{\Phi }}_{k,k-1}=e^{\mathit{F}\cdot \left(t_k-t_{k-1}\right)}$. ${\mathit{G}}_{SINS}$ is the design matrix that relates the error states with noise sources.

2.2.2 Measurement model

The LC GNSS/INS utilizes the GNSS receiver-derived position and velocity (denoted as ${\mathit{r}}_k^{GNSS}$ and ${\mathit{v}}_k^{GNSS}$, respectively) as the reference values, which are subsequently compared with the INS outputs (denoted as ${\mathit{r}}_k^{IMU}$ and ${\mathit{v}}_k^{IMU}$) to estimate navigation errors and biases in inertial sensors. To this end, we employ an EKF wherein the differences between the reference values and the INS outputs are utilized as inputs. At time instant $k$, the EKF measurement $\delta {\mathit{z}}_k^{LC}$ can be expressed as Equation 12.

$\delta {\mathit{z}}_k^{LC}=\left(\begin{array}{c}\hfill \delta {\mathit{z}}_r\hfill \\ \hfill \delta {\mathit{z}}_v\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathit{r}}_k^{IMU}-{\mathit{r}}_k^{GNSS}\hfill \\ \hfill {\mathit{v}}_k^{IMU}-{\mathit{v}}_k^{GNSS}\hfill \end{array}\right)(12)$

As shown in Figure 3, GNSS antenna and IMU are fixed at different positions, forming the lever-arm vector ${\mathit{\ell }}^b$ from IMU center to GNSS phase center. The measurement model is derived as Equation 13 with the lever-arm effect corrections. In Figure 3b, the final GNSS lever arm vector for this vehicle is [1.00, 0.50, 0.80] (m).

$\delta {\mathit{z}}_k^{LC}={\mathit{H}}_k^{LC}\cdot \delta {\mathit{x}}_k+{\mathit{e}}_{LC}(13)$

where ${\mathit{e}}_{LC}={\left({\mathit{e}}_r,{\mathit{e}}_v\right)}^{\text{T}}$ denotes the GNSS position and velocity noises with covariance matrix $E\left[{\left({\mathit{e}}_{ri}^{\text{T}},{\mathit{e}}_{vi}^{\text{T}}\right)}^{\text{T}}\cdot \left({\mathit{e}}_{rk}^{\text{T}},{\mathit{e}}_{vk}^{\text{T}}\right)\right]={\mathit{R}}_k{\delta }_{ik}$. ${\delta }_{ik}$ denotes the Kronecker Delta function, $\delta {\mathit{z}}_k^{LC}$ is measurement vector and ${\mathit{H}}_k^{LC}$ is the design matrix.

$\delta {\mathit{z}}_k^{LC}=\left(\begin{array}{c}\hfill \delta {\mathit{z}}_r\hfill \\ \hfill \delta {\mathit{z}}_v\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathit{r}}_{IMU}^n-{\mathit{r}}_{GNSS}^n+{\mathit{C}}_b^n{\mathit{\ell }}^b\hfill \\ \hfill {\mathit{v}}_{IMU}^n-{\mathit{v}}_{GNSS}^n-\left({\mathit{\omega }}_{in}^n\times \right){\mathit{C}}_b^n{\mathit{\ell }}^b-{\mathit{C}}_b^n\left({\mathit{\ell }}^b\times \right){\mathit{\omega }}_{ib}^b\hfill \end{array}\right)(14)$

${\mathit{H}}_k^{LC}=\left(\begin{array}{ccccc}\hfill {\mathit{I}}_{3\times 3}\hfill & \hfill {\mathbf{0}}_{3\times 3}\hfill & \hfill \left({\mathit{C}}_b^n{\mathit{\ell }}^b\right)\times \hfill & \hfill {\mathbf{0}}_{3\times 3}\hfill & \hfill {\mathbf{0}}_{3\times 3}\hfill \\ \hfill {\mathbf{0}}_{3\times 3}\hfill & \hfill {\mathit{I}}_{3\times 3}\hfill & \hfill -\left[\begin{array}{c}\hfill \left({\mathit{\omega }}_{in}^n\times \right)\left({\mathit{C}}_b^n{\mathit{\ell }}^b\times \right)\hfill \\ \hfill +{\mathit{C}}_b^n\left({\mathit{\ell }}^b\times {\mathit{\omega }}_{ib}^b\right)\times \hfill \end{array}\right]\hfill & \hfill -{\mathit{C}}_b^n\left({\mathit{\ell }}^b\times \right)\hfill & \hfill {\mathbf{0}}_{3\times 3}\hfill \end{array}\right)(15)$

Figure 3

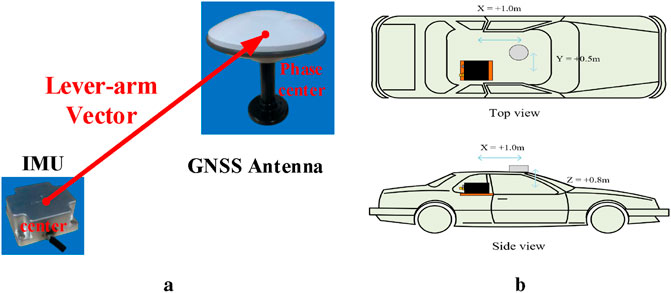
Figure 3. The lever-arm vector description. (a) The lever-arm vector ${\mathit{\ell }}^b$ from IMU center to GNSS phase center. (b) Description with vehicles.

2.2.3 Kalman filter

The state-space model for LC GNSS/INS can be expressed more straightforward in a simpler linear form shown in Equation 16.

$\delta {\mathit{x}}_k={\mathbf{\Phi }}_{k,k-1}\delta {\mathit{x}}_{k-1}+{\mathbf{\Gamma }}_{k,k-1}{\mathit{\zeta }}_{k-1}(16)$

$\delta {\mathit{z}}_k={\mathit{H}}_k\delta {\mathit{x}}_k+{\mathit{e}}_k(17)$

Assuming the state-space model is exact and the measurement noises follow a zero-mean Gaussian distribution, it is possible to solve Equations 16, 17 through standard KF. This approach is based on optimizing the objective function formulated in Equation 18.

$\delta {\mathit{x}}_k^{+}=\mathrm{arg\; min}\left({‖\delta {\mathit{x}}_k-\delta {\mathit{x}}_k^{-}‖}_{{\left({\mathit{P}}_k^{-}\right)}^{-1}}^2+{‖{\mathit{H}}_k\delta {\mathit{x}}_k-\delta {\mathit{z}}_k‖}_{{\mathit{R}}_k^{-1}}^2\right)(18)$

where ${‖\delta \mathit{x}‖}_A^2\delta {\mathit{x}}^{\text{T}}\cdot \mathit{A}\cdot \delta \mathit{x}$ is the estimated state before measurement update. $\delta {\mathit{x}}_k^{-}$ and $\delta {\mathit{x}}_k^{+}$ is the estimated state after measurement update. ${\mathit{P}}_k^{-}$ is the covariance matrix of the predicted state. We define ${\mathbf{\Lambda }}_{X_k^{-}}={\left({\mathit{P}}_k^{-}\right)}^{-\frac{1}{2}}\left(\delta {\mathit{x}}_k-\delta {{\mathit{x}}_k}^{-}\right)$ and ${\mathbf{\Lambda }}_k={\mathit{R}}_k^{-\frac{1}{2}}\left({\mathit{H}}_k\delta {\mathit{x}}_k-\delta {\mathit{z}}_k\right)$, then Equation 19 is obtained.

${\mathit{x}}_k^{+}=\mathrm{arg\; min}\left({\mathbf{\Lambda }}_{X_k^{-}}^{\text{T}}{\left({\mathit{P}}_k^{-}\right)}^{-1}{\mathbf{\Lambda }}_{X_k^{-}}+{\mathbf{\Lambda }}_k^{\text{T}}{\mathit{R}}_k^{-1}{\mathbf{\Lambda }}_k\right)(19)$

The solution of standard KF (i.e., optimal estimates of navigation errors and inertial sensor biases) is obtained by solving this least-square problem. However, it is important to note that this solution is highly sensitive to model errors. Therefore, in the LC GNSS/INS system, a standard KF is utilized, as illustrated in Figure 4.

Figure 4

Figure 4. The standard EKF applied in LC GNSS/INS.

2.3 Common tigtly coupled GNSS/INS architecture

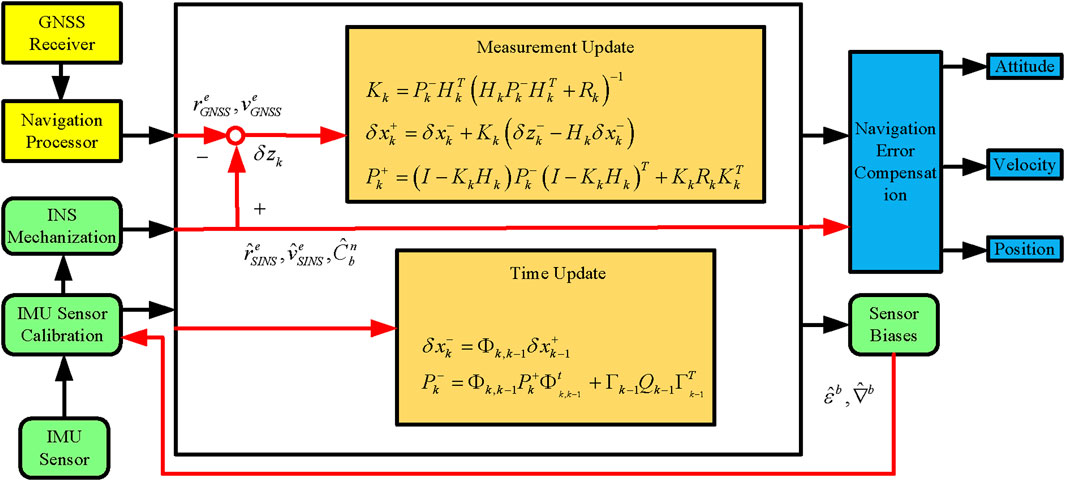
Unlike conventional LC integration, the TC model utilizes raw GNSS observations such as pseudorange, doppler shift, carrier-phase, instead of relying on GNSS solutions such as position and velocity. This approach enables more comprehensive data fusion. Figure 5 presents the structure of the TC GNSS/INS algorithm. and highlights the differences between LC and TC in the yellow dashed box.

Figure 5

Figure 5. The schematic of the LC GNSS/INS diagram.

2.3.1 System dynamics analysis model

In the TC system model, GNSS-related error states $\delta {\mathit{x}}_{GNSS}$ (e.g., receiver clock offset $\delta \left(c\delta t_{Offset}\right)$ and clock drift $\delta \left(c\delta t_{Drift}\right)$) should also be included in the filter error state $\delta \mathit{x}$, apart from the error states $\delta {\mathit{x}}_{SINS}$ related to SINS. $\delta {\mathit{x}}_{SINS}$ is the same as $\delta {\mathit{x}}_{LC}$, which depicts the dynamics of INS error. Moreover, there is no direct interaction between GNSS and SINS error states, while they are actually related by the measurement model. Therefore, the system model for GNSS/MEMS-SINS TC integrated navigation can be represented as Equation 20.

$\delta \dot{\mathit{x}}=\left(\begin{array}{c}\hfill \delta {\dot{\mathit{x}}}_{SINS}\hfill \\ \hfill \delta {\dot{\mathit{x}}}_{GNSS}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill {\mathit{F}}_{SINS}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{F}}_{GNSS}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \delta {\mathit{x}}_{SINS}\hfill \\ \hfill \delta {\mathit{x}}_{GNSS}\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill {\mathit{G}}_{GNSS}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathit{G}}_{GNSS}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathit{\zeta }}_{SINS}\hfill \\ \hfill {\mathit{\zeta }}_{GNSS}\hfill \end{array}\right)(20)$

where $\delta {\mathit{x}}_{SINS}={\left[\mathit{\varphi },\delta {\mathit{r}}^n,\delta {\mathit{v}}^n,{\mathit{\epsilon }}^b,{\mathbf{\nabla }}^b\right]}^{\text{T}}$ denotes the SINS error state vector and $\delta {\mathit{x}}_{GNSS}={\left[\delta \left(c\delta t_{Offset}\right),\delta \left(c\delta t_{Drift}\right)\right]}^{\text{T}}$ is the GNSS error state vector. ${\mathit{F}}_{SINS}$ and ${\mathit{F}}_{GNSS}$ are the state transition matrixs; ${\mathit{\zeta }}_{SINS}$ and ${\mathit{\zeta }}_{GNSS}$ are the process noise vectors with the covariance matrix ${\mathit{Q}}_{SINS}$ and ${\mathit{Q}}_{GNSS}$, respectively. The difference between LC and TC models is the dynamics for receiver clock errors. Clock offset and drift are established according to Equation 21.

$\left\{\begin{array}{c}\delta \left(c\dot{\delta }{t}_{Offset}\right)=\delta \left(c\delta t_{Drift}\right)+{\eta }_{Offset}\hfill \\ \delta \left(c\dot{\delta }{t}_{Drift}\right)={\eta }_{Drift}\hfill \end{array}\right.(21)$

where $c\delta t_{Offset}$ is the receiver clock offset. $c\delta t_{Drift}$ is the clock drift. Given the above modeling, ${\mathit{F}}_{SINS}$, ${\mathit{G}}_{GNSS}$, and ${\mathit{\zeta }}_{GNSS}$ can be given by Equation 22.

${\mathit{F}}_{GNSS}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],{\mathit{G}}_{GNSS}=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\mathit{\zeta }}_{GNSS}=\left[\begin{array}{c}\hfill {\eta }_{Offset}\hfill \\ \hfill {\eta }_{Drift}\hfill \end{array}\right](22)$

where ${\eta }_{Offset}$ set denotes the driven noise of clock offset with the spectral density $q_{Offset}=h_0{c}^2/2$. ${\eta }_{Drift}$ is the driven noise of clock drift with the spectral density $q_{Drift}=c^2\cdot 2{\pi }^2\cdot h_{-2}$. $h_0$ and $h_{-2}$ are the Allan variance parameters for the clock error and their typical values are $2.0\times 10^{-19}$ and $2.0\times 10^{-20}$.

2.3.2 Measurement model

The TC GNSS/INS integration method utilizes raw observations such as pseudorange ${\tilde{\rho }}_{GNSS}^{\left(n\right)}$ and doppler $\tilde{\cdot }{\rho }_{GNSS}^{\left(n\right)}$ obtained from the GNSS receiver as a reference. The differences between these raw observations, the computed pseudoranges ${\widehat{\rho }}_{SINS}^{\left(n\right)}$, pseudorange rates $\widehat{\cdot }{\rho }_{SINS}^{\left(n\right)}$ from the INS algorithm’s estimated position and velocity of the user are used as inputs to an EKF. The EKF is used to estimate the navigation errors and inertial sensors’ biases. The KF measurement at time instant $k$ can be expressed as Equation 23.

$\delta {\mathit{z}}_k^{TC}=\left(\begin{array}{c}\hfill \delta {\mathit{z}}_p\hfill \\ \hfill \delta {\mathit{z}}_{\dot{p}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\left(\begin{array}{cccc}\hfill {\widehat{\rho }\widehat{\rho }}_{SINS}^{\left(1\right)}-{\widehat{\rho }}_{GNSS}^{\left(1\right)}\hfill & \hfill {\widehat{\rho }}_{SINS}^{\left(2\right)}-{\widehat{\rho }}_{GNSS}^{\left(2\right)}\hfill & \hfill \cdot \cdot \cdot \hfill & \hfill {\widehat{\rho }}_{SINS}^{\left(m\right)}-{\widehat{\rho }}_{GNSS}^{\left(m\right)}\hfill \end{array}\right)}^{\text{T}}\hfill \\ \hfill {\left(\begin{array}{cccc}\hfill \widehat{\cdot }{\rho }_{SINS}^{\left(1\right)}-\widehat{\cdot }{\rho }_{GNSS}^{\left(1\right)}\hfill & \hfill \widehat{\cdot }{\rho }_{SINS}^{\left(2\right)}-\widehat{\cdot }{\rho }_{GNSS}^{\left(2\right)}\hfill & \hfill \cdot \cdot \cdot \hfill & \hfill \widehat{\cdot }{\rho }_{SINS}^{\left(m\right)}-\widehat{\cdot }{\rho }_{GNSS}^{\left(m\right)}\hfill \end{array}\right)}^{\text{T}}\hfill \end{array}\right)(23)$

where $\delta z_{\rho }$ and $\delta z_{\dot{\rho }}$ represent pseudorange and doppler KF measurements, respectively; m denotes the number of the visible satellites. For the raw observations of the $n$th GNSS satellite, systematic error corrections are needed.

$\left\{\begin{array}{c}{\tilde{\rho }}_{GNSS}^{\left(n\right)}={\rho }^{\left(n\right)}+c\delta t^{\left(n\right)}-I^{\left(n\right)}-T\left(n\right)\hfill \\ \tilde{\cdot }{\rho }_{GNSS}^{\left(n\right)}={\dot{\rho }}^{\left(n\right)}+\delta f^{\left(n\right)}\hfill \end{array}\right.(24)$

where ${\tilde{\rho }}_{GNSS}^{\left(n\right)}$ and $\tilde{\cdot }{\rho }_{GNSS}^{\left(n\right)}$ are the corrected pseudorange and doppler measurements at GNSS antenna phase center, respectively; ${\rho }^{\left(n\right)}$ and ${\dot{\rho }}^{\left(n\right)}$ are the raw pseudorange and doppler measurements, $n=\mathrm{1,2},\dots ,m$. $c\delta t^{\left(n\right)}$, $\delta f^{\left(n\right)}$, $I^{\left(n\right)}$, and $T^{\left(n\right)}$ are the corrections for satellite clock offset, satellite clock drift, ionosphere propagation errors, and troposphere propagation errors, respectively, which can be obtained from the broadcasted GNSS ephemeris. The corresponding predicted pseudorange and doppler from the user’s position and velocity estimated by INS algorithm are expressed in Equation 25.

$\left\{\begin{array}{c}{\widehat{\rho }}_{GNSS}^{\left(n\right)}=\sqrt{{\left({\mathit{r}}^{\left(n\right)}-{\mathit{r}}_{GNSS}\right)}^{\text{T}}\left({\mathit{r}}^{\left(n\right)}-{\mathit{r}}_{GNSS}\right)}+c\delta t_{Offset}\hfill \\ \widehat{\cdot }{\rho }_{SINS}^{\left(n\right)}=\left({\mathit{v}}^{\left(n\right)}-{\mathit{v}}_{GNSS}\right){\mathit{u}}^{\left(n\right)}+c\delta t_{Drift}\hfill \end{array}\right.(25)$

where ${\mathit{r}}^{\left(n\right)}$ and ${\mathit{v}}^{\left(n\right)}$ are the position and velocity of the $n$th satellite at the time of GNSS signal transmission, calculated from GNSS ephemeris; ${\mathit{r}}_{GNSS}$ and ${\mathit{v}}_{GNSS}$ are the position and velocity of the GNSS antenna at the time of signal arrival, calculated from SINS outputs; the line-of-sight (LOS) vector is ${\mathit{u}}^{\left(n\right)}=-\left({\mathit{r}}^{\left(n\right)}-{\mathit{r}}_{GNSS}\right)/‖\left({\mathit{r}}^{\left(n\right)}-{\mathit{r}}_{GNSS}\right)‖$. The GNSS antenna center ${\mathit{r}}_{\mathit{GNSS}}$ and the IMU measurement center ${\mathit{r}}_{\mathit{SINS}}$, which need lever-arm effect correction, are usually different position shown in Figure 3. The INS-derived position and velocity at the GNSS antenna center are obtained by Equation 26.

$\left\{\begin{array}{c}{\mathit{r}}_{\mathit{GNSS}}={\mathit{r}}_{SINS}+{\mathit{C}}_b^n{\mathit{\ell }}^b\hfill \\ {\mathit{v}}_{GNSS}={\mathit{v}}_{SINS}-\left({\mathit{\omega }}_{in}^n\times \right){\mathit{C}}_b^n{\mathit{\ell }}^b-{\mathit{C}}_b^n\left({\mathit{\ell }}^b\times \right){\mathit{\omega }}_{ib}^b\hfill \end{array}\right.(26)$

To obtain Equation 27, substitute Equation 26 into Equation 25 and perform Taylor series expansion.

$\left\{\begin{array}{c}{\widehat{\rho }}_{SINS}^{\left(n\right)}-{\rho }_{GNSS}^{\left(n\right)}=-{\mathit{u}}^{\left(n\right)}{\mathit{C}}_n^e\delta {\mathit{r}}^n+\delta \left(c\delta t_{Offset}\right)+e_{\rho }^{\left(n\right)}\hfill \\ \widehat{\cdot }{\rho }_{SINS}^{\left(n\right)}-\tilde{\cdot }{\rho }_{GNSS}^{\left(n\right)}=-{\mathit{u}}^{\left(n\right)}{\mathit{C}}_n^e\delta {\mathit{v}}^n+\delta \left(c\delta t_{Drift}\right)+e_{\dot{\rho }}^{\left(n\right)}\hfill \end{array}\right.(27)$

Then, Equation 27 can be written in the matrix form as expressed in Equation 28.

$\delta {\mathit{z}}_k^{TC}={\mathit{H}}_k^{TC}\cdot \delta {\mathit{x}}_k+{\mathit{e}}_k^{TC}(28)$

where ${\mathit{e}}_k^{TC}={\left(e_{\rho }^{\left(1\right)} \cdots e_{\rho }^{\left(m\right)}{e}_{\dot{\rho }}^{\left(1\right)} \cdots e_{\dot{\rho }}^{\left(m\right)}\right)}^{\text{T}}$ denotes the observation noises vector; the measurement design matrix ${\mathit{H}}_k^{TC}$ is written in Equation 29.

${\mathit{H}}_k^{TC}=\left(\begin{array}{ccccc}\hfill -{\mathit{u}}^{\left(1\right)}{\mathit{C}}_n^e\hfill & \hfill {\mathbf{0}}_{1\times 3}\hfill & \hfill {\mathbf{0}}_{1\times 9}\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill -{\mathit{u}}^{\left(m\right)}{\mathit{C}}_n^e\hfill & \hfill {\mathbf{0}}_{1\times 3}\hfill & \hfill {\mathbf{0}}_{1\times 9}\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill {\mathbf{0}}_{1\times 3}\hfill & \hfill -{\mathit{u}}^{\left(1\right)}{\mathit{C}}_n^e\hfill & \hfill {\mathbf{0}}_{1\times 9}\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mathbf{0}}_{1\times 3}\hfill & \hfill -{\mathit{u}}^{\left(m\right)}{\mathit{C}}_n^e\hfill & \hfill {\mathbf{0}}_{1\times 9}\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)(29)$

Based on the preceding derivations, it is evident that the Tightly Coupled (TC) GNSS/INS integration method outperforms the Loosely Coupled (LC) approach in several key areas. Firstly, the TC framework implicitly accounts for variations in satellite geometry through the measurement model, effectively incorporating the effects of Position Dilution of Precision (PDoP). This provides the TC system with greater robustness against unfavorable satellite configurations. Secondly, TC integration maintains the ability to provide continuous navigation support even when fewer than four satellites are visible, which is a critical advantage in challenging environments. Nevertheless, a limitation of the traditional TC approach is its inherent vulnerability to GNSS measurement outliers, as it lacks built-in mechanisms to reject or mitigate such anomalies.

3 Evaluation: performance and computational complexity

This section is dedicated to evaluating and contrasting the performance and computational burden of LC and TC GNSS/INS integration strategies. To facilitate this comparison, our team developed an outdoor pre-experiment platform, which enabled us to assess and validate both approaches. Some initial experimental results, accompanied by a brief analysis, have already been presented. In the subsequent content, a deeper investigation of the pre-experiment is conducted to identify the potential causes of HI GNSS/INS anomalies.

3.1 Performance comparison

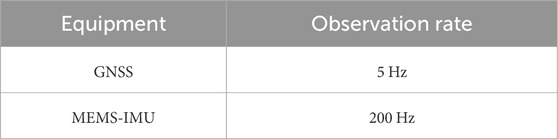
The pre-experiment was carried out on the campus of Peking University (PKU) in Beijing, China. As shown in Figure 6, the Programmable Logic (PL) of ZynqⓇ SoC is used for GNSS baseband signal processing and MEMS-IMU data collection. While GNSS positioning algorithm, INS mechanization and ESKF are implemented with Processing System (PS) of the chip. Table 2 gives the observation rate of GNSS receiver and MEMS-IMU. In Figure 7a, we designed and assembled a dedicated experimental system. The GNSS/MEMS-IMU navigation unit (blue component) executes both LC and TC algorithms independently under identical environmental conditions to derive their respective position outputs. Since the performance of the IMU plays a crucial role in the positioning accuracy of GNSS/INS integration, we include detailed specifications of the MEMS-IMU employed in the test. These specifications are summarized in Table 3. Additionally, a u-blox F9P receiver was utilized to capture high-precision position data, serving as the ground truth reference.

Figure 6

Figure 6. The details of the equipment used.

Table 2

Table 2. The observation rate of MEMS-IMU and GNSS receiver in pre-experiment.

Figure 7

Figure 7. Experiment description. (a) Experiment setup. (b) Planned trajectories.

Table 3

Table 3. Specifications of MEMS-IMU in pre-experiment.

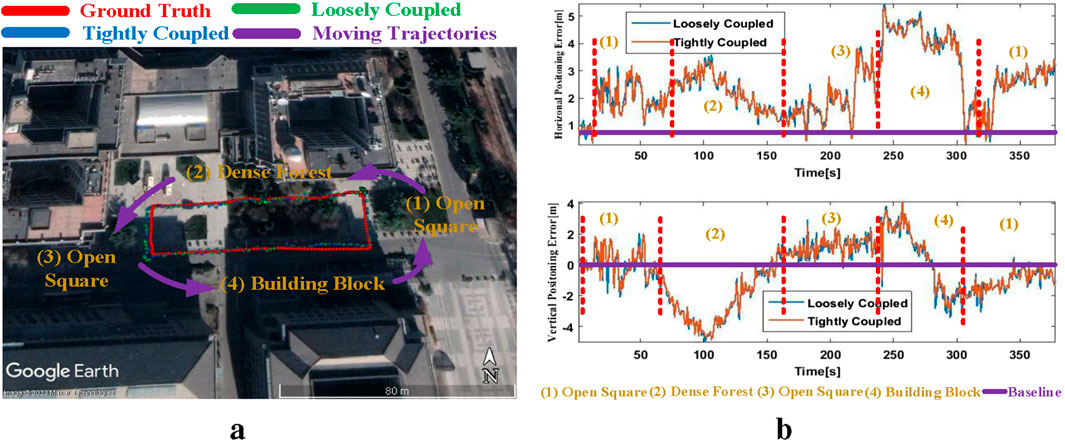
As illustrated in Figure 7b, the receiver travels from Area One to Area Two, corresponding to an open square and dense forest. This route allows for the assessment of positioning performance under varying GNSS signal conditions. The resulting trajectories are visualized using Google Earth. Figure 8a presents the movement paths derived from the receiver shown in Figure 7a. Figure 8b depicts the horizontal and vertical position errors, clearly indicating that dense vegetation and surrounding buildings negatively affect positioning accuracy. The trajectory in Figure 8a reveals that the receiver traverses four distinct environments, eventually forming a closed-loop path. These four regions and their corresponding baselines are approximately marked in Figure 8b. It is evident that both LC and TC achieve lower positioning errors in the open square (1) and open square (3), confirming that the quality of GNSS signals has a direct influence on accuracy. This further highlights that LC performs more reliably when signal conditions are favorable.

Figure 8

Figure 8. Experiment description. (a) Trajectories shown on Google Earth. (b) Position errors.

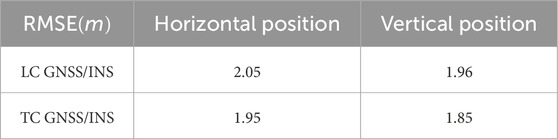
To quantitatively assess this impact, we adopted the Root Mean Square Error (RMSE) as the evaluation metric. As defined in Equation 30, RMSE is commonly utilized to measure the discrepancy between the observed position $P_{obs}$ and the ground truth $P_{gt}$. The results presented in Table 4 show that the RMSE of TC GNSS/INS is lower than that of LC GNSS/INS, suggesting that the TC approach achieves superior positioning accuracy.

Table 4

Table 4. RMSE analysis of position error.

$\text{RMSE}=\sqrt{\frac{1}{m}{\displaystyle \sum _{i-1}^m}{\left(P_{obs}-P_{gt}\right)}^2}(30)$

The results of this pre-experiment demonstrate that both LC and TC methods exhibit a significant improvement in positioning accuracy when operating in environments with strong GNSS signals, such as open squares. Under practical conditions, the positioning error of TC GNSS/INS in these areas is observed to be smaller than that of LC GNSS/INS. This finding indicates that LC is capable of delivering high-precision positioning when GNSS signal conditions are favorable. Moreover, the comparative analysis between LC and TC suggests that LC remains a dependable solution for real-world navigation tasks in scenarios where signal quality is sufficient. Hence, it can be concluded that the quality of GNSS signals is a decisive factor in achieving reliable and accurate navigation.

3.2 Computational complexity evaluation

The results of the pre-experiment reveal that GNSS signal quality plays a pivotal role in the performance of both LC and TC systems in real-world scenarios. TC exhibits greater robustness under varying signal conditions, while LC is capable of achieving acceptable positioning accuracy when GNSS signals remain strong and stable. Notably, TC leverages Kalman filtering for more sophisticated GNSS data processing, which enhances accuracy but also introduces higher computational costs. In contrast, LC features a straightforward structure and ease of implementation, making it highly practical for resource-constrained applications. Against this backdrop, this study aims to investigate the potential advantages of combining the complementary features of LC and TC. Before delving into the integration strategy, it is essential to first analyze and compare the computational complexity of the LC and TC frameworks, as presented in the following part.

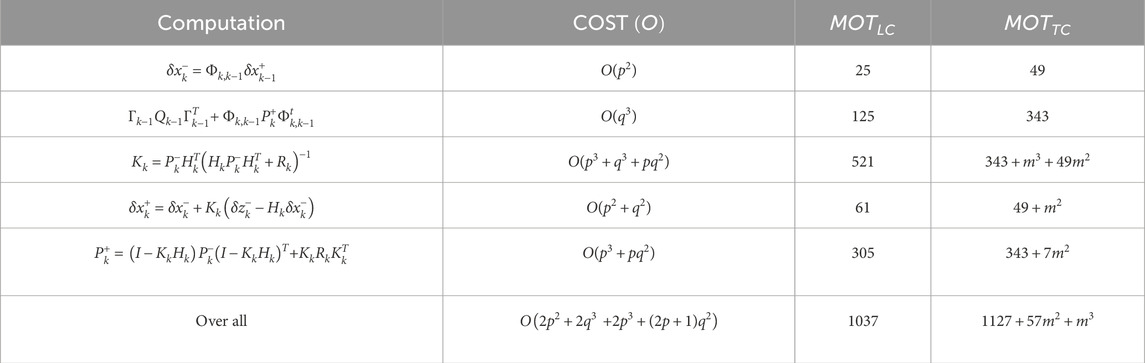
The computational complexity of the KF correlates with the dimensions of the state $p$ and the dimensions of the measurement $q$, respectively. $m$ is the value of NoS. For LC, the dimensions of the state of the KF $p_{LC}$ is 5 and the dimensions of the measurement of the KF $q_{LC}$ is 6 (according to Equation 9; Equation 12). For TC, the dimensions of the state of the KF $p_{TC}$ is 7 and the dimensions of the measurement of the KF $q_{TC}$ is $2m(m\ge 4)$ (according to Equation 20; Equation 21; Equation 23; Equation 24). Table 5 presents a quantitative comparison of the computational complexity associated with the Kalman Filter in both LC and TC GNSS/INS systems. Notation $O$ is commonly used to express the worst-case time complexity of an algorithm. It is the longest time it takes for an algorithm to execute under the worst-case scenario. $MO{T}_{LC}$ and $MO{T}_{TC}$ represents the multiplication operations times (MOT) of KF in LC and TC, respectively.

Table 5

Table 5. Computational complexity analysis of Kalman filter in LC and TC.

The over all COST $\left(O\right)$ of the computational complexity of the KF is $O(2p^2+2q^3+2p^3+(2p+1)q^2)$. A more detailed observation of satellite signals using the Kalman Filter leads to increased computational complexity, especially when incorporating the expanded state variables in the TC framework. The exact multiplication operation times (MOT) for both LC and TC can be explicitly computed. For instance, the $MO{T}_{TC}=3984$ when $m=4$, which is significantly higher than $MO{T}_{LC}=1037$. As a result, LC demonstrates a clear advantage over TC in terms of computational efficiency. From the complexity analysis, it is evident that LC significantly outperforms TC in terms of computational load, while still maintaining satisfactory positioning accuracy under favorable GNSS signal conditions. The pre-experiment has comparatively evaluated both LC and TC with respect to positioning performance and computational complexity, highlighting the respective strengths and limitations of each approach. Considering the critical role these methods play in engineering practice, a balanced evaluation between accuracy and efficiency is of great importance. Building upon the insights gained, this study introduces the HI GNSS/INS integration strategy.

4 Hybrid integration of GNSS/INS

4.1 Hybrid integration of GNSS/INS architecture

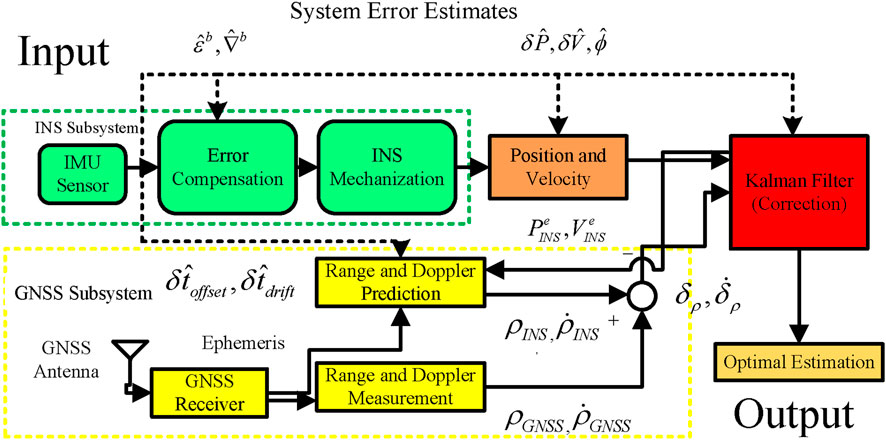
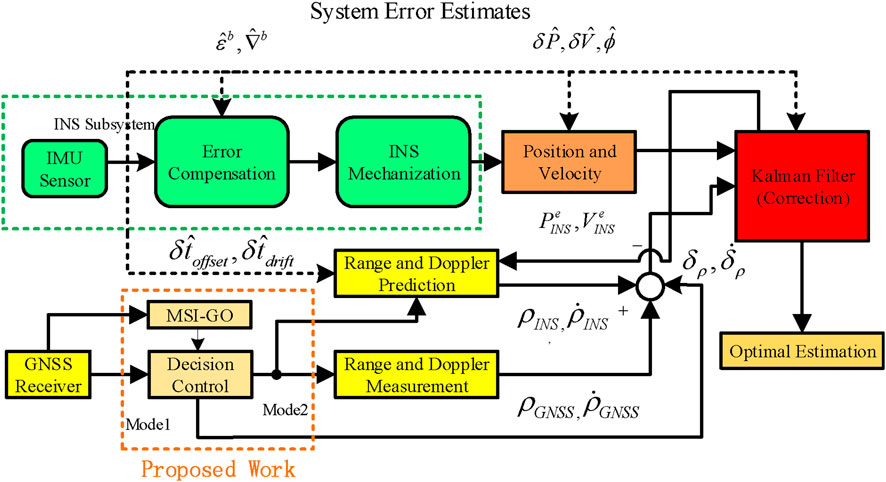
The HI GNSS/INS system leverages the strengths of both LC and TC approaches. By dynamically switching between positioning modes under the management of the MSI-GO, HI GNSS/INS achieves a balance between positioning accuracy and computational efficiency. As illustrated in Figure 9, the system architecture integrates both LC and TC modes. The components proposed in this study are highlighted within the brown dashed box in Figure 9.

Figure 9

Figure 9. The schematic of the HI GNSS/INS diagram.

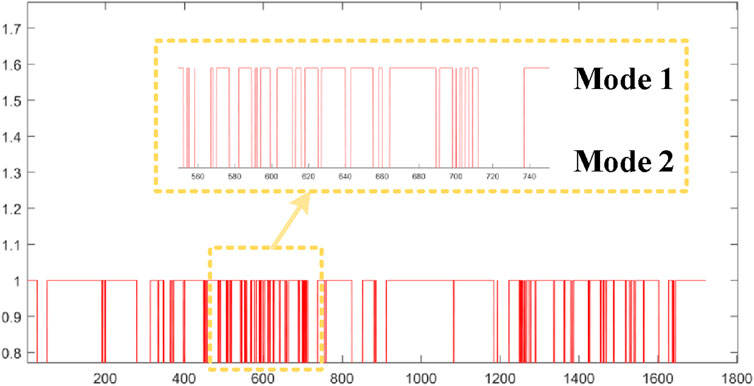
MSI-GO functions primarily as a mode selection mechanism, relying on Position Dilution of Precision (PDoP) and the Number of Satellites (NoS) as key indicators. The selection criteria are formulated based on the evaluation of position outputs and satellite observation data from both LC and TC modes over a specific time window. A detailed mathematical formulation of this process is provided in Section 4.2. The operational workflow of MSI-GO involves continuously monitoring GNSS signal conditions upon reception of satellite data, generating control signals, and subsequently determining the appropriate system mode. The output of MSI-GO is a decision matrix, denoted as $\mathit{D}$, where the value of 1 indicates that the system switches to TC mode, and the value of 0 corresponds to LC mode.

Although the overall architecture of the HI GNSS/INS system remains relatively straightforward, its key innovation lies in the integration of the MSI-GO module for intelligent mode selection. As such, it is crucial to conduct an in-depth investigation into two core aspects of the HI GNSS/INS framework: positioning accuracy and computational complexity. Initially, MSI-GO performs a quantitative evaluation of positioning accuracy and GNSS signal quality under both LC and TC modes to determine which modes meet predefined accuracy thresholds. This process ensures that the system maintains optimal positioning performance. Furthermore, if the LC mode meets the required accuracy standard, MSI-GO generates a control signal that prompts the system to operate in the LC combination mode. Given the previously analyzed computational complexity of LC and TC, this strategy enables the system to significantly reduce the computational complexity of the system. A comprehensive mathematical formulation of MSI-GO within the HI GNSS/INS system is presented in the subsequent section.

4.2 Multiple state inspection of GNSS observations (MSI-GO)

MSI-GO is primarily based on two observations: PDoP and NoS. The generation process of MSI-GO parameters ($\text{MSI}$-$\text{P}$) is described. The $\mathit{P}\mathit{D}\mathit{o}\mathit{P}$ and $\mathit{N}\mathit{o}\mathit{S}$ written as Equation 31 are data matrix of PDoP and NoS respectively.

$\left[\begin{array}{c}\hfill \mathit{P}\mathit{D}\mathit{o}\mathit{P}\hfill \\ \hfill \mathit{N}\mathit{o}\mathit{S}\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill PDo{P}_1\hfill & \hfill PDo{P}_2\hfill & \hfill \cdots \hfill & \hfill PDo{P}_M\hfill \\ \hfill No{S}_1\hfill & \hfill No{S}_2\hfill & \hfill \cdots \hfill & \hfill No{S}_M\hfill \end{array}\right](31)$

The ${\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{LC}$, ${\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{TC}$ and $\mathit{P}\mathit{o}{\mathit{s}}_{GT}$ are position results of LC, TC GNSS/INS and ground truth, respectively. These data are both measured. The decision matrix $\mathit{D}$ can be obtained based the function ${\mathit{f}}_{dec}$ given by Equation 32 and Equation 33.

$\mathit{D}={\mathit{f}}_{dec}\left({\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{LC},{\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{TC},\mathit{P}\mathit{o}{\mathit{s}}_{GT}\right)=\left\{\begin{array}{c}{D}_M=0,\frac{\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{Mea}^{LC}-\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{GT}}{\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{Mea}^{TC}-\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{GT}}<MS{I}_{Thr}\hfill \\ D_M=1,\frac{\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{Mea}^{LC}-\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{GT}}{\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{Mea}^{TC}-\mathit{P}\mathit{o}{{\mathit{s}}^{\left(M\right)}}_{GT}}\ge MS{I}_{Thr}\hfill \end{array}\right.(32)$

$\mathit{D}=\left[\begin{array}{cccc}\hfill D_1\hfill & \hfill D_2\hfill & \hfill \cdots \hfill & \hfill D_M\hfill \end{array}\right](33)$

where $M$ in Equation 31, Equation 32 and Equation 33 is the total number of epochs.

The $MS{I}_{Thr}$ plays a crucial role in ${\mathit{f}}_{dec}$ as it is a constant that effectively balances the precision and computational complexity. Specifically, a larger $MS{I}_{Thr}$ value enhances the precision, while a smaller $MS{I}_{Thr}$ value reduces the computational complexity. In practical applications, the value of $MS{I}_{Thr}$ can be adjusted according to the precision requirements of the position system. By substituting Equation 31 and Equation 33 into Equation 34, the resulting value of $\text{MSI}$-$\text{P}$ can be obtained.

$\begin{array}{c}\text{MSI}-\text{P}=\left[\begin{array}{c}\hfill PDo{P}_{MSI}\hfill \\ \hfill No{S}_{MSI}\hfill \end{array}\right]=\left(\left[\begin{array}{c}\hfill \mathit{P}\mathit{D}\mathit{o}\mathit{P}\hfill \\ \hfill \mathit{N}\mathit{o}\mathit{S}\hfill \end{array}\right]\cdot {\mathit{D}}^{\mathrm{T}}\right)/\mathbf{\Omega }\hfill \end{array}(34)$

where $\mathbf{\Omega }={\displaystyle {\sum }_{i=1}^M}\left[D_i\ne 0\right]$.

As shown in Equation 34, the computation of $\text{MSI}$-$\text{P}$ consists of two primary steps: (1) First, all PDoP and NoS values that satisfy the predefined positioning accuracy criteria are selected. (2) Next, the average of these qualified MSI-GO parameters is computed to derive the final $\text{MSI}$-$\text{P}$ value. The initial step ensures that the system maintains positioning accuracy under the current GNSS signal conditions as assessed by MSI-GO. The second step guarantees that the MSI-GO mode selection strategy remains stable and representative over a broader temporal window. This design principle aligns with the operational characteristics of the HI GNSS/INS framework.

5 Simulation

5.1 Data generation

The HI GNSS/INS system relies on accurately synchronized GNSS and INS data. To validate the effectiveness of the proposed method, we employ the MATLAB-based open-source software GINav in conjunction with the publicly available CPT dataset. GINav is a versatile GNSS/INS data processing platform that supports integrated navigation analysis. It is capable of handling multi-constellation and multi-frequency GNSS data, making it well-suited for our evaluation tasks [24]. It provides a flexible and user-friendly platform for testing newly developed algorithms and experimental features. The CPT dataset, used in this study, was collected in a suburban driving environment. The data acquisition system includes a Trimble R10 GNSS receiver and a tactical-grade IMU, with high-precision reference solutions provided by the NovAtel SPAN-CPT system. This dataset enables comprehensive evaluation of various GNSS/INS navigation modes. In this work, we adopt LC SPP (Standard Point Positioning)/INS and TC SPP/INS configurations to validate the performance of the proposed HI GNSS/INS system. The data processing procedure is directly aligned with the mathematical formulation of the MSI-GO algorithm presented earlier. The trajectories of LC and TC, corresponding to ${\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{LC}$ and ${\mathit{P}\mathit{o}\mathit{s}}_{Mea}^{TC}$ are displayed on Google Earth as illustrated in Figure 10. Figure 11 shows the position errors of LC and TC which are corresponding to Equation 32. These data will be used in Equation 32 to obtain $\mathit{D}$. Furthermore, the results are consistent with the theoretical analysis and the observations made in the pre-experiment.

Figure 10

Figure 10. Position results of LC and TC. (a) Position results of LC. (b) Position results of TC.

Figure 11

Figure 11. Position errors. (a) Position errors of LC GNSS/INS. (b) Position errors of TC GNSS/INS.

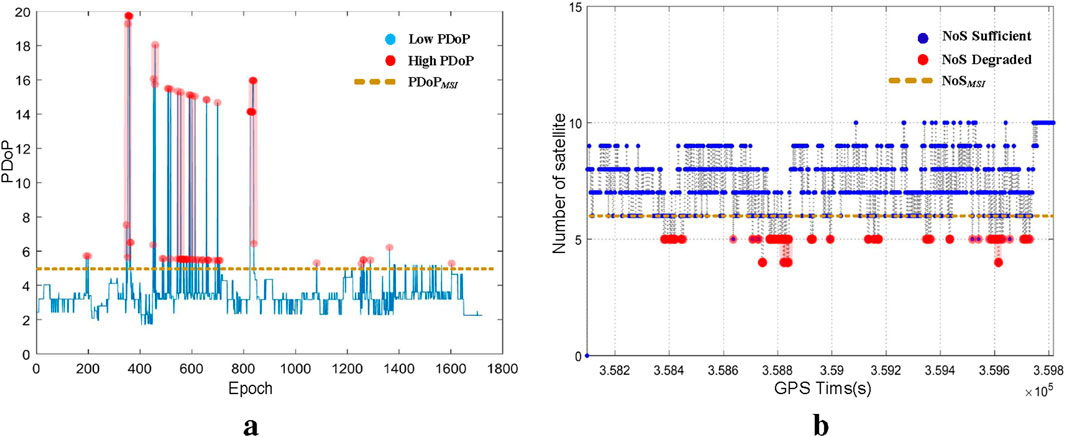
Figure 12 illustrates the PDoP and NoS values for LC and TC within the HI GNSS/INS framework. These datasets correspond to the parameters defined in Equation 31 and are utilized in the calculation of the $\text{MSI}-\text{P}$ matrix as shown in Equation 34. Additionally, Figure 12 visually highlights the substantial fluctuations in GNSS signal quality encountered during real-world positioning scenarios. For example, in Figure 12a, the PDoP value enclosed by the red circle indicates poor satellite geometry and degraded signal quality. An effective $PDo{P}_{MSI}$ metric should be sensitive to such fluctuations in order to adapt to signal degradation. Likewise, an ideal $No{S}_{MSI}$ should be capable of recognizing signal quality deterioration when the number of visible satellites is low, as shown in Figure 12b.

Figure 12

Figure 12. MSI-GO parameters analysis. (a) PDoP. (b) NoS.

5.2 Results

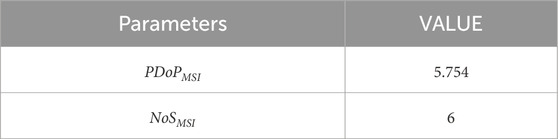
The specific results of the $\text{MSI}$-$\text{P}$ calculation and the position result of HI GNSS/INS are presented in this section. Figure 13 presents the values of $\mathit{D}$ in every epoch along with $x$-axis. The total number of epochs $M$ is 1721. Figure 13 shows the changes of $\mathit{D}$ between 0 and 1. The denser red lines represent more significant changes in GNSS signal quality, which match the locations of drastic changes in PDoP shown in Figure 12a. This suggests that $\mathit{D}$ accurately reflects changes in GNSS signal quality.

Figure 13

Figure 13. The values of $\mathit{D}$ in every epoch.

Based on Equation 34 and $\mathit{D}$, it is able to compute $PDo{P}_{MSI}$ and $No{S}_{MSI}$. In this paper, the $MS{I}_{Thr}$ is set as $97\%$. Table 6 presents the value of $PDo{P}_{MSI}$ and $No{S}_{MSI}$. It indicates that if $PDo{P}_{MSI}<5.754$ and $No{S}_{MSI}\ge 6$, the MSI-GO will will assess that the current GNSS signal quality is good and output a control matrix to operate HI GNSS/INS in LC mode. Moreover, the values of $PDo{P}_{MSI}$ and $No{S}_{MSI}$ shows that the control of $\mathit{D}$ is generally consistent with the GNSS signal quality depicted in Figure 12. As shown in Figure 12a, when $PDo{P}_{MSI}>5.754$, it can be basically considered that the GNSS signal is in a poor quality stage. Similarly, Figure 12a also reflects that the GNSS signal quality sharply decreases when there are only 4 or 5 available satellites. Therefore, the values given in Table 6 are theoretically consistent with the previous analysis.

Table 6

Table 6. Values of MSI-GO parameters.

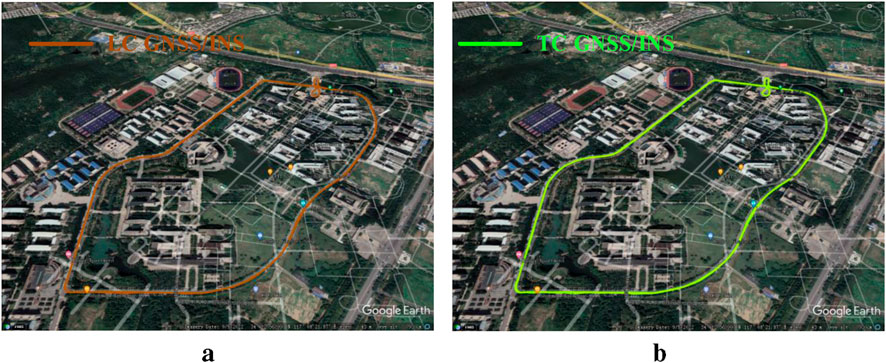
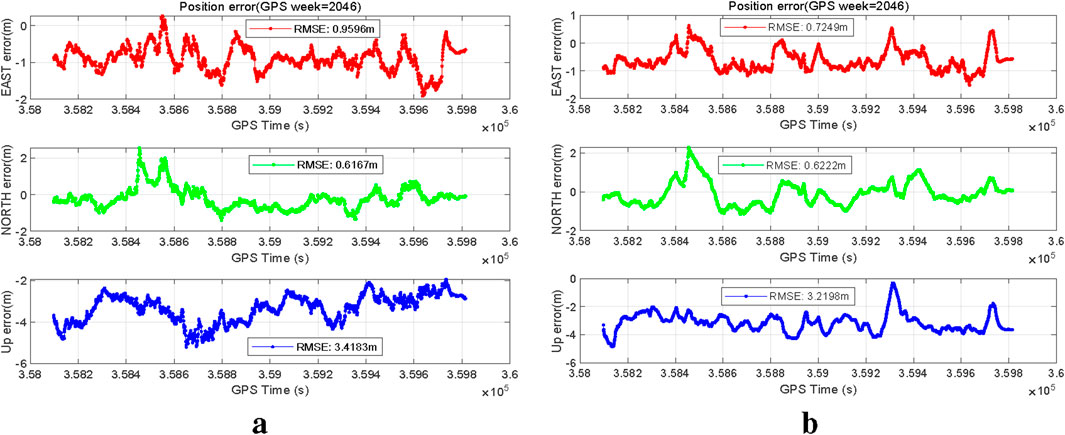
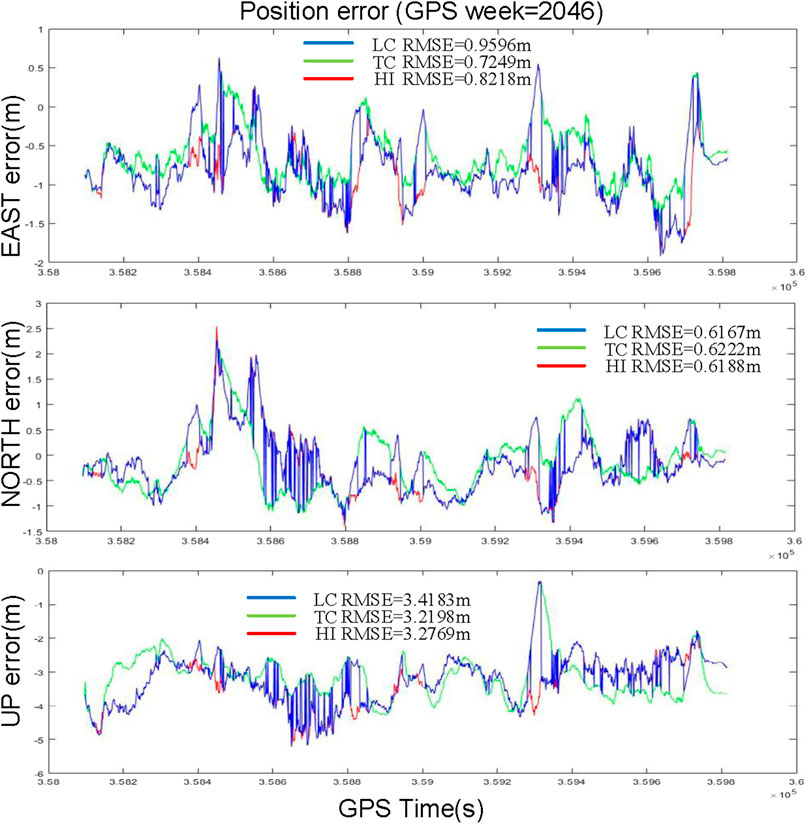
Figure 14 presents the trajectory results of the HI GNSS/INS system, which overall exhibits satisfactory positioning performance. Figure 15 compares the positioning errors of LC, TC, and HI. As shown, the RMSE values of HI in the east, north, and up directions are moderately distributed. This suggests that under the control of MSI-GO, HI employs a mode-switching strategy that maintains acceptable positioning accuracy while moderately compromising accuracy to achieve lower computational cost.

Figure 14

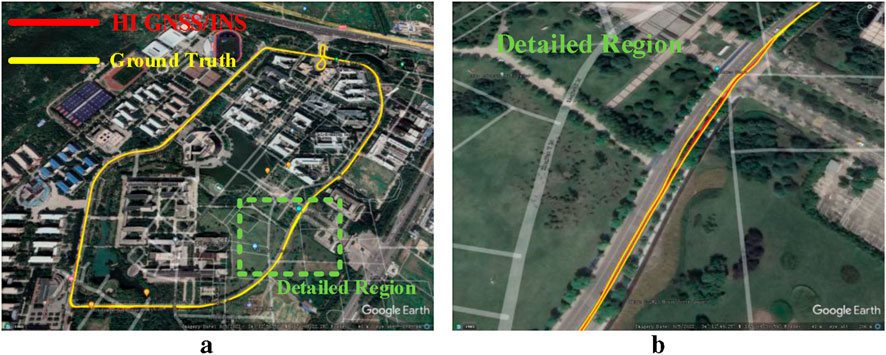
Figure 14. Trajectories of HI GNSS/INS. (a) Trajectories shown on Google Earth. (b) Trajectories in detailed region.

Figure 15

Figure 15. The position errors of HI-GNSS/INS.

In other words, the adaptive mode-switching mechanism of HI effectively reduces computational complexity without significantly degrading positioning performance, thus improving the overall system efficiency. This strategy is especially beneficial in scenarios where system resources are limited and ultra-high positioning accuracy is not a strict requirement. Moreover, the relatively moderate RMSE values indicate that the trade-off strategy adopted by HI does not significantly impair system performance, making it a practical solution for real-world applications.

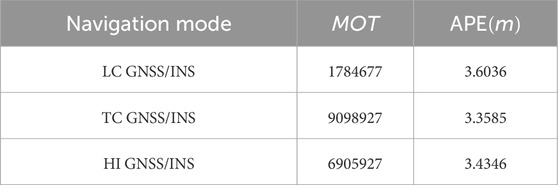
To provide a more intuitive evaluation of the positioning performance of HI, the Average Position Error (APE), defined in Equation 35, is introduced. APE quantifies the positional deviation in terms of three-dimensional distance. Furthermore, computational complexity is assessed by integrating the Number of Satellites (NoS) observed in each epoch. The results shown in Table 7 indicate that the HI system achieves lower computational complexity compared to TC, while also delivering better positioning accuracy than LC. These results highlight the strong practical potential of the HI GNSS/INS approach in real-world applications.

$\text{APE}=\sqrt{{\left(\text{RMS}{\text{E}}_{EAST}\right)}^2+{\left(\text{RMS}{\text{E}}_{NORTH}\right)}^2+{\left(\text{RMS}{\text{E}}_{UP}\right)}^2}(35)$

Table 7

Table 7. Performance analysis of HI GNSS/INS.

The results presented in Table 7 indicate that the HI GNSS/INS system, under the control of MSI-GO, achieves a favorable trade-off by reducing computational complexity at the expense of a slight loss in positioning accuracy. This has significant implications for the design of positioning systems intended for use in computationally constrained environments, offering a practical strategy to balance accuracy and processing demands. In summary, the HI GNSS/INS framework provides a promising approach for developing navigation systems capable of maintaining reliable performance under limited computational resources. By leveraging this strategy, system designers can achieve a balance between efficiency and accuracy, enabling broader applicability and improved adaptability across various practical scenarios.

5.3 Discussion

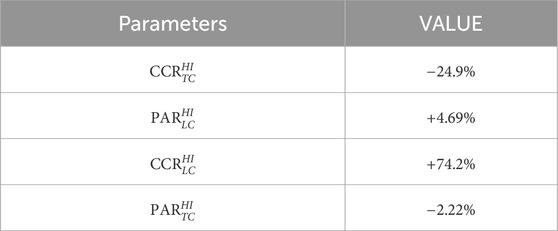
Based on the positioning results, a quantitative evaluation of positioning accuracy and computational complexity can be conducted, allowing for direct comparison with LC GNSS/INS and TC GNSS/INS systems. Subsequently, the limitations and potential drawbacks of the HI GNSS/INS approach are discussed. To facilitate this comparison, the Computational Complexity Ratio (CCR) and the Position Accuracy Ratio (PAR) are defined and formulated in Equation 36 and Equation 37, respectively.

${\text{CCR}}_{Mode2}^{Mode1}=\frac{MO{T}_{Mode1}-MO{T}_{Mode2}}{MO{T}_{Mode2}}\times 100\%(36)$

${\text{PAR}}_{Mode2}^{Mode1}=-\frac{\text{AP}{\text{E}}_{Mode1}-\text{AP}{\text{E}}_{Mode2}}{\text{AP}{\text{E}}_{Mode2}}\times 100\%(37)$

CCR represents the ratio of the reduction in computational complexity of $Mode1$ relative to $Mode2$. The greater the CCR, the diminished the level of computational complexity. Similarly, PAR denotes the proportion of enhancement in position accuracy for $Mode1$ to $Mode2$. A larger value of PAR indicates a higher position accuracy. Table 8 presents the specific results of ${\text{CCR}}_{TC}^{HI}$, ${\text{PAR}}_{LC}^{HI}$, ${\text{CCR}}_{LC}^{HI}$, ${\text{PAR}}_{TC}^{HI}$. Comparing to LC and TC, HI boost the position accuracy by $4.69\%$ and reduce computational complexity by around $24.9\%$. Furthermore, it is worth noting the magnitude of the numerical value ${\text{PAR}}_{TC}^{HI}=-2.22\%$. In the previous configuration, we mentioned setting the $MS{I}_{Thr}$ as $97\%$, while the corresponding $MS{I}_{Thr}$ here is actually $1-\left|{\text{PAR}}_{TC}^{HI}\right|=97.78\%$. This demonstrates that HI is able to achieve a balance between position accuracy and computational complexity through the $MS{I}_{Thr}$ control of MSI-GO which is entirely consistent with our previous theoretical analysis. Moreover, the sum of $\left|{\text{CCR}}_{TC}^{HI}\right|$ and $\left|{\text{CCR}}_{LC}^{HI}\right|$ is $24.9\%+74.2\%=99.1\%\approx 1$. This is attributed to the fact that HI alternates between LC and TC modes, leading to a computational complexity that is higher than LC but lower than TC. This behavior is consistent with the fundamental operating principle of the HI system.

Table 8

Table 8. HI GNSS/INS performance evaluation.

Moreover, the results confirm that HI is capable of effectively balancing positioning accuracy and computational complexity across varying GNSS signal conditions. In addition, Table 5 provides the per-epoch computational costs for LC and TC. The ratio of LC to TC epochs under MSI-GO was observed during the experiments. The reported 25% in Table 8 saving for HI was estimated by combining these two components, rather than from separately measured wall-clock runtime. The thresholds used in the experiments were selected from observable statistics of PDoP and NoS to approximate the knee of this trade-off, striking a balance between accuracy and runtime. Importantly, no ground truth was used during threshold selection, so the design avoids overfitting and preserves generalizability. The reported results already include the LC baseline (lowest cost, highest error), the TC baseline (highest cost, lowest error), and the HI policy operating point in between. These three points effectively capture the outer bounds and the achieved compromise. Any ablation sweep of thresholds would simply interpolate between these reported endpoints, reproducing the monotonic trade-off already demonstrated in the results.

Although the HI GNSS/INS technology demonstrates strong potential for navigation applications, several limitations must be addressed to fully realize its capabilities: (1) First, the current HI GNSS/INS framework is not capable of real-time operation. Achieving real-time functionality requires the integration of various complex processes and system-level optimizations, which warrant further research and development. (2) Second, the validation and deployment of HI GNSS/INS are constrained by the limited diversity of test environments. To ensure system robustness and reliability, it is crucial to assess its performance under a wide range of challenging conditions, such as varying GNSS signal strengths, environmental dynamics, and application contexts. In addition, more inclusive data acquisition and analysis strategies should be adopted to ensure adaptability across diverse user needs and usage scenarios. (3) Third, the selection of the optimal $MS{I}_{Thr}$ threshold for different parameters requires deeper mathematical investigation and multidimensional parameter tuning. Furthermore, incorporating novel functions and algorithms could broaden the system’s adaptability and operational scope, making it more capable of addressing various real-world navigation demands.

In conclusion, further research and development are essential to build a reliable and efficient HI GNSS/INS system capable of real-time operation. Moreover, enhancements in testing and evaluation methodologies are required to thoroughly verify the system’s robustness and reliability under diverse conditions. Despite these challenges, the design of MSI-GO lays a solid foundation for the continued refinement of HI GNSS/INS technology and presents promising opportunities for future advancements. In particular, a deeper exploration of the theoretical basis of MSI-GO is critical, and continued research in this domain is both necessary and valuable.

6 Conclusion

In this work, we propose a Hybrid Integration (HI) GNSS/INS framework that effectively combines the strengths of traditional LC and TC methods. The core innovation of the HI GNSS/INS system lies in its adoption of MSI-GO, which enables feature-based learning from GNSS observations. This mechanism allows the system to autonomously switch to the most suitable operating mode based on real-time signal characteristics, thereby reducing computational burden while maintaining high positioning accuracy. Simulation results demonstrate that the proposed HI GNSS/INS system achieves superior overall performance compared to conventional LC and TC approaches. Notably, the HI system reduces computational complexity by approximately $25\%$ relative to TC mode, while also improving positioning accuracy by about $5\%$ over LC mode. In summary, the HI GNSS/INS framework offers a significant advancement in integrated navigation, making it a promising solution for resource-constrained environments such as autonomous vehicles, unmanned aerial vehicles (UAVs), and maritime navigation systems.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SW: Writing – original draft, Writing – review and editing. HH: Data curation, Methodology, Writing – original draft. FT: Formal Analysis, Project administration, Writing – original draft. BZ: Funding acquisition, Resources, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article.

Acknowledgements

The authors would like to thank the editors and reviewers for their efforts in supporting the publication of this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from the Laboratory of Science and Technology on Marine Navigation and Control, China State Shipbuilding Corporation (Grant No. 2024010104). The funder had the following involvement in the study: researching on algorithms related to GNSS/INS integrated navigation.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Boguspayev N, Akhmedov D, Raskaliyev A, Kim A, Sukhenko A. A comprehensive review of gnss/ins integration techniques for land and air vehicle applications. Appl Sci (2023) 13:4819. doi:10.3390/app13084819

CrossRef Full Text | Google Scholar

2. Li X, Xia C, Li S, Zhou Y, Shen Z, Qin Z. A filter-based integration of gnss, ins, and stereo vision in tight mode with optimal smoothing. IEEE Sensors J (2023) 23:23238–54. doi:10.1109/JSEN.2023.3295816

CrossRef Full Text | Google Scholar

3. Yang C, Shi W, Chen W. Robust M–m unscented kalman filtering for gps/imu navigation. J Geodesy (2019) 93:1093–104. doi:10.1007/s00190-018-01227-5

CrossRef Full Text | Google Scholar

4. Shuai Q, Pang Q, Tang F, Niu Z, Zhu B. An enhanced precise carrier phase positioning method for vehicle navigation. IEEE Access (2025) 13:122484–95. doi:10.1109/ACCESS.2023.3285818

CrossRef Full Text | Google Scholar

5. Xiao K, Sun F, He M, Zhang L, Zhu X. Inertial aided bds triple-frequency integer ambiguity rounding method. Adv Space Res (2021) 67:1638–55. doi:10.1016/j.asr.2020.12.013

CrossRef Full Text | Google Scholar

6. Wu Y, Wang J, Hu D. A new technique for ins/gnss attitude and parameter estimation using online optimization. IEEE Trans Signal Process (2014) 62:2642–55. doi:10.1109/tsp.2014.2312317

CrossRef Full Text | Google Scholar

7. Xia C, Li X, He F, Li S, Zhou Y. Accurate and rapidly-convergent gnss/ins/lidar tightly-coupled integration via invariant ekf based on two-frame group. IEEE Trans Automation Sci Eng (2025) 22:7992–8005. doi:10.1109/TASE.2024.3476069

CrossRef Full Text | Google Scholar

8. Wen ZC, Li Y, Guo XL, Zhang XX. Design and evaluation of gnss/ins tightly-coupled navigation software for land vehicles. The Int Arch Photogrammetry, Remote Sensing Spat Inf Sci XLVI-3/W1-2022 (2022) 213–8. doi:10.5194/isprs-archives-XLVI-3-W1-2022-213-2022

CrossRef Full Text | Google Scholar

9. Zhao J, Sun W, Ding W, Li Y, Sun P, Sun P. Vehicle cooperative positioning with tightly coupled gnss/ins/uwb integration based on improved multiple fading factors and adaptive cost function. IEEE Trans Intell Transportation Syst (2025) 26:9740–54. doi:10.1109/TITS.2025.3575812

CrossRef Full Text | Google Scholar

10. Yokota Y, Ishikawa T, Watanabe S-i., Nakamura Y. Kilometer-scale sound speed structure that affects gnss-a observation: case study off the kii channel. Front Earth Sci (2020) 8:331–2020. doi:10.3389/feart.2020.00331

CrossRef Full Text | Google Scholar

11. Wang H, Tang F, Wei J, Zhu B, Wang Y, Zhang K. Online semi-supervised transformer for resilient vehicle gnss/ins navigation. IEEE Trans Vehicular Technology (2024) 73:16295–311. doi:10.1109/TVT.2024.3422680

CrossRef Full Text | Google Scholar

12. Wang S, Zhan X, Zhai Y, Liu B. Fault detection and exclusion for tightly coupled gnss/ins system considering fault in state prediction. Sensors (Basel) (2020) 20:590. doi:10.3390/s20030590

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chang J, Zhang Y, Fan S, Huang F, Xu D, Hsu L-T. An anti-spoofing model based on mvm and mccm for a loosely-coupled gnss/ins/lidar kalman filter. IEEE Trans Intell Vehicles (2024) 9:1744–55. doi:10.1109/TIV.2023.3335356

CrossRef Full Text | Google Scholar

14. Lv C, Yang J, Ben Y, Li Q, Wang K, Yao J. Residual clustering analysis-based fault detection and exclusion for gnss/ins tightly coupled integration. IEEE Sensors J (2025) 25:7053–67. doi:10.1109/JSEN.2025.3526803

CrossRef Full Text | Google Scholar

15. Niu X, Zhang Q, Gong L, Liu C, Zhang H, Shi C, et al. Development and evaluation of gnss/ins data processing software for position and orientation systems. Surv Rev (2015) 47:87–98. doi:10.1179/1752270614y.0000000099

CrossRef Full Text | Google Scholar

16. Zhu F, Xiao T, Xu Z, Zhang Y, Lv J, Guo F, et al. Uncertainty modeling for plane and line features to improve consistency in rtk/ins/lidar integrated navigation. IEEE Trans Intell Transportation Syst (2024) 25:21002–20. doi:10.1109/TITS.2024.3474093

CrossRef Full Text | Google Scholar

17. Wang D, Dong Y, Li Z, Li Q, Wu J. Constrained mems-based gnss/ins tightly coupled system with robust kalman filter for accurate land vehicular navigation. IEEE Trans Instrumentation Meas (2020) 69:5138–48. doi:10.1109/tim.2019.2955798

CrossRef Full Text | Google Scholar

18. Shen K, Wang M, Fu M, Yang Y, Yin Z. Observability analysis and adaptive information fusion for integrated navigation of unmanned ground vehicles. IEEE Trans Ind Electronics (2020) 67:7659–68. doi:10.1109/tie.2019.2946564

CrossRef Full Text | Google Scholar

19. Zeng Y, Lu Z, Xie Y, Ren B, Yu Y, Ni S. Overview of development and challenges of attitude determination for rotary wing uavs based on gnss. Front Phys (2025) 13:1487136–2025. doi:10.3389/fphy.2025.1487136

CrossRef Full Text | Google Scholar

20. Shao XY, Gao BB, Gao SS, Gao R, Zhang J. Variational bayesian-based adaptive unscented particle filter for bds/ins integration. In: Proceedings of 2017 ieee 7th international conference on electronics information and emergency communication iceiec (2017). p. 37–40.

Google Scholar

21. Wang H, Wei J, Qin J, Zhu N, Ren M, Zhao Z, et al. Dynamic process noise covariance adjustment in gnss/ins integrated navigation using gru-sac for enhanced positioning accuracy. IEEE Trans Intell Transportation Syst (2025) 26:9047–64. doi:10.1109/TITS.2025.3540205

CrossRef Full Text | Google Scholar

22. Wu Z, Li X, Shen Z, Xu Z, Li S, Zhou Y, et al. A failure-resistant, lightweight, and tightly coupled gnss/ins/vision vehicle integration for complex urban environments. IEEE Trans Instrumentation Meas (2024) 73:1–13. doi:10.1109/TIM.2024.3406814

CrossRef Full Text | Google Scholar

23. Shen Z, Li X, Li X (2024). Advancing high-precision navigation: leveraging homogeneous sensors in tightly coupled ppp-rtk/imu integration. IEEE Trans Ind Electron, 71, 15100–10. doi:10.1109/TIE.2024.3363741

CrossRef Full Text | Google Scholar

24. Chen K, Chang G, Chen C. Ginav: a matlab-based software for the data processing and analysis of a gnss/ins integrated navigation system. GPS Solutions (2021) 25:108. doi:10.1007/s10291-021-01144-9

CrossRef Full Text | Google Scholar

25. Zhang Q, Niu X, Zhang H, Shi C. Algorithm improvement of the low-end gnss/ins systems for land vehicles navigation. Math Probl Eng (2013) 2013:1–12. doi:10.1155/2013/435286

CrossRef Full Text | Google Scholar

26. Wen W, Pfeifer T, Bai X, Hsu L-T. Factor graph optimization for gnss/ins integration: a comparison with the extended kalman filter. NAVIGATION: J Inst Navigation (2021) 68:315–31. doi:10.1002/navi.421

CrossRef Full Text | Google Scholar

27. Chang Y, Wang Y, Shen Y, Ji C. A new fuzzy strong tracking cubature kalman filter for ins/gnss. GPS Solutions (2021) 25:120. doi:10.1007/s10291-021-01148-5

CrossRef Full Text | Google Scholar

28. Zhang Q, Niu X, Chen Q, Zhang H, Shi C. Using allan variance to evaluate the relative accuracy on different time scales of gnss/ins systems. Meas Sci Technology (2013) 24:085006. doi:10.1088/0957-0233/24/8/085006

CrossRef Full Text | Google Scholar

29. Han H, Wang J, Wang J, Tan X. Performance analysis on carrier phase-based tightly-coupled gps/bds/ins integration in gnss degraded and denied environments. Sensors (Basel) (2015) 15:8685–711. doi:10.3390/s150408685

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Falco G, Pini M, Marucco G. Loose and tight gnss/ins integrations: comparison of performance assessed in real urban scenarios. Sensors (Basel, Switzerland) (2017) 17:E255. doi:10.3390/s17020255

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhu Z, Jiang C, Bo Y. Performance enhancement of gnss/mems-imu tightly integration navigation system using multiple receivers. IEEE Access (2020) 8:52941–9. doi:10.1109/access.2020.2981769

CrossRef Full Text | Google Scholar

32. Jiang C, Zhang S, Li H, Li Z. Performance evaluation of the filters with adaptive factor and fading factor for gnss/ins integrated systems. GPS Solutions (2021) 25:130. doi:10.1007/s10291-021-01165-4

CrossRef Full Text | Google Scholar

33. Elsheikh M, Abdelfatah W, Nourledin A, Iqbal U, Korenberg M. Low-cost real-time ppp/ins integration for automated land vehicles. Sensors (Basel) (2019) 19:4896. doi:10.3390/s19224896

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Vagle N, Broumandan A, Lachapelle G. Multiantenna gnss and inertial sensors/odometer coupling for robust vehicular navigation. IEEE Internet Things J (2018) 5:4816–28. doi:10.1109/JIOT.2018.2822264

CrossRef Full Text | Google Scholar

35. Xu Y, Wang K, Jiang C, Li Z, Yang C, Liu D, et al. Motion-constrained gnss/ins integrated navigation method based on bp neural network. Remote Sensing (2023) 15:154. doi:10.3390/rs15010154

CrossRef Full Text | Google Scholar

36. Ma Y, Fang J, Wang W, Li J. Decoupled observability analyses of error states in ins/gps integration. J Navigation (2014) 67:473–94. doi:10.1017/s0373463313000829

CrossRef Full Text | Google Scholar

37. Niu Z, Nie P, Tao L, Sun J, Zhu B. Rtk with the assistance of an imu-based pedestrian navigation algorithm for smartphones. Sensors (2019) 19:3228. doi:10.3390/s19143228

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Song X, Liao S, Wang X, Lu C, Wang M, Miao C. A high precision autonomous navigation algorithm of uav based on mems sensor. In: 2019 IEEE international conference on unmanned systems (ICUS) (2019). p. 904–8. doi:10.1109/ICUS48101.2019.8996061

CrossRef Full Text | Google Scholar

39. Specht M, Specht C, Stateczny A, Burdziakowski P, Dąbrowski P, Lewicka O. Study on the positioning accuracy of the gnss/ins system supported by the rtk receiver for railway measurements. Energies (2022) 15:4094. doi:10.3390/en15114094

CrossRef Full Text | Google Scholar

40. Stateczny A, Specht C, Specht M, Brčić D, Jugović A, Widźgowski S, et al. Study on the positioning accuracy of gnss/ins systems supported by dgps and rtk receivers for hydrographic surveys. Energies (2021) 14:7413. doi:10.3390/en14217413

CrossRef Full Text | Google Scholar

41. Won DH, Lee E, Heo M, Lee S-W, Lee J, Kim J, et al. Selective integration of gnss, vision sensor, and ins using weighted dop under gnss-challenged environments. IEEE Trans Instrumentation Meas (2014) 63:2288–98. doi:10.1109/TIM.2014.2304365

CrossRef Full Text | Google Scholar

42. Tang F, Zhang S, Zhu B, Sun J. Enhanced lidar odometry for autonomous vehicular positioning system using local feature enhancement and global motion constraint. IEEE Trans Vehicular Technology (2025) 1–16. doi:10.1109/TVT.2025.3566776

CrossRef Full Text | Google Scholar

43. Li G, Tang F, Sun J, Sun Y, Zhu B. Implementation of zupt aided gnss/mems-imu deeply coupled navigation system. In: 2023 international conference on microwave and millimeter wave Technology (ICMMT) (2023). p. 1–3. doi:10.1109/ICMMT58241.2023.10276622

CrossRef Full Text | Google Scholar

44. Tang F, Zhu B, Sun J. Gradient enhancement techniques and motion consistency constraints for moving object segmentation in 3d lidar point clouds. Remote Sensing (2025) 17:195. doi:10.3390/rs17020195

CrossRef Full Text | Google Scholar

45. Tang F, Zhang S, Zhu B, Sun J. Outdoor large-scene 3d point cloud reconstruction based on transformer. Front Phys (2024) Volume:1474797–2024. doi:10.3389/fphy.2024.1474797

CrossRef Full Text | Google Scholar

46. Tang F, Wang Z, Cheng Y. Simultaneous parameter and state estimation with extended kalman filter for dynamic parameters. In: 2024 IEEE MTT-S International Wireless Symposium (IWS) (2024). p. 1–3. doi:10.1109/IWS61525.2024.10713488

CrossRef Full Text | Google Scholar

47. Tang F, Li G, Sun Y, Sun J, Zhu B. Comparison of performance between loosely and tightly coupled gnss/ins in real scenarios. In: 2023 international conference on microwave and millimeter wave Technology (ICMMT) (2023). p. 1–3. doi:10.1109/ICMMT58241.2023.10276464

CrossRef Full Text | Google Scholar

48. Shkel AM, Wang Y (2021). Strapdown inertial navigation mechanism. 37–46. doi:10.1002/9781119699910.ch3

CrossRef Full Text | Google Scholar