Estimation of the effect of Tsallis non-extensive statistics on the 14C(n,γ)15C reaction rate

The total cross-section of the radiative neutron capture reaction ¹⁴С(n,γ₀₊₁)¹⁵C—for energies ranging from 10 meV to 5 MeV—is considered. Calculations performed in the framework of the modified potential cluster model with forbidden states show an agreement of total cross-section σ (23.3 keV) = 4.75 μb with the presently recommended value 4.86(48) μb by Ma et al., 2020. The efficiency of carbon isotope ¹⁵C production is illustrated by the ¹⁴С(n,γ₀₊₁)¹⁵C reaction rate calculated at temperatures from T₉ = 0.001 to T₉ = 10. The conventional Maxwell–Boltzmann weighted reaction rate ${〈\sigma v〉}_{\text{MB}}$ of the present work is comparable, with less than 10% accuracy, with the latest calculations by Ma et al., 2020 and Bhattacharyya et al., 2021. The estimation of non-extensive effects is implemented using our data on the reaction rate ${〈\sigma v〉}_{\text{MB}}$ as reference values. The efficiency of carbon isotope production in radiative capture reactions ^12-14С(n,γ)^13-15C is estimated based on the calculated reaction rates. The influence of the Maxwellian-weighted ^12-14C(n,γ)^13-15C reaction rates on the ratios ¹²C/¹³C and ¹³C/¹⁴C is examined. Tsallis statistics is applied for the first time to the calculation of the ¹⁴С(n,γ₀)¹⁵C reaction rate with values of non-extensive parameter 0.7 ≤ q ≤ 1.3 on the background of Maxwell–Boltzmann statistics corresponding to q = 1. The reaction rate ${〈\sigma v〉}_q$ shows a factor ∼4 increase for q = 0.7 and a factor ∼0.6 decrease for q = 1.3 compared to q = 1.

1 Introduction

The role of carbon isotope ¹⁴С in the stellar environment of asymptotic giant branch (AGB) stars was examined nearly 30 years ago by Forestini and Charbonnel, 1997, as part of research concerning the nucleosynthesis of light elements in low-metallicity intermediate-mass stars of $3-7M_{\odot }$ [1, 2]. We found it very interesting how the authors incorporated the isotope ¹⁴С into the scenario of AGB star evolution as some of their perspectives can now be validated with contemporary data. To reconstruct the AGB evolution, the network of neutron-, proton-, and ⁴He-induced reactions was considered on some selected nuclides, particularly ¹⁴С(n,γ), ¹⁴С(p,γ), ¹⁴С(α,γ), and ¹⁴С(α,n) processes, with ¹⁴С as the seed nucleus [1, 2]. The production of ¹⁴С is provided by two reactions: ¹³C(n,γ)¹⁴С and ¹⁴N(n,p)¹⁴C, so it is important to briefly discuss the status of these processes today.

The results of [1] are presented as an estimation of isotope abundance in carbon pockets:

${}^{12}\mathrm{C}/{}^{13}\mathrm{C}=44\pm 3,{}^{13}\mathrm{C}/{}^{14}\mathrm{C}>1400,{}^{14}\mathrm{N}/{}^{15}\mathrm{N}>5300.(1)$

These numbers turned out to be reference values, to some extent, for subsequent studies of AGB stars. Some original papers and reviews provide observables for the ¹²C/¹³C and ¹⁴N/¹⁵N ratios in AGB stars [3–6]. Note that ratios in Equation 1 strongly depend on the mutually connected reaction chains, such as neutron-induced reactions

${}^{12}\mathrm{C}\left(n,\gamma \right){}^{13}\mathrm{C}\left(n,\gamma \right){}^{14}\mathrm{C}\left(n,\gamma \right){}^{12}\mathrm{C}\left({\mathrm{\beta }}^{-}\right){}^{15}\mathrm{N},(2)$

where the evolution of carbon isotopes ^12-15C occurs, and finally nitrogen ¹⁵N is created. Hydrogen burning, ^12-14C(p,γ)^13-15N, is the source of nitrogen isotopes, providing the ¹⁴N/¹⁵N ratio while also regulating the carbon fractions. We are not concerned with the mechanism of ⁴He combustion since it mainly relates to the outer helium shell of AGB stars, which is beyond the scope of the present work.

We intend to discuss [5], purposely, the situation with the radiative neutron capture reaction ¹⁴С(n,γ)¹⁵C in the context of the following questions:

i. how reliable is the reaction rate determined today?;

ii. how may modern data on the reaction rate change the isotopic ratio (Equation 1)?;

iii. are there any reasons to shift from the traditional Maxwell–Boltzmann (MB) weighted reaction rate to non-extensive statistics?

While calculating the ratios (Equation 1), Forestini and Charbonnel, 1997 [1], used as input information for the constructed network the rate of the ¹⁴С(n,γ)¹⁵C reaction obtained in [7], which was nearly a factor of 5 lower than that of the earlier calculations in [8]. As a result, it was concluded that the reaction ¹⁴С(n,γ)¹⁵C(β⁻)¹⁵N plays an insignificant role in the formation of ¹⁵N, with the process of radiative capture of protons ¹⁴С(p,γ)¹⁵N dominating.

This “factor of 5 difference” triggered, to some extent, the following year’s experimental study of the cross section of ¹⁴С(n,γ)¹⁵C reaction [9–12]. The value of the total cross section σ(E) at $E_{\mathrm{c}.\mathrm{m}.}=23.3\text{keV}$ is a benchmark today for comparing experimental methods and theoretical models. We suggest, for analysis, the set of results for $\sigma \left(23.3\text{keV}\right)$ from [7, 9, 11–19, 49] and the recently published data by [20].

To determine the consistency of the results on the MB-weighted rate of the ¹⁴С(n,γ)¹⁵C reaction, we use data from [7, 8, 11, 18, 19] along with the present model calculations to address question (i). Since we employed the modified potential cluster model (MPCM) (see, for details, [21, 22]), the comparison of rates for the neutron-induced reactions ^12-14С(n,γ)^13-15C calculated within the same framework provides a way to re-estimate the ¹³C/¹⁴C ratio (ii).

Question (iii) is a new issue in the study of the ¹⁴С(n,γ)¹⁵C reaction. The subject of non-equilibrium phenomena in the context of stars is related to the application of non-extensive Tsallis statistics, as suggested in [23]. For the first time, [24] (final version, 2017 [25]), pointed out the strong sensitivity of thermonuclear reaction rates of light nuclei during Big Bang nucleosynthesis to the non-extensive parameter q. Further investigations concern the effect of Tsallis statistics on primordial BBN in the context of addressing the lithium problem [26, 27]. A summary of the research [24, 25] suggested extending the study of non-extensive effects to the formation of nuclei with masses beyond the BB seeds, i.e., with $\mathit{A}>7$. The authors foresee a possible new comprehension of the synthesis of heavy elements. In the present work, we applied the formalism of Tsallis statistics [24, 25] to illustrate its effect on the ¹⁴С(n,γ)¹⁵C reaction rate.

2 Elements of MPCM input data for the ¹⁴C(n,γ₀₊₁)¹⁵C reaction

The details of the study of the ¹⁴С(n,γ₀₊₁)¹⁵C reaction in the framework of the MPCM are presented in [28]. In this study, we still consider radiative E1 neutron capture on ¹⁴С, scattering p-waves to the ground state (GS) and first excited state (1^st ES) of ¹⁵C, with respective quantum numbers ${}^{2}P_{1/2}{+}^2{P}_{3/2}{\to }^2{S}_{1/2}$ and ${}^{2}P_{3/2}{\to }^2{D}_{5/2}$. The interaction potential used for the calculation of continuum and bound states is of the Gauss type

$V\left(r,JLS\right)=-V_0\left(JLS\right)\exp \left\{-\alpha \left(JLS\right)r^2\right\},(3)$

where V₀ is the potential depth and α is a parameter defining the asymptotic decrease in the potential at long relative distances r. Parameters V₀ and α in Equation 3 are fitted for the bound states so that they match the channel binding energy Е_b, charge radius R_ch, and matter radius R_m. A set of parameters is found for each partial wave with quantum numbers JLS. The nodal or nodeless r-dependence of the relative wave functions is determined by the classification of orbital symmetry using Young diagrams, as implemented for the $n{+}^{14}\mathrm{C}$ system in [28].

Another experimental characteristic is the asymptotic normalization coefficient $A_{NC}$ (ANC), which is related to the dimensional asymptotic constant C via the spectroscopic factor $S_F$ as follows: $A_{NC}^2=S_F\times C^2$ [29]. We work in the formalism of the dimensionless asymptotic constant $C_w$, which is related to C by $C_w=C/\sqrt{2k_o}$, where the wave number $k_0$ corresponds to the channel binding energy $E_{\mathrm{b}}={\mathrm{\hslash }}^2{k}_o^2/2\mu$ and $\mu$ is the reduced mass. The asymptotic constant $C_w$ is determined by matching the numerical radial function to the analytical Whittaker function: ${\mathrm{\chi }}_L\left(r\right)=\sqrt{2k_0}{C}_w{W}_{-\eta L+1/2}\left(2k_{0}r\right)$. In the case of neutron-induced reactions, $\eta =0$. The corresponding results are provided in Table 1.

Table 1

Table 1. Parameters of the ground and excited state potential for ¹⁵C nucleus in the n¹⁴C channel and results of MPCM calculations of Е_b, R_ch, R_m, and C_w with the listed parameters V₀ and α.

To calculate R_ch(¹⁵C) and R_m(¹⁵C), we follow the definitions from [21]. The input numerical information includes the masses of the constituent particles, m_n = 1.008665 amu and $m_{{14}_{\mathrm{C}}}$ = 14.003242 amu; the averaged value of R_ch(¹⁴C) = 2.48 fm from [30–32]; and the latest data for R_m(¹⁴C) = 2.367(35) fm from[33]. The recent experimental data on the ground state charge R_ch and matter radius R_m for ¹⁵C, presented in Table 2, show good agreement with the MPCM results (see Table 1).

Table 2

Table 2. Data on the experimentally measured charge radius R_ch and matter radius R_m of ¹⁵C.

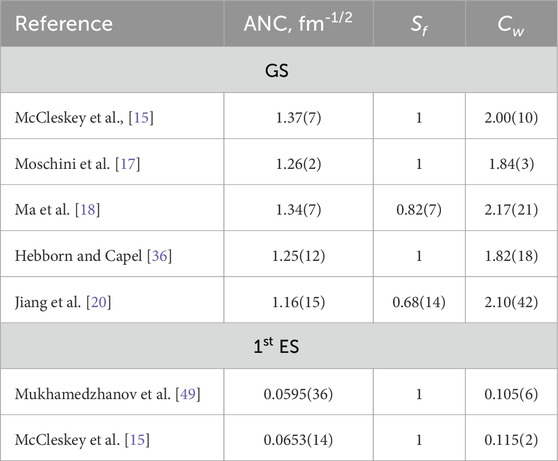
The results for C_w in Table 1 were obtained over the interval 7–27 fm. Selected later data on the ANC and their recalculated values for C_w, presented in Table 3, show reasonable agreement with the MPCM results for the GS, as well as for the first excited state.

Table 3

Table 3. Asymptotic constant data for ¹⁵C in the n¹⁴C channel.

Initially, we proceeded from the data in work [37], where for the resonant states ²P_1/2 at 3.103 MeV and ²P_3/2 at 4.657 MeV, the reaction ¹⁴С(n,γ)¹⁵C does not occur, which means that these states are excited or formed in stripping or pickup reactions. In some studies, the narrow resonance at 3.103 MeV (Г_n = 42 keV) is included in ¹⁴С(n,γ)¹⁵C cross-section calculations as a Breit–Wigner resonance; for example, see recent references [18, 20]. Their estimates show that its contribution is very small, even compared to the capture to the first excited state.

In the present study, we assume the ²P_1/2 and ²P_3/2 states to be non-resonant in the n + ¹⁴C channel. Since in the MPCM, the partial ²P waves do not contain forbidden states [22, 28], which are present in the spectrum of solutions of the Schrödinger equation only as bound states and require sufficiently deep attractive potentials [21], we assume the corresponding potentials to be zero.

Our choice of the zero depth for the P-wave scattering interaction potentials is supported by Ref. [16], where the role of different interaction parameters sets in the continuum $n{+}^{14}\mathrm{C}$ channel is examined for the Coulomb breakup of ¹⁵C, and from these data the radiative capture ¹⁴С(n,γ₀)¹⁵C cross sections are recalculated.

3 Total cross sections of the n¹⁴C capture reaction

Comparison of the total cross sections for the ¹⁴С(n,γ₀₊₁)¹⁵C reaction, calculated using the MPCM potential parameters from Table 1, with experimental data is presented in Figure 1a. It is clearly observed that there is a noticeable input from the (n,γ₁) capture to the first ES starting from energies $E_{\mathrm{c}.\mathrm{m}.}\sim 1\text{MeV}$.

Figure 1

Figure 1. Total cross sections of the ¹⁴С(n,γ₀₊₁)¹⁵C reaction. Experiment: , [20]; , [12]; , [11]; , [10]; , [9]; , [7]. Curves: MPCM calculations. (a) E_c.m. = 5 keV–5 MeV. (b) E_c.m. = 10⁻⁸–5 MeV; green dash-dotted curve–results of [28].

Note that the data by [12] are the result of a recalculation of the Coulomb breakup of ¹⁵C and corresponds to the photodisintegration reaction ${}^{15}\mathrm{C}{\left(\stackrel{\sim }{\gamma },n\right)}^{14}\mathrm{C}$ by virtual photons. When compared to direct photodisintegration by real γ-quanta, the results may differ. In general, it should be acknowledged that the measurement errors are very large, and all experimental points refer to the GS radiative capture ¹⁴С(n,γ₀)¹⁵C process.

Figure 1b illustrates the total cross sections for E_c.m. shows the results from our earlier work [28]. These cross sections are somewhat lower than the present cross sections since in [28], the radial matrix elements for the cross sections were calculated only up to 30 fm. Based on the low binding energy $E_{\mathrm{b}}$ of the n¹⁴C system, we have extended the integration interval for the overlapping integrals up to a distance of 100 fm.

The energy dependence of σ(E_c.m.) at $E_{\mathrm{c}.\mathrm{m}.}\le 10\text{keV}$ (red solid curve in Figure 1b) can be approximated by the simple functional form:

${\sigma }_{ap}\left(\mathrm{\mu }\mathrm{b}\right)=A\sqrt{E_{\mathrm{c}.\mathrm{m}.}\left(\text{keV}\right)}.(4)$

The constant A = 1.002 μb·keV^-1/2 in equation 4 is determined from a single point of $\sigma \left(E_{\mathrm{c}.\mathrm{m}.}\right)$ at the minimum energy of 10 MeV. The value $A=0.782\mathrm{\mu }\mathrm{b}·{\text{keV}}^{-1/2}$ obtained earlier in [28] is approximately 20% lower. The accuracy of approximation (Equation 4) is estimated as $M\left(E\right)=\left|\left[{\sigma }_{ap}\left(E\right)-{\sigma }_{theor}\left(E\right)\right]/{\sigma }_{theor}\left(E\right)\right|$. The relative deviation of the calculated theoretical cross section ${\sigma }_{theor}\left(E\right)$ and its approximation ${\sigma }_{ap}\left(E\right)$ by the above function at energies less than 10 keV does not exceed 0.8%. Relation (Equation 4) allows determining the value of the thermal cross section: ${\sigma }_{th}\left(25.3\text{meV}\right)\simeq 0.005\mathrm{\mu }\mathrm{b}$.

The thermal cross section is too small to be measured; therefore, the available experimental value of $\sigma \left(E_{\mathrm{c}.\mathrm{m}.}\right)$ at $E_{\mathrm{c}.\mathrm{m}.}=23.3\text{keV}$ is a benchmark for comparing different experimental methods and the results obtained from various theoretical models. The summary at $\sigma \left(23.3\text{keV}\right)$ is presented in Table 4. We note the good agreement of our calculations with the data of [16], [18], [19], and with the evaluated values suggested as the presently recommended values.

Table 4

Table 4. Comparison of the ¹⁴C neutron capture cross sections at $E_{\mathrm{c}.\mathrm{m}.}=23.3\text{keV}$.

Figure 2 shows the neutron capture cross section divided by E^1/2, i.e., $S_n\left(E\right)=\sigma \left(E\right)/\sqrt{E}$. It should be noted that the theoretical calculations [13, 18] and the present MPCM results agree well. At an energy of 10⁻⁸ MeV, S_n(E) = 1.002 μb·keV^-1/2 for the total cross section and S_n(E) = 0.949 μb·keV^-1/2 for capture to the GS, corresponding to ∼95% dominance. The contribution of the first ES is ∼5% at low energies.

Figure 2

Figure 2. Total cross sections of the radiative n¹⁴С capture divided by E^1/2. The inset shows the comparison of the theoretical calculations of [13, 18] and the MPCM results.

4 ¹⁴C(n,γ₀₊₁)¹⁵C reaction rate

The astrophysical rate of the ¹⁴С(n,γ₀₊₁)¹⁵C reaction, calculated in MPCM, is shown in Figure 3. We approximated the MPCM reaction rates using an expression of the form $\left(T_9={10}^9\mathrm{K}\right)$:

$\begin{array}{ll}\hfill N_A〈\sigma v〉& =a_1/T_9^{2/3}\exp \left(-a_2/T_9^{1/3}\right)\left(1.0+a_3{T}_9^{1/3}+a_4{T}_9^{2/3}+a_5{T}_9+a_6{T}_9^{4/3}+a_7{T}_9^{5/3}\right)\hfill \\ \hfill & +a_8{T}_9^{a_9}.\hfill \end{array}(5)$

Figure 3

Figure 3. Rate of the ¹⁴C(n,γ)¹⁵C reaction. MPCM reaction rates: red solid curve, –GS + first ES; blue dashed curve, GS. Inset: comparison of the reaction rates from [18] (dot magenta curve), [11] (dash-dot-dot blue curve), and [19] (dash-dot black curve) normalized to the MPCM rate.

Corresponding parameters a_i for the GS and total reaction rates are provided in Table 5 according (Equation 5). The approximation yields χ² = 0.0005 and χ² = 0.0006, respectively, with an accuracy of 5% for the calculated reaction rates.

Table 5

Table 5. Reaction rate approximation parameters for (Equation 5).

The inset in Figure 3 shows a comparison of present results and reaction rates calculated by [11], [18], and [19] normalized to the rate of the present work. The rate [18] based on the ANC formalism in the interval $T_9=0.003-5$ shows agreement with the MPCM rate within +5% on average, which is very close to that of [11]. The reaction rate in [19] derived from the Coulomb dissociation data is near ∼10% lower than the MPCM rate at the temperatures of $T_9=0.01-1$. In summary, the results of the MPCM are in very good agreement with the modern data from [18, 19].

In Figure 3, we do not present the results from [20] directly, but we compare our reaction rate with the tabulated data of [20]. The authors note that their rate is ∼25% lower than that provided in [11] and ∼2.5–4 times higher than that provided in [7]. Comparison with our rate shows that our data exceeds the rate from [20] by a factor of 1.20. We may conclude that our results are more consistent with those reported in [11, 18, 19].

5 ^12-14C(n,γ)^13-15C reaction rates and ¹²C/¹³C and ¹³C/¹⁴C ratios

Answer to question (i): The MPCM passed the cross-check; therefore, reliable data on the rate of the ¹⁴С(n,γ₀₊₁)¹⁵C reaction may be considered well determined today within ∼10% accuracy. This conclusion allows us to discuss possible corrections to the isotopic ratios ¹²C/¹³C, ¹³C/¹⁴C, and ¹⁴N/¹⁵N, following sequence 2 by comparing the early values from Ref. [1] (Equation 1) and addressing question (ii). The first observation concerns the near factor-of-5 difference in the reaction rates reported by [7] and [8], as shown in Figure 4. This difference changes the ratio ${}^{13}\mathrm{C}{/}^{14}\mathrm{C}>1400$ to ${}^{13}\mathrm{C}{/}^{14}\mathrm{C}>280$. Results obtained by Wiescher et al. 25 years ago have been confirmed today.

Figure 4

Figure 4. Comparison of MPCM results with the modeless calculations implemented by [7] and [8].

Further changes in isotopic ratios may come from the results on reaction rates of the radiative neutron capture on carbon isotopes ¹²C(n,γ)¹³C [38] ¹³C(n,γ)¹⁴C [39], and ¹⁴C(n,γ)¹⁵C (present work) calculated in the same model—MPCM. These rates are shown in Figure 5.

Figure 5

Figure 5. Comparison of the astrophysical ¹²C(n,γ_0+1+2+3)¹³C [38], ¹³C(n,γ₀₊₁₊₂)¹⁴C [39], and ¹⁴C(n,γ₀₊₁)¹⁵C reaction rates in the range T₉ = 0.01–10. Colored areas correspond to the interchange of the reaction rates (see comments in text).

Radiative neutron capture reactions may change the balance of ¹³C/¹⁴C as the ratio of reaction rates $R_{{}^{13}\mathrm{C}/{}^{14}\mathrm{C}}\left(T_9\right)={〈\sigma v〉}_{{}^{12}\mathrm{C}{\left(n,\gamma \right)}^{13}\mathrm{C}}/{〈\sigma v〉}_{{}^{13}\mathrm{C}{\left(n,\gamma \right)}^{14}\mathrm{C}}$ at temperatures $T_9=0.01-0.025$ varies in the range of 2.9–3.2. These rates become equal at $T_9\simeq 0.2$ $\left(R_{{}^{13}\mathrm{C}/{}^{14}\mathrm{C}}=1\right)$, and then, up to $T_9\simeq 1.5$, the production of ¹⁴C exceeds the creation of ¹³C ($R_{{}^{13}\mathrm{C}/{}^{14}\mathrm{C}}\simeq 0.5$ at $T_9\simeq 1.1$).

Comparison of ¹³C(n,γ₀₊₁₊₂)¹⁴C and ¹⁴C(n,γ₀₊₁)¹⁵C rates in Figure 5 shows the temperature intervals where slow production of ¹⁵C exceeds the creation of ¹⁴C. The low energy interval is T₉ = 0.1–0.2, which refers to the equality of the corresponding reaction rates ${〈\sigma v〉}_{{}^{13}\mathrm{C}{\left(n,\gamma \right)}^{14}\mathrm{C}}={〈\sigma v〉}_{{}^{14}\mathrm{C}{\left(n,\gamma \right)}^{15}\mathrm{C}}$ with values of ≃ 290 and ≃ 620 cm³mol^-1s^-1 at the edges. At temperatures T₉ ≳ 3, the rate of ¹⁵C production noticeably prevails over the rate of ¹⁴C formation. It is not meaningful to discuss the unobservable ratio of ¹⁴C/¹⁵C isotopes, but the relative enhancement in the ¹⁴C(n,γ₀₊₁)¹⁵C reaction rate may, to some extent, affect the nitrogen ratio ¹⁴N/¹⁵N.

The production of ¹⁴С in low-metallicity AGB stars is provided by two reactions: ¹³C(n,γ)¹⁴С and ¹⁴N(n,p)¹⁴C [40, 41]. Measurements by Wallner et al. [41] reported cross section at 23.3 keV ${\sigma }_{n,\gamma }=6.7\mathrm{\mu }\mathrm{b}$, ${\sigma }_{n,p}=1.74\text{\hspace{0.17em}mb}$, and ${\sigma }_{n,p}/{\sigma }_{n,\gamma }=260$. The recent measurements of the Maxwellian averaged cross sections (MACS) derived from the n_TOF cross section reported the value ${\sigma }_{n,p}^{\text{MACS}}=1.77\pm 0.04\text{\hspace{0.17em}mb}$ [42] for the $kT=25\text{\hspace{0.5em}keV}$, while the data from [41] are ${\sigma }_{n,p}^{\text{MACS}}=2.03\pm 0.04\text{\hspace{0.17em}mb}$ and ${\sigma }_{n,\gamma }^{\text{MACS}}=20.6\pm 2.7\mathrm{\mu }\mathrm{b}$. Corresponding ratios ${\sigma }_{n,p}^{\text{MACS}}$/ ${\sigma }_{n,\gamma }^{\text{MACS}}$ are 98.5 and 86, respectively. The difference in MACS between Wallner et al. [41] and Torres et.al. [41] becomes noticeable for $kT>15\text{\hspace{0.5em}keV}$ and reaches a factor ∼3 at $kT=100\text{\hspace{0.5em}keV}$.

In simpler terms, the ratio of these two reactions ¹³C(n,γ)¹⁴С and ¹⁴N(n,p)¹⁴C is approximately two orders of magnitude. Hence, the relative concentrations of accumulated nuclei ¹³C and ¹⁴N set the balance between these two reactions, which provides the abundance of ¹⁴C sufficient for a change in the elemental content of carbon pockets. Reaction ¹⁴N(n,p)¹⁴C changes the ratio ¹⁴N/¹⁵N, and at the same time, this ratio may be affected by increasing the number of ¹⁵N via the reaction ${}^{14}\mathrm{С}{\left(n,\gamma \right)}^{15}\mathrm{C}{\left({\beta }^{-}\right)}^{15}\mathrm{N}$.

6 Rate of the ¹⁴C(n,γ₀)¹⁵C reaction with Tsallis statistics

It has been established that thermal pulses arise during the evolution of AGB stars and lead to temperature and density fluctuations in the convective envelope, which can locally disrupt the equilibrium particles’ velocity distribution [1, 2]. The Maxwell–Boltzmann distribution may also be violated due to turbulence and sudden energetic events, such as helium and hydrogen flashes. This provides the motivation for applying Tsallis statistics [23–25], κ-distributions [43–45], and superstatistics [46] when calculating nuclear reaction rates in AGB models.

The application of Tsallis statistics is our first step toward examining non-extensive effects in stellar plasma, for example, the ¹⁴С(n,γ₀)¹⁵C reaction, which may be incorporated into the analysis of the processes occurring in the carbon pockets of AGB stars [1, 4, 6]. The reason for applying Tsallis statistics concerns several aspects. The interpretation of non-extensive parameter q in the velocity distribution f_q(v) is quite straightforward; i.e., in case, q > 1, the Maxwell–Boltzmann f_MB(v) symmetric distribution is violated due to a damping in the number of particles with high energies, whereas case q < 1 implies an enhancement in the low energy component in the f_q(v) distribution compared to the f_MB(v). We also find that the Tsallis formalism is rather simple in application for calculating reaction rate integrals as it allows for convergent control of the results to those of the Maxwell–Boltzmann distribution.

Following [24] and [25], we recalculated the rate of the ¹⁴С(n,γ)¹⁵C reaction simulating the non-extensive effect of Tsallis statistics versus the Maxwell–Boltzmann by changing the velocity distribution from f_MB(v) to f_q(v). Explicit expressions and normalizing conditions for the velocity distributions of non-relativistic particles with an energy $E=\mu v^2/2$ in the center-of-mass system are

$f_{MB}\left(v\right)=4\pi {\left(\frac{\mu }{2\pi kT}\right)}^{3/2}{e}^{-\frac{\mu v^2}{2kT}}{v}^2,{\displaystyle \underset{0}{\overset{\infty }{\int }}}{f}_{MB}\left(v\right)dv=1,(6)$

$f_q\left(v\right)=B_{q}4\pi {\left(\frac{\mu }{2\pi kT}\right)}^{\frac{3}{2}}{\left[1-\left(q-1\right)\frac{\mu v^2}{2kT}\right]}^{\frac{1}{q-1}}{v}^2,\int f_q\left(q\right)dv=1.(7)$

Note that $\underset{q\to 1}{\lim }{\left[1-\left(q-1\right)\frac{E}{kT}\right]}^{\frac{1}{q-1}}=e^{-\frac{E}{kT}}$, so the case $q=1$ of the non-extensive parameter refers to the MB velocity distribution. Normalizing condition in Equation 7 allows us to calculate analytically the normalizing constants B_q and express them via the gamma-function $\mathrm{\Gamma }\left(z\right)$:

$B_q={\left(1-q\right)}^{3/2}\frac{\mathrm{\Gamma }\left(\frac{1}{1-q}\right)}{\mathrm{\Gamma }\left(\frac{1}{1-q}-\frac{3}{2}\right)},\text{\hspace{1em}if\hspace{1em}}\frac{1}{3}\le q<1,(8)$

$B_q={\left(q-1\right)}^{3/2}\left(\frac{1}{q-1}+\frac{3}{2}\right)\left(\frac{1}{q-1}+\frac{1}{2}\right)\frac{\mathrm{\Gamma }\left(\frac{1}{q-1}+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(\frac{1}{q-1}+1\right)},\text{\hspace{1em}if\hspace{0.5em}}q>1.(9)$

In the case of $q<1$, there is no limit of particles by the energy, i.e., $E_{\max }=\infty$. In the case of $q>1$, the kinetic energy is limited as $E_{\max }=\frac{kT}{q-1}$, kT = 0.086173·T₉ (MeV). In Table 6, a few values of B_q (Equations 8, 9) and E_max are presented.

Table 6

Table 6. Normalizing constants B_q and values of E_max (for $q>1$).

The integral over the Maxwellian-weighted cross section (Equation 6) determines the reaction rate, which was derived in detail by Iliadis and is provided in a general form [47]:

$N_A〈\sigma v〉=N_A{\left(\frac{8}{\pi \mu }\right)}^{1/2}{\left(kT\right)}^{-3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}}\sigma \left(E\right)E\exp \left(-\frac{E}{kT}\right)dE.(10)$

Equation 10 along with substituted numerical values for the constants is expressed as:

$N_A{〈\sigma v〉}_{\text{MB}}=3.7313·{10}^4{\mu }^{-1/2}{T_9}^{-3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}}\sigma \left(E\right)E\exp \left(-11.605E/T_9\right)dE.(11)$

In the case of Tsallis statistics and following definition for f_q(v) distribution (Equation 7), Equation 11 can be transformed to

$N_A{〈\sigma v〉}_q=B_q·3.7313·{10}^4{\mu }^{-1/2}{T_9}^{-3/2}{\displaystyle \underset{0}{\overset{E_{\max }}{\int }}}\sigma \left(E\right)E{\left[1-\left(q-1\right)·11.605E/T_9\right]}^{\frac{1}{q-1}}dE.(12)$

In Figure 6 the results of the calculated ${〈\sigma v〉}_q$ reaction rate of the radiative neutron capture to the GS of the ¹⁵C nucleus for the interval of non-extensive parameter $0.7\le q\le 1.3$ are presented. It is clear that the case $q>1$ corresponds to the inequality ${〈\sigma v〉}_q<{〈\sigma v〉}_{\text{MB}}$, which can be explained by looking at the E_max values of q in Table 6 and the energy dependence of the total cross section $\sigma \left(E\right)$ in Figure 1. Since no cut-off of integrand in Equation 12 in the case of $q<1$, the corresponding reaction rates are related as ${〈\sigma v〉}_q>{〈\sigma v〉}_{\text{MB}}$.

Figure 6

Figure 6. Reaction rates calculated for the Tsallis statistics: $q>1$ – blue band, $q<1$ – red band relative to the Maxwellian-Boltzmann rate–black solid curve.

Figure 7 shows the numerical difference in reaction rates, considering the effect of the non-equilibrium Tsallis distribution compared to the MB distribution for $0.9\le q\le 1.1$. The difference in rates ${〈\sigma v〉}_q/{〈\sigma v〉}_{\text{MB}}$ is ∼4%–35% increase for $0.99\le q\le 1.1$ and ∼4–20% decrease for $1.01\le q\le 1.10$. Figure 6 shows a factor ∼4 increase in ${〈\sigma v〉}_q$ for $q=0.7$ and a factor ∼0.6 decrease for $q=1.3$.

Figure 7

Figure 7. Ratio of the Tsallis reaction rates to the Maxwell–Boltzmann rate.

In [20] Jiang et al., implemented the calculated ¹⁴С(n,γ)¹⁵C reaction rate ${〈\sigma v〉}_{MB}$ for the estimation of the ¹⁵N abundance, which results in ∼20% increase of nitrogen-15 production, but only ∼0.2% impact on the final abundances of heavy elements with A > 90. As we mentioned above, the present ${〈\sigma v〉}_{MB}$ rate for this reaction is ∼1.2 times higher than reported in [20]. If we assume the non-extensive parameter q = 0.7, the increasing factor for the reaction rate ${〈\sigma v〉}_q$ is ∼5; therefore, ¹⁵N abundance may increase much higher than estimations based on the rate by Jiang et al., 2025. Note that the value q = 0.7 refers to a rather strong enhancement of the high-energy tails, which may arise from extreme events in the AGB environment.

Note that we have implemented a simplified calculation procedure, assuming that the effect of the center-of-mass correction, introduced by [26, 27], is not essential, as the seed nucleus ¹⁴C is much heavier than the light species with comparable masses involved at the stage of primordial BBN.

7 Conclusion

In summary, we show that the MPCM results on ¹⁴С(n,γ₀₊₁)¹⁵C are in good agreement with those reported in [18, 19]. Benchmark cross section $\sigma \left(23.3\text{keV}\right)$ = 4.75 μb matches the presently recommended value 4.86(48) μb reported in [18]. The Maxwellian-weighted reaction rates calculated in the MPCM agree within ∼±10% deviations with the independent calculations of [8, 11, 18], and [19], therefore, the data on the MB rate of the ¹⁴C(n,γ)¹⁵C reaction can be considered well determined today.

The obtained values of reaction rates can be confidently conceived as the reference ones for the re-estimation of ¹²C/¹³C, ¹³C/¹⁴C, and ¹⁴N/¹⁵N via the neutron-induced reactions ¹²C(n,γ_0+1+2+3)¹³C, ¹³C(n,γ₀₊₁₊₂)¹⁴C, and ¹⁴C(n,γ₀₊₁)¹⁵C calculated in MPCM. We determined the temperature windows where the interchange of reaction rates is observed: ${〈\sigma v〉}_{{}^{13}\mathrm{C}{\left(n,\gamma \right)}^{14}\mathrm{C}}>{〈\sigma v〉}_{{}^{12}\mathrm{C}{\left(n,\gamma \right)}^{13}\mathrm{C}}$ at T₉ = 0.2–1.5; ${〈\sigma v〉}_{{}^{14}\mathrm{C}{\left(n,\gamma \right)}^{15}\mathrm{C}}>{〈\sigma v〉}_{{}^{13}\mathrm{C}{\left(n,\gamma \right)}^{14}\mathrm{C}}$ at AGB stars’ actual temperatures T₉ = 0.1–0.2 and at higher values T₉ ≳ 3.

Here, in order to finalize the values of isotopic ratios, it is reasonable to consider the reaction rates ^12-14C(n,γ)^13-15C together with the proton-induced reactions ^12-14C(p,γ)^13-15N calculated in the same model. We took a step forward toward this goal by calculating the MPCM rate for the ¹²C(p,γ)¹³N reaction [48].

The Tsallis statistics allow one to vary the numerical values of the ¹⁴С(n,γ₀₊₁)¹⁵C reaction rate, as illustrated in the present calculations for the range of the non-extensive parameter $0.7\le q\le 1.3$. This provides a tool for the re-estimation of astrophysical processes occurring in low-metallicity AGB stars, in particular, the production and depletion carbon isotopes as reflected in the observed ¹³C/¹⁴C ratio. Note that the value of the ¹³C/¹⁴C ratio directly affects the ratio of nitrogen isotope yields, ¹⁴N/¹⁵N. Comparing these results with studies of BBN reactions [25–27], the effect of non-extensivity in the case of the ¹⁴С(n,γ₀)¹⁵C reaction is moderate—not orders of magnitude—but can produce a maximum factor of ∼1.35 increase or ∼0.8 decrease in the MB reaction rate for $0.9\le q\le 1.1$. One reason for this moderate effect may be that, in the case of BBN, charged particles of comparable mass are involved in the reactions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AT: Conceptualization, Supervision, Writing – review and editing. NB: Formal analysis, Writing – original draft. BY: Data curation, Writing – review and editing. SD: Software, Validation, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP19676483).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Forestini M, Charbonnel C. Nucleosynthesis of light elements inside thermally pulsing AGB stars. Astron Astrophys Suppl Ser (1997) 123:241–72. doi:10.1051/aas:1997348

CrossRef Full Text | Google Scholar

2. Forestini M, Guelin M, Cernicharo J. ¹⁴C in AGB stars: the case of IRC+10216. Astron Astrophys (1997) 317:883–8.

Google Scholar

3. Karakas AI, Lattanzio JC. The dawes review 2: nucleosynthesis and stellar yields of Low- and intermediate-mass single stars. Publ Astron Soc Aust 31:e030. (2014) doi:10.1017/pasa.2014.21

CrossRef Full Text | Google Scholar

4. Palmerini S, Busso M, Vescovi D, Naselli E, Pidatella A, Mucciola R, et al. Presolar grain isotopic ratios as constraints to nuclear and stellar parameters of asymptotic giant branch star nucleosynthesis. Astrophys J (2021) 921:7. doi:10.3847/1538-4357/ac1786

CrossRef Full Text | Google Scholar

5. Herwig F. Evolution of asymptotic giant branch stars. Annu Rev Astron Astrophys (2005) 43:435–79. doi:10.1146/annurev.astro.43.072103.150600

CrossRef Full Text | Google Scholar

6. Choplin A, Siess L, Goriely S. Proton ingestion in asymptotic giant branch stars as a possible explanation for J-type stars and AB2 grains. Astron Astrophys (2024) 691:L7. doi:10.1051/0004-6361/202451013

CrossRef Full Text | Google Scholar

7. Beer H, Wiescher M, Kaeppeler F, Goerres J, Koehler PE. A measurement of the C-14(n, gamma)C-15 cross section at a stellar temperature of kT = 23.3 keV. Astrophys J (1992) 387:258. doi:10.1086/171077

CrossRef Full Text | Google Scholar

8. Wiescher M, Gorres J, Thielemann F-K. Capture reactions on C-14 in nonstandard big bang nucleosynthesis. Astrophys J (1990) 363:340. doi:10.1086/169348

CrossRef Full Text | Google Scholar

9. Horvath A, Weiner J, Galonsky A, Deak F, Higurashi Y, Ieki K, et al. Cross section for the astrophysical ¹⁴C(n,γ)¹⁵C reaction via the inverse reaction. Astrophys J (2002) 570:926–33. doi:10.1086/339726

CrossRef Full Text | Google Scholar

10. Reifarth R, Heil M, Plag R, Besserer U, Dababneh S, Dörr L, et al. Stellar neutron capture rates of ¹⁴C. Nucl Phys A (2005) 758:787–90. doi:10.1016/j.nuclphysa.2005.05.141

CrossRef Full Text | Google Scholar

11. Reifarth R, Heil M, Forssén C, Besserer U, Couture A, Dababneh S, et al. The ¹⁴C(n,γ) cross section between 10 keV and 1 MeV. Phys Rev C (2008) 77:015804. doi:10.1103/PhysRevC.77.015804

CrossRef Full Text | Google Scholar

12. Nakamura T, Fukuda N, Aoi N, Imai N, Ishihara M, Iwasaki H, et al. Neutron capture cross section of ¹⁴C of astrophysical interest studied by coulomb breakup of ¹⁵C. Phys Rev C (2009) 79:035805. doi:10.1103/PhysRevC.79.035805

CrossRef Full Text | Google Scholar

13. Timofeyuk NK, Baye D, Descouvemont P, Kamouni R, Thompson IJ. ¹⁵C−¹⁵F charge symmetry and the ¹⁴C(n,γ)¹⁵C reaction puzzle. Phys Rev Lett (2006) 96:162501. doi:10.1103/PhysRevLett.96.162501

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Summers NC, Nunes FM. Extracting (n,γ) direct capture cross sections from coulomb dissociation: application to ¹⁴C(n,γ)¹⁵C. Phys Rev C (2008) 78:011601. doi:10.1103/PhysRevC.78.011601

CrossRef Full Text | Google Scholar

15. McCleskey M, Mukhamedzhanov AM, Trache L, Tribble RE, Banu A, Eremenko V, et al. Determination of the asymptotic normalization coefficients for ¹⁴C + n ↔ ¹⁵C, the ¹⁴C(n,γ)¹⁵C reaction rate, and evaluation of a new method to determine spectroscopic factors. Phys Rev C (2014) 89:044605. doi:10.1103/PhysRevC.89.044605

CrossRef Full Text | Google Scholar

16. Capel P, Nollet Y. Reconciling coulomb breakup and neutron radiative capture. Phys Rev C (2017) 96:015801. doi:10.1103/PhysRevC.96.015801

CrossRef Full Text | Google Scholar

17. Moschini L, Yang J, Capel P. ¹⁵C: from halo effective field theory structure to the study of transfer, breakup, and radiative-capture reactions. Phys Rev C (2019) 100:044615. doi:10.1103/PhysRevC.100.044615

CrossRef Full Text | Google Scholar

18. Ma T, Guo B, Pang D, Li Z, Su Y, Li X, et al. New determination of astrophysical ¹⁴C(n, γ)¹⁵C reaction rate from the spectroscopic factor of ¹⁵C. Sci China Phys Mech Astron (2020) 63:212021. doi:10.1007/s11433-019-9411-2

CrossRef Full Text | Google Scholar

19. Bhattacharyya A, Datta U, Rahaman A, Chakraborty S, Aumann T, Beceiro-Novo S, et al. Neutron capture cross sections of light neutron-rich nuclei relevant for r-process nucleosynthesis. Phys Rev C (2021) 104:045801. doi:10.1103/PhysRevC.104.045801

CrossRef Full Text | Google Scholar

20. Jiang Y, He Z, Luo Y, Xin W, Chen J, Li X, et al. New determination of the ¹⁴C(n,γ)¹⁵C reaction rate and its astrophysical implications. Astrophys J (2025) 989:231. doi:10.3847/1538-4357/ade5b3

CrossRef Full Text | Google Scholar

21. Dubovichenko SB, Uzikov YN. Astrophysical S-factors of reactions with light nuclei. Phys Particles Nuclei (2011) 42:251–301. doi:10.1134/S1063779611020031

CrossRef Full Text | Google Scholar

22. Dubovichenko SB. Radiative neutron capture: primordial nucleosynthesis of the universe. Berlin: De Gruyter (2019).

Google Scholar

23. Tsallis C. Possible generalization of boltzmann-gibbs statistics. J Stat Phys (1988) 52:479–87. doi:10.1007/BF01016429

CrossRef Full Text | Google Scholar

24. Hou SQ, He JJ, Parikh A, Daid K, Bertulani C. Big-bang nucleosynthesis verifies classical maxwell-boltzmann distribution (2014) Available online at: http://arxiv.org/abs/1408.4422 (Accessed Feburary 07, 2025).

Google Scholar

25. Hou SQ, He JJ, Parikh A, Kahl D, Bertulani CA, Kajino T, et al. Non-extensive statistics to the cosmological lithium problem. Astrophys J (2017) 834:165. doi:10.3847/1538-4357/834/2/165

CrossRef Full Text | Google Scholar

26. Kusakabe M, Kajino T, Mathews GJ, Luo Y. On the relative velocity distribution for general statistics and an application to big-bang nucleosynthesis under tsallis statistics. Phys Rev D (2019) 99:043505. doi:10.1103/PhysRevD.99.043505

CrossRef Full Text | Google Scholar

27. Bertulani CA. Shubhchintak. Primordial nucleosynthesis with non-extensive statistics. Eur Phys J Spec Top (2024) 233:2831–42. doi:10.1140/epjs/s11734-024-01216-0

CrossRef Full Text | Google Scholar

28. Dubovichenko S, Dzhazairov-Kakhramanov A, Afanasyeva N. Radiative neutron capture on ⁹Be, ¹⁴C, ¹⁴N, ¹⁵N and ¹⁶O at thermal and astrophysical energies. Int J Mod Phys E (2013) 22:1350075. doi:10.1142/S0218301313500754

CrossRef Full Text | Google Scholar

29. Mukhamedzhanov AM, Tribble RE. Connection between asymptotic normalization coefficients, subthreshold bound states, and resonances. Phys Rev C (1999) 59:3418–24. doi:10.1103/PhysRevC.59.3418

CrossRef Full Text | Google Scholar

30. Yamaguchi T, Hachiuma I, Kitagawa A, Namihira K, Sato S, Suzuki T, et al. Scaling of charge-changing interaction cross sections and point-proton radii of neutron-rich carbon isotopes. Phys Rev Lett (2011) 107:032502. doi:10.1103/PhysRevLett.107.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zhao JW, Sun B-H, Tanihata I, Xu JY, Zhang KY, Prochazka A, et al. Charge radii of ¹¹⁻¹⁶C, ¹³⁻¹⁷N and ¹⁵⁻¹⁸O determined from their charge-changing cross-sections and the mirror-difference charge radii. Phys Lett B (2024) 858:139082. doi:10.1016/j.physletb.2024.139082

CrossRef Full Text | Google Scholar

32. Zhao JW, Sun B-H, Tanihata I, Terashima S, Prochazka A, Xu JY, et al. Isospin-dependence of the charge-changing cross-section shaped by the charged-particle evaporation process. Phys Lett B (2023) 847:138269. doi:10.1016/j.physletb.2023.138269

CrossRef Full Text | Google Scholar

33. Li LY, Tu XL, Zhang JT, Zhang GQ. Nuclear matter distribution radius compilation and evaluation: NMRCE2025. At Data Nucl Data Tables (2025) 166:101747. doi:10.1016/j.adt.2025.101747

CrossRef Full Text | Google Scholar

34. Kanungo R, Horiuchi W, Hagen G, Jansen GR, Navratil P, Ameil F, et al. Proton distribution radii of ^12-19C illuminate features of neutron halos. Phys Rev Lett (2016) 117:102501. doi:10.1103/PhysRevLett.117.102501

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Dobrovolsky AV, Korolev GA, Tang S, Alkhazov GD, Colò G, Dillmann I, et al. Nuclear matter distributions in the neutron-rich carbon isotopes ¹⁴⁻¹⁷C from intermediate-energy proton elastic scattering in inverse kinematics. Nucl Phys A (2021) 1008:122154. doi:10.1016/j.nuclphysa.2021.122154

CrossRef Full Text | Google Scholar

36. Hebborn C, Capel P. Halo effective field theory analysis of one-neutron knockout reactions of ¹¹Be and ¹⁵C. Phys Rev C (2021) 104:024616. doi:10.1103/PhysRevC.104.024616

CrossRef Full Text | Google Scholar

37. Ajzenberg-Selove F. Energy levels of light nuclei A = 13–15. Nucl Phys A (1991) 523:1–196. doi:10.1016/0375-9474(91)90446-D

CrossRef Full Text | Google Scholar

38. Dubovichenko SB, Burkova NA. Rate of radiative n¹²C decay at temperatures from 0.01 T₉ to 10 T₉. Russ Phys J (2021) 64:216–27. doi:10.1007/s11182-021-02319-0

CrossRef Full Text | Google Scholar

39. Dubovichenko SB. n¹³C capture reaction rate. Russ Phys J (2022) 65:208–15. doi:10.1007/s11182-022-02624-2

CrossRef Full Text | Google Scholar

40. Lugaro M, Herwig F, Lattanzio JC, Gallino R, Straniero O. Process nucleosynthesis in asymptotic giant branch stars: a test for stellar evolution. Astrophys J (2003) 586:1305–19. doi:10.1086/367887

CrossRef Full Text | Google Scholar

41. Wallner A, Bichler M, Buczak K, Dillmann I, Käppeler F, Karakas A, et al. Accelerator mass spectrometry measurements of the ¹³C(n,γ)¹⁴C and ¹⁴N(n,p)¹⁴C cross sections. Phys Rev C (2016) 93:045803. doi:10.1103/PhysRevC.93.045803

CrossRef Full Text | Google Scholar

42. Torres-Sánchez P, Praena J, Porras I, Sabaté-Gilarte M, Lederer-Woods C, Aberle O, et al. Measurement of the ¹⁴N(n,p)¹⁴C cross section at the CERN n_TOF facility from subthermal energy to 800 keV. Phys Rev C (2023) 107:064617. doi:10.1103/PhysRevC.107.064617

CrossRef Full Text | Google Scholar

43. Kong H, Xie H, Liu B, Tan M, Luo D, Li Z, et al. Enhancement of fusion reactivity under Non-Maxwellian distributions: effects of drift-ring-beam, slowing-down, and kappa super-thermal distributions. Plasma Phys Control Fusion (2024) 66:015009. doi:10.1088/1361-6587/ad1008

CrossRef Full Text | Google Scholar

44. Squarer BI, Presilla C, Onofrio R. Enhancement of fusion reactivities using Non-Maxwellian energy distributions. Phys Rev E (2024) 109:025207. doi:10.1103/PhysRevE.109.025207

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Livadiotis G. Kappa distributions: statistical physics and thermodynamics of space and astrophysical plasmas. Universe (2018) 4:144. doi:10.3390/universe4120144

CrossRef Full Text | Google Scholar

46. Ourabah K. Reaction rates in quasiequilibrium states. Phys Rev E (2025) 111:034115. doi:10.1103/PhysRevE.111.034115

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Iliadis C. Nuclear physics of stars. Second. Weinheim, Germany: Wiley-VCH Verlag GmbH and Co. KGaA (2015).

Google Scholar

48. Dubovichenko SB, Burkova NA, Tkachenko AS, Samratova A. Reaction rate of radiative p¹²C capture in a modified potential cluster model. Chin Phys C (2025) 49:044104. doi:10.1088/1674-1137/ada34d

CrossRef Full Text | Google Scholar

49. Mukhamedzhanov AM, Burjan V, Gulino M, Hons V, Kroha Z, McCleskey M, et al. Asymptotic normalization coefficients from the ¹⁴C(d,p)¹⁵C reaction. Phys. Rev. C (2011) 84:024616. doi:10.1103/PhysRevC.84.024616

CrossRef Full Text | Google Scholar