Model calculation of charged galactic cosmic ray radiation dose during a flight to Mars

The radiation exposure from galactic cosmic rays (GCRs) presents a significant challenge for human spaceflight to Mars. In this study, we employ our previously published GCR radiation dose calculation model to estimate the GCR radiation dose rates during a Mars mission from the Earth. Using this model, we calculate the absorbed dose rates of GCRs during the flight to Mars and compare our results with observational data from the Mars Science Laboratory Radiation Assessment Detector (MSL-RAD) and computational results from the Badhwar-O’Neill (BON) GCR model. First, we compute the energy spectrum of GCRs during the Earth-to-Mars transit using the GCR modulation model. Then, using the fluence-to-dose conversion coefficients (FDCCs) from ICRP 123, the absorbed dose rates of 15 human organs/tissues during the Earth-to-Mars transit are calculated to represent the general absorbed dose rate of the body (in water). Furthermore, considering the contributions of different elements and the underestimation of the model in 2012, we calculate the total absorbed dose rates of charged GCRs in silicon during the flight. Our results generally align with the BON11 model (excluding pions) and are consistently $\sim$20% lower than the central value of the MSL-RAD/B observational data within expected uncertainties. This work may provide help for the future mission with radiation protection.

1 Introduction

Galactic cosmic rays (GCRs) are high-energy particles originating from outside the solar system, consisting primarily of protons, helium nuclei, and heavier ions [1]. These particles travel at close to the speed of light and can penetrate spacecraft shielding, posing significant radiation risks to both astronauts and electronic equipment [2]. GCR radiation poses a significant concern for long-duration space missions, such as a Mars expedition, due to the extended exposure duration and the current inadequacy of shielding technologies to effectively mitigate the impact of such high-energy particles [3]. Understanding and accurately predicting GCR radiation doses are therefore critical for ensuring the safety of future manned missions to Mars and beyond.

The radiation environment in free space differs significantly from that on Earth’s surface. On Earth, the shielding effect of the ground limits GCR exposure to a 2$\pi$ geometry. Furthermore, the presence of Earth’s magnetic field and atmosphere significantly reduces the harmful effects of GCR radiation on humans and the environment. However, once outside the protective shield of Earth, during interplanetary travel, humans are exposed to substantially higher levels of GCR radiation, which poses serious health risks [4]. For example, in the International Space Station (ISS), typical GCR dose rates range from 90 to 110 $\mu$Gy/day, excluding the influence of the South Atlantic Anomaly (SAA). In deep space near Earth, typical GCR dose rates increase to 250–500 $\mu$Gy/day, reflecting the significantly higher radiation levels encountered during interplanetary travel [5]. In terms of observational data, the Radiation Assessment Detector (RAD) on board the Mars Science Laboratory (MSL) provided valuable observations of the GCR radiation doses during the spacecraft’s journey to Mars [6]. [3] reported measurements of the energetic particle radiation environment inside the MSL during its cruise to Mars from 6 December 2011, to 14 July 2012, offering important insights for future human missions to Mars. In addition, several GCR modulation models have been developed to predict GCR radiation doses under various conditions. These include the Badhwar-O’Neill (BON) model, the Heliospheric Modulation Model (HelMod), and the Cosmic Ray Effects on Micro-Electronics (CREME96) model, among others (e.g., [2,7]). These models estimate radiation exposure by incorporating factors such as solar modulation, spacecraft shielding, and particle transport [8]. However, the discrepancies between the observed and simulated data highlight the need for further refinement of these models [9].

The radiation environment in free space and exposure to GCR radiation are considered among the primary health risks for future long-duration human exploration missions [5]. [10] estimated the GCR radiation dose rates around the lunar surface, using a GCR radiation dose calculation model. Although the modeling results generally agreed with spacecraft observation, they underestimated the observations in the year 2012 (indicated as underestimation of the model in 2012 hereafter). In this study, following [10], we employ numerical simulations using the GCR modulation model developed in previous work [11–13] to calculate the GCR energy spectra for the four predominant GCR nuclei (protons, helium, oxygen, and iron ions) during the Earth-to-Mars transit. By combining these simulation results with the FDCCs from ICRP Publication 123 [4,14,15] and considering the contributions of different elements (based on the contribution percentages in Table 1 of [10]), as well as the underestimation of the model in 2012, we derive time-dependent GCR absorbed dose rates during the transit period, accounting for all 26 GCR nuclei. In Section 2, we introduce the methodology for calculating the GCR radiation dose during a flight to Mars. In Section 3, we present the calculated results and compare them with observations. Finally, in Section 4, we provide a summary and discussion of our study.

2 Methodology

2.1 Experiment

The RAD on the MSL rover “Curiosity” is a comprehensive instrument designed to measure the energetic particle radiation environment. The RAD instrument, which includes a telescope comprising silicon detectors (A, B, C) and scintillators (D, E, F), provides comprehensive measurements of the radiation field. Detector B provides the absorbed dose rate in silicon for charged particles, while detector E, due to its tissue-equivalent composition, provides a more biologically relevant tissue dose rate and is also more sensitive to neutrons. During the cruise to Mars, RAD was housed inside the spacecraft, enabling it to measure the mixed field of primary galactic cosmic rays and secondary particles generated in the spacecraft shielding. This makes its data particularly relevant for assessing the radiation exposure for a crewed mission in a similarly shielded vehicle [6].

2.2 GCR model

This study extends our prior GCR dose model, which computes radiation dose by numerically solving the Parker transport equation to obtain GCR fluxes and converting them to dose rates using ICRP 123 FDCCs, a methodology validated against lunar radiation data (LRO/CRaTER, Chang’E-4/LND) [10]. For the present study, we validate the model against the Mars transit radiation environment using data from the MSL-RAD.

Building upon this work, we employ the GCR modulation model developed by Shen & Qin [11–13] to calculate the GCR energy spectra. The primary advancement here is the application of this model to the specific trajectory and time period of an Earth-to-Mars transit. This section provides a concise overview of the model implementation; for complete methodological details and theoretical foundations, we refer the reader to our prior publications.

2.2.1 Transport equation

The transport of GCRs in the heliosphere is fundamentally modulated by solar activity. This process is governed by the Parker transport equation [16], which accounts for diffusion, convection, particle drifts, and adiabatic energy changes of charged particles in the heliospheric magnetic field,

$\frac{\partial f}{\partial t}=-\left({\mathit{V}}_{\text{sw}}+⟨{\mathit{V}}_{\text{d}}⟩\right)\cdot \nabla f+\nabla \cdot \left({\mathit{K}}_{\text{s}}\cdot \nabla f\right)+\frac{1}{3}\left(\nabla \cdot {\mathit{V}}_{\text{sw}}\right)\frac{\partial f}{\partial \ln p},(1)$

here, $f(\mathit{r},p,t)$ represents the omnidirectional distribution function of cosmic rays, where $\mathit{r}$ is the spatial position in heliocentric coordinates, $p$ is particle momentum (typically in GeV/c), and $t$ is time. Key parameters include: $V_{\text{sw}}$, solar wind velocity ($\sim$400–800 km/s in the ecliptic plane); $⟨V_{\text{d}}⟩$, pitch-angle-averaged drift velocity; ${\mathit{K}}_{\text{s}}$, symmetric diffusion tensor component. The differential flux $j$ is related to the distribution function through $j=p^{2}f$. The right-hand side terms represent convection, drifts, diffusion, and adiabatic energy changes, respectively.

2.2.2 Source spectrum

Since our GCR model does not include modulation effects beyond the heliospheric termination shock, for high energy particles, we follow previous studies [11–13] by setting the modulation boundary at the termination shock (assumed to be at 85 AU) and adopting an input spectrum [17]. Following [10], we express the GCR source at 85 AU as follows: for protons source, the local interstellar spectrum (LIS) by [17] is applied,

$j_s=j_{\text{LIS}}=J_0{p}_0^{2.6}p{\left(m_0^2{c}^2+p^2\right)}^{-1.8},(2)$

for heavy ion sources (He–Fe), the model from [13] is used,

$j_s=j_0{\beta }^{\delta }{\left(\frac{E+E_0}{E_c}\right)}^{-\gamma },(3)$

where $J_0$ is a normalization constant, $p_0$ = 1 GeV/$c$, $p$ is the particle momentum, $c$ is the speed of light, and $m_0$ is the particle mass. $E_0$ represents the rest energy per nucleon, $E_c$ = 1 GeV ${\text{n}}^{-1}$, and $j_0$, $\delta$ and $\gamma$ are free parameters (values provided in Table 2 of [13]).

2.2.3 Numerical methods

To numerically solve the Parker transport equation, we employ the time-backward Markov stochastic process method developed by [18]. This approach transforms the partial differential equation (Equation 1) into the following set of stochastic differential equations [18,19]:

$\mathrm{d}{x}_i=A_i\left(x_i\right)\mathrm{d}s+{\displaystyle \sum _j}{B}_{ij}\left(x_i\right)\cdot \mathrm{d}{W}_i,(4)$

where $x_i$ $(i\in (r,\theta ,\varphi ,P))$ are Itô processes, $\mathrm{d}{W}_i\sim \mathcal{N}(\mathrm{0,1})$, $A$ is a multidimensional vector governing continuous slow variations, and $B_{ij}$ is a matrix describing the rapidly varying stochastic process, all of the variables can be obtained from the transport equation of cosmic rays [11,18,20,21].

We track the trajectories of multiple pseudo-particles in the backward direction from the observer’s position until they reach the outer boundary, and calculate their intensities using the GCR source spectrum (Equations 2, 3) in conjunction with the stochastic process method (Equation 4). For each month, we assume a locally static heliosphere, where the interplanetary conditions (e.g., $B$, $\delta B$, $P_A$, ${\mathit{V}}_{\text{sw}}$) at position $\mathit{r}$ and time $t$ are determined by the states at the source surface $r_s$ at an earlier time, as outlined by [22]. Consequently, we implement a time-delayed heliosphere model, as proposed in previous studies [11–13], and solve the transport equation at monthly intervals.

2.3 Radiation dose rates model

Following [10], we have the radiation dose rates model as below.

Considering the particle differential flux $j(\mathit{r},E,t)$ and the fluence-to-absorbed-dose conversion coefficients (absorbed-FDCCs) $d_{\text{T,R}}(E)$, with the coefficients evaluated for an isotropic irradiation on a water phantom, the absorbed dose rate can be written as:

$D_{\text{t}}=\frac{1}{n_{\text{T}}}{\displaystyle \sum _{\text{T}=1}^{n_{\text{T}}}}{\displaystyle \sum _{\text{R}}}{\int }_E{\int }_{\mathrm{\Omega }}{d}_{\text{T,R}}\left(E\right)j\left(\mathit{r},E,t\right)\mathrm{d}\mathrm{\Omega }\mathrm{d}E,(5)$

where $j(\mathit{r},E,t)$ is the particle differential flux (in units of ${\text{m}}^{-2}$ ${\text{s}}^{-1}$ ${\text{sr}}^{-1}$ ${\text{GeV}}^{-1}$/n⁻¹); the absorbed-FDCCs $d_{\text{T,R}}(E)$, as released by [4]; [14,15], are in units of pGy ${\text{cm}}^2$; T represents a given organ/tissue; R represents the radiation type; $\mathrm{\Omega }$ is the solid angle, and $n_{\mathrm{T}}$ is the number of organs/tissues. Here, because the true particle differential flux $j(\mathit{r},E,t)$ is inaccessible, we evaluate Equation 5 with the differential flux simulated by our GCR modulation program, $j^{\mathrm{s}\mathrm{i}\mathrm{m}}(\mathit{r},E,t)$, where label “$\mathrm{m}\mathrm{o}\mathrm{d}$” indicates “simulation”.

For a given organ/tissue T and radiation type R, we use our GCR modulation model to calculate the differential flux $j(\mathit{r},E,t)$ of the four predominant GCR nuclei (protons, helium, oxygen, and iron ions) during the Earth-to-Mars transit. According to Equation 5, we combine the differential flux $j(\mathit{r},E,t)$ with the absorbed-FDCCs $d_{\mathrm{T},\mathrm{R}(E)}$ from ICRP Publication 123 [4,14,15], with $\mathrm{\Omega }=4\pi$, energy $E$ ranging from 1 MeV/nucleon to 100 GeV/nucleon, and R $\in$ H, He, O, Fe, and $n_{\mathrm{T}}=15$, to obtain the time-dependent absorbed dose rates for the four main GCRs during the transit, $D_{\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}}$. Here, we obtain the simulated differential flux, $j^{\mathrm{s}\mathrm{i}\mathrm{m}}(\mathit{r},E,t)$, of the four predominant GCR nuclei (H, He, O, Fe) by numerically solving the Parker modulation equation for GCRs. Among them, following [10], we adopt the approximation that energy deposition is nearly uniform across all tissues under high-energy GCR irradiation. This approximation allows us to use the averaged value over 15 organs/tissues as a representative whole-body dose rate. Next, following [10], to save computational resources and improve efficiency, we incorporate the radiation doses from the remaining 22 nuclei ($\sim$26.5%) into the results for the four main GCR nuclei based on the pre-calculated contribution percentages of radiation absorbed doses (listed in Table 1 of [10]). This approach, which uses the heavy ion oxygen ($\sim$8.5%) as a key reference, represents the total radiation absorbed dose rates for all 26 GCR nuclei (H to Fe). We assume this as the modeling results of the absorbed dose rate $D_{\mathrm{t}}^{\mathrm{m}\mathrm{o}\mathrm{d}}$, which serves as an approximation to the true absorbed dose rates $D_{\mathrm{t}}$. From [10], the model systematically underestimates the true physical quantity, so the total radiation absorbed dose rates with correction, $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$, during the Mars transit in free space (in silicon) can be obtained with

$D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}=\lambda D_{\mathrm{t}}^{\mathrm{m}\mathrm{o}\mathrm{d}}.(6)$

Here $\lambda$ denotes a correction factor that compensates for the systematic underestimation, as illustrated in Figure 7 of [10], which was attributed to the oversimplified GCR modulation model failing to accurately capture the relatively weak solar activity around 2012 during Solar Cycle 24 (as indicated by long-term sunspot data), leading to underestimated flux and dose. We have adopted $\lambda =1.321$ to account for the underestimation observed in 2012, and we adhere to the water-silicon conversion factor of 1.333, both as recommended by [10]. Furthermore, to consider the secondary charged particle radiation produced by GCR interactions inside the spacecraft, the total absorbed dose rate inside the spacecraft, $D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$, during the journey to Mars can be written as

$D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}=\alpha D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}},(7)$

with a scale factor $\alpha$. This empirical factor $\alpha$ link our free-space GCR dose calculation with the in-situ measurement by primarily accounting for the net contribution of secondary charged particles from spacecraft shielding.

3 Results

In the following, we present observational and numerical results for the radiation absorbed dose rates of GCRs during a flight to Mars (in silicon). The MSL spacecraft was launched to Mars on 26 November 2011. During most of the 253-day, 560-million-kilometer cruise to Mars, the RAD instrument made detailed measurements of the energetic particle radiation environment inside the spacecraft [23]. In the following, we use the dosimetry data from the MSL-RAD silicon detector B, as our model focuses on the dose rate from GCR charged particles in free space (excluding neutral particles such as neutrons), which aligns with the measurement capability of detector B. The data are sourced from the digitization of Figure 5 in [23], with the radioisotope thermoelectric generator (RTG) background already subtracted. The radiation measurements during the 7-month cruise to Mars exhibit characteristic variability patterns - including $\sim$27-day solar rotation effects, Forbush decreases, and SEP spikes. We have filtered the dataset by removing the five identified SEP events to ensure our analysis focuses exclusively on GCR-induced variations. A complete list of these SEP events can be found in the cruise phase analysis by [24]. Considerable work has been done comparing the measured and calculated dose rates (e.g., [25,26]). [3] reported that the BON11 GCR flux model used the HZETRN radiation transport code to calculate the dose rate of GCRs during the flight to Mars and estimated the contribution from pions and their decay products (including muons, electrons, and $\gamma$ rays) during the flight to Mars [27,28].

Figure 1 shows the GCR radiation absorbed dose rate (in silicon) with the horizontal axis tracking the spacecraft’s transit time from Earth to Mars. The silver solid line with solid circles represents the absorbed dose rate detected by MSL-RAD/B, while the black solid line shows the smoothed result. As can be seen from the figure, the observed values of absorbed dose rate exhibit relatively severe fluctuations, which may be caused by local disturbances in the space environment. The blue solid and dash-dotted lines represent the modeling results from the BON11 model, without and with pion contributions, respectively [3].

Figure 1

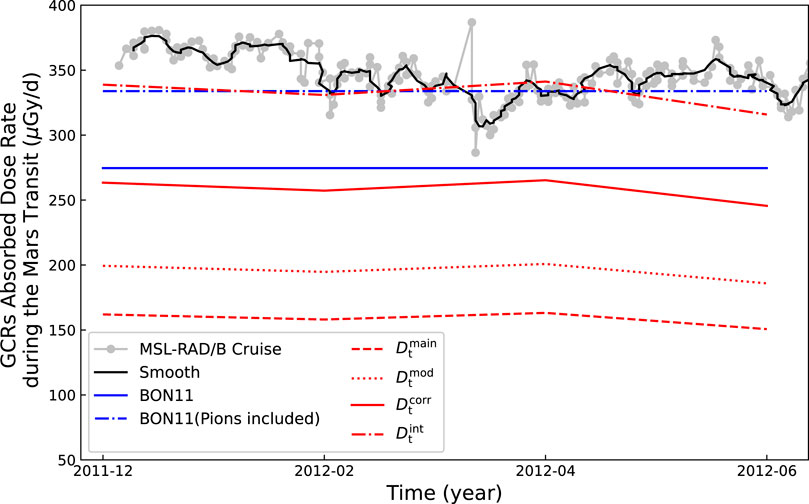
Figure 1. The GCRs radiation absorbed dose rates during a flight to Mars (in silicon). The silver solid line with solid circles represents the absorbed dose rate detected by MSL-RAD/B, while the black solid line shows the smoothed result. The blue solid and dash-dotted lines show the modeling results from the BON11 model without and with pion contributions, respectively. The red dashed line indicates the absorbed dose rates from the four main GCR particles calculated by our model, $D_{\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}}$. The red dotted line represents the absorbed dose rates for 26 GCR particles from the model, $D_{\mathrm{t}}^{\mathrm{m}\mathrm{o}\mathrm{d}}$. The red solid line shows the correct modeling results incorporating the 2012 underestimation, according to [10], $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$. The red dash-dotted line represents the scaling results, $D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$, using an optimal factor $\alpha$ that forces the mean to equal the observed mean.

In order to calculate the absorbed dose rates, we performed numerical simulations to solve the modulation model, i.e., the Parker transport equation of GCRs in the heliosphere, Equation 1, during the MSL spacecraft’s traveling from the Earth to the Mars. Figure 2 illustrates the interplanetary conditions, including the solar tilt angle, magnetic turbulence magnitude $(\delta b)$, sunspot numbers, and spacecraft position in heliosphere, as a function of time during the Earth-to-Mars transit period (December 2011 - June 2012). These parameters – solar tilt angle, magnetic turbulence magnitude $(\delta b)$, and spacecraft position in heliosphere – are also key inputs for our model of GCR modulation. The top panel shows the computed tilt angle of the heliospheric current sheet (HCS) for the new model from the WSO (http://wso.stanford.edu/Tilts.html). The second panel shows the square root of the magnetic field variances (magnetic turbulence magnitude) calculated following [10]. The third panel shows the monthly sunspot number from the WDC-SILSO (https://www.sidc.be/SILSO/datafiles). The bottom panel shows the radial distance of the MSL spacecraft from the Sun (https://omniweb.gsfc.nasa.gov/coho/helios/heli.html). In summary, the period was characterized by a fluctuating heliospheric current sheet (HCS) tilt, which is inversely related to radiation intensity; that is, the greater the tilt, the weaker the radiation. There was also increasing magnetic turbulence, which similarly correlates with weaker radiation as its magnitude grows. Additionally, there was a near-term decrease in sunspot numbers, despite the ongoing ascent of the current solar cycle, and this reduction in sunspot activity is associated with weaker radiation. Conversely, there was an increase in solar distance, which is directly related to radiation intensity; the greater the distance from the Sun, the stronger the radiation observed. During this period, the overall variation in absorbed dose rates (in silicon) is the combined effect of these several factors. We input these parameters into our numerical model to obtain numerical results.

Figure 2

Figure 2. Interplanetary conditions during the Earth-to-Mars transit (December 2011 - June 2012). Top panel: Tilt angle of the heliospheric current sheet from the WSO website using the new model. Second panel: Square root of the magnetic field variances, representing the magnetic turbulence magnitude. Third panel: Monthly sunspot number from WDC-SILSO. Bottom panel: Radial distance of the MSL spacecraft from the Sun.

In Figure 1, we present the GCR absorbed dose rates (in silicon) as predicted by our model. The red dashed line represents the absorbed dose rates due to the four main GCR species-hydrogen (H), helium (He), oxygen (O), and iron (Fe)-calculated using simulations based on the GCR modulation equation, denoted as $D_{\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}}$. The red dotted line corresponds to the absorbed dose rates for a comprehensive set of 26 GCR particles, as forecasted by the model, labeled $D_{\mathrm{t}}^{\mathrm{m}\mathrm{o}\mathrm{d}}$. The red solid line illustrates the modeled results after correction, $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$, which incorporates the 2012 underestimation factor, as detailed by [10]. The red dash-dotted line depicts the results, $D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$, obtained by scaling the corrected dose rates $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$ with an optimized scaling factor $\alpha =1.286$. This scaling factor $\alpha$ was determined by forcing the model mean to equal the observational data, which corresponds to a relative difference $RD$ = 2.51% against the observational average. The silicon detector B detects a mixed radiation field of GCR and secondary particles inside the spacecraft, whereas our model is specifically for charged GCR in free space. Therefore, we propose that this scaling is primarily due to the secondary charged particle radiation resulting from GCR interactions with the spacecraft, which is not accounted for in our model. Additionally, other factors, such as uncertainties in estimating less abundant particle species, organ-averaging, and the constant water-to-silicon conversion coefficient, could also partially contribute to the observed discrepancy.

The results from Figure 1 indicate that, after correcting for the underestimation noted by [10], the results of $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$ closely align with the BON11 model without pions, both of which are slightly lower than the MSL-RAD/B observed data, showing a reduction of $\sim$20% compared to the background trend value inferred from the MSL-RAD/B observations within expected uncertainties. In contrast, the BON11 model with pions yields results that are very similar to the background trend value of the observations. These findings suggest that the secondary charged particle radiation (e.g., from pions) produced by GCR interactions inside the spacecraft during the journey to Mars significantly impacts the overall radiation dose rate. Assuming that the influence of secondary charged particle radiation produced by interactions of GCRs within the spacecraft can be represented by a scaling factor, we have adjusted our model $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$, the scaling factor $\alpha =1.286$ to match the observed data, thus creating the scaled model $D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$. We acknowledge that detector E provides a more comprehensive measure of the total dose, including neutral secondaries, and is recommended for future studies aiming to model the complete internal radiation field. Our analysis demonstrates that the results of the model $D_{\mathrm{t}}^{\mathrm{i}\mathrm{n}\mathrm{t}}$ are in good agreement with the background trend value of the observations. Specifically, the GCR radiation levels exhibit a general, albeit slight, decreasing trend. This is consistent with the approach to the solar maximum of Solar Cycle 24 during this period [24], a pattern that is captured by both our model and the MSL-RAD observations. Furthermore, by comparing the interplanetary environment during the flight shown in Figure 2 with our radiation simulation results in Figure 1, it is evident that the modulation of GCRs is complex and influenced by multiple interplanetary factors.

4 Summary and discussion

In this study, we calculate the charged GCR radiation absorbed dose rate during a flight to Mars in free space, based on the GCR radiation dose rate model developed in previous work by [10]. Firstly, we use the GCR modulation model to calculate the differential flux $j(\mathit{r},E,t)$ of the four predominant GCR nuclei (protons, helium, oxygen, and iron ions) during the Earth-to-Mars transit from December 2011 to June 2012. Next, using Equation 5, we combine the differential flux $j(\mathit{r},E,t)$ with the absorbed-FDCCs $d_{\mathrm{T},\mathrm{R}}(E)$ from ICRP Publication 123 [4,14,15], where $\mathrm{\Omega }=4\pi$, $E$ ranges from 1 MeV/nucleon to 100 GeV/nucleon, R $\in$ H, He, O, Fe, and $n_{\mathrm{t}}=15$, to obtain the time-dependent simulated absorbed dose rates for the four main GCR nuclei $(\sim 73.5\%)$ during the transit, $D_{\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}}$. To save computing resources and improve efficiency, as done by [10], we use the calculated heavy ion oxygen ($\sim$8.5%) as a reference and incorporate the radiation doses from the remaining 22 particles ($\sim$26.5%) into the results for the four main GCR nuclei, yielding the radiation absorbed dose rates for all 26 GCR nuclei (H to Fe), $D_{\mathrm{t}}^{\mathrm{m}\mathrm{o}\mathrm{d}}$. Finally, based on the results in Figure 7 of [10] that reveal a $\sim$24.3% underestimation in our 2012 GCR absorbed dose model, we corrected for this underestimation proportionally to obtain the final modeling charged GCR absorbed dose rates (in silicon) for free space during the Mars transit, $D_{\mathrm{t}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}$ with Equation 6. Our simulation results are similar to those of BON11 without pions, both being slightly lower than the observed data from MSL-RAD/B during the flight. However, the results from BON11 with pions in the simulation, align well with the observed central values from MSL-RAD/B. Furthermore, considering that the MSL-RAD was placed inside the spacecraft during the Mars transit, it was exposed to a complex shielding environment, which resulted in significant secondary charged particle effects, such as those from pions, that contributed substantially to the radiation levels. To quantitatively account for the net effect of these unmodeled processes, we empirically determined a scaling factor $(\alpha )$ through an average fitting procedure that minimizes the discrepancy between our model results and the MSL-RAD observations. This empirically-derived factor $\alpha$ = 1.286 was optimized to bring the total radiation dose rate for the 26 particles into closer alignment with the measured data, with Equation 7. This approach allowed us to quantify the aggregate radiation contribution from secondary charged particles generated by GCRs within the spacecraft’s shielding. This suggests that the radiation effects of secondary charged particles (e.g., from pions) generated by GCRs inside the spacecraft during the Mars flight should be carefully considered as well.

The scaling factor $\alpha$ introduced in this study aims to correct discrepancies between model results and measurements from the MSL-RAD silicon detector B. It is important to note that silicon detector B is primarily sensitive to charged particles and insensitive to neutral particles such as neutrons and $\gamma$ rays. Therefore, factor $\alpha$ primarily quantifies dose discrepancies attributable to unmodeled charged secondary particles (e.g., pions) and other potential systematic model errors, rather than representing the total contribution from all secondary particles. To accurately assess the total absorbed dose within spacecraft shielding (encompassing all charged particles and neutral components), data from MSL-RAD plastic scintillator detector E is both necessary and more appropriate. Detector E’s tissue-equivalent properties and sensitivity to neutral particles (neutrons, $\gamma$ rays) enable it to provide dosimetric data more directly relevant to human radiation effects. Consequently, in future work, we will employ detector E measurements as a key benchmark for developing and validating advanced models capable of fully simulating the radiation fields of primary and all secondary particles within shielded environments. It should be noted that the MSL-RAD dose rates include particles from the spacecraft’s RTG power supply, which emits a steady background of neutrons and $\gamma$ rays. The RTG background contributions require correction for the data from detector B. In contrast, the influence on the dose measured by detector E is negligible because its energy threshold is high enough to exclude this background.

The discrepancies between our simulation results and observational data primarily stem from the following sources: First, inaccuracies in the GCR modulation model arise due to an oversimplified representation of magnetic turbulence and the heliospheric structure, along with insufficient consideration of localized and transient solar variations. These limitations diminish the model’s ability to fully reproduce the observed particle fluxes. Second, uncertainty is introduced in the estimation of contributions from less abundant particle species. Rather than performing explicit numerical simulations for these minor components, we relied on widely accepted abundance ratios from established literature, which may not capture the specific environmental conditions during the observation period. Third, the calculation of dose averages across 15 organs/tissues specified by the ICRP reference phantoms [4] –while providing a representative whole-body value–may overlook anatomical variations and tissue–specific energy deposition patterns, potentially introducing inaccuracies in biological dose estimation. Fourth, the use of a constant conversion coefficient between water and silicon-based dose measurements neglects energy-dependent and material-specific effects in radiation energy deposition. This simplification fails to fully represent the complex particle interactions within different detector and tissue materials. Finally, methodological differences between computational dose assessments and physical measurements contribute to the discrepancies. While our simulation follows ICRP guidelines for radiation protection quantities, the MSL-RAD measurements were obtained using a silicon detector located inside the MSL spacecraft during its journey to Mars, positioned directly beneath the descent stage and above the heat shield. This difference in phantom geometry, material composition, and shielding configuration between computational models and physical detectors introduces inherent inconsistencies in dose comparisons. Our model is currently primarily used for calculating GCR radiation doses in free space and does not yet account for secondary particle effects under different shielding conditions. Therefore, future work will require the use of a dedicated simulation model, such as GEANT4, to evaluate radiation doses under various shielding conditions. For such validation, measurements from the MSL-RAD scintillator detector E will be prioritized, as its tissue-equivalent composition and heightened sensitivity to low-energy secondary particles (e.g., electrons, gammas, and neutrons) provide a more relevant benchmark for assessing the total absorbed dose inside a spacecraft.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

DL: Writing – original draft. GQ: Writing – review and editing.

Funding

The authors declare that financial support was received for the research and/or publication of this article. DL and GQ acknowledge support from the National Natural Science Foundation of China (NSFC) (Grant No. 42374190), the Shenzhen Science and Technology Program (Grant No. JCYJ20250604145503005 and Grant No. JCYJ20210324132812029), the National Key Research and Development Program of China (Grant Nos. 2021YFA0718600 and 2022YFA1604600), the Shenzhen Key Laboratory Launching Project (Grant No. ZDSYS20210702140800001), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB 41000000).

Acknowledgements

The work was carried out at National Supercomputer Center in Tianjin, and the calculations were performed on TianHe-3F.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Simpson JA. Elemental and isotopic composition of the galactic cosmic rays. Annu Rev Nucl Part Sci (1983) 33:323–82. doi:10.1146/annurev.ns.33.120183.001543

CrossRef Full Text | Google Scholar

2. Durante M, Cucinotta FA. Physical basis of radiation protection in space travel. Rev Mod Phys (2011) 83:1245–81. doi:10.1103/revmodphys.83.1245

CrossRef Full Text | Google Scholar

3. Zeitlin C, Hassler DM, Cucinotta FA, Ehresmann B, Wimmer-Schweingruber RF, Brinza DE, et al. Measurements of energetic particle radiation in transit to Mars on the Mars science. Science (2013) 340(6136):1080–4. doi:10.1126/science.1235989

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Dietze G, Bartlett D, Cool D, Cucinotta F, Jia X, McAulay I, et al. ICRP PUBLICATION 123: assessment of radiation exposure of astronauts in space. Ann ICRP (2013) 42:1–339. doi:10.1016/j.icrp.2013.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Berger T, Matthiä D, Burmeister S, Zeitlin C, Rios R, Stoffle N, et al. Long term variations of galactic cosmic radiation on board the international space station, on the moon and on the surface of Mars. J Space Weather Space Clim (2020) 10:34. doi:10.1051/swsc/2020028

CrossRef Full Text | Google Scholar

6. Hassler DM, Zeitlin C, Wimmer-Schweingruber RF, Böttcher S, Martin C, Andrews J, et al. The radiation assessment detector (RAD) investigation. Space Sci Rev (2012) 170:503–58. doi:10.1007/s11214-012-9913-1

CrossRef Full Text | Google Scholar

7. Mrigakshi AI, Matthiä D, Berger T, Reitz G, Wimmer-Schweingruber RF. How galactic cosmic ray models affect the estimation of radiation exposure in space. Adv Space Res (2013) 51(5):825–34. doi:10.1016/j.asr.2012.10.017

CrossRef Full Text | Google Scholar

8. Schwadron NA, Boyd AJ, Kozarev K, Golightly M, Spence H, Townsend LW, et al. Galactic cosmic ray radiation hazard in the unusual extended solar minimum between solar cycles 23 and 24. Space Weather (2010) 8(A6):S00E04. doi:10.1029/2010sw000567

CrossRef Full Text | Google Scholar

9. Cucinotta FA, Schimmerling W, Wilson JW, Peterson LE, Badhwar GD, Saganti PB, et al. Space radiation cancer risks and uncertainties for Mars missions. Radiat Res (2001) 156(5):682–8. doi:10.1667/0033-7587(2001)156[0682:srcrau]2.0.co;2

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lyu D, Qin G, Shen Z -N. Long-term variation of the galactic cosmic ray radiation dose rates. Space Weather (2024) 22(1):e2023SW003804. doi:10.1029/2023sw003804

CrossRef Full Text | Google Scholar

11. Qin G, Shen ZN. Modulation of galactic cosmic rays in the inner heliosphere, comparing with PAMELA measurements. ApJ (2017) 846:56. doi:10.3847/1538-4357/aa83ad

CrossRef Full Text | Google Scholar

12. Shen ZN, Qin G. Modulation of galactic cosmic rays in the inner heliosphere over solar cycles. ApJ (2018) 854:137. doi:10.3847/1538-4357/aaab64

CrossRef Full Text | Google Scholar

13. Shen ZN, Qin G, Zuo P, Wei F. Modulation of galactic cosmic rays from helium to nickel in the inner heliosphere. ApJ (2019) 887:132. doi:10.3847/1538-4357/ab5520

CrossRef Full Text | Google Scholar

14. Sato T, Endo A, Zankl M, Petoussi-Henss N, Niita K. Fluence-to-dose conversion coefficients for neutrons and protons calculated using the PHITS code and ICRP/ICRU adult reference computational phantoms. Phys Med Biol (2009) 54:1997–2014. doi:10.1088/0031-9155/54/7/009

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sato T, Endo A, Niita K. Fluence-to-dose conversion coefficients for heavy ions calculated using the PHITS code and the ICRP/ICRU adult reference computational phantoms. Phys Med Biol (2010) 55:2235–46. doi:10.1088/0031-9155/55/8/008

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Parker EN. The passage of energetic charged particles through interplanetary space. Planet Space Sci (1965) 13:9–49. doi:10.1016/0032-0633(65)90131-5

CrossRef Full Text | Google Scholar

17. Webber WR, Cummings AC, McDonald FB, Stone EC, Heikkila B, Lal N. Galactic cosmic ray H and he nuclei energy spectra measured by voyagers 1 and 2 near the heliospheric termination shock in positive and negative solar magnetic polarity cycles. J.Geophys Res Space Phys (2008) 113:A10108. doi:10.1029/2008ja013395

CrossRef Full Text | Google Scholar

18. Zhang M. A markov stochastic process theory of cosmic-ray modulation. ApJ (1999) 513:409–20. doi:10.1086/306857

CrossRef Full Text | Google Scholar

19. Kopp A, Büsching I, Strauss RD, Potgieter MS. A stochastic differential equation code for multidimensional fokker-planck type problems. Computer Phys Commun (2012) 183:530–42. doi:10.1016/j.cpc.2011.11.014

CrossRef Full Text | Google Scholar

20. Qin G, Zhang M, Dwyer JR. Effect of adiabatic cooling on the fitted parallel mean free path of solar energetic particles. ApJ (2006) 111:A08101. doi:10.1029/2005ja011512

CrossRef Full Text | Google Scholar

21. Pei C, Bieber JW, Burger RA, Clem J. A general time-dependent stochastic method for solving Parker’s transport equation in spherical coordinates. J Geophys Res Space Phys (2010) 115:A12107. doi:10.1029/2010ja015721

CrossRef Full Text | Google Scholar

22. Potgieter MS, Vos EE, Boezio M, De Simone N, Di Felice V, Formato V. Modulation of galactic protons in the heliosphere during the unusual solar minimum of 2006 to 2009. Sol Phys (2014) 289:391–406. doi:10.1007/s11207-013-0324-6

CrossRef Full Text | Google Scholar

23. Zeitlin C, Hassler DM, Wimmer-Schweingruber RF, Ehresmann B, Appel J, Berger T, et al. Calibration and characterization of the radiation Assessment detector (RAD) on curiosity. Space Sci Rev (2016) 201:201–33. doi:10.1007/s11214-016-0303-y

CrossRef Full Text | Google Scholar

24. Löwe JL, Khaksarighiri S, Wimmer-Schweingruber RF, Hassler DM, Ehresmann B, Guo J, et al. Nowcasting solar energetic particle events for Mars missions. Space Weather (2025) 23(4):e2025SW004372. doi:10.1029/2025sw004372

CrossRef Full Text | Google Scholar

25. Schwadron NA, Townsend L, Kozarev K, Dayeh MA, Cucinotta F, Desai M, et al. Earth-moon-mars radiation environment module framework. Space Weather (2010) 8(10):S00E02. doi:10.1029/2009sw000523

CrossRef Full Text | Google Scholar

26. McKenna LS, Gonçalves P, Keating A, Matthiä D. Overview of energetic particle hazards during prospective manned missions to Mars. Planet Space Sci (2012) 63:123–32. doi:10.1016/j.pss.2011.06.017

CrossRef Full Text | Google Scholar

27. O'Neill PM. Badhwar–O’Neill 2010 galactic cosmic ray flux model—revised. IEEE Trans Nucl Sci (2010) 57(6):3148–53. doi:10.1109/TNS.2010.2083688

CrossRef Full Text | Google Scholar

28. Wilson JW, Badavi FF, Cucinotta FA, Shinn JL, Badhwar GD, Silberberg R, et al. HZETRN:Description of a free-space ion and nucleon transport and shielding computer program. Hampton, Virginia: NASA sti/recon technical report (1995). Langley Research Center • Hampton, Virginia.

Google Scholar