Quantum tunneling and barrier hopping in MgTi2O5 nanoparticles: a study of AC/DC conductivity and dielectric response

The electrical conductivity and dielectric characteristics were investigated across a frequency range of 200–5 MHz and a temperature range of 318 K to 433K for MgTi₂O₅ nanoparticles (NPs). The electrical conductivity data displayed two dominant conduction mechanisms: a quantum mechanical tunneling model (QMT) and the correlated barrier hopping model (CBH). The activation energy values derived from the Direct Current (DC) Conductivity were 0.15 and 0.27 eV. In addition, the activation energy values derived from the Alternating Current (AC) Conductivity decreased as frequency increased from 0.13 to 0.014 eV due to the improvement of electronic jumps among localized states. Additionally, dielectric investigation of MgTi₂O₅ NPs within the frequency range from (200 – 5 MHz) and the temperature range from (318K–433K) revealed that both real (ε₁) and imaginary (ε₂) components of a dielectric permittivity decrease as the frequency increased and increased as a temperature increased due to thermal motion of electrons, which is related to the polarization mechanism.

1 Introduction

Pseudobrookite MgTi₂O₅ of the Bbmm space group (1) is a common crystalline phase in TiO₂ glass ceramics (2). MgTi₂O₅ is unique because it can host transitional metal ions in two octahedral cavities while processing refractoriness and high refractive index (2). Furthermore, this material exhibits high thermal stability, cation order-disorder behavior, high permittivity, and dielectric losslessness (3), as well as good mechanical characteristics. The MgTi₂O₅ compound also has low thermal expansion, good temperature stability, and low cost (4, 5). MgTi₂O₅ compound is usually used in many applications like a catalyst (6), white pigment (2), photocatalyst (7), pseudobrookit phase stabilizer for the Al₂TiO₅ compounds, thermistor (8), buffering layers between Silicon substrates and Platinum thin films (9), a red-emitting phosphor (Mg Ti₂O₅:Eu) (10), sodium-ion batteries, water purification (11) due to its unique properties. Several methods have been used to manufacture MgTi₂O₅, including, conventional high-temperature (12), sol-gel (13), and citrate gel route, simultaneous hydrolysis (14).

M.A. Ehasn et al. reported the characteristics of MgTi₂O₅ thin films synthesized by a heterobimetallic single molecular precursor (15), including X-ray diffraction, energy dispersive X-ray spectroscopy, field emission gun-scanning electron spectroscopy, and X-ray photoelectron spectroscopy. Moreover, the optical examination revealed that the MgTi₂O₅ compound had a direct bandgap of about 3.4 eV. Photoelectrochemical (PEC) measurements of MgTi₂O₅ electrodes revealed a maximum photocurrent anodic density of approximately 400 μA/cm² at a voltage of 0.7 V vs. Ag/Ag.Cl/3 M KCl, during simulated sunshine exposure. So, MgTi₂O₅ has application in optoelectronics. The characteristics of MgTi₂O₅ prepared by a microwave method, investigated by XRD, TG/DTA, and FTIR, reported by G. Çelik, revealed that the material has an orthorhombic structure and thermal stability (16). T. Selvamani reported the synthesis of MgTi₂O₅ NPs using a simple hydrothermal post-annealing process (11). The material exhibits a direct allowed transition with an optical band gap of about 3.35 eV. The study reveals that sonophotocatalytic activity degraded crystal violet more effectively than photocatalytic and sonocatalytic activities. So, this material is used in water treatment. H. W. Son (17) reported the investigation of MgTi₂O₅ ceramics sintered at 1,100 °C–1,200 °C. This study reveals that the material has a high density and flexural strength of 99%. The characterization analysis of MgTi₂O₅ NPs growth using the co-precipitation technique was reported by S. Elnobi (18), including thermal analysis (TG/DSC), XRD, SEM, TEM, and EDX. Structural characterization revealed that the average crystallite size of the synthesized MgTi₂O₅ nanoparticles ranges between 27 and 37 nm. Morphological analysis via SEM and TEM imaging confirmed a quasi-spherical particle geometry. The direct band gap value 3.81 + 0.01 eV was estimated from the diffuse reflectance spectra. The DC conductivity was measured across a temperature range of 303–503 K, revealing that thermal activation is the primary mechanism driving conductivity. Besides, MgTi₂O₅ NPs have a high antibacterial capability (18).

Investigating charge transport processes holds significant value both for advancing technological applications (19) and deepening our fundamental understanding of material behavior. Measuring electrical conductivity (DC and AC) can provide us with information about the mechanisms of charge transport. DC conductivity reflects the movement of free charges in a constant external electric field. Moreover, AC conductivity measurements are particularly useful for probing the characteristics of materials with limited charge mobility.

Despite the extensive research on the structural, optical, and catalytic properties of MgTi₂O₅, its charge transport behavior—particularly under alternating current (AC) conditions—remains insufficiently understood. Given the compound’s promising dielectric characteristics, thermal stability, and potential for integration into microelectronic and optoelectronic devices (19), a deeper understanding of its frequency- and temperature-dependent electrical response is essential. AC conductivity and impedance spectroscopy offer powerful tools to probe localized charge dynamics, dielectric relaxation, and conduction mechanisms, which are critical for optimizing material performance (18, 20, 21) in real-world applications such as capacitors, sensors, and energy storage systems. This study focuses on exploring how the dielectric properties of MgTi₂O₅ nanoparticles vary with temperature and frequency, using impedance spectroscopy across a frequency range from 200 Hz to 5 MHz and a temperature range of 318 K–433 K. The conduction mechanism model is defined from the AC conductivity measurements. Moreover, activation energy values and the dielectric permittivity components can be determined from these measurements.

2 Experimental procedure

Previous work illustrated in detail the synthesis of MgTi₂O₅ NPs using the aqueous co-precipitation method and the characterization of the prepared samples (18).

To prepare MgTi₂O₅ samples for AC conductivity measurements, we grind the MgTi₂O₅samples to a fine powder and then press the powder into a pellet with a diameter of 10 mm and a thickness of 2 mm. The two electrodes were formed on a polished pellet surface using silver paste as ohmic contacts. The AC conductivity was obtained using an automated LCR meter program (Hioki model 3,536). Experimental measurements were conducted over a temperature range of 318K–433 K and a frequency range of 200 Hz - 5 MHz.

3 Results and discussion

3.1 Investigation of frequency-dependent conductivity

Figure 1 illustrates the frequency-dependent behavior of total conductivity (σ_tot) across the temperature interval of 318K–433 K, expressed using Jonscher’s law of the universal power (22):

$\sigma \left(\omega \right)={\sigma }_{dc}+{\sigma }_{ac}={\sigma }_{dc}+A{\omega }^s(1)$

$\omega$ represents the angular frequency, whereas A is a constant coefficient, and symbol s represents the exponent of frequency that is almost equal to a value of less than one. A and (s) are temperature-dependent factors. The curve distinctly exhibits two regimes; in the low-frequency domain, the electrical conductivity remains invariant with respect to frequency, corresponding to the DC conductivity regime commonly referred to as the plateau region. In this regime, enhanced grain boundary activity suppresses electron hopping, leading to reduced conductivity due to higher resistivity. So, the sample is suitable for use in microwave devices (23). At high values of frequencies, the electrical conductivity increases progressively with frequency, indicating a frequency-dependent response typical of the dispersion region. This phenomenon arises from the hopping or quantum tunneling of charge carriers, such as small polarons, between localized electronic states within the mobility gap. In addition, increasing the temperature enhances their conductivity. This revealed that MgTi₂O₅ nanoparticles have semiconductor properties over the range of frequencies (24).

Figure 1

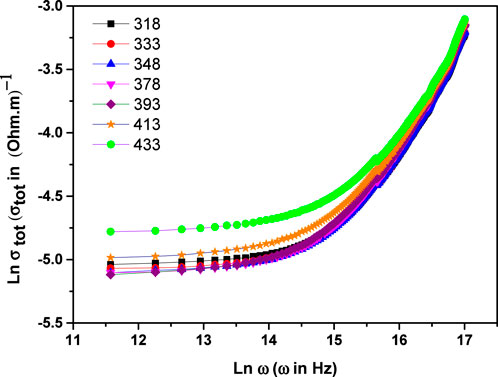
Figure 1. The frequency-dependent electrical conductivity (${\sigma }_{tot}$) at various temperatures for MgTi₂O₅ NPs.

3.1.1 Conduction mechanism

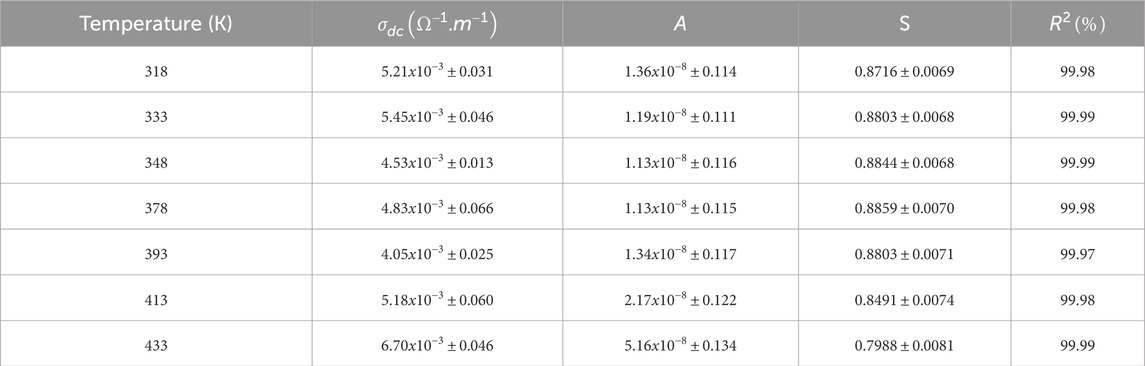
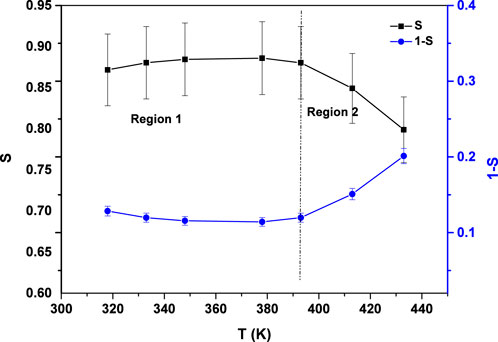
The conduction mechanism can be elucidated by analyzing the temperature and frequency dependence of the frequency exponent (s). To interpret the AC conductivity behavior under varying thermal and frequency conditions, four theoretical models have been proposed. According to the QMT model, the frequency exponent s remains temperature-independent and typically approximates a value near 0.8. According to the CBH model, the frequency exponent s exhibits a temperature-dependent decline, decreasing progressively as temperature increases. In the overlapping large polaron tunneling (OLPT) model, the frequency exponent s initially decreases with rising temperature, reaching a minimum at a specific threshold, beyond which it increases again—demonstrating dependence on both temperature and frequency. Meanwhile, the non-overlapping small polaron tunneling (NSPT) model indicates a temperature-dependent increase in s with thermal elevation.

Using the equation of Jonscher’s universal power law (22):

${\sigma }_{ac}=A{\omega }^s(2)$

The frequency exponent s and pre-exponential factor A are evaluated from the slope and intercept, respectively, of the linear fit to the plot of $\mathit{Ln}{\sigma }_{ac}$ versus $\mathit{Ln}\omega$, across the temperature range of 318–433 K. Table 1 summarizes the fitting parameters derived from the experimental AC conductivity data. Figure 2 depicts the temperature-dependent behavior of the frequency exponent s, emphasizing its variation across the examined thermal range. First, the frequency exponent s remains nearly constant at approximately 0.88 over the temperature range of 318–393 K, indicating temperature independence and suggesting that the QMT model governs the conduction mechanism in this regime (24). According to the QMT model, it is assumed that no lattice distortions related to the carrier motion contribute to the ac conductivity. The frequency exponent s is theoretically expected to remain unaffected by temperature variations, while exhibiting a clear dependence on the frequency (25). Second, within the temperature range of 393–433 K, the frequency exponent s exhibits a declining trend with increasing temperature, consistent with the CBH model. This behavior reflects a conduction mechanism in which charge carriers hop between localized sites, overcoming potential barriers through thermally activated hopping (26). It is clear from these results that the QMT model provides an excellent fit of dominant tunneling conduction in a lower temperature region, whereas the CBH model demonstrates the thermally activated conduction at a higher temperature region.

Table 1

Table 1. Fitting parameters from Jonscher’s Power law with 95% confidence interval level.

Figure 2

Figure 2. Temperature dependence of (s) and (1-s) for MgTi₂O₅ NPs.

According to the QMT model, the exponent s remains unaffected by changes in both temperature and frequency (27).

$s=1-\frac{4}{\mathit{Ln}\left(\omega {\tau }_o\right)}(3)$

${\tau }_o$ denotes the relaxation time of a polaron.

Within the CBH model, electrical conduction occurs through either single polaron or bipolaron hopping mechanisms, which causes disorder in their surrounding medium by displacing atoms away from their equilibrium locations, resulting in structural flaws (28). The CBH model expresses the exponent s as the following formula (29).

$s=1-\frac{6K_{B}T}{W_H-K_{B}T\left(\mathit{Ln}\frac{1}{\omega {\tau }_o}\right)}(4)$

Where $W_H$ represents the polaron’s binding energy, while polarons move from one atomic position to another. In the case of a single polaron, the hopping energy $W_H$ is typically about one-fourth of the optical band gap, where in the case of bipolaron hopping, it tends to be nearly equal to the full energy gap (30). For a high value of $\frac{W_H}{K_{B}T}$ , the above Equation 4 is expressed by (29):

$s=1-\frac{6K_{B}T}{W_H}(5)$

$1-s=\frac{6K_{B}T}{W_H}(6)$

As illustrated in Figure 2, plotting (1-s) against absolute temperature T yields a straight line, from which the slope is used to determine the hopping energy $W_H$. The calculated average polaron binding energy $W_H$ is approximately 0.275 eV.

Additionally, the CBH model describes the hopping distance using the following relation (30):

$R_{\omega }=\frac{4n{e}^2}{\pi {\epsilon }_o{\epsilon }_r\left[W_H-K_{B}T\left(\mathit{Ln}\frac{1}{\omega {\tau }_o}\right)\right]}(7)$

Here, n denotes the number of polarons involved in the hopping process, where n = 1 corresponds to single polaron hopping and n = 2 to a bipolaron hopping. Based on the results, the hopping energy $W_H$ is found to be nearly equal to the optical energy gap, indicating that bipolaron hopping predominantly governs the conduction mechanism.

Based on the CBH model, the Austin-Mott relation can be utilized to determine the AC conductivity ${\sigma }_{ac}\left(\omega \right)$, which results from electron hopping between localized states N (EF) at the Fermi level (31). At the Fermi level, the following equation describes the relationship between ${\sigma }_{ac}\left(\omega \right)$ and N (EF).

${\sigma }_{ac}\left(\omega \right)=\frac{\pi }{3}{e}^2{K}_{B}T{\alpha }^{-5}{\left[N\left(E_F\right)\right]}^2\omega {\left[\ln \left(\frac{{\upsilon }_{ph}}{\omega }\right)\right]}^4(8)$

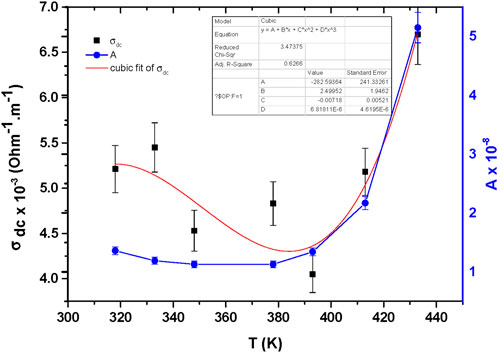
Figure 3 shows a relationship between both pre-exponential factor A, and DC conductivity versus temperature. It is noticed, the pre-exponential factor A increases exponentially significantly with temperature from 1.36 × 10⁻⁸ at 318K to 5.16 × 10⁻⁸ at 433K. this behavior may be due to enhanced hopping probability and carrier mobility at elevated temperature as well as, a transition from tunneling to thermally hopping reinforcing the CBH mechanism at elevated temperature. While, for DC conductivity σ_dc variation with temperature, it is clear, an initial decrease of σ_dc values from 318K to 393K, reach a maximum value 4.05 × 10⁻³ (Ohm^-1.m^-1) at 393K and raise sharply again with elevated temperature reaching 6.7 × 10⁻³ (Ohm^-1.m^-1) at 433K. This behavior is demonstrating two conduction mechanism exist in MgTi₂O₅ NPs in temperature range from 318K to 433K.

Figure 3

Figure 3. σ_dc, and pre-exponential factor A versus temperature.

3.2 Study the temperature-dependent electrical conductivity

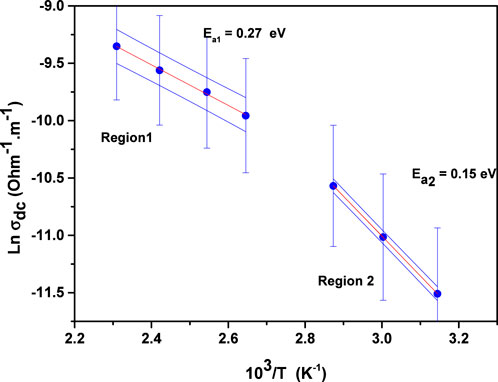
The variation of DC conductivity with temperature can be interpreted using the Arrhenius relation (32):

${\sigma }_{dc}={\sigma }_o\mathit{exp}\frac{-E_a}{K_{B}T}(9)$

In this relation, ${\sigma }_o$ refers to the DC conductivity at T = 0K, $E_a$ denotes the activation energy, T is the temperature in kelvin, and $K_B$ is the Boltzmann constant.

The value of $E_a$ and ${\sigma }_o$ can be determined by plotting the relationship between $\mathit{Ln}{\sigma }_{dc}$ and $\frac{{10}^3}{T}$ as shown in Figure 4. The curve clearly indicates that DC conductivity increases with rising temperature. The curve is divided into two linear regions corresponding to high- and low-temperature ranges (393 K–433 K) and (318 K–393 K), respectively, which refer to two conduction mechanisms in this temperature range. At higher temperatures, the activation energy is approximately $0.27\pm 0.0122$eV, with 95% confidence interval level corresponding to the bipolaron hopping mechanism, as reported by S.D.Kang et al (33), by increasing the temperature, a bipolaron can be easily formed. At lower temperatures, it decreases to around $0.15\pm 0.06104$eV, with 95% confidence interval level corresponding to a small polaron hopping mechanism, which involves charge carriers jumping between adjacent localized sites with minimum lattice deformations. According to G. P. Triberis (34), at low temperatures, the small polaron hopping dominates in disordered materials as a result of a limited thermal energy as well as a strong electron–photon coupling. These results of activation energy match with other oxides, including SnO₂ NPs (26), which have an activation energy of 0.307 eV in the temperature range (353–433)K, and AlTi₂O₅ have Ea from 0.09–0.15 eV at temperature range (110–290)K (35)

Figure 4

Figure 4. DC Conductivity versus inverse temperature $\raisebox{1ex}{${10}^3$}\!\left/ \!\raisebox{-1ex}{$T$}\right.$ of MgTi₂O₅ NPs.

According to Equation 1, AC conductivity is derived by eliminating the DC contribution from the total conductivity. Its variation with temperature can be examined through the Arrhenius Law (32):

${\sigma }_{ac}={\sigma }_o\mathit{exp}-\frac{\Delta E_{ac}}{K_{B}T}(10)$

${\sigma }_{ac}$ is the AC conductivity, ${\sigma }_o$ refers to the AC conductivity at T = 0K, $\Delta E_{ac}$ refers to an activation energy of AC conductivity, $K_B$ is a Boltzmann constant, and T denotes an absolute temperature. By plotting the relationship between $\ln {\sigma }_{ac}$ versus $\raisebox{1ex}{${10}^3$}\!\left/ \!\raisebox{-1ex}{$T$}\right.$, both of $\Delta E_{ac}$ and ${\sigma }_o$ values can be extracted from the slope and intercept of the linear fit at different values of frequency, respectively.

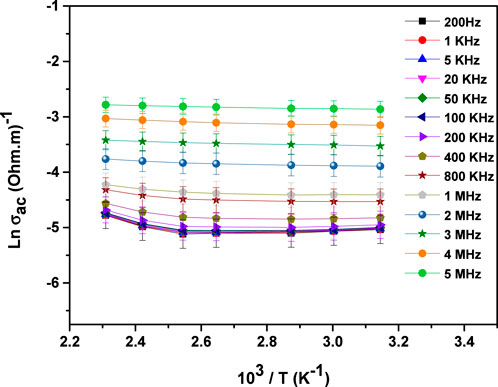
Figure 5 illustrates the temperature-dependent behavior of AC conductivity in MgTi₂O₅ at various frequencies. The observed increase in conductivity with rising temperature suggests a thermally activated conduction mechanism (36).

Figure 5

Figure 5. AC Conductivity vs. Temperature for MgTi₂O₅ NPs at various frequencies.

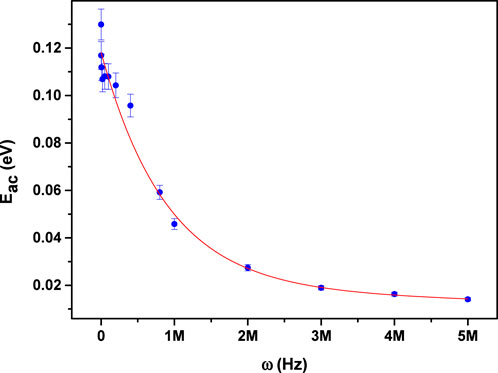
Figure 6 illustrates how the AC activation energy $\Delta E_{ac}$ varies with frequency $\left(\omega \right)$, revealing an exponential decline in $\Delta E_{ac}$ as the frequency rises. This decline in AC activation energy $\Delta E_{ac}$ with increasing frequency could be attributed to a greater rate of electronic transitions between localized states, facilitated by the enhanced energy available at higher (31). Similar behavior is observed in other materials, including both amorphous and crystalline types, where frequency significantly affects the conduction mechanism. This underscores the predominance of hopping conductivity, as charge carriers tend to move between localized states more effectively at higher frequencies (37).

Figure 6

Figure 6. The AC activation energy $\Delta E_{ac}$ variation versus frequency for MgTi₂O₅ NPs.

3.3 Analysis of dielectric properties

Examining dielectric permittivity is crucial for gaining insight into the properties of materials. The complex permittivity, denoted as ${\epsilon }^{*}$ , is expressed as follows (26):

${\epsilon }^{*}={\epsilon }_1+i{\epsilon }_2(11)$

${\epsilon }_1$ represents the real part of a material’s complex permittivity which indicates its capacity to store energy when subjected to an external electric field. ${\epsilon }_2$ represents the imaginary part of the dielectric permittivity, which accounts for the energy loss or dissipation within the dielectric material when subjected to an external electric field. Measurements of the complex permittivity components ε₁ and ε₂ were obtained by

${\epsilon }_1=\frac{C_{p}d}{{\epsilon }_{o}A}(12)$

${\epsilon }_2={\epsilon }_1\tan \delta (13)$

The symbols $C_p$, d, A, and ${\epsilon }_o$ represent the sample’s capacitance, thickness, surface area, and the permittivity of free space, respectively capacitance and loss tangent values were computed from the dielectric measurements at temperatures ranging from (318K–433K) and frequencies ranging from 200 Hz to – 5 MHz.

Figures 7, 8 illustrate how the real (${\epsilon }_1$) and imaginary (${\epsilon }_2$) components of dielectric permittivity for MgTi₂O₅ nanoparticles vary with frequency across different temperatures. As shown, both ε₁ and ε₂ exhibit higher values at lower frequencies, followed by a sharp decline with increasing frequency, eventually stabilizing at higher frequency ranges.

Figure 7

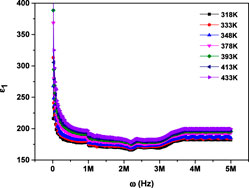
Figure 7. Variation of the real component of dielectric permittivity with frequency for MgTi₂O₅ NPs at various temperatures.

Figure 8

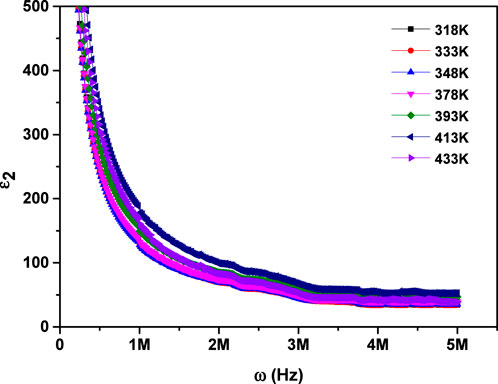
Figure 8. Dependence of the imaginary component of dielectric permittivity on frequency for MgTi₂O₅ NPs at various temperatures.

This behavior is explained using many types of polarization, including; electronic, ionic, orientational, and interfacial. (38, 39). At lower frequencies, the dipoles within the material have sufficient time to align completely with the externally applied electric field, resulting in maximum or total polarization. As the frequency rises, the rapid oscillation of the external electric field causes dipoles to struggle with maintaining full alignment. This partial alignment, driven by the swift rotation of dipoles, results in a reduction in orientational polarization. At higher frequencies (around 10⁶ Hz), dipoles can no longer maintain full alignment with the oscillating electric field due to its rapid variation. As a result, their contribution becomes frequency-independent and stabilizes. In this regime, interfacial polarization emerges as the predominant mechanism influencing the dielectric response (26, 31). Moreover, at a given frequency, both ε₁ and ε₂ exhibit an upward trend with rising temperature. This behavior can be attributed to enhanced thermal agitation of electrons, which plays a key role in the polarization process. At lower temperatures, limited electron mobility restricts their ability to align with the electric field. However, as temperature increases, electrons gain sufficient energy to reorient more effectively, resulting in greater polarization and consequently higher values of ε₁ and ε₂ (40).

Figure 9 illustrates how the dielectric loss tangent (tan δ) varies with frequency across different temperature conditions. The figure revealed an exponential decrease of $\mathit{tan}\delta$ as frequency increased. The dielectric loss tangent graph shows the same trend as the dielectric constant’s behavior. At low frequency, $\mathit{tan}\delta$ has a higher value, whereas it diminishes at high values of frequencies. The reduction in tan δ at higher frequencies can be attributed to the inability of charge carriers to keep pace with the rapidly oscillating electric field. Once the frequency surpasses a certain threshold, the rate of charge hopping lags behind the field variation, resulting in diminished energy dissipation and thus a lower dielectric loss tangent (28).

Figure 9

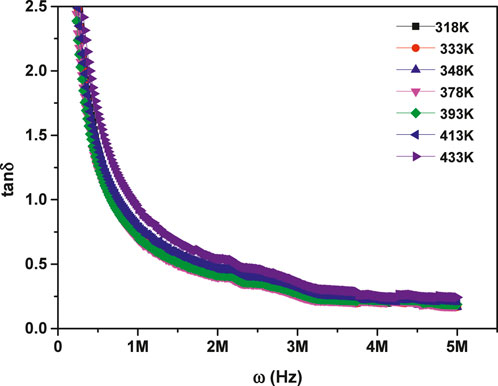
Figure 9. Frequency-dependent behavior of the dielectric loss tangent for MgTi₂O₅ NPs at various temperatures.

4 Conclusion

The electrical and dielectric behavior of MgTi₂O₅ nanoparticles was systematically investigated across a temperature range of 318–433 K and a frequency span of 200 Hz to 5 MHz. The AC conductivity exhibited a frequency-dependent trend consistent with the power law relation, ${\sigma }_{ac}=A{\omega }^s$. Analysis revealed the presence of two distinct conduction mechanisms: Quantum Mechanical Tunneling (QMT) and the Correlated Barrier Hopping (CBH) model. Both the real (ε₁) and imaginary (ε₂) components of dielectric permittivity were found to be significantly high at low frequencies, decreasing with increasing frequency. The nanoparticles demonstrated pronounced dispersive AC conductivity, along with a strong dependence of dielectric properties on both frequency and temperature. These effects, amplified by nanoscale dimensions and surface interactions, highlight the potential of MgTi₂O₅ NPs for use in advanced dielectric and electronic device applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AS: Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review and editing. HW: Investigation, Methodology, Validation, Writing – review and editing. AI: Funding acquisition, Investigation, Methodology, Writing – review and editing. MAE-S: Formal Analysis, Investigation, Methodology, Visualization, Writing – review and editing.

Funding

The authors declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2025.1728372/full#supplementary-material

References

1. Pauling L. VII. The crystal structure of pseudobrookite. Z für Kristallographie (1930) 73:97–112. doi:10.1524/zkri.1930.73.1.97

CrossRef Full Text | Google Scholar

2. Matteucci F, Cruciani G, Dondi M, Gasparotto G, Tobaldi DM. Crystal structure, optical properties and colouring performance of karrooite MgTi₂O₅ ceramic pigments. J Solid State Chem (2007) 180:3196–210. doi:10.1016/j.jssc.2007.08.029

CrossRef Full Text | Google Scholar

3. Purohit RD, Saha S. Synthesis of magnesium dititanate by citrate gel route and its characterization. Ceram Int (1999) 25:475–7. doi:10.1016/S0272-8842(98)00062-5

CrossRef Full Text | Google Scholar

4. Suzuki Y, Morimoto M. Porous MgTi₂O₅/MgTiO₃ composites with narrow pore-size distribution: in situ processing and pore structure analysis. J Ceram Soc Jpn (2010) 118:819–22. doi:10.2109/jcersj2.118.819

CrossRef Full Text | Google Scholar

5. Suzuki Y, Morimoto M. Uniformly porous MgTi₂O₅ with narrow pore-size distribution: in situ processing, microstructure and thermal expansion behavior. J Ceram Soc Jpn (2010) 118:1212–6. doi:10.2109/jcersj2.118.1212

CrossRef Full Text | Google Scholar

6. Lopez T, Hernandez-Ventura J, Aguilar DH, Quintana P. Thermal phase stability and catalytic properties of nanostructured TiO₂-MgO sol–gel mixed oxides. J Nanosci Nanotech (2008) 8:6608–17. doi:10.1166/jnn.2008.18434

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kapoor PN, Uma S, Rodriguez S, Klabunde KJ. Aerogel processing of MTi₂O₅ (m=Mg, Mn, Fe, Co, Zn, sn) compositions using single source precursors: synthesis, characterization and photocatalytic behavior. J Mol Catal A: Chem (2005) 229:145–50. doi:10.1016/j.molcata.2004.11.008

CrossRef Full Text | Google Scholar

8. Weise EK, Lesk IA. On the electrical conductivity of some alkaline Earth titanates. J Chem Phys (1953) 21:801–6. doi:10.1063/1.1699036

CrossRef Full Text | Google Scholar

9. Lee C-H, Kim S-I. The characteristics of magnesium titanate thin film as buffer layer by electron beam evaporation. Integ Ferroelectr (2003) 57:1265–70. doi:10.1080/10584580390259821

CrossRef Full Text | Google Scholar

10. Komimami H, Tanaka M, Hara K, Nakanishi Y, Hatanaka Y. Synthesis and luminescence properties of Mg-Ti-O: Eu red-emitting phosphors. Phys Status Solidi C (2006) 3:2758–61. doi:10.1002/pssc.200669655

CrossRef Full Text | Google Scholar

11. Selvamani T, Anandan S, Asiri AM, Maruthamuthu P, Ashokkumar M. Preparation of MgTi₂O₅ nanoparticles for sonophotocatalytic degradation of triphenylmethane dyes. Ultrason Sonochem (2021) 75:105585. doi:10.1016/j.ultsonch.2021.105585

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Purohit RD, Saha S. Synthesis of magnesium dititanate by citrate gel route and its characterisation. Ceram Int (1999) 25:475–7. doi:10.1016/s0272-8842(98)00062-5

CrossRef Full Text | Google Scholar

13. López T, Hernández J, Gómez R, Bokhimi X, Boldú JL, Muñoz E, et al. Synthesis and characterization of TiO₂−MgO mixed oxides prepared by the sol−Gel method. Langmuir (1999) 15:5689–93. doi:10.3390/ma12050698

CrossRef Full Text | Google Scholar

14. Yamaguchi O, Yamamoto S. Kinetics of the formation of alkoxy-derived MgO_0.2TiO₂ and MgO.TiO₂. Ceram Int (1981) 7:73–4. doi:10.1016/0272-8842(81)90018-3

CrossRef Full Text | Google Scholar

15. Ali Ehsan M, Naeem R, McKee V, Saeed Hakeem A, Mazhar M. MgTi₂O₅ thin films from single molecular precursor for photoelectrochemical water splitting. Solar Energy Mater & Solar Cells (2017) 161:328–37. doi:10.1016/j.solmat.2016.12.015

CrossRef Full Text | Google Scholar

16. Çelik G, Kurtulus F. Fast microwave synthesis and characterization of MgTi₂O₅. Int J Mater Res (2015) 106:311–3. doi:10.3139/146.111175

CrossRef Full Text | Google Scholar

17. Son H-W, Maki RSS, Kim B-N, Suzuki Y. High-strength pseudobrookite-type MgTi₂O₅ by spark plasma sintering. J Ceram Soc Jpn (2016) 124:838–40. doi:10.2109/jcersj2.16058

CrossRef Full Text | Google Scholar

18. Elnobi S, Abuelwafa AA, Abd El-sadek MS, Wasly HS. Facile synthesis and physical properties of magnesium dititanate nanoparticles for antibacterial applications. Indian J Phys (2024) 7:2417–27. doi:10.1007/s12648-023-03028-9

CrossRef Full Text | Google Scholar

19. Siva Jahnavi V, Kumar Tripathy S, Ramalingeswara AVN. Rao 2019 structural, optical, magnetic and dielectric studies of SnO₂ nano particles in real time applications. Physica B: Condensed Matter (2019) 565:61–72. doi:10.1016/j.physb.2019.04.020

CrossRef Full Text | Google Scholar

20. Suzuki Y, Shinoda Y. Magnesium dititanate (MgTi₂O₅) with pseudobrookite structure: a review. Sci Technol Adv Mater (2011) 12:034301. doi:10.1088/1468-6996/12/3/034301

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Son HW, Guo Q, Suzuki Y, Kim BN, Mori T. Thermoelectric properties of MgTi₂O₅/TiN conductive composites prepared via reactive spark plasma sintering for high-temperature functional applications. Scripta Materialia (2020) 178:44–50. doi:10.1016/j.scriptamat.2019.11.008

CrossRef Full Text | Google Scholar

22. Dhahri A, Dhahri E, Hlil EK. Electrical conductivity and dielectric behaviour of nanocrystalline La_0.6Gd_0.1Sr_0.3Mn_0.75Si_0.25O₃. RSC Adv (2018) 8:9103–11. doi:10.1039/c8ra00037a

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Aman S, Ahmad N, Almutairi BS, Tahir MB, Ali HE. Study of gadolinium substituted barium-based spinel ferrites for microwave applications. J Electron Mater (2023) 52:4149–61. doi:10.1007/s11664-023-10396-9

CrossRef Full Text | Google Scholar

24. Ben Yahya S, Barillé R, Louati B. Synthesis, optical and ionic conductivity studies of a lithium cobalt germanate compound. RSC Adv (2022) 12:6602–14. doi:10.1039/d2ra00721e

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hossain MS, Islam R, Khan KA. Electrical conduction mechanisms of undoped and vanadium doped ZnTe thin films. Chalcogenide Lett (2008) 5:1–9.

Google Scholar

26. Saad Ebied M, Abd El-sadek MS, Salwa AS. Structural and dielectric properties of green synthesized SnO2 nanoparticles. Phys Scr (2025) 100:015989. doi:10.1088/1402-4896/ad9ee8

CrossRef Full Text | Google Scholar

27. Kumar A, Singh S. Electrical properties and conduction mechanisms of Ba_0.75Sr_0.25Ti_1-xZr_xO₃ ceramics synthesized by sol-gel route. Ceramics Int (2024) 50:29476–85. doi:10.1016/j.ceramint.2024.05.242

CrossRef Full Text | Google Scholar

28. Elliott SR. A theory of AC conduction in chalcogenide glasses. Phil Mag (1977) 36:1291–304. doi:10.1080/14786437708238517

CrossRef Full Text | Google Scholar

29. Meena R, Dhaka RS. Dielectric properties and impedance spectroscopy of NASICON type Na₃Zr₂Si₂PO₁₂. Ceramics Int (2022) 23:35150–9. doi:10.1016/j.ceramint.2022.08.111

CrossRef Full Text | Google Scholar

30. Saleh AM, Hraibat S, Kitaneh RL, Abu-Samreh M, Musameh S. Dielectric response and electric properties of organic semiconducting phthalocyanine thin films. J Semiconductors (2012) 8:082002. doi:10.1088/1674-4926/33/8/082002

CrossRef Full Text | Google Scholar

31. Hamood R, Abd El-sadek MS, Gadalla A. Facile synthesis, structural, electrical and dielectric properties of CdSe/CdS core-shell quantum dots. Vacuum (2018) 157:291–8. doi:10.1016/j.vacuum.2018.08.050

CrossRef Full Text | Google Scholar

32. Moustafa MG, Saad HMH, Ammar MH. Insight on the weak hopping conduction produced by titanium ions in the lead borate glassy system. Mater Res Bull (2021) 140:111323. doi:10.1016/j.materresbull.2021.111323

CrossRef Full Text | Google Scholar

33. Kang SD, Dylla M, Snyder GJ. Thermopower-conductivity relation for distinguishing transport mechanisms: polaron hopping in CeO₂ and band conduction in SrTiO₃. Phys Rev B (2018) 97:235201. doi:10.1103/physrevb.97.235201

CrossRef Full Text | Google Scholar

34. Triberis GP. A conductivity study on V2O5 layers deposited from gels. J non-crystalline Sol (1988) 104:135–8. doi:10.1016/0022-3093(88)90192-5

CrossRef Full Text | Google Scholar

35. Takahama R, Arizono M, Indo D, Yoshinaga T, Terakra C, Takeshita N, et al. Magnetic and transport properties of the pseudobrookite Al1−xTi2+xO5 single crystals. JPS Conf Proc (2023) 38:011114. doi:10.7566/JPSCP.38.011114

CrossRef Full Text | Google Scholar

36. Yakuphanoglu F, Aydogdu Y, Schatzschneider U, Rentschler E. DC and AC conductivity and dielectric properties of the metal-radical compound: aqua[bis(2-dimethylaminomethyl-4-NIT-phenolato)] copper(II). Solid State Commun (2003) 128:63–7. doi:10.1016/s0038-1098(03)00651-3

CrossRef Full Text | Google Scholar

37. El-Nahass MM, Atta AA, El-Zaidia EFM, Farag AAM, Ammar AH. Electrical conductivity and dielectric measurements of Co MTPP. Mater Chem Phys (2014) 143:490–4. doi:10.1016/j.matchemphys.2013.08.038

CrossRef Full Text | Google Scholar

38. Darwish AAA, El-Nahass MM, Bekheet AE. AC electrical conductivity and dielectric studies on evaporated nanostructured InSe thin films. J Alloys Compd (2014) 586:142–7. doi:10.1016/j.jallcom.2013.10.054

CrossRef Full Text | Google Scholar

39. Sharma A, Mehta N. Analysis of dielectric relaxation in glassy Se and Se₉₈M₂ (M = Ag, Cd and Sn) alloys. Eur Phys J Appl Phys (2012) 59:10101–7. doi:10.1051/epjap/2012120184

CrossRef Full Text | Google Scholar

40. Deger D, Ulutas K. Conduction and dielectric polarization in Se thin films. Vacuum (2003) 72:307–12. doi:10.1016/j.vacuum.2003.08.008

CrossRef Full Text | Google Scholar