Magnetohydrodynamic Free Stream and Heat Transfer of Nanofluid Flow Over an Exponentially Radiating Stretching Sheet With Variable Fluid Properties

1. Introduction

Because of a stretching surface, studying fluid dynamics is essential as it has many practical and industrial applications. In a number of industrial and manufacturing processes, material production occurs and involves sheets of metal, and polymer. For instance, cooling an infinite metal plate in a cooling bath, the boundary layer along material handling conveyors, plastic sheet aerodynamic extrusion, the boundary layer along a liquid film in condensation procedures, paper manufacturing, glass blowing, steel spinning and plastic film drawing.

Boundary layer for incompressible flow on a moving flat plate was studied by Sakiadis [1]. The study focused on the flow through a moving flat plate while considered static fluid contrary to the work by Blasius [2] who considered flow over a fixed plate. The study carried out by Crane [3] diverted to the study of boundary layer flow of a fluid with high viscosity and uniform density on a plate being stretched linearly. Magyari and Keller [4] conducted the research on an exponentially stretching steady surface to explore heat and mass transfer in the boundary layers but without variable fluid properties and MHD consideration. Elbashbeshy [5], who researched the features of flow and heat transfer over an exponentially stretching permeable sheet, adds a different dimension to this inquiry. The considered research is without the characteristics of MHD and varying fluid properties. Many researchers have extended the work for different flow model. But most of those studies have been focusing on constant fluid properties. The analysis of boundary layer flow with variable fluid properties on a moving flat plate in a parallel free stream was studied by Bachok et al. [6]. They computed solution numerically. Andersson and Aarseth [7] investigated the properties of fluid under the influence of temperature.

Magnetohydrodynamics (MHD) is the study of the flow of electrically conducting fluids in an electro-magnetic-fields. MHD flow research is of significant concern in contemporary processes of metallurgy and metalworking. Makinde et al. [8] examined the MHD flow of variable viscosity of nanofluid over a radially stretching sheet. They indicated that Brownian motion enhances the rate of mass transfer. Mukhopadhyay et al. [9] carried out the study of investigation of magnetic field effects on a fluid flow with variable viscosity on heated surface. They reported that the fluid velocity reduces as the viscosity declines. The influence of temperature on viscosity during heating surface was investigated by Elbashbeshay and Bazid [10] and evaluated solution with the help of a shooting method. The effect of variable fluid properties on the hydro-magnetic flow and heat transfer over a nonlinearly stretching sheet was discussed by Popley et al. [11]. They have numerically addressed their problem. Similarly, the influence of a study of temperature-dependent fluid properties on MHD free stream flow and heat transfer over a nonlinearly stretching sheet was studied by Prasad et al. [12].

Some important applications for radiative heat transfer are the MHD accelerator, high temperature plasmas, power generation devices and cooling of nuclear reactors. Many procedures occur in engineering areas at higher temperatures and understanding the transfer of radiative heat becomes very crucial for the design of appropriate equipment. Heat transfer assessment of boundary layer flow with radiation is also vital in electrical power generation, astrophysical flows, solar power technology, and other industrial areas. Raptis et al. [13] recorded the impact of thermal radiation over a semi-infinite stationary plate on the MHD flow of a viscous fluid. Devi and Reddy [14] presented analysis of the radiation and mass transfer effects on MHD boundary layer flow due to an exponentially stretching sheet with heat source. Mukhopadhyay [15] discussed the slip effects on MHD flow over an radiating exponentially stretching sheet with suction/blowing. The influence of radiation effect over an exponentially stretching sheet was studied by Ishak [16] and Mabood et al. [17]. Bidin and Nazar [18] carried out a numerical study to investigate the effect of thermal radiation on boundary layer flow over an exponentially stretching sheet. Poornima and Reddy [19] presented an analysis of the radiation effects on MHD free convective boundary layer flow of nanofluids over a nonlinear stretching sheet. Most of the above studies have not discussed variable fluid properties and radiation simultaneously.

Because of the unique physical and chemical properties of nanometer-sized products, nanofluids have many applications in the industrial sector. Nanofluids are composites of solid-liquid materials, typically 1–100 nm, consisting of powerful nanoparticles or liquid-suspended nanofibers. The term nanofluid was suggested by Choi [20]. He revealed that supplying a tiny quantity of nanoparticles to conventional fluids (<1 percent by volume fraction) improved the heat conductivity of the fluid by ~2 times. Nield and Kuznestov [21] studied convected boundary layer flow of nanofluid in a porous medium. They considered natural convection past a vertical flat plate. Khan et al. [22] presented non-aligned MHD stagnation point flow of nanofluid with variable viscosity over a stretching sheet with radiation effect. They found that non-alignment of the reattachment point decreases with an increase in magnetic parameter M. Bachok et al. [23] discussed stagnation-point and heat transfer flow over an exponentially stretching/shrinking sheet in a nanofluid. They discovered that the solution obtained for shrinking sheet is not unique. Nada et al. [24] examined the effect of nanofluid while variable properties are taken into account. They considered enclosures for the studies. Malik et al. [25] studied Casson nanofluid's boundary layer flow over a cylinder that stretches exponentially and found solution numerically. Eid [26] addressed the impact of chemical reaction over an exponentially stretching sheet on the MHD boundary layer flow of two-phase nanofluid. They found that thermal boundary layer is dependent on the reaction and source parameter. Gangaiah et al. [27] examined the MHD flow of nanofluid in the presence of viscous dissipation and chemical reaction over an exponentially stretching sheet. They showed that thermal boundary layer depends on viscous dissipation parameter. The effect of different variables like variable viscosity, buoyancy and variable thermal conductivity on mixed convection heat transfer due to an exponentially stretching sheet was discussed by Abel et al. [28]. They obtained solution numerically. In Yousif et al. [29] and Ellahi et al. [30], they have discussed MHD Carreau and non-Newtonian nanofluid flow over an exponentially and slippery walls, respectively. Unsteady flow with CNT-based MHD nanofluid, variable viscosity and a permeable shrinking surface have been discussed in Ahmed et al. [31]. See also Thoi et al. [32] for a different fluid flow aspect in a Y-shaped fin. Previous studies mostly concern with nanofluid with variable viscosity but these are devoid of variable thermal conductivity.

There exists a very extensive literature with and without nanofluid on the topic of a constant fluid properties. But not many studies were dedicated to explore the effects of variable fluid properties on nanofluid flow. To bridge that gap, the present research focuses on the effects of variable viscosity and variable thermal conductivity on the boundary layer nanofluid flow. The structure of the paper is as follows. In section 2, we formulate the fundamental physical problem's mathematical model. The constant and variable fluid characteristics are discussed in section 3. The numerical methods are outlined in section 4. Results and analysis are presented in section 5. Conclusion of the current work is drawn at the end in section 6.

2. Problem Formulation

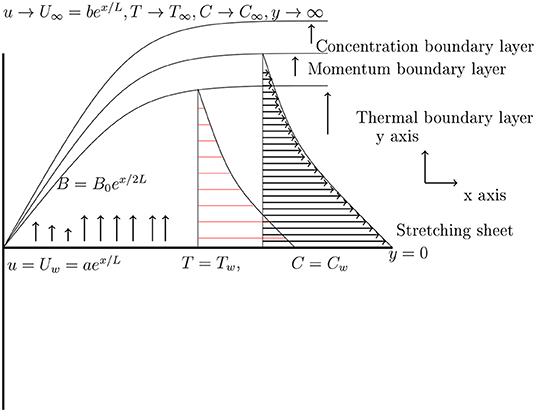
We consider a laminar, MHD nanofluid flow over an exponentially stretching sheet with thermal radiation. The sheet is situated at y = 0. A variable magnetic field $B(x)=B_o{e}^{\frac{x}{2L}}$ has been applied normal to the sheet. Figure 1 is the geometry of the flow, in which x-axis is along and y-axis is taken as normal to the sheet.

FIGURE 1

Figure 1. Structure of the flow problem.

Let $U_w=a{e}^{\frac{x}{L}}$ is the wall velocity, whereas $U_{\infty }=b{e}^{\frac{x}{L}}$ is a free stream velocity, in which stretching parameters a, b > 0. The sheet has been kept at constant wall temperature T_w and T_∞ refers to the ambient temperature. Under the hypothesis of a low magnetic Reynolds number, the induced magnetic field is ignored. The boundary layer equations with Buongiorno model [33] which regulate the above flow are:

$\begin{array}{ll}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,& (1)\end{array}$

$\begin{array}{ll}u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=U_{\infty }\frac{d{U}_{\infty }}{dx}+\frac{1}{\rho }\frac{\partial }{\partial y}(\frac{\mu \partial u}{\partial y})-\frac{\sigma B^2}{\rho }(u-U_{\infty }),& (2)\end{array}$

$\begin{array}{ll}\begin{array}{c}\hfill u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{1}{\rho c_p}\frac{\partial }{\partial y}(\frac{k\partial T}{\partial y})+\\ \hfill \tau (D_B\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}{(\frac{\partial T}{\partial y})}^2)-\frac{1}{\rho c_p}\frac{\partial q_r}{\partial y},\end{array}& (3)\end{array}$

$\begin{array}{ll}u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2},& (4)\end{array}$

where the coordinates of velocities (u, v) are along x− and y− axes, respectively. μ is a fluid viscosity coefficient, B(x) is a variable magnetic field along the y− axis. Here T is the temperature, C is the nanoparticles concentration, c_p is the specific heat constant, D_B is the Brownian motion coefficient, D_T is the thermophoretic diffusion coefficient, $\tau =\frac{{(\rho c)}_p}{{(\rho c)}_f}$ is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the fluid and q_r is the radiative heat flux. Appropriate boundary conditions complete the above system by:

$\begin{array}{l}u=U_w(x)=a{e}^{\frac{x}{L}},v=0,T=T_w,C=C_w\text{at}y=0\\ u\to U_{\infty }=b{e}^{x/L},T\to T_{\infty },C\to C_{\infty }\text{as}y\to \infty & (5)\end{array}$

Using the following similarity transformation on above equations which are defined as:

$\begin{array}{c}\hfill \eta =\sqrt{\frac{a}{2\nu L}}{e}^{\frac{x}{2L}}y,\psi =\sqrt{2a\nu L}{e}^{\frac{x}{2L}}f(\eta ),\theta =\frac{T-T_{\infty }}{T_w-T_{\infty }},\\ \hfill u=a{e}^{\frac{x}{L}}{f}^{\prime }(\eta ),v=-\sqrt{\frac{\nu a}{2L}}{e}^{\frac{x}{2L}}(f(\eta )+\eta f^{\prime }(\eta )).& (6)\end{array}$

Equation (1) is identically satisfied. Moreover, when above similarity variables used in Equations (2), (3), and (4) which yields:

$\begin{array}{ll}{(\frac{\mu }{{\mu }_o}{f}^{″})}^{\prime }+2({\lambda }^2-{(f^{\prime })}^2)+f{f}^{″}-M(f^{\prime }-\lambda )=0,& (7)\end{array}$

$\begin{array}{ll}(1+\frac{4}{3}{R}_d){(\frac{k}{k_o}{\theta }^{\prime })}^{\prime }+P{r}_o(f{\theta }^{\prime }-f^{\prime }\theta +N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{({\theta }^{\prime })}^2)=0,& (8)\end{array}$

$\begin{array}{ll}{\varphi }^{″}+\frac{N_t}{N_b}{\theta }^{″}+L_e(f{\varphi }^{\prime }-f^{\prime }\varphi )=0.& (9)\end{array}$

The boundary conditions transformed into:

$\begin{array}{ll}f(0)=0,f^{\prime }(0)=1,\theta (0)=1,f^{\prime }(\infty )=\lambda ,\theta (\infty )=0,\varphi (0)=1,\varphi (\infty )=0,& (10)\end{array}$

where $M=\frac{2\sigma B_0^{2}L}{\rho a}$ is a magnetic parameter, $\lambda =\frac{b}{a}$ is a ratio of the free stream velocity to the velocity of the stretching sheet, $P{r}_o=\frac{{\mu }_o{c}_{p_o}}{k_o}$ is the Prandtl number, $N_b=\frac{\tau D_B(C_w-C_{\infty })}{\nu }$ is the Brownian motion parameter, $N_t=\frac{\tau D_T(T_w-T_{\infty })}{T_{\infty }\nu }$ is the thermophoresis parameter, $R_d=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k_0{k}^{*}}$ denotes the radiation parameter and $L_e=\frac{\nu }{D_B}$ is the Lewis number.

3. Analysis on Fluid Properties

This section comprises of two subsections. Firstly, an overview of the constant fluid properties will be presented followed by the discussion on variable fluid properties.

3.1. Case A: Constant Fluid Properties

For this case, Equations (7), (8), and (9) can be adjusted as follows to incorporate constant fluid properties:

$\begin{array}{ll}{f}^{‴}+2({\lambda }^2-{(f^{\prime })}^2)+f{f}^{″}-M(f^{\prime }-\lambda )=0& (11)\end{array}$

$\begin{array}{ll}(1+\frac{4}{3}{R}_d){\theta }^{″}+P{r}_o(f{\theta }^{\prime }-f^{\prime }\theta +N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{({\theta }^{\prime })}^2)=0& (12)\end{array}$

$\begin{array}{ll}{\varphi }^{″}+\frac{N_t}{N_b}{\theta }^{″}+L_e(f{\varphi }^{\prime }-f^{\prime }\varphi )=0& (13)\end{array}$

3.2. Case B: Variable Fluid Properties

For this case, viscosity and thermal conductivity in Equations (7), (8), and (9) is considered variable and taken as a function of a temperature. For viscosity we write:

$\begin{array}{ll}\mu (T)=\frac{{\mu }_{ref}}{1+\gamma (T-T_{ref})},& (14)\end{array}$

where we follow Andersson and Aarseth [7] and reference within to write above expression (14). In above γ is a fluid property. If T_o ≈ T_ref then above formula (14) becomes:

$\begin{array}{ll}\mu =\frac{{\mu }_o}{1-\frac{T-T_o}{{\theta }_r(T_w-T_o)}}=\frac{{\mu }_o}{1-\frac{\theta (\eta )}{{\theta }_r}},& (15)\end{array}$

here ${\theta }_r=\frac{-1}{\gamma (T_w-T_o)}$. If the above viscosity relation is incorporated in the Equation (7), then it can be rewritten as:

$\begin{array}{ll}\frac{{\theta }_r}{(\theta r-\theta )}{f}^{‴}+\frac{f^{″}{\theta }^{\prime }{\theta }_r}{{({\theta }_r-\theta )}^2}+2({\lambda }^2-{(f^{\prime })}^2)+f{f}^{″}-M(f^{\prime }-\lambda )=0.& (16)\end{array}$

The variable thermal conductivity is expressed in terms of temperature by following Prasad et al. [12] as:

$\begin{array}{ll}k(T)=k_o(1+ϵ\theta )& (17)\end{array}$

Under this above relation the mathematical form of Equation (8) can be described as:

$\begin{array}{l}(1+\frac{4}{3}{R}_d)((1+ϵ\theta ){\theta }^{″}+ϵ{({\theta }^{\prime })}^2)\\ +P_{r_o}(f{\theta }^{\prime }-f^{\prime }\theta +N_b{\theta }^{\prime }{\varphi }^{\prime }+N_t{({\theta }^{\prime })}^2)=0.& (18)\end{array}$

To measure the roughness, heat transfer rate and mass transfer rate onto the surface, we calculate the skin friction coefficient C_f the local Nusselt number Nu_x and the local Sherwood number Sh_x, respectively, i.e.,

$\begin{array}{ll}{C}_f=\frac{{\tau }_w}{\rho U_w^2}=\frac{f^{″}(0)}{\sqrt{2R{e}_x}},& (19)\end{array}$

$\begin{array}{ll}N{u}_x=-\frac{x{q}_w}{T_w-T_{\infty }}=-\sqrt{\frac{xR{e}_x}{2L}}{\theta }^{\prime }(0),& (20)\end{array}$

$\begin{array}{ll}S{h}_x=-\frac{x{j}_w}{C_w-C_{\infty }}=-\sqrt{\frac{xR{e}_x}{2L}}{\varphi }^{\prime }(0).& (21)\end{array}$

4. Numerical Procedure

4.1. Shooting Method

To apply the shooting technique to Cases A and B together with the boundary conditions, we transformed boundary value problem (BVP) into an initial value problem (IVP) and convert higher order ODEs into a system of first order ODEs. The Newton-Raphson technique was used to locate the root. After that, the order five Runge-Kutta method was implemented to determine the IVP solution. The shooting method is implemented in MATLAB. For Cases A and B, the system of first order ODEs are written as,

(a) Case A:

$\begin{array}{c}\hfill f=y_1,f^{\prime }=y_2,f^{″}=y_3,f^{‴}=y_3^{\prime }=-2({\lambda }^2-y_2^2)-y_1{y}_3\\ \hfill +M(y_2-\lambda ),\\ \hfill y_4=\theta ,y_5={\theta }^{\prime },{\theta }^{″}=y_5^{\prime }=-\frac{P{r}_o}{(1+\frac{4}{3})R_d}(y_1{y}_5-y_2{y}_4+N_b{y}_5{y}_7\\ \hfill +N_t{y}_5^2),\\ \hfill y_6=\varphi ,y_7={\varphi }^{\prime },{\varphi }^{″}=y_7^{\prime }=-L_e(y_1{y}_7-y_2{y}_6)-\frac{N_t}{N_b}{y}_5^{\prime }.\end{array}$

(b) Case B:

$\begin{array}{l}f=y_1,f^{\prime }=y_2,f^{″}=y_3,f^{‴}=y_3^{\prime }=\frac{(y_3{y}_5)}{(y_4-{\theta }_r)}\\ +\frac{(y_4-{\theta }_r)}{{\theta }_r}(2({\lambda }^2-y_2^2)+y_1{y}_3-M(y_2-\lambda )),\\ y_4=\theta ,y_5={\theta }^{\prime },{\theta }^{″}=y_5^{\prime }=\frac{-ϵy_5^2}{1+ϵy_4}\\ -\frac{P_{r_o}}{(1+ϵy_4)(1+\frac{4}{3}{R}_d)}(y_1{y}_5-y_2{y}_4+N_b{y}_5{y}_7+N_t{y}_5^2),\\ y_6=\varphi ,y_7={\varphi }^{\prime },{\varphi }^{″}=y_7^{\prime }=-L_e(y_1{y}_7-y_2{y}_6)-\frac{N_t}{N_b}{y}_5^{\prime }.\end{array}$

4.2. bvp4c

Using MATLAB bvp4c algorithm, BVP can even be solved. bvp4c solver employs the collocation technique in the background. It manages to find a solution after supplying initial guess, domain size and the number of points. Please see reference [34] for more detail and examples.

5. Results and Discussion

In Table 1, we compute the local Nusselt number and compared its values with published results for distinct parameters Prandtl number Pr₀, radiation parameter Rd and magnetic parameter M.

TABLE 1

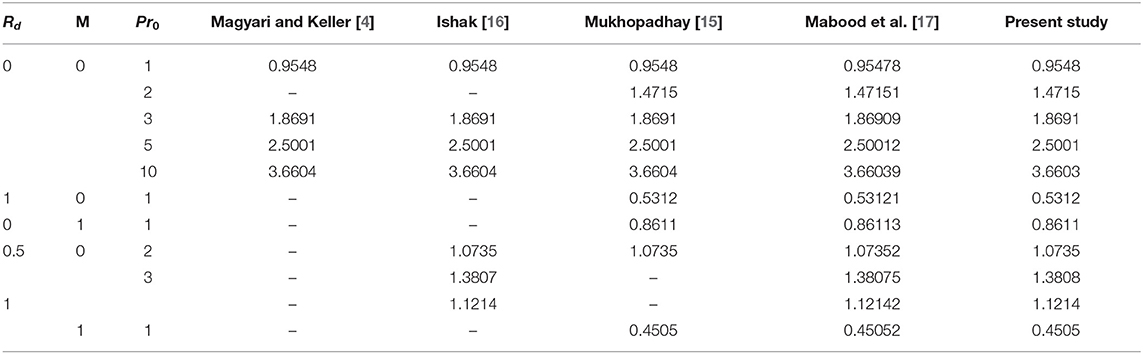
Table 1. (For Case A) Comparison of −θ′(0) for different values of M, R_d and Pr₀, when λ = N_b = N_t = L_e = 0.

Table 2 illustrates that the skin friction coefficient is not significantly changed whereas the local Nusselt number drops for ϵ and increases for the values of λ. The local Sherwood number grows with the rise of λ and ϵ. It is observed in Table 3 that the local Nusselt and the Sherwood numbers rises with a rise of λ but the skin friction coefficient held opposite behavior. For fixed values of λ = 0, 0.5 and an increase in viscosity parameter θ_r brings the increasing change in the skin friction coefficient but the local Nusselt and Sherwood numbers has shown decreasing behavior. Table 4 demonstrates that as Pr_o and R_d rises, there is a negligible change in the skin friction coefficient. But the local Nusselt numbers decreases and local Sherwood number increases by increasing the values of radiation parameter R_d. Moreover, the local Nusselt number increases by increasing Prandtl number but the local Sherwood number decreases.

TABLE 2

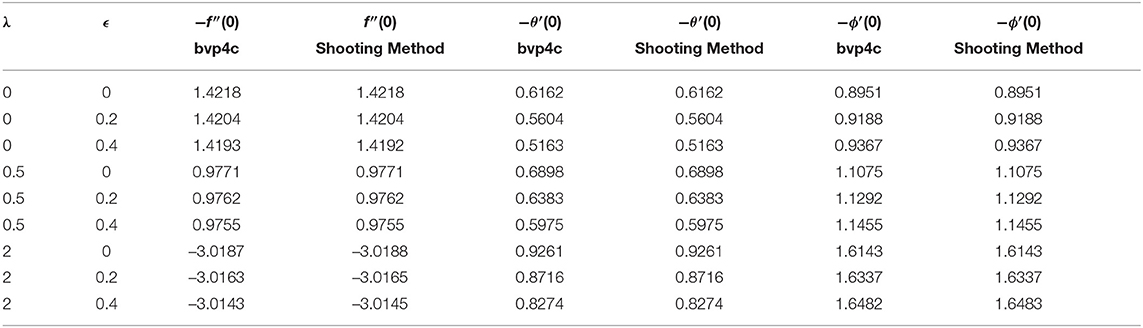
Table 2. (For Case B) Comparison of the values of f″(0), θ′(0) and ϕ′(0) for different values of ϵ and λ when M = λ = R_d = 0, Pr₀ = 1, θ_r = −5, L_e = 1.3.

TABLE 3

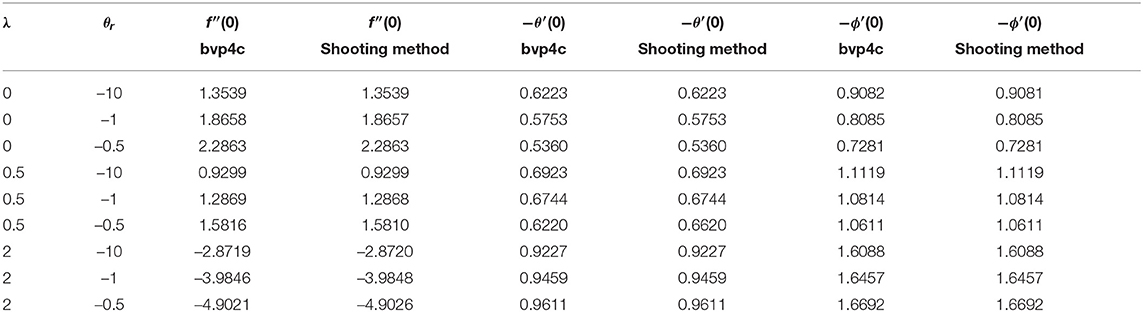
Table 3. (For Case B) Comparison of the values of f″(0) and θ′(0) for different values of θ_r and λ when M = 0, Pr₀ = 10, ϵ = 0.

TABLE 4

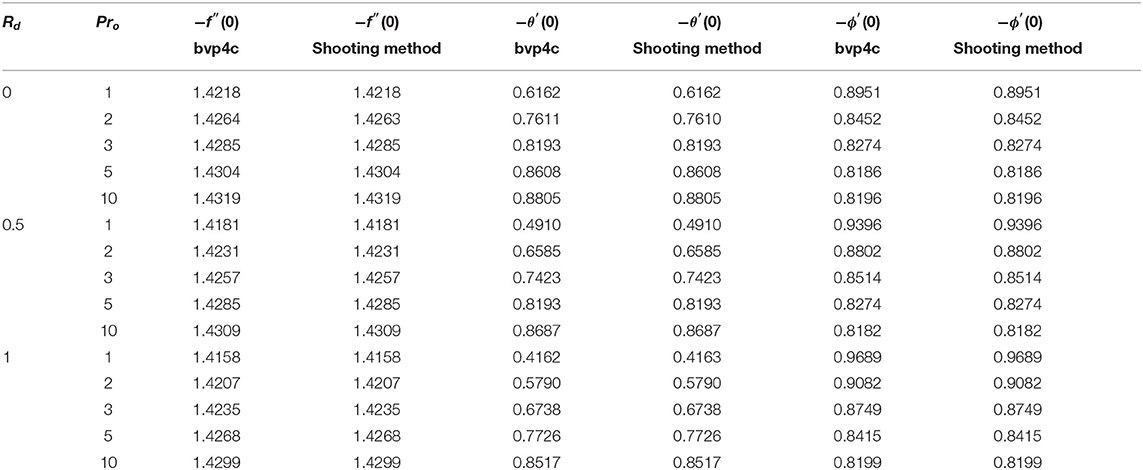
Table 4. (For Case B) Comparison of the values of f″(0) and θ′(0) for different values of R_d and Pr₀ when M = λ = ϵ = 0, θ_r = −5, N_b = 0.8, N_t = 0.5, L_e = 1.3.

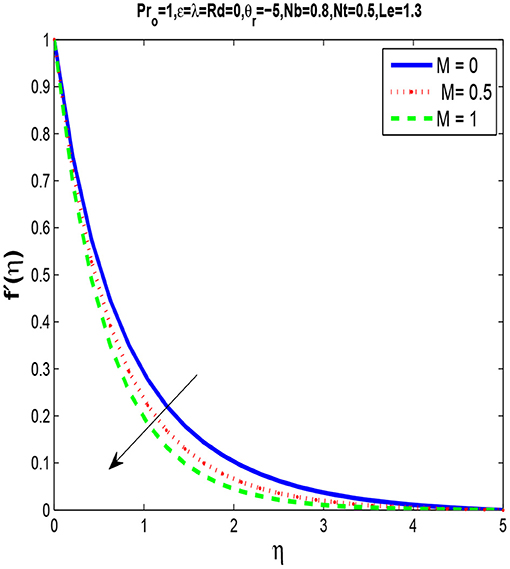
Figure 2 shows that the momentum boundary layer thickness is reduced with the increase in M. It happens because of a transverse magnetic field as it opposes the phenomenon of transport. The Lorentz force generates resistance to the fluid flow with a rise of M and slows down the velocity.

FIGURE 2

Figure 2. Velocity profile f′(η) for different M (For Case B).

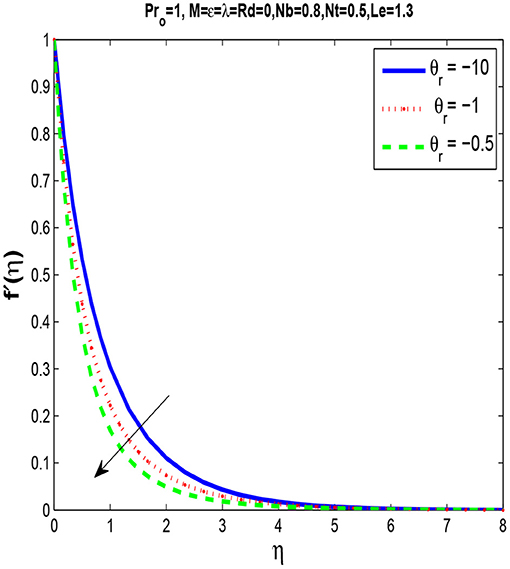
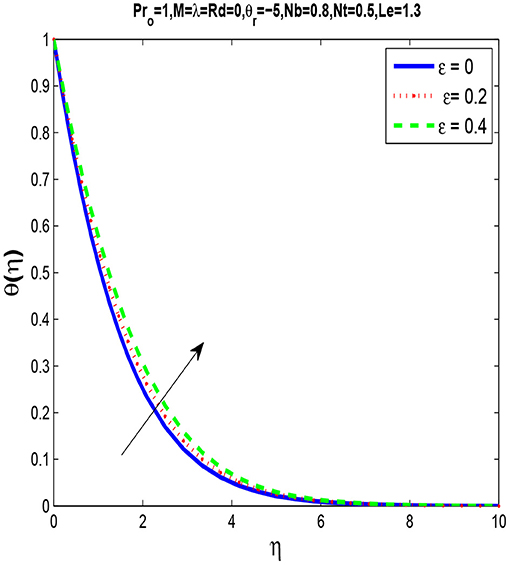
In Figure 3, we observe that by rising the viscosity parameter θ_r, a momentum boundary layer thins. Figure 4 shows that there is a rise in temperature profile with an increase in thermal conductivity parameter ϵ.

FIGURE 3

Figure 3. Velocity profile f′(η) for different θ_r (For Case B).

FIGURE 4

Figure 4. Temperature profile θ(η) for different ϵ (For Case B).

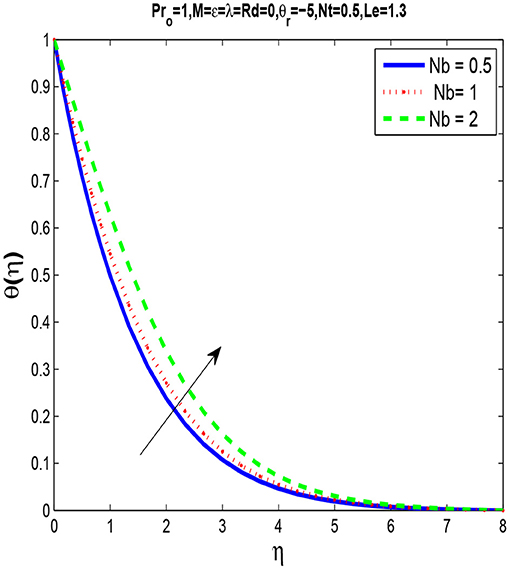
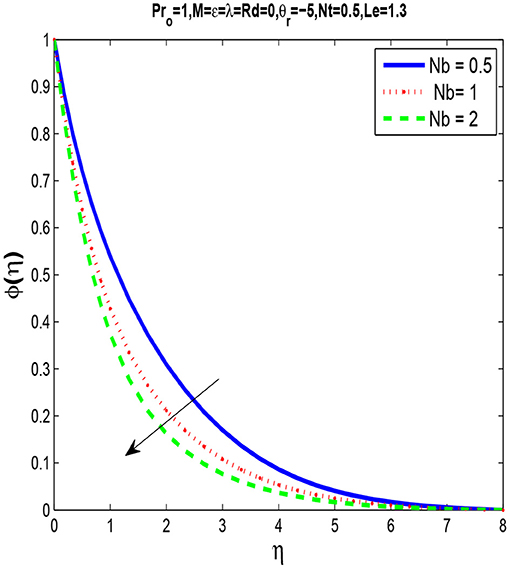
Figures 5, 6 are plotted for different values of Brownian motion parameter N_b and we observe that by increasing N_b thermal boundary layer thickness increases while concentration boundary layer decrease by increasing N_b.

FIGURE 5

Figure 5. Temperature profile θ(η) for different N_b (For Case B).

FIGURE 6

Figure 6. The concentration profile ϕ(η) for different N_b (For Case B).

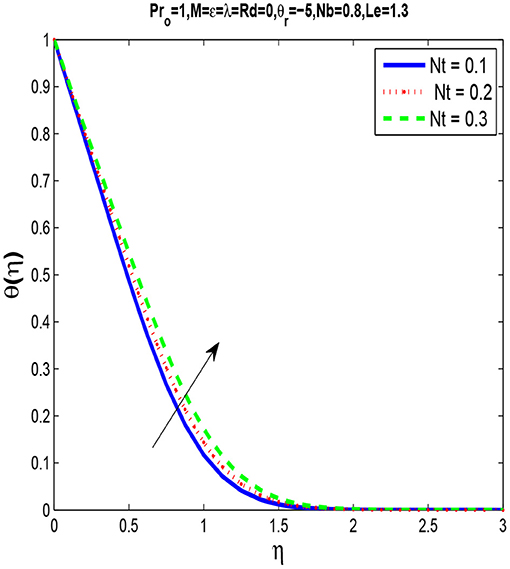
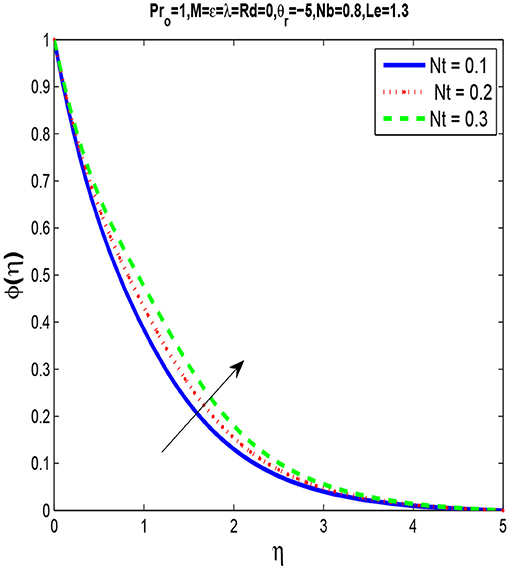
As seen in Figures 7, 8 that by increasing thermophoresis parameter N_t, temperature and concentration profiles increases.

FIGURE 7

Figure 7. Temperature profile θ(η) for different N_t (For Case B).

FIGURE 8

Figure 8. Concentration profile ϕ(η) for different N_t (For Case B).

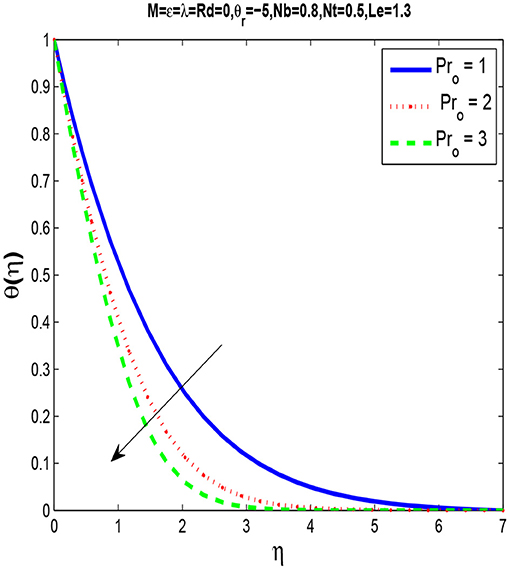
Figure 9 indicates that by increasing Pr_o the thermal boundary layer thickness decreases. This is because, when Pr_o increases, the thermal diffusivity decreases and thus the heat is diffused away from the heated surface more slowly and in consequence increase the temperature gradient at surface.

FIGURE 9

Figure 9. Temperature profile θ(η) for different Pr_o (For Case B).

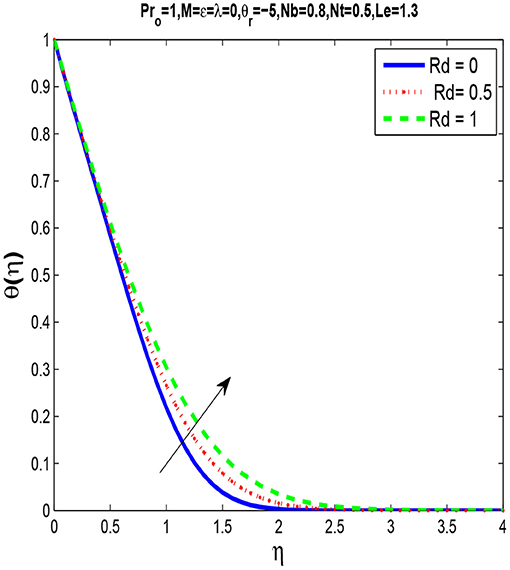
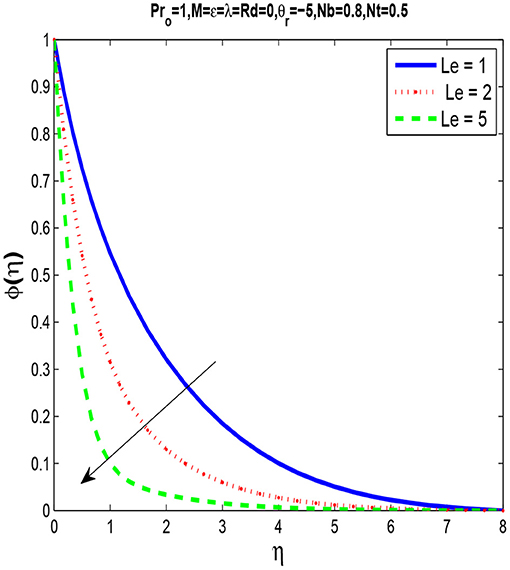
Figure 10 shows that temperature and thermal boundary layer thickness increases when the radiation parameter intensifies. Figure 11 describe the influence of the Lewis number Le on concentration profile. We observe that by increasing Le there is decrease in concentration profile. Lewis number is the ratio of Prandtl number and Schmidt number, so with the increase in Lewis number Le, molecular diffusivity decreases. As a result, increase in Le the nanoparticle fraction is lowered.

FIGURE 10

Figure 10. Temperature profile θ(η) for different Rd (For Case B).

FIGURE 11

Figure 11. Concentration profile ϕ(η) for different Le (For Case B).

6. Conclusions

The current study offers the findings of a two-dimensional MHD flow of an incompressible fluid through an exponentially stretched sheet whereas treating viscosity and thermal conductivity constant in Case A and variable for Case B. The significance of various parameters on velocity, temperature and concentration is examined. The study's main results for Case B are as follows:

• Momentum boundary layer thickness decrease by increasing fluid viscosity parameter θ_r and magnetic parameter M.

• Thermal boundary layer thickness increases by increasing the thermal conductivity parameters ϵ, Brownian motion parameter N_b and thermophoretic parameter N_t.

• Thermal boundary layer thickness decreases by increasing the Prandtl number Pr₀ whereas increases for radiation parameter Rd.

• Concentration boundary layer thickness increases by increasing thermophoretic parameter N_t whereas decreases by increasing Brownian motion parameter N_b and Lewis number Le.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MI collected the data and wrote the paper. MF made the analysis of the paper. TI made the geometry of problem and arrange the setting of the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Sakiadis BC. Boundary layer behavior on continuous solid surfaces: I. Boundary layer equations for two-dimensional and axisymmetric flow. AIChE J. (1961) 7:26–8. doi: 10.1002/aic.690070108

CrossRef Full Text | Google Scholar

2. Blasius H. Grenzschichten in Flussigkeiten mit Kleiner Reibung. Z Angew Math Phys. (1908) 56:1–37.

3. Crane LK. Flow past a stretching plate. Z Angew Math Phys. (1961) 7:21–8.

Google Scholar

4. Magyari E, Keller B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D Appl Phys. (1999) 32:577.

Google Scholar

5. Elbashbeshy EMA. Heat transfer over an exponentially stretching continuous surface with suction. Arch Mechan. (2001) 53:643–51.

Google Scholar

6. Norfifah B, Ishak A, Pop I. Boundary layer flow and heat transfer with variable fluid properties on a moving flat plate in a parallel free stream. J Appl Math. (2012) 2012:372623. doi: 10.1155/2012/372623

CrossRef Full Text | Google Scholar

7. Andersson HI, Jan B. Aarseth. Sakiadis flow with variable fluid properties revisited. Int J Eng Sci. (2007) 45:554–61. doi: 10.1016/j.ijengsci.2007.04.012

CrossRef Full Text | Google Scholar

8. Makinde OD, Mabood F, Khan WA, Tshehla MS. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J Mol Liquids. (2016) 219:624–30. doi: 10.1016/j.molliq.2016.03.078

CrossRef Full Text | Google Scholar

9. Mukhopadhyay S, Layek GC, Samad SkA. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int J Heat Mass Transfer. (2005) 48:4460–6. doi: 10.1016/j.ijheatmasstransfer.2005.05.027

CrossRef Full Text | Google Scholar

10. Elbashbeshy EMA, Bazid MAA. The effect of temperature-dependent viscosity on heat transfer over a continuous moving surface. J Phys D Appl Phys. (2000) 33:2716. doi: 10.1088/0022-3727/33/21/309

CrossRef Full Text | Google Scholar

11. Poply V, Singh P, Yadav AK. A study of Temperature-dependent fluid properties on MHD free stream flow and heat transfer over a non-linearly stretching sheet. Proc Eng. (2015) 127:391–7. doi: 10.1016/j.proeng.2015.11.386

CrossRef Full Text | Google Scholar

12. Prasad KV, Vajravelu K, Datti PS. The effects of variable fluid properties on the hydro-magnetic flow and heat transfer over a non-linearly stretching sheet. Int J Thermal Sci. (2010) 49:603–10. doi: 10.1016/j.ijthermalsci.2009.08.005

CrossRef Full Text | Google Scholar

13. Raptis A, Christos P, Takhar HS. Effect of thermal radiation on MHD flow. Appl Math Comput. (2004) 153:645–9. doi: 10.1016/S0096-3003(03)00657-X

CrossRef Full Text | Google Scholar

14. RLV Renuka D, Poornima T, Bhaskar Reddy N, Venkataramana S. Radiation and mass transfer effects on MHD boundary layer flow due to an exponentially stretching sheet with heat source. Int J Eng Innovative Technol. (2014) 3:33–9.

15. Mukhopadhyay S. Slip effects on MHD boundary layer flow over an exponentially stretching sheet with suction/blowing and thermal radiation. Ain Shams Eng J. (2013) 4:485–91. doi: 10.1016/j.asej.2012.10.007

CrossRef Full Text | Google Scholar

16. Ishak A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malaysiana. (2011) 40:391–5.

Google Scholar

17. Mabood F, Khan WA, Md Ismail AI. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J King Saud Univ Eng Sci. (2017) 29:68–74. doi: 10.1016/j.jksues.2014.06.001

CrossRef Full Text | Google Scholar

18. Bidin B, Nazar R. Numerical solution of the boundary layer flow over an exponentially stretching sheet with thermal radiation. Eur J Sci Res. (2009) 33:710–7.

Google Scholar

19. Poornima T, Bhaskar Reddy N. Radiation effects on MHD free convective boundary layer flow of nanofluids over a nonlinear stretching sheet. Adv Appl Sci Res. (2013) 4:190–202.

Google Scholar

20. Choi SUS, Eastman JA. Enhancing Thermal Conductivity of Fluids With Nanoparticles. Argonne National Lab. (1995).

Google Scholar

21. Nield DA, Kuznetsov AV. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int J Heat Mass Transf. (2009) 52:5792–5. doi: 10.1016/j.ijheatmasstransfer.2009.07.024

CrossRef Full Text | Google Scholar

22. Khan WA, Makinde OD, Khan ZH. Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat. Int J Heat Mass Transf. (2016) 96:525–34. doi: 10.1016/j.ijheatmasstransfer.2016.01.052

CrossRef Full Text | Google Scholar

23. Bachok N, Ishak A, Pop I. Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. Int J Heat Mass Transf. (2012) 55:8122–8. doi: 10.1016/j.ijheatmasstransfer.2012.08.051

CrossRef Full Text | Google Scholar

24. Abu-Nada E, Masoud Z, Oztop HF, Campo A. Effect of nanofluid variable properties on natural convection in enclosures. Int J Therm Sci. (2010) 49:479–91. doi: 10.1016/j.ijthermalsci.2009.09.002

CrossRef Full Text | Google Scholar

25. Malik MY, Naseer M, Nadeem S, Rehman A. The boundary layer flow of Casson nanofluid over a vertical exponentially stretching cylinder. Appl Nanosci. (2014) 4:869–73. doi: 10.1007/s13204-013-0267-0

CrossRef Full Text | Google Scholar

26. Eid MR. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J Mol Liquids. (2016) 220:718–25. doi: 10.1016/j.molliq.2016.05.005

CrossRef Full Text | Google Scholar

27. Gangaiah T, Saidulu N, Venkata Lakshmi A. Magnetohydrodynamic flow of nanofluid over an exponentially stretching sheet in presence of viscous dissipation and chemical reaction. J Nanofluids. (2018) 7:439–48. doi: 10.1166/jon.2018.1465

CrossRef Full Text | Google Scholar

28. Abel M. Mahantesh S, Nandeppanavar M, Basanagouda V. Effects of variable viscosity, buoyancy and variable thermal conductivity on mixed convection heat transfer due to an exponentially stretching surface with magnetic field. Proc Natl Acad Sci India Sec A Phys Sci. (2017) 87:247–56. doi: 10.1007/s40010-016-0338-1

CrossRef Full Text | Google Scholar

29. Yousif MA, Farhan Ismael H, Abbas T, Ellahi R. Numerical study of momentum and heat transfer of MHD Carreau nanofluid over an exponentially stretched plate with internal heat source/sink and radiation. Heat Transf Res. (2019) 50:649–58. doi: 10.1615/HeatTransRes.2018025568

CrossRef Full Text | Google Scholar

30. Ellahi R, Zeeshan A, Hussain F, Abbas T. Thermally charged MHD Bi-phase flow coatings with non-Newtonian nanofluid and Hafnium particles along slippery walls. Coatings. (2019) 9:300. doi: 10.3390/coatings9050300

CrossRef Full Text | Google Scholar

31. Ahmed Z, Nadeem S, Saleem S, Ellahi R. Numerical study of unsteady flow and heat transfer CNT-based MHD nanofluid with variable viscosity over a permeable shrinking surface. Int J Numer Methods Heat Fluid Flow. (2019). doi: 10.1108/HFF-04-2019-0346. [Epub ahead of print].

CrossRef Full Text | Google Scholar

32. Nguyen-Thoi T, Bhatti MM, Ali JA, Mustafa Hamad S, Sheikholeslami M, Shafee A, Haq R. Analysis on the heat storage unit through a Y-shaped fin for solidification of NEPCM. J Mol Liquids. (2019) 292:111378. doi: 10.1016/j.molliq.2019.111378

CrossRef Full Text | Google Scholar

33. Buongiorno J. Convective transport in nanofluids. J Heat Transf. (2006) 128:240–50.

Google Scholar

34. Shampine LF, Kierzenka J, Reichelt MW. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor Notes. (2000) 2000:1–27.

Google Scholar

Nomenclature