- 1Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States
- 2Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States
Single atom catalysts (SACs) are emergent catalytic materials that have the promise of merging the scalability of heterogeneous catalysts with the high activity and atom economy of homogeneous catalysts. Computational, first-principles modeling can provide essential insight into SAC mechanism and active site configuration, where the sub-nm-scale environment can challenge even the highest-resolution experimental spectroscopic techniques. Nevertheless, the very properties that make SACs attractive in catalysis, such as localized d electrons of the isolated transition metal center, make them challenging to study with conventional computational modeling using density functional theory (DFT). For example, Fe/N-doped graphitic SACs have exhibited spin-state dependent reactivity that remains poorly understood. However, spin-state ordering in DFT is very sensitive to the nature of the functional approximation chosen. In this work, we develop accurate benchmarks from correlated wavefunction theory (WFT) for relevant octahedral complexes. We use those benchmarks to evaluate optimal DFT functional choice for predicting spin state ordering in small octahedral complexes as well as models of pyridinic and pyrrolic nitrogen environments expected in larger SACs. Using these guidelines, we determine Fe/N-doped graphene SAC model properties and reactivity as well as their sensitivities to DFT functional choice. Finally, we conclude with broad recommendations for computational modeling of open-shell transition metal single-atom catalysts.
Introduction
Single atom catalysts (SACs) (Yang et al., 2013) are emergent catalytic materials (Yang et al., 2013; Liang et al., 2015, 2017) that have the promise of merging the scalability of heterogeneous catalysts with the high activity and atom economy of homogeneous catalysts, but the reactivity of SACs is poorly understood (Figure 1). Fe/N-doped graphene SACs have been demonstrated for critical transformations such as selective hydrocarbon oxidation (Liu et al., 2017), including ambient methane to methanol conversion (Cui et al., 2018), and as non-Pt oxygen reduction reaction (ORR) electrocatalysts (Li et al., 2016; Chen et al., 2017; Yang et al., 2018). The short-lived, variable SAC active sites that are fundamentally sub-nm-scale challenge the resolution of spectroscopic techniques (Fei et al., 2015; Wang and Zhang, 2016), making first-principles modeling essential to mechanistic study.
Figure 1. Iron catalysts in three classes: homogeneous tetraphenyl porphyrin (Top), N-doped graphene single atom catalysts (SACs, Middle), and heterogeneous hematite (Bottom). In all cases, carbon is shown in gray, nitrogen in blue, iron in purple, and oxygen in red.
For these emerging catalysts, changing synthesis (Liu et al., 2017) or reaction (Li et al., 2016; Zitolo et al., 2017) conditions changes the distribution of SAC coordination geometries, and the most reactive species for key reactions (e.g., ORR or selective partial hydrocarbon oxidation) remain under debate (Zitolo et al., 2015; Zhu et al., 2017; Yang et al., 2018). In selective partial hydrocarbon oxidation, spin-state-dependent reactivity of Fe/N-doped graphene SACs has been observed, with an intermediate, five-coordinate Fe(III)-N-C catalyst more reactive and selective (Liu et al., 2017) than low-spin or high-spin Fe active sites with four- or six-fold coordination. The fundamental source of this spin-state dependent reactivity remains unknown. In SAC electrocatalysts (Fei et al., 2015; Qiu et al., 2015; Zitolo et al., 2015, 2017; Back et al., 2017; Chen et al., 2017; Cheng et al., 2017; Zhang et al., 2017a,b; Zhu et al., 2017; Gao et al., 2018; Jiang et al., 2018; Wang et al., 2018; Zhang et al., 2018), changes in applied potential (e.g., in ORR) have been suggested to change the Fe SAC active site, possibly through a change in spin state (Zitolo et al., 2017).
Although perhaps surprising in the context of heterogeneous catalysis, strong spin-state dependence in reactivity is well-known in homogeneous catalyst (Schröder et al., 2000) analogs. Thus, it follows that paradigms that work in coordination chemistry might apply to SACs as well. The near-octahedral coordination environment around a metal center produces distinct quantum mechanical spin states (i.e., local metal magnetic moments) that are determined by the ligand-field strength as well as oxidation state and metal identity (Tsuchida, 1938). Different spin states often have distinct reaction barriers (Schröder et al., 2000; Schwarz, 2017) in a paradigm known as two-state reactivity (TSR) (Shaik et al., 1995; Schröder et al., 2000; Schwarz, 2017). TSR was first identified for Fe+ ions, where oxidation of H2 or CH4 to H2O or CH3OH, respectively, is limited by spin inversion from a steep ground state, high spin (HS) surface to a more reactive but excited state low spin (LS) surface. For cases such as iron-oxo porphyrin systems that have nearly degenerate spin states, different pathways can indeed lead to distinct products (Kamachi and Yoshizawa, 2003; Ji et al., 2015).
In minimal model single-site catalysts, we recently demonstrated (Gani and Kulik, 2018) that bond elongation or compression has an effect similar to modulating ligand field strength, which could also alter ground state spin and reactivity in an interconnected manner. Most Fe(II)/N complexes have near degenerate HS and LS states because nitrogen ligands are of intermediate field strength, but small changes in the N-N separation of bidentate ligands that make up the octahedral complex are known to tune the experimental ground state of the material (Phan et al., 2017). In metal-doped graphene, strain has been predicted to change the ground state spin (Huang et al., 2011). Even changes in orientation of ligands (i.e., one equatorial swapped with one axial) have been experimentally observed to change the favored ground state spin of related molecular complexes (Andris et al., 2016).
The confined nature of metal d states and interactions with localized p orbitals from organic ligand atoms impart properties to open-shell SACs in a manner more closely resembling the chemical bonding of homogeneous catalysts than bulk metal counterparts. These very features, i.e., quantum size effects (Yang et al., 2013) at an open shell, high-valent metal atom, that make SACs reactive for essential catalytic transformations (Qiao et al., 2011; Yang et al., 2013; Zitolo et al., 2015, 2017; Zhang et al., 2018) also make conventional computational tools used in heterogeneous catalysis (i.e., plane wave, semi-local density functional theory, or DFT) ill-suited to predictive SAC study. Well-localized electrons are disproportionately affected by self-interaction error in approximate DFT (Cohen et al., 2011; Kulik, 2015), leading to an imbalanced treatment of differing spin and oxidation states (Ganzenmüller et al., 2005; Kulik et al., 2006; Droghetti et al., 2012; Ioannidis and Kulik, 2015, 2017; Mortensen and Kepp, 2015; Gani and Kulik, 2017).
Despite evidence of the importance of spin in homogeneous (Abram et al., 2014; Zhu et al., 2016; Schwarz, 2017) and SAC catalysts (Liu et al., 2017), most first-principles studies of SACs (Chu et al., 2015; Ma et al., 2016; Xu et al., 2018) have avoided directly quantifying the role of metal center spin in reactivity, with few exceptions (Impeng et al., 2014; Fong et al., 2018; Sirijaraensre and Limtrakul, 2018). In most studies, the magnetic moment is calculated with a semi-local DFT functional known to produce erroneous magnetic moments (Kulik, 2015; Ioannidis and Kulik, 2017; Janet et al., 2017; Wilbraham et al., 2017) and the magnetization is often allowed to vary along the reaction coordinate (Xu et al., 2018). However, in confined metal centers, spin states are well defined and transitions between spin states occur with low probability because they are quantum mechanically forbidden. Spin state transitions can become kinetically limiting (Shaik et al., 1995; Schröder et al., 2000; Schwarz, 2017), explaining unexpected experimental reactivity (Andris et al., 2016). Within the homogeneous catalysis community (Harvey, 2014; Hernández-Ortega et al., 2015), significant effort has been made to develop tools to assess whether spin crossover is kinetically limiting, but this is not the case in SACs.
Unfortunately, given the importance of spin in predicting reactivity, spin state ordering is highly sensitive to the exchange-correlation functional employed in approximate DFT (Ganzenmüller et al., 2005; Kulik et al., 2006; Droghetti et al., 2012; Ioannidis and Kulik, 2015, 2017; Mortensen and Kepp, 2015). Semi-local (e.g., generalized gradient approximation, GGA) DFT functionals widely employed for their good cost/accuracy balance for many properties consistently stabilize overly-delocalized, covalent states (Autschbach and Srebro, 2014). GGAs thus favor the increased bonding in low-spin over high-spin states (Kulik, 2015; Gani and Kulik, 2017; Ioannidis and Kulik, 2017; Janet et al., 2017; Wilbraham et al., 2017). Hybrid functionals, which incorporate an admixture of HF exchange, are employed in organic chemistry to correct delocalization errors (Kümmel and Kronik, 2008). In transition metal catalysis, the fraction of HF exchange required, as judged by comparison to experiment or accurate correlated wavefunction theory (WFT) reference, is strongly system dependent (Bruschi et al., 2004; Ganzenmüller et al., 2005; Smith et al., 2005; Bowman and Jakubikova, 2012; Droghetti et al., 2012; Ioannidis and Kulik, 2015; Verma et al., 2017).
Thus, in this work, we carry out highly accurate correlated wavefunction theory calculations to develop benchmarks for transition metal complex spin state ordering with ligands that model the environment observed in single atom catalysts. Using these benchmarks, we identify trends in DFT functional performance, and then we evaluate how these observations influence predictions of the stability, reactivity, and ground state identity in models of Fe(II)/N-doped graphene SACs. Finally we provide our conclusions and outlook, including recommendations for computational modeling in this emergent space of single atom catalysis.
Computational Details
Octahedral Transition Metal Complexes
Initial structures of octahedral transition metal (TM) complexes with H2O, NH3, pyridine, and pyrrole ligands were built with the molSimplify toolkit (Ioannidis et al., 2016) with both ligand force-field pre-optimization and trained metal-ligand bond length features enabled. For the hexa-aqua and hexa-ammine complexes, M(II) Ti-Ni and M(III) V-Cu ions were studied, but the pyrrole and pyridine ligands were only studied in complex with Fe(II) or Fe(III). The formal charges assigned to the ligands were neutral in all cases except for pyrrole, which was deprotonated and given a −1 charge. High-spin (HS)-low-spin (LS) states studied in this work were defined as: triplet-singlet for d2 Ti(II)/V(III) and d8 Ni(II)/Cu(III), quartet-doublet for d3 V(II)/Cr(III) and d7 Co(II)/Ni(III), quintet-singlet for d4 Cr(II)/Mn(III) and d6 Fe(II)/Co(III), and sextet-doublet for d5 Mn(II)/Fe(III). Intermediate-spin (IS) states were also studied: triplet d4 Cr(II)/Mn(III) or d6 Fe(II)/Co(III) and quartet d5 Mn(II)/Fe(III).
Fe/N-Doped Graphene SAC Finite Models
Two possible Fe(II) coordination environments in finite graphitic SAC models were investigated with DFT, and in both the metal is coordinated by four nitrogen atoms substituted in the graphene structure. In both cases, we employed a hydrogen-atom-terminated graphene flake to avoid increasing computational cost in accordance with prior SAC computational studies that used finite models (Xu et al., 2018). First, a FeN4C10 compound (chemical formula: C36N4H16Fe) was studied in which all coordinating nitrogen atoms were in six-membered rings (i.e., pyridinic N). This structure is formed by removing two adjacent C atoms from C42H16 and replacing the four C atoms surrounding the vacancy with N atoms. This active site would correspond to two adjacent point defects in graphene, as has been observed experimentally (Banhart et al., 2011). A second compound, FeN4C12 (chemical formula: C40N4H16Fe), was also studied in which all coordinating nitrogen atoms were in five-membered rings (i.e., pyrrolic N). This structure was formed by removing two C atoms from a C46H16 structure, which contains two seven-membered rings in the center surrounded by four five-membered rings. Thus, this structure would require vacancy migration that has also been experimentally observed (Banhart et al., 2011). The two C atoms were removed from where the seven membered rings are joined, and the four inward-facing C atoms that are part of the five-membered rings were replaced with N atoms. All initial coordinates were generated by drawing the 2D structures with ChemDraw and converting the xml structures to 3D coordinates with the molSimplify (Ioannidis et al., 2016) interface to OpenBabel (O'Boyle et al., 2011) followed by force field optimization with the universal force field (Rappé et al., 1992). Singlet, triplet, and quintet spin states were studied, and all simulations had zero net charge.
Fe/N-Doped Graphene SAC Periodic Models
Periodic analogs to the flake models were studied starting from a 4 × 4 supercell of graphene at its experimental lattice parameter (Trucano and Chen, 1975). A smaller supercell than suggested (i.e., 7 × 7) in previous work (Krasheninnikov et al., 2009) was used for computational efficiency, and future work should focus on the effect of supercell size on dopant properties. The pyridinic (chemical formula: FeN4C18) SAC model was created following the same vacancy/N-atom replacement approach as in the finite case. For the pyrrolic (chemical formula: FeN4C20) SAC model, we started from the pyridinic case, inserting C atoms into the five-membered FeN2C2 ring. Next, we adjusted the adjacent six-membered rings into five-membered rings to create pyrrolic N atoms. In this small supercell, an eight-membered C ring was then formed next to the five membered rings. Neutral systems were studied by spin polarized, fixed magnetization periodic calculations in singlet, triplet, and quintet states.
Localized Basis Set DFT Calculations
Transition Metal Complexes
All LS, IS, and HS complexes were geometry optimized with DFT using the PBE0 (default 25% exchange) global hybrid GGA functional (Adamo and Barone, 1999) with the def2-TZVP basis set (Weigend and Ahlrichs, 2005) in ORCA v.4.0 (Neese, 2018). Singlet states were calculated in a restricted formalism, whereas all remaining calculations were open shell and required level shifting (Saunders and Hillier, 1973) in select cases to aid self-consistent field convergence typically with a value of 1.0 eV but as large as 100.0 eV in one case ([Mn(NH3)6]2+). The optimizations were carried out using the BFGS algorithm in redundant internal coordinates implemented to the default tolerances of 3 × 10−4 hartree/bohr for the maximum gradient and 5 × 10−6 hartree for the change in self-consistent field (SCF) energy between steps. All calculations at other levels of theory or with differing functional definitions were obtained as single point energies on these optimized geometries. The effect of Hartree-Fock (HF) exchange fraction choice on spin-state energetics within DFT was investigated by altering the fraction in a modified form of the PBE0 global hybrid. The HF exchange fraction was varied from as low as 0% [i.e., a pure PBE GGA (Perdew et al., 1996)] to as high as 100% HF exchange in increments of 10–20%, as indicated in the text, again using the def2-TZVP basis set. In previous work (Gani and Kulik, 2016), we found tuning range-separation parameters in range-corrected hybrids to have a comparable effect on density and energetics of transition metal complexes to global exchange tuning, and therefore we focus on only global exchange tuning in this work.
Fe/N-Doped Graphene Flake Models
Geometry optimizations and single-point energy calculations were performed with ORCA v4.0. All DFT methodology was kept the same as for transition metal complexes, including geometry optimizing at PBE0 (25% exchange) and carrying out single points at modified exchange fractions in PBE0 in 10% increments in conjunction with the def2-TZVP basis set, except as noted below. All singlet, triplet, and quintet calculations were carried out in an unrestricted formalism. All calculations employed the resolution of the identity (RI) (Baerends et al., 1973; Whitten, 1973; Dunlap et al., 1979; Eichkorn et al., 1995, 1997; Kendall and Fruchtl, 1997) and the chain-of-sphere (COSX)(Neese et al., 2009) approximations with the auxiliary basis set def2/J (Weigend, 2006) and def2-TZVP/C (Hellweg et al., 2007) for all atoms to accelerate the calculations while introducing marginal errors (Kossmann and Neese, 2009). Molecular structures and orbitals were visualized and plotted with VESTA (Momma and Izumi, 2011).
Periodic DFT Calculations
All systems were calculated with both the PBE (Perdew et al., 1996) semi-local GGA functional and the HSE06 (Heyd et al., 2003, 2006) local, range-separated GGA hybrid using the plane wave, periodic boundary condition Quantum-ESPRESSO (Paolo et al., 2009) code. Norm-conserving pseudopotentials for C, N, and Fe were generated with OPIUM (Rappe et al., 1990). The wavefunction and charge density cutoffs employed were 50 Ry and 200 Ry, respectively. A Monkhorst-Pack k-point grid of 8 × 8 × 1 was used for efficiency after confirming convergence of total energies with k-point mesh size. Total energies were converged to 0.1 meV and forces were converged to 1 meV/Å. Quantum-ESPRESSO post-processing tools were employed to visualize the spin density and projected density of states. Variable cell relaxation was employed to obtain final lattice parameters with PBE GGA for the pyridinic (result: 8.34 Å × 7.55 Å) and pyrrolic (result: 8.35 Å) models. A vacuum between each SAC layer of 10 Å was included along with a dipole correction to limit periodic image effects (Bengtsson, 1999). The HSE06 calculations were obtained as single point energies applied to these structures.
Correlated WFT
Complete active-space second-order perturbation theory (CASPT2) (Andersson et al., 1992) calculations were performed with OpenMolcas1 (Aquilante et al., 2016) on M(II)/M(III) hexa-aqua and hexa-ammine octahedral complexes. Calculations were carried out with two active space definitions: the standard active space and an extended active space. For the standard active space, we followed literature recommendations for TM complexes (Pierloot, 2003; Veryazov et al., 2011) to include five orbitals with TM 3d character, two σ bonding orbitals describing covalent metal-ligand bonding, and five double-shell d orbitals for mid-row and later transition metals [i.e., Mn(II/III) and later]. For n 3d electrons, the standard active space is (n + 4, 7) (i.e., for Sc-Cr) or (n + 4, 12) (i.e., for Mn-Cu). In the extended active space, we followed additional literature recommendations (Wilbraham et al., 2017) to include the metal 3s orbital and an unoccupied counterpart, giving an active space of (n + 6, 9) (i.e., for Sc-Cr) or (n + 6, 14) (i.e., for Mn-Ni). Relativistic atomic natural orbital (ANO-rcc) basis sets (Roos et al., 2004, 2005) contracted to [7s6p5d3f2g1h] for the metal center, [4s3p2d1f] for O and N, and [3s1p] for H were used together with the scalar relativistic Douglas-Kroll Hamiltonian (Douglas and Kroll, 1974; Hess, 1986). The 10 core orbitals were frozen in all calculations. An imaginary level shift (Forsberg and Malmqvist, 1997) of 0.1 was used, and a zeroth-order Hamiltonian empirical correction, i.e., the IPEA shift (Ghigo et al., 2004), was set as 0.5 a.u. or varied as described in the main text to identify the effect on spin state energetics. For difficult to converge complete active space self-consistent field iterations, a level shift was applied to the Hamiltonian with shift value 1.0.
Results and Discussion
Spin State Ordering in Model Complexes
Correlated WFT Results
We first conducted correlated wavefunction theory (WFT) calculations to generate reference spin-splitting energies of model first row octahedral transition metal complexes. Our focus is on weak field hexa-aqua and hexa-ammine complexes that are small (i.e., 19–25 atoms in size) and of comparable ligand field strength to the coordination environment in SACs. Although CASPT2 is often the method of choice for predicting spin state energetics for molecules that are either too large or multireference in character to be comfortably treated with CCSD(T) (Pierloot et al., 2017), a number of calculation parameters can strongly influence the CASPT2 predictions. Specifically, spin state energetics can be influenced by the active space choice and the formulation of the zeroth-order Hamiltonian, i.e., the value of the IPEA shift (Ghigo et al., 2004). Here, we investigate the effects of both of these factors and then select reference results for DFT calculations.
Several studies (Kepenekian et al., 2009; Lawson Daku et al., 2012; Vela et al., 2016; Pierloot et al., 2017) have shown that the standard IPEA shift of 0.25 a.u. in CASPT2 overstabilizes high spin states. However, there is no universal agreement about the best solution to this problem. Some (Kepenekian et al., 2009; Lawson Daku et al., 2012; Vela et al., 2016) have recommended increasing the IPEA shift to 0.5–0.7 a.u. based on comparison with experimental or MRCI results, whereas others (Pierloot et al., 2017) recommend the standard IPEA value because increased IPEA can reduce the high spin bias but only at the expense of deteriorating the CASPT2 description of valence correlation. To understand the effect of IPEA shift, we obtained CASPT2 spin-splitting energies with IPEA shifts of 0.0, 0.50, and 1.5 a.u. and standard active spaces (Figure 2 and see Computational Details). For all complexes, increasing IPEA shifts the high-spin/low-spin splitting toward more positive values, reducing high spin stabilization. The range of energetics calculated with different IPEA values for each complex provides a measure of IPEA sensitivity of each transition metal complex's spin-splitting energy (Figure 2). The IPEA sensitivity is consistently largest for cases where the high spin state has four more unpaired electrons than the low spin state (i.e., Cr2+ through Co3+).
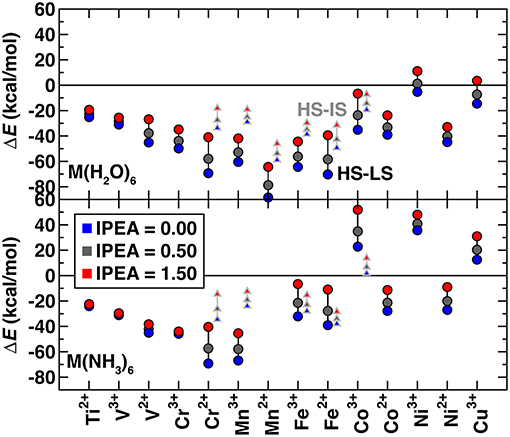
Figure 2. CASPT2 spin splitting energetics in kcal/mol for ΔEH−L (circles) and ΔEH−I (triangles), as indicated in inset, of hexa-aqua (top) and hexa-ammine (bottom) transition metal complexes. Results are shown for 3 IPEA shifts: 0.00 (blue symbols), 0.50 (dark gray symbols), and 1.50 (red symbols) a.u.. Both M(II) and M(III) complexes are shown sorted by the number of 3d electrons, from Ti2+ to Cu3+.
To focus only on spin state definitions in which the high spin state has two more unpaired electrons, we compare the high spin/low spin splitting, ΔEH−L, for early and late TMs with the high spin/intermediate spin splitting, ΔEH−I, for mid-row TMs. For these two electron differences, we observe similar sensitivities, with a ca. 10–20 kcal/mol positive shift when the IPEA is changed from 0.0 to 1.5 a.u. (Figure 2). This observation excludes only very early or late TM complexes that have smaller sensitivities. In comparison, the 4 electron-difference cases have higher sensitivities of around 30 kcal/mol or more (Figure 2). Overall, most early- and mid-row complexes remain high spin regardless of the IPEA shift (i.e., below the zero axis in Figure 2). The smaller energetic differences between states in later TM complexes [e.g., hexa-aqua Ni(III)] mean that the IPEA shift can change the ground state from high spin to low spin for very large IPEA shifts. For subsequent calculations, we selected the 0.5 a.u. IPEA shift but note that variation across the commonly employed range of 0.0–0.5 a.u. can shift the predicted ΔEH−L (ΔEH−I) spin-splitting for mid-row [e.g., Fe(II/III)] complexes by around 10 (3) kcal/mol (Figure 2).
We next investigated the effect of use of a standard active space vs. a more extended active space in the CASPT2 calculations of ΔEH−L and ΔEH−I using the 0.5 a.u. IPEA shift (Supplementary Table 1). For most complexes, the energetic difference due to active space change is on the order of a few kcal/mol, which suggests that the calculation is converged with respect to active space size, as motivated in previous work (Wilbraham et al., 2017). The major outlier identified is [Mn(NH3)6]2+, which is strongly low-spin in the standard active space but becomes high-spin like hexa-aqua Mn(II) with the extended active space, exhibiting greater active space dependence than had been observed in Mn(II) porphyrins (Yang et al., 2016) (Supplementary Table 1). This discrepancy is likely caused by orbital rotation of some active orbitals into the inactive metal 3s/4s orbitals, as suggested in recent work (Radoń and Drabik, 2018) on aqua complexes. After removing this outlier, the mean absolute difference between the standard and extended active space results for all ΔEH−L and ΔEH−I combinations is 3.3 kcal/mol for the hexa-aqua and 5.9 kcal/mol for the hexa-ammine complexes. The mean signed error is near zero for the hexa-aqua cases, and weakly negative (ca. −3 kcal/mol) for the hexa-ammines (Supplementary Table 1). Generally, discrepancies are smallest for the hexa-aqua complexes throughout and especially small for the early or late TMs (e.g., Ti2+-V2+ and Ni3+-Cu3+), typically as little as 0–2 kcal/mol (Supplementary Table 1). In mid-row cases, there is no universal preference as to whether ΔEH−L or ΔEH−I has more active space dependence.
Given the small size of the studied octahedral complexes, we selected the extended active space calculations as reference values for comparison to DFT. Use of the larger active space changed some ground state spin assignments. When calculated with the extended active space, almost all hexa-aqua complexes are high spin, excluding only weakly low spin [Ni(H2O)6]3+ with a ΔEH−L of 0.49 kcal/mol. The slightly stronger ligand field in the hexa-ammine complexes produces some additional LS late-TM complexes [e.g., Co(III) and Cu(III)] along with the analogous Ni(III) complex. Examining isoelectronic metals generally reveals that the later, more oxidized metal has only a weak high-spin-stabilizing effect that is smaller than the ligand-field effect in cases where the two metals converge to similar electronic states (Figure 2 and Supplementary Table 1).
DFT Functional Performance
Despite the high accuracy of CASPT2 for treating spin state energetics in TM complexes, the high computational cost and sensitivity to active space definition and parameters limit its application on SACs. We thus sought to identify the extent to which DFT functionals can be selected or tuned to reproduce the spin-splitting energetics obtained with CASPT2. We focused on the exchange fraction within the global hybrid PBE0 (Adamo and Barone, 1999), motivated by previous observations of comparable behavior in tuning range-separated hybrids (Gani and Kulik, 2016), global hybrids with a different correlation functional (Ioannidis and Kulik, 2015), or those that incorporate meta-GGA exchange (Ioannidis and Kulik, 2017).
From all complexes studied with CASPT2, we narrowed our focus to those containing nominally 3–7 3d electrons (i.e., V2+ to Ni3+) that are most likely to be good candidates for understanding spin-state dependent single atom catalysis. We determined the effect of varying PBE0 exchange fraction on both ΔEH−L and ΔEH−I for the relevant subset (i.e., 4–6 3d electrons). In accordance with prior work (Droghetti et al., 2012; Ioannidis and Kulik, 2015), we anticipated the sensitivity of these quantities to exchange fraction and the optimal exchange fraction to minimize error with respect to CASPT2 to be chemistry dependent. However, we aimed to identify if these trends can be readily rationalized (Gani and Kulik, 2017) or learned (Janet and Kulik, 2017) for use in SAC modeling.
As expected (Droghetti et al., 2012; Ioannidis and Kulik, 2015; Zhao and Kulik, 2018), spin-state energetics vary linearly with exchange fraction over a wide range (i.e., 0–50%) and high-spin states are stabilized with increasing exchange fraction for all transition metal complexes studied (Supplementary Tables 2–3). We quantified the exchange sensitivity of the spin-splitting energetics (Ioannidis and Kulik, 2015) by an approximate linear fit:
We use the unit notation HFX corresponding to the variation from 0 to 100% exchange. To maximize correspondence in quantities compared, we evaluate exchange sensitivity of all spin states that differ by two paired electrons: ΔEH−L for V(II)/Cr(III) and Co(II)/Ni(III) and ΔEH−I for the remaining complexes (ΔEH−L values are also tabulated in Supplementary Table 3). The exchange sensitivity of two-electron-difference spin-state ordering for [M(H2O)6]2+ complexes is relatively invariant to 3d filling (i.e., varying only 2–4 kcal/(mol·HFX), see Figure 3). Conversely, hexa-ammine Mn(II), Fe(II), and Co(II) complexes have increased spin-splitting exchange sensitivity over the earlier TM complexes (Figure 3). For both ligand fields, the M(III) complexes are even more varied, with the least exchange sensitivity being observed in either late or early transition metal complexes (Figure 3). These observations are consistent with the fact that these complexes should have the least difference in electron delocalization between the two spin states, reducing exchange sensitivity (Gani and Kulik, 2017). Although M(III) complexes are more variable, isoelectronic +2/+3 complexes do have somewhat comparable exchange sensitivity (Figure 3). In comparing ΔEH−L for all complexes, exchange sensitivity is universally higher for these mid-row cases due to the enhanced sensitivity of the four-electron difference energetics (e.g., [M(H2O)6]2+: −57 kcal/(mol·HFX) for Mn vs. −25 kcal/(mol·HFX) for V, see Supplementary Figure 1).
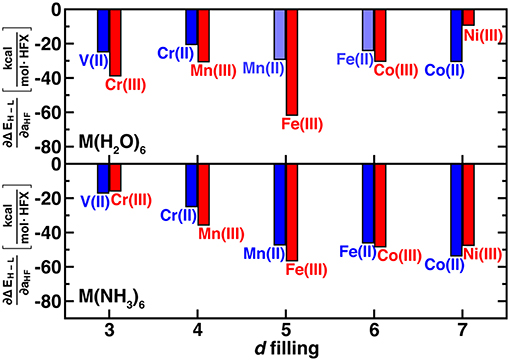
Figure 3. Sensitivity of spin-state splitting with respect to HF exchange (i.e., ∂ΔEH−L/∂aHF, in kcal/mol.HFX) for hexa-aqua (top) and hexa-ammine (bottom) transition metal complexes. Both M(II) and M(III) complexes are shown grouped by their nominal d filling from 3 to 7 3d electrons for V(II) to Ni(III). For the 4, 5, and 6 d-electron cases, the energy gap corresponds to high-spin/intermediate-spin rather than high-spin/low-spin. Shaded bars indicate that spin contamination could not be eliminated for both spin states and sensitivity may not be reliable.
The remaining question is whether the exchange fraction can be appropriately tuned within a modified form of PBE0 to obtain ΔEH−L and ΔEH−I values that match CASPT2 results. Comparing the range of spin-splitting energies obtained from 0 to 100% exchange to the CASPT2 extended active space values generally reveals that high exchange fractions (c.a. 40%) are required to reproduce CASPT2 results (Figure 4 and ΔEH−L-only results shown in Supplementary Figure 2). With the exception of Ni(III) or V(II)/Cr(III) hexa-ammines, pure PBE GGA ΔE values are much more positive (i.e., low-spin biased) than the WFT results (Figure 4). Increasing exchange thus in most cases improves agreement with WFT, but the optimal exchange fraction for reproducing the CASPT2 result varies significantly for the different complexes (Figure 4). For five of the cases [e.g., midrow Mn(II)(H2O)6, Fe(II)(NH3)6, and Co(II)(H2O)6], the optimal exchange fraction is larger than 0.4, whereas the majority of the remaining complexes would require exchange fractions of 0.0-0.4 to recover the CASPT2 value (Figure 4). Only three complexes [i.e., V(II)(H2O)6, Cr(III)(H2O)6, and Ni(III)(H2O)6] have an optimal exchange fraction corresponding to typically applied (Ioannidis and Kulik, 2015) values of around 10–30%.
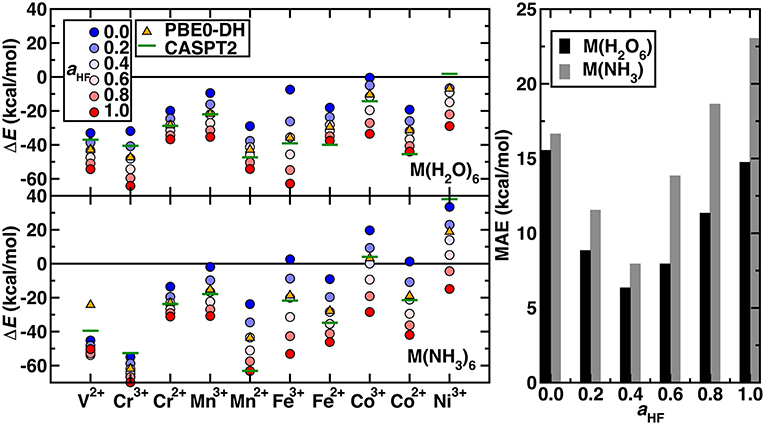
Figure 4. (Left) Spin-splitting energetics (in kcal/mol) corresponding to ΔEH−I for Cr2+-Co3+ and ΔEH−L for all other cases shown for hexa-aqua (Top) and hexa-ammine (Bottom) complexes. Modified PBE0 GGA hybrid results are shown as circles. The exchange fraction, aHF, is colored from blue for 0.0 (pure GGA) to red for 1.0 (full HF exchange), according to the inset legend. Reference CASPT2 results with the extended active space and IPEA shift of 0.5 a.u. are shown as green horizontal lines. The PBE0-DH results are shown as orange triangles. (Right) MAE (in kcal/mol) at several exchange fractions for the hexa-aqua and hexa-ammine complexes indicated at left.
Considering overall performance on the 20 TM complexes, incorporating any exact exchange reduces the mean absolute error (MAE) of spin-splitting energies with respect to WFT. From PBE to 20% to 40% exchange, the MAE decreases monotonically from 17 to 12 to 8 kcal/mol for hexa-ammines and comparably (i.e., 16 to 9 to 6 kcal/mol) for hexa-aquas (Figure 4). Increasing HF exchange higher than 40% increases the MAE again for both ligand fields. For these two weak ligand fields, the optimal exchange fraction is more metal dependent than ligand field dependent, producing comparable optimal exchange values for fixed metal and oxidation state (Figure 4). Recent work (Wilbraham et al., 2018) has suggested double hybrids (DH, i.e., with MP2 long-range correlation) could improve predictions of spin-state ordering. We selected the PBE0-DH, which contains 50% global HF exchange for comparison to GGA global hybrid results (Figure 4). The PBE0-DH results are comparable to those obtained with a modified PBE0 global hybrid GGA with 40% exchange (i.e., MAE of 8 kcal/mol for hexa-ammine complexes and 6 kcal/mol for hexa-aqua complexes, see Supplementary Table 4). Given the higher computational cost and scaling of the double hybrids, tuned GGA hybrids would remain a preferable choice for modeling larger systems.
Comparison of Nitrogen-Containing Ligands
So far, we have studied model complexes and confirmed the importance of incorporating exact exchange in DFT functionals to reproduce correlated WFT reference spin-splitting energetics. We next considered the transferability of exchange sensitivity of DFT spin-splitting energetics to octahedral transition metal complexes that contain coordination environments similar to Fe/N-doped graphene SAC models. The two ligands we used to represent these environments were pyridine (py) in which the coordinating nitrogen is in a six membered carbon-containing ring and pyrrole (pyr) in which the coordinating nitrogen is in a five membered carbon-containing ring (Figure 5 inset and see Computational Details). With a pure PBE GGA, all complexes except for hexa-pyr Fe(II) are low spin, whereas exchange fractions above ~15% instead result in all ground states being assigned as high spin (Figure 5). The trend with exchange is again linear as in the hexa-ammine complexes, although the linearity is slightly reduced for Fe(II) vs. Fe(III) complexes (Figure 5).
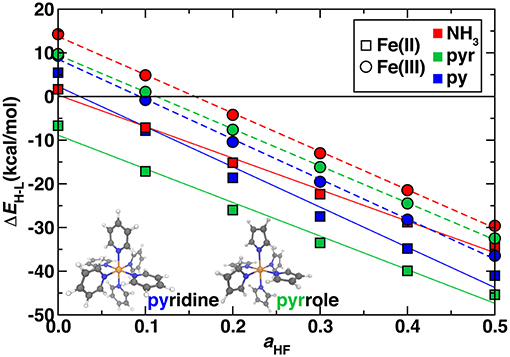
Figure 5. Sensitivity to HF exchange fraction (aHF) of high-spin/low-spin splitting (ΔEH−L, in kcal/mol) for Fe(II) (squares) and Fe(III) (circles) homoleptic octahedral transition metal complexes with NH3 (red symbols), pyridine (blue symbols), and pyrrole (green symbols) ligands. The structures of pyridine and pyrrole compounds are shown in inset in ball and stick (gray carbon, blue nitrogen, white hydrogen, and orange for iron). A zero axis is shown that indicates change in favored ground state spin.
The ΔEH−L values are within ~7 kcal/mol for all complexes of the same oxidation state across the full range of exchange due to the relatively similar ligand field strengths of the N-containing ligands and comparable metal-ligand bond lengths (Supplementary Table 5). However, the hexa-ammines are generally the most low-spin-favoring, whereas the SAC-like nitrogen complexes have a slightly increased high-spin bias. In analogy to ligand field arguments for ΔEH−L, exchange sensitivities, , of spin splitting are also comparable for ammonia, pyridine and pyrrole complexes (Figure 5). For , NH3 and pyrrole are very similar in both Fe(II) [−72 and −77 kcal/(mol·HFX)] and Fe(III) [−88 and −85 kcal/(mol·HFX)], whereas pyridine has slightly larger slope of −92 kcal/(mol·HFX) in both oxidation states. These observations are consistent with the previously observed greater sensitivity to the ligand identity than to oxidation state for Fe(II)/Fe(III) (Ioannidis and Kulik, 2015). Due to the similar spin-splitting energetics and sensitivities to exchange, we expect that our observations on hexa-ammine complexes are applicable to pyridinic and pyrrolic nitrogen-containing complexes and materials as well. Thus, for larger SAC models, we recommend either typical exchange fractions for qualitative ground state spin assignment (i.e., high spin) or higher exchange fractions (ca. 40–50%) that were needed in the hexa-ammine cases to reproduce WFT results quantitatively.
Graphene Flake Models of SACs
Fe/N-doped graphitic SACs are expected on the basis of experimental spectroscopic characterization (Zitolo et al., 2015; Chen et al., 2017; Liu et al., 2017) to consist of Fe metal centers coordinated by pyridinic or pyrrolic nitrogen atoms. These experimental observations come from a combination of aberration corrected scanning tunneling electron microscopy to confirm well-isolated metal sites as well as numerous spectroscopic techniques (e.g., X-ray absorption spectroscopy) to confirm the metal coordination (Zitolo et al., 2015; Chen et al., 2017; Liu et al., 2017). Although the most reactive SAC active site remains an open question, we consider in this work two limits in finite graphene flake SAC models that contain either four pyridinic (FeN4C10) or pyrrolic (FeN4C12) N atoms (Figure 6). Due to the rigidity of the graphene flakes, singlet Fe(II) pyridinic (py) and pyrrolic (pyr) Fe-N bond lengths are shorter than the corresponding py or pyr octahedral complexes (py: 1.90 vs. 2.08 Å or pyr: 1.97 Å vs. 2.11 Å, see Supplementary Tables 5–6). This rigidity in the SAC models without any displacement of iron from the plane that has been observed in porphyrins (Sahoo et al., 2015) also leads to average Fe-N distances being invariant to spin state. There is a marginal (ca 0.01 Å) increase from singlet to quintet spin states for the FeN4C10 SAC in comparison to large (ca. 0.16–0.20 Å) bond length increases from singlet to quintet in the Fe(II)(py)6 complex (Supplementary Tables 5–6). The Fe-N distances are shorter in pyridinic FeN4C10 than in pyrrolic FeN4C12 (i.e., 1.90 Å vs. 1.96 Å) due to smaller N-N separations (FeN4C10: 2.61 Å and 2.75 Å, FeN4C12: 2.75 Å). Despite this difference in N-N separation, which has previously been noted to influence experimental spin state ordering (Phan et al., 2017), the PBE0 ground state spin is triplet in both models (Supplementary Table 7).
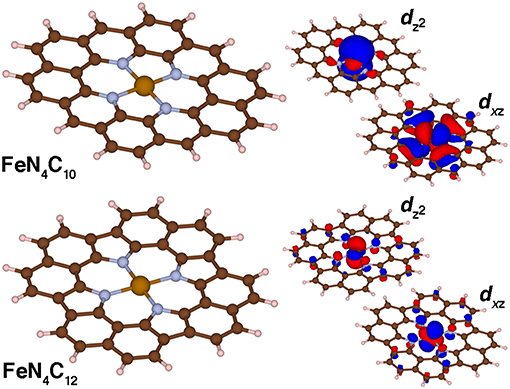
Figure 6. Molecular structures (left) and singly occupied dxz and dz2 spin-up molecular orbitals (right) for FeN4C10 and FeN4C12 graphene flake SAC models in the triplet state. The positive and negative phases of the wavefunction are shown in red and blue, respectively. An isosurface of 0.01 e/Bohr3 was used for the orbitals of FeN4C10 and of 0.03 e/Bohr3 for those of FeN4C12 for clarity. All structures are shown in ball and stick representation with carbon in brown, hydrogen in white, nitrogen in light blue, and iron in orange.
The two singly occupied orbitals in both triplet SAC models correspond to the dxz and dz2 orbitals consistent with expectations for square-planar coordinated triplet Fe(II) (Figure 6). Small differences are observed in the orbital character due to the lower symmetry for the pyridinic FeN4C10 flake: in this case, dxz and dyz degeneracy is broken (Figure 6). The longer N-N separation along the x-axis leads to a pure dxz orbital vs. dxz and dyz mixing for the case of pyrrolic FeN4C12 (Figure 6). In both cases, weak coupling is observed between the metal-centered orbitals and p-orbitals of both the N and C atoms in the graphene flake (Figure 6).
For both SAC models at the PBE0 level of theory, singlet and quintet states reside ~4–6 kcal/mol and 12 kcal/mol above the triplet ground state, respectively, and thus singlet-quintet ΔEH−L is around +6–8 kcal/mol (Supplementary Table 7). These observations contrast with the octahedral models: ΔEH−L for Fe(II)(py)6 is −15 kcal/mol and is −30 kcal/mol for Fe(II)(pyr)6 (Supplementary Table 4). These differences can be traced to several factors, including the coordination number (4 vs. 6) in the models as well as rigidity of the graphene flakes that compress Fe-N bonds to values more commensurate with equilibrium low-spin geometries. Finally, examining the electronic structure of the SAC models reveals distribution of spin not just on the metal but also on the flake in the high spin states, particularly for the pyrrolic FeN4C12 models (Supplementary Tables 8, 9). Even in the triplet ground state this is apparent with a magnetic moment of 2.2 μB, close to that expected (i.e., 2 μB) for FeN4C10, but with a larger 2.7 μB on Fe for FeN4C12 (Supplementary Tables 8, 9). The singlet FeN4C12 is also open shell with a 1.4–2.0 μB magnetic moment on Fe (Supplementary Table 9). In contrast with the molecular complexes, the quintets are particularly poorly described by a localized metal spin, with a reduced Fe moment vs. the triplet state of around 2.4 μB on Fe for FeN4C12 and a comparable one of 2.2 μB on Fe for FeN4C10. Although spin contamination can be expected with increasing HF exchange fraction, comparison of these moments across 0–50% exchange does not ever produce a pure 4 μB moment on Fe for the quintet FeN4C12 (Supplementary Table 9). This observation could be due to low-lying unoccupied states on graphene that are populated instead of the metal states, especially in these models and at this level of theory, as is known to occur in porphyrins as well (Fujii, 2002).
Beyond PBE0 (25%) results on the graphene SAC models, we considered properties over a range that spans from typical values in periodic catalysis modeling (i.e., 0%) to larger values (40%) motivated by our octahedral complex studies (see section Spin State Ordering in Model Complexes). Over this 0–40% range of exchange fractions, singlet and triplet states become destabilized with respect to high-spin quintet states (Figure 7). The reduced dependence of spin-state ordering observed here on exchange fraction in comparison to the octahedral complexes is due to differences in coordination number and rigidity of the SAC models. Intermediate Fe spin states were observed experimentally (Liu et al., 2017) for N-doped graphitic SACs using Mössbauer spectroscopy. Although high HF exchange fractions favoring quintet states for both SAC models would suggest inconsistencies with experiment, it is important to recall that the magnetic moments of the Fe metal are intermediate in both triplet and quintet states. Therefore, high HF exchange fractions are in fact stabilizing the simultaneous presence of spin on the graphene coupled to an intermediate Fe center (Supplementary Tables 8, 9). In both FeN4C12 at low exchange fractions and FeN4C10 over a larger range of 0-100% exchange, higher order than typically linear sensitivities are observed to % exchange (Supplementary Figure 3). For FeN4C12, the anti-ferromagnetically coupled metal spin on Fe varies significantly (i.e., 0.6 μB) and discontinuously, leading to less smooth energetic variations (Figure 7). For the FeN4C10 model where spin states are more well defined, the variations are instead linear over the expected range of HF exchange (Droghetti et al., 2012; Ioannidis and Kulik, 2015; Zhao and Kulik, 2018).
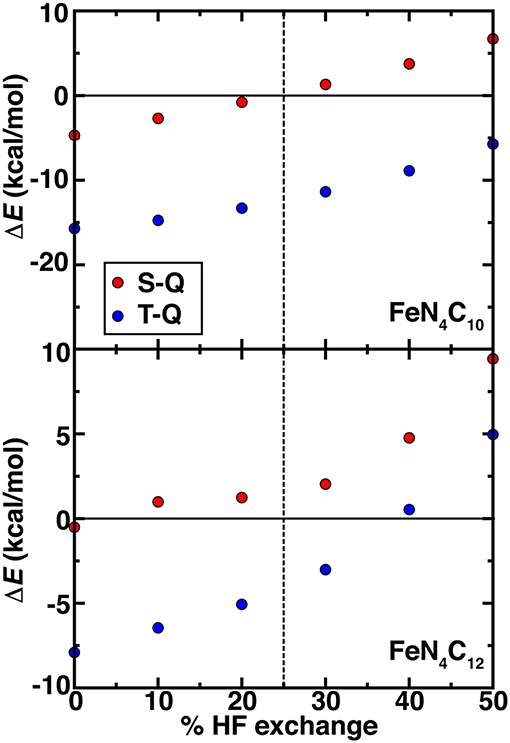
Figure 7. Spin-splitting energetics (in kcal/mol) for singlet-quintet (S-Q, red circles) or triplet-quintet (T-Q, blue circles) spin states vs. % HF exchange for pyridinic (FeN4C10, top) and pyrrolic (FeN4C12, bottom) SAC models. The 25% exchange in standard PBE0 is indicated as a vertical dashed line.
High-valent Fe(IV) = O intermediates are expected to be essential for catalytic transformations at N-doped graphitic SACs (Liu et al., 2017). Thus, we examined the spin-state-, model-, and exchange-fraction-dependence of reaction energetics for Fe(IV) = O formation. Here, we employed N2O as a model oxidant, but results are comparable when assuming the oxygen atom comes from triplet O2 (Figure 8 and Supplementary Figures 4–6). Overall, pyridinic SACs form more stable oxo species across the range of HF exchange and spin states than pyrrolic SACs (Figure 8). Although activation energies would be needed to make firmer statements about relative active site model reactivity, the endothermic reaction energies for the intermediate spin FeN4C12 above 20% exchange (ca. +10 kcal/mol at 40% exchange) suggest that the pyrrolic model could potentially be unreactive with N2O oxidant (Figure 8). Regardless of spin state or model, increasing exchange fraction makes formation of oxo intermediates less favorable due to the penalty for delocalization (Gani and Kulik, 2017).
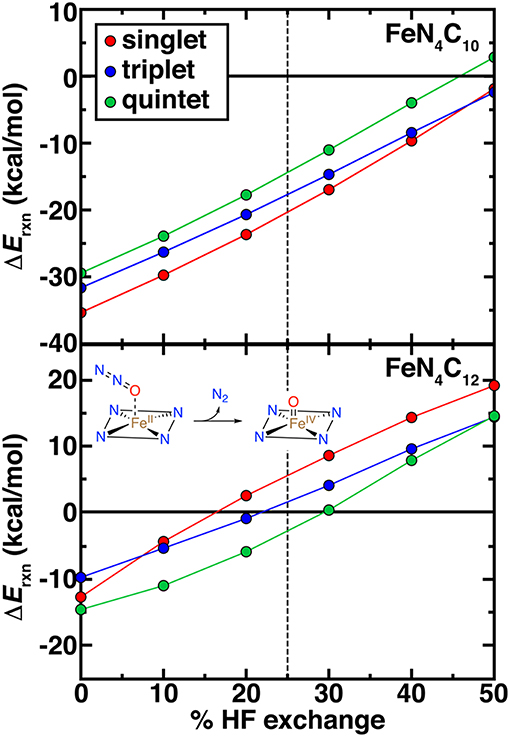
Figure 8. Reaction energetics (ΔErxn, in kcal/mol) for oxo formation from N2O oxidant vs. % HF exchange for pyridinic (FeN4C10, top) and pyrrolic (FeN4C12, bottom) SAC models. The reaction is shown in inset. In each case, singlet (red circles), triplet (blue circles), and quintet (green circles) oxo formation energies are shown. The 25% exchange in standard PBE0 is indicated as a vertical dashed line.
Determination of ground state spin from DFT of the pristine Fe(II)/N SAC model and the Fe(IV) = O intermediate should be carried out with caution, noting that spin (ca. 0.5–1.0 μB) arises on the O atom in triplet and quintet states of both Fe(IV) = O SAC models but not in the singlet states (Supplementary Tables 8, 9). Although spin on the oxo species can be expected and even linked to catalytic efficiency (Liu et al., 2009; Quesne et al., 2014), these states cannot readily be described within a single Kohn-Sham determinant in DFT (Koch and Holthausen, 2015). Overall, spin state ordering of the bare Fe(II) SAC is largely preserved in the Fe(IV) = O intermediate, with singlet and triplet Fe(IV) = O states being weakly stabilized by around 3–5 kcal/mol with respect to the bare Fe(II) case for the pyridinic SACs (Supplementary Figure 4). In the pyrrolic case, the opposite occurs, potentially due to the loss of spin on the ring in triplet pyrrolic Fe(IV) = O (Supplementary Table 9 and Figure 4). Nevertheless, further investigation of kinetic barriers is merited in future work, as close spin state ordering of both the Fe(IV) = O and pristine Fe(II) intermediates combined with comparable differences of around 5–10 kcal/mol between reaction energetics in each spin state could give rise to spin-state dependent reactivity with distinct product formation (Kamachi and Yoshizawa, 2003; Ji et al., 2015). Finally, it is noteworthy that at 0% exchange (i.e., pure PBE), singlet FeN4C12 is predicted to produce a slightly more stable Fe(IV) = O than the triplet, the same ordering that is observed for FeN4C10 albeit at −10 to −15 kcal/mol in the former case vs. −30 to −35 kcal/mol in the latter case (Figure 8). At the 40% exchange motivated by our careful CASPT2 characterization of Fe-N bonds (see section Comparison of Nitrogen-Containing Ligands), or even at the 25% exchange fraction motivated in stronger ligand field cases (Ioannidis and Kulik, 2017), conclusions are different. Namely, at these higher exchange fractions: (i) the triplet oxo is more stable for pyrrolic SACs than the singlet, whereas the ordering remains the same for the pyridinic case, and (ii) neither form exothermically for the pyrrolic case at these exchange fractions.
Periodic Modeling of SACs
We validated our choice of finite SAC flakes by comparing to periodic models of both pyridinic and pyrrolic SAC active sites (Figure 9). We focused on the triplet intermediate spin state favored both in our finite models and in experiment (Liu et al., 2017). Shorter Fe-N 1.91 Å vs. 1.97 Å Fe-N bond lengths are observed for the pyridinic model than for the pyrrolic models, consistent with the finite models. It is more straightforward to localize the magnetic moment to the metal in these periodic systems than was observed for the molecular models (Supplementary Table 10 and Supplementary Figure 7). For the triplet cases, spin density is nearly exclusively observed on the metal center (Figure 9). In both pyridinic and pyrrolic periodic models, use of the hybrid functional leads to less electron density on the Fe center than when a GGA is employed, consistent with prior observations (Gani and Kulik, 2016; Zhao and Kulik, 2018) (Supplementary Table 10).
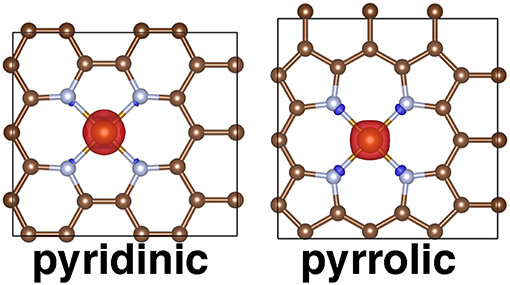
Figure 9. Periodic structures for pyridinic and pyrrolic periodic SAC models in the triplet state with spin density shown. Positive spin density is shown in red and negative spin density is shown in blue, with an isosurface value of 0.03 e/Bohr3. All structures are shown in ball and stick representation with carbon in brown, nitrogen in light blue, and iron in orange.
We compared the electronic structure of the pyridinic and pyrrolic SAC active site models by determining the projected density of states (PDOS) decomposed by N 2p, C 2p, and Fe 3d contributions with the HSE06 hybrid functional (Figure 10). Qualitatively, the occupied orbitals and symmetries confirm observations made on the finite graphene flake models with PBE0, which may be expected if short range effects dominate as HSE06 and PBE0 both incorporate 25% exchange in the short range mixed with pure PBE exchange. That is, the pyridinic system again has singly occupied dz2 and dxz orbitals and no occupation of the dxy state. The pyrrolic system also differs from the pyridinic by having degenerate dxz and dyz states, consistent with the molecular flakes (Figure 10). Generally, agreement is more variable for other spin states, where convergence of the magnetic state is sensitive to starting conditions in the periodic calculation (Supplementary Figures 8–9). In the pyridinic case, dyz states span the Fermi level, whereas the 3d states are well separated in the pyrrolic SAC (Figure 10). The pyrrolic 3d states also mix more deeply into the C and N 2p bands, whereas in the pyridinic case, most 3d states sit at the top of the occupied C/N 2p bands (Figure 10). Overall, these observations support the use of finite models at higher levels of theory for consistent modeling, due to the unique challenges of modeling periodic systems with such methods (Janet et al., 2017). More analysis in larger supercells with variable graphene defects will be necessary in future work to strengthen this conclusion.
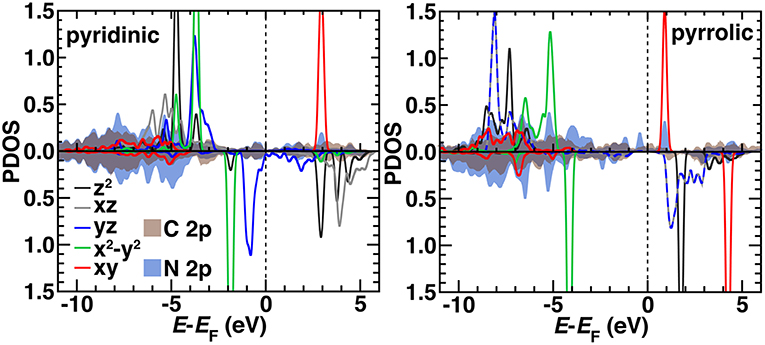
Figure 10. The HSE06 projected density of states (PDOS) for spin up (Top) and down (Bottom, reflected curves) triplet pyridinic (Left) and pyrrolic (Right) SAC models. The 3d Fe orbital PDOS are shown as indicated in inset legends as solid curves except for yz and xz in the pyrrolic case, which are shown as dashed lines due to their degeneracy. The average PDOS for a 2p orbital from C (brown) or N (dark blue) are shown as translucent shaded regions. All energy levels (in eV) are aligned to the Fermi level (EF), which is shown as a vertical dashed line. Some d levels have been truncated by the y-axis range to be able to compare to the broader C 2p and N 2p features.
Conclusions and Outlook
We have presented an overview of the effect of computational model choice on the properties of octahedral transition metal complexes and emergent single atom catalyst (SAC) materials made from Fe centers in N-doped graphene. The octahedral transition metal complexes chosen mimic the ligand field environment observed in the SAC models but remain tractable for study with multi-reference wavefunction theory. Observations from the hexa-aqua and hexa-ammine complex studies revealed that spin state ordering of mid-row complexes could be sensitive both to the IPEA shift chosen and whether an extended active space was used, whereas late and early transition metals were far less sensitive. Then using these extended active space CASPT2 results as a benchmark, we observed that nearly all transition metal complexes benefitted from increased HF exchange. In fact, errors with respect to exchange fraction chosen monotonically decreased from 0 to 40% but with no improvement for higher exchange fractions. The 40% exchange hybrid results had comparable accuracy to the more computationally demanding double hybrid PBE0-DH.
The HF exchange tuning study confirmed the comparable behavior of Fe(II) complexes with ammonia, pyridine, and pyrrole ligands due to the overriding role of the metal, oxidation state, and ligand connecting atom in determining functional sensitivity. Comparison to CASPT2 results on the hexa-ammine system motivated us to propose higher exchange fractions (ca. 40% rather than 25% in PBE0) to be essential to counteract the low-spin bias in semi-local DFT. Using these benchmarks, we then evaluated the effect of DFT functional tuning on finite graphitic SAC models with pyridine or pyrrole nitrogen atoms. In these square planar SAC geometries, rigid structures compressed the Fe-N bond length, reducing exchange sensitivity of spin state ordering but otherwise confirming the observations in the octahedral complexes (i.e., favoring higher spin configurations and destabilizing singlet states). We observed that at the recommended higher exchange fractions, the formation of an oxo intermediate from N2O became unfavorable at the pyrrolic SAC active site. We also observed changes in spin state ordering of the most stable oxo intermediates. Thus, incorporation of exchange can alter predictions of reactivity at SAC active sites. Finally, we confirmed that these observations were not sensitive to choice of a finite SAC model by comparing to periodic SAC models where similar electron configurations were observed.
Overall, predictions of reactivity and spin state ordering are highly sensitive to the functional employed. We have shown that this sensitivity is broadly transferable across different ligand environments as long as the metal and direct ligating atom are kept constant. This observation can be leveraged to obtain DFT functional performance on smaller models where correlated WFT is tractable. Additionally, smaller flake models may be amenable to direct WFT calculation with methods not covered in this work. Spin state exchange sensitivity can be expected to be depressed in cases where the SAC is fully rigid and prevents expansion of the metal-ligand bond when the spin state changes. The highly ordered, symmetric cases here are expected to be the limit in this rigidity argument, and more disordered SAC models or more flexible active sites (e.g., graphitic carbon nitride) are expected to be more sensitive. Still, some outstanding challenges remain in understanding the extent to which spin arising on the graphene itself could be physical and also impart reactivity or whether it arises due to increased static correlation error for hybrid DFT. Furthermore, in periodic simulations with larger supercells than studied in this work it will become essential to employ range-separated hybrids with HF exchange only in the short range, and the comparison to CASPT2 results to range-separated hybrid tuning will be essential here. Overall, modeling in SACs will continue to benefit from this multi-level approach in assessing method accuracy and sensitivity and how method choice impacts predictions of active site geometry and reactivity.
Author Contributions
HK designed the research. FL, TY, JY, EX, and AB carried out the research. FL, TY, JY, and HK wrote and revised the manuscript.
Funding
The authors acknowledge support by the Department of Energy under grant number DE-SC0018096 for the work on density functional theory and the support of FL and AB. The authors also acknowledge the National Science Foundation under grant number CBET-1704266 for the support of TY. HK holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank Adam H. Steeves for providing a critical reading of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2019.00219/full#supplementary-material
Footnotes
1. ^OpenMolcas. Available online at: https://gitlab.com/Molcas/OpenMolcas.git (accessed June 6, 2018).
References
Abram, S.-L., Monte-Pérez, I., Pfaff, F. F., Farquhar, E. R., and Ray, K. (2014). Evidence of two-state reactivity in alkane hydroxylation by lewis-acid bound copper–nitrene complexes. Chem. Commu. 50, 9852–9854. doi: 10.1039/C4CC03754E
Adamo, C., and Barone, V. (1999). Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170. doi: 10.1063/1.478522
Andersson, K., Malmqvist, P. Å., and Roos, B. O. (1992). Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 96, 1218–1226. doi: 10.1063/1.462209
Andris, E., Jašík, J., Gómez, L., Costas, M., and Roithová, J. (2016). Spectroscopic characterization and reactivity of triplet and quintet iron (IV) oxo complexes in the gas phase. Angewandte Chemie Int. Ed. 55, 3637–3641. doi: 10.1002/anie.201511374
Aquilante, F., Autschbach, J., Carlson, R. K., Chibotaru, L. F., Delcey, M. G., De Vico, L., et al. (2016). Molcas 8: new capabilities for multiconfigurational quantum chemical calculations across the periodic table. J. Comput. Chem. 37, 506–541. doi: 10.1002/jcc.24221
Autschbach, J., and Srebro, M. (2014). Delocalization error and “functional tuning” in Kohn–Sham calculations of molecular properties. Acc. Chem. Res. 47, 2592–2602. doi: 10.1021/ar500171t
Back, S., Lim, J., Kim, N.-Y., Kim, Y.-H., and Jung, Y. (2017). Single-atom catalysts for CO2 electroreduction with significant activity and selectivity improvements. Chem. Sci. 8, 1090–1096. doi: 10.1039/C6SC03911A
Baerends, E. J., Ellis, D. E., and Ros, P. (1973). Self-consistent molecular Hartree-Fock-Slater calculations - I. the computational procedure. Chem. Phys. 2, 41–51. doi: 10.1016/0301-0104(73)80059-X
Banhart, F., Kotakoski, J., and Krasheninnikov, A. V. (2011). Structural defects in graphene. ACS Nano 5, 26–41. doi: 10.1021/nn102598m
Bengtsson, L. (1999). Dipole correction for surface supercell calculations. Phys. Rev. B 59, 12301–12304. doi: 10.1103/PhysRevB.59.12301
Bowman, D. N., and Jakubikova, E. (2012). Low-spin versus high-spin ground state in pseudo-octahedral iron complexes. Inorg. Chem. 51, 6011–6019. doi: 10.1021/ic202344w
Bruschi, M., De Gioia, L., Zampella, G., Reiher, M., Fantucci, P., and Stein, M. (2004). A theoretical study of spin states in Ni-S4 complexes and models of the [NiFe] hydrogenase active site. J. Biol. Inorgan. Chem. 9, 873–884. doi: 10.1007/s00775-004-0588-2
Chen, Y., Ji, S., Wang, Y., Dong, J., Chen, W., Li, Z., et al. (2017). Isolated single iron atoms anchored on N-doped porous carbon as an efficient electrocatalyst for the oxygen reduction reaction. Angewandte Chemie 129, 7041–7045. doi: 10.1002/ange.201702473
Cheng, Q., Yang, L., Zou, L., Zou, Z., Chen, C., Hu, Z., et al. (2017). Single cobalt atom and N codoped carbon nanofibers as highly durable electrocatalyst for oxygen reduction reaction. ACS Catal. 7, 6864–6871. doi: 10.1021/acscatal.7b02326
Chu, M., Liu, X., Sui, Y., Luo, J., and Meng, C. (2015). Unique reactivity of transition metal atoms embedded in graphene to CO, NO, O2 and O adsorption: a first-principles investigation. Molecules 20, 19540–19553. doi: 10.3390/molecules201019540
Cohen, A. J., Mori-Sánchez, P., and Yang, W. (2011). Challenges for density functional theory. Chem. Rev. 112, 289–320. doi: 10.1021/cr200107z
Cui, X., Li, H., Wang, Y., Hu, Y., Hua, L., Li, H., et al. (2018). Room-temperature methane conversion by graphene-confined single iron atoms. Chem 4, 1902–1910. doi: 10.1016/j.chempr.2018.1005.1006
Douglas, M., and Kroll, N. M. (1974). Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 82, 89–155. doi: 10.1016/0003-4916(74)90333-9
Droghetti, A., Alfè, D., and Sanvito, S. (2012). Assessment of density functional theory for iron (II) molecules across the spin-crossover transition. J. Chem. Phys. 137:124303. doi: 10.1063/1.4752411
Dunlap, B. I., Connolly, J. W. D., and Sabin, J. R. (1979). Some approximations in applications of X-alpha theory. J. Chem. Phys. 71, 3396–3402. doi: 10.1063/1.438728
Eichkorn, K., Treutler, O., Ohm, H., Haser, M., and Ahlrichs, R. (1995). Auxiliary basis-sets to approximate coulomb potentials. Chem. Phys. Lett. 240, 283–289. doi: 10.1016/0009-2614(95)00621-A
Eichkorn, K., Weigend, F., Treutler, O., and Ahlrichs, R. (1997). Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials. Theor. Chem. Acc. 97, 119–124. doi: 10.1007/s002140050244
Fei, H., Dong, J., Arellano-Jiménez, M. J., Ye, G., Dong Kim, N., Samuel, E. L. G., et al. (2015). Atomic cobalt on nitrogen-doped graphene for hydrogen generation. Nat. Commun. 6:8668. doi: 10.1038/ncomms9668
Fong, A., Vandervelden, C., Scott, S. L., and Peters, B. (2018). Computational support for Phillips catalyst initiation via Cr–C bond homolysis in a chromacyclopentane site. ACS Catal. 8, 1728–1733. doi: 10.1021/acscatal.7b03724
Forsberg, N., and Malmqvist, P.-Å. (1997). Multiconfiguration perturbation theory with imaginary level shift. Chem. Phys. Lett. 274, 196–204. doi: 10.1016/S0009-2614(97)00669-6
Fujii, H. (2002). Electronic structure and reactivity of high-valent oxo iron porphyrins. Coord. Chem. Rev. 226, 51–60. doi: 10.1016/S0010-8545(01)00441-6
Gani, T. Z. H., and Kulik, H. J. (2016). Where does the density localize? convergent behavior for global hybrids, range separation, and DFT+U. J. Chem. Theory Comput. 12, 5931–5945. doi: 10.1021/acs.jctc.6b00937
Gani, T. Z. H., and Kulik, H. J. (2017). Unifying exchange sensitivity in transition metal spin-state ordering and catalysis through bond valence metrics. J. Chem. Theory Comput. 13, 5443–5457. doi: 10.1021/acs.jctc.7b00848
Gani, T. Z. H., and Kulik, H. J. (2018). Understanding and breaking scaling relations in single-site catalysis: methane-to-methanol conversion by Fe(IV)=O. ACS Catal. 8, 975–986. doi: 10.1021/acscatal.7b03597
Ganzenmüller, G., Berkaïne, N., Fouqueau, A., Casida, M. E., and Reiher, M. (2005). Comparison of density functionals for differences between the high- (T2g5) and low- (A1g1) spin states of iron(II) compounds. IV. Results for the ferrous complexes [Fe(L)(‘NHS4’)]. J. Chem. Phys. 122:234321. doi: 10.1063/1.1927081
Gao, Z.-Y., Yang, W.-J., Ding, X.-L., Lv, G., and Yan, W.-P. (2018). Support effects on adsorption and catalytic activation of O 2 in single atom iron catalysts with graphene-based substrates. Phys. Chem. Chem. Phys. 20, 7333–7341. doi: 10.1039/C7CP08301G
Ghigo, G., Roos, B. O., and Malmqvist, P.-Å. (2004). A modified definition of the zeroth-order hamiltonian in multiconfigurational perturbation theory (CASPT2). Chem. Phys. Lett. 396, 142–149. doi: 10.1016/j.cplett.2004.08.032
Harvey, J. N. (2014). Spin-forbidden reactions: computational insight into mechanisms and kinetics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 4, 1–14. doi: 10.1002/wcms.1154
Hellweg, A., Hattig, C., Hofener, S., and Klopper, W. (2007). Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 117, 587–597. doi: 10.1007/s00214-007-0250-5
Hernández-Ortega, A., Quesne, M. G., Bui, S., Heyes, D. J., Steiner, R. A., Scrutton, N. S., et al. (2015). Catalytic mechanism of cofactor-free dioxygenases and how they circumvent spin-forbidden oxygenation of their substrates. J. Am. Chem. Soc. 137, 7474–7487. doi: 10.1021/jacs.5b03836
Hess, B. A. (1986). Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators. Phys. Rev. A 33:3742. doi: 10.1103/PhysRevA.33.3742
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215. doi: 10.1063/1.1564060
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2006). Erratum: hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 124:219906. doi: 10.1063/1.2204597
Huang, B., Yu, J., and Wei, S.-H. (2011). Strain control of magnetism in graphene decorated by transition-metal atoms. Phys. Rev. B 84:075415. doi: 10.1103/PhysRevB.84.075415
Impeng, S., Khongpracha, P., Warakulwit, C., Jansang, B., Sirijaraensre, J., Ehara, M., et al. (2014). Direct oxidation of methane to methanol on Fe–O modified graphene. RSC Adv. 4, 12572–12578. doi: 10.1039/C3RA47826B
Ioannidis, E. I., Gani, T. Z., and Kulik, H. J. (2016). molSimplify: A toolkit for automating discovery in inorganic chemistry. J. Comput. Chem. 37, 2106–2117. doi: 10.1002/jcc.24437
Ioannidis, E. I., and Kulik, H. J. (2015). Towards quantifying the role of exact exchange in predictions of transition metal complex properties. J. Chem. Phys. 143:034104. doi: 10.1063/1.4926836
Ioannidis, E. I., and Kulik, H. J. (2017). Ligand-field-dependent behavior of meta-GGA exchange in transition-metal complex spin-state ordering. J. Phys. Chem. A 121, 874–884. doi: 10.1021/acs.jpca.6b11930
Janet, J. P., and Kulik, H. J. (2017). Predicting electronic structure properties of transition metal complexes with neural networks. Chem. Sci. 8, 5137–5152. doi: 10.1039/C7SC01247K
Janet, J. P., Zhao, Q., Ioannidis, E. I., and Kulik, H. J. (2017). Density functional theory for modelling large molecular adsorbate-surface interactions: a mini-review and worked example. Mol. Simul. 43, 327–345. doi: 10.1080/08927022.2016.1258465
Ji, L., Faponle, A. S., Quesne, M. G., Sainna, M. A., Zhang, J., Franke, A., et al. (2015). Drug metabolism by cytochrome P450 enzymes: what distinguishes the pathways leading to substrate hydroxylation over desaturation? Chem. A Euro. J. 21, 9083–9092. doi: 10.1002/chem.201500329
Jiang, K., Siahrostami, S., Zheng, T., Hu, Y., Hwang, S., Stavitski, E., et al. (2018). Isolated Ni single atoms in graphene nanosheets for high-performance CO2 reduction. Energy Environ. Sci. 11, 893–903. doi: 10.1039/C7EE03245E
Kamachi, T., and Yoshizawa, K. (2003). A theoretical study on the mechanism of camphor hydroxylation by compound I of cytochrome P450. J. Am. Chem. Soc. 125, 4652–4661. doi: 10.1021/ja0208862
Kendall, R. A., and Fruchtl, H. A. (1997). The impact of the resolution of the identity approximate integral method on modern ab initio algorithm development. Theor. Chem. Acc. 97, 158–163. doi: 10.1007/s002140050249
Kepenekian, M., Robert, V., and Le Guennic, B. (2009). What zeroth-order hamiltonian for CASPT2 adiabatic energetics of Fe (II) N 6 architectures? J. Chem. Phys. 131:114702. doi: 10.1063/1.3211020
Koch, W., and Holthausen, M. C. (2015). A Chemist's Guide to Density Functional Theory. Weinheim: John Wiley & Sons.
Kossmann, S., and Neese, F. (2009). Comparison of two efficient approximate Hartree-Fock approaches. Chem. Phys. Lett. 481, 240–243. doi: 10.1016/j.cplett.2009.09.073
Krasheninnikov, A. V., Lehtinen, P. O., Foster, A. S., Pyykkö, P., and Nieminen, R. M. (2009). Embedding transition-metal atoms in graphene: structure, bonding, and magnetism. Phys. Rev. Lett. 102:126807. doi: 10.1103/PhysRevLett.102.126807
Kulik, H. J. (2015). Perspective: treating electron over-delocalization with the DFT+U method. J. Chem. Phys. 142:240901. doi: 10.1063/1.4922693
Kulik, H. J., Cococcioni, M., Scherlis, D. A., and Marzari, N. (2006). Density functional theory in transition-metal chemistry: a self-consistent hubbard U approach. Phys. Rev. Lett. 97:103001. doi: 10.1103/PhysRevLett.97.103001
Kümmel, S., and Kronik, L. (2008). Orbital-dependent density functionals: theory and applications. Rev. Mod. Phys. 80, 3–60. doi: 10.1103/RevModPhys.80.3
Lawson Daku, L. V. M., Aquilante, F., Robinson, T. W., and Hauser, A. (2012). Accurate spin-state energetics of transition metal complexes. 1. CCSD (T), CASPT2, and DFT study of [M (NCH) 6] 2+(M= Fe, Co). J. Chem. Theory Comput. 8, 4216–4231. doi: 10.1021/ct300592w
Li, J., Ghoshal, S., Liang, W., Sougrati, M.-T., Jaouen, F., Halevi, B., et al. (2016). Structural and mechanistic basis for the high activity of Fe-N-C catalysts toward oxygen reduction. Energy Environ. Sci. 9, 2418–2432. doi: 10.1039/C6EE01160H
Liang, J. X., Wang, Y. G., Yang, X. F., Xing, D. H., Wang, A. Q., Zhang, T., et al. (2017). “Recent advances in single-atom catalysis,” in Encyclopedia of Inorganic and Bioinorganic Chemistry, ed R. A. Scott (Hoboken, NJ: Wiley).
Liang, S., Hao, C., and Shi, Y. (2015). The power of single-atom catalysis. ChemCatChem 7, 2559–2567. doi: 10.1002/cctc.201500363
Liu, H. N., Llano, J., and Gauld, J. W. (2009). A DFT study of nucleobase dealkylation by the DNA repair enzyme AlkB. J. Phys. Chem. B 113, 4887–4898. doi: 10.1021/jp810715t
Liu, W., Zhang, L., Liu, X., Liu, X., Yang, X., Miao, S., et al. (2017). Discriminating catalytically active FeNx species of atomically dispersed Fe–N–C catalyst for selective oxidation of the C–H bond. J. Am. Chem. Soc. 139, 10790–10798. doi: 10.1021/jacs.7b05130
Ma, D. W., Wang, Q., Yan, X., Zhang, X., He, C., Zhou, D., et al. (2016). 3d transition metal embedded C2N monolayers as promising single-atom catalysts: a first-principles study. Carbon 105, 463–473. doi: 10.1016/j.carbon.2016.04.059
Momma, K., and Izumi, F. (2011). VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276. doi: 10.1107/S0021889811038970
Mortensen, S. R., and Kepp, K. P. (2015). Spin propensities of octahedral complexes from density functional theory. J. Phys. Chem. A 119, 4041–4050. doi: 10.1021/acs.jpca.5b01626
Neese, F. (2018). Software update: the ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8:e1327. doi: 10.1002/wcms.1327
Neese, F., Wennmohs, F., and Hansen, A. (2009). Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method. J. Chem. Phys. 130:114108. doi: 10.1063/1.3086717
O'Boyle, N. M., Banck, M., James, C. A., Morley, C., Vandermeersch, T., and Hutchison, G. R. (2011). Open babel: an open chemical toolbox. J. Cheminform. 3:33. doi: 10.1186/1758-2946-3-33
Paolo, G., Stefano, B., Nicola, B., Matteo, C., Roberto, C., Carlo, C., et al. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Conden. Matter 21:395502. doi: 10.1088/0953-8984/21/39/395502
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Phan, H., Hrudka, J. J., Igimbayeva, D., Lawson Daku, L. v. M., and Shatruk, M. (2017). A simple approach for predicting the spin state of homoleptic Fe (II) tris-diimine complexes. J. Am. Chem. Soc. 139, 6437–6447. doi: 10.1021/jacs.7b02098
Pierloot, K. (2003). The CASPT2 method in inorganic electronic spectroscopy: from ionic transition metal to covalent actinide complexes. Mol. Phys. 101, 2083–2094. doi: 10.1080/0026897031000109356
Pierloot, K., Phung, Q. M., and Domingo, A. (2017). Spin state energetics in first-row transition metal complexes: contribution of (3s3p) correlation and its description by second-order perturbation theory. J. Chem. Theory Comput. 13, 537–553. doi: 10.1021/acs.jctc.6b01005
Qiao, B., Wang, A., Yang, X., Allard, L. F., Jiang, Z., Cui, Y., et al. (2011). Single-atom catalysis of CO oxidation using Pt 1/FeO x. Nat. Chem. 3:634–641. doi: 10.1038/nchem.1095
Qiu, H. J., Ito, Y., Cong, W., Tan, Y., Liu, P., Hirata, A., et al. (2015). Nanoporous graphene with single-atom nickel dopants: an efficient and stable catalyst for electrochemical hydrogen production. Angewandte Chem Int. Edit. 54, 14031–14035. doi: 10.1002/anie.201507381
Quesne, M. G., Latifi, R., Gonzalez-Ovalle, L. E., Kumar, D., and de Visser, S. P. (2014). Quantum mechanics/molecular mechanics study on the oxygen binding and substrate hydroxylation step in AlkB repair enzymes. Chem. Euro. J. 20, 435–446. doi: 10.1002/chem.201303282
Radoń, M., and Drabik, G. (2018). Spin states and other ligand-field states of aqua complexes revisited with multireference ab initio calculations including solvation effects. J. Chem. Theory Comput. 14, 4010–4027. doi: 10.1021/acs.jctc.8b00200
Rappé, A. K., Casewit, C. J., Colwell, K., Goddard, I. I. I. W. A., and Skiff, W. (1992). UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035. doi: 10.1021/ja00051a040
Rappe, A. M., Rabe, K. M., Kaxiras, E., and Joannopoulos, J. D. (1990). Optimized pseudopotentials. Phys. Rev. B 41, 1227–1230. doi: 10.1103/PhysRevB.41.1227
Roos, B. O., Lindh, R., Malmqvist, P.-Å., Veryazov, V., and Widmark, P.-O. (2004). Main group atoms and dimers studied with a new relativistic ANO basis set. J. Phys. Chem. A 108, 2851–2858. doi: 10.1021/jp031064+
Roos, B. O., Lindh, R., Malmqvist, P.-Å., Veryazov, V., and Widmark, P.-O. (2005). New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 109, 6575–6579. doi: 10.1021/jp0581126
Sahoo, D., Quesne, M. G., de Visser, S. P., and Rath, S. P. (2015). Hydrogen-bonding interactions trigger a spin-flip in iron (III) porphyrin complexes. Angewandte Chem Int. Edit. 54, 4796–4800. doi: 10.1002/anie.201411399
Saunders, V. R., and Hillier, I. H. (1973). A 'Level-Shifting' method for converging closed shell Hartree-Fock wave functions. Int. J. Quantum Chem. 7, 699–705. doi: 10.1002/qua.560070407
Schröder, D., Shaik, S., and Schwarz, H. (2000). Two-state reactivity as a new concept in organometallic chemistry. Acc. Chem. Res. 33, 139–145. doi: 10.1021/ar990028j
Schwarz, H. (2017). Ménage-à-trois: single-atom catalysis, mass spectrometry, and computational chemistry. Catal. Sci. Technol. 7, 4302–4314. doi: 10.1039/C6CY02658C
Shaik, S., Danovich, D., Fiedler, A., Schröder, D., and Schwarz, H. (1995). Two-state reactivity in organometallic gas-phase ion chemistry. Helv. Chim. Acta 78, 1393–1407. doi: 10.1002/hlca.19950780602
Sirijaraensre, J., and Limtrakul, J. (2018). Theoretical investigation on reaction pathways for ethylene epoxidation on Ti-decorated graphene. Struct. Chem. 29, 159–170. doi: 10.1007/s11224-017-1015-y
Smith, D. M., Dupuis, M., and Straatsma, T. (2005). Multiplet splittings and other properties from density functional theory: an assessment in iron–porphyrin systems. Mol. Phys. 103, 273–278. doi: 10.1080/00268970512331317309
Trucano, P., and Chen, R. (1975). Structure of graphite by neutron diffraction. Nature 258:136–137. doi: 10.1038/258136a0
Tsuchida, R. (1938). Absorption spectra of co-ordination compounds. I. Bull. Chem. Soc. Jpn. 13, 388–400. doi: 10.1246/bcsj.13.388
Vela, S., Fumanal, M., Ribas-Ariño, J., and Robert, V. (2016). On the zeroth-order hamiltonian for CASPT 2 calculations of spin crossover compounds. J. Comput. Chem. 37, 947–953. doi: 10.1002/jcc.24283
Verma, P., Varga, Z., Klein, J. E., Cramer, C. J., Que, L., and Truhlar, D. G. (2017). Assessment of electronic structure methods for the determination of the ground spin states of Fe (II), Fe (III) and Fe (IV) complexes. Phys. Chem. Chem. Phys. 19, 13049–13069. doi: 10.1039/C7CP01263B
Veryazov, V., Malmqvist, P. Å., and Roos, B. O. (2011). How to select active space for multiconfigurational quantum chemistry? Int. J. Quantum Chem. 111, 3329–3338. doi: 10.1002/qua.23068
Wang, A., and Zhang, T. (2016). Water splitting: taking cobalt in isolation. Nat. Energy 1:15019. doi: 10.1038/nenergy.2015.19
Wang, J., Zhang, H., Wang, C., Zhang, Y., Wang, J., Zhao, H., et al. (2018). Co-synthesis of atomic Fe and few-layer graphene towards superior ORR electrocatalyst. Energy Storage Mater. 12, 1–7. doi: 10.1016/j.ensm.2017.11.004
Weigend, F. (2006). Accurate coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 8, 1057–1065. doi: 10.1039/b515623h
Weigend, F., and Ahlrichs, R. (2005). Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–3305. doi: 10.1039/b508541a
Whitten, J. L. (1973). Coulombic potential-energy integrals and approximations. J. Chem. Phys. 58, 4496–4501. doi: 10.1063/1.1679012
Wilbraham, L., Adamo, C., and Ciofini, I. (2018). Communication: evaluating non-empirical double hybrid functionals for spin-state energetics in transition-metal complexes. J. Chem. Phys. 148:041103. doi: 10.1063/1.5019641
Wilbraham, L., Verma, P., Truhlar, D. G., Gagliardi, L., and Ciofini, I. (2017). Multiconfiguration pair-density functional theory predicts spin-state ordering in iron complexes with the same accuracy as complete active space second-order perturbation theory at a significantly reduced computational cost. J. Phys. Chem. Lett. 8, 2026–2030. doi: 10.1021/acs.jpclett.7b00570
Xu, H., Cheng, D., Cao, D., and Zeng, X. C. (2018). A universal principle for a rational design of single-atom electrocatalysts. Nat. Catal. 1, 339–348. doi: 10.1038/s41929-018-0063-z
Yang, L., Cheng, D., Xu, H., Zeng, X., Wan, X., Shui, J., et al. (2018). Unveiling the high-activity origin of single-atom iron catalysts for oxygen reduction reaction. Proc. Natl. Acad. Sci. 115:6626. doi: 10.1073/pnas.1800771115
Yang, T., Quesne, M. G., Neu, H. M., Cantú Reinhard, F., n,. G, Goldberg, D. P., et al. (2016). Singlet versus triplet reactivity in an Mn (v)–oxo species: testing theoretical predictions against experimental evidence. J. Am. Chem. Soc. 138, 12375–12386. doi: 10.1021/jacs.6b05027
Yang, X.-F., Wang, A., Qiao, B., Li, J., Liu, J., and Zhang, T. (2013). Single-atom catalysts: a new frontier in heterogeneous catalysis. Acc. Chem. Res. 46, 1740–1748. doi: 10.1021/ar300361m
Zhang, C., Sha, J., Fei, H., Liu, M., Yazdi, S., Zhang, J., et al. (2017a). Single-atomic ruthenium catalytic sites on nitrogen-doped graphene for oxygen reduction reaction in acidic medium. ACS Nano 11, 6930–6941. doi: 10.1021/acsnano.7b02148
Zhang, L., Jia, Y., Gao, G., Yan, X., Chen, N., Chen, J., et al. (2018). Graphene defects trap atomic Ni species for hydrogen and oxygen evolution reactions. Chem 4, 285–297. doi: 10.1016/j.chempr.2017.12.005
Zhang, Z., Gao, X., Dou, M., Ji, J., and Wang, F. (2017b). Biomass derived n-doped porous carbon supported single fe atoms as superior electrocatalysts for oxygen reduction. Small 13:1604290. doi: 10.1002/smll.201604290
Zhao, Q., and Kulik, H. J. (2018). Where does the density localize in the solid state? divergent behavior for hybrids and DFT+U. J. Chem. Theory Comput. 14, 670–683. doi: 10.1021/acs.jctc.7b01061
Zhu, B., Guan, W., Yan, L.-K., and Su, Z.-M. (2016). Two-state reactivity mechanism of benzene C–C activation by trinuclear titanium hydride. J. Am. Chem. Soc. 138, 11069–11072. doi: 10.1021/jacs.6b02433
Zhu, C., Fu, S., Shi, Q., Du, D., and Lin, Y. (2017). Single-atom electrocatalysts. Angewandte Chemie Int. Edit. 56:13944. doi: 10.1002/anie.201703864
Zitolo, A., Goellner, V., Armel, V., Sougrati, M.-T., Mineva, T., Stievano, L., et al. (2015). Identification of catalytic sites for oxygen reduction in iron-and nitrogen-doped graphene materials. Nat. Mater. 14:937. doi: 10.1038/nmat4367
Keywords: density functional theory, catalysis, single atom catalysis, spin state crossover, transition metal chemistry
Citation: Liu F, Yang T, Yang J, Xu E, Bajaj A and Kulik HJ (2019) Bridging the Homogeneous-Heterogeneous Divide: Modeling Spin for Reactivity in Single Atom Catalysis. Front. Chem. 7:219. doi: 10.3389/fchem.2019.00219
Received: 20 December 2018; Accepted: 20 March 2019;
Published: 16 April 2019.
Edited by:
Sam P. De Visser, University of Manchester, United KingdomReviewed by:
Daniel Glossman-Mitnik, Advanced Materials Research Center, MexicoMatthew George Quesne, Cardiff University, United Kingdom
Copyright © 2019 Liu, Yang, Yang, Xu, Bajaj and Kulik. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heather J. Kulik, aGprdWxpa0BtaXQuZWR1
 Fang Liu
Fang Liu Tzuhsiung Yang
Tzuhsiung Yang Jing Yang
Jing Yang Eve Xu1
Eve Xu1 Akash Bajaj
Akash Bajaj Heather J. Kulik
Heather J. Kulik