Molecular Beam Scattering Experiments as a Sensitive Probe of the Interaction in Bromine–Noble Gas Complexes

Introduction

The knowledge of the nature and the characterization of the role of the intermolecular halogen bond (XB) is presently recognized to be of great relevance in many areas of fundamental and applied research, including materials engineering, biochemistry, molecular recognition, drug design, and supra-molecular Chemistry (Gilday et al., 2015; Han et al., 2017).

In order to disentangle the effect of the XB on the molecular dynamics, it is necessary to identify the interaction components involved and to provide their radial and angular dependences. This information, seldom available in the literature, can obtained by investigating in detail prototypical systems, whose features are necessary to formulate interaction models useful for the description of the force fields in systems at increasing complexity and of applied interest (Cappelletti et al., 2015).

The weakly bound complexes Ng–X₂, formed by a noble gas (Ng) and a di-halogen molecule X₂ (X = Cl, Br, I), have been considered as prototypes of particular relevance for investigating energy transfer mechanisms and for the characterization of the fundamental role of the intermolecular interaction components (Baturo et al., 2017; Li et al., 2017) leading to the formation of the weak intermolecular halogen bond (Desiraju et al., 2013). Moreover, for the identification of basic selectivity in energy transfer processes, the X₂ moiety has been considered both the ground ($X^2{\Sigma }_g^{+}$) and in the excited ($B^3{\Pi }_u$) electronic state (Janda et al., 1998; Rohrbacher et al., 2000; Delgado-Barrio et al., 2006; Beswick et al., 2012), and related potential energy surfaces (PES) have been classified as X (ground) and B (excited).

Extensive spectroscopic and theoretical studies (see, for instance, Jahn et al., 1996; Buchachenko et al., 2000; Prosmiti et al., 2002a,b; de Lara-Castells et al., 2004; Boucher et al., 2005; Garcia-Vela, 2005; Carrillo-Bohórquez et al., 2016) have been devoted to the characterization of the stability of the Ng–Br₂ adducts in the limiting collinear and T-shaped configurations and of the predissociation dynamics induced by electronic, vibrational, and rotational excitations.

Nowadays, it is clear that in the ground-state PES, both the collinear and T-shaped isomers have comparable binding energy and are separated by a significant saddle region. By contrast, in the electronically excited PES, the T-shaped configuration is the most stable one, as typical of most of the atom-diatom complexes bound by van der Waals (vdW) forces (de Lara-Castells et al., 2004; Garcia-Vela, 2005; Pirani et al., 2019). The origin of this difference in the topography of the PES is still being debated because it depends on a delicate balance between the involved interaction components. In particular, open questions concern the proper identification of the principal interaction terms, their modeling, and their dependence on the atomic or molecular partners involved within the complex.

Recently, we performed an integrated experimental/theoretical investigation on Ng–Cl₂ systems with the goal of adequately addressing some of the above-mentioned open questions (Nunzi et al., 2019; Pirani et al., 2019). In particular, we have found that for such systems, the most relevant features of the X ground-state PESs are mainly determined by the anisotropic halogen bond components, which operate even in the case of the lightest He–Cl₂. Such components concur to stabilize the collinear configuration selectively by charge transfer (CT) and polar flattening (PF) effects, which are specific interaction features of XB. Ab initio calculations have revealed that both CT and PF contributions miss in the electronic excited B PESs, where the formed adducts show typical vdW behavior. This observation is consistent with the behavior of other atom–diatom systems, as Ng–O₂ and Ng–N₂ complexes, dominated by size repulsion and dispersion/induction attraction (Aquilanti et al., 1995).

The present manuscript reports and discusses the results of a new experimental investigation, focused on the X ground PES of the He–, Ne–, and Ar–Br₂ systems, carried out with the molecular beam (MB) technique applied under the same conditions of recent experiments on Ng–Cl₂. The analysis of these new scattering data has been performed by extending the methodology applied to the rationalization of data measured for homologous systems formed with the Cl₂ moiety (Nunzi et al., 2019; Pirani et al., 2019). In particular, the main components, characterizing the interaction potential between Ng and Br₂, have been identified and their radial angular dependences represented through the adoption of semi-empirical/empirical equations involving only a few parameters, each one with a defined physical meaning. As for Ng–Cl₂ systems, we have found that X ground-state PES in Ng–Br₂ adducts is mainly determined by anisotropic halogen bond components, concurring to stabilize selectively the collinear configuration by CT and PF effects. The model has also been applied to predict the behavior of Kr– and Xe–Br₂ systems, for which MB experiments cannot be carried out under sufficiently high angular and velocity resolution conditions, obtainable for lighter Ng atoms, which are proper to resolve quantum interference effects in the scattering. Such an extension has been achieved by simply exploiting the change of parameters involved when one is moving along the Ng–Br₂ homologous family of systems. Finally, the features the obtained PES have been compared with results from the literature.

Experimental Apparatus and Scattering Results

Gas-phase scattering experiments have been carried out in order to measure the velocity dependence of the integral cross section. The availability of the projectile (here, He, Ne, and Ar) in a large speed range is of great relevance to perform measurements as a function of the collision velocity. On the other hand, the choice of temperature and pressure of the target with a defined mass [here, Br₂ (X,¹${\Sigma }_{\text{g}}^{+}$)] is crucial to achieve in the experiments angular and velocity resolution conditions proper to resolve quantum interference effects, as those giving the “glory” oscillations, observable in the velocity dependence of the integral cross section. The collected experimental results probe in detail, and an internally consistent way, the absolute scale of the interaction both at long and intermediate distance ranges, where, respectively, the attraction dominates and the potential well occurs (Pirani and Vecchiocattivi, 1982; Pirani et al., 2008). Therefore, such results provide direct information on some basic features of the X PESs and allow a direct comparison with other X PESs, recently characterized in detail for the corresponding Ng–Cl₂ systems (Nunzi et al., 2019; Pirani et al., 2019).

The experiments have been performed with an MB apparatus, with the objective of measuring the total (elastic + inelastic) integral cross section Q as a function of the selected MB velocity v. Such an apparatus has been extensively described in the past (Aquilanti et al., 1992; Cappelletti et al., 2002, 2015, 2016a,b). Briefly, it is composed of a set of differentially pumped vacuum chambers, where MB, in the present case formed by Ng atoms, is generated by the gas expansion from a nozzle, maintaining its temperature in the range of 77–600 K and total pressure in the source within 7–20 mbar, in order to avoid cluster formation and to cover a wide range of collision velocities. Under such conditions, the MB emerges with near-effusive or moderate supersonic character, and it is analyzed in velocity by a mechanical selector and collides at a “nominal” velocity, v, with the stationary target gas (Br₂) contained in the scattering chamber at a pressure not larger than 2 × 10⁻⁴ mbar in order to assure the occurrence of single collision events. The chamber is kept at room temperature to avoid condensation effects of the target gas on the walls and to maintain a sufficiently high rotational temperature of the target molecules. The latter condition is critical to limit anisotropy effects in the scattering and then to better resolve frequency and amplitude of the glory oscillatory pattern. MB is detected downstream by a quadrupole mass spectrometer, coupled with an ion counting device. At each selected velocity, v, of the projectile atoms, the quantity to be measured is the MB attenuation I/I₀, where I represents the MB intensity detected with the target in the scattering chamber (filled at the chosen pressure) and I₀ that without it (empty chamber). From the measurement of the ratio I/I₀, it is possible to determine the value of the integral cross section Q(v) through the Lambert–Beer law: calibration methodology and reference data are given in Nenner et al. (1975), Aquilanti et al. (1976), Pirani and Vecchiocattivi (1977).

The Q(v) values, measured for He–, Ne–, and Ar–Br₂ systems as a function of the selected MB velocity v, are reported in Figure 1. In all cases, the cross sections are plotted as Q(v)· v^2/5 to emphasize the “glory” quantum interference and to more efficiently analyze the scattering cross sections in terms of a smooth component and an oscillating part. The He–, Ne–, and Ar–Br₂ systems exhibit absolute scales of the observables and interference patterns that are very different, thus revealing significant variations in the intermolecular interactions.

FIGURE 1

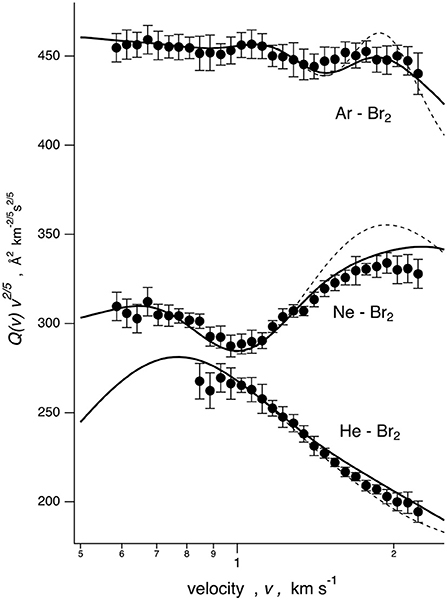
Figure 1. Integral cross sections Q(v) for Ng atom projectiles colliding at each selector velocity with Br₂ targets. Data are plotted as Q(v)· v^2/5 to emphasize the glory patterns. Solid line: cross sections calculated with the full PES, including in the formulation of the various interaction components taken into account in the data analysis. Dashed line: calculation with the spherically averaged PES.

The analysis of Q(v) (see next sections) provided a quantitative characterization of the strength of the intermolecular interaction both at long range, obtained from the velocity dependence of the average value of Q(v), and in the potential well region, probed by the resolved glory structure (Pirani and Vecchiocattivi, 1982; Pirani et al., 2008).

During the analysis, center-of-mass (CM) cross section values have been calculated within the semi-classical Jeffreys–Wentzel–Kramers–Brillouin approximation (Child, 1974) from the assumed intermolecular interaction potential V (see next section), and afterwards convoluted in the laboratory frame to make a direct comparison with the measured Q(v) (Cappelletti et al., 2002).

During a trial-and-error procedure, the parameters defining the basic features of V have been tested and fine-tuned in order to obtain the best comparison between experimental and calculated data. This phenomenological analysis (see the next section) has been guided also by available results obtained in the past on a large variety of atom–molecule systems (Pirani et al., 2019).

Potential Parametrization and Data Analysis

For the Ng–Br₂ systems, we adopted a formulation of PES based on what recently developed for the homologous systems with Cl₂ (Nunzi et al., 2019). In particular, the total intermolecular potential V has been defined as the sum of three contributions, identified as vdW, V_vdW, three bodies, V_3B, and CT, V_CT, each one related to fundamental features of the partners involved in the interaction.

The electronic polarizability is the fundamental chemical–physical property determining both dispersion/induction attraction and Pauli (exchange or particle size) repulsion and can be employed in semi-empirical correlation formulas (Cambi et al., 1991) for the modeling of a large variety of non-covalent intermolecular interactions. Accordingly, the anisotropic V_vdW component has been represented in terms of two pairwise additive potential contributions, Ng–Br_i, where the Br_i interaction centers coincide with the bromine atoms of the Br₂ molecule. As emphasized for the representation of Cl atoms in Cl₂ (Nunzi et al., 2019), also for these “effective” Br atoms, involved in a stable Br–Br chemical bond, we assumed an anisotropic component of the electronic polarizability different from that of the isolated Br atom. On the other side, the value obtained by summing the average polarizability of the “effective” Br atoms is kept consistent with that of the Br₂ molecule (Maroulis and Makris, 1997). To adequately describe the repulsion contributions related to the strongly anisotropic Br₂ electron density, mostly determined by the outer valence electrons in the π* molecular orbitals, we included in the formulation of V a three-body term, V_3B. Finally, a third interaction component, V_CT, has been included and associated with CT effects, which directly influences the formation of the intermolecular bond (Pirani et al., 2000; Belpassi et al., 2009; Cappelletti et al., 2012).

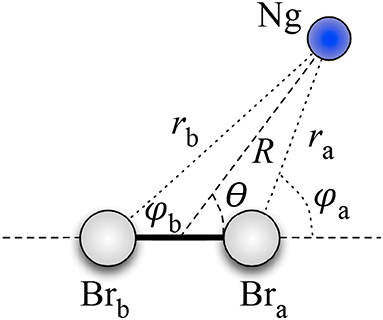
Therefore, assuming as R the distance between Ng and the CM of Br₂, and as θ the angle between the vector R and the Br–Br bond axis (see Figure 2), for the Ng–Br₂ adducts in the X ground states, we defined the anisotropic intermolecular potential V(R, θ) as the combination of three main components:

$\begin{array}{ll}V(R,\theta )=V_{vdW}(R,\theta )+V_{CT}(R,\theta )+V_{3B}(R,\theta )& (1)\end{array}$

Such components indirectly include the role of less important contributions.

FIGURE 2

Figure 2. Coordinate systems for the Ng–Br₂ systems under study.

In more detail, V_vdW has been represented as the sum of two Ng–Br_i (i = a, b) pairwise additive contributions:

$\begin{array}{ll}{V}_{vdW}(R,\theta )=V_{Ng-B{r}_a}(r_a,{\phi }_a)+V_{Ng-B{r}_b}(r_b,{\phi }_b)& (2)\end{array}$

where a and b identify the two different Br atoms, r_a and r_b are the distances between Ng and Br_a/Br_b, and ϕ_aand ϕ_b are the angles between r_a/r_b and the Br₂ bond axis. Accordingly, each atom–atom pair term has been formulated as an improved Lennard Jones (ILJ) function (Pirani et al., 2008):

$\begin{array}{l}{V}_{Ng-Bri}(r_i,{\phi }_i)=\epsilon ({\phi }_i)[\frac{6}{n(r_i,{\phi }_i)-6}·{\left(\frac{r_m({\phi }_i)}{r_i}\right)}^{n(r_i,{\phi }_i)}\\ -\frac{n(r_i,{\phi }_i)}{n(r_i,{\phi }_i)-6}·{\left(\frac{r_m({\phi }_i)}{r_i}\right)}^6]& (3)\end{array}$

where the ε(φ_i) and r_m(φ_i) parameters are generated by the following relationships:

$\begin{array}{ll}\epsilon ({\phi }_i)={\epsilon }_{\parallel }·{cos}^2({\phi }_i)+{\epsilon }_{\perp }·{sin}^2({\phi }_i)& (4)\end{array}$

$\begin{array}{ll}{r}_m({\phi }_i)={r_m}_{\parallel }·{cos}^2({\phi }_i)+{r_m}_{\perp }·{sin}^2({\phi }_i)& (5)\end{array}$

The symbols ∥ and ⊥ refer, respectively, to the parallel (φ_i = 0) and perpendicular (φ_i = π/2) configurations within each Ng–Br_i pair. The factor n(r_i, φ_i), which modulates simultaneously the “fall off” of the repulsion and the radial dependence of the intermediate and long-range attraction, depends on β, an additional parameter related to the hardness of both partners (Capitelli et al., 2007). It is expressed as,

$\begin{array}{ll}n(r_i,{\phi }_i)=\beta +4·{\left(\frac{r_i}{r_m({\phi }_i)}\right)}^2& (6)\end{array}$

Note that the partial long-range attraction coefficient, C_6i = $\epsilon ({\phi }_i)·r_m^6({\phi }_i),$ provides the asymptotic behavior of each ILJ contribution, while the global attraction coefficient is simply given as the sum of the two angular averaged C_6i components.

The values of the ε and r_m parameters have been predicted in an internally consistent way for the three Ng–Br₂ systems from the polarizability components (Cambi et al., 1991). They have been tested, and when necessary, fine-tuned, by exploiting the comparison of calculated cross sections with experimental results. During the analysis, the additional constraint of providing global average asymptotic attractions in substantial agreement (within about 10%) with those reported by Olney et al. (1997) has been imposed. As previously done for other systems involving other halogen atoms (Bartocci et al., 2015; Cappelletti et al., 2015; Nunzi et al., 2019), the zero-order values of _{rm ∥} have been decreased by about 4% to account for the PF effect in the X ground state of Br₂. Such an effect must be related to the peculiar electronic charge distribution of Br along the Br–Br bond direction pointing at the approaching Ng in the collinear isomer (see next section). The decreasing of _{rm ∥} has been accompanied by an of e_∥ in order to maintain the C₆ coefficient constant.

The second term in Equation 1, V_3B(R, θ), has been formulated as,

$\begin{array}{ll}{V}_{3B}(R,\theta )=-A_{3B}{(sin2\theta )}^2·e^{-3.0·R}& (7)\end{array}$

and it has been enclosed to properly represent the angular dependence of the full PES, especially in the proximity of the saddle point, where the molecular repulsion by occupied π* orbitals is more prominent. The functional form of V_3B has been improved with respect to that reported by Nunzi et al. (2019) to guarantee a second derivative equal to zero at θ = 90.

Finally, the third term, V_CT(R,θ), has been defined as,

$\begin{array}{ll}{V}_{CT}(R,\theta )={\displaystyle \sum _{i=a,b}}{A}_{CT}·{cos}^4({\phi }_i)·e^{-3.0·r_i}& (8)\end{array}$

The dynamical treatment used for the data analysis, adopted for many other atom–molecule systems and summarized in the Supporting Information (SI), allows a good reproduction of the measured cross sections for all the investigated systems by mostly adjusting A_3B and A_CT values, while keeping unaltered (or variable in limited ranges) the other parameters. The final values are reported in Table 1.

TABLE 1

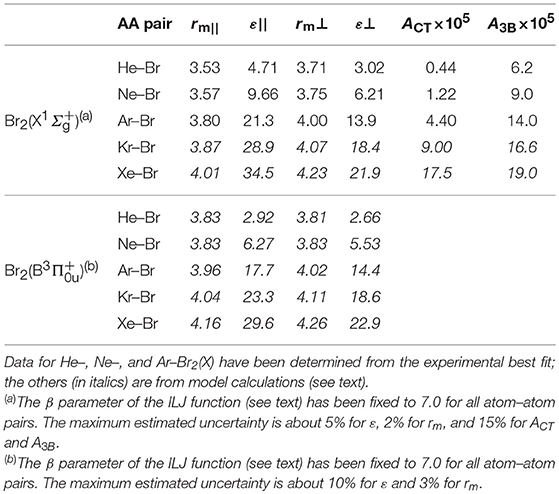
Table 1. Potential parameters (ε, A_CT, A_3B in meV, and r_m in Å) employed for the formulation of the Ng–Br atom–atom pairwise interaction for Ng–Br₂ systems in the (${\text{X}}^1{\Sigma }_{\text{g}}^{+}$) ground and (${\text{B}}^3{\Pi }_{0\text{u}+}$) excited states.

Discussion

Cross sections, calculated with the full PES based on the potential parameters of Table 1, are compared with the experimental data in Figure 1. In the same figure is also reported, as a dashed line, a calculation based on the spherically averaged PES. In Figures 3, 4, some details are given on the dynamical model employed and on the sensitivity of the experiment to the PES features. Results are presented for the case of Ne–Br₂, chosen as a representative. Specifically in Figure 3, scattering cross sections derived from selected cuts of the PESs are reported together with those obtained combining them according to those obtained according to the IOS (infinite-order sudden) approximation and to the dynamical regime adopted, whose details are reported by Nunzi et al. (2019) and also summarized in Supporting Information.

FIGURE 3

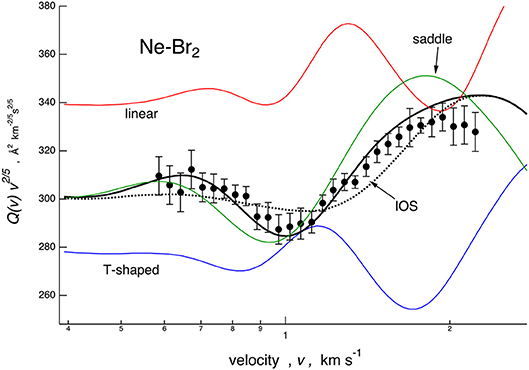
Figure 3. Comparison for Ne–Br₂ system between experimental cross section data, plotted as Q(v)· v^2/5 and reported as a function of the molecular beam (MB) velocity v, and calculations performed considering the interaction in the three selected limiting configurations (colored lines), the infinite-order sudden (IOS) approximation (dotted line), and the full treatment employed for the data analysis (solid line, see text).

FIGURE 4

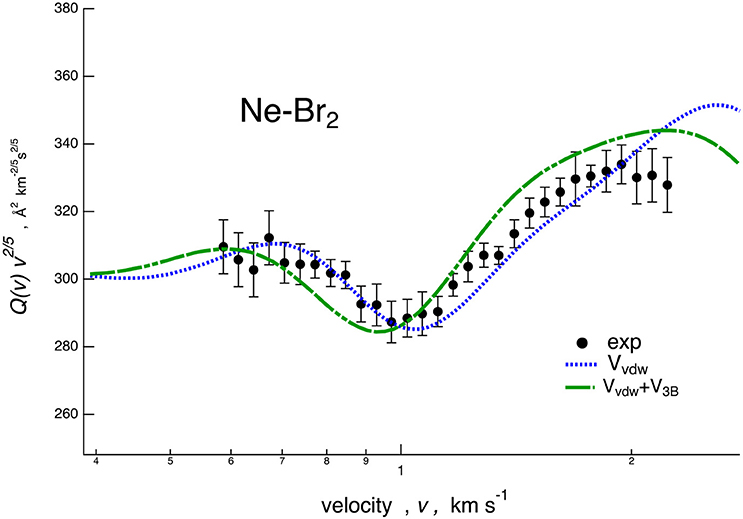
Figure 4. Comparison for Ne–Br₂ system between experimental cross section data, plotted as Q(v)· v^2/5 and reported as a function of the MB velocity v, and calculations performed considering a potential energy surface (PES) including only the van der Waals component plus PF contribution (V_vdW, dotted line) and the additional three-body contribution (V_vdW+V_3B, dashed line).

The IOS calculations are very sensitive to the anisotropy of the PES and must be considered correct to describe the scattering when the collisions are “sudden”: this typically occurs at high relative collision velocities. The data treatment exploited in the present work combines the IOS results with cross sections calculated with the spherically averaged PES, probed in the present investigation by collisions confined at low velocities (see Figure 1) by means of a switching function operative in the intermediate velocity range (see the Supplementary Information). Therefore, this treatment exploits the concept that present observables are basically determined by anisotropic elastic collisions and that inelastic events, occurring at orbital angular momentum values smaller than those probed by the present experiments, play a minor role (Aquilanti et al., 1998). The combined calculations reproduce the amplitude satisfactorily and the frequency of the glory patterns very well, experimentally resolved for all investigated systems, and this represents an important reliability test for all proposed PESs. They have been formulated in an internally consistent way and using few parameters, all related to basic physical properties of the interacting partners. In particular, the parameters that define V_vdW depend on the polarizability components of Br₂ and scale also according to that of Ng, while the significant effect of V_3Bmanifests along the direction of π* molecular orbitals, occupied by more outer electrons of Br₂.

In Figure 4, we report the results of a sensitivity test for the Ne–Br₂ case. In particular, a calculation has been performed with a PES including the term and the PF effect (V_vdW, blue dotted) and further adding the three-body term (V_vdW + V_3B, green dashed). These incomplete PESs fail in reproducing the correct location of the calculated glory interference extrema.

The average strength of V_CT increases from He to Ar, accordingly with the ionization potential of Ng. It must also depend on the electron affinity of Br₂, which is slightly larger with respect to that of Cl₂. Moreover, its angular dependence is strongly modulated by the PF and by the so-called σ-hole in the electron density of the halogen molecule (Clark et al., 2007; Kol and Hobza, 2016).

In order to illustrate the main basic features of the PESs characterized in this paper, the interaction energy for selected configurations of Ng–Br₂ systems is plotted as a function of the Ng–Br₂ distance, R, in Figure 5.

FIGURE 5

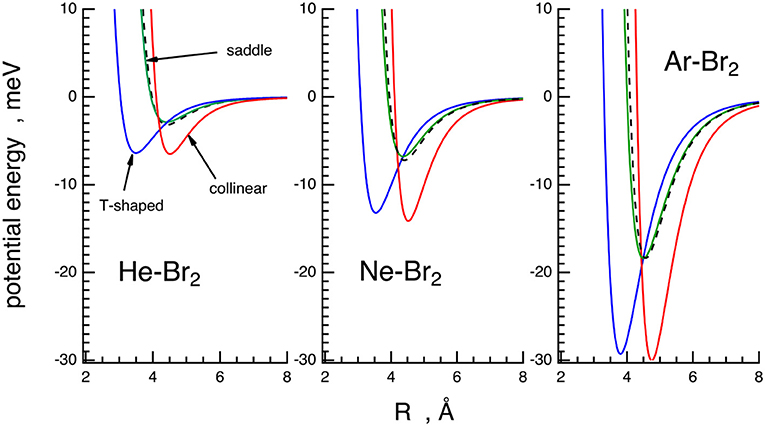
Figure 5. Potential energy curves (energy vs. Ng–Br₂ distance) of the X ground state for the Ng–Br₂ complexes in the three selected configurations obtained from the phenomenological PESs. T-shaped (θ = 90, blue solid line), collinear (θ = 0, red solid line), saddle (θ values in Table 2, green solid line). The spherically averaged interactions are reported for comparison (black dashed lines).

These results can be compared with those obtained for the analogous Ng–Cl₂ systems recently (Nunzi et al., 2019; Pirani et al., 2019). When passing from Cl₂ to Br₂ adducts, the relative anisotropy, obtained by scaling the absolute anisotropy for the average interaction, is very similar, but the absolute interaction is higher for the Br₂ family. The variation can be attributed to the simultaneous increase of all the basic components, here represented as V_vdW, V_3B, and V_CT, due to the combined change of electronic polarizability and of the extension of external charge distribution when moving from Cl₂ to Br₂.

In Table 2, the main features of the obtained PESs, namely, binding energy and equilibrium distance for the three basic configurations of each system, are given for the noble gas–Br₂(X) systems. In the table are also reported significant results from the literature, mostly from ab initio calculations, available for the He, Ne, and Ar cases.

TABLE 2

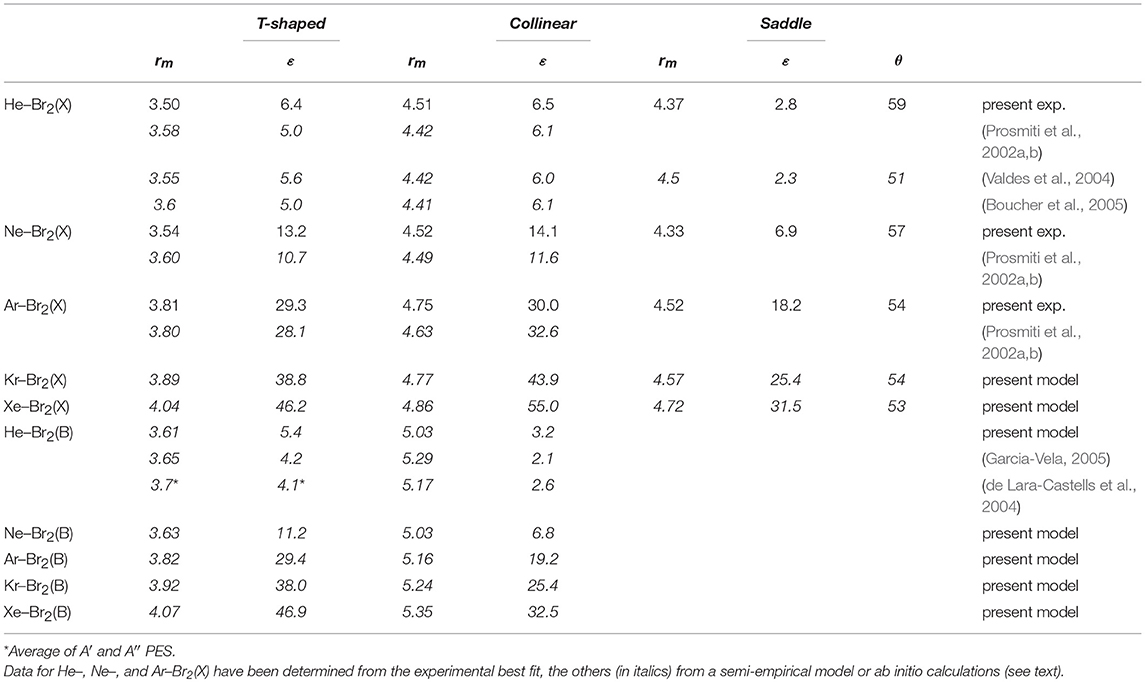
Table 2. Potential well depth (ϵ, in meV) and well location r_m (in Å) for the Ng–Br₂ complexes for the (${\text{X}}^1{\Sigma }_{\text{g}}^{+}$) ground and (${\text{B}}^3{\Pi }_{0\text{u}+}$) excited states of Br₂ representative of the intermolecular bond stability and length in the three basic configurations.

Within the same approach, we have also predicted the interaction parameters for Kr–Br₂ and Xe–Br₂ systems, whose values have been enclosed in Tables 1, 2. Specifically, the vdW r_m , ε, and the A_3B parameters of Kr– and Xe– cases (Table 1) have been obtained by a direct scaling of those of the lighter rare gases' parameters, utilizing the noble gas polarizabilities and correlation formulas of general validity (Cambi et al., 1991). The CT parameter A_CT has been obtained through correlation formulas for the CT component (see Pirani et al., 2000 and references therein), utilizing the ionization potential of the noble gases and the electron affinity of the halogen molecule (Pirani et al., 2000).

The agreement with literature data is, in general, very good. The present results for the He–Br₂ and Ne–Br₂ cases show slightly deeper well depths.

The minimum energy path, MEP, describing the angular dependence of the binding energy evaluated at each equilibrium distance is given in Figure 6. The MEP has been easily obtained here by exploiting the adopted analytical formulation of the interaction.

FIGURE 6

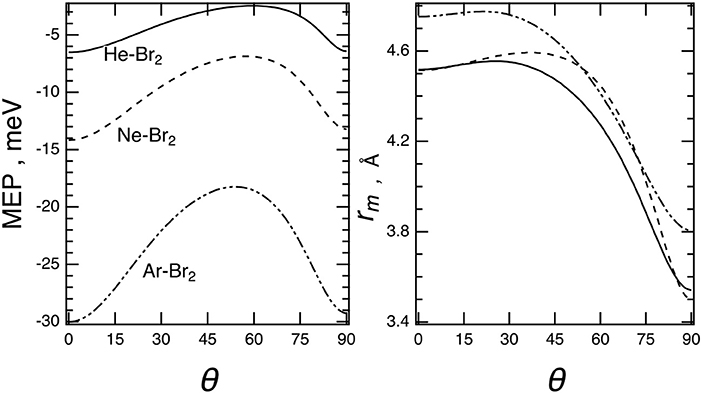
Figure 6. Minimum energy path, MEP (left), and equilibrium distances, r_m (right), vs. the angular variable θ for the Ng–Br₂ complexes (Ng = He, Ne, Ar) predicted by the present potential formulation for the ground (X) electronic states of Br₂.

The angular trend of the interaction component V_vdW, V_3B, and V_CT, is reported for Ne–Br₂ in Figure 7. From the figure, it can be clearly seen that V_vdW alone would provide a T-shaped configuration (θ = 90°) much more stable than the collinear (θ = 0°); on the other side, the V_CT term is responsible for the change in stability of the collinear configuration with respect to the perpendicular one. The effect of the V_3B term manifests itself at an intermediate angle and affects mostly the relative stability of the saddle configuration.

FIGURE 7

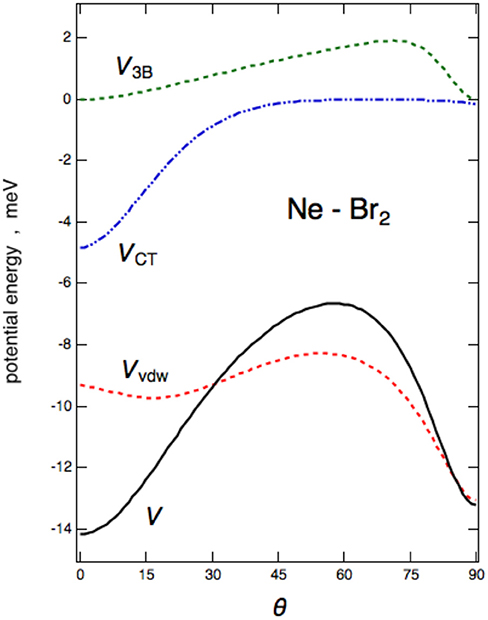
Figure 7. Interaction energies for the V_vdW, V_3B, and V_CT components vs. the angular variable θ are reported for the Ne–Br₂(X) case.

The phenomenological approach has also been extended to obtain, within the same framework adopted for the systems involving Cl₂, an analytical formulation of the PESs for the complete family of the Ng(¹S₀)–Br₂($B^3{\Pi }_{0\text{u}+}$) systems. Upon excitation in the triplet B state, leading an electron from the π* to the σ* molecular orbital, a consistent charge rearrangement is attained in the Br₂ molecule, accomplishing an increase in the polarizability and its anisotropy with respect to that of the ground state. Since the excitation energy for Br₂ is very similar to that of Cl₂, we assumed for Br₂ the same change in polarizability as for Cl₂, for which reliable values are available (Beneventi et al., 1993; Nunzi et al., 2019; Pirani et al., 2019). For the ground electronic state of Br₂, the average polarizability value and its anisotropy have been taken from the literature (Maroulis and Makris, 1997). The interaction potential in the triplet B state has been modeled by considering exclusively the occurrence of a vdW interaction, which can be represented with a pairwise additive approach. The potential parameters (r_m , ε) have been estimated on the basis of polarizability and correlation formulas (Cambi et al., 1991).

The estimated parameters for the excited B state are reported in Table 1. For the He–Br₂ system, the relative anisotropy of the present PES for the B state (i.e., the difference between perpendicular and parallel configuration divided by the average value) is in good agreement with that obtained by ab initio calculations (de Lara-Castells et al., 2004; Garcia-Vela, 2005).

In conclusion, we have found, trough a detailed experimental investigation, that the noble gas–Br adducts are affected by a selective emergence of the intermolecular halogen bond, as recently demonstrated for the companion noble gas–Cl₂ systems (Nunzi et al., 2019; Pirani et al., 2019). In particular, it has been confirmed that for these systems, XB's peculiar effect comes into play only in the collinear configuration of the ground-state PES. The obtained results extend the phenomenology and knowledge of the intriguing weak XB.

The present study also provided a simple and accurate analytical formulation of the PESs, describing the intermolecular interaction both in the ground X and in the excited electronic B state of Br₂. The PES has been represented as a combination of three basic interaction components, each one modulated by few and well-defined physical parameters. The model potential provided the force fields in the full space of the relative configurations and is then suitable for molecular dynamics simulations of fundamental phenomena, such as energy transfer processes.

Author Contributions

DC and FP contributed conception and design of the study. DC, FP, and SF conducted data collection and analysis. DC wrote the first draft of the manuscript. DC and FP wrote sections of the manuscript. All the authors contributed to the development of the experimental facility and analysis instruments. All authors contributed to manuscript revision, read and approved the submitted version.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

DC, AN, AC, and FP thank MIUR and the University of Perugia for financial support through the AMIS project (Dipartimenti di Eccellenza−2018–2022).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2019.00320/full#supplementary-material

References

Aquilanti, V., Ascenzi, D., Cappelletti, D., de Castro, M., and Pirani, F. (1998). Scattering of aligned molecules. The potential energy surfaces for the Kr–O2 and Xe–O2 Systems. J. Chem. Phys. 109, 3898−3910. doi: 10.1063/1.476989

CrossRef Full Text | Google Scholar

Aquilanti, V., Ascenzi, D., Cappelletti, D., Franceschini, S., and Pirani, F. (1995). Scattering of rotationally aligned oxygen molecules and the measurement of anisotropies of van der Waals forces. Phys. Rev. Lett. 74, 2929–2932. doi: 10.1103/PhysRevLett.74.2929

PubMed Abstract | CrossRef Full Text | Google Scholar

Aquilanti, V., Cappelletti, D., Lorent, V., Luzzatti, E., and Pirani, F. (1992). The ground and lowest excited states of XeCl by atomic beam scattering. Chem. Phys. Lett. 192, 153–160. doi: 10.1016/0009-2614(92)85445-G

CrossRef Full Text | Google Scholar

Aquilanti, V., Liuti, G., Pirani, F., Vecchiocattivi, F., and Volpi, G. G. (1976). Absolute total elastic cross sections for collisions of oxygen atoms with the rare gases at thermal energies. J. Chem. Phys. 65, 4751–4755. doi: 10.1063/1.432928

CrossRef Full Text | Google Scholar

Bartocci, A., Belpassi, L., Cappelletti, D., Falcinelli, S., Grandinetti, F., Tarantelli, F., et al. (2015). Catching the role of anisotropic electronic distribution and charge transfer in halogen bonded complexes of noble gases. J. Chem. Phys. 142:184304. doi: 10.1063/1.4919692

PubMed Abstract | CrossRef Full Text | Google Scholar

Baturo, V. V., Lukashov, S. S., Poretsky, S. A., and Pravilov, A. M. (2017). The RgI(2) (ion-pair states) van der Waals complexes. Eur. Phys. J. D 71:227. doi: 10.1140/epjd/e2017-80142-6

CrossRef Full Text | Google Scholar

Belpassi, L., Tarantelli, F., Pirani, F., Candori, P., and Cappelletti, D. (2009). Experimental and theoretical evidence of charge transfer in weakly bound complexes of water. Phys. Chem. Chem. Phys. 11, 9970–9975. doi: 10.1039/b914792f

PubMed Abstract | CrossRef Full Text | Google Scholar

Beneventi, L., Casavecchia, P., Volpi, G. G., Bieler, C. R., and Janda, K. C. (1993). The HeCl2 potential: a combined scattering–spectroscopic study. J. Chem. Phys. 98, 178–185. doi: 10.1063/1.464652

CrossRef Full Text | Google Scholar

Beswick, J. A., Halberstadt, N., and Janda, K. C. (2012). Structure and dynamics of noble gas–halogen and noble gas ionic clusters: when theory meets experiment. Chem. Phys. 399, 4–16. doi: 10.1016/j.chemphys.2011.05.026

CrossRef Full Text | Google Scholar

Boucher, D. S., Strasfeld, D. B., Loomis, R. A., Herbert, J. M., Ray, S. A., and McCoy, A. B. (2005). Stabilization and rovibronic spectra of the T-shaped and linear ground-state conformers of a weakly bound rare-gas–homonuclear dihalogen complex: He–Br2. J. Chem. Phys. 123:104312. doi: 10.1063/1.2006675

PubMed Abstract | CrossRef Full Text | Google Scholar

Buchachenko, A. A., Gonzalez-Lezana, T., Hernandez, M. I., de Lara Castells, M. P., Delgado-Barrio, G., and Villarreal, P. (2000). Blueshifts of the B < –X excitation spectra of He79Br2 using a DIM-based potential. Chem. Phys. Lett. 318, 578–584. doi: 10.1016/S0009-2614(99)01452-9

CrossRef Full Text | Google Scholar

Cambi, R., Cappelletti, D., Pirani, F., and Liuti, G. (1991). Generalized correlations in terms of polarizability for van der Waals interaction potential parameter calculations. J. Chem. Phys. 95, 1852–1861. doi: 10.1063/1.461035

CrossRef Full Text | Google Scholar

Capitelli, M., Cappelletti, D., Colonna, G., Gorse, C., Laricchiuta, A., Liuti, G., et al. (2007). On the possibility of using model potentials for collision integral calculations of interest for planetary atmospheres. Chem. Phys. 338, 62–68. doi: 10.1016/j.chemphys.2007.07.036

CrossRef Full Text | Google Scholar

Cappelletti, D., Aquilanti, V., Bartocci, A., Nunzi, F., Tarantelli, F., Belpassi, L., et al. (2016a). Interaction of O2 with CH4, CF4, and CCl4 by molecular beam scattering experiments and theoretical Calculations. J. Phys. Chem. A. 120, 5197–5207. doi: 10.1021/acs.jpca.6b00948

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappelletti, D., Bartocci, A., Grandinetti, F., Falcinelli, S., Belpassi, L., Tarantelli, F., et al. (2015). Experimental evidence of chemical components in the bonding of helium and neon with neutral molecules. Chem. Eur. J. 21, 6234–6240. doi: 10.1002/chem.201406103

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappelletti, D., Bartolomei, M., Pirani, F., and Aquilanti, V. (2002). Molecular beam scattering experiments on benzene–rare gas systems: probing the potential energy surfaces for the C6H6–He, –Ne, and –Ar dimers. J. Phys. Chem. A. 106, 10764–10772. doi: 10.1021/jp0202486

CrossRef Full Text | Google Scholar

Cappelletti, D., Falcinelli, S., and Pirani, F. (2016b). The intermolecular interaction in D2–CX4 and O2–CX4 (X = F, Cl) systems: molecular beam scattering experiments as a sensitive probe of the selectivity of charge transfer component. J. Chem. Phys. 145:134305. doi: 10.1063/1.4964092

PubMed Abstract | CrossRef Full Text | Google Scholar

Cappelletti, D., Ronca, E., Belpassi, L., Tarantelli, F., and Pirani, F. (2012). Revealing charge-transfer effects in gas-phase water chemistry. Acc. Chem. Res. 45, 1571–1580. doi: 10.1021/ar3000635

PubMed Abstract | CrossRef Full Text | Google Scholar

Carrillo-Bohórquez, O., Valdés, A., and Prosmiti, R. (2016). Temperature dependence of HeBr2 isomers' stability through rovibrational multiconfiguration time-dependent Hartree calculations. J. Phys. Chem. A. 120, 9458–9464. doi: 10.1021/acs.jpca.6b09107

PubMed Abstract | CrossRef Full Text | Google Scholar

Child, M. S. (1974). Molecular Collision Theory. Oxford: Clarendon Press.

Google Scholar

Clark, T., Hennemann, M., Murray, J. S., and Polizer, P. (2007). Halogen bonding: the sigma-hole. J. Mol. Model. 13, 291–296. doi: 10.1007/s00894-006-0130-2

PubMed Abstract | CrossRef Full Text | Google Scholar

de Lara-Castells, M. P., Buchachenko, A. A., Delgado-Barrio, G., and Villarreal, P. (2004). The open-shell interaction of He with B3Πu(0+) state of Br2: an ab initio study and its comparison with diatomics-in-molecule perturbation model. J. Chem. Phys. 120, 2182–2192. doi: 10.1063/1.1636716

PubMed Abstract | CrossRef Full Text | Google Scholar

Delgado-Barrio, G., Prosmiti, R., Valdes, A., and Villarreal, P. (2006). An overview on potential energy surfaces of rare-gas dihalogen van der Waals clusters. Phys. Scripta 73, C57–C63. doi: 10.1088/0031-8949/73/1/N11

CrossRef Full Text | Google Scholar

Desiraju, G. R., Ho, P. S., Kloo, L., Legon, A. C., Marquardt, R., Metrangolo, P., et al. (2013). Definition of the halogen bond (IUPAC recommendations 2013). Pure Appl. Chem. 85, 1711–1713. doi: 10.1351/PAC-REC-12-05-10

CrossRef Full Text | Google Scholar

Garcia-Vela, A. (2005). An empirical potential energy surface for the He–Br2 (B3Πu) van der Waals complex. J. Phys. Chem. A. 109, 5545–5552. doi: 10.1021/jp051167n

CrossRef Full Text | Google Scholar

Gilday, L. C., Robinson, S. W., Barendt, T. A., Langton, M. J., Mullaney, B. R., and Beer, P. D. (2015). Halogen bonding in supramolecular chemistry. Chem. Rev. 115, 7118–7195. doi: 10.1021/cr500674c

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Z. M., Czap, G., Chiang, C. L., Xu, C., Wagner, P. J., Wei, X. Y., et al. (2017). Imaging of halogen bond in self-assembled halogenbenzenes on silver. Science 358, 206–210. doi: 10.1126/science.aai8625

PubMed Abstract | CrossRef Full Text | Google Scholar

Jahn, D. G., Barney, W. S., Cabalo, J., Clement, S. G., Rohrbacher, A., Slotterback, T. J., et al. (1996). High resolution spectroscopy of the He79Br2 van der Waals molecule: an experimental and theoretical study. J. Chem. Phys. 104, 3501–3510. doi: 10.1063/1.471055

CrossRef Full Text | Google Scholar

Janda, K. C., Djahandideh, D., Roncero, O., and Halberstadt, N. (1998). The B < - X spectrum of ArCl2: linear and perpendicular isomers. Chem. Phys. 239, 177–186. doi: 10.1016/S0301-0104(98)00276-6

CrossRef Full Text | Google Scholar

Kol,ár, M. H., and Hobza, P. (2016). Computer modeling of halogen bond and other σ-hole interactions. Chem. Rev. 116, 5155–5187. doi: 10.1021/acs.chemrev.5b00560

CrossRef Full Text | Google Scholar

Li, S., Zheng, R., Chen, S. J., Chen, Y., and Chen, P. (2017). Investigations of the Rg–BrCl (Rg = He, Ne, Ar, Kr, Xe) binary van der Waals complexes: ab initio intermolecular potential energy surfaces, vibrational states and predicted pure rotational transition frequencies. Spectrochim. Acta A Mol. Biomol. Spectrosc. 174, 105–117. doi: 10.1016/j.saa.2016.11.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Maroulis, G., and Makris, C. (1997). On the electric properties of Br₂. Mol. Phys. 91, 333–341. doi: 10.1080/002689797171625

CrossRef Full Text | Google Scholar

Nenner, T., Tien, H., and Fenn, J. B. (1975). Total cross section measurements for the scattering of argon by aliphatic hydrocarbons. J. Chem. Phys. 63, 5439–5444. doi: 10.1063/1.431278

CrossRef Full Text | Google Scholar

Nunzi, F., Cesario, D., Belpassi, L., Tarantelli, F., Roncaratti, L. F., Falcinelli, S., et al. (2019). An insight into the halogen-bond nature of noble gas–chlorine systems by molecular beam scattering experiments, ab initio calculations and charge displacement analysis. Phys. Chem. Chem. Phys. 21, 7330–7340. doi: 10.1039/C9CP00300B

PubMed Abstract | CrossRef Full Text | Google Scholar

Olney, T. N., Cann, C. G., Cooper, G., and Brion, C. E. (1997). Absolute scale determination for photoabsorption spectra and the calculation of molecular properties using dipole sum-rules. Chem. Phys. 223, 59–98. doi: 10.1016/S0301-0104(97)00145-6

CrossRef Full Text | Google Scholar

Pirani, F., Brizi, S., Roncaratti, L. F., Casavecchia, P., Cappelletti, D., and Vecchiocattivi, F. (2008). Beyond the Lennard-Jones model: a simple and accurate potential function probed by high resolution scattering data useful for molecular dynamics simulations. Phys. Chem. Chem. Phys. 10, 5489–5503. doi: 10.1039/b808524b

PubMed Abstract | CrossRef Full Text | Google Scholar

Pirani, F., Cappelletti, D., Falcinelli, S., Cesario, D., Nunzi, F., Belpassi, L., et al. (2019). The selective emergence of halogen bond in the ground and excited states of noble-gas–Cl₂ systems. Angew. Chemie Int. Ed. Engl. 58, 4195–4199. doi: 10.1002/anie.201812889

CrossRef Full Text | Google Scholar

Pirani, F., Giulivi, A., Cappelletti, D., and Aquilanti, V. (2000). Coupling by charge transfer: role in bond stabilization for open-shell systems and ionic molecules and in harpooning and proton attachment processes. Mol. Phys. 98, 1749–1762. doi: 10.1080/00268970009483379

CrossRef Full Text | Google Scholar

Pirani, F., and Vecchiocattivi, F. (1977). Absolute total elastic cross sections for collisions of He with Ne, Ar, Kr, and Xe. J. Chem. Phys. 66, 372–373. doi: 10.1063/1.433644

CrossRef Full Text | Google Scholar

Pirani, F., and Vecchiocattivi, F. (1982). A fast and accurate semiclassical calculation of the total elastic cross section in the glory energy range. Mol. Phys. 45, 1003–1013. doi: 10.1080/00268978200100771

CrossRef Full Text | Google Scholar

Prosmiti, R., Cunha, C., Buchachenko, A. A., Delgado-Barrio, G., and Villarreal, P. (2002a). Vibrational predissociation of NeBr₂ (X, v = 1) using an ab initio potential energy surface. J. Chem. Phys. 117, 10019–10025. doi: 10.1063/1.1519001

CrossRef Full Text | Google Scholar

Prosmiti, R., Cunha, C., Villarreal, P., and Delgado-Barrio, G. (2002b). Ab initio ground state potential energy surfacesfor Rg–Br₂ (Rg = He, Ne, Ar) complexes J. Chem. Phys. 116, 9249–9254. doi: 10.1063/1.1473800

CrossRef Full Text | Google Scholar

Rohrbacher, A., Halberstadt, N., and Janda, K. C. (2000). The dynamics of noble gas–halogen molecules and clusters. Annu. Rev. Phys. Chem. 51, 405–433. doi: 10.1146/annurev.physchem.51.1.405

PubMed Abstract | CrossRef Full Text | Google Scholar

Valdes, A., Prosmiti, R., Villarreal, P., and Delgado-Barrio, G. (2004). He–Br₂ complex: ground-state potential and vibrational dynamics from ab initio calculations. Mol. Phys. 102, 2277–2283. doi: 10.1080/00268970412331290634

CrossRef Full Text | Google Scholar