Non-poissonian Distribution of Point Mutations in DNA

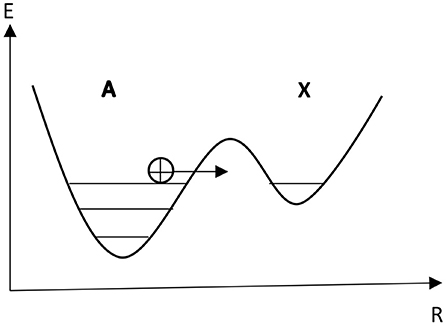
In general, for chemical reactions occurring in systems, where fluctuations are not negligibly small, it is necessary to introduce a master equation for distribution of probability of fluctuations. It has been established that the monomolecular reactions of a type as A ↔ X are described by the master equation, which leads to a Poisson distribution with the variance equal to the average value N₀. However, the consideration of the Löwdin mechanism as autocatalytic non-linear chemical reactions such as A + X ↔ 2X and the corresponding master equation lead to a non-Poissonian probability distribution of fluctuations. In the presented work, first-order autocatalysis has been applied to the Löwdin's mechanism of spontaneous mutations in DNA. Describing double proton transfers between complimentary nucleotide bases along the chain by first-order autocatalytic reactions, the corresponding master equation for protons in tautomeric states becomes non-linear, and at non-equilibrium conditions this leads to the non-Poissonian distribution of spontaneous mutations in DNA. It is also suggested that the accumulation of large fluctuations of successive cooperative concerted protons along the chain may produce higher non-linearities which could have a significant impact on some biochemical processes, occurring in DNA.

Introduction

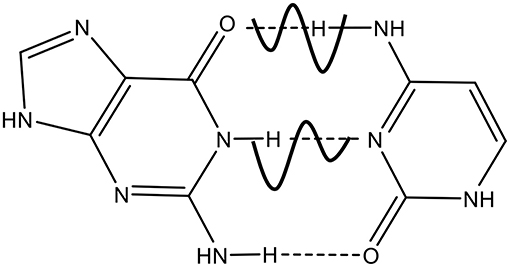
The role of mutations in DNA is crucial for human aging, metabolic and degenerative disorders and cancer, as well as for biological evolution of living systems (Löwdin, 1966; Friedberg et al., 2006). The point mutations caused by the substitution of one nucleotide base for another may occur during DNA replication by DNA polymerases, the performance of which is very important for genome integrity and transmission of genetic information in all living organisms. Although DNA replicates with high fidelity, DNA polymerase can make mistakes with the average frequency in the range of (10⁻⁷–10⁻⁹) per base pair per cell division (Drake et al., 1998). Spontaneous mutations are point mutations caused by the substitution of one nucleotide base of DNA for another one occurring due to endogenous factors during normal cell metabolism. The rare tautomeric hypothesis (Watson and Crick, 1953a,b; Topal and Fresco, 1976; Bebenek et al., 2011; Wang et al., 2011) originally proposed by J. Watson and F. Crick (Watson and Crick, 1953a,b) is considered as a possible mechanism of formation of spontaneous mutations suggesting the existence of different chemical forms of nucleotide bases, so called tautomers, in which the protons occupy in one of its tautomeric forms. The origination of mutagenic tautomers has not been completely established, although three possible mechanisms are discussed: (1) intramolecular single proton transfer in DNA bases (Basu et al., 2005; Gorb et al., 2005; Zhao et al., 2006; Brovarets and Hovorun, 2010, 2011; Brovarets et al., 2012); (2) proton transfer in a single base assisted by water molecules (Gorb and Leszczynski, 1998a,b; Kim et al., 2007; Fogarasi, 2008; Michalkova et al., 2008; Furmanchuk et al., 2011; Markova et al., 2017); (3) Löwdin's mechanism of double proton tunneling (DPT) between complimentary bases (Löwdin, 1963, 1966) (Figure 1).

FIGURE 1

Figure 1. G-C → G* − C*: DPT in the double potential wells.

Based on the rare tautomeric hypothesis by Watson-Crick, Löwdin (Löwdin, 1963, 1966) suggested that spontaneous mutations in DNA occur due to double proton transfer between two complementary bases along intermolecular H-bonds by quantum tunneling. Thus, each proton in the connecting hydrogen bonds can be in one of two quantum states, in deep or shallow potential wells. Following the pioneering works of Löwdin, the tautomeric base pairs (A^*-T^*, G^*-C^*) have been extensively studied in terms of their lifetime, the probability of occurrence and the energy by using different theoretical approaches (Florian et al., 1995; Florian and Leszczynski, 1996; Gorb et al., 2004; Villani, 2005, 2010; Ceron-Carrasco et al., 2009a,b; Brovarets et al., 2012), including DFT calculations, ab initio MP2, quantum mechanics. All these calculated findings substantially support the Watson-Crick's tautomeric hypothesis of the origin of spontaneous point mutations, constrained by thermodynamic and kinetic criteria (Florian et al., 1994; Dabkowska et al., 2005; Brovarets et al., 2012) to be relevant to spontaneous mutations. Based on the Löwdin's mechanism, the probability of formation of spontaneous mutations was calculated from the kinetics of double proton transfer during DNA replication by taking into account 2D Marcus theory of double proton transfer (DPT) (Turaeva and Brown-Kennerly, 2015). The model allows to establish the spontaneous mutation probability as a function of temperature, replication rate and solvent. It was also established that there are different factors impacting on DNA mutations, including external electric fields (Ceron-Carrasco et al., 2014), metallic cations (Ceron-Carrasco et al., 2012), even the genetic sequence (Ceron-Carrasco and Jacquemin, 2015) through the hydrogen transfers between the complimentary nucleotide bases in DNA. In the framework of Lowdin's mechanism of spontaneous mutation formation, we can suppose that those factors directly or indirectly change the potential barrier relief for proton transfers, leading to the change of the mutation rate and the distribution of mutations along the chain.

In the present work, we will show that the Löwdin's mechanism of spontaneous mutations results in a non-Poissonian distribution function of mutagenic tautomeric forms of DNA by using first-order autocatalysis. It is well-known that the first- and higher order autocatalysis was applied to different biological processes, including reproduction (Eigen, 1971; Biebricher et al., 1983; Schuster, 2018), cooperation (Higgs and Lehman, 2015; Schuster, 2018), chirality of biological molecules (Frank, 1953). The autocatalytic reaction of first order was applied to reproduction of RNA and DNA molecules (Biebricher et al., 1983), giving rise to their exponential growth with different reproducing variants leading to natural selection. The correct and error-prone RNA replication leading to point mutations was also described by the autocatalytic reaction of first order by introducing the mutation matrix with the assumption of uniform error rate (Eigen, 1971). Catalyzed replication leading to cooperation among replicators was described by the autocatalytic reaction of second order (Higgs and Lehman, 2015). In general, according to the evolution model (Schuster, 2018), the characteristic features of the first order autocatalysis include selection and optimization, while the second order autocatalysis covers oscillations, deterministic chaos, spontaneous pattern formation and high sensitivity to stochastic phenomena caused by small particle numbers. So, competitive reproduction gives rise to selection, but catalyzed reproduction is needed for cooperation of competitors.

In our model, the autocatalytic reaction of first order is applied to the process of double proton transfer in DNA, which gives a non-Poissonian distribution of tautomeric states of hydrogens along the chain which as a result of replication leads to spontaneous mutations.

The search of experiments on the distribution function of spontaneous mutations to verify our model leads to the Luria-Delbruck's experiments and distribution of mutants (Luria and Delbrück, 1943), that gives a non-Poissonian relationship for the distribution of mutant bacteria colonies consistent with the experimentally obtained values, in which the variance was considerably greater than the mean. We suppose that the non-Poissonian character of the distribution function of tautomeric forms of nucleotide bases can be counted toward the Löwdin's mechanism of origin of spontaneous mutations formation, since the intramolecular single proton transfer in DNA bases describing by the monomolecular reactions of a type as A ⇔ X is described by the master equation, leading to the Poissonian distribution, where the variance is equal to the average value N₀.

Stochastic Model of Spontaneous Mutation Formation

In general case, for chemical reactions occurring in systems, where fluctuations are not considered negligible small, it is necessary to introduce a master-equation for distribution of probability (Gardiner, 1983; Haken, 1983). Analyzing a monomolecular reaction of a type as A ⇔ X on the base of the master equation the Poisson distribution function with average value of N₀ can be derived. It is well-known that at considering the reactions of A + X ⇔ 2X the corresponding kinetic equations for markovian processes become non-linear and this peculiarity leads to the non-Poissonian distribution functions. This result was proved by Nicolis and Prigogine (Nicolis and Prigogine, 1977) and caused a great scientific interest. The process of generation of spontaneous mutations in DNA through double proton transition during the replication can be treated as first-order autocatalytic chemical reactions, described by the following reaction scheme:

$\begin{array}{ll}A\begin{array}{c}{k}_1\\ \iff \\ k_{-1}\\ \end{array}X& (1)\end{array}$

$\begin{array}{ll}A+X\begin{array}{c}{k}_2\\ \iff \\ k_{-2}\\ \end{array}2X& (2)\end{array}$

Here A denotes protons along the DNA strand which are in their regular stable position, X is the protons in the tautomeric state (Figure 2), k and k₋ are the rate constants of forward and reverse chemical reactions, respectively. The first reaction corresponds to the processes of the transfer of a proton from the regular position into the tautomeric state and vice versa, while the second reaction corresponds to the generation of tautomeric forms of nucleotide bases due to the interaction of the single proton in the tautomeric state with the regular proton and its relaxation into the single proton tautomeric state.

FIGURE 2

Figure 2. The double-well potential for a single proton tunneling.

Denoting the number of protons in the tautomeric state by N, we can establish a master-equation for the distribution of fluctuations P(N, t) in the following general form:

$\begin{array}{l}\dot{P}\left(N,t\right)=w\left(N,N-1\right)P\left(N-1,t\right)\\ +w\left(N,N+1\right)P\left(N+1,t\right)-\{w\left(N+1,N\right)\\ +w\left(N-1,N\right)\}P\left(N,t\right).& (3)\end{array}$

Here w is the transition probability per unit time. The crux of the master equation is to determine the transition rates explicitly for each chemical reaction. We investigate all transitions leading to N or going away from it. For spontaneous mutations in DNA we consider two types of transition—the tautomeric proton generation (N → N + 1, N – 1 → N) and the tautomeric proton annihilation (N + 1 → N, N → N − 1) for both chemical reactions. We will show in detail the derivation of total transition rate for the first reaction (1).

1. In the direction k₁ (“birth” of a tautomeric proton X). The number of the transitions per second is equal to the occupational probability, P(N, t), multiplied by the transition probability per second, ω(N + 1, N), which is the product of the linear density of regular protons N_A along the DNA strand and the reaction rate k₁. So, for transition → N + 1, we have w(N + 1, N) = k₁N_AL. Here L is the length of DNA. In the same way the transition rate is calculated for transition N − 1 → N: w(N, N − 1) = k₁N_AL.

For this reaction the total transition rate is received in the following form:

$\begin{array}{ll}{k}_1{N}_{A}LP(N-1,t)-k_1{N}_{A}LP(N,t).& (4)\end{array}$

2. In a similar way, we can find the reverse process of the first reaction. Here the number of tautomeric protons is decreased by 1 (“death” of a metastable proton X). Considering the “death” process for transitions N + 1 → N and N → N − 1, in the reverse k _{− 1} direction (“death” of X) the total transition rate is equal to:

$\begin{array}{ll}{k}_{-1}\frac{(N+1)}{L}LP(N+1,t)-k_{-1}\frac{N}{L}LP(N,t).& (5)\end{array}$

3. For the reaction (2), in the k₂ direction (“birth” of a tautomeric proton X), the total transition rate can be written:

$\begin{array}{ll}{k}_2{N}_A\frac{N-1}{L}LP(N-1,t)-k_2{N}_A\frac{N}{L}LP(N,t).& (6)\end{array}$

4. For the reaction (2) in the k₋₂ direction (“death” of a tautomeric proton X), the total transition rate can be written:

$\begin{array}{ll}{k}_{-2}\frac{(N+1)N}{L^2}LP(N+1,t)-k_{-2}\frac{N(N-1)}{L^2}LP(N,t).& (7)\end{array}$

Thus, by taking into account (Equations 4–7) the transition rates for the reactions (1) and (2) are given:

$\begin{array}{ll}\omega (N,N-1)=k_1{N}_{A}L+k_2{N}_A\frac{N-1}{L}L;& (8)\end{array}$

$\begin{array}{ll}\omega (N,N+1)=k_{-1}\frac{(N+1)}{L}L+k_{-2}\frac{(N+1)N}{L^2}L;& (9)\end{array}$

$\begin{array}{ll}\omega (N+1,N)=k_1{N}_{A}L+k_2{N}_A\frac{N}{L}L;& (10)\end{array}$

$\begin{array}{ll}\omega (N-1,N)=k_{-1}\frac{N}{L}L+k_{-2}\frac{N(N-1)}{L^2}L.& (11)\end{array}$

The stationary solution of the master equation (3) is determined as Eigen (1971):

$\begin{array}{l}P(N)=P(0){\displaystyle \prod _{n=0}^{N-1}}\frac{\omega (n+1,n)}{\omega (n,n+1)}\\ =P(0){\displaystyle \prod _{n=0}^{N-1}}\frac{k_1{N}_A{L}^2+k_2{N}_{A}nL}{k_{-1}(n+1)L+k_{-2}(n+1)n}.& (12)\end{array}$

Let us denote the probabilities of two transitions by the following expressions:

$\begin{array}{ll}\{\begin{array}{l}\omega \left(N,N-1\right)={\omega }_{+}\left(N\right)\\ \omega \left(N,N+1\right)={\omega }_{-}\left(N\right).\end{array}\hfill & (13)\end{array}$

The condition of extremes of stationary P(N) is Haken (1983):

$\begin{array}{ll}\frac{{\omega }_{+}(N_0+1)}{{\omega }_{-}(N_0)}=1.& (14)\end{array}$

We can find the extreme solutions N₀ of P(N) from the following expression which is received by rewriting (Equation 14) by taking into account Equations (13), (8), and (9):

$\begin{array}{ll}\frac{k_1{N}_A{L}^2+k_2{N}_A{N}_{0}L}{k_{-1}(N_0+1)L+k_{-2}(N_0+1)N_0}=1.& (15)\end{array}$

The solution of Equation (15) for N₀ can be received:

$\begin{array}{ll}{N}_0^{1,2}=\frac{-(k_{-2}+k_{-1}L-k_2{N}_{A}L)\pm \sqrt{{(k_{-2}+k_{-1}L-k_2{N}_{A}L)}^2-4k_{-2}(k_{-1}L-k_1{N}_A{L}^2)}}{2k_{-2}}.& (16)\end{array}$

The positive value of N₀ can be obtained if k _{− 2} + k _{− 1}L < k₂N_AL. The plot of the probability P(N) represents the curve with two maxima. By assuming that the transfer of the second proton takes place almost instantaneously compared to its reverse process, which corresponds to the large ratio of k₂/k₋₂, we can receive the probability distribution function with one maximum (Figure 3):

$\begin{array}{ll}{N}_0=\frac{k_{-1}-k_1{N}_{A}L}{k_2{N}_A-k_{-1}}.& (17)\end{array}$

It is seen from Equation (17) that N_o is positive when the transfer of proton from the regular position into the tautomeric state proceeds slower than its reverse reaction (1), while the second proton is transferred almost instantaneously (2) compared to the reverse process of the first reaction (1).

FIGURE 3

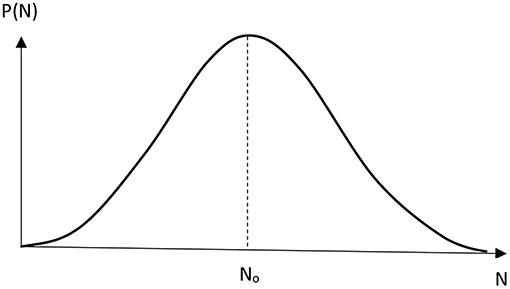
Figure 3. Non-poissonian distribution function P(N) of spontaneous mutations in DNA by Löwdin's mechanism.

If the principle of detailed balance is satisfied for both chemical reactions (1) and (2), then the Poisson distribution function for fluctuations can be deduced (Haken, 1983). We must write the detailed balance equations then for both reactions (1) and (2):

$\begin{array}{ll}{\omega }_1(N,N-1)P(N-1)={\omega }_1(N-1,N)P(N);& (18)\end{array}$

$\begin{array}{ll}{\omega }_2(N,N-1)P(N-1)={\omega }_2(N-1,N)P(N).& (19)\end{array}$

Dividing Equation (18) by Equation (19) and using the explicit expressions (Equations 8 and 11), we find the relation:

$\begin{array}{ll}\frac{k_1{N}_A}{k_{-1}N/L}=\frac{k_2{N}_A}{k_{-2}N/L}\equiv \frac{\mu }{N}.& (20)\end{array}$

Here μ is a constant. By using Equation (20) we can rewrite the detailed balance equation:

$\begin{array}{ll}\omega (N,N-1)=\frac{\mu }{N}\omega (N-1,N).& (21)\end{array}$

By inserting Equation (21) into Equation (12) at normalization condition of P(0) we find the Poisson distribution:

$\begin{array}{ll}P(N)=\frac{{\mu }^N}{N!}{e}^{-\mu }.& (22)\end{array}$

In general, however, for non-equilibrium processes, where the detailed balance principle is not valid, the character of distribution function P(N) (Equation 12) is non-Poissonian (Gardiner, 1983; Haken, 1983). Since double proton transfers during the DNA replication are far from equilibrium, a non-Poissonian distribution for tautomeric forms should be well founded. These results can be used to support the mechanism of the origin of spontaneous mutations in DNA based on concerted double proton transfers between complimentary nucleotide bases during the DNA replication instead of single proton transfers in a single base.

Conclusion

In this work, we applied first-order autocatalysis to the Löwdin's mechanism of spontaneous mutation formation, in which concerted double proton transfers in DNA lead to the formation of tautomeric forms nucleotide bases during the DNA replication. The stochastic model results in a master-equation for the distribution function of tautomeric nucleotide bases, the stationary solution of which is a non-Poissonian function with the assumption that the processes of double proton transfers during DNA replication are far from equilibrium conditions. We suppose that these peculiarities of Löwdin's mechanism of spontaneous mutation formation should be taken into account in the discussion of the origin of spontaneous mutation formation. It is interesting to note the possibility of accumulation of point mutations locally on DNA due to the cooperation effect between tautomeric hydrogens. The cooperation effect should increase the order of autocatalytic reactions. Such fluctuations can be possible due to the U-negative effect (Anderson, 1975), which can lead to the formation of a solitary wave or a soliton on the chain at a certain distance between metastable proton pairs (Golo et al., 2001). The soliton can move along the chain and impacts on different biochemical processes, occurring in DNA, including its replication, proofreading and so on. At realization of such effect, the rate constants of the reactions (1) and (2) become the function of distance between the point mutations along the chain. This perspective of fluctuations will be considered in our future research.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary material.

Author Contributions

NT was the author of the idea about application of stochastic theory to spontaneous mutations in DNA and the main contributor of the manuscript. BO was the author of the idea about the possibility of soliton generation in DNA based on accumulation of metastable proton fluctuations.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anderson, P. W. (1975). Model of the electronic structure of amorphous semiconductors. Phys. Rev. Lett. 34:953. doi: 10.1103/PhysRevLett.34.953

CrossRef Full Text | Google Scholar

Basu, S., Majumdar, R., Das, G. K., and Bhattacharyya, D. (2005). Energy barrier and rates of tautomeric transitions in DNA bases: ab initio quantum chemical study. Indian J. Biochem. Biophys. 42, 378–385.

Google Scholar

Bebenek, K., Pedersen, L. C., and Kunkel, T. A. (2011). Replication infidelity via a mismatch with Watson-Crick geometry. Proc. Natl. Acad. Sci. U.S.A. 108, 1862–1867. doi: 10.1073/pnas.1012825108

PubMed Abstract | CrossRef Full Text | Google Scholar

Biebricher, C. K., Eigen, M., and Gardiner, W. C. (1983). Kinetics of RNA replication. Biochemistry 22, 2544–2559. doi: 10.1021/bi00279a036

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovarets, O. O., and Hovorun, D. M. (2010). How stable are the mutagenic tautomers of DNA bases? Biopolym. Cell 26, 72–76. doi: 10.7124/bc.000147

CrossRef Full Text | Google Scholar

Brovarets, O. O., and Hovorun, D. M. (2011). Intramolecular tautomerization and the conformational variability of some classical mutagens – cytosine derivatives: quantum chemical study. Biopolym. Cell 27, 221–230. doi: 10.7124/bc.0000BD

CrossRef Full Text | Google Scholar

Brovarets, O. O., Kolomiets, I. M., and Hovorun, D. M. (2012). “Elementary molecular mechanisms of the spontaneous point mutations in DNA: a novel quantum-chemical insight into the classical understanding,” in Quantum Chemistry–Molecules for Innovations, ed T. Tada (InTech), 59–102. doi: 10.5772/35743. Available online at: https://www.intechopen.com/books/quantum-chemistry-molecules-for-innovations/elementary-molecular-mechanisms-of-the-spontaneous-point-mutations-in-dna-a-novel-quantum-chemical-i

CrossRef Full Text | Google Scholar

Ceron-Carrasco, J. P., Cerezo, J., and Jacquemin, D. (2014). How DNA is damaged by external electric fields: selective mutatio vs. random degradation. Phys. Chem. Chem. Phys. 18, 8243–8246. doi: 10.1039/C3CP54518K

CrossRef Full Text | Google Scholar

Ceron-Carrasco, J. P., and Jacquemin, D. (2015). DNA spontaneous mutation and its role in the evolution of GC-content: assessing the impact of the genetic sequence. Phys. Chem. Chem. Phys. 17, 7754–7760. doi: 10.1039/C4CP05806B

PubMed Abstract | CrossRef Full Text | Google Scholar

Ceron-Carrasco, J. P., Requena, A., and Jacquemin, D. (2012). Impact of DFT functionals on the predicted magnesium-DNA interaction: an ONIOM study. Theor. Chem. Acc. 131:1188. doi: 10.1007/s00214-012-1188-9

CrossRef Full Text | Google Scholar

Ceron-Carrasco, J. P., Requena, A., Michaux, C., Perpete, E. A., and Jacquemin, D. (2009a). Effects of hydration on the proton transfer mechanism in the adenine-thymine base pair. J. Phys. Chem. A 113, 7892–7898. doi: 10.1021/jp900782h

PubMed Abstract | CrossRef Full Text | Google Scholar

Ceron-Carrasco, J. P., Requena, A., Zuniga, J., Michaux, C., Perpete, E. A., and Jacquemin, D. (2009b). Intermolecular proton transfer in microhydrated guanine-cytosine base pair: a new mechanism for spontaneous mutation in, DNA. J. Phys. Chem. A 113, 10549–10556. doi: 10.1021/jp906551f

CrossRef Full Text | Google Scholar

Dabkowska, I., Gutowski, M., and Rak, J. (2005). Interaction with glycine increases stability of a mutagenic tautomer of uracil. a density functional theory study. J. Am. Chem. Soc. 127, 2238–2248. doi: 10.1021/ja048730k

PubMed Abstract | CrossRef Full Text | Google Scholar

Drake, J. W., Charlesworth, B., Charlesworth, D., and Crow, J. F. (1998). Rates of spontaneous mutation. Genetics 148, 1667–1686.

PubMed Abstract | Google Scholar

Eigen, M. (1971). Self-organization of matter and the evolution of biological macromolecules. Naturwissenschaften 58, 465–523. doi: 10.1007/BF00623322

CrossRef Full Text | Google Scholar

Florian, J., Hrouda, V., and Hobza, P. (1994). Proton transfer in the adenine-thymine base pair. J. Am. Chem. Soc. 116, 1457–1460. doi: 10.1021/ja00083a034

CrossRef Full Text | Google Scholar

Florian, J., and Leszczynski, J. (1996). Spontaneous DNA mutations induced by proton transfer in the guanine·cytosine base pairs: an energetic perspective. J. Am. Chem. Soc. 118, 3010–3017. doi: 10.1021/ja951983g

CrossRef Full Text | Google Scholar

Florian, J., Leszczynski, J., and Scheiner, S. (1995). Ab initio study of the structure of guanine- cytosine base pair conformers in gas phase and polar solvents. Mol. Phys. 84, 469–480. doi: 10.1080/00268979500100321

CrossRef Full Text | Google Scholar

Fogarasi, G. (2008). Water-mediated tautomerization of cytosine to the rare imino form: an ab initio dynamics study. Chem. Phys. 349, 204–209. doi: 10.1016/j.chemphys.2008.02.016

CrossRef Full Text | Google Scholar

Frank, F. C. (1953). On spontaneous asymmetric synthesis. Biochem. Acta 11:459. doi: 10.1016/0006-3002(53)90082-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedberg, E. C., Walker, G. C., Siede, W., Wood, R. D., Schultz, R. A., and Ellenberger, T. (2006). DNA Repair and Mutagenesis 2nd Edn. Washington, DC: ASM Press.

Google Scholar

Furmanchuk, A., Isayev, O., Gorb, L., Shishkin, O. V., Hovorun, D. M., and Leszczynski, J. (2011). Novel view on the mechanism of water-assisted proton transfer in the DNA bases: bulk water hydration. Phys. Chem. Chem. Phys. 13, 4311–4317. doi: 10.1039/c0cp02177f

PubMed Abstract | CrossRef Full Text | Google Scholar

Gardiner, C. W. (1983). Handbook of Stochastic Methods for Physics Chemistry and the Natural Sciences. New, York, NY: Springer.

Google Scholar

Golo, V. L., Kats, E. I., and Peyrard, M. (2001). Concerted motion of protons in hydrogen bonds of DNA-type molecules. J. Exp. Theor. Phy. Lett. 73:202. doi: 10.1134/1.1368715

CrossRef Full Text | Google Scholar

Gorb, L., Kaczmarek, A., Gorb, A., Sadlej, A. J., and Leszczynski, J. (2005). Thermodynamics and kinetics of intramolecular proton transfer in guanine. post Hartree-Fock study. J. Phys. Chem. B 109, 13770–13776. doi: 10.1021/jp050394m

PubMed Abstract | CrossRef Full Text | Google Scholar

Gorb, L., and Leszczynski, J. (1998a). Intramolecular proton transfer in monohydrated tautomers of cytosine: an ab initio post-Hartree–Fock study. Int. J. Quant. Chem. 70, 855–862. https://doi.org/10.1002/(SICI)1097-461X(1998)70:4/5<855::AID-QUA31>3.0.CO;2-Y

Google Scholar

Gorb, L., and Leszczynski, J. (1998b). Intramolecular proton transfer in mono- and dihydrated tautomers of guanine: an ab initio post Hartree-Fock study. J. Am. Chem. Soc. 120, 5024–5032. doi: 10.1021/ja972017w

CrossRef Full Text | Google Scholar

Gorb, L., Podolyan, Y., Dziekonski, P., Sokalski, W. A., and Leszczynsky, J. (2004). Double- proton transfer in adenine-thymine and guanine-cytosine base pairs. a post- Hartree-Fock ab initio study. J. Am. Chem. Soc. 126, 10119–10129. doi: 10.1021/ja049155n

PubMed Abstract | CrossRef Full Text | Google Scholar

Haken, H. (1983). Synergetics. An introduction: Nonequilibrium Phase Transitions and Self-Organization in Physics Chemistry and Biology. New York, NY: Springer.

Google Scholar

Higgs, P. G., and Lehman, N. (2015). The RNA world: molecular cooperation at the origins of life. Nat. Rev. Genet. 16, 7–17. doi: 10.1038/nrg3841

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H.-S., Ahn, D.-S., Chung, S.-Y., Kim, S. K., and Lee, S. (2007). Tautomerization of adenine facilitated by water: computational study of microsolvation. J. Phys. Chem. A 111, 8007–8012. doi: 10.1021/jp074229d

PubMed Abstract | CrossRef Full Text | Google Scholar

Löwdin, P.-O. (1963). Proton tunneling in DNA and its biological implications. Rev. Mod. Phys. 35, 724–732. doi: 10.1103/RevModPhys.35.724

CrossRef Full Text | Google Scholar

Löwdin, P.-O., (eds.). (1966). “Quantum genetics and the aperiodic solid: some aspects on the biological problems of heredity, mutations, aging, and tumors in view of the quantum theory of the DNA molecule,” in: Advances in Quantum Chemistry, Vol. 2 (New York, NY; London: Academic Press), 213–360.

Google Scholar

Luria, S. E., and Delbrück, M. (1943). Mutations of bacteria from virus sensitivity to virus resistance. Genetics 28, 491–511.

PubMed Abstract | Google Scholar

Markova, N., Pejov, L., Stoyanova, N., and Enchev, V. (2017). Hybrid MC/QC simulations of water-assisted proton transfer in nucleosides. Guanosine and its analog acyclovir. J. Biomol. Struct. Dyn. 35, 1168–1188. doi: 10.1080/07391102.2016.1179594

PubMed Abstract | CrossRef Full Text | Google Scholar

Michalkova, A., Kosenkov, D., Gorb, L., and Leszczynski, J. (2008). Thermodynamics and kinetics of intramolecular water assisted proton transfer in Na+-1-methylcytosine water complexes. J. Phys. Chem. B 112, 8624–8633. doi: 10.1021/jp801807x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicolis, G., and Prigogine, I. (1977). Self-Organization in Nonequilibrium Systems 170, New York, NY: Wiley.

Google Scholar

Schuster, P. A. (2018). Mathematical model of Evolution MATCH Commun. Math. Comput. Chem. 80, 547–585 doi: 10.1007/s12064-010-0110-z

CrossRef Full Text | Google Scholar

Topal, M. D., and Fresco, J. R. (1976). Complementary base pairing and the origin of substitution mutations. Nature 263, 285–289. doi: 10.1038/263285a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Turaeva, N., and Brown-Kennerly, V. (2015). Marcus model of spontaneous point mutation in DNA. Chem. Phy. 461, 106–110. doi: 10.1016/j.chemphys.2015.09.005

CrossRef Full Text | Google Scholar

Villani, G. (2005). Theoretical investigation of hydrogen transfer mechanism in the adenine, thymine base pair. Chem. Phys. 316, 1–8. doi: 10.1016/j.chemphys.2005.04.030

CrossRef Full Text | Google Scholar

Villani, G. (2010). Theoretical investigation of hydrogen atom transfer in the cytosine- guanine base pair and its coupling with electronic rearrangement. concerted vs stepwise mechanism. J. Phys. Chem. B. 114, 9653–9662. doi: 10.1021/jp102457s

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Hellinga, H. W., and Beese, L. S. (2011). Structural evidence for the rare tautomer hypothesis of spontaneous mutagenesis. Proc. Natl. Acad. Sci. U.S.A. 108, 17644–17648. doi: 10.1073/pnas.1114496108

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. D., and Crick, F. H. (1953a). The structure of DNA. Cold Spring Harbor Symp. Quant. Biol. 18, 123–131. doi: 10.1101/SQB.1953.018.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Watson, J. D., and Crick, F. H. (1953b). Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature 171, 737–738. doi: 10.1038/171737a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Z.-M., Zhang, Q. R., Gao, C. Y., and Zhuo, Y. Z. (2006). Motion of the hydrogen bond proton in cytosine and the transition between its normal and imino states. Phys. Lett. A 359, 10–13. doi: 10.1016/j.physleta.2006.06.004

CrossRef Full Text | Google Scholar