- Department of Physics, Assam University, Silchar, India
A detailed density functional theory investigation of He2-encapsulated fullerene C36 and C40 has been presented here. When confinement takes place, He-He bond length shortens and a non-covalent type of interaction exists between two He atoms. Energy decomposition analysis shows that though an attractive interaction exists in free He2, when it is confined inside the fullerenes, repulsive interaction is observed due to the presence of dominant repulsive energy term. Fullerene C40, with greater size, makes the incorporation of He2 much easier than C36 as confirmed from the study of boundary crossing barrier. In addition, we have studied the possibility of using He2-incorporated fullerene as acceptor material in dye-sensitized solar cell (DSSC). Based on the highest energy gap, He2@C40 and bare C40 fullerenes are chosen for this purpose. Dye constructed with He2@C40 as an acceptor has the highest light-harvesting efficiency and correspondingly will possess the maximum short circuit current as compared to pure C40 acceptor.
Introduction
Ever since the discovery of fullerene (Kroto et al., 1985), it has been studied extensively due to its fascinating properties, leading to versatile applications in various fields of nano and opto- electronics (Bhusal et al., 2016; Paul et al., 2017, 2018a,b; Qu et al., 2019), besides being used as sensors (Jaroš et al., 2019; Parey et al., 2019) and hydrogen storage devices (Chandrakumar and Ghosh, 2008; Srinivasu and Ghosh, 2012). Fullerenes are also known to exist in different isomeric forms (Małolepsza et al., 2007; Zhao et al., 2018). Insertion of various atoms and molecules into the fullerene cage has attracted a lot of interest in the scientific community and is designated as the endohedral fullerenes. It is believed that the endohedrally trapped species can manipulate different properties and affect the reactivities of the fullerene cage as well (Ravinder and Subramanian, 2011, 2012). Thus, this class of fullerenes is studied both theoretically and experimentally, having their extensive use in the field of electronics, medicine, and nanotechnology (Guha and Nakamoto, 2005; Martín, 2006; Yamada et al., 2010). They can also serve the purpose of being an acceptor in photovoltaic devices (Osuna et al., 2011). Reactivity pattern of a system (atoms and molecules) significantly changes due to confinement (Chattaraj and Sarkar, 2003; Sarkar et al., 2009, 2012; Khatua et al., 2014c; Deb et al., 2016a,b); as a result, stability increases and reduces the activation barrier. The encapsulated atoms or molecules can be either metal, non-metal, or noble gas (Ng). Noble gases, due to their closed electronic shell configuration, are generally reluctant of forming any chemical compound. However, it is possible to successfully encapsulate them inside fullerenes using techniques, such as ion bombardment (Weiske et al., 1991), molecular surgery (Saunders et al., 1994), and involving high pressure and high-temperature methods. Synthesis of the first xenon-containing molecule opened a way and interest for the researchers that noble gases are eligible to take part in chemical reactions (Bartlett, 1962). Ng-containing compound HNgY (Ng = Ar, Kr, Xe; Y = electron-withdrawing group) has been successfully synthesized by Pettersson et al. (1998). Literature survey also reveals that Feldman et al. has prepared hydrides and other Ng-related compounds (Feldman and Sukhov, 1996; Feldman et al., 1997). A number of theoretical studies on Ng have also been done apart from experimental investigations (Pan et al., 2013a,b,c, 2014a,b,c, 2015a,b,c; Saha et al., 2015; Ghara et al., 2016; Ayub, 2017). Inclusion and exclusion of Ng inside fullerene cages have been reported (Saunders et al., 1993; Hummelen et al., 1995), where an intermediate is formed by the rupture of one or more bonds, thus making an open window for the encapsulation of these noble gas atoms, although some disagreement is also set forth (Haaland et al., 2004). Experimental studies show that noble gases put inside the hollow cavity of C60 acquire an activation barrier energy as high as 90 kcal/mol−1 during its dissociation (Becker et al., 1996). Ng atoms are not only encapsulated inside larger fullerene cages (C60, C70), but they can also be successfully trapped inside much smaller cages such as C10H10, C20H20, C32, etc. (Darzynkiewicz and Scuseria, 1997; Jiménez-Vázquez et al., 2001; Zou et al., 2010; Chakraborty et al., 2016; Sekhar et al., 2017). Further studies on trapping two Ng atoms forming an Ng dimer (Ng2) inside fullerene have been first theoretically predicted by Giblin et al. (1997) and just after a year, He and Ne dimers are experimentally spotted into C70 fullerene (Khong et al., 1998; Laskin et al., 1998). Confinement of Ng dimers in C60 fullerene starting from He to Xe atoms have been studied theoretically by some groups (Krapp and Frenking, 2007; Fernández et al., 2014; Khatua et al., 2014b), where it was found that the Ng-Ng bond distances relatively get smaller when the Ng2 molecule is trapped inside the cage as compared to the bond distances of the isolated dimer (Krapp and Frenking, 2007). However, as a whole, these systems are thermodynamically not stable owing to the exclusion of the Ng atoms. In a study as reported by Krapp and Frenking (2007) a genuine chemical bond is found to exist between the two Xe atoms when its dimer is confined inside the C60 cage, while for its lighter analogs, i.e., He and Ne, the presence of weak van der Waals interaction is detected. Cerpa et al. (2009) have studied the effect of confinement on the electronic interaction between He-He bond in the host C20H20 and their results followed that a shorter He-He bond does not always indicate a chemical bond. Not only are the carbon related compounds considered as the hosts for entrapping the Ng atoms and their dimers, but hosts constituted with other elements such as B40 cage (Pan et al., 2018), B12N12 (Khatua et al., 2014a; Paul et al., 2019), B16N16 (Khatua et al., 2014a), , and (Sekhar et al., 2017) are also reported. Encapsulation of Ng and Ng2 in B12N12 and B16N16 fullerenes show that the dimer He2 undergoes not only vibration and translation, but also rotation inside the cage. These investigations on noble gases encourage further comprehensive study on their confinement with different host materials.
Fullerenes possessed with electron-deficient characteristics are used as electron acceptors in a solar cell device (Liu and Troisi, 2011; Eom et al., 2014; Leng et al., 2014; Shimata et al., 2016). Dye-sensitized solar cell (DSSC) (O'Regan and Grätzel, 1991) is one of the widely used organic solar cells because it offers the possibility to convert light photons to electrical energy at a low cost. A dye in a DSSC consists of three parts: an electron-rich donor, a spacer, and an electron-deficient acceptor. Among the acceptors, [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) has been widely investigated (Liu and Troisi, 2011). Apart from fullerene C60 in PCBM, C70 cage is also used (Leng et al., 2014). Endohedral fullerenes can be used in designing solar cells (Ross et al., 2009) where the confined atoms are supposedly contributing to the efficiencies of the carrier transport (Yamada et al., 2010).
Inspired by all these works on noble gas, herein, we have investigated the influence of He2 molecule when trapped inside C36 and C40 fullerenes by calculating the energetic stability, bonding analysis, energy decomposition analysis, distortion energy, and boundary-crossing barrier energy of He2@CX (X = 36, 40). A glimpse of the UV-visible absorption spectra of He2@CX is presented. Finally, considering the energetically most stable fullerene among the two (He2@C40), various parameters associated with the study of a dye-sensitized solar cell have been investigated. To make a comparison, pristine C40 fullerene is considered for this particular case study.
Computational Details
All the structures have been optimized using density functional theory (DFT) methodology as implemented in Gaussian 09 program package (Frisch et al., 2009), using M05-2X functional (Hohenstein et al., 2008). We have used 6-31+g(d,p) basis set for the C atoms and def2-TZVP basis set for the He atoms.
Dissociation energy (De) and distortion energy (Ed) are calculated using the relations:
where ECX is the total energy of pristine CX fullerenes, EHe2@CX is the total energy of the He2 encapsulated fullerenes (i.e., He2@C36 and He2@C40), ECX(expanded) is the energy calculated by removing the He2 dimer and evaluating single point energy of the expanded CX fullerenes, and EHe2 is the energy of He2 dimer.
The boundary-crossing barrier of the He2 dimer through one hexagonal face of the fullerenes has been obtained by scanning the potential energy surface at different distances from the center of the fullerene cages. GAMESS software (Schmidt et al., 1993) has been implemented in calculation of energy decomposition analysis. Multiwfn software (Lu and Chen, 2011) is used to perform the topological analysis of electron density. Time-dependent density functional theory (TDDFT) has been employed to check the absorption spectra for the first 40 excited state transitions of the fullerenes and GaussSum software (O'Boyle et al., 2008) has been used for plotting. For calculating solar cell parameters, we have considered B3LYP functional and 6–31 g basis set for all the atoms.
Results and Discussion
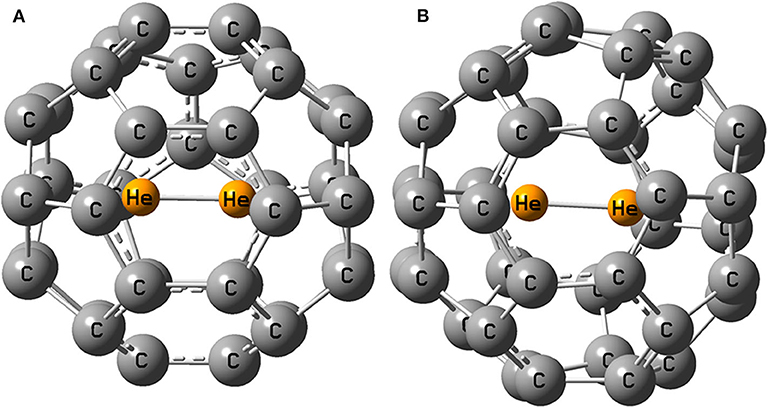
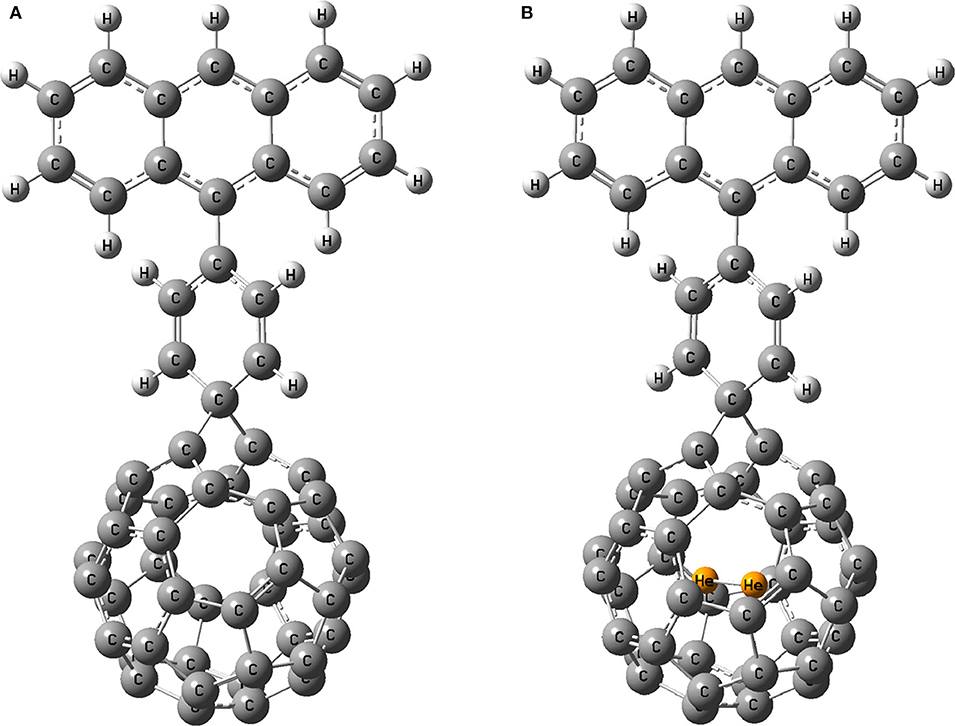
The optimized structure of He2 dimer encapsulated fullerenes are shown in Figure 1 below.
Upon optimization, He2 dimer orients itself in the middle of the fullerene cage in such a way that it can move through the midpoint of a six-membered ring easily when put inside C36 and C40 cages. In the beginning, empty C36 and C40 fullerenes (Figure S1) possess D2d and D2 symmetry, respectively. On enclosing He2 inside them, the symmetry of C36 (i.e., He2@C36) changes to C2 but C40 (i.e., He2@C40) successfully retains its original symmetry D2. The highest dissociation energy is found when He2 is encapsulated inside C36 cage (−53.1 kcal/mol) and naturally, the least is found for C40 fullerene, having a value of −45.6 kcal/mol. Negative values of dissociation energy reveal that He2 encapsulation in them is not favorable. It should be noted that cage distortion and Pauli repulsion plays an important role in destabilization. However, with the increase in the size of the fullerene cage (C36 < C40), destabilization decreases due to enlargement of space inside the cavity. Hence, it may be inferred that larger cages may lead toward favoring He2 encapsulation in them. This result is also supported by the values of energy gap of He2-incorporated C36 and C40 fullerenes. The larger fullerene C40 records a value of 3.980 eV, whereas C36 has 3.028 eV energy gap when they both hold the He2 dimer inside them, indicating that He2@C40 is more stable than He2@C36 owing to its greater energy gap in comparison.
Distortion Energy
The encapsulation of the He2 dimer inside the fullerene cages expands the surface area of the fullerene cage and this expansion may increase the binding energy of the system. The calculated distortion energy for He2@C36 is 1.6 kcal/mol and for He2@C40 is 1.7 kcal/mol. Thus, He2 dimer has to expend this amount of energy barriers to get encapsulated inside the fullerene cages, as can be seen from the distortion energy values.
Structural Properties and Bonding Analysis
In order to get an idea about how the confinement of He2 affects itself as well as the fullerene encaging it, we have calculated the bond lengths of the He2 dimer both in unconfined and confined state. We have also performed electron density analysis, which will further strengthen the results. The equilibrium bond length for an isolated He2 is calculated to be 2.666 Å, which is exactly same as that of Khatua et al. (2014a). As expected, confinement reduces the bond length of He2 dimer, which is found from the investigation. More specifically, when He2 is entrapped inside C36, its bond length diminishes to 1.520 Å, while with the larger C40 cage, it has a value of 1.546 Å.
To understand the nature of interaction between the two He atoms both inside and outside fullerene C36 and C40 and surrounding C atoms when He2 is placed inside the cages, the electron density analysis at the bond critical point (BCP) was performed (Deb et al., 2018) by employing the Bader's atoms-in-molecules theory (Bader, 1990). The corresponding topological descriptors are tabulated in Table 1 and the contour plot of the Laplacian of electron densities at the BCPs are shown in Figure 2. At the BCP, depletion and accumulation of electron density [ρ(rc)] can be well understood from the positive and negative values of the Laplacian of electron density , respectively. Thus, when the magnitude of , a covalent or shared bond is formed between two atoms while a non-covalent bond is expected when . This criterion is helpful in explaining the bonding nature in many systems, but for the systems involving heavier atoms or with 3d orbitals, considering only is not adequate to describe the nature of bonding connecting the heavier atoms. Therefore, some more topological descriptors like the local kinetic energy density [G (rc)], local potential energy density [V (rc)], and local electron energy density [H(rc)], including two ratios −G (rc)/V (rc) and G (rc)/ρ(rc), become essential to knowing the bonding nature. Based on these parameters, Cremer and Kraka (1984) proposed that if ∇2ρ(rc) > 0 and H(rc) < 0, then the nature of bonding is partially covalent. It is also stated that if the ratio −G (rc)/V (rc) falls in the range 0.5–1, then there exists some degree of covalent character (partial covalent type) and if −G (rc)/V (rc) > 1, a purely non-covalent type of interaction is formed. Further, the magnitude of G (rc)/ρ(rc) < 1 is also indicative of the presence of covalency in any bond.

Table 1. Electron density descriptors (in au) at the bond critical points (BCPs) in between some selected bonds of He2, He2@CX (X = 36, 40).
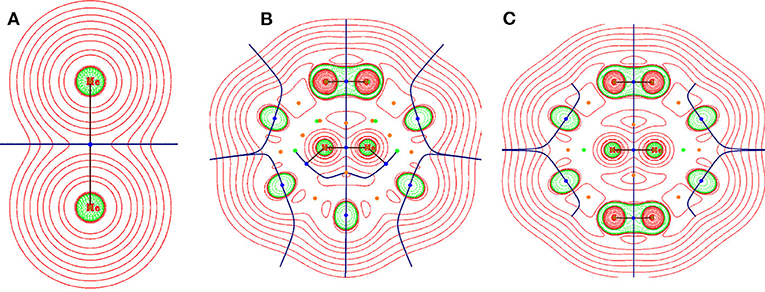
Figure 2. Contour plot representation of Laplacian of electron density at a particular plane of (A) He2, (B) He2@C36, and (C) He2@C40. Red region depicts the area having ∇2 ρ(rc) > 0 and green region depicts the area having ∇2 ρ(rc) < 0.
Present case deals with two types of bonds, i.e., one between He-He (in He2 and He2@C36, He2@C40) and another between He-C (in He2@C36 and He2@C40); corresponding labeled figure is provided in Figure S2. From Table 1, it is seen that both ∇2ρ(rc) and H(rc) have values > 0, which means that a non-covalent type of bonding exists between them. The ratios −G (rc)/V (rc) and G (rc)/ρ(rc) both have a value > 1, which again emphasizes the finding that a non-covalent type of interaction is present between both He-He and He-C bonds. It should be mentioned here that along with positive ∇2ρ(rc), the magnitude of ρ(rc) at the BCP is also lower than 0.1 au, which is the threshold value for ρ(rc) considered here, and again confirms that the studied bonds are not of covalent type. Now examining the He-He bonds in the two host fullerenes C36 and C40, one can find that the ρ(rc) value of He-He bond present in C36 is the highest between the two hosts, recording a value of 0.045 au. However, it may be noted that for unconfined He2, the values of ρ(rc), ∇2ρ(rc), G (rc), V (rc), and H (rc) are very small and almost close to zero, but when it gets confined inside the cages, the values are considerably increased. This indicates that confinement of He2 inside fullerene C36 and C40 has affected its various parameters.
Energy Decomposition Analysis
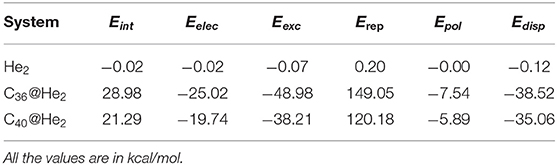
To examine the interdependence of He2 inside C36 and C40 fullerene cages, we studied the interaction energy and the different contributing energy terms in connection with the total interaction obtained from all-electron calculations using localized molecular orbital energy decomposition analysis (LMO-EDA). To make a comparison, we also checked the interaction energy for an unconfined He2 dimer. The interaction energy (Eint) can be decomposed into five energy components: electrostatic (Eelec), exchange (Eexc), repulsion (Erep), polarization (Epol), and dispersion (Edisp). This particular study will shed light into the attractive (negative Eint) or repulsive (positive Eint) nature of interaction between the He2 molecule and the concerned fullerene cages. For the He2-entrapped C36 and C40 fullerenes, He2 molecule is considered as one fragment and the associated fullerene as the other. Here, the electrostatic energy represents the classical Coulomb interaction, the exchange energy includes the Pauli repulsion. The repulsion energy deals with the contribution coming from the exchange of parallel spin electrons between the two fragments. The energy gained due to the orbital relaxation of one fragment because of the existence of other fragment having undistorted charge distribution in the former fragment's proximity is accounted for the polarization energy. Lastly, the dispersion energy comes from the instantaneous correlation of fluctuating electron density distribution between the two fragments. From Table 2, we may find that attractive nature of interaction is found when two He atoms form a He2 dimer, which is clear from its negative interaction energy. However, the situation is changed as soon as the dimer gets confined inside the two fullerene cages and records a positive value of interaction energy. In case of free He2 dimer, all the energy components are less in magnitude, with zero contribution coming from the polarization energy. Now, coming to the confined He2 inside the cages, it can be seen that Eelec, Eexc, Epol, and Edisp energies are attractive in nature. Of all the attractive terms, Eexc contributes the most toward the total attraction energy, the second leading contributor being Edisp for both the systems. The electrostatic energy makes the third-highest attractive contribution and the polarization term with a smaller value (as compared to other attractive terms) is put in the last of all. However, the Pauli repulsion energy component, Erep, is so repulsive with the highest magnitude (positive) among all other energy terms that it makes the net interaction energy term positive and thus overall repulsive interaction energy is found for He2 incorporated fullerenes. The highest repulsive energy is found for He2@C36 (149.05 kcal/mol), whereas He2@C40 records much less repulsive energy than He2@C36, with a value 120.18 kcal/mol. It may be noted here that the steep rise in the destabilizing Pauli repulsive energy term in the case of He2-entrapped C36 and C40 fullerene and a positive interaction energy is due to the compression of bond distance in He2 dimer confined inside the cages in comparison to the isolated He2 dimer. One important finding is that when compared to He2 entrapped in B12N12 and B16N16 cages (Khatua et al., 2014a), the total interaction energy is much lowered in the present study owing to the increase in the size of the fullerene cages. This may indicate that larger cages can accommodate He2 dimer easily and may at some point stabilize the whole system.
Barrier Crossing Energy
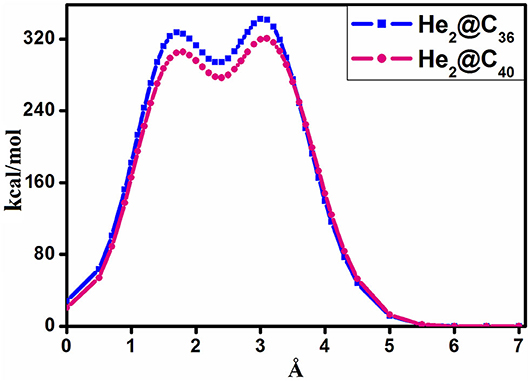
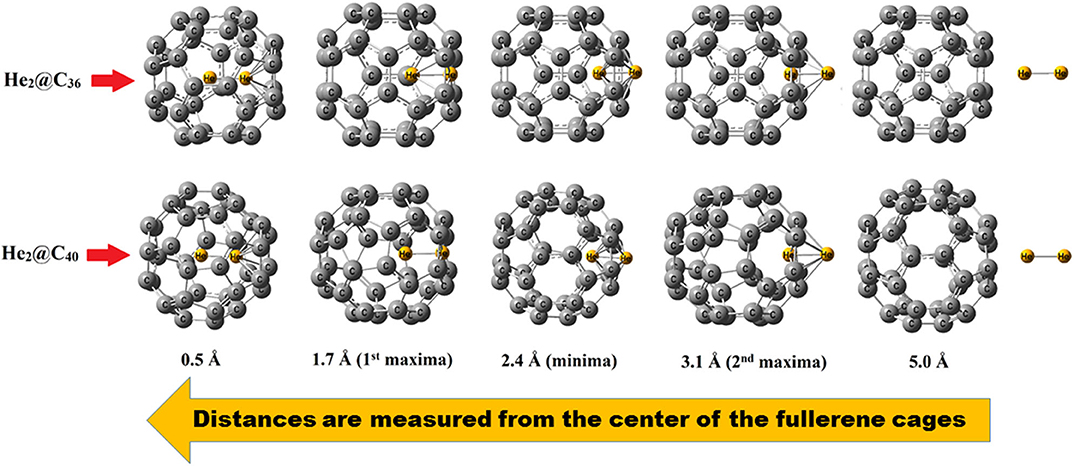
The barrier crossing energy of He2@C36 and He2@C40 fullerenes have been depicted in Figure 3. The potential of an atom or a molecule to enter/exit into/from a fullerene cage is measured by speculating the boundary-crossing barriers. The corresponding energies provide information about the permeability and kinetic barrier of the atom or the molecule for crossing the boundary of the fullerene cage. Thus, to observe the movement of He2 through C36 and C40 fullerenes, the boundary-crossing barrier has been studied. Also, five pictures of He2 encapsulation in fullerenes are shown in Figure 4. Now, since an easy translation of the dimer into the cage can be done through a six-membered ring (instead of five-membered ring), the scanning process for its barrier crossing is calculated through a hexagon only. From Figure 3, we may observe that there are two peaks for each of the curves, with the second one (2nd maxima) from left much steeper than the first one (1st maxima). The barrier crossing energy is calculated in such a way that at the beginning the He2 dimer is put at a distance of 7 Å from the center and then it is moved toward the cage to finally get placed in the center of the fullerene cage. The energy along this path is noted and the resulting curve is shown in Figure 3. The presence of two peaks is due to the two He atoms, which enter through the cage. The first peak from right (2nd maxima) corresponds to the energy when the first He atom passes through the cage, then the energy comes down slightly corresponding to the valley between two peaks, where the two He atoms are equally placed, one inside and another outside the surface of the cage. After that, when the second He atom just reaches the surface of the fullerene cage, the corresponding energy again rises (1st maxima), but with a relatively lower magnitude than that of the former peak value. Thereafter the energy value gradually decreases as the He2 dimer reaches the center of the cage, where it takes the minimum energy position. Among the two cages, namely fullerene C36 and C40, it is clear from Figure 3 that He2 dimer possesses lower barrier crossing energy when it enters the C40 fullerene as compared to C36. Thus, it is obvious that with increase in the size of the cage, it becomes comparatively easier for the He2 dimer to be encapsulated inside it. Moreover, high energy barrier for the encapsulation process of any atom/molecule to be confined inside any closed complex suggests their kinetic stability, and once these encapsulated clusters are formed, they cannot dissociate into fragments owing to higher kinetic barrier (Sekhar et al., 2017). Here in this study, both the He2 encapsulated fullerenes, He2@C36 (327. 3 kcal/mol at 1st maxima and 342.2 kcal/mol at 2nd maxima) and He2@C40 (305.4 kcal/mol at 1st maxima and 320.4 kcal/mol at 2nd maxima), have a much higher energy barrier when the two He atoms of the constituting He2 dimer cross the surface of the fullerene cages. Thus, they may be considered as kinetically stable systems.
Absorption Spectra
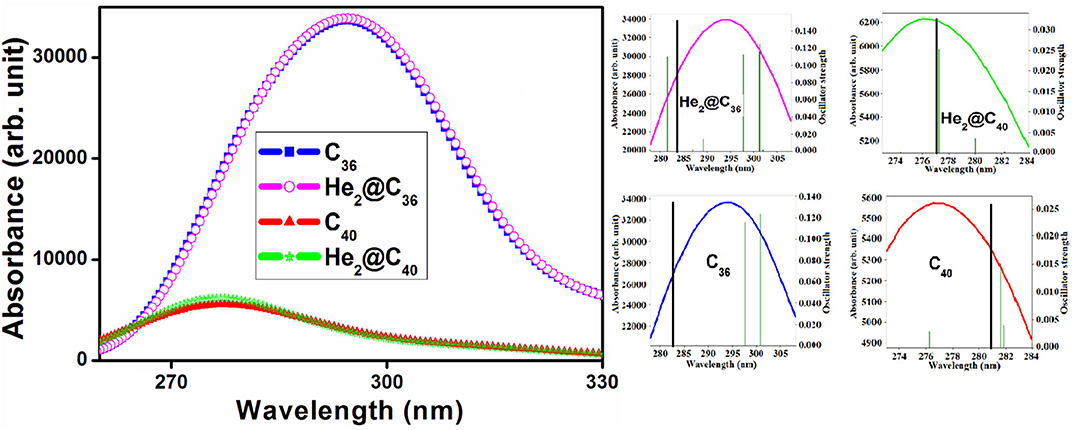
Table S1 provides the maximum absorption wavelength (λmax), corresponding transition energy (E0), highest oscillator strength (fmax), and the major electronic transitions of the He2 encapsulated C36 and C40 fullerenes along with their empty counterparts. The associated absorption spectra are provided in Figure 5. Also, to get a clear view of the highest absorption peak and highest oscillator strength of both bare and He2-encapsulated fullerenes, a zoom plot is provided. We may see that both the He2-encaged fullerenes possess absorption maxima in the ultraviolet (UV) region of the spectra with their λmax values of 283.652 and 277.090 nm for He2@C36 and He2@C40, respectively. One may observe that the highest oscillator strength of He2 confined C36 cage (0.1521) is much higher than that of C40 cage (0.0324). In addition, the corresponding λmax of He2@C36 is red-shifted toward a higher wavelength compared to He2@C40. Again, from the absorption spectra, it should be pointed out that the maximum absorption of the empty fullerenes, i.e., C36 (282.572 nm) and C40 (280.669 nm), also occur in the UV region, having slight displacement of the peaks with respect to their He2-confined analogs. C36, He2@C36 has higher intensity of absorption compared to C40, He2@C40. This is because the former set (C36 and He2@C36) has recorded a much higher value of oscillator strength, which significantly increased its absorption maxima with respect to the later set (C40 and He2@C40). In addition, the increment in the oscillator strength of C36 and He2@C36 occurs may be due to higher value of transition dipole moment, which ultimately puts an impact on the intensity of the highest electronic transition (Wang et al., 2015).
The shift in the absorption maxima (either blue or red) depends on various factors; for example, the electronic structure (Yanagisawa et al., 2013; Giri et al., 2014), implementation of gas or solvent phase (Giri et al., 2014), orientation of embedded molecule inside any closed cage (Wang et al., 2018), substitution of donor or acceptors (Ma et al., 2019), and sometimes dependency on the method of calculation is also observed (Cárdenas-Jirón et al., 2017). Here, in this case, may be the electronic structure (symmetry, orientation of He2 inside the fullerenes) plays an important role in this shift. In addition, red shift of the absorption spectra is also associated with a smaller energy gap (HOMO-LUMO gap) (Giri et al., 2014). Thus, He2@C36 (3.028 eV) with comparatively lower value of energy gap than He2@C40 (3.980 eV), has its absorption maxima red shifted toward the greater wavelength region. These systems with their maximum absorption peak falling in the UV region are usable in designing UV light protection devices.
Solar Cell Parameters
The most stable He2 encapsulated fullerene (He2@C40) among the two hosts is chosen as the acceptor for designing a solar cell device. To make a comparison, its free counterpart, pristine C40, is also taken as another acceptor. For the study, anthracene as donor and benzene as spacer are being used. For simplicity, we name the dye with acceptor as pristine C40 as D1 and that with He2@C40 as D1@He2. The optimized dyes are shown in Figure 6.
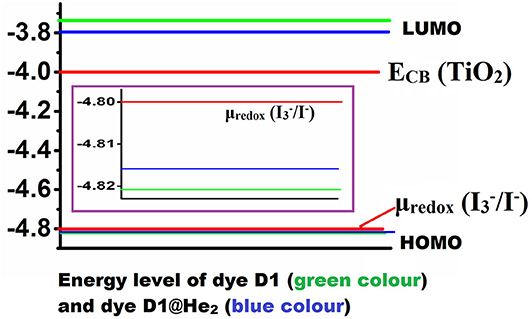
The energy levels of a dye molecule, which primarily indicates its HOMO and LUMO, play a very important role in its performance as a solar cell and the corresponding energy level diagram of the dyes is shown in Figure 7 (HOMO level of the dyes is zoomed). Eventually, the HOMO level of the dye must lie below the redox potential of couple (μredox = −4.80 eV), while the LUMO level must be placed above the conduction band (CB) edge of TiO2 semiconductor (ECB = −4.00 eV) (Qin et al., 2007). We found that the HOMO level of both the dyes lie just below the redox potential of couple, with a magnitude of −4.821 eV (for D1) and −4.816 eV (for D1@He2), which confirms that charge regeneration of the dyes is possible. The LUMO value of dye, D1, is calculated to be −3.736 eV, while that of D1@He2 is −3.795 eV. This means the LUMO levels of both the dyes lie above the conduction band of TiO2, and thus electron injection from the excited dyes to the conduction band of the semiconductor (TiO2) will become easier. However, on comparing the HOMO and LUMO values of both the dyes, one may observe that the LUMO of D1 acquires some appreciable changes when He2 dimer is inserted in the acceptor (i.e., D1@He2 dye), but there is very less change in the HOMO energy. Therefore, it can be inferred that changing the acceptor can only affect the LUMO energy level of the dye. Moreover, dye D1 with comparatively higher LUMO value than D1@He2 will help to increase the open-circuit voltage, opening a path to improve the efficiency of the dye-sensitized solar cell. The energy gap of dyes D1 and D1@He2 are calculated to be 1.085 and 1.021 eV, respectively. Thus, dye D1@He2 with a relatively smaller energy gap and a comparatively higher light-harvesting efficiency will show a better result.
Absorption Properties
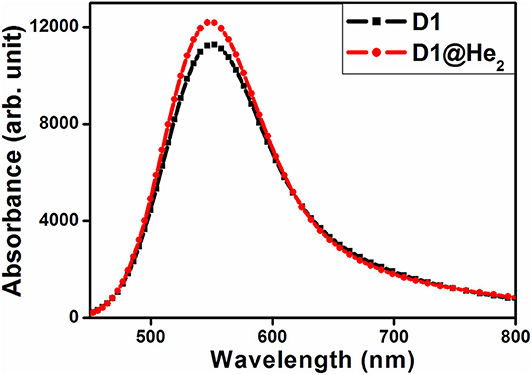
Here we have calculated the UV-visible absorption spectra of both the dyes (Figure 8) considering the lowest 40 transitions and results are provided in Table S2. One may observe that the maximum absorption wavelength corresponding to the highest oscillator strength (0.1456) of D1 dye falls at 547.126 nm with major transitions from HOMO → LUMO+3 (55%), HOMO → LUMO+5 (20%). For dye D1@He2, the highest oscillator strength increases to 0.1570 and there is a blue shift of the maximum absorption peak as compared to dye D1, located at 545.897 nm. There are two major transitions found for D1@He2 dye that take place from HOMO → LUMO+3 (53%) and HOMO → LUMO+5 (20%). Both the dyes show absorption in the visible region occurring at around 550 nm. From this study, we can infer that He2 dimer incorporation inside C40 increases the oscillator strength of dye D1. Thus, based on the study of absorption spectra, it is found that dye D1@He2 possesses a comparatively higher light-harvesting efficiency resulting a greater photocurrent response.
Short-Circuit Current and Open-Circuit Voltage
The short circuit current (JSC) (Zhang et al., 2012) is given by the relation
It greatly depends on the light-harvesting efficiency (LHE) and electron injection efficiency (ϕinject). For the systems differing only in the choice of dyes, ηcollect can be assumed constant.
On the other hand, ϕinject is related to the free energy of electron injection from the excited states of dye to the semiconductor surface (ΔGinject), which can be expressed as
ΔGinject can be estimated using the following equation (Katoh et al., 2004),
where represents the excited state oxidation potential of the dye, represents the ground state oxidation potential of the dye, E0 is the vertical transition energy corresponding to the maximum absorption wavelength of the dye, and ECB refers to the conduction band edge of the semiconductor (TiO2).
The computed results of various quantities involved in the calculation of JSC are provided in Table 3 for both the dyes. With the increase in the magnitude of , ΔGinject increases, which ultimately increases the ϕinject. Out of the two dyes, dye with the He2 dimer records the highest LHE value and thus will have a tendency to absorb more photons, which will lead to a higher magnitude of the short circuit current in comparison to dye D1. Also, according to a study (Islam et al., 2003), the electron injection efficiency of a dye is approximately equal to 1 when |ΔGinject| > 0.2. Here, we can see that both the dyes have a value of ΔGinject, which are much higher than 0.2. Thus, both of them possess sufficient driving force for electron injection to the semiconductor TiO2.
The open-circuit voltage (VOC) of a dye molecule can be evaluated approximately by finding the difference in energy between the LUMO energy level of the dye and the conduction band edge ECB of the semiconductor substrate, which may be represented by the mathematical relation (Sang-aroon et al., 2012),
The eVOC values of the dyes are given in Table 3. The equation indicates that higher the magnitude of the LUMO level of the dye, the higher open-circuit voltage (VOC) it will generate. From Table 3 we can see that dye D1 records greater value of eVOC than its He2 dimer encapsulated counterpart, which has a comparatively higher value of ΔGinject. This may be due to the fact that too high value of ΔGinject leads to energy redundancy, making a fall in the value of VOC (Li et al., 2017). Hence though the dye D1@He2 has a higher ΔGinject, but it possesses a smaller value of VOC than dye D1.
Non-linear Optical Properties
To explore the relationship between the efficiency of the dye molecules and their non-linear optical (NLO) properties, the isotropic polarizability of the dyes has been calculated. The response of any system when it is subjected to an external electric field is characterized by the study of NLO properties of that system (Deb et al., 2020). In case of dye D1, the isotropic polarizability is found to be 574.045 au, while for the dye D1@He2 the value increases to 577.945 au. This means that inclusion of a He2 dimer inside C40 acceptor improves the dye's polarizability. In addition, dyes having higher magnitudes of polarizability possibly will create strong interaction with its surroundings and will increase the local concentration of acceptor. Thus, the local concentration of the acceptor of the dye D1@He2, i.e., C40@He2 is increased on the semiconductor surface, which in turn will increase the possibility of this acceptor to perforate into the dye adsorption layer.
Conclusion
Density functional theory has been implemented to assess the various properties of He2 dimer when encaged inside two fullerene cages, C36 and C40. Our study shows that when He2 is confined in the cages, its bond length considerably decreases. The compression in bond length is more when C36 holds the dimer as compared to that of its relatively larger counterpart, C40 fullerene. Non-covalent type of interaction exists between the He-He bond, whether in isolated or confined inside the cages, which is confirmed from the electron density analysis. From energy decomposition analysis it is observed that attractive interaction is found for He2 dimer, but after being encapsulated in the fullerenes, the interaction becomes repulsive. The presence of larger repulsive energy compared to the other attractive energy terms may be responsible for this change in the case of He2@C36 and He2@C40. Fullerene C40 bearing a larger cavity makes He2 incorporation energetically much easier than that of C36 as observed from the investigation of barrier crossing energy. Absorption spectra analysis of both the He2@CX shows that they can be potentially used as UV light protectors since they possess absorption maxima in the UV region. Next, we designed a DSSC with free C40 and He2 confined C40 as acceptors. Charge regeneration and electron injection, which are the two most important qualities, are being fulfilled here by the dyes. In addition, both the dyes show an absorption peak in the visible region, which is another criterion for a DSSC. He2@C40, when used as acceptor, records the highest LHE value and thus will have a higher magnitude of JSC. NLO properties of the dyes are also calculated, and we found that the dye with He2-confined C40 acceptor has greater polarizability and thus will have higher possibility to perforate into the dye adsorption layer. This indicates that He2 incorporation inside fullerene really has a good effect on different properties.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
DP has played the lead role in data collection, analysis, visualization, and writing original draft. HD has played a supporting role in data extraction and formal analysis. US has a lead role in supervision, funding and software, and supporting role in conceptualization. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
DP thanks, University Grant Commission for her fellowship. US would like to thank DST, New Delhi, India for providing the financial support from SERB project (File No. EMR/2016/006764).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00621/full#supplementary-material
References
Ayub, K. (2017). Binding affinity and permeation of X12Y12 nanoclusters for helium and neon. J. Mol. Liquids 244, 124–134. doi: 10.1016/j.molliq.2017.08.118
Becker, L., Poreda, R. J., and Bada, J. L. (1996). Extraterrestrial helium trapped in fullerenes in the sudbury impact structure. Science 272, 249–252. doi: 10.1126/science.272.5259.249
Bhusal, S., Zope, R. R., Bhatta, S., and Baruah, T. (2016). Electronic and optical properties of VSc2N@C68 fullerene. J. Phys. Chem. C 120, 27813–27819. doi: 10.1021/acs.jpcc.6b08904
Cárdenas-Jirón, G., Borges-Martínez, M., Sikorski, E., and Baruah, T. (2017). Excited states of light-harvesting systems based on fullerene/graphene oxide and porphyrin/smaragdyrin. J. Phys. Chem. C 121, 4859–4872. doi: 10.1021/acs.jpcc.6b12452
Cerpa, E., Krapp, A., Flores-Moreno, R., Donald, K. J., and Merino, G. (2009). Influence of endohedral confinement on the electronic interaction between He atoms: a He2@C20H20 case study. Chem. Eur. J. 15, 1985–1990. doi: 10.1002/chem.200801399
Chakraborty, D., Pan, S., and Chattaraj, P. K. (2016). Encapsulation of small gas molecules and rare gas atoms inside the octa acid cavitand. Theor. Chem. Acc. 135:119. doi: 10.1007/s00214-016-1876-y
Chandrakumar, K. R. S., and Ghosh, S. K. (2008). Alkali-metal-induced enhancement of hydrogen adsorption in C60 fullerene: an ab initio study. Nano Lett. 8, 13–19. doi: 10.1021/nl071456i
Chattaraj, P. K., and Sarkar, U. (2003). Effect of spherical confinement on chemical reactivity. J. Phys. Chem. A 107, 4877–4882. doi: 10.1021/jp034321j
Cremer, D., and Kraka, E. (1984). Chemical bonds without bonding electron density? Does the difference electron-density analysis suffice for a description of the chemical bond? Angew. Chem. Int. Ed. Engl. 23, 627–628. doi: 10.1002/anie.198406271
Darzynkiewicz, R. B., and Scuseria, G. E. (1997). Noble gas endohedral complexes of C60 buckminsterfullerene. J. Phys. Chem. A 101, 7141–7144. doi: 10.1021/jp971323t
Deb, J., Bhattacharya, B., Paul, D., and Sarkar, U. (2016b). Interaction of nitrogen molecule with pristine and doped graphyne nanotube. Phys. E 84, 330–339. doi: 10.1016/j.physe.2016.08.006
Deb, J., Bhattacharya, B., and Sarkar, U. (2016a). Confinement of water molecule inside (2, 2) graphyne nanotube. AIP Conf. Proc. 1731:050081. doi: 10.1063/1.4947735
Deb, J., Paul, D., and Sarkar, U. (2020). Density functional theory investigation of nonlinear optical properties of T-graphene quantum dots. J. Phys. Chem. A 124, 1312–1320. doi: 10.1021/acs.jpca.9b10241
Deb, J., Paul, D., Sarkar, U., and Ayers, P. W. (2018). Characterizing the sensitivity of bonds to the curvature of carbon nanotubes. J. Mol. Model. 24:249. doi: 10.1007/s00894-018-3793-6
Eom, S. H., Baek, M.-J., Park, H., Yan, L., Liu, S., You, W., et al. (2014). Roles of interfacial modifiers in hybrid solar cells: inorganic/polymer bilayer vs inorganic/polymer: fullerene bulk heterojunction. ACS Appl. Mater. Interfaces 6, 803–810. doi: 10.1021/am402684w
Feldman, V., Sukhov, F., and Orlov, A. Y. (1997). Further evidence for formation of xenon dihydride from neutral hydrogen atoms: a comparison of ESR and IR spectroscopic results. Chem. Phys. Lett. 280, 507–512. doi: 10.1016/S0009-2614(97)01208-6
Feldman, V. I., and Sukhov, F. F. (1996). Formation and decay of transient xenon dihydride resulting from hydrocarbon radiolysis in a xenon matrix. Chem. Phys. Lett. 255, 425–430. doi: 10.1016/0009-2614(96)00346-6
Fernández, I., Solà, M., and Bickelhaupt, F. M. (2014). Origin of reactivity trends of noble gas endohedral fullerenes Ng2@C60 (Ng = He to Xe). J. Chem. Theory Comput. 10, 3863–3870. doi: 10.1021/ct500444z
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09, Revision D.01. Wallingford, CT: Gaussian, Inc.
Ghara, M., Pan, S., Deb, J., Kumar, A., Sarkar, U., and Chattaraj, P. K. (2016). A computational study on structure, stability and bonding in noble gas bound metal nitrates, sulfates and carbonates (Metal = Cu, Ag, Au). J. Chem. Sci. 128, 1537–1548. doi: 10.1007/s12039-016-1150-9
Giblin, D. E., Gross, M. L., Saunders, M., Jiménez-Vázquez, H., and Cross, R. J. (1997). Incorporation of helium into endohedral complexes of C60 and C70 containing noble-gas atoms: a tandem mass spectrometry study. J. Am. Chem. Soc. 119, 9883–9890. doi: 10.1021/ja971104l
Giri, S., Moore, C. H., Mcleskey, J. T., and Jena, P. (2014). Origin of red shift in the photoabsorption peak in MEH-PPV polymer. J. Phys. Chem. C 118, 13444–13450. doi: 10.1021/jp5030069
Guha, S., and Nakamoto, K. (2005). Electronic structures and spectral properties of endohedral fullerenes. Coord. Chem. Rev. 249, 1111–1132. doi: 10.1016/j.ccr.2004.11.017
Haaland, A., Shorokhov, D. J., and Tverdova, N. V. (2004). Topological analysis of electron densities: is the presence of an atomic interaction line in an equilibrium geometry a sufficient condition for the existence of a chemical bond? Chem. Eur. J. 10, 4416–4421. doi: 10.1002/chem.200400663
Hohenstein, E. G., Chill, S. T., and Sherrill, C. D. (2008). Assessment of the performance of the M05-2X and M06-2X exchange-correlation functionals for noncovalent interactions in biomolecules. J. Chem. Theory Comput. 4, 1996–2000. doi: 10.1021/ct800308k
Hummelen, J. C., Prato, M., and Wudl, F. (1995). There is a hole in my bucky. J. Am. Chem. Soc. 117, 7003–7004. doi: 10.1021/ja00131a024
Islam, A., Sugihara, H., and Arakawa, H. (2003). Molecular design of ruthenium(II) polypyridyl photosensitizers for efficient nanocrystalline TiO2 solar cells. J. Photochem. Photobiol. A 158, 131–138. doi: 10.1016/S1010-6030(03)00027-3
Jaroš, A., Bonab, E. F., Straka, M., and Foroutan-Nejad, C. (2019). Fullerene-based switching molecular diodes controlled by oriented external electric fields. J. Am. Chem. Soc. 141, 19644–19654. doi: 10.1021/jacs.9b07215
Jiménez-Vázquez, H. A., Tamariz, J., and Cross, R. J. (2001). Binding energy in and equilibrium constant of formation for the dodecahedrane compounds He@C20H20 and Ne@C20H20. J. Phys. Chem. A 105, 1315–1319. doi: 10.1021/jp0027243
Katoh, R., Furube, A., Yoshihara, T., Hara, K., Fujihashi, G., Takano, S., et al. (2004). Efficiencies of electron injection from excited N3 dye into nanocrystalline semiconductor (ZrO2, TiO2, ZnO, Nb2O5, SnO2, In2O3) films. J. Phys. Chem. B 108, 4818–4822. doi: 10.1021/jp031260g
Khatua, M., Pan, S., and Chattaraj, P. K. (2014a). Confinement induced binding of noble gas atoms. J. Chem. Phys. 140:164306. doi: 10.1063/1.4871800
Khatua, M., Pan, S., and Chattaraj, P. K. (2014b). Movement of Ng2 molecules confined in a C60 cage: an ab initio molecular dynamics study. Chem. Phys. Lett. 610-611, 351–356. doi: 10.1016/j.cplett.2014.06.052
Khatua, M., Sarkar, U., and Chattaraj, P. K. (2014c). Reactivity dynamics of a confined molecule in presence of an external magnetic field. Int. J. Quantum Chem. 115, 144–157. doi: 10.1002/qua.24801
Khong, A., Jiménez-Vázquez, H. A., Saunders, M., Cross, R. J., Laskin, J., Peres, T., et al. (1998). An NMR study of He2 inside C70. J. Am. Chem. Soc. 120, 6380–6383. doi: 10.1021/ja980142h
Krapp, A., and Frenking, G. (2007). Is this a chemical bond? a theoretical study of Ng2@C60 (Ng = He, Ne, Ar, Kr, Xe). Chem. Eur. J. 13, 8256–8270. doi: 10.1002/chem.200700467
Kroto, H. W., Heath, J. R., O'Brien, S. C., Curl, R. F., and Smalley, R. E. (1985). C60: buckminsterfullerene. Nature 318, 162–163. doi: 10.1038/318162a0
Laskin, J., Peres, T., Lifshitz, C., Saunders, M., Cross, R. J., and Khong, A. (1998). An artificial molecule of Ne2 inside C70. Chem. Phys. Lett. 285, 7–9. doi: 10.1016/S0009-2614(97)01473-5
Leng, C., Qin, H., Si, Y., and Zhao, Y. (2014). Theoretical prediction of the rate constants for exciton dissociation and charge recombination to a triplet state in PCPDTBT with different fullerene derivatives. J. Phys. Chem. C 118, 1843–1855. doi: 10.1021/jp410562u
Li, Y., Li, Y., Song, P., Ma, F., Liang, J., and Sun, M. (2017). Screening and design of high-performance indoline-based dyes for DSSCs. RSC Adv. 7, 20520–20536. doi: 10.1039/C6RA28396A
Liu, T., and Troisi, A. (2011). Absolute rate of charge separation and recombination in a molecular model of the P3HT/PCBM interface. J. Phys. Chem. C 115, 2406–2415. doi: 10.1021/jp109130y
Lu, T., and Chen, F. (2011). Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592. doi: 10.1002/jcc.22885
Ma, N., Lv, M., Liu, T., Song, M., Liu, Y., and Zhang, G. (2019). Second-order nonlinear optical properties of [60] fullerene-fused dihydrocarboline derivates: a theoretical study on switch effect. J. Mater. Chem. C 7, 13052–13058. doi: 10.1039/C9TC04126E
Małolepsza, E., Witek, H. A., and Irle, S. (2007). Comparison of geometric, electronic, and vibrational properties for isomers of small fullerenes C20-C36. J. Phys. Chem. A 111, 6649–6657. doi: 10.1021/jp068529r
Martín, N. (2006). New challenges in fullerene chemistry. Chem. Commun. 20, 2093–2104. doi: 10.1039/B601582B
O'Boyle, N. M., Tenderholt, A. L., and Langner, K. M. (2008). cclib: a library for package-independent computational chemistry algorithms. J. Comput. Chem. 29, 839–845. doi: 10.1002/jcc.20823
O'Regan, B., and Grätzel, M. (1991). A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 353, 737–740. doi: 10.1038/353737a0
Osuna, S., Swart, M., and Solà, M. (2011). The reactivity of endohedral fullerenes. What can be learnt from computational studies? Phys. Chem. Chem. Phys. 13, 3585–3603. doi: 10.1039/C0CP01594F
Pan, S., Contreras, M., Romero, J., Reyes, A., Merino, G., and Chattaraj, P. K. (2013a). C5 and O2 as noble gas trapping agents. Chem. Eur. J. 19, 2322–2329. doi: 10.1002/chem.201203245
Pan, S., Ghara, M., Kar, S., Zarate, X., Merino, G., and Chattaraj, P. K. (2018). Noble gas encapsulated B40 cage. Phys. Chem. Chem. Phys. 20, 1953–1963. doi: 10.1039/C7CP07890K
Pan, S., Gupta, A., Mandal, S., Moreno, D., Merino, G., and Chattaraj, P. K. (2015a). Metastable behavior of noble gas inserted tin and lead fluorides. Phys. Chem. Chem. Phys. 17, 972–982. doi: 10.1039/C4CP03856H
Pan, S., Gupta, A., Saha, R., Merino, G., and Chattaraj, P. K. (2015b). A coupled-cluster study on the noble gas binding ability of metal cyanides versus metal halides (Metal = Cu, Ag, Au). J. Comp. Chem. 36, 2168–2176. doi: 10.1002/jcc.24190
Pan, S., Jalife, S., Kumar, R. M., Subramanian, V., Merino, G., and Chattaraj, P. K. (2013b). Structure and stability of (NG)n CN3 clusters and comparison with (NG)BeY0/+. ChemPhysChem 15, 2511–2517. doi: 10.1002/cphc.201300357
Pan, S., Jalife, S., Romero, J., Reyes, A., Merino, G., and Chattaraj, P. K. (2013c). Attractive Xe-Li interaction in Li-decorated clusters. Comput. Theor. Chem. 1021, 62–69. doi: 10.1016/j.comptc.2013.06.026
Pan, S., Mandal, S., and Chattaraj, P. K. (2015c). Cucurbit[6]uril: a possible host for noble gas atoms. J. Phys. Chem. B 119, 10962–10974. doi: 10.1021/acs.jpcb.5b01396
Pan, S., Moreno, D., Cabellos, J. L., Merino, G., and Chattaraj, P. K. (2014a). An ab initio study on the stability of NgnBe2N2, NgnBe3N2, and NgBeSiN2 clusters (Ng = He-Rn). ChemPhysChem 15, 2618–2625. doi: 10.1002/cphc.201402101
Pan, S., Moreno, D., Cabellos, J. L., Romero, J., Reyes, A., Merino, G., and Chattaraj, P. K. (2014b). In quest of strong Be-Ng bonds among the neutral Ng-Be complexes. J. Phys. Chem. A 118, 487–494. doi: 10.1021/jp409941v
Pan, S., Moreno, D., Merino, G., and Chattaraj, P. K. (2014c). Stability of noble-gas-bound clusters. ChemPhysChem 15, 3554–3564. doi: 10.1002/cphc.201402370
Parey, V., Jyothirmai, M. V., Kumar, E. M., Saha, B., Gaur, N. K., and Thapa, R. (2019). Homonuclear B2/B3 doped carbon allotropes as a universal gas sensor: possibility of CO oxidation and CO2 hydrogenation. Carbon 143, 38–50. doi: 10.1016/j.carbon.2018.10.060
Paul, D., Deb, J., Bhattacharya, B., and Sarkar, U. (2017). Density functional theory study of pristine and transition metal doped fullerene. AIP Conf. Proc. 1832:050107. doi: 10.1063/1.4980340
Paul, D., Deb, J., Bhattacharya, B., and Sarkar, U. (2018a). Electronic and optical properties of C24, C12X6Y6, and X12Y12 (X = B, Al and Y = N, P). J. Mol. Model. 24:204. doi: 10.1007/s00894-018-3735-3
Paul, D., Deb, J., Bhattacharya, B., and Sarkar, U. (2018b). The influence of the substitution of transition metals on pristine C20: a DFT study. Int. J. Nano. Sci. 16:1760026. doi: 10.1142/S0219581X17600262
Paul, D., Deb, J., and Sarkar, U. (2019). Influence of noble gas atoms on B12N12 fullerene: a DFT study. AIP Conf. Proc. 2115:030171. doi: 10.1063/1.5113010
Pettersson, M., Lundell, J., Khriachtchev, L., Isoniemi, E., and Räsänen, M. (1998). HXeSH, the first example of a xenon-sulfur bond. J. Am. Chem. Soc. 120, 7979–7980. doi: 10.1021/ja981032d
Qin, P., Yang, X., Chen, R., Sun, L., Marinado, T., Edvinsson, T., et al. (2007). Influence of π-conjugation units in organic dyes for dye-sensitized solar cells. J. Phys. Chem. C 111, 1853–1860. doi: 10.1021/jp065550j
Qu, M., Qin, G., Du, A., Fan, J., and Sun, Q. (2019). B80 fullerene: a promising metal-free photocatalyst for efficient conversion of CO2 to HCOOH. J. Phys. Chem. C 123, 24193–24199. doi: 10.1021/acs.jpcc.9b07562
Ravinder, P., and Subramanian, V. (2011). Studies on the encapsulation of various anions in different fullerenes using density functional theory calculations and Born-Oppenheimer molecular dynamics simulation. J. Phys. Chem. A 115, 11723–11733. doi: 10.1021/jp203421v
Ravinder, P., and Subramanian, V. (2012). Role of encapsulation of Na+ and F− ions on the Diels-Alder reactivity of C32. J. Phys. Chem. A 116, 6870–6878. doi: 10.1021/jp3015244
Ross, R. B., Cardona, C. M., Guldi, D. M., Sankaranarayanan, S. G., Reese, M. O., Kopidakis, N., et al. (2009). Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 8, 208–212. doi: 10.1038/nmat2379
Saha, R., Pan, S., Merino, G., and Chattaraj, P. K. (2015). Comparative study on the noble-gas binding ability of BeX clusters (X = SO4, CO3, O). J. Phys. Chem. A 119, 6746–6752. doi: 10.1021/acs.jpca.5b03888
Sang-aroon, W., Saekow, S., and Amornkitbamrung, V. (2012). Density functional theory study on the electronic structure of monascus dyes as photosensitizer for dye-sensitized solar cells. J. Photochem. Photobiol. A 236, 35–40. doi: 10.1016/j.jphotochem.2012.03.014
Sarkar, U., Giri, S., and Chattaraj, P. K. (2009). Dirichlet boundary conditions and effect of confinement on chemical reactivity. J. Phys. Chem. A 113, 10759–10766. doi: 10.1021/jp902374d
Sarkar, U., Khatua, M., and Chattaraj, P. K. (2012). A tug-of-war between electronic excitation and confinement in a dynamical context. Phys. Chem. Chem. Phys. 14, 1716–1727. doi: 10.1039/C1CP22862E
Saunders, M., Jiménez-Vázquez, H. A., Cross, R. J., Mroczkowski, S., Gross, M. L., Giblin, D. E., et al. (1994). Incorporation of helium, neon, argon, krypton, and xenon into fullerenes using high pressure. J. Am. Chem. Soc. 116, 2193–2194. doi: 10.1021/ja00084a089
Saunders, M., Jiménez-Vázquez, H. A., Cross, R. J., and Poreda, R. J. (1993). Stable compounds of helium and neon: He@C60 and Ne@C60. Science 259, 1428–1430. doi: 10.1126/science.259.5100.1428
Schmidt, M. W., Baldridge, K. K., Boatz, J. A., Elbert, S. T., Gordon, M. S., Jensen, J. H., et al. (1993). General atomic and molecular electronic structure system. J. Comput. Chem. 14, 1347–1363. doi: 10.1002/jcc.540141112
Sekhar, P., Ghosh, A., Joshi, M., and Ghanty, T. K. (2017). Noble gas encapsulated endohedral zintl ions Ng@ and Ng@ (Ng = He, Ne, Ar, and Kr): a theoretical investigation. J. Phys. Chem. C 121, 11932–11949. doi: 10.1021/acs.jpcc.7b03294
Shimata, Y., Ide, M., Tashiro, M., Katouda, M., Imamura, Y., and Saeki, A. (2016). Charge dynamics at heterojunction between face-on/edge-on PCPDTBT and PCBM bilayer: interplay of donor/acceptor distance and local charge carrier mobility. J. Phys. Chem. C 120, 17887–17897. doi: 10.1021/acs.jpcc.6b04827
Srinivasu, K., and Ghosh, S. K. (2012). Transition metal decorated porphyrin-like porous fullerene: promising materials for molecular hydrogen adsorption. J. Phys. Chem. C 116, 25184–25189. doi: 10.1021/jp3047517
Wang, L., Wang, W.-Y., Qiu, Y.-Q., and Lu, H.-Z. (2015). Second-order nonlinear optical response of electron donor-acceptor hybrids formed between corannulene and metallofullerenes. J. Phys. Chem. C 119, 24965–24975. doi: 10.1021/acs.jpcc.5b06870
Wang, L., Ye, J.-T., Wang, H.-Q., Xie, H.-M., and Qiu, Y.-Q. (2018). Third-order nonlinear optical properties of endohedral fullerene (H2)2@C70 and (H2O)2@C70 accompanied by the prospective of novel (HF)2@C70. J. Phys. Chem. C 122, 6835–6845. doi: 10.1021/acs.jpcc.8b00623
Weiske, T., Boehme, D. K., and Schwarz, H. (1991). Injection of helium atoms into doubly and triply charged carbon (C60) cations. J. Phys. Chem. 95, 8451–8452. doi: 10.1021/j100175a011
Yamada, M., Akasaka, T., and Nagase, S. (2010). Endohedral metal atoms in pristine and functionalized fullerene cages. Acc. Chem. Res. 43, 92–102. doi: 10.1021/ar900140n
Yanagisawa, S., Yasuda, T., Inagaki, K., Morikawa, Y., Manseki, K., and Yanagida, S. (2013). Intermolecular interaction as the origin of red shifts in absorption spectra of zinc-phthalocyanine from first-principles. J. Phys. Chem. A 117, 11246–11253. doi: 10.1021/jp407608w
Zhang, J., Li, H.-B., Sun, S.-L., Geng, Y., Wu, Y., and Su, Z.-M. (2012). Density functional theory characterization and design of high-performance diarylamine-fluorenedyes with different π spacers for dye-sensitized solar cells. J. Mater. Chem. 22, 568–576. doi: 10.1039/C1JM13028E
Zhao, D., Liu, S., Rong, C., Zhong, A., and Liu, S. (2018). Toward understanding the isomeric stability of fullerenes with density functional theory and the information-theoretic approach. ACS Omega 3, 17986–17990. doi: 10.1021/acsomega.8b02702
Keywords: noble gas dimer, fullerene, encapsulation, DFT, solar cell
Citation: Paul D, Dua H and Sarkar U (2020) Confinement Effects of a Noble Gas Dimer Inside a Fullerene Cage: Can It Be Used as an Acceptor in a DSSC? Front. Chem. 8:621. doi: 10.3389/fchem.2020.00621
Received: 27 April 2020; Accepted: 15 June 2020;
Published: 06 August 2020.
Edited by:
Sudip Pan, University of Marburg, GermanyReviewed by:
Shubin Liu, University of North Carolina at Chapel Hill, United StatesSantanab Giri, Haldia Institute of Technology, India
Copyright © 2020 Paul, Dua and Sarkar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Utpal Sarkar, dXRwYWxjaGVtaWl0a2dwQHlhaG9vLmNvbQ==
 Debolina Paul
Debolina Paul Utpal Sarkar
Utpal Sarkar