- School of Material Sciences and Engineering, Hebei University of Technology, Tianjin, China
We report the presence of a Weyl fermion in VI3 monolayer. The material shows a sandwich-like hexagonal structure and stable phonon spectrum. It has a half-metal band structure, where only the bands in one spin channel cross the Fermi level. There are three pairs of Weyl points slightly below the Fermi level in spin-up channel. The Weyl points show a clean band structure and are characterized by clear Fermi arcs edge state. The effects of spin-orbit coupling, electron correlation, and lattice strain on the electronic band structure were investigated. We find that the half-metallicity and Weyl points are robust against these perturbations. Our work suggests VI3 monolayer is an excellent Weyl half-metal.
Introduction
In recent years, Weyl semimetals (WSMs) have attracted extensive research attentions (Wan et al., 2011; Lv et al., 2015; Shekhar et al., 2015; Soluyanov et al., 2015; Sun et al., 2015; Weng et al., 2015; Deng et al., 2016; Koepernik et al., 2016; Wu et al., 2016; Kumar et al., 2017). In a WSM, at least one of the time reversal and inversion symmetry is broken. The crossing points, namely, Weyl nodes, appear in pairs with different chirality (Ruan et al., 2016a,b). Such chiral anomaly can induce interesting transport properties such as anomalous Hall effect and negative magnetoresistance (Liu et al., 2013; Son and Spivak, 2013; Liu and Vanderbilt, 2014; Hirayama et al., 2015; Huang et al., 2015). Besides, Weyl nodes can be classified into two categories, namely, types I and II, according to the tilt degree of band crossing. Type I WSMs with traditional band dispersion follow the Lorentz symmetry (Wan et al., 2011; Lv et al., 2015; Shekhar et al., 2015; Sun et al., 2015; Weng et al., 2015). However, for type II WSMs (Soluyanov et al., 2015; Deng et al., 2016; Koepernik et al., 2016; Wu et al., 2016; Kumar et al., 2017), the Weyl cones are completely tilted. The tilted Weyl cones can cause the coexistence of electron-like pocket and hole-like pocket at the same energy level. As the results, type II WSMs have different physical phenomena from type I ones, including modified anomalous Hall conductivity, direction-dependent chiral anomaly, and momentum space Klein tunneling (Koshino, 2016; O'Brien et al., 2016; Yu et al., 2016; Zyuzin and Tiwari, 2016).
Up to now, a large number of WSMs have been reported, and some of which have been confirmed in experiments such as TaAs (Lv et al., 2015), NbP (Shekhar et al., 2015), and NbAs (Yang et al., 2019). These examples are all three-dimensional (3D) non-magnetic materials. Recently, WSMs in two-dimensional (2D) materials and magnetic materials have received increasing interests. For 2D WSMs, the interest arises from the promising applications in spintronic nanodevices (You et al., 2019). For magnetic WSMs, the interest comes from the novel interplay between the non-trivial band topology and the magnetic ordering (Xu et al., 2011; Kübler and Felser, 2016; Wang et al., 2016; Chen et al., 2019; He et al., 2019; Jin et al., 2020; Meng et al., 2020a,b,c). Recently, the VI3 material (Kong et al., 2019; Tian et al., 2019; Huang et al., 2020; Long et al., 2020; Zhang et al., 2020), both in 3D and 2D, has attracted great attention. The 3D VI3 material is a ferromagnetic insulator, which is a layered material (Kong et al., 2019). In addition, 3D VI3 compound has a R3 phase at room temperature, and experimental evidence suggests that it may undergo a structure phase transition at 78 K (Huang et al., 2020). Importantly, 2D VI3 had been proved by Long et al. (2020) to be a ferromagnetic half-metal and provides an excellent candidate material for electronic devices. In this work, we report that VI3 monolayer is an excellent 2D WSM. We have systematically investigated the stability, magnetism, and band topology of VI3 monolayer. We find VI3 monolayer is dynamically stable and naturally has the ferromagnetic ordering. The band structure suggests VI3 monolayer is a half-metal, which holds fully spin-polarized conducting electrons. Especially, there exists a band crossing near the Fermi level, which forms three pairs of Weyl fermions in the spin-up band structure. We have further investigated the effects of spin-orbit coupling (SOC), electron correlation, and lattice strain on the electronic band structure. In addition, the non-trivial edge states for the Weyl points are clearly identified. These results suggest VI3 monolayer can serve as a good platform to investigate Weyl states in 2D.
Computational Methods and Details
The first-principles calculations in this work are performed by using the Vienna ab initio Simulation Package (Blochl, 1994; Kresse and Joubert, 1999). The exchange-correlation potential is adopted by the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof functional (Perdew et al., 1996). For the crystal structure of VI3 monolayer, we built a vacuum with the thickness >18 Å to avoid potential interactions between layers. The cutoff energy is set as 500 eV. The Brillouin zone is sampled by a Monkhorst–Pack k-mesh with size of 15 × 15 × 1. To account for the Coulomb interaction, the GGA + U method is applied during our calculations (Anisimov et al., 1991). For the V-3d orbitals, the U value is chosen as 3eV. The phonon spectra are calculated by using the PHONOPY code (Togo et al., 2008).
Results and Discussion
Before studying the structure and electronic band of the monolayer VI3, we want to point out that the layered compound VI3 has already been synthesized by chemical vapor transport method experimentally. The specific synthesis process can be found in Kong et al. (2019). In addition, monolayer VI3 is very promising to be exfoliated from its bulk phase (Miro et al., 2014).
Next, we study the structure of single-layer VI3. Figures 1A,B show the top and side views of the geometric structure of VI3 monolayer. Figure 1C shows the Brillouin zone (BZ) of monolayer VI3. In the structure, each V atom bonds with six I atoms, forming the hexagonal structure. From the side view, we can observe that the material has a triple-layered form, with one V layer sandwiched by two I layers. The circled regions in (A) and (B) show the unit cell of VI3 monolayer, which contains two V atoms and six I atoms. The Cr2C compound shows a hexagonal structure with space group P3M1. The lattice constant of VI3 monolayer is a = b = 7.13 Å. The bond length of V-I is 2.80 Å, and that of I-I is 4.13 Å. These values are very close to the reported results of He et al. (2016). We have calculated the phonon spectrum of VI3 monolayer, as displayed in Figure 1D. We find no negative frequency phonons in all the highly symmetric k paths. This suggests that the VI3 monolayer can be stable.
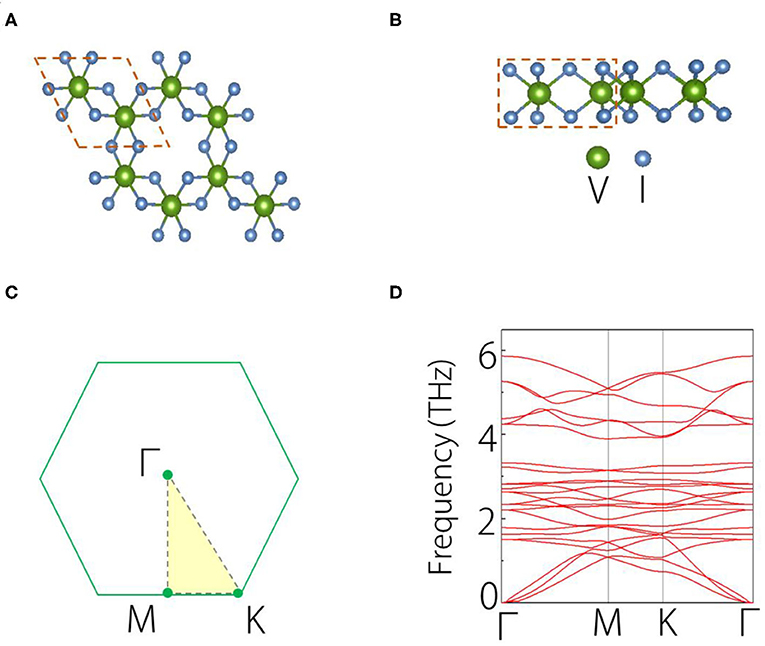
Figure 1. (A) Top view and (B) side views of VI3 monolayer, the dotted line circles the primitive cell. (C) Brillouin zone for VI3 monolayer. (D) Calculated phonon spectrum of VI3 monolayer.
Before studying the band structure of VI3 monolayer, we first verify its magnetic ground state. In VI3 monolayer, the magnetic moments are mainly contributed by the 3d transition element V. Here, we consider three potential magnetization directions of V moment, including [001], [010], and [100]. Our calculation results show that the [001] magnetization direction has the lowest energy. Then, in the [001] direction, we considered four magnetic configurations including ferromagnet (FM), Néel antiferromagnet (AFM), stripe AFM, and zigzag AFM. Our calculation results show that the energy of FM is lower than that of other magnetic structures in VI3 monolayer. The total magnetic moment is 4 μB per unit cell, which is almost contributed by the V atoms. In addition, we have calculated the exchange energy ΔE of VI3 monolayer, which is approximately 28 meV. Then, we can estimate the Curie temperature (Tc) according to the following equation:
In (1), the parameter “C” represents the number of magnetic atoms in unit cell, and “kB” represents the Boltzmann constant. We calculated that the Curie temperature Tc value of VI3 monolayer is 106 K, which is comparable with the Monte Carlo simulations (98 K) (He et al., 2016).
Here, we discuss the electronic band structure of VI3 monolayer. At first, we did not consider SOC in the calculations. The band structures are shown in Figures 2A,B. In the spin-up band structure, we find one band crosses the Fermi level, manifesting a metallic signature (Figure 2A). In the spin-down band structure, we can find a band gap around the Fermi level, manifesting the insulating signature (Figure 2B). Therefore, VI3 monolayer is in fact a half-metal. In particular, the half-metal gap is about 2.98 eV (Figure 2B), which is much layer than previously reported half-metals in 2D including YN2 (1.35eV) (Liu et al., 2017) and Na2C (0.77eV) monolayer (Ji et al., 2018). In the spin-up band structure, we notice there shows a band crossing point (P) in the M–K path, slightly below the Fermi level (Figure 2B). By checking the density of states, we find the states near the Fermi level mostly come from the d orbitals of V atom.
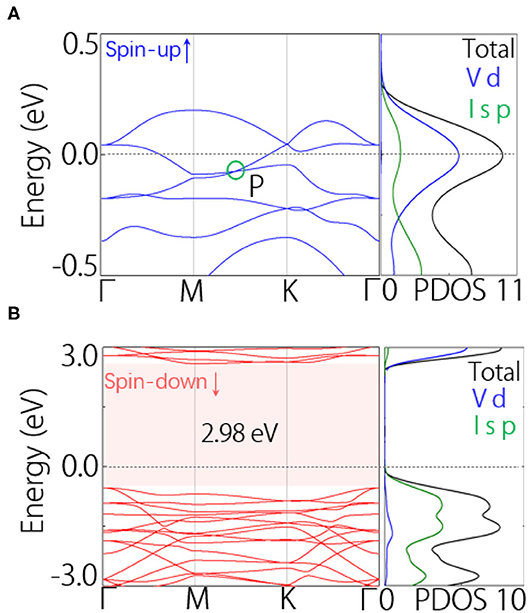
Figure 2. (A) Spin-up and (B) spin-down band structures of VI3 monolayer without SOC. In (A,B), the total and projected density of states (PDOS) are also shown.
Figure 3A shows the orbital-projected band structure near the crossing point P. We can observe the band inversion of the two bands, suggesting the non-trivial band topology in VI3 monolayer. Then we take into account the SOC effect in the calculation. The comparison of band structure between SOC and without SOC is shown in Figures 3B,C. We can find that the band crossing retains under SOC, even though its position has slightly changed. Without SOC, the crossing point locates at 0.04 eV below the Fermi level; under SOC, it locates at 0.08 eV below the Fermi level. Because the band crossing happens in two bands, the band crossing in fact forms Weyl points. To be noted, in VI3 monolayer, the time reversal is broken, but the inversion symmetry is retained; hence, the Weyl points are time-reversal–breaking Weyl points.
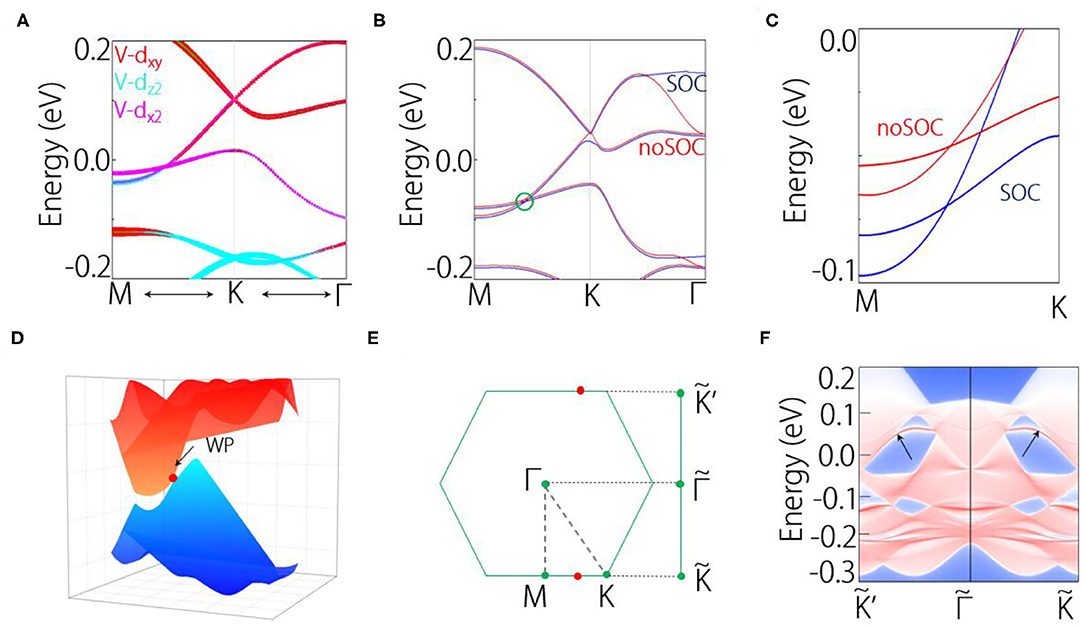
Figure 3. (A) Orbital-projected band structure near the crossing point P. (B,C) Comparison of band structure between SOC and without SOC, where (C) is the enlarged band structure. (D) 3D band dispersions near the Weyl point. (E) 2D Brillouin zone and its projection to the edge. (F) Edge states of VI3 monolayer.
In Figure 3D, we show the 3D plotting of band structure near the Weyl point. We can find that the Weyl cone is titled. Because of the preserved inversion symmetry, there are in total three pairs of such Weyl points in the system. From the symmetry analysis, the Weyl points in monolayer VI3 are protected by the C3v symmetry. It is worth noticing that Weyl points have many special physical phenomena, such as modified anomalous Hall conductivity, direction-dependent chiral anomaly, momentum space Klein tunneling (Koshino, 2016; O'Brien et al., 2016; Yu et al., 2016; Zyuzin and Tiwari, 2016). However, the Weyl fermions have been rarely found in 2D materials. Therefore, the VI3 monolayer reported here can be a good platform to study the Weyl fermions in 2D. In addition, in Figure 3E, the orbital projection is performed on (010) surface, we have also identified the Fermi arc edge states of the Weyl points, as shown in Figure 3F. This further verifies the non-trivial band topology in VI3 monolayer.
Finally, we discuss the effects of electron correlation and lattice strain on the half-metal band structure and the Weyl points. In Figure 4A, we show the positions of the conduction band minimum and the valence band maximum with shifting the U-values of V atom from 0 to 6 eV. The results show that VI3 monolayer is always a ferromagnetic half-metal, and the spin-down band gap will increase with increasing the U-values. For the Weyl points, we find they can exist when U-values are at 2–4 eV. Figure 4B shows the positions of the Weyl points at different U-values. Similarly, in Figures 4C,D, we show the strain effects on the half-metal band structure and the Weyl points. We can find that the half-metal band structure can retain from 4% compressive stain to 4% tensile strain (Figure 4C). Meanwhile, as shown in Figure 4D, we find the Weyl points can exist from 1% compressive stain to 2% tensile strain (Figure 4D). These results show that the half-metal band structure and the Weyl points are in some degree robust against electron correlation effects and lattice strain.
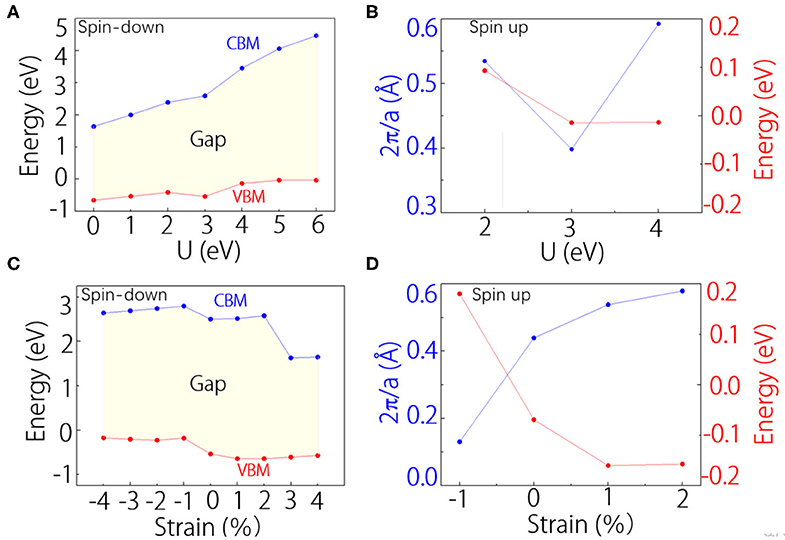
Figure 4. (A) The curves of the valence band maximum (VBM) and the conduction band minimum (CBM) under different U-values in the spin-down channel. The shadowed area shows the band gap. (B) The position of Weyl points under different U-values. (C,D) Similar with (A,B), but for the changes under different stains.
Summary
We have reported the Weyl fermion in 2D VI3 monolayer. The phonon spectrum suggests VI3 monolayer is dynamically stable. We have verified that VI3 monolayer has the ferromagnetic ground state. In the ground state, we find VI3 monolayer has a half-metal band structure with the half-metallic gap as large as 2.98 eV; thus, the conducting electrons can be fully spin-polarized. Very interestingly, VI3 monolayer shows three pairs of Weyl points near the Fermi level, locating in the spin-up band structure. Importantly, the three pairs of Weyl points show clear Fermi arcs on the edge. Moreover, we verify that the half-metal band structure and the Weyl points in VI3 monolayer are robust against proper electron correlation effects and lattice strain. These properties make VI3 monolayer have promising applications in spintronic nanodevices.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
This project was conceived by XZ and GL. TJ, HZ, and CL completed theoretical model and first principles calculations with the help from XZ and XD. TJ and WM performed the data analysis and designed the manuscript with the assistances from XZ and GL. This manuscript was written by TJ and XZ with important inputs from GL and XD. This project was supervised by GL. All authors discussed the results and commented on the manuscript.
Funding
This work was supported by Nature Science Foundation of Hebei Province (Nos. E2019202107 and E2019202222), National Natural Science Foundation of China (Grants No. 11904074). XZ acknowledges the financial support from Young Elite Scientists Sponsorship Program by Tianjin.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Anisimov, V. I., Zaanen, J., and Andersen, O. K. (1991). Band theory and mott insulators: Hubbard U instead of stoner I. Phys. Rev. B 44:943. doi: 10.1103/PhysRevB.44.943
Blochl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50:17953. doi: 10.1103/PhysRevB.50.17953
Chen, C., Yu, Z. M., Li, S., Chen, Z., Sheng, X. L., and Yang, S. A. (2019). Weyl-loop half-metal in Li2 (FeO3) 2. Phys. Rev. B 99:075131. doi: 10.1103/PhysRevB.99.075131
Deng, K., Wan, G. L., Deng, P., Zhang, K. N., Ding, E. Y., Yan, M. Z., et al. (2016). Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 12, 1105–1110. doi: 10.1038/nphys3871
He, J. J., Ma, S. Y., Lyu, P., and Nachtigall, P. (2016). Unusual Dirac half-metallicity with intrinsic ferromagnetism in vanadium trihalide monolayers. J. Mater. Chem. C 4, 2518–2526. doi: 10.1039/C6TC00409A
He, T. L., Zhang, X. M., Meng, W. Z., Jin, L., Dai, X. F., and Liu, G. D. (2019). Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 7, 12657–12663. doi: 10.1039/C9TC04046C
Hirayama, M., Okugawa, R., Ishibashi, S., Murakami, S., and Miyake, T. (2015). Weyl node and spin texture in trigonal tellurium and selenium. Phys. Rev. Lett. 114:206401. doi: 10.1103/PhysRevLett.114.206401
Huang, C. X., Wu, F., Yu, S. L., Jena, P., and Kan, E. (2020). Discovery of twin orbital-order phases in ferromagnetic semiconducting VI3 monolayer. Phys. Chem. Phys. 22, 512–517. doi: 10.1039/C9CP05643B
Huang, X., Zhao, L., Long, Y., Wang, P., Chen, D., Yang, Z., et al. (2015). Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5:031023. doi: 10.1103/PhysRevX.5.031023
Ji, W. X., Zhang, B. M., Zhang, S. F., Zhang, C. W., Ding, M., Wang, P., et al. (2018). Na2C monolayer: a novel 2p Dirac half-metal with multiple symmetry-protected Dirac cones. Nanoscale 10, 13645–13651. doi: 10.1039/C8NR02761G
Jin, L., Zhang, X. M., He, T. L., Meng, W. Z., Dai, X. F., and Liu, G. D. (2020). Ferromagnetic two-dimensional metal-chlorides MCl (M= Sc, Y, and La): candidates for Weyl nodal line semimetals with small spin-orbit coupling gaps. App. Sur. Sci. 520:146376. doi: 10.1016/j.apsusc.2020.146376
Koepernik, K., Kasinathan, D., Efremov, D. V., Khim, S., Borisenko, S., Buchner, B., et al. (2016). TaIrTe4: a ternary type-II Weyl semimetal. Phys. Rev. B 93:201101. doi: 10.1103/PhysRevB.93.201101
Kong, T., Stolze, K., Timmons, E. I., Tao, J., Ni, D., Guo, S., et al. (2019). VI3-a new layered ferromagnetic semiconductor. Adv Mater. 31:1808074. doi: 10.1002/adma.201808074
Koshino, M. (2016). Cyclotron resonance of figure-of-eight orbits in a type-II Weyl semimetal. Phys. Rev. B 94:035202. doi: 10.1103/PhysRevB.94.035202
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmentedwave method. Phys. Rev. B 59:1758. doi: 10.1103/PhysRevB.59.1758
Kübler, J., and Felser, C. (2016). Non-collinear antiferromagnets and the anomalous Hall effect. Europhys. Lett. 114:47005. doi: 10.1209/0295-5075/114/47005
Kumar, N., Sun, Y., Xu, N., Manna, K., Yao, M. Y., Suss, V., et al. (2017). Extremely high magnetoresistance and conductivity in the type-II Weyl semimetals WP2 and MoP2. Nat. Commun. 8:1642. doi: 10.1038/s41467-017-01758-z
Liu, C. X., Ye, P., and Qi, X. L. (2013). Chiral gauge field and axial anomaly in a Weyl semimetal. Phys. Rev. B 87:235306. doi: 10.1103/PhysRevB.87.235306
Liu, Z. F., Liu, J. Y., and Zhao, J. J. (2017). YN2 monolayer: novel p-state Dirac half metal for high-speed spintronics. Nano Res. 10, 1972–1979. doi: 10.1007/s12274-016-1384-3
Liu, J, and Vanderbilt, D. (2014). Weyl semimetals from noncentrosymmetric topological insulators. Phys. Rev. B 90:155316. doi: 10.1103/PhysRevB.90.155316
Long, C., Wang, T., Jin, H., Wang, H., and Dai, Y. (2020). Stacking-independent ferromagnetism in Bilayer VI3 with Half-metallic characteristic. J. Phys. Chem. Lett. 11, 2158–2164. doi: 10.1021/acs.jpclett.0c00065
Lv, B. Q., Weng, H. M., Fu, B. B., Wang, X. P., Miao, H., Ma, J., et al. (2015). Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5:031013. doi: 10.1103/PhysRevX.5.031013
Meng, W. Z., Zhang, X. M., He, T. L., Dai, X. F., Jin, L., and Liu, G. D. (2020b). Crystal Structures, electronic structures and topological signatures in equiatomic TT'X compounds (T = Sc, Zr, Hf; T' = Co, Pt, Pd, Ir, Rh; X = Al, Ga, Sn). J. Phy. Chem. C 124, 7378–7385. doi: 10.1021/acs.jpcc.0c00303
Meng, W. Z., Zhang, X. M., He, T. L., Dai, X. F., Jin, L., Liu, Y., et al. (2020a). Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J. Adv. Res. 24, 523–528. doi: 10.1016/j.jare.2020.05.026
Meng, W. Z., Zhang, X. M., Liu, Y., Dai, X. F., and Liu, G. D. (2020c). Lorentz-violating type-II Dirac fermions in full-Heusler compounds XMg2Ag (X=Pr, Nd, Sm). New J. Phys. 22:073061. doi: 10.1088/1367-2630/ab9d55
Miro, P., Audiffred, M., and Heine, T. (2014). An atlas of two-dimensional materials. Chem. Soc. Rev. 43, 6537–6554. doi: 10.1039/C4CS00102H
O'Brien, T. E., Diez, M., and Beenakker, C. W. J. (2016). Magnetic breakdown and Klein tunneling in a type-II Weyl semimetal. Phys. Rev. Lett. 116:236401. doi: 10.1103/PhysRevLett.116.236401
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Ruan, J., Jian, S. K., Yao, H., Zhang, H., Zhang, S. C., and Xing, D. (2016a). Symmetry-protected ideal 14 Weyl semimetal in HgTe-class materials. Nat. Commun. 7:11136. doi: 10.1038/ncomms11136
Ruan, J., Jian, S. K., Zhang, D., Yao, H., Zhang, H., Zhang, S. C., et al. (2016b). Ideal Weyl Semimetals in the Chalcopyrites CuTlSe2, AgTlTe2, AuTlTe2, and ZnPbAs2. Phys. Rev. Lett. 116:226801. doi: 10.1103/PhysRevLett.116.226801
Shekhar, C., Nayak, A. K., Sun, Y., Schmidt, M., Nicklas, M., Leermakers, I., et al. (2015). Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 11, 645–649. doi: 10.1038/nphys3372
Soluyanov, A. A., Gresch, D., Wang, Z. J., Wu, Q. S., Troyer, M., Dai, X., et al. (2015). Type-II Weyl semimetals. Nature 527, 495–498. doi: 10.1038/nature15768
Son, D. T., and Spivak, B. Z. (2013). Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88:104412. doi: 10.1103/PhysRevB.88.104412
Sun, Y., Wu, S. C., and Yan, B. H. (2015). Topological surface states and Fermi arcs of the noncentrosymmetric Weyl semimetals TaAs, TaP, NbAs, and NbP. Phys. Rev. B 92:115428. doi: 10.1103/PhysRevB.92.115428
Tian, S. J., Zhang, J. F., Li, C. H., Ying, T. P., Li, S. Y., Zhang, X., et al. (2019). Ferromagnetic van der Waals crystal VI3. J. Am. Chem. Soc. 141, 5326–5333. doi: 10.1021/jacs.8b13584
Togo, A., Oba, F., and Tanaka, I. (2008). First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-Type SiO2 at high pressures. Phys. Rev. B 78:134106. doi: 10.1103/PhysRevB.78.134106
Wan, X., Turner, A. M., Vishwanath, A., and Savrasov, S. Y. (2011). Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83:205101. doi: 10.1103/PhysRevB.83.205101
Wang, Z. J., Vergniory, M. G., Kushwaha, S., Hirschberger, M., Chulkov, E. V., Ernst, A., et al. (2016). Time-reversal-breaking weyl fermions in magnetic heusler alloys. Phys. Rev. Lett. 117:236401. doi: 10.1103/PhysRevLett.117.236401
Weng, H. M., Fang, C., Fang, Z., Bernevig, B. A., and Dai, X. (2015). Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5:011029. doi: 10.1103/PhysRevX.5.011029
Wu, Y., Mou, D. X., Jo, N. H., Sun, K. W., Huang, L. N., Bud'ko, S. L., et al. (2016). Observation of Fermi arcs in the type-II Weyl semimetal candidate WTe2. Phys. Rev. B 94:121113. doi: 10.1103/PhysRevB.94.121113
Xu, G., Weng, H. M., Wang, Z. J., Dai, X., and Fang, Z. (2011). Chern $HALL effect in HgCr2Se4. Phys. Rev. Lett. 107:186806. doi: 10.1103/PhysRevLett.107.186806
Yang, H. F., Yang, L. X., Liu, Z. K., Sun, Y., Chen, C., Peng, H., et al. (2019). Topological Lifshitz transitions and Fermi arc manipulation in Weyl semimetal NbAs. Nat. Commu. 10:3478. doi: 10.1038/s41467-019-11491-4
You, J. Y., Chen, C., Zhang, Z., Sheng, X. L., Yang, S. Y. A., and Su, G. (2019). Two-dimensionalWeyl half-semimetal and tunable quantum anomalous Hall effect. Phys. Rev. B 100:64408. doi: 10.1103/PhysRevB.100.064408
Yu, Z. M., Yao, Y., and Yang, S. Y. A. (2016). Predicted unusual magnetoresponse in type-II Weyl semimetals. Phys. Rev. Lett. 117:077202. doi: 10.1103/PhysRevLett.117.077202
Zhang, F., Mi, W., and Wang, X. (2020). Spin-dependent electronic structure and magnetic anisotropy of 2D ferromagnetic Janus Cr2I3X3 (X = Br, Cl) monolayers. Adv. Electron. Mater. 6:1900778. doi: 10.1002/aelm.201900778
Keywords: topological semimetal, 2D materials, first-principles calculations, half-metal, Weyl state
Citation: Jia T, Meng W, Zhang H, Liu C, Dai X, Zhang X and Liu G (2020) Weyl Fermions in VI3 Monolayer. Front. Chem. 8:722. doi: 10.3389/fchem.2020.00722
Received: 30 June 2020; Accepted: 14 July 2020;
Published: 26 August 2020.
Edited by:
Gokhan Surucu, Middle East Technical University, TurkeyCopyright © 2020 Jia, Meng, Zhang, Liu, Dai, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoming Zhang, emhhbmd4aWFvbWluZzg3QGhlYnV0LmVkdS5jbg==; Guodong Liu, Z2RsaXUxOTc4QDEyNi5jb20=
 Taoyuan Jia
Taoyuan Jia Xiaoming Zhang
Xiaoming Zhang Guodong Liu
Guodong Liu