Implementation of Laplace Transformed MP2 for Periodic Systems With Numerical Atomic Orbitals

We present an implementation of the canonical and Laplace-transformed formulation of the second-order Møller–Plesset perturbation theory under periodic boundary conditions using numerical atomic orbitals. To validate our approach, we show that our results of the Laplace-transformed MP2 correlation correction for the total energy and the band gap are in excellent agreement with the results of the canonical MP2 formulation. We have calculated the binding energy curve for the stacked trans-polyacetylene at the Hartree–Fock + MP2 level as a preliminary application.

1. Introduction

The second-order Møller–Plesset perturbation theory (MP2) is a post-Hartree–Fock approach to take the electron correlation effect into account. Although it is very simple in form, it can capture around 90% of the correlation energy (Bartlett and Stanton, 2007); so the MP2 method is still of high interest in the quantum chemistry (Schütz et al., 1999; Kobayashi and Nakai, 2006; Bartlett and Stanton, 2007) and solid-state physics communities (Suhai, 1983, 1992; Sun and Bartlett, 1996; Pisani et al., 2008; Marsman et al., 2009; Schäfer et al., 2018).

However, the O(N⁵) calculation scaling of the original (canonical) MP2 method has limited the application of the MP2 method in large systems. A series of algorithms have been proposed to speed up the calculations, such as local MP2 method (Saebø and Pulay, 1993; Pisani et al., 2005, 2008; Maschio, 2011), Lapace-transformed MP2 method (Häser and Almlöf, 1992; Häser, 1993; Ayala and Scuseria, 1999; Ayala et al., 2001; Schäfer et al., 2018), or resolution of the identity (RI) MP2 method (Katouda and Nagase, 2010; Ren et al., 2012). The local MP2 method proposed by Pulay (1983) and Saebø and Pulay (1993) has been efficiently implemented (Schütz et al., 1999) in the MOLPRO code for molecules, then the periodic version of the local MP2 method has been implemented (Pisani et al., 2005, 2008; Maschio, 2011) in the CRYSCOR code and in the CP2K code (Usvyat et al., 2018) for extended systems. Since the spatially localized orbitals or Wannier functions are adopted, the computational scaling of the local MP2 method is O(N). The Laplace-transformed MP2 method is originally proposed by Häser and Almlöf (1992) and Häser (1993), and have been implemented for both the molecule (Ayala and Scuseria, 1999) and extended systems (Ayala et al., 2001) in the GAUSSIAN suite of programs. The localized atomic orbitals have been employed and the computational scaling is also O(N). The Laplace-transformed MP2 method has been combined with the resolution of identity (RI) technique to further improve the computational efficiency (Izmaylov and Scuseria, 2008). Further rigorous integral screening scheme (Lambrecht et al., 2005) has been introduced on top of the Laplace-transformed MP2 to perform the calculations for a system comprising 1,000 atoms (Doser et al., 2008). Recently, the Laplace-transformed MP2 method has also been implemented (Schäfer et al., 2018) in VASP using stochastic orbitals.

So far, most of the implementations of the MP2 are adopting the Gaussian-type orbital (GTO) as the basis set. However, in the calculation of the periodic system, too diffused GTO with a long tail will increase the number of cells in the auxiliary supercell, and therefore the computational cost will increase. Compared with GTO, the numerical atomic orbital (NAO) is strictly localized, which could naturally leads to lower order scaling of computational time vs. system size. Here in this work, we have implemented the canonical MP2 and Laplace-transformed MP2 for the extended systems using NAO, and the results obtained by these two approaches are consistent. Furthermore, we have investigated the MP2 correlation correction to the band structure with both the canonical and Laplace-transformed formulation; our implementation has been validated by comparing the MP2 correlation correction of the total energy and the band gap to the literature values.

The remainder of this paper is organized as follows. The fundamental theoretical framework and the implementation details for the canonical and Laplace transformed MP2 are presented in section 2. The benchmark calculations are presented in section 3. In section 4, we summarize our main achievement and highlight the possible future research direction related to this work.

2. Method

2.1. Numerical Atomic Orbitals

The numerical atomic orbital is defined by a product of a numerical radial function and a spherical harmonic

$\begin{array}{ll}{\chi }_{Ilmn}(\text{r})={\phi }_{Iln}(r){\text{Y}}_{lm}(\widehat{r}).& (1)\end{array}$

By solving the one-dimension radial Schrödinger equation

$\begin{array}{ll}(-\frac{1}{2}\frac{1}{r}\frac{{\text{d}}^2}{\text{d}{r}^2}r+\frac{l(l+1)}{2r^2}+V(r)+V_{cut}){\phi }_{Iln}(r)={ϵ}_l{\phi }_{Iln}(r),& (2)\end{array}$

we can get the radial part of the numerical atomic orbital φ_Iln(r), where V(r) denotes the electrostatic potential for orbital φ_Iln(r), and V_cut ensures a smooth decay of each radial function, which is strictly zero outside a confining radius r_cut.

In order to perform the Hartree–Fock and MP2 calculation, the electron repulsion integrals (ERIs) are needed:

$\begin{array}{ll}({\chi }_{\mu }{\chi }_{\nu }|{\chi }_{\lambda }{\chi }_{\sigma })={\displaystyle \int {\displaystyle \int \frac{{\chi }_{\mu }(r){\chi }_{\nu }(r){\chi }_{\lambda }(r^{\prime }){\chi }_{\sigma }(r^{\prime })}{|r-r^{\prime }|}}}drd{r}^{\prime }& (3)\end{array}$

we use NAO2GTO scheme described to calculate them as shown in the following section.

2.2. The NAO2GTO Scheme to Calculate ERIs

In the NAO2GTO scheme, we fit the NAO with GTOs, then we calculate the ERIs analytically; in this way, the strict cutoff of the atomic orbitals is satisfied with NAO and the construction of Hartree-Fock exchange (HFX) matrix can scale linearly with the system sizes (Shang et al., 2011). Since the angular part of the NAOs is spherical harmonic, while the GTOs are Cartesian harmonic function, a transformation between the Cartesian and spherical harmonic functions is performed within the NAO2GTO scheme.

2.3. Canonical MP2 Formulation

In extended systems, the normalized crystal orbital ψ_i(k, r) is a linear combination of Bloch functions ϕ_μ(k, r):

$\begin{array}{ll}{\psi }_i(\text{k},\text{r})={\displaystyle \sum _{\mu }}{C}_{\mu ,i}(\text{k}){\varphi }_{\mu }(\text{k},\text{r})& (4)\end{array}$

$\begin{array}{ll}{\varphi }_{\mu }(k,r)=\frac{1}{\sqrt{N}}{\displaystyle \sum _R{\chi }_{\mu }^R}(r)e^{ik·(R+r_{\mu })}& (5)\end{array}$

in which N is the number of cells in extended systems, μ is the index of the atomic orbitals, i refers to the crystal orbital index, R denotes the cells in the extended systems (auxiliary supercell), ${\chi }_{\mu }^{\text{R}}(\text{r})={\chi }_{\mu }(\text{r}-\text{R}-{\text{r}}_{\mu })$ refers to the atomic orbital whose center is displaced from the cell R by r_μ, and C_{μ, i}(k) are the coefficients of the crystal orbitals.

The MP2 correlation correction for the total energy of the unit cell is

$\begin{array}{ll}\begin{array}{ll}{E}_{\text{mp2}}\hfill & =-\frac{1}{N}{\displaystyle \sum _i{\displaystyle \sum _j{\displaystyle \sum _a{\displaystyle \sum _b\frac{1}{V_k^4}}}}}{\displaystyle \int d{k}_i}{\displaystyle \int d{k}_j}{\displaystyle \int d{k}_a}\hfill \\ \hfill & {\displaystyle \int d{k}_b}\frac{(IA|JB){[2(IA|JB)-(IB|JA)]}^{*}}{{ϵ}_a(k_a)+{ϵ}_b(k_b)-{ϵ}_i(k_i)-{ϵ}_j(k_j)}\hfill \end{array}& (6)\end{array}$

in which we use labeling i,j for occupied orbitals and a,b for unoccupied orbitals. I/J refer to the composite index (i,k_i)/(j,k_j), V_k is the volume of the Brillouin zone, and ϵ_i(k_i) is the Hartree–Fock eigenvalue for the eigenstate ψ_i(k_i). It should be noted that by using the identity ($\sum _{\text{R}}expi\text{k}·\text{R}=N{\delta }_{\text{k},0}$) derived with the Born–von Karman periodic boundary condition, we can remove one dimension integration over k_j since k_j = T(−k_i + k_a + k_b), where T is the translation operator. The formalism of summation over 3-fold k points and over 4-fold k points (Equation 6) give the same results.

Similarly, the MP2 correlation correction (${ϵ}_g{({\text{k}}_g)}^{(2)}$) to the Hartree–Fock eigenstate ψ_g(k_g) can be written as

$\begin{array}{ll}{ϵ}_g{({\text{k}}_g)}^{(2)}={ϵ}_g{({\text{k}}_g)}^{\text{MP2}}-{ϵ}_g{({\text{k}}_g)}^{\text{HF}}=U(g)+V(g)& (7)\end{array}$

$\begin{array}{ll}U(g)=-{\displaystyle \sum _{i,a,b}\frac{1}{V_k^3}}{\displaystyle \int d{k}_i}{\displaystyle \int d{k}_a}{\displaystyle \int d{k}_b}\frac{(IA|GB){[2(IA|GB)-(IB|GA)]}^{*}}{{ϵ}_a(k_a)+{ϵ}_b(k_b)-{ϵ}_i(k_i)-{ϵ}_g(k_g)}& (8)\end{array}$

$\begin{array}{ll}V(g)={\displaystyle \sum _{i,j,a}\frac{1}{V_k^3}}{\displaystyle \int d{k}_i}{\displaystyle \int d{k}_j}{\displaystyle \int d{k}_a}\frac{(IA|JG){[2(IA|JG)-(IG|JA)]}^{*}}{{ϵ}_a(k_a)+{ϵ}_g(k_g)-{ϵ}_i(k_i)-{ϵ}_j(k_j)}& (9)\end{array}$

When ψ_g(k_g) is the occupied orbital at the valance band maximum (VBM), we can see U(g) < 0, V(g) > 0 and |U(g)| < |V(g)|, then the MP2 renormalization of the VBM is positive and will move the VBM orbital upward. When ψ_g(k_g) is the unoccupied orbital at the conduction band minimum (CBM), we have |U(g)| > |V(g)|, so the MP2 renormaliztion of the CBM is negative, and will move the CBM downward. In total, the MP2 renormalization of the band gap is negative, and the MP2 band gap is smaller than the Hartree-Fock band gap.

2.4. Laplace-Transformed MP2 Formulation

The Laplace transform is defined as:

$\begin{array}{ll}\frac{1}{x}={\displaystyle {\int }_0^{\infty }}{e}^{-xt}\text{d}t,x>0& (10)\end{array}$

which can be used to remove the denominator in the canonical MP2 formulation:

$\begin{array}{ll}\frac{1}{{ϵ}_a(k_a)+{ϵ}_b(k_b)-{ϵ}_i(k_i)-{ϵ}_j(k_j)}={\displaystyle \int e^{[{ϵ}_i(k_i)+{ϵ}_j(k_j)-{ϵ}_a(k_a)-{ϵ}_b(k_b)]t}\text{d}t}& (11)\end{array}$

The integration in Equation (10) can either be done by using a least square fitting method (Häser and Almlöf, 1992; Häser, 1993) or by using a Jacobian transform (Ayala and Scuseria, 1999; Kobayashi and Nakai, 2006) of the Laplace integration variable in order to transform the integration range [0, ∞) into the finite range [0, 1]. Here, we use the transform as follows:

$\begin{array}{ll}{\displaystyle {\int }_0^{\infty }}{e}^{-xt}\text{d}t={\displaystyle {\int }_0^1}{e}^{-xt}\frac{\text{d}t}{\text{d}r}\text{d}r={\displaystyle {\int }_0^1}f(r)\text{d}r& (12)\end{array}$

in which the Jacobian transform is

$\begin{array}{ll}t=\frac{r^3-0.9r^4}{{(1-r)}^2}+r^{2}tan(\frac{\pi r}{2})& (13)\end{array}$

Then the final integration (${\int }_0^{1}f(r)\text{d}r$) in Equation (12) in evaluated with Romberg quadrature method, which uses refinements of the extended trapezoidal rule to reduce error in definite integrals.

In this way, the E_mp2 correlation correction energy can be written as a new integration form:

$\begin{array}{l}{E}_{\text{mp2}}=-{\displaystyle \int d}t{\displaystyle \sum _{\mu 0,\nu R_{\nu },\lambda R_{\lambda },\sigma R_{\sigma }}{T}_{\mu ,\lambda ,\nu ,\sigma }^{0R_{\lambda }{R}_{\nu }{R}_{\sigma }}}(t)[2({\chi }_{\mu }^0{\chi }_{\lambda }^{R_{\lambda }}|{\chi }_{\nu }^{R_{\nu }}{\chi }_{\sigma }^{R_{\sigma }})\\ -({\chi }_{\mu }^0{\chi }_{\sigma }^{R_{\sigma }}|{\chi }_{\nu }^{R_{\nu }}{\chi }_{\lambda }^{R_{\lambda }})]& (14)\end{array}$

where μ,ν,σ,λ and the following λ,δ,τ,κ refer to the indexes of the atomic orbitals. $({\chi }_{\mu }^0{\chi }_{\sigma }^{{\text{R}}_{\sigma }}|{\chi }_{\nu }^{{\text{R}}_{\nu }}{\chi }_{\lambda }^{{\text{R}}_{\lambda }})$ is the electron repulsion integrals defined as

$\begin{array}{ll}({\chi }_{\mu }^0{\chi }_{\sigma }^{R_{\sigma }}|{\chi }_{\nu }^{R_{\nu }}{\chi }_{\lambda }^{R_{\lambda }})={\displaystyle \int {\displaystyle \int \frac{{\chi }_{\mu }^0(r){\chi }_{\sigma }^{R_{\sigma }}(r){\chi }_{\nu }^{R_{\nu }}(r^{\prime }){\chi }_{\lambda }^{R_{\lambda }}(r^{\prime })}{|r-r^{\prime }|}}}drd{r}^{\prime }.& (15)\end{array}$

and

$\begin{array}{l}{T}_{\mu ,\lambda ,\nu ,\sigma }^{{\text{R}}_{\mu }{\text{R}}_{\lambda }{\text{R}}_{\nu }{\text{R}}_{\sigma }}(t)=\\ {\displaystyle \sum _{\gamma {\text{R}}_{\gamma },\delta {\text{R}}_{\delta },\tau {\text{R}}_{\tau },\kappa {\text{R}}_{\kappa }}}& X_{\mu \gamma }^{{\text{R}}_{\mu }{\text{R}}_{\gamma }}{X}_{\nu \delta }^{{\text{R}}_{\nu }{\text{R}}_{\delta }}{Y}_{\lambda \kappa }^{{\text{R}}_{\lambda }{\text{R}}_{\kappa }}{Y}_{\sigma \tau }^{{\text{R}}_{\sigma }{\text{R}}_{\tau }}({\chi }_{\gamma }^{{\text{R}}_{\gamma }}{\chi }_{\kappa }^{{\text{R}}_{\kappa }}|{\chi }_{\delta }^{{\text{R}}_{\delta }}{\chi }_{\tau }^{{\text{R}}_{\tau }})& (16)\end{array}$

The 4-fold k points are treated independently within $X_{\gamma \mu }^{{\text{R}}_{\gamma }{\text{R}}_{\mu }}$ and $Y_{\lambda \kappa }^{{\text{R}}_{\lambda }{\text{R}}_{\kappa }}$:

$\begin{array}{ll}{X}_{\gamma \mu }^{R_{\gamma }{R}_{\mu }}={\displaystyle \sum _i^{occ}\frac{1}{V_k}}{\displaystyle \int d{k}_i{C}_{\gamma i}^{*}(k_i)C_{\mu i}(k_i)e^{({ϵ}_i-{ϵ}_f)t}{e}^{i{k}_i(R_{\mu }-R_{\gamma })}}& (17)\end{array}$

$\begin{array}{ll}{Y}_{\lambda \kappa }^{R_{\lambda }{R}_{\kappa }}={\displaystyle \sum _a^{unocc}\frac{1}{V_k}}{\displaystyle \int d{k}_a}{C}_{\lambda a}^{*}(k_a)C_{\kappa a}(k_a)e^{-({ϵ}_a-{ϵ}_f)t}{e}^{i{k}_a(R_{\kappa }-R_{\lambda })}& (18)\end{array}$

In this way, the 4-fold integration over k-points in Equation (6) can be reduced to 1-dimensional k-points integral as shown in Equations (17) and (18). Furthermore, the locality of the atomic basis function can be adopted for the calculation of $T_{\mu ,\lambda ,\nu ,\sigma }^{{\text{R}}_{\mu }{\text{R}}_{\lambda }{\text{R}}_{\nu }{\text{R}}_{\sigma }}$ and electron repulsion integrals, and the total computational scaling could be O(N · N_k) if the distant screening between these ERIs are applied. Here in this work, such distance screening has not been used, so our implementation results in a $O(N^2·N_k)$ scaling. It is worth noting that in order to keep the exponential value ($e^{({ϵ}_i)t}$) in Equation (17)/Equation (18) to be smaller than unity, we have inserted the Fermi energy level into the exponential factor ($e^{({ϵ}_i-{ϵ}_f)t}$) in order to make the calculation to be more stable.

Based on Equations (7) and (10), we have the Laplace-transformed MP2 correlation correction (${ϵ}_g{({\text{k}}_g)}^{(2)}$) for the eigenstate:

$\begin{array}{ll}\begin{array}{ll}{ϵ}_g{(k_g)}^{(2)}\hfill & ={\displaystyle \int dt{\displaystyle \sum _{\mu 0,\nu R_{\nu },\lambda R_{\lambda },\sigma R_{\sigma }}{G}_{\mu ,\lambda ,\nu ,\sigma }^{0R_{\nu }{R}_{\lambda }{R}_{\sigma }}}(t)[2({\chi }_{\mu }^0{\chi }_{\lambda }^{R_{\lambda }}|{\chi }_{\nu }^{R_{\nu }}{\chi }_{\sigma }^{R_{\sigma }})}\hfill \\ \hfill & -({\chi }_{\mu }^0{\chi }_{\sigma }^{R_{\sigma }}|{\chi }_{\nu }^{R_{\nu }}{\chi }_{\lambda }^{R_{\lambda }})]\hfill \end{array}& (19)\end{array}$

$\begin{array}{l}{G}_{\mu ,\lambda ,\nu ,\sigma }^{{\text{R}}_{\mu }{\text{R}}_{\lambda }{\text{R}}_{\nu }{\text{R}}_{\sigma }}(t)={\displaystyle \sum _{\gamma {\text{R}}_{\gamma },\delta {\text{R}}_{\delta },\tau {\text{R}}_{\tau },\kappa {\text{R}}_{\kappa }}}{X}_{\mu \gamma }^{{\text{R}}_{\mu }{\text{R}}_{\gamma }}{Y}_{\lambda \kappa }^{{\text{R}}_{\lambda }{\text{R}}_{\kappa }}({\chi }_{\gamma }^{{\text{R}}_{\gamma }}{\chi }_{\kappa }^{{\text{R}}_{\kappa }}|{\chi }_{\delta }^{{\text{R}}_{\delta }}{\chi }_{\tau }^{{\text{R}}_{\tau }})\\ \times (-W_{\nu \delta }^{{\text{R}}_{\nu }{\text{R}}_{\delta }}{Y}_{\sigma \tau }^{{\text{R}}_{\sigma }{\text{R}}_{\tau }}+X_{\nu \delta }^{{\text{R}}_{\nu }{\text{R}}_{\delta }}{Z}_{\sigma \tau }^{{\text{R}}_{\sigma }{\text{R}}_{\tau }})& (20)\end{array}$

$\begin{array}{ll}{W}_{\gamma \mu }^{{\text{R}}_{\gamma }{\text{R}}_{\mu }}=C_{\gamma g}^{*}({\text{k}}_g)C_{\mu g}({\text{k}}_g)e^{({ϵ}_g)t}{e}^{i{\text{k}}_g({\text{R}}_{\mu }-{\text{R}}_{\gamma })}& (21)\end{array}$

$\begin{array}{ll}{Z}_{\lambda \kappa }^{{\text{R}}_{\lambda }{\text{R}}_{\kappa }}=C_{\lambda g}^{*}({\text{k}}_g)C_{\kappa g}({\text{k}}_g)e^{-({ϵ}_g)t}{e}^{i{\text{k}}_g({\text{R}}_{\kappa }-{\text{R}}_{\lambda })}& (22)\end{array}$

Similarly, in order to keep the exponential value to be smaller than unity and avoid computational divergence, we inserted the VBM/CBM value into the exponential factor when calculated the MP2 reformulation of the VBM/CBM.

The canonical and Laplace-transformed MP2 methods described above have been implemented in the Order-N performance HONPAS code (Qin et al., 2014).

3. Results

In order to validate our implementation, we perform benchmark calculations for 1-dimensional systems. We use norm-conserving pseudopotentials generated with the Troullier–Martins scheme to represent the interaction between core ion and valence electrons. The single-zeta (SZ), double-zeta (DZ), and double-zeta polarized (DZP) basis sets are generated using SIESTA. Then the NAOs are fitted with GTOs to perform the Hartree–Fock calculation as discussed in Shang et al. (2011).

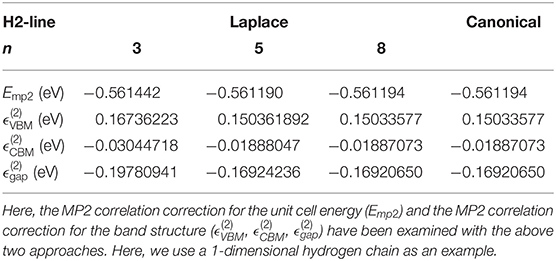
First, we use a 1-dimensional hydrogen chain as an example to make the comparison between the results of canonical MP2 and those of Laplace-transformed MP2. The lattice parameter for the 1-dimensional H chain is set to 2.6 Å, and the H-H bond length is set to 1.346 Å. The SZ basis set is adopted, so that there are only two atomic orbitals in the unit cell. The Brillouin zone is sampled by 1 × 1 × 6 k-points. The unit cell is a 20 × 20 × 2.6 Åbox, and the real-space integration mesh is set to be 100 Ry. In the Laplace-transformed MP2 method, the Romberg method is adopted to perform the final integration. The accuracy of integration results depends on the order of Romberg integration (n), since the results of the Romberg integration are obtained in a recursive manner, $R(n,j)=R(n,j-1)+\frac{R(n,j-1)-R(n-1,j-1)}{4^{j-1}-1}$. As shown in Table 1, when the order of Romberg integration increases from 3 to 8, the MP2 correlation correction for the unit cell energy (E_mp2) as well as the MP2 correlation correction for the band structure (${ϵ}_{\text{VBM}}^{(2)}$, ${ϵ}_{\text{CBM}}^{(2)}$, ${ϵ}_{\text{gap}}^{(2)}$) are converged to the results of canonical MP2. When using the media precision parameter (n = 5) in Laplace- transformed MP2, we get a absolute/relative error of 4 × 10⁻⁶ eV/0.0007% for the correlation of the unit cell energy (E_mp2), and we get a absolute/relative error of 3 × 10⁻⁵ eV/0.02% for the MP2 correlation correction for the band gap (${ϵ}_{\text{gap}}^{(2)}$). Overall, we find an excellent agreement between the Laplace-transformed MP2 and the canonical MP2 benchmark results.

TABLE 1

Table 1. The comparison between the results of canonical MP2 and those of Laplace-transformed MP2.

We also examine the relative error between the results of Laplace-transformed MP2 and those of canonical MP2 with respect to the basis set size (SZ, DZ, DZP), as shown in Table 2 with ethylene molecule as an example. Again, we find an excellent agreement between the Laplace-transformed MP2 and the canonical MP2 benchmark results.

TABLE 2

Table 2. The relative error between the results of canonical MP2 and those of Laplace-transformed MP2 with different basis set.

Second, we perform the Laplace-transformed MP2 calculation for the 1D polymer trans-polyacetylene as shown in Table 3. The order of Romberg integration is set to be n = 5. The SZ basis set is adopted in our calculation. The Brillouin zone is sampled by 1 × 1 × 30 k-points. The real-space integration mesh is set to be 200 Ry. We compare our calculated MP2 correlation correction for the total energy per unit cell with the one obtained in Sun and Bartlett (1996). The G3 geometry parameters as listed in Sun and Bartlett (1996) are adopted to keep the geometry to be the same for comparison. We get an absolute/relative error of 0.26 eV/8% for the correlation correction of the unit cell energy (E_mp2). The difference comes from the usage of the different basis set, since in Sun and Bartlett (1996), the STO-3G basis set is used, whose shape is different from the SZ basis that we are using. For a similar reason, when using the same G6 geometry parameter of trans-polyacetylene (Sun and Bartlett, 1996), we get an absolute/relative error of 0.09 eV/7% for the correlation correction of the band gap (${ϵ}_{\text{gap}}^{(2)}$) when compared with Sun's result.

TABLE 3

Table 3. The comparison between our results and those from the literature (Sun and Bartlett, 1996).

We then investigate the performance and scaling of our implementation, and we show timings for the trans-polyacetylene molecules with variable number of atoms in Figure 1. We find a linear scaling for the calculation of ERIs and an O(N²) scaling for the calculation of the Laplace-transformed MP2. This is not too surprising, since we can see from Equation (14) that there are two loops over the ERIs for the calculation of Laplace-transformed MP2, so we get the O(N²) scaling.

FIGURE 1

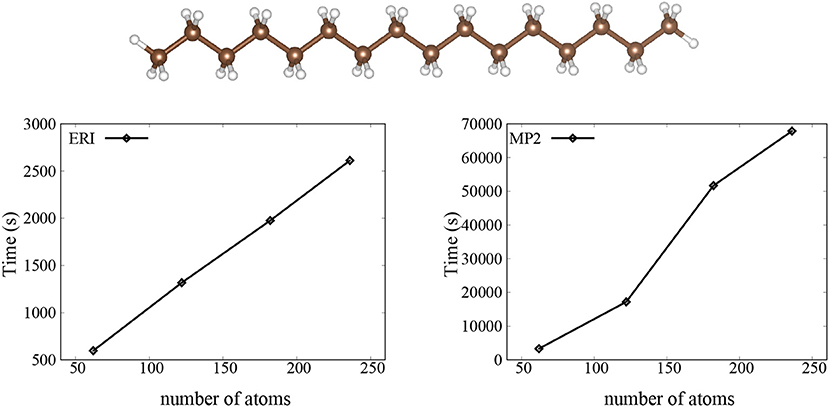
Figure 1. The CPU time for the ERI and MP2 calculation using SZ basis set. Here, the trans-polyacetylene molecules are used as the test systems.

Finally, we show the calculated binding-energy curves as functions of the distance between two trans-polyacetylene chains with the PBC-MP2 method. Although the MP2 theory gives overestimation of the dispersion interaction energy (Tkatchenko et al., 2009), it is still a superior starting point for the dispersion correction compared to Hartree–Fock and semi-local density functional theory (DFT). As shown in Figure 2, the MP2 method results in a binding states. On the contrary, Hartree–Fock and PBE functional fail to identify any binding between the two chains. We can see in Figure 2 that the energy profile calculated with Hartree–Fock and PBE functional shows a repulsive behavior as the two chains are brought closer together.

FIGURE 2

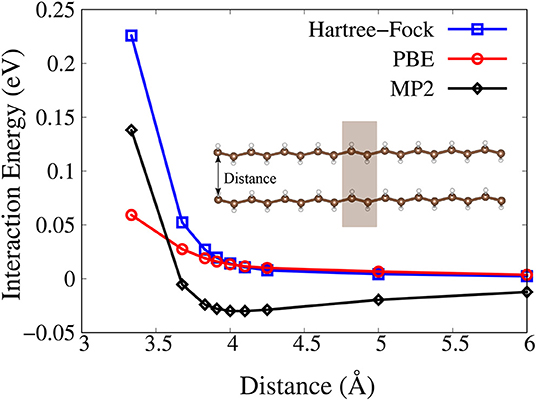
Figure 2. Interaction energy as functions of the distance between two trans-polyacetylene chains as predicted by the Hartree-Fock (blue), PBE (red), and MP2 (black) method. The unit cell is marked with shaded box.

4. Conclusions

We have implemented the canonical and Laplace-transformed algorithms to calculate the MP2 correlation correction for the total energy and the band gap of periodic systems in HONPAS code with numerical atomic orbitals. The results obtained by the canonical MP2 and Laplace-transformed MP2 are consistent with each other. We have also validated the implementation by comparing the results with the literature data. We have studied the binding-energy curves for the two stacked trans-polyacetylene chains, which shows the MP2 method can well describe the correlation energy and the long-range van der Waals interactions. Future work will address the application of the Laplace-transformed MP2 method to 3-dimensional periodic systems in the HONPAS code.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

JY designed and directed the project. HS developed the theoretical formalism, carried out the implementation, and performed the numerical simulations. Both JY and HS contributed to the final version of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by CARCH4205, CARCH4411, and by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDC01040100) and by National Natural Science Foundation of China (Grant No. 22003073).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

HS acknowledges Georg Kresse for inspiring discussions. HS thanks the Tianhe-2 Supercomputer Center for computational resources.

References

Ayala, P. Y., Konstantin, K. N., Kudin, N., and Scuseria, G. E. (2001). Atomic orbital laplace-transformed second-order Møller-plesset theory for periodic systems. J. Chem. Phys. 115, 9698–9707. doi: 10.1063/1.1414369

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayala, P. Y., and Scuseria, G. E. (1999). Linear scaling second-order Moller–Plesset theory in the atomic orbital basis for large molecular systems. J. Chem. Phys. 110, 3660–3671. doi: 10.1063/1.478256

CrossRef Full Text | Google Scholar

Bartlett, R. J., and Stanton, J. F. (2007). “Applications of post-hartree-fock methods: a tutorial,” in Reviews in Computational Chemistry, eds K.B. Lipkowitz and D.B. Boyd. doi: 10.1002/9780470125823.ch2

CrossRef Full Text | Google Scholar

Doser, B., Lambrecht, D. S., and Ochsenfeld, C. (2008). Tighter multipole-based integral estimates and parallel implementation of linear-scaling AO–MP2 theory. Phys. Chem. Chem. Phys. 10, 3335–3344. doi: 10.1039/b804110e

PubMed Abstract | CrossRef Full Text | Google Scholar

Häser, M. (1993). Møller-Plesset (MP2) perturbation theory for large molecules. Theor. Chim. Acta 87, 147–173. doi: 10.1007/BF01113535

CrossRef Full Text | Google Scholar

Häser, M., and Almlöf, J. (1992). Laplace transform techniques in Møller-Plesset perturbation theory. J. Chem. Phys. 96, 489–494. doi: 10.1063/1.462485

CrossRef Full Text | Google Scholar

Izmaylov, A. F., and Scuseria, G. E. (2008). Resolution of the identity atomic orbital Laplace transformed second order Møller–Plesset theory for nonconducting periodic systems. Phys. Chem. Chem. Phys. 10, 3421–3429. doi: 10.1039/b803274m

PubMed Abstract | CrossRef Full Text | Google Scholar

Katouda, M., and Nagase, S. (2010). Application of second-order Møller-Plesset perturbation theory with resolution-of-identity approximation to periodic systems. J. Chem. Phys. 133, 1–9. doi: 10.1063/1.3503153

PubMed Abstract | CrossRef Full Text | Google Scholar

Kobayashi, M., and Nakai, H. (2006). Implementation of Surján's density matrix formulae for calculating second-order Møller–Plesset energy. Chem. Phys. Lett. 420, 250–255. doi: 10.1016/j.cplett.2005.12.088

CrossRef Full Text | Google Scholar

Lambrecht, D. S., Doser, B., and Ochsenfeld, C. (2005). Rigorous integral screening for electron correlation methods. J. Chem. Phys. 123:184102. doi: 10.1063/1.2079987

CrossRef Full Text | Google Scholar

Marsman, M., Grüneis, A., Paier, J., and Kresse, G. (2009). Second-order Møller-Plesset perturbation theory applied to extended systems. I. Within the projector-augmented-wave formalism using a plane wave basis set. J. Chem. Phys. 130, 1–10. doi: 10.1063/1.3126249

PubMed Abstract | CrossRef Full Text | Google Scholar

Maschio, L. (2011). Local MP2 with density fitting for periodic systems: a parallel implementation. J. Chem. Theory Comput. 7, 2818–2830. doi: 10.1021/ct200352g

PubMed Abstract | CrossRef Full Text | Google Scholar

Pisani, C., Busso, M., Capecchi, G., Casassa, S., Dovesi, R., Maschio, L., et al. (2005). Local-MP2 electron correlation method for nonconducting crystals. J. Chem. Phys. 122:94113. doi: 10.1063/1.1857479

PubMed Abstract | CrossRef Full Text | Google Scholar

Pisani, C., Maschio, L., Casassa, S., Halo, M., Schütz, M., and Usvyat, D. (2008). Periodic local MP2 method for the study of electronic correlation in crystals: Theory and preliminary applications. J. Comput. Chem. 29, 2113–2124. doi: 10.1002/jcc.20975

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulay, P. (1983). Localizability of dynamic electron correlation. Chem. Phys. Lett. 100, 151–154. doi: 10.1016/0009-2614(83)80703-9

CrossRef Full Text | Google Scholar

Qin, X., Shang, H., Xiang, H., Li, Z., and Yang, J. (2014). HONPAS: a linear scaling open-source solution for large system simulations. Int. J. Quantum Chem. 115, 647–655. doi: 10.1002/qua.24837

CrossRef Full Text | Google Scholar

Ren, X., Rinke, P., Blum, V., Wieferink, J., Tkatchenko, A., Sanfilippo, A., et al. (2012). Resolution-of-identity approach to Hartree–Fock, hybrid density functionals, RPA, MP2 and GW with numeric atom-centered orbital basis functions. New J. Phys. 14:053020. doi: 10.1088/1367-2630/14/5/053020

CrossRef Full Text | Google Scholar

Saebø, S., and Pulay, P. (1993). Local treatment of electron correlation. Annu. Rev. Phys. Chem. 44, 213–236. doi: 10.1146/annurev.pc.44.100193.001241

CrossRef Full Text | Google Scholar

Schäfer, T., Ramberger, B., and Kresse, G. (2018). Laplace transformed MP2 for three dimensional periodic materials using stochastic orbitals in the plane wave basis and correlated sampling. J. Chem. Phys. 148:064103. doi: 10.1063/1.5016100

PubMed Abstract | CrossRef Full Text | Google Scholar

Schütz, M., Hetzer, G., and Werner, H.-J. (1999). Low-order scaling local electron correlation methods. I. Linear scaling local MP2. J. Chem. Phys. 111, 5691–5705. doi: 10.1063/1.479957

CrossRef Full Text | Google Scholar

Shang, H., Li, Z., and Yang, J. (2011). Implementation of screened hybrid density functional for periodic systems with numerical atomic orbitals: basis function fitting and integral screening. J. Chem. Phys. 135:034110. doi: 10.1063/1.3610379

PubMed Abstract | CrossRef Full Text | Google Scholar

Suhai, S. (1983). Perturbation theoretical investigation of electron correlation effects in infinite metallic and semiconducting polymers. Int. J. Quantum Chem. 23, 1239–1256. doi: 10.1002/qua.560230414

CrossRef Full Text | Google Scholar

Suhai, S. (1992). Structural and electronic properties of infinitecis andtrans polyenes: perturbation theory of electron correlation effects. Int. J. Quantum Chem. 42, 193–216. doi: 10.1002/qua.560420112

CrossRef Full Text | Google Scholar

Sun, J., and Bartlett, R. J. (1996). Second-order many-body perturbation-theory calculations in extended systems. J. Chem. Phys. 104, 8553–8565. doi: 10.1063/1.471545

CrossRef Full Text | Google Scholar

Tkatchenko, A., DiStasio, R. A., Head-Gordon, M., and Scheffler, M. (2009). Dispersion-corrected Moller–Plesset second-order perturbation theory. J. Chem. Phys. 131:094106. doi: 10.1063/1.3213194

PubMed Abstract | CrossRef Full Text | Google Scholar

Usvyat, D., Maschio, L., and Schütz, M. (2018). Periodic and fragment models based on the local correlation approach. WIREs Comput. Mol. Sci. 8:e1357. doi: 10.1002/wcms.1357

CrossRef Full Text | Google Scholar