Exciton Modulation in Perylene-Based Molecular Crystals Upon Formation of a Metal-Organic Interface From Many-Body Perturbation Theory

Excited-state processes at organic-inorganic interfaces consisting of molecular crystals are essential in energy conversion applications. While advances in experimental methods allow direct observation and detection of exciton transfer across such junctions, a detailed understanding of the underlying excitonic properties due to crystal packing and interface structure is still largely lacking. In this work, we use many-body perturbation theory to study structure-property relations of excitons in molecular crystals upon adsorption on a gold surface. We explore the case of the experimentally-studied octyl perylene diimide (C8-PDI) as a prototypical system, and use the GW and Bethe-Salpeter equation (BSE) approach to quantify the change in quasiparticle and exciton properties due to intermolecular and substrate screening. Our findings provide a close inspection of both local and environmental structural effects dominating the excitation energies and the exciton binding and nature, as well as their modulation upon the metal-organic interface composition.

Organic-inorganic interfaces play a key role in energy conversion and transfer processes (Wasielewski, 1992; Grätzel, 2001). Photoexcitations in the organic component typically generate bound electron and hole pairs, i.e., excitons, which serve as the main energy carriers and can effectively transfer energy across the interface (Ginley and Cahen, 2011). In particular, organic molecular crystals, composed of aromatic organic molecules bound together by van der Waals interactions (Klauk, 2006; Kronik and Neaton, 2016), are widely studied due to their easily adjustable characteristics and tunable excitonic properties (Sato et al., 1981; Smith and Michl, 2013; Luo et al., 2020), with relatively long diffusion lengths (Wan et al., 2015; Penwell et al., 2017; Schnedermann et al., 2019; Delor et al., 2020) stemming from their crystal structure, for example through singlet fission processes and the formation of long-lived triplet states (Wilson et al., 2013; Rao and Friend, 2017; Gish et al., 2019). The coupling between excitonic properties in molecular crystals and their underlying crystal packing and symmetry offers desirable tunability of their exciton relaxation processes and can lead to extended energy-transfer efficiency through material and interface design (Refaely-Abramson et al., 2017; Troisi and Orlandi, 2005; Cocchi et al., 2018; Arias et al., 2016; Cudazzo et al., 2012; Rangel et al., 2016). Of particular interest are the family of perylene diimide (PDI) molecular crystals, composed of a perylene body and an imide group and assembled by π-π interaction (Würthner et al., 2016; Schierl et al., 2018; Krieg et al., 2019; Santosh et al., 2010). Crystal packing and symmetry in PDI crystals vary strongly depending on their residues, allowing structural control of the exciton nature and diffusion length (Würthner et al., 2016; Schierl et al., 2018; Eaton et al., 2013; Zhang et al., 2018; Piland and Bardeen, 2015; Hestand and Spano, 2018; Oleson et al., 2019; Carter and Grossman, 2020; Wei et al., 2020), for example via a change in the imide substitution (Le et al., 2018; Felter et al., 2019). A commonly studied PDI crystal in organic optoelectronics is octyl-PDI (C8-PDI) (Felter et al., 2019; O’Brien et al., 2011; Krauss et al., 2009), shown in Figure 1A. The intermolecular interaction nature in this crystal gives rise to strongly bound excitons on one hand, and significant exciton dispersion on the other, making it a natural candidate for efficient exciton transfer upon formation of an organic-inorganic interface (Le et al., 2018; Cotton et al., 2020). In particular, C8-PDI single crystals and monolayers serve as a gate dielectric interface in working metal-organic devices, and the subtle details of interface design and structural inhomogeneity on charge and energy transfer efficiency within such junctions have been widely explored (Youn et al., 2012; Liscio et al., 2013; Ciccullo et al., 2015).

FIGURE 1

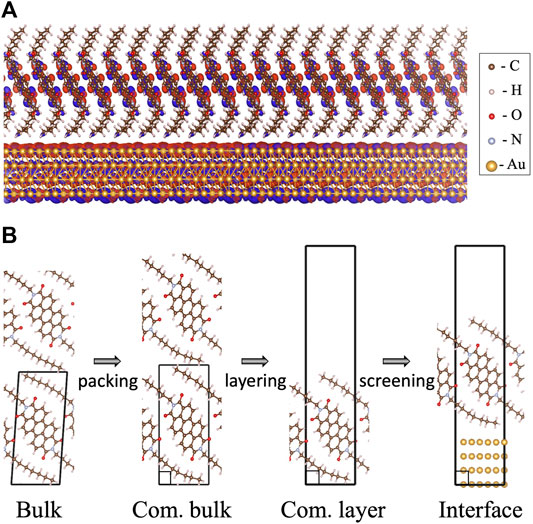
FIGURE 1. (A) The examined C8-PDI@Au metal-organic interface composed of an organic monolayer, commensurate with a four-layer Au (111) surface. The charge distribution computed for the lowest bound singlet exciton is also shown. (B) The different structural modifications of the interface compositions as examined in this work: C8-PDI intermolecular packing, layering, and adsorption on Au surface. The four main structures discussed in the text are termed as “bulk”, for the experimental triclinic crystal structure (Briseno et al., 2007); “com. bulk”, for an artificial construction of a commensurate phase; “com. layer”, for a monolayer structure of the commensurate phase; and “interface”, for an interface formed between the commensurate monolayer and four layers of Au (111).

These control capabilities at the atomistic level call for a computational examination of the change in excitonic properties stemming from the underlying structure, and in particular upon experimentally-accessible structural modifications. Such excitonic properties can be reliably computed using many-body perturbation theory (MBPT) within the GW and Bethe-Salpeter equation framework (GW-BSE) (Hybertsen and Louie, 1986; Rohlfing and Louie, 2000; Deslippe et al., 2012), a Green’s function based ab initio approach. GW-BSE computations have the predictive power required to relate the change in crystal packing to electronic and excitonic interaction nature. As such, this method has been applied in recent years to study quasiparticle and excitonic properties in bulk organic molecular crystals (Cudazzo et al., 2012; Sharifzadeh et al., 2012; Cudazzo et al., 2013; Sharifzadeh et al., 2013; Refaely-Abramson et al., 2015; Cudazzo et al., 2015; Kronik and Neaton, 2016; Rangel et al., 2016; Refaely-Abramson et al., 2017; Cocchi et al., 2018; Rangel et al., 2018). However, its explicit application on a metal-organic PDI interface is far from trivial, as it is highly computationally demanding. Nevertheless, such investigation can supply a comprehensive ab initio understanding of the relation between the structural changes at the various steps of interface construction - from the freestanding phase to an adsorbate on a metal surface - and the changes in quasiparticle and excitation properties dominating the energy transfer mechanisms.

In this study, we explore the change in excitonic properties in the C8-PDI organic molecular crystal upon structural modifications associated with metal-organic interface formation. For this, we investigate a series of systems, from the bulk molecular crystal with modified unit cells, through a monolayer structure, and finally an organic-inorganic interface formed by the adsorption of the C8-PDI monolayer on Au (111) surface. We use GW-BSE to study the quasiparticle and optical excitation energies in each system, and analyze the involved electron-hole binding as a function of intermolecular packing and layering. We demonstrate a close relationship between exciton localization and molecular arrangement in the crystal, manifesting the importance of intermolecular interactions beyond the Frenkel excitonic picture. We further investigate the effect of interlayer screening on the fundamental and optical gaps, and the resulting exciton binding energy. We show that while the quasiparticle energies are strongly affected by intermolecular and interlayer interactions, the optical excitation energies are far less sensitive to these structural modifications, demonstrating that the long-range nature of the interaction dominates the former and the short-range nature of the interaction dominates the latter. As a result, the computed exciton binding energy strongly depends on the crystal modifications. Our study presents an ab initio structure-sensitive understanding of excitonic properties in the C8-PDI@Au organic-inorganic interface, as a prototypical example which sheds light on the excited-state phenomena associated with the exciton transfer processes across such interfaces.

The paper is organized as follows: We first present the GW-BSE computational approaches used. Then we discuss the bulk C8-PDI quasiparticle and excitonic properties, emphasizing the exciton dispersion and the singlet and triplet state localization, and explore the effect of intermolecular packing upon unit cell modification to a commensurate structure. Finally, we examine variations in the excitonic picture in a freestanding layer, as opposed to the bulk structure, and upon adsorption on an Au substrate. The main steps in the structural modification explored are demonstrated in Figure 1B.

1 Computational Methods

We perform structural relaxation and compute initial electronic wavefunctions and energies, using density functional theory (DFT) (Kohn and Sham, 1965) and the Perdew-Burke-Ernzerhof (PBE) (Perdew et al., 1996) exchange-correlation functional, as implemented in the Quantum Espresso package (Giannozzi et al., 2017) (see full computational details in the SI). The DFT Kohn-Sham eigenvalues and eigenfunctions are then taken as the first guess for the MBPT calculations. We use the GW approximation to compute the quasiparticle energies and bandstructure (Hybertsen and Louie, 1986; Deslippe et al., 2012; Hedin, 1965), where we calculate self-energy corrections via Σ = iGW, for G the single-particle Green’s function and W the screened Coulomb interaction, $W_{\mathbf{G}{\mathbf{G}}^{\prime }}(\mathbf{q};0)={\epsilon }_{\mathbf{G}{\mathbf{G}}^{\prime }}^{-1}(\mathbf{q};0)v(\mathbf{q}+{\mathbf{G}}^{\prime }),$ where G, G′ are reciprocal lattice vectors, v is the bare Coulomb interaction, and ɛ_GG′(q; 0) is the dielectric function of the system for interaction wavevector q and zero frequency, evaluated via (Hybertsen and Louie, 1986; Deslippe et al., 2012):

${\epsilon }_{\mathbf{G}{\mathbf{G}}^{\prime }}(\mathbf{q};0)={\delta }_{\mathbf{G}{\mathbf{G}}^{\prime }}-v(\mathbf{q}+\mathbf{G}){\chi }_{\mathbf{G}{\mathbf{G}}^{\prime }}^0(\mathbf{q};0),(1)$

with ${\chi }_{\mathbf{G}{\mathbf{G}}^{\prime }}^0(\mathbf{q};0)$ the non-interacting electronic polarizability calculated using the random-phase approximation.

Optical excitations and excitonic properties are computed through the BSE formalism (Rohlfing and Louie, 1998; Rohlfing and Louie, 2000)

$\begin{array}{c}\left(E_{c\mathbf{k}+\mathbf{Q}}-E_{v\mathbf{k}}\right)A_{vc\mathbf{k}\mathbf{Q}}^S+\sum _{v^{\prime }{c}^{\prime }{\mathbf{k}}^{\prime }}⟨v\mathbf{k};c\mathbf{k}+\mathbf{Q}|K^{eh}|v^{\prime }{\mathbf{k}}^{\prime };c^{\prime }{\mathbf{k}}^{\prime }+\mathbf{Q}⟩A_{v^{\prime }{c}^{\prime }{\mathbf{k}}^{\prime }\mathbf{Q}}^S\hfill \\ ={\mathrm{\Omega }}_{\mathbf{Q}}^S{A}_{vc\mathbf{k}\mathbf{Q}}^S\hfill \end{array}(2)$

for a hole state $\left|v\mathbf{k}⟩\right.⟩$ and an electron state $\left|c\mathbf{k}+\mathbf{Q}⟩\right.⟩$, where k is the crystal momentum and Q is the exciton center-of-mass momentum. S indexes the exciton state at momentum Q. $A_{vc\mathbf{k}\mathbf{Q}}^S$ is the amplitude of the free electron-hole pair. E_ck+Q and E_vk are the quasiparticle energies calculated within the GW approximation; ${\mathrm{\Omega }}_{\mathbf{Q}}^S$ is the excitation energy; and K^eh is the electron-hole interaction kernel. Exciton dispersion is obtained by solving the BSE at different exciton momenta Q following the methodology developed in Refs. (Gatti and Sottile, 2013; Qiu et al., 2015). The GW-BSE exciton wavefunction can be represented as $\left|{\mathrm{\Psi }}_{S,\mathbf{Q}}⟩\right.⟩={\sum }_{vc\mathbf{k}}{A}_{vc\mathbf{k}\mathbf{Q}}^S\left|c\mathbf{k}+\mathbf{Q}⟩\right.⟩\left|v\mathbf{k}⟩\right.⟩$.

We compute the dielectric screening at the C8-PDI@Au interface using two approaches. The first is a direct calculation using G₀W₀ for the interface, which is highly computationally challenging and is made possible due to recent advances both in large-scale computing capabilities and associated code development (Del Ben et al., 2019). As a comparison, we also compute the dielectric function of the interface using a recently developed substrate screening GW approach (Liu et al., 2019). In this approach, the non-interacting polarizability of the interface is approximated by the summation of the separately calculated polarizabilies of the substrate (Au) and adsorbate (C8-PDI), i.e.,

${\chi }_{\mathrm{t}\mathrm{o}\mathrm{t},\mathbf{G}{\mathbf{G}}^{\prime }}^0(\mathbf{q};0)\approx {\chi }_{\mathrm{m}\mathrm{o}\mathrm{l},\mathbf{G}{\mathbf{G}}^{\prime }}^0(\mathbf{q};0)+{\chi }_{\mathrm{s}\mathrm{u}\mathrm{b},\mathbf{G}{\mathbf{G}}^{\prime }}^0(\mathbf{q};0),(3)$

where ${\chi }_{\text{mol}}^0$ and ${\chi }_{\text{sub}}^0$ are the polarizabilities associated with the standalone molecular layer and metal substrates, respectively. This approximation holds for systems with weak hybridization between the adsorbate and the substrate (Liu et al., 2019; Xuan et al., 2019; Adeniran et al., 2020). The goal is to assess the validity of Eq. 3 against a direct GW calculation of the interface, to determine the nature of the surface effect on quasiparticle and exciton properties of the C8-PDI.

As shown in Figure 1B, we mainly study four different structures: (i) “bulk”, a bulk crystal in its experimentally resolved triclinic unit cell and relaxed atomic coordinates; (ii) “com. bulk”, a modified bulk structure in an orthorhombic lattice, so that it is commensurate with the lattice of the Au substrate; (iii) “com. layer”, a layered orthorhombic structure with large vacuum, taken as one molecular layer along the c axis from (ii); and (iv) “interface”, the C8-PDI monolayer from (iii) adsorbed on four layers of Au (111) surface, with each layer consisting of 2 × 3 Au atoms and an adsorption height of 3.18 Å. Such thickness of the simulated Au surface was previously found to sufficiently capture wavefunction hybridization and dielectric screening effects (Liu et al., 2017; Refaely-Abramson et al., 2019). We apply periodic boundary conditions to all structures, and fully relax the internal coordinates for each one of the structures. For (i) and (ii), the calculations were carried out using the converged parameters of a (8 × 4 × 4) k-point grid and 600 bands in the summation to compute the dielectric matrix, as well as a kinetic energy cutoff of 80 Ry and a dielectric cutoff of 10 Ry. The calculation of the absorption spectrum was carried out via an interpolation to a finer (12 × 6 × 6) k-point grid. For (iii) and (iv), the calculations used a k-point grid of (8 × 4 × 1) and 1,000 bands in the summation to compute the dielectric matrix, as well as the same cutoffs as (i) and (ii). (i)-(iii) used a semiconductor screening treatment of the q → 0 limit and (iv) used a metallic screening, as implemented in the BerkeleyGW package (Deslippe et al., 2012). Furthermore, (iii) and (iv) used a slab truncation for the Coulomb interaction.

2 Crystal Packing Effect on Exciton Nature

We begin with investigating the electronic and excitonic properties of the bulk C8-PDI system, using the experimentally-resolved crystal structure (Briseno et al., 2007), shown in Figure 2A (see full structural details in the SI). Figure 2B shows the computed GW quasiparticle bandstructure for this system (solid, red line). The three frontier electronic bands shown, valence (v₁), conduction (c₁), and second conduction (c₂), dominate the low-lying excitonic spectra we discuss in this work. The computed GW quasiparticle gap is 2.6 eV, with an expected large self-energy correction on top of the DFT (PBE) gap of 1.1 eV. The quasiparticle bands are well isolated, as typical in molecular crystals due to the molecular-like nature of the material (Refaely-Abramson et al., 2013; Kronik and Neaton, 2016); still, we note a significant band dispersion of ∼0.7 eV for the valence band between k-points X and Γ and 0.3 eV for the conduction bands between C and X, reflecting non-negligible intermolecular electronic coupling.

FIGURE 2

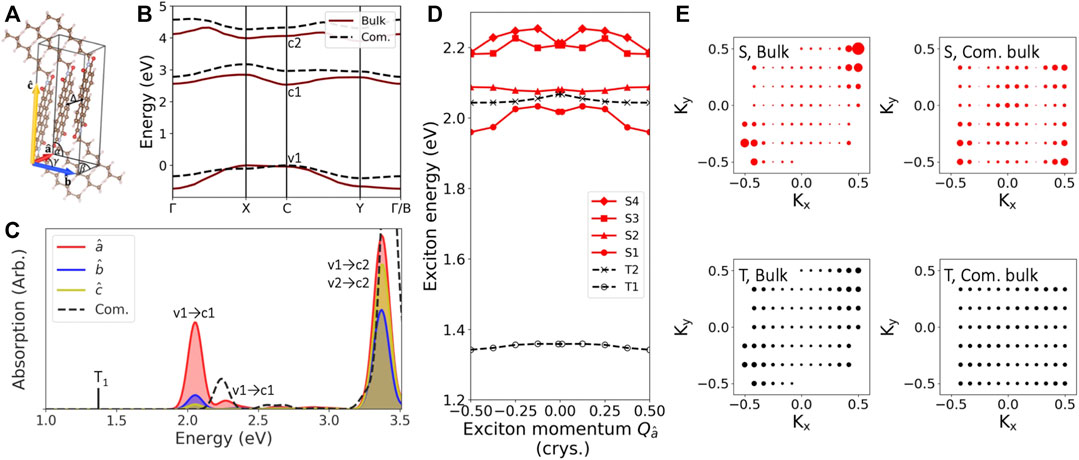
FIGURE 2. Structural and excitation properties of the bulk C8-PDI molecular crystal: (A) The unit cell showing the crystallographic parameters, which are modified among the various bulk structures examined. Δ denotes the intermolecular distance. (B) Computed GW quasiparticle bandstrcuture for the bulk (solid red) and the commensurate bulk (dashed black) structures. (C) Computed GW-BSE absorption spectra with the polarization of the light aligned along different cell directions. The low-lying triplet state is also shown (black line). Solid lines are for the bulk structure, and dashed black line is for the commensurate bulk structure. (D) Exciton bandstructure of the four lowest singlet states (solid red) and the two lowest triplet states (dashed black) of the bulk structure. (E) Exciton coefficients as a function of electron momentum in the (K_x, K_y) crystal plane for the lowest singlet and triplet states, of both the bulk and the commensurate bulk structures.

To explore the effect of intermolecular orientation, we computed different bulk structures through variation of relative intermolecular distance and the crystallographic parameters of the unit cell (see SI for full details). Our motivation to vary these parameters is twofold: first, to explore the effect of molecular packing on the quasiparticles and excitons; second, to look into the effect of changes in unit cell vectors, which are needed to achieve proper commensurateness between the unit cell of the C8-PDI crystal and that of the Au surface. In order to maintain minimal strain within the Au surface, we only vary the PDI cell parameters. For the case of a single C8-PDI molecule per cell, this results in a modified cell (“com. bulk” in Figure 1B), in which the intermolecular distance grows compared to the original structure. Here we explore the limiting case of an orthorhombic molecular crystal unit cell, although a monoclinic cell leads to very similar results (see SI). By allowing more molecules per cell, commensurate layers can be achieved with smaller atomic modifications, however, performing GW-BSE calculations on these large supercells in an accurate manner is highly computationally challenging. The associated structures and the computed GW bandstructures for each of these cells in its bulk form are given in Supplementary Table S1; Supplementary Figure S1.

Since the electronic and excitonic states stem from the molecular building blocks, the effect of such unit-cell modification is not trivial and depends on the level of the electronic and excitonic wavefunction localization. Upon structural reorganization from the “bulk” structure to the “com. bulk” cell that is commensurate with the Au surface, the intermolecular distance increases from 3.4 Å to 3.6 Å, and the cell angle γ (Figure 2A) changes from 82^◦ to 90^◦. As a result, the computed GW quasiparticle gap increases by 0.4 eV and the band dispersion decreases by 0.35 eV, as shown in Figure 2B. Two other bulk structures with intermediate variations reveal a gradual modification between these values (see SI).

The strong structural dependence of the quasiparticle band dispersion reveals a somewhat surprisingly large effect of the molecular packing and orientation on the quasiparticle and exciton picture. It stems from intermolecular interactions and screening, which vary significantly with intermolecular distances and relative orientation. Figure 2C shows the computed BSE absorption spectra of the “bulk” structure, with a low-energy singlet peak at 2.05 eV, in good agreement with the experimental value of ∼2.2 eV (Le et al., 2018; Felter et al., 2019). The absorption spectra along the three main polarization directions are shown in different colors, with the main optically-active dipole transitions along the $\widehat{a}$ axis, namely through the π − π stacking direction, and the least active direction along the c axis. The low-lying triplet exciton is found at 1.4 eV, shown with a black line. As a comparison, the absorption computed for the commensurate bulk structure is shown as well (dashed black line). As shown in Table 1, comparing the “com. bulk” structure with the “bulk” structure, the lowest singlet excitation energy increases by 0.19 eV; however, the lowest triplet excitation energy increases by only 0.06 eV.

TABLE 1

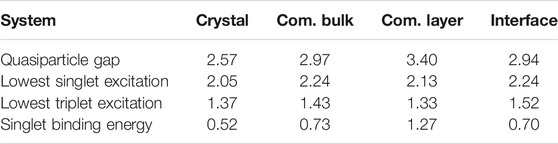
TABLE 1. Quasiparticle and optical excitation energies from GW-BSE for the various structures examined. All energies are in eV.

We further examine the effect of intermolecular coupling on the exciton nature by investigating the exciton dispersion, where the center-of-mass momentum Q represents the momentum difference between the hole and the excited electron, which is taken into account in the BSE, Eq. 2; (Qiu et al., 2015). Figure 2D shows the computed exciton bandstructure along the optically-active $\widehat{a}$ direction (other crystal directions are shown in the SI). The exciton band shape varies along the reciprocal space due to indirect transitions occurring between the Γ and X points. At small exciton momentum Q, the lowest singlet exciton, S₁, shows a parabolic behavior, with effective mass of 0.35m_e (for m_e the electron mass). Higher singlet excitons are also shown, revealing varying levels of localization. As expected, the low-lying triplet state has a larger effective mass of 2.7m_e, supporting its higher degree of real-space localization, as typical in organic molecular crystals (Rangel et al., 2016; Refaely-Abramson et al., 2017).

Figure 2E shows the exciton coefficients ($A_{vc\mathbf{k}}^S$ in Eq. 2) for the Q = 0 transition as a function of quasiparticle momentum in the (K_x , K_y) crystal plane. The lowest singlet state shows high localization in momentum space at the C point ([0.5,0.5,0] in reciprocal space), suggesting spatial delocalization. On the contrary, for the lowest triplet state, the exciton coefficients are nearly uniform within the Brillouin zone, pointing to spatial localization. In the commensurate bulk structure, the same singlet excitons are more spread in reciprocal space, reflecting increased real-space localization. The triplet state is localized in both structures and experiences a smaller change due to the structural modification, compared to the singlet state. The sizable differences between singlet and triplet localization is coupled to the short-range exchange in C8-PDI, dominating intermolecular electron-hole coupling (Rohlfing and Louie, 2000; Rangel et al., 2016). Upon changes in intermolecular packing, induced exciton localization leads to enhanced exchange interactions. Our results thus reveal strong state- and structure-dependence of the exciton nature in bulk C8-PDI, as an outcome of the intermolecular interactions dominating the electron-hole coupling.

3 Dimensionality and Interface Effects on Exciton Binding

Next, we study the effect of crystal layering and surface adsorption on the excitation energies. As shown in Table 1, for the commensurate structure, the quasiparticle gap of a freestanding C8-PDI layer increases by ∼0.4 eV, while both the singlet and triplet exciton energies decrease by ∼0.1 eV, compared to the commensurate bulk structure. This results in a significant increase of the exciton binding energy, an expected result due to the strong dimensionality effect on the dielectric screening, as we further elaborate in the discussion section below. From a computational point of view, constructing a monolayer is motivated by its subsequent adsorption on Au substrate within a computationally tractable periodic cell. In the following we directly compare the charged and neutral excitations of the freestanding layer with the adsorbed one, to gain direct insight into the Au screening effect on exciton binding.

To capture the dielectric screening at the C8-PDI@Au interface, we compare two approaches: an explicit GW calculation of the entire interface, with the simulation cell presented in Figure 1; and a substrate screening GW approach (Liu et al., 2019), in which the polarizabilities of the two parts of the interface are computed separately and then combined in the interface cell, as we discuss in the methods section. Our motivation is to verify the validity of the substrate screening approximation for the C8-PDI@Au interface. If this is true, we can conclude that the effect of the Au substrate merely provides a dielectric media that renormalizes the quasiparticle and excitation energies within the C8-PDI molecular layer, rather than altering the nature of the quasiparticle orbitals and excitons of the C8-PDI via orbital hybridization.

Figure 3A shows the computed GW quasiparticle projected density of states (pDOS) of the full interface at high symmetry k-points onto C8-PDI (purple) and Au (orange) atomic orbitals. Dashed black lines represent the pDOS associated with the freestanding C8-PDI layer, which we align with the pDOS onto C8-PDI at the resonance corresponding to the highest occupied molecular orbital (at about −0.8 eV in Figure 3A). The quasiparticle gap associated with the molecular levels is reduced by 0.46 eV compared to the monolayer, due to the Au surface. The associated valence and conduction electronic charge distributions for the PDI-localized interface wavefunctions are well separated from the Au states, demonstrating the negligible interface hybridization in this system. The change in quasiparticle energies is a direct outcome of interface screening. Figure 3B compares the computed dielectric function ɛ₀₀ (Eq. 1) of the commensurate bulk, layered, and interface systems for the head elements, namely G = G′ = 0. At large interaction distance q, corresponding to short-range interactions in real space, the dielectric function reaches the expected limit of ɛ = 1. At small q, however, the dielectric function increases significantly due to the Au screening, while remaining close to unity for the freestanding layer due to its reduced dimensionality.

FIGURE 3

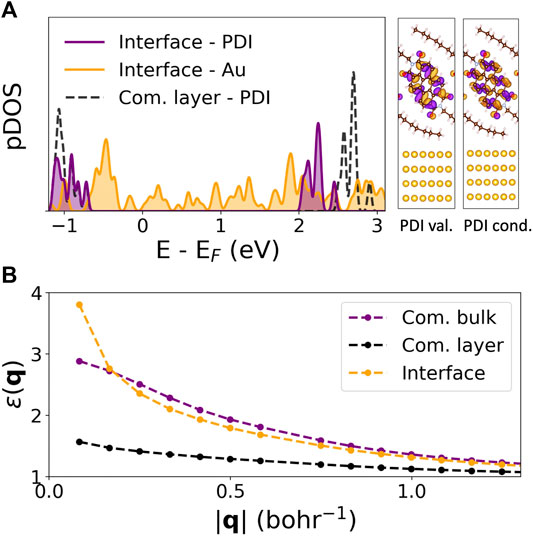
FIGURE 3. Quasiparticle and dielectric properties of the C8-PDI@Au interface: (A) GW pDOS on C8-PDI (purple) and Au (orange) atomic orbitals, compared to the freestanding molecular layer (dashed black). The right panel shows the electronic distributions of the PDI-localized valence and conduction states. (B) Computed GW dielectric function, ɛ(q), for the commensurate bulk (purple), commensurate layer (black), and the interface structure (orange).

The computed GW quasiparticle gap resulting from the substrate screening approach is 2.95 eV, which is in very good agreement with the direct calculation (2.94 eV). Additionally, in Supplementary Figure S5, we compare the diagonal elements of the non-interacting polarizability of the interface (${\chi }_{\text{tot}}^0$) computed using the two approaches, and find that they agree very well. We can infer from these results that there is negligible orbital hybridization at the C8-PDI@Au interface, and that the Au substrate simply provides a dielectric environment that effectively screens the molecular crystal. We expect that the substrate screening approach, based on the additivity of the non-interacting polarizability of the interface (Liu et al., 2019; Xuan et al., 2019), is applicable to other systems without significant orbital hybridization or covalent bonding.

We believe this conclusion could help us understand the physical interface where a C8-PDI monolayer in its pristine bulk lattice (rather than the artificial commensurate lattice as we did in this work) is adsorbed on Au (111). From a computational perspective, such a physical interface is incommensurate and is prohibitively expensive to calculate. However, based on the conclusion achieved in this section, we can infer what would happen if we were modelling the incommensurate physical interface: all the properties associated to the exciton wavefunctions of the C8-PDI bulk crystal as reported in Figure 2 will be qualitatively unchanged in the interface, thanks to the negligible orbital hybridization. The exciton binding energies will be renormalized due to the dielectric screening of the Au substrate.

4 Discussion and Conclusion

Our results demonstrate the effect of intermolecular and surface screening on both quasiparticle and exciton properties via a step-by-step structural variation. Specifically, we look closely at the exciton nature as a function of molecular crystal packing and dielectric environment, as summarized in Figure 4. For the case of Frenkel-like molecular excitons, the exciton nature should stay roughly unchanged upon changes in crystal packing, as the environmental effect will be mainly manifested through an effective dielectric constant (Sharifzadeh et al., 2012; Cudazzo et al., 2013). Nonetheless, we find that the bulk C8-PDI excitons do have dispersion and are crystal-momentum dependent, reflecting non-negligible excitonic coupling beyond the Frenkel picture. The dispersion is more enhanced in singlet states compared to triplet states due to the exchange interaction, as observed before in related organic molecular crystals (Rangel et al., 2016; Refaely-Abramson et al., 2017; Rangel et al., 2018). On top of this effect, the dielectric screening induces further variations: upon crystal layering, the quasiparticle gap increases, and upon surface adsorption it renormalizes, while the exciton energies remain largely unchanged. This is a direct outcome of the non-local screening that dominates the quasiparticle energies, compared to local screening that dominates the electron-hole binding in the low-lying excitons. These dielectric effects are captured in the GW calculation through an explicit evaluation of the dielectric function (Hybertsen and Louie, 1986; Deslippe et al., 2012). As shown in Figure 3B, the dielectric functions of the various structures are similar at the short-range interaction regime and differ greatly at the long-range interaction regime.

FIGURE 4

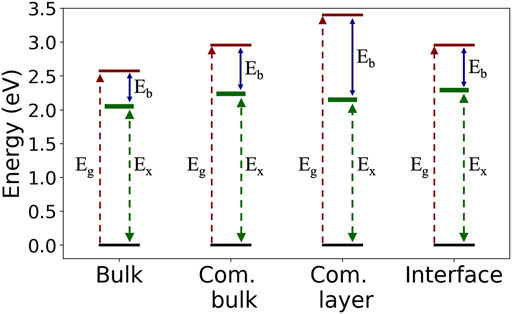
FIGURE 4. Summary of the computed GW quasiparticle gap, E_g; optical gap, E_x; and the exciton binding energy, E_b, in the four examined structures.

Table 1 indicate the strong sensitivity of the charged quasiparticle excitation energies (as reflected in gaps) to the dielectric environment and the weak sensitivity of the neutral excitation energy (as reflected in optical transitions in the case of strong electron-hole coupling) to the environment (Kronik et al., 2012; Refaely-Abramson et al., 2015). The change in the optical gaps and the exciton binding energies between the C8-PDI monolayer and the C8-PDI@Au interface points to a significant decrease in the exciton binding energy upon formation of the interface with Au. This effect is expected, as the enhanced screening has a significant influence on the quasiparticle gap (Neaton et al., 2006; Egger et al., 2015; Liu et al., 2017). On the other hand, simple metal surfaces tend to have a much weaker influence on the optical excitations localized within the adsorbate (Spataru, 2013; Deilmann and Thygesen, 2019).

Importantly, the computational approach we employed here is not limited to cases of weak hybridization at the interface, and can be hence further used to investigate other types of PDI interfaces where the exciton separation mechanisms are expected to involve significant charge-transfer components. For example, triplet exciton transfer across C8-PDI and SiO₂ interfaces was recently suggested to be strongly coupled to changes in intermolecular interactions due to surface hybridization (Cotton et al., 2020). In addition, few recent studies explored the role of surface passivation in modifying and controlling the efficiency of exciton transfer from acene molecular crystals adsorbed on silicon substrates (Einzinger et al., 2019; Daiber et al., 2020). The relation between interface bonding, charge and exciton localization far from and at the junction, and the resulting energy-transfer efficiency at PDI-based junctions is intriguing, and the results we present here for the case of weak metal-organic coupling can be thought of as a computational test case at the weakly interacting regime. Our results thus demonstrate that the GW-BSE approach offers a reliable tool to explore interface effects on excitonic properties at organic-inorganic interfaces with various levels of interface hybridization.

To conclude, we studied the effect of structural modifications on quasiparticle and exciton nature in the C8-PDI molecular crystal and its interface with Au. We explored the excitonic properties of the bulk system in detail, and investigated the effect of crystal packing and interface dielectric screening, building a structural modification route from the bulk structure to a heterogeneous interface. Our results demonstrate that while the quasiparticle band gap undergoes significant variations upon the structural modification and surface adsorption, the optical gap is much less affected by them, leading to strong structural sensitivity of the exciton binding energies. Our methods allow us to quantify this effect, and relate it to the specifics of local and non-local structural modifications.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

LS performed most of the DFT, GW, and GW-BSE computations presented in this work. OA performed the interface calculations using the substrate screening GW approach. GV performed DFT and GW examination to explore additional packing effects. Z-FL constructed and led the substrate screening GW calculations. SR-A is the corresponding author in this work and instructed the DFT, GW, and GW-BSE computations. All authors contributed to the manuscript writing.

Funding

This research was supported by a grant from the United States-Israel Binational Science Foundation (BSF), Jerusalem, Israel, awarded to Z-FL and SR-A (Grant Number 2018113). OA acknowledges A. Paul and Carole C. Schaap Endowed Distinguished Graduate Award and Rumble Fellowship from Wayne State University. Z-FL acknowledges start-up funds and an Ebbing faculty development award from Wayne State University. SR-A is an incumbent of the Leah Omenn Career Development Chair, and acknowledges research grants from the Peter and Patricia Gruber Awards and an Alon Fellowship. This research used computational resources within a PRACE Allocation Grant, Project No. 2019204916, at the Barcelona Supercomputing Center (BSC-CNS), as well as at the Chemfarm cluster at the Weizmann Institute of Science and at the Center for Functional Nanomaterials, which is a U.S. Department of Energy Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. Additional computational resources were provided by the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Boris Rybtchinski and Angelica Elkan for valuable discussions, Mark Vilensky for administrative support, and Diana Qiu and Felipe da Jornada for helpful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.743391/full#supplementary-material

References

Adeniran, O., Refaely-Abramson, S., and Liu, Z. F. (2020). Layer-Dependent Quasiparticle Electronic Structure of the P3HT: PCBM Interface From a First-Principles Substrate Screening GW Approach. J. Phys. Chem. C 124 (25), 13592–13601. doi:10.1021/acs.jpcc.0c03543

CrossRef Full Text | Google Scholar

Arias, D. H., Ryerson, J. L., Cook, J. D., Damrauer, N. H., and Johnson, J. C. (2016). Polymorphism Influences Singlet Fission Rates in Tetracene Thin Films. Chem. Sci. 7, 1185–1191. doi:10.1039/c5sc03535j

PubMed Abstract | CrossRef Full Text | Google Scholar

Briseno, A. L., Mannsfeld, S. C. B., Reese, C., Hancock, J. M., Xiong, Y., Jenekhe, S. A., et al. (2007). Perylenediimide Nanowires and Their Use in Fabricating Field-Effect Transistors and Complementary Inverters. Nano Lett. 7, 2847–2853. doi:10.1021/nl071495u

PubMed Abstract | CrossRef Full Text | Google Scholar

Carter, K.-J. B., and Grossman, J. C. (2020). Design Rules for Transparent Push-Pull Electron Acceptors: A Case Study on Perylenediimide Derivatives. J. Phys. Chem. Lett. 11, 9265–9271. doi:10.1021/acs.jpclett.0c02485

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciccullo, F., Savu, S.-A., Gerbi, A., Bauer, M., Ovsyannikov, R., Cassinese, A., et al. (2015). Chemisorption, Morphology, and Structure of a N-type Perylene Diimide Derivative at the Interface with Gold: Influence on Devices from Thin Films to Single Molecules. Chem. Eur. J. 21, 3766–3771. doi:10.1002/chem.201404901

PubMed Abstract | CrossRef Full Text | Google Scholar

Cocchi, C., Breuer, T., Witte, G., and Draxl, C. (2018). Polarized Absorbance and Davydov Splitting in Bulk and Thin-Film Pentacene Polymorphs. Phys. Chem. Chem. Phys. 20, 29724–29736. doi:10.1039/c8cp06384b

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotton, D. E., Moon, A. P., and Roberts, S. T. (2020). Using Electronic Sum-Frequency Generation to Analyze the Interfacial Structure of Singlet Fission-Capable Perylenediimide Thin Films. J. Phys. Chem. C 124, 11401–11413. doi:10.1021/acs.jpcc.0c01025

CrossRef Full Text | Google Scholar

Cudazzo, P., Gatti, M., and Rubio, A. (2012). Excitons in Molecular Crystals from First-Principles many-body Perturbation Theory: Picene versus Pentacene. Phys. Rev. B 86, 195307. doi:10.1103/physrevb.86.195307

CrossRef Full Text | Google Scholar

Cudazzo, P., Gatti, M., Rubio, A., and Sottile, F. (2013). Frenkel versus Charge-Transfer Exciton Dispersion in Molecular Crystals. Phys. Rev. B 88, 195152. doi:10.1103/physrevb.88.195152

CrossRef Full Text | Google Scholar

Cudazzo, P., Sottile, F., Rubio, A., and Gatti, M. (2015). Exciton Dispersion in Molecular Solids. J. Phys. Condens. Matter 27, 113204. doi:10.1088/0953-8984/27/11/113204

CrossRef Full Text | Google Scholar

Daiber, B., Maiti, S., Ferro, S. M., Bodin, J., van den Boom, A. F. J., Luxembourg, S. L., et al. (2020). Change in Tetracene Polymorphism Facilitates Triplet Transfer in Singlet Fission-Sensitized Silicon Solar Cells. J. Phys. Chem. Lett. 11, 8703–8709. doi:10.1021/acs.jpclett.0c02163

PubMed Abstract | CrossRef Full Text | Google Scholar

Deilmann, T., and Thygesen, K. S. (2019). Important Role of Screening the Electron-Hole Exchange Interaction for the Optical Properties of Molecules Near Metal Surfaces. Phys. Rev. B 99, 045133. doi:10.1103/physrevb.99.045133

CrossRef Full Text | Google Scholar

Del Ben, M., da Jornada, F. H., Canning, A., Wichmann, N., Raman, K., Sasanka, R., et al. (2019). Large-scale GW Calculations on Pre-exascale HPC Systems. Comp. Phys. Commun. 235, 187–195. doi:10.1016/j.cpc.2018.09.003

CrossRef Full Text | Google Scholar

Delor, M., Weaver, H. L., Yu, Q., and Ginsberg, N. S. (2020). Imaging Material Functionality through Three-Dimensional Nanoscale Tracking of Energy Flow. Nat. Mater. 19, 56–62. doi:10.1038/s41563-019-0498-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Deslippe, J., Samsonidze, G., Strubbe, D. A., Jain, M., Cohen, M. L., and Louie, S. G. (2012). BerkeleyGW: A Massively Parallel Computer Package for the Calculation of the Quasiparticle and Optical Properties of Materials and Nanostructures. Comp. Phys. Commun. 183, 1269–1289. doi:10.1016/j.cpc.2011.12.006

CrossRef Full Text | Google Scholar

D. S. Ginley, and D. Cahen (Editors) (2011). Fundamentals of Materials for Energy and Environmental Sustainability (Cambridge University Press).

Eaton, S. W., Shoer, L. E., Karlen, S. D., Dyar, S. M., Margulies, E. A., Veldkamp, B. S., et al. (2013). Singlet Exciton Fission in Polycrystalline Thin Films of a Slip-Stacked Perylenediimide. J. Am. Chem. Soc. 135, 14701–14712. doi:10.1021/ja4053174

CrossRef Full Text | Google Scholar

Egger, D. A., Liu, Z.-F., Neaton, J. B., and Kronik, L. (2015). Reliable Energy Level Alignment at Physisorbed Molecule-Metal Interfaces from Density Functional Theory. Nano Lett. 15, 2448–2455. doi:10.1021/nl504863r

PubMed Abstract | CrossRef Full Text | Google Scholar

Einzinger, M., Wu, T., Kompalla, J. F., Smith, H. L., Perkinson, C. F., Nienhaus, L., et al. (2019). Sensitization of Silicon by Singlet Exciton Fission in Tetracene. Nature 571, 90–94. doi:10.1038/s41586-019-1339-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Felter, K. M., Caselli, V. M., Günbaş, D. D., Savenije, T. J., and Grozema, F. C. (2019). Interplay between Charge Carrier Mobility, Exciton Diffusion, Crystal Packing, and Charge Separation in Perylene Diimide-Based Heterojunctions. ACS Appl. Energ. Mater. 2, 8010–8021. doi:10.1021/acsaem.9b01490

PubMed Abstract | CrossRef Full Text | Google Scholar

Gatti, M., and Sottile, F. (2013). Exciton Dispersion from First Principles. Phys. Rev. B 88, 155113. doi:10.1103/physrevb.88.155113

CrossRef Full Text | Google Scholar

Giannozzi, P., Andreussi, O., Brumme, T., Bunau, O., Buongiorno Nardelli, M., Calandra, M., et al. (2017). Advanced Capabilities for Materials Modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901. doi:10.1088/1361-648x/aa8f79

PubMed Abstract | CrossRef Full Text | Google Scholar

Gish, M. K., Pace, N. A., Rumbles, G., and Johnson, J. C. (2019). Emerging Design Principles for Enhanced Solar Energy Utilization with Singlet Fission. J. Phys. Chem. C 123, 3923–3934. doi:10.1021/acs.jpcc.8b10876

CrossRef Full Text | Google Scholar

Grätzel, M. (2001). Photoelectrochemical Cells. Nature 414, 338–344. doi:10.1038/35104607

PubMed Abstract | CrossRef Full Text | Google Scholar

Hedin, L. (1965). New Method for Calculating the One-Particle Green’s Function With Application to the Electron-Gas Problem. Phys. Rev. 139, A796. doi:10.1103/PhysRev.139.A796

CrossRef Full Text | Google Scholar

Hestand, N. J., and Spano, F. C. (2018). Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 118, 7069–7163. doi:10.1021/acs.chemrev.7b00581

PubMed Abstract | CrossRef Full Text | Google Scholar

Hybertsen, M. S., and Louie, S. G. (1986). Electron Correlation in Semiconductors and Insulators: Band Gaps and Quasiparticle Energies. Phys. Rev. B 34 (8), 5390. doi:10.1103/PhysRevB.34.5390

PubMed Abstract | CrossRef Full Text | Google Scholar

Klauk, H. (2006). Organic Electronics: Materials, Manufacturing, and Applications. John Wiley & Sons.

Kohn, W., and Sham, L. J. (1965). Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

Krauss, T. N., Barrena, E., de Oteyza, D. G., Zhang, X. N., Major, J., Dehm, V., et al. (2009). X-ray/Atomic Force Microscopy Study of the Temperature-dependent Multilayer Structure of PTCDI-C8 Films on SiO2. J. Phys. Chem. C 113, 4502–4506. doi:10.1021/jp808037w

CrossRef Full Text | Google Scholar

Krieg, E., Niazov-Elkan, A., Cohen, E., Tsarfati, Y., and Rybtchinski, B. (2019). Noncovalent Aqua Materials Based on Perylene Diimides. Acc. Chem. Res. 52, 2634–2646. doi:10.1021/acs.accounts.9b00188

PubMed Abstract | CrossRef Full Text | Google Scholar

Kronik, L., and Neaton, J. B. (2016). Excited-State Properties of Molecular Solids from First Principles. Annu. Rev. Phys. Chem. 67, 587–616. doi:10.1146/annurev-physchem-040214-121351

PubMed Abstract | CrossRef Full Text | Google Scholar

Kronik, L., Stein, T., Refaely-Abramson, S., and Baer, R. (2012). Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals. J. Chem. Theor. Comput. 8, 1515–1531. doi:10.1021/ct2009363

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, A. K., Bender, J. A., Arias, D. H., Cotton, D. E., Johnson, J. C., and Roberts, S. T. (2018). Singlet Fission Involves an Interplay between Energetic Driving Force and Electronic Coupling in Perylenediimide Films. J. Am. Chem. Soc. 140, 814–826. doi:10.1021/jacs.7b11888

PubMed Abstract | CrossRef Full Text | Google Scholar

Liscio, F., Albonetti, C., Broch, K., Shehu, A., Quiroga, S. D., Ferlauto, L., et al. (2013). Molecular Reorganization in Organic Field-Effect Transistors and its Effect on Two-Dimensional Charge Transport Pathways. ACS nano 7, 1257–1264. doi:10.1021/nn304733w

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z.-F., da Jornada, F. H., Louie, S. G., and Neaton, J. B. (2019). Accelerating GW-Based Energy Level Alignment Calculations for Molecule-Metal Interfaces Using a Substrate Screening Approach. J. Chem. Theor. Comput. 15, 4218–4227. doi:10.1021/acs.jctc.9b00326

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z.-F., Egger, D. A., Refaely-Abramson, S., Kronik, L., and Neaton, J. B. (2017). Energy Level Alignment at Molecule-Metal Interfaces from an Optimally Tuned Range-Separated Hybrid Functional. J. Chem. Phys. 146, 092326. doi:10.1063/1.4975321

CrossRef Full Text | Google Scholar

Luo, X., Han, Y., Chen, Z., Li, Y., Liang, G., Liu, X., et al. (2020). Mechanisms of Triplet Energy Transfer Across the Inorganic Nanocrystal/Organic Molecule Interface. Nat. Commun. 11, 1. doi:10.1038/s41467-019-13951-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Neaton, J. B., Hybertsen, M. S., and Louie, S. G. (2006). Renormalization of Molecular Electronic Levels at Metal-Molecule Interfaces. Phys. Rev. Lett. 97, 216405. doi:10.1103/physrevlett.97.216405

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Brien, D. B., Anglin, T. C., and Massari, A. M. (2011). Surface Chemistry and Annealing-Driven Interfacial Changes in Organic Semiconducting Thin Films on Silica Surfaces. Langmuir 27, 13940. doi:10.1021/la202443u

PubMed Abstract | CrossRef Full Text | Google Scholar

Oleson, A., Zhu, T., Dunn, I. S., Bialas, D., Bai, Y., Zhang, W., et al. (2019). Perylene Diimide-Based Hj- and hJ-Aggregates: The Prospect of Exciton Band Shape Engineering in Organic Materials. J. Phys. Chem. C 123, 20567–20578. doi:10.1021/acs.jpcc.9b04429

CrossRef Full Text | Google Scholar

Penwell, S. B., Ginsberg, L. D. S., Noriega, R., and Ginsberg, N. S. (2017). Resolving Ultrafast Exciton Migration in Organic Solids at the Nanoscale. Nat. Mater 16, 1136–1141. doi:10.1038/nmat4975

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Ernzerhof, M., and Burke, K. (1996). Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 105, 9982–9985. doi:10.1063/1.472933

CrossRef Full Text | Google Scholar

Piland, G. B., and Bardeen, C. J. (2015). How Morphology Affects Singlet Fission in Crystalline Tetracene. J. Phys. Chem. Lett. 6, 1841–1846. doi:10.1021/acs.jpclett.5b00569

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, D. Y., Cao, T., and Louie, S. G. (2015). Nonanalyticity, Valley Quantum Phases, and Lightlike Exciton Dispersion in Monolayer Transition Metal Dichalcogenides: Theory and First-Principles Calculations. Phys. Rev. Lett. 115, 176801. doi:10.1103/physrevlett.115.176801

PubMed Abstract | CrossRef Full Text | Google Scholar

Rangel, T., Berland, K., Sharifzadeh, S., Brown-Altvater, F., Lee, K., Hyldgaard, P., et al. (2016). Structural and Excited-State Properties of Oligoacene Crystals from First Principles. Phys. Rev. B 93, 115206. doi:10.1103/physrevb.93.115206

CrossRef Full Text | Google Scholar

Rangel, T., Rinn, A., Sharifzadeh, S., da Jornada, F. H., Pick, A., Louie, S. G., et al. (2018). Low-lying Excited States in Crystalline Perylene. Proc. Natl. Acad. Sci. U.S.A. 115, 284–289. doi:10.1073/pnas.1711126115

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, A., and Friend, R. H. (2017). Harnessing Singlet Exciton Fission to Break the Shockley-Queisser Limit. Nat. Rev. Mater. 2, 17063. doi:10.1038/natrevmats.2017.63

CrossRef Full Text | Google Scholar

Refaely-Abramson, S., da Jornada, F. H., Louie, S. G., and Neaton, J. B. (2017). Origins of Singlet Fission in Solid Pentacene from an Ab Initio Green's Function Approach. Phys. Rev. Lett. 119, 267401. doi:10.1103/physrevlett.119.267401

PubMed Abstract | CrossRef Full Text | Google Scholar

Refaely-Abramson, S., Jain, M., Sharifzadeh, S., Neaton, J. B., and Kronik, L. (2015). Solid-State Optical Absorption From Optimally Tuned Time-Dependent Range-Separated Hybrid Density Functional Theory. Phys. Rev. B 92 (8), 081204. doi:10.1103/PhysRevB.92.081204

CrossRef Full Text | Google Scholar

Refaely-Abramson, S., Liu, Z.-F., Bruneval, F., and Neaton, J. B. (2019). First-Principles Approach to the Conductance of Covalently Bound Molecular Junctions. J. Phys. Chem. C 123, 6379–6387. doi:10.1021/acs.jpcc.8b12124

CrossRef Full Text | Google Scholar

Refaely-Abramson, S., Sharifzadeh, S., Jain, M., Baer, R., Neaton, J. B., and Kronik, L. (2013). Gap Renormalization of Molecular Crystals From Density-Functional Theory. Phys. Rev. B 88, 081204. doi:10.1103/physrevb.88.081204

CrossRef Full Text | Google Scholar

Rohlfing, M., and Louie, S. G. (2000). Electron-hole Excitations and Optical Spectra from First Principles. Phys. Rev. B 62, 4927–4944. doi:10.1103/physrevb.62.4927

CrossRef Full Text | Google Scholar

Rohlfing, M., and Louie, S. G. (1998). Electron-Hole Excitations in Semiconductors and Insulators. Phys. Rev. Lett. 81, 2312–2315. doi:10.1103/physrevlett.81.2312

CrossRef Full Text | Google Scholar

Santosh, G., Shirman, E., Weissman, H., Shimoni, E., Pinkas, I., Rudich, Y., et al. (2010). Photofunctional Self-Assembled Nanostructures Formed by Perylene Diimide−Gold Nanoparticle Hybrids. J. Phys. Chem. B 114, 14389–14396. doi:10.1021/jp100662b

CrossRef Full Text | Google Scholar

Sato, N., Seki, K., and Inokuchi, H. (1981). Polarization Energies of Organic Solids Determined by Ultraviolet Photoelectron Spectroscopy. J. Chem. Soc. Faraday Trans. 2 77, 1621. doi:10.1039/f29817701621

CrossRef Full Text | Google Scholar

Schierl, C., Niazov-Elkan, A., Shimon, L. J., Feldman, Y., Rybtchinski, B., and Guldi, D. M. (2018). Singlet Fission in Self-Assembled PDI Nanocrystals. Nanoscale 10, 20147–20154. doi:10.1039/C8NR04155E

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnedermann, C., Sung, J., Pandya, R., Verma, S. D., Chen, R. Y. S., Gauriot, N., et al. (2019). Ultrafast Tracking of Exciton and Charge Carrier Transport in Optoelectronic Materials on the Nanometer Scale. J. Phys. Chem. Lett. 10, 6727–6733. doi:10.1021/acs.jpclett.9b02437

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharifzadeh, S., Biller, A., Kronik, L., and Neaton, J. B. (2012). Quasiparticle and Optical Spectroscopy of the Organic Semiconductors Pentacene and PTCDA from First Principles. Phys. Rev. B 85, 125307. doi:10.1103/physrevb.85.125307

CrossRef Full Text | Google Scholar

Sharifzadeh, S., Darancet, P., Kronik, L., and Neaton, J. B. (2013). Low-Energy Charge-Transfer Excitons in Organic Solids from First-Principles: The Case of Pentacene. J. Phys. Chem. Lett. 4, 2197–2201. doi:10.1021/jz401069f

CrossRef Full Text | Google Scholar

Smith, M. B., and Michl, J. (2013). Recent Advances in Singlet Fission. Annu. Rev. Phys. Chem. 64, 361–386. doi:10.1146/annurev-physchem-040412-110130

PubMed Abstract | CrossRef Full Text | Google Scholar

Spataru, C. D. (2013). Electronic and Optical gap Renormalization in Carbon Nanotubes Near a Metallic Surface. Phys. Rev. B 88, 125412. doi:10.1103/physrevb.88.125412

CrossRef Full Text | Google Scholar

Troisi, A., and Orlandi, G. (2005). Band Structure of the Four Pentacene Polymorphs and Effect on the Hole Mobility at Low Temperature. J. Phys. Chem. B 109, 1849–1856. doi:10.1021/jp0457489

CrossRef Full Text | Google Scholar

Wan, Y., Guo, Z., Zhu, T., Yan, S., Johnson, J., and Huang, L. (2015). Cooperative Singlet and Triplet Exciton Transport in Tetracene Crystals Visualized by Ultrafast Microscopy. Nat. Chem 7, 785–792. doi:10.1038/nchem.2348

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasielewski, M. R. (1992). Photoinduced Electron Transfer in Supramolecular Systems for Artificial Photosynthesis. Chem. Rev. 92, 435–461. doi:10.1021/cr00011a005

CrossRef Full Text | Google Scholar

Wei, W., Ouyang, S., and Zhang, T. (2020). Perylene Diimide Self-Assembly: From Electronic Structural Modulation to Photocatalytic Applications. J. Semicond. 41, 091708. doi:10.1088/1674-4926/41/9/091708

CrossRef Full Text | Google Scholar

Wilson, M. W. B., Rao, A., Ehrler, B., and Friend, R. H. (2013). Singlet Exciton Fission in Polycrystalline Pentacene: From Photophysics toward Devices. Acc. Chem. Res. 46, 1330–1338. doi:10.1021/ar300345h

PubMed Abstract | CrossRef Full Text | Google Scholar

Würthner, F., Saha-Möller, C. R., Fimmel, B., Ogi, S., Leowanawat, P., and Schmidt, D. (2016). Perylene Bisimide Dye Assemblies as Archetype Functional Supramolecular Materials. Chem. Rev. 116, 962–1052. doi:10.1021/acs.chemrev.5b00188

PubMed Abstract | CrossRef Full Text | Google Scholar

Xuan, F., Chen, Y., and Quek, S. Y. (2019). Quasiparticle Levels at Large Interface Systems from Many-Body Perturbation Theory: The XAF-GW Method. J. Chem. Theor. Comput. 15, 3824–3835. doi:10.1021/acs.jctc.9b00229

PubMed Abstract | CrossRef Full Text | Google Scholar

Youn, J., Dholakia, G. R., Huang, H., Hennek, J. W., Facchetti, A., and Marks, T. J. (2012). Influence of Thiol Self-Assembled Monolayer Processing on Bottom-Contact Thin-Film Transistors Based on N-type Organic Semiconductors. Adv. Funct. Mater. 22, 1856–1869. doi:10.1002/adfm.201102312

CrossRef Full Text | Google Scholar

Zhang, G., Zhao, J., Chow, P. C. Y., Jiang, K., Zhang, J., Zhu, Z., et al. (2018). Nonfullerene Acceptor Molecules for Bulk Heterojunction Organic Solar Cells. Chem. Rev. 118, 3447–3507. doi:10.1021/acs.chemrev.7b00535

PubMed Abstract | CrossRef Full Text | Google Scholar