- Department of Chemical Engineering, Imperial College London, London, United Kingdom
Mechanochemistry utilizes mechanical forces to activate chemical bonds. It offers environmentally benign routes for both (bio) organic and inorganic syntheses. However, direct comparison of mechanochemistry results is often very challenging. In mechanochemical synthetic protocols, ball mill setup (mechanical design and grinding vessel geometry) in addition to experimental parameters (milling frequency, duration, ball count and size) vary broadly. This fact poses a severe issue to further progress in this exciting research area because ball mill setup and experimental parameters govern how much kinetic energy is transferred to a chemical reaction. In this work, we address the challenge of comparing mechanochemical reaction results by taking the energy dose provided by ball mills as a unified metric into account. In this quest, we applied kinematic modeling to two ball mills functioning under distinct working principles to express the energy dose as a mathematical function of the experimental parameters. By examining the effect of energy dose on the extent of the mechanocatalytic depolymerization (MCD) of lignocellulosic biomass (beechwood), we found linear correlations between yield of water-soluble products (WSP) and energy dose for both ball mills. Interestingly, when a substrate layer is formed on the grinding jar wall and/or grinding medium, a weak non-linear correlation between water-soluble products yield and energy dose is identified. We demonstrate that the chemical reaction’s best utilization of kinetic energy is achieved in the linear regime, which presents improved WSP yields for given energy doses. In the broader context, the current analysis outlines the usefulness of the energy dose as a unified metric in mechanochemistry to further the understanding of reaction results obtained from different ball mills operating under varied experimental conditions.
Introduction
Mechanochemistry employs mechanical forces to drive chemical reactions, which can be sustained by milling, grinding, or extrusion with no need for bulk dissolution of reactants, thus opening up new avenues for the design of organic reactions (Stolle et al., 2011; Do and Friščić, 2016; Hernández and Bolm, 2017). Importantly, mechanochemistry enables chemical reactivity inaccessible in solution. In this instance, solvent-free catalytic routes to depolymerize cellulose (Hick et al., 2010; Meine et al., 2012; Hilgert et al., 2013; Shrotri et al., 2013; Zhang and Jerome, 2013; Käldström et al., 2014a; Liao et al., 2014; Schüth et al., 2014; Yabushita et al., 2014; Dornath et al., 2015; Shrotri et al., 2015; Dong et al., 2016; Schneider et al., 2016; Yu et al., 2016; Schneider et al., 2017b; Furusato et al., 2018; Karam et al., 2018; Kobayashi and Fukuoka, 2018), lignocellulosic biomass (Meine et al., 2012; Carrasquillo-Flores et al., 2013; Käldström et al., 2014a; Käldström et al., 2014b; Schüth et al., 2014; Loustau-Cazalet et al., 2016; Schneider et al., 2017a), and more recently, technical lignins (Kleine et al., 2013; Dabral et al., 2015; Brittain et al., 2018; Dabral et al., 2018) constitute outstanding examples demonstrating the potential of mechanochemistry to enable chemical reactivity inaccessible in solution under ambient conditions. These routes are known as mechanocatalytic depolymerization (MCD). Recently, atomistic modeling provided in-depth insight into the impact of mechanical forces on the MCD of cellulose and lignin (Amirjalayer et al., 2019). On the one hand, mechanical forces are proposed to produce conformational changes in the pyranic ring, activating latent states in the MCD of cellulose, facilitating the glycosidic bond cleavage (Schüth et al., 2014). In this manner, compared to a thermally activated process, the mechanochemical conversion was predicted to decrease the activation barrier by a factor of five (Amirjalayer et al., 2019). On the other hand, the cleavage of the most common lignin linkages (β-O-4 aryl alkyl ether) seems to be favored by stretching forces (Patel et al., 2020). Stretching of polymeric lignin chains may also be achieved by friction in a ball mill.
Experimentally, MCD of lignocellulose is performed by subjecting dry (ligno)cellulosic biomass, impregnated with strong acids (e.g., H2SO4, HCl, p-toluenosulfonic acid) or mixed with solid acids (e.g. kaolinites), to ball milling for a duration of 1–3 h. Under optimized conditions, this procedure fully converts lignocellulosic materials into water-soluble products (WSP) via acid-catalyzed depolymerizing reactions on cellulose, hemicellulose, and lignin (Hick et al., 2010; Meine et al., 2012). Other chemical processes also happen together with MCD, contributing to the water solubility of the reaction products. Notably, the formation of α(1→6)-oligoglucosaccharides from cellulose and hemicellulose enhances the water solubility of the products (Shrotri et al., 2013; Dornath et al., 2015). In addition, native lignin also undergoes depolymerization (Calvaruso et al., 2017b). Therefore, WSP obtained from lignocellulose is a complex mixture of oligosaccharides and depolymerized lignin oligomers. Under low severity conditions (pH 1, 140°C for 1 h), the WSP can easily undergo further saccharification in aqueous medium, leading to lignin precipitation. As a result, an acidified solution of C5 and C6 sugars is obtained while water-soluble lignin species are removed from solution by the precipitation of lignin (Käldström et al., 2014a; Käldström et al., 2014b; Calvaruso et al., 2017a; Calvaruso et al., 2017b). In effect, MCD of lignocellulosic materials holds great promise as an entry-point process for integrated fractionation processes yielding sugars and lignins for the sustainable manufacture of chemicals and biofuels.
Despite the promise, progress in this exciting research area is still slowed down by difficulties in comparing results across the literature. When comparing reaction data, the description of milling conditions is insufficient to allow a direct analysis because the energy dose provided by a ball mill also depends on its mechanical design and grinding vessel geometry, which are often not provided. Therefore, to advance mechanochemistry in its breadth and depth, it is urgent to apply mathematical models to determine the energy dose provided by ball mills as a function of process parameters, thus generating a unified metric to analyze the reaction results.
Several studies have been dedicated to determining the kinetic energy dose that ball mills provide in metal alloying (Burgio et al., 1991; Magini et al., 1993; Magini et al., 1994; Magini et al., 1996). Despite the valuable insights gained in metal alloying, the application of kinematic modeling of ball mills to determine the energy dose provided by a mill to reactants in organic reactions is still in its infancy. Kinematic modeling of planetary ball mills provides the velocity and acceleration of a ball in a grinding jar, allowing for the determination of the energy dose supplied by a mill to a powder. Kinematic equations are derived from specific parameters of the mill mechanical designs, expressing the energy dose as a function of experimental parameters, e.g., milling frequency, duration, ball count and size (Burgio et al., 1991; Magini et al., 1993; Magini et al., 1994; Magini et al., 1996). Based on the collision theory, the modeling considers the mill mechanical design of a mill in addition to the geometry of a grinding vessel. During the impacts on the jar walls, a ball transfers its kinetic energy to the powder. In the kinematic modeling, the impact events are taken as the dominant energy transfer mechanism. In this instance, friction is not accounted for in the kinematic equations of planetary mills. In practice, the operation conditions of a planetary mill are optimized by a trial-and-error approach to minimize friction, preventing excessive heat generation, which may cause the thermal decomposition of organic molecules and polymers.
We recently explored the concepts underlining the kinematic modeling to determine the energy dose provided by a high energy mill, shedding light on the macroscopic relations between energy dose and WSP yield obtained from the MCD of α-cellulose and beechwood acidified by H2SO4 impregnation (Kessler et al., 2018). Herein, we explore the energy dose as a unified explanatory variable to compare the results from MCD of beechwood acidified with H2SO4 performed in ball mills of different working principles under varied milling conditions. In this report, the presentation of results and discussion is organized into four parts. The first presents the mechanical design of the mills and the geometry of the grinding jars. The second describes the key aspects to consider in the kinematic modeling of planetary mills. Using energy dose as a unified metric of the milling parameters, the third part compares the results of 47 experiments performed in the planetary mill. The fourth part quantitatively examines two datasets obtained from different ball mill setups operating under varied milling conditions, providing detailed insight into the relationship between WSP yield and energy dose.
Materials and Methods
Materials
Beechwood chips (approximately 2 × 2 × 6 mm in dimension, Räuchergold® KL 2–16 provided by J. Rettenmaier and Söhne), diethyl ether (for synthesis, VWR Chemicals); sulfuric acid (95%, VWR Chemicals) were used as received.
Acidification of Beechwood by H2SO4 Impregnation
Beechwood (20 g) was suspended in a 0.125 mol/L sulfuric acid solution in diethyl ether (160 ml) under magnetic stirring (300 rpm) at room temperature for 2 h. Next, diethyl ether was removed under reduced pressure by using a rotary evaporator (Heidolph Rotary Evaporator Hei VAP series). The solvent-free, acid-impregnated substrate was immediately used in the MCD experiments.
MCD Experiments Carried out in a Planetary Ball Mill
A planetary ball mill (Pulverisette seven premium line, Fritsch) equipped with stainless steel milling jars (80 ml filling capacity) and stainless steel balls were used. An experimental set was generated by varying rotational speed, milling time, and ball count and size. The milling parameters of the experiments are summarized in Supplementary Table S1 (Supplementary Material). The H2SO4-impregnated beechwood (6.4 g per jar) together with the defined number of milling balls were added to the jars and milled for the specified time. During the milling process, the jar temperature was held between 35 and 45°C by applying cooling cycles (in which the milling was paused until the jar cooled down to 35°C). The process times specified in Supplementary Table S1 apply exclusively to the milling with the set speed. The milled substrate was removed from the jars in a fume hood. WSP yield was determined directly in sequence.
MCD Experiments Carried out in a High Energy Ball Mill
A high-energy ball mill (Emax mill, Retsch) equipped with stainless-steel milling jars (50 ml filling capacity) and stainless-steel balls were employed. An experimental set was generated by varying rotational speed, milling time, and ball count and size. The milling parameters of the experiments are listed in Supplementary Table S2 (Supplementary Material). The H2SO4-impregnated beechwood (4 g per jar) together with the defined number of milling balls were added to the jars and milled for the specified time. During the milling process, the jar temperature was controlled between 35 and 45°C by using an external cooling system attached to the mill (VWR RC-10 digital chiller). The process times specified in Supplementary Table S2 apply exclusively to the milling with the set speed. The milled substrate was removed from the jars in a fume hood. WSP yield was determined directly in sequence.
Determination of WSP Yield
To a weighed centrifuge tube (50 ml Greiner Bio-One, polypropylene conical base centrifuge tube), the milled H2SO4-impregnated beechwood (1 g, weighed at a 0.1 mg precision) was added to the tube and suspended in distilled water (10 ml). The mixture was sonicated in an ultrasonic bath at room temperature for a total of 30 min (VWR USC 1200 HF ultrasonic bath operating at a frequency of 132 kHz). During the sonication, the centrifuge tube was manually shaken once in a while. Next, the mixture was centrifuged at 9,000 rpm (relative centrifugal force, RCF: 8,694) for 10 min in a Sigma 3–18 L centrifuge. The supernatant (WSP solution) was separated from the remnant solid. The centrifuge tube containing the insoluble residue was dried overnight at 40°C under reduced pressure (1 mbar). The weight of the centrifuge tube containing the dried solid residue was determined. The mass of solid residue (
Where:
Digital Optical Microscopy and Particle Size Determination
Imaging and particle size determination was carried out on a Keyence VHX-5000 digital microscope. A total of 3,800–3,900 particles were measured. The particle size distribution was estimated from the maximum diameter of the particles.
Results and Discussion
Mechanical Design of the Mills and Geometry of the Grinding Jars
The energy dose supplied by the mills depends on the mechanical design of the milling device and the geometry of the grinding jars (Burgio et al., 1991; Magini et al., 1993; Magini et al., 1994; Magini et al., 1996). In this section, we present the key features of the mechanical design of the planetary mill and the high-energy Emax mill. Figure 1 shows a simplified schematic representation of the two mills, indicating ball-wall impact points and ball-wall friction zones in the jar during the mill operation. The characteristic parameters of the two ball mills are listed in Table 1.
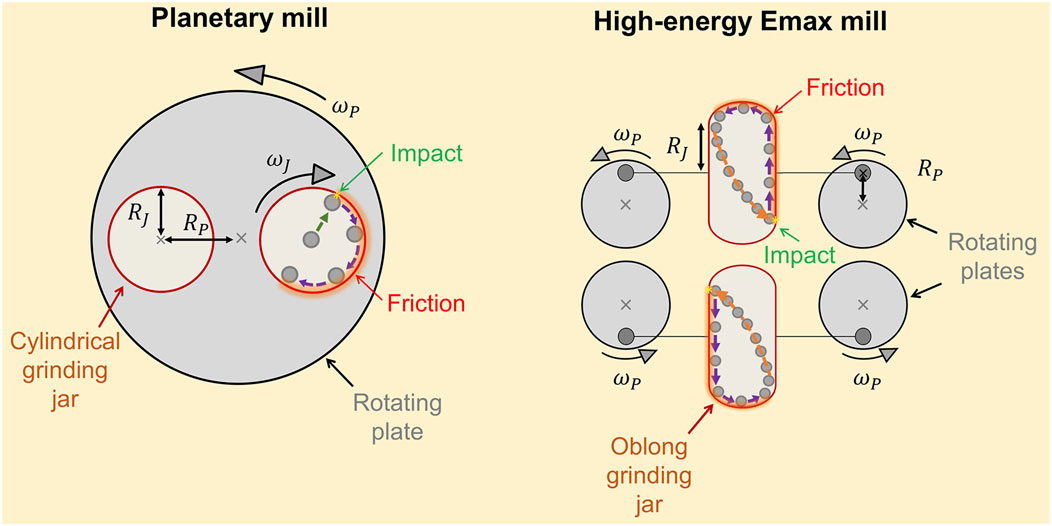
FIGURE 1. Simplified representation of the key features of the mechanical design of the planetary mill (left) and the high-energy Emax mill (right). In this schematic representation, the trajectory of a ball for each grinding jar geometry is presented. The asterisk “*” in yellow color represents ball-wall impact points, and the blue arrows indicate the idealized moviment of the ball on the wall creating a ball-wall friction zone. For clarity, no representation of the grinding medium bulk is presented. However, ball-ball friction becomes substantial when loading the jar with a large number of balls of small diameter. Detailed information about the internal dimensions of the jars is presented in Supplementary Figure S1 (Supplementary Material).
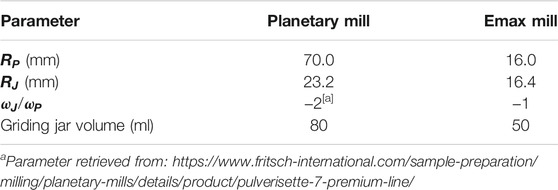
TABLE 1. Characteristic parameters of the planetary ball mill (“Pulverissete 7 Premium Line”) and the high-energy Emax ball mill (Retsch GmbH).
The planetary ball mill employs cylindrical grinding jars (Figure 1, left). The jars present an internal radius indicated by
The high-energy Emax mill is designed to operate with oblong grinding jars (Figure 1, right). They are each fixed on two plates which are synchronously rotating with an
Kinematic Modeling of Planetary Mills
Burgio et al. (1991) and Magini et al. (1993), Magini et al. (1994), Magini et al. (1996) presented the kinematic modeling of planetary ball mills to determine the velocity of a ball
Owing to momentum transfer, the ball velocity becomes
The energy transferred to the substrate from one ball during one collision (
However, the operation of planetary mills involves more than one ball. This implies that some balls will inevitably impede the impacts of others with the inner wall of the grinding jar. This reciprocal hindering depends on the degree of filling of the grinding jar. To account for the operation of the ball milling with multiple balls as the grinding medium, a yield coefficient (
Burgio et al. derived the yield coefficient from analytical relations (Burgio et al., 1991). In short,
Finally,
The collision frequency,
Where
where
Replacing (5), (7) and (12) in (13), the expression for calculating the energy dose E becomes Eq. 14:
Finally, considering that
The adaption of the kinematic model from a planetary ball mill to the high-energy Emax mill was detailed in our previous work (Kessler et al., 2018). To account for the Emax mill operation, the relation
Energy Dose as a Unified Metric for Comparing Mechanochemical Reaction Results
To examine the effect of the kinetic energy dose upon the WSP yield obtained from the MCD of H2SO4-impregnated beechwood, a total number (n) of 47 experiments were performed in a planetary mill operating under varied conditions, i.e., different ball diameters (4–20 mm), ball counts (4–391), rotational speeds (400–800 rpm), and milling durations (0.18–4.4 h), as listed in Supplementary Table S1. Figure 2 presents a chart correlating the WSP yields with the respective energy doses provided by the planetary ball mill in each experiment.
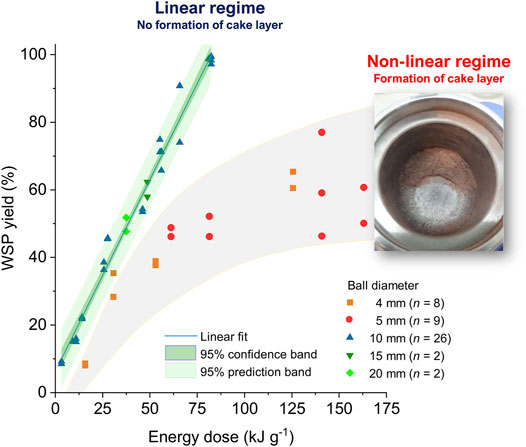
FIGURE 2. Dependence of WSP yield on the kinetic energy dose provided to H2SO4-impregnated beechwood by the planetary mill (Pulverisette seven premium, Fritsch) employing varied conditions as listed in Supplementary Table S1. Unlike the regions presented in green tones, which represent the 95% confidence band and 95% prediction band, the region highlighted in gray is solely intended to serve as a guide for the eyes, qualitatively outlining the data dispersion for the results obtained from MCD in the non-linear regime.
From the WSP yield vs. energy dose chart, a linear and a non-linear regime for the dependence of WSP yield on the kinetic energy dose were identified for the MCD of H2SO4-impregnated beechwood. For the linear regime, WSP yields rose from 9% at 3.3 kJ g−1 to 99% at 81.1 kJ g−1. Notably, a low data dispersion was obtained, as indicated by the adjusted r2 value (0.9834). Within the upper and lower 95% confidence bounds, the predicted values for the mean WSP yields are distributed ±2–3% around the fitted curve. In turn, within the upper and lower 95% prediction bounds, a new data point is expected to lie in a region ±7–8% around the fitted curve. The linear regime was observed when performing the MCD experiments employing a griding medium composed of balls of a diameter equal to or higher than 10 mm. For these (relatively) large balls, the overall ball surface area of the grinding medium is minimized. Hence, ball-ball friction occurring in the bulk of the grinding medium is reduced, ensuring a dominant energy transfer through the impact of the balls against the jar wall.
In stark contrast, no linear correlation was found in the highly scattered dataset obtained from the MCD of H2SO4-impregnated beechwood carried out using a grinding medium composed of balls of 4- or 5-mm in diameter. Interestingly, for the non-linear regime, WSP yields increased from 8% at 15.7 kJ g−1 to highly scattered values around 60% for energy doses between 125–165 kJ g−1. No further improvement in the WSP yields could be achieved by prolonging the milling duration or increasing the rotational speed. Hence, a limitation of the depolymerization extent (to a WSP yield of around 63%) is visible for the MCD of H2SO4-impregnated beechwood carried out employing a grinding medium composed of balls of 4- or 5-mm in diameter. The observation appears to be associated with the formation of a solid deposit (also known as cake layer or coating layer) on the grinding jar wall and/or grinding medium, as depicted in the inset of Figure 2. The cake layer has different mechanical properties than wood chips or sawdust in the initial milling stages of the H2SO4-impregnated beechwood. As a result, the formation of a thick layer of substrate buffers the ball-wall collision. The mechanism underlining the cake layer formation remains poorly understood in mechanochemistry. However, it is clear from Figure 2 that operating the ball mill for MCD in the linear regime, in which no cake layer is formed, corresponds to the best utilization of kinetic energy by the chemical reaction, boosting the WSP yield for a given energy dose provided by a ball mill.
Comparison of MCD Results Obtained in Different Ball Mill Setups
The strong correlation between WSP yield and energy dose provided by the planetary mill indicates that the energy dose serves as a “compounded” explanatory variable, enabling a direct comparison of results obtained from experiments carried out in a planetary mill under varied experimental conditions. This section expands our analysis by comparing results obtained from ball mills of different operation principles. In this quest, we revisited the previously reported data obtained from the MCD of H2SO4-impregnated beechwood carried out in a high-energy Emax mill (Kessler et al., 2018). The high-energy Emax mill also produces a high-frequency impact of the griding medium against the jar walls like a planetary ball mill. Nonetheless, the operating mechanism of the high-energy Emax mill results in intensified frictional forces owing to the jar geometry and movement. The kinematic modeling of the ball mills solely includes the impact component as the energy transfer mechanism. In this manner, the comparison of MCD results obtained from the planetary mill and high energy Emax mill also provides qualitative but still critical insight into the effect of high friction on the MCD process. Figure 3 presents a chart comparing MCD data from the experiments carried out in the high-energy Emax mill or planetary ball mill (linear regime) under varied conditions and the linear fit for each dataset. The linear fit parameters are presented in Table 2.
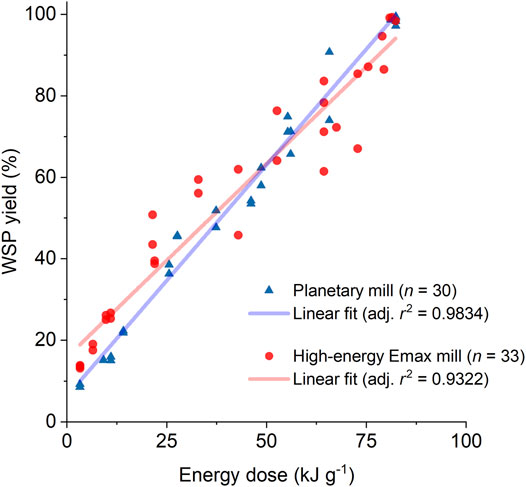
FIGURE 3. Comparison of MCD data from the experiments carried out in the high-energy Emax mill (Kessler et al., 2018) and the planetary ball mill (displaying the results from the linear regime) under varied conditions, and the linear fit for each dataset. Milling conditions are listed in Supplementary Table S1 and Supplementary Table S2.
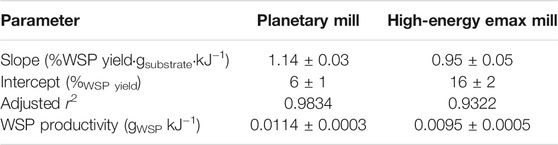
TABLE 2. Linear regression parameters derived from the MCD datasets for the experiments carried out in the planetary and high-energy Emax mill, presented in Figure 3.
For MCD of H2SO4-impregnated beechwood carried out in the high energy Emax mill, the WSP yields linearly increased with the energy dose provided by the mill (from 14% at 3.3 kJ g−1–99% at 81.5 kJ g−1). In stark contrast to the planetary mill experiments, no cake layer was formed in the high-energy Emax mill experiments, even when using a grinding medium composed of balls equal to or smaller than 5-mm in diameter. However, the results from the experiments carried out in the Emax mill presented a data dispersion larger than those from the experiments performed in the planetary mill, as indicated by the smaller adjusted r2 value (0.9322 vs. 0.9834). F-test using the linear fit showed that the differences in the datasets are statistically relevant (p = 0.003). Likewise, the slopes are statistically different (p = 0.002). From the slopes obtained from the linear fitting, we derived the WSP productivity (expressed in gWSP kJ−1) by multiplying the slope value by a factor of 0.01 (to convert the percentual yield into decimal yield), followed by algebraic simplification. For the MCD performed in the planetary mill, the WSP productivity was 20% higher than that found for the high-energy Emax mill (0.0114 ± 0.0003 gWSP kJ−1 vs. 0.0095 ± 0.0005 gWSP kJ−1, respectively). This difference is probably associated with the increased component of frictional forces provided by the Emax mill. Tentatively, the frictional forces would counteract the impact forces by realigning the polymer chains, thus reverting the conformational changes required for the activation of cellulose towards depolymerizing reactions (Schüth et al., 2014; Amirjalayer et al., 2019).
As also shown in Table 2, the intercept values are different [planetary mill: 6 ± 1% vs. high-energy Emax mill: 16 ± 2%). The intercepts present the WSP yield extrapolated at “time zero.” In the initial stage of the MCD process, it is natural to expect a redistribution of the acid catalyst impregnated in the beechwood chips when reducing the chip size from a millimetric down to a micrometric scale (Kaufman Rechulski et al., 2015). In effect, we expect the homogenization of acid catalyst distribution on the substrate to be a critical factor accounting for the difference in the intercept values, as the depolymerizing reactions on lignocellulose proceed very slowly when milling the substrate with no added acid catalyst. Notably, it takes over 1,000 h to achieve full conversion of cellulosic fibers into WSP by milling the substrate with no added catalyst] (Steurer and Hess, 1944; Grohn, 1958; Grohn and Schierbaum, 1958; Simionescu and Vasiliu-Oprea, 1969; Oprea, 1978).
To assess the impact of the different mills on the communition of H2SO4-impregnated beechwood chips, MCD was carried out in each ball mill operating under conditions to provide a low energy dose of 3.3 kJ mol−1. In sequence, the substrate was examined by digital optical microscopy at ×300 and ×800 magnification to determine the particle size distribution. Figure 4 displays the typical appearance of the particles and the particle size distribution obtained for each experiment.
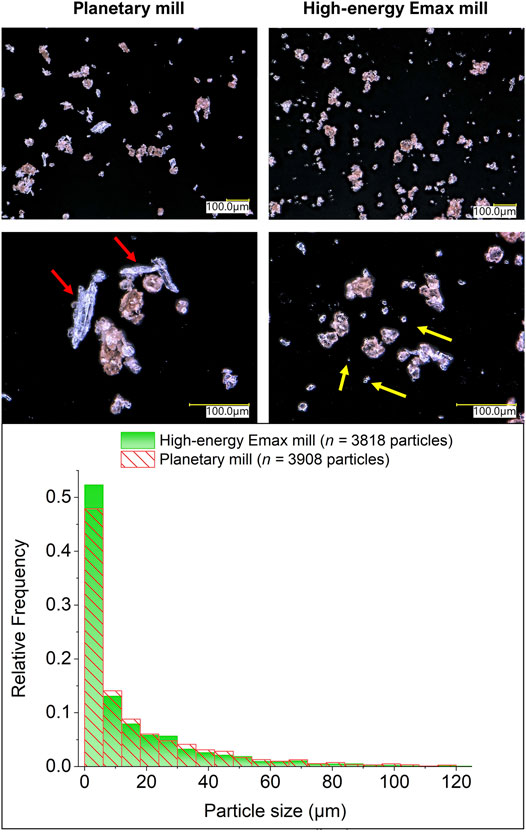
FIGURE 4. Digital optical micrographs and size particle distribution for H2SO4-impregnated beechwood processed at low energy dose (3.3 kJ mol−1) in different mills. The arrows in yellow color indicate small particles (1–6 μm) typically formed by the H2SO4-impregnated beechwood processed in a high-energy Emax mill. The arrows in red color indicate substantial residual particles (50–125 μm) typically obtained by processing H2SO4-impregnated beechwood in the planetary mill at a low energy dose.
Two classes of particles can be identified in the images in Figure 4. In the first, fibrous particles, which are white/translucent in appearance, are seen. In the second, small reddish-brown rugged aggregates are found. In detail, the powder product obtained in the planetary mill shows many large white fibrous particles next to the reddish-brown aggregates. In stark contrast, the powder product obtained in the high-energy Emax mill is a (relatively) homogeneous mixture of small reddish-brown aggregates with only very few fibrous white particles identified. In line with these qualitative observations, the particle distribution for the powder product obtained in the high-energy Emax mill shows a more prominent population of particle size smaller than 6 μm, compared to the particle size distribution for the powder product obtained in the planetary mill. In addition, the powder product obtained in the planetary shows populations of particles larger than 6 μm consistently higher than those present in the powder product from the high-energy Emax mill.
Overall, these observations substantiate the working hypothesis that the high-energy Emax mill reduces the size of beechwood chips more extensively than the planetary mill. As a result, we propose that the “initial stage” mass transfer process involved in the homogenization of the acid catalyst content on the substrate is more effective in the high-energy Emax mill, explaining the higher initial WSP yield for the MCD performed in the Emax mill at low energy doses. However, when the mass transfer limitations are relaxed, that is, when homogenization of the acid content is achieved, the WSP yield becomes governed by the intricacies of the energy dose transfer underlined by the operation principle of each ball mill setup.
Conclusion
We demonstrated the energy dose as a unified metric to compare the results from MCD of H2SO4-impregnated beechwood performed in different ball mill setups operating under varied experimental parameters. The data comparison provided in-depth insight into the macroscopic relationships between the WSP yield and energy dose provided by a ball mill. Notably, linear correlations between WSP yields and energy dose were observed for the experiments carried out in both ball mills. These correlations show that the MCD carried out in a planetary mill presents a WSP productivity higher than that in a high-energy Emax mill by 20%. However, when a cake layer is formed on the grinding jar and/or the grinding medium, the productivity of WSP per energy dose markedly decreases. This observation indicates that the mechanochemical reactions should be performed under conditions that prevent the cake layer formation. Under such conditions, the best use of the energy dose by the chemical conversion is reached. Moreover, provided no cake layer is formed, we expect that the MCD of other types of lignocellulosic materials should also observe a linear correlation between WSP yield and energy dose, owing to the MCD process to be agnostic to the type of lignocellulosic substrate (Meine et al., 2012; Käldström et al., 2014a; Käldström et al., 2014b).
In the broader context, using the energy dose as a unified metric offers a productive avenue to understand the effects of mill setup and operational parameters upon the outcomes of mechano-assisted chemical reactions. Such data analysis is conducive to translating optimal process settings from one milling device to another via rational experiment design. In fact, beginning with the energy dose values required to achieve a certain chemical conversion extent, the macroscopic correlations between product yield and energy dose enable the translation of milling parameters between ball mills by employing the energy dose as an educated guess in the experiment design. Such a rational design of experiments holds promise to supersede the time-consuming trial-and-error approaches in the current practice of organic and inorganic syntheses assisted by mechanical forces.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
RR conceived the idea and managed the project. MK designed and performed the experiments, analyzed data, and drafted the manuscript. MK and RR discussed the results and reviewed the manuscript.
Funding
This work was financially supported by ERC Consolidator Grant “Ligninfirst” (Grant agreement ID: 725762).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to Prof Valeria Garbin (Department of Chemical Engineering, Delft University of Technology, Netherlands) for fruitful discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.816553/full#supplementary-material
References
Amirjalayer, S., Fuchs, H., and Marx, D. (2019). Understanding the Mechanocatalytic Conversion of Biomass: A Low‐Energy One‐Step Reaction Mechanism by Applying Mechanical Force. Angew. Chem. Int. Ed. 58, 5232–5235. doi:10.1002/anie.201811091
Brittain, A. D., Chrisandina, N. J., Cooper, R. E., Buchanan, M., Cort, J. R., Olarte, M. V., et al. (2018). Quenching of Reactive Intermediates during Mechanochemical Depolymerization of Lignin. Catal. Today 302, 180–189. doi:10.1016/j.cattod.2017.04.066
Burgio, N., Iasonna, A., Magini, M., Martelli, S., and Padella, F. (1991). Mechanical Alloying of the Fe−Zr System. Correlation between Input Energy and End Products. Il Nuovo Cimento D 13, 459–476. doi:10.1007/BF02452130
Calvaruso, G., Clough, M. T., Rechulski, M. D. K., and Rinaldi, R. (2017a). On the Meaning and Origins of Lignin Recalcitrance: A Critical Analysis of the Catalytic Upgrading of Lignins Obtained from Mechanocatalytic Biorefining and Organosolv Pulping. ChemCatChem 9, 2691–2700. doi:10.1002/cctc.201700473
Calvaruso, G., Clough, M. T., and Rinaldi, R. (2017b). Biphasic Extraction of Mechanocatalytically-Depolymerized Lignin from Water-Soluble Wood and its Catalytic Downstream Processing. Green. Chem. 19, 2803–2811. doi:10.1039/C6GC03191A
Carrasquillo-Flores, R., Käldström, M., Schüth, F., Dumesic, J. A., and Rinaldi, R. (2013). Mechanocatalytic Depolymerization of Dry (Ligno)cellulose as an Entry Process for High-Yield Production of Furfurals. ACS Catal. 3, 993–997. doi:10.1021/cs4001333
Dabral, S., Mottweiler, J., Rinesch, T., and Bolm, C. (2015). Base-catalysed Cleavage of Lignin β-O-4 Model Compounds in Dimethyl Carbonate. Green. Chem. 17, 4908–4912. doi:10.1039/c5gc00186b
Dabral, S., Wotruba, H., Hernández, J. G., and Bolm, C. (2018). Mechanochemical Oxidation and Cleavage of Lignin β-O-4 Model Compounds and Lignin. ACS Sustain. Chem. Eng. 6, 3242–3254. doi:10.1021/acssuschemeng.7b03418
Do, J.-L., and Friščić, T. (2016). Mechanochemistry: A Force of Synthesis. ACS Cent. Sci. 3, 13–19. doi:10.1021/ACSCENTSCI.6B00277
Dong, Y., Schneider, L., Hu, T., Jaakkola, M., Holm, J., Leveque, J. M., et al. (2016). Direct Acid-Catalysed Mechanical Depolymerisation of Fibre Sludge to Reducing Sugars Using Planetary Milling. Biomass Bioenergy 86, 36–42. doi:10.1016/j.biombioe.2016.01.006
Dornath, P., Cho, H. J., Paulsen, A., Dauenhauer, P., and Fan, W. (2015). Efficient Mechano-Catalytic Depolymerization of Crystalline Cellulose by Formation of Branched Glucan Chains. Green. Chem. 17, 769–775. doi:10.1039/C4GC02187H
Furusato, S., Takagaki, A., Hayashi, S., Miyazato, A., Kikuchi, R., and Oyama, S. T. (2018). Mechanochemical Decomposition of Crystalline Cellulose in the Presence of Protonated Layered Niobium Molybdate Solid Acid Catalyst. ChemSusChem 11, 888–896. doi:10.1002/cssc.201702305
Grohn, H., and Schierbaum, F. (1958). Enzymatische Abbauversuche an schwinggemahlenem Holz und Zellstoff. Holzforschung 12, 65–73. doi:10.1515/hfsg.1958.12.3.65
Grohn, H. (1958). Mechanochemical Degradation of Cellulose by Vibratory Grinding. J. Polym. Sci. 30, 551–559. doi:10.1002/pol.1958.1203012146
Hernández, J. G., and Bolm, C. (2017). Altering Product Selectivity by Mechanochemistry. J. Org. Chem. 82, 4007–4019. doi:10.1021/acs.joc.6b02887
Hick, S. M., Griebel, C., Restrepo, D. T., Truitt, J. H., Buker, E. J., Bylda, C., et al. (2010). Mechanocatalysis for Biomass-Derived Chemicals and Fuels. Green. Chem. 12, 468–474. doi:10.1039/B923079C
Hilgert, J., Meine, N., Rinaldi, R., and Schüth, F. (2013). Mechanocatalytic Depolymerization of Cellulose Combined with Hydrogenolysis as a Highly Efficient Pathway to Sugar Alcohols. Energy Environ. Sci. 6, 92–96. doi:10.1039/C2EE23057G
Käldström, M., Meine, N., Farès, C., Schüth, F., and Rinaldi, R. (2014b). Deciphering ‘water-Soluble Lignocellulose' Obtained by Mechanocatalysis: New Insights into the Chemical Processes Leading to Deep Depolymerization. Green. Chem. 16, 3528–3538. doi:10.1039/C4GC00004H
Käldström, M., Meine, N., Farès, C., Rinaldi, R., and Schüth, F. (2014a). Fractionation of ‘water-Soluble Lignocellulose' into C5/C6 Sugars and Sulfur-free Lignins. Green. Chem. 16, 2454–2462. doi:10.1039/c4gc00168k
Karam, A., Amaniampong, P. N., García Fernández, J. M., Oldani, C., Marinkovic, S., Estrine, B., et al. (2018). Mechanocatalytic Depolymerization of Cellulose with Perfluorinated Sulfonic Acid Ionomers. Front. Chem. 6, 74. doi:10.3389/fchem.2018.00074
Kaufman Rechulski, M. D., Käldström, M., Richter, U., Schüth, F., and Rinaldi, R. (2015). Mechanocatalytic Depolymerization of Lignocellulose Performed on Hectogram and Kilogram Scales. Ind. Eng. Chem. Res. 54, 4581–4592. doi:10.1021/acs.iecr.5b00224
Kessler, M., Woodward, R. T., Wong, N., and Rinaldi, R. (2018). Kinematic Modeling of Mechanocatalytic Depolymerization of α‐Cellulose and Beechwood. ChemSusChem 11, 552–561. doi:10.1002/cssc.201702060
Kleine, T., Buendia, J., and Bolm, C. (2013). Mechanochemical Degradation of Lignin and Wood by Solvent-free Grinding in a Reactive Medium. Green. Chem. 15, 160–166. doi:10.1039/C2GC36456E
Kobayashi, H., and Fukuoka, A. (2018). Development of Solid Catalyst-Solid Substrate Reactions for Efficient Utilization of Biomass. Bull. Chem. Soc. Jpn. 91, 29–43. doi:10.1246/bcsj.20170263
Liao, Y., Liu, Q., Wang, T., Long, J., Zhang, Q., Ma, L., et al. (2014). Promoting Hydrolytic Hydrogenation of Cellulose to Sugar Alcohols by Mixed Ball Milling of Cellulose and Solid Acid Catalyst. Energy Fuels 28, 5778–5784. doi:10.1021/ef500717p
Loustau-Cazalet, C., Sambusiti, C., Buche, P., Solhy, A., Bilal, E., Larzek, M., et al. (2016). Innovative Deconstruction of Biomass Induced by Dry Chemo-Mechanical Activation: Impact on Enzymatic Hydrolysis and Energy Efficiency. ACS Sustain. Chem. Eng. 4, 2689–2697. doi:10.1021/acssuschemeng.6b00194
Magini, M., Burgio, N., Iasonna, A., Martelli, S., Padella, F., and Paradiso, E. (1993). Analysis of Energy Transfer in the Mechanical Alloying Process in the Collision Regime. J. Mater. Synth. Process. 1, 135–144.
Magini, M., Colella, C., Guo, W., Iasonna, A., Martelli, S., and Padella, F. (1994). Some Hints about Energy Transfer in the Mechanosynthesis of Materials. Int. J. Mechanochem. Mech. Alloying 1, 14–25.
Magini, M., Iasonna, A., and Padella, F. (1996). Ball Milling: an Experimental Support to the Energy Transfer Evaluated by the Collision Model. Scripta Mater. 34, 13–19. doi:10.1016/1359-6462(95)00465-3
Mahler, S., and Pankratz, J. (2011). Laboratory Vibration Grinding Mill Having Inclined Grinding Bowls. US Patent 8,042,754 B2.
Meine, N., Rinaldi, R., and Schüth, F. (2012). Solvent-Free Catalytic Depolymerization of Cellulose to Water-Soluble Oligosaccharides. ChemSusChem 5, 1449–1454. doi:10.1002/cssc.201100770
Patel, D. H., Marx, D., and East, A. L. L. (2020). Improving the Yield and Rate of Acid‐Catalyzed Deconstruction of Lignin by Mechanochemical Activation. ChemPhysChem 21, 2660–2666. doi:10.1002/CPHC.202000671
Schneider, L., Haverinen, J., Jaakkola, M., and Lassi, U. (2016). Solid Acid-Catalyzed Depolymerization of Barley Straw Driven by Ball Milling. Bioresour. Technol. 206, 204–210. doi:10.1016/j.biortech.2016.01.095
Schneider, L., Haverinen, J., Jaakkola, M., and Lassi, U. (2017a). Effective Saccharification of Lignocellulosic Barley Straw by Mechanocatalytical Pretreatment Using Potassium Pyrosulfate as a Catalyst. Bioresour. Technol. 234, 1–7. doi:10.1016/j.biortech.2017.03.020
Schneider, L., Haverinen, J., Jaakkola, M., and Lassi, U. (2017b). Pretreatment and Fractionation of Lignocellulosic Barley Straw by Mechanocatalysis. Chem. Eng. J. 327, 898–905. doi:10.1016/j.cej.2017.06.175
Schüth, F., Rinaldi, R., Meine, N., Käldström, M., Hilgert, J., and Rechulski, M. D. K. (2014). Mechanocatalytic Depolymerization of Cellulose and Raw Biomass and Downstream Processing of the Products. Catal. Today 234, 24–30. doi:10.1016/j.cattod.2014.02.019
Shrotri, A., Lambert, L. K., Tanksale, A., and Beltramini, J. (2013). Mechanical Depolymerisation of Acidulated Cellulose: Understanding the Solubility of High Molecular Weight Oligomers. Green. Chem. 15, 2761–2768. doi:10.1039/C3GC40945G
Shrotri, A., Kobayashi, H., and Fukuoka, A. (2015). Efficient Catalytic Conversion of Cellulose to Platform Chemicals Using Mechanical Treatment. J. Jpn. Petrol. Inst. 58, 1–8. doi:10.1627/jpi.58.1
Simionescu, C., and Vasiliu-Oprea, C. (1969). Kinetics of Mechanochemical Decomposition of Cellulose by Vibratory Milling. Cellul. Chem. Technol. 3, 361–381.
Steurer, E., and Hess, K. (1944). The Process of Formation and the Mechano-chemical Degradation of High Polymers by Vibratory Milling. Z. Phys. Chem. 193, 248–257.
Stolle, A., Szuppa, T., Leonhardt, S. E. S., and Ondruschka, B. (2011). Ball Milling in Organic Synthesis: Solutions and Challenges. Chem. Soc. Rev. 40, 2317–2329. doi:10.1039/c0cs00195c
Yabushita, M., Kobayashi, H., Hara, K., and Fukuoka, A. (2014). Quantitative Evaluation of ball-milling Effects on the Hydrolysis of Cellulose Catalysed by Activated Carbon. Catal. Sci. Technol. 4, 2312–2317. doi:10.1039/c4cy00175c
Yu, Y., Long, Y., and Wu, H. (2016). Near-Complete Recovery of Sugar Monomers from Cellulose and Lignocellulosic Biomass via a Two-Step Process Combining Mechanochemical Hydrolysis and Dilute Acid Hydrolysis. Energy Fuels 30, 1571–1578. doi:10.1021/acs.energyfuels.5b02196
Keywords: mechanocatalysis, mechanochemistry, biorefinery, lignocellulose acid-hydrolysis, depolymerization, kinematic model, ball mill, energy dose
Citation: Kessler M and Rinaldi R (2022) Kinetic Energy Dose as a Unified Metric for Comparing Ball Mills in the Mechanocatalytic Depolymerization of Lignocellulose. Front. Chem. 9:816553. doi: 10.3389/fchem.2021.816553
Received: 16 November 2021; Accepted: 23 November 2021;
Published: 03 January 2022.
Edited by:
Tomas Ramirez Reina, University of Surrey, United KingdomReviewed by:
Cristina Megías-Sayago, Université de Strasbourg, FranceJose Luis Santos Muñoz, KU Leuven, Belgium
Copyright © 2022 Kessler and Rinaldi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roberto Rinaldi, ci5yaW5hbGRpMUBpbXBlcmlhbC5hYy51aw==
 Martin Kessler
Martin Kessler Roberto Rinaldi
Roberto Rinaldi