Theoretical laser cooling feasibility study of ZrH molecule at the fine structure level

A theoretical electronic structure calculation of the ZrH molecule is conducted via ab initio Complete Active Space Self-Consistent Field and the Multireference Configuration Interaction with Davidson correction calculation (CASSCF/MRCI + Q). The adiabatic potential energy curves (PECs) for the 53 low-lying electronic states in the representations of ^2s+1Λ^(+/−) and Ω^(+/−) for ZrH molecule have been investigated along with the internuclear distance R_e, the harmonic frequency ω_e, the dipole moment μ, the rotational constant B_e and the electronic transition energy with respect to the ground state T_e. are calculated. By using the canonical function approach, the vibrational energy E_v, the rotational constants B_v, the centrifugal constants D_v, and the turning points R_min and R_max have been calculated up to the vibrational level v = 18. Based on the investigated data, the Franck−Condon factors, the Einstein coefficient, the radiative lifetimes, and the vibrational branching ratio for the transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2 have been calculated. The large value of the radiative lifetimes in (ms) for these transitions proves that this molecule is not a good candidate for direct laser cooling.

1 Introduction

The characteristics of metal-hydrogen bonds and the function of metal d orbitals have led to an increase in the number of theoretical and experimental studies on transition metal hydrides. Both electron correlation and relativistic effects become significant for heavier transition metal hydrides. Generally speaking, low-lying electronic states with a variety of spatial and spin symmetries are closely clustered together in transition metal hydrides. This makes transition metal hydrides one of the most challenging possibilities for theoretical research, especially when combined with the electron correlation (McLean, 1983; Kraussand, 1985; Balasubraman et al., 1988; Balasubramanian et al., 1987; Hay and Martin, 1985).

Moreover, in the considered molecule, massive nuclear spins in the transition elements can produce complicated structural patterns with magnetic hyperfine structures (James et al., 1993). Chemistry may lead from the spectroscopy of these systems to better understand the bonding of transition metals, high-temperature chemical processes, and luminous chemical reactions (Langhoff and Bauschlicher, 1988; Korek and Hamdan, 2008). With a theoretical ab initio investigation, the electronic structures of diatomic molecules are required for astrophysics, astrochemistry, and laser cooling studies (Thompson and Ziurys, 2001).

The goal of the current study is to conduct a thorough theoretical analysis of several low-lying electronic states of the ZrH molecule, taking relativistic, electron correlation, and spin-orbit effects into account. SCF/SDCI/CPF calculations on two electronic states of ZrH have been performed by Langhoff et al. (1987a) without spin-orbit effects included. In this work, we perform a full active space (CASSCF/MRCI + Q) that incorporates the spin-orbit term on 36 electronic states of ZrH. To the best of our knowledge, there has been little theoretical and no experimental research done on the zirconium hydride ZrH molecule. This provided us with a strong incentive to examine the electronic structure of this molecule, as well as its spectroscopic characteristics and ro-vibrational studies. In the current work, the ab intio approach with an entire active space consistent field has been used to investigate the potential energy curves (PECs) of 53 electronic states for ZrH molecule in the ^2s+1Λ^(+/−) and Ω^(+/−) representations. All these calculations are followed by a ro-vibrational analysis in order to determine the values of vibrational energy E_v, the rotational constant B_v, the centrifugal distortion constant D_v, and the turning point abscissas R_min and R_max. Based on these investigated data, the Franck−Condon factors, the Einstein coefficient, the radiative lifetimes, and the vibrational branching ratio are determined for the transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2.

2 Computational methods

The state average Complete Active Self Consistent Field (CASSCF)/Multireference Configuration Interaction (MRCI + Q) has been used to investigate the doublet and quartet electronic states of the ZrH molecule with and without the spin-orbit coupling. By using the Breit-Pauli operator and the ECP spin-orbit operator for the Zr-atom, the total Hamiltonian H_t = H_e + W_SO is diagonalized with the help of the Born-Oppenheimer approximation along with the spin-orbit perturbation. The lowest energies have been calculated for the spin-orbit coupling states Ω = 1/2, 3/2, and 5/2. With the graphical interface, GABEDIT (Werner et al., 2025), and the computational chemistry program MOLPRO (Allouche, 2011), these calculations have been accomplished. For the ZrH molecule, the ECP28MDF basis set (Peterson et al., 2007) is used for the Zr atom with 12 valence electrons distributed as 4s² 4p⁶ 5s² 4d^2, and the aug-cc-pV5Z basis set (Dunning, 1989) is considered for the H atom with one valence electron 1s¹. Before we choose our basis set, we run several trials to choose the most accurate degeneracy between the states in the first and fourth symmetry. The ECP28MDF basis set and the aug-cc-pV5Z basis set gave the best degeneracy results.

As the MOPRO program can work only with the Abelian point group, the ZrH molecule is treated in C_2v instead of ${\mathrm{C}}_{\infty }$ v. The active space for the considered ZrH molecule is 6σ (Zr: 4d_0, 4d₂₊, 5P₀, 5s₁; H:1s,2s), 2π (Zr: 4d_{± 1,} 5p _{± 1}) and 1δ (Zr: 5d_2-), where the corresponding irreducible representation is 6a₁, 2b₁, 2b₂, and 1a₂ noted by [6,2,2,1], In order to obtain the potential energy curves, the estimated energy points are connected using the avoided-crossing rule for electronic states that belong to the same irreducible representation of the single/double point group ${\mathrm{C}}_{\infty \mathrm{V}}$. The one-dimensional Born-Oppenheimer Schrödinger equation is used to obtain the spectroscopic constants including R_e (equilibrium bond length), T_e (transition energy), ω_e (harmonic constant) and B_e (rotational constant). Due to the lack of experimental data on the ZrH molecule and its corresponding spectroscopic constants (R_e, T_e, ω_e, and B_e), the comparison between our obtained results with any other experimental result was not possible.

3 Results and discussion

For the spin-free ZrH molecule, the potential energy curves (PEC) using MRCI calculation for 22 doublet and quartet electronic states are investigated and plotted in Figures 1, 2 as a function of internuclear distance R in the ranges 1.20 Å ≤ R ≤ 2.20 Å and 1.20 Å ≤ R ≤ 4.80Å, respectively. For the spin-orbit coupling of the ZrH molecule, we investigated 31 electronic states where the corresponding potential energy curves are plotted in Figures 3a,b, where the ranges of energies are −46.902 → −46.862 Hartree and −46.857 → −46.841 Hartree, respectively. For the considered molecule ZrH, all of the studied states with spin-free and spin-orbit coupling are bound states, with depth potential energy curves indicating the strength of the bond and the stability of this molecule.

Figure 1

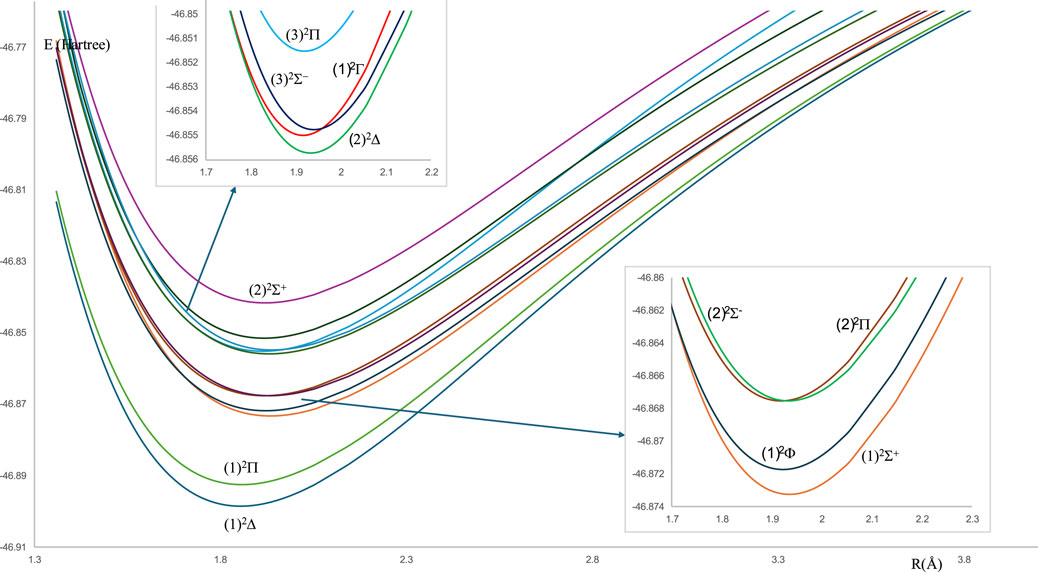
Figure 1. The spin-free potential energy curves of the doublet electronic states of the ZrH molecule.

Figure 2

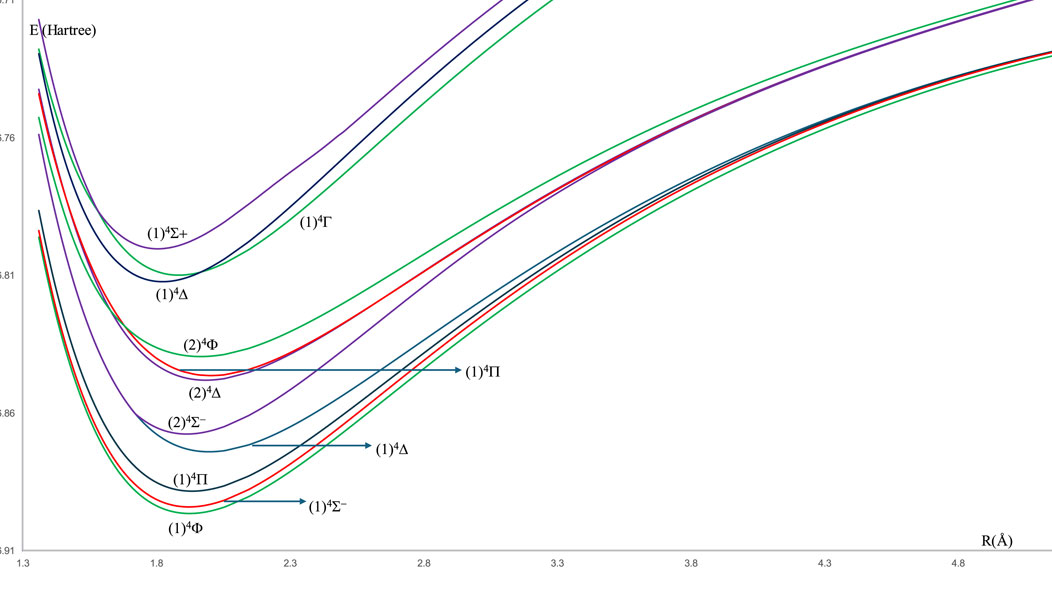
Figure 2. The spin-free potential energy curves of the quartet electronic states of the ZrH molecule.

Figure 3

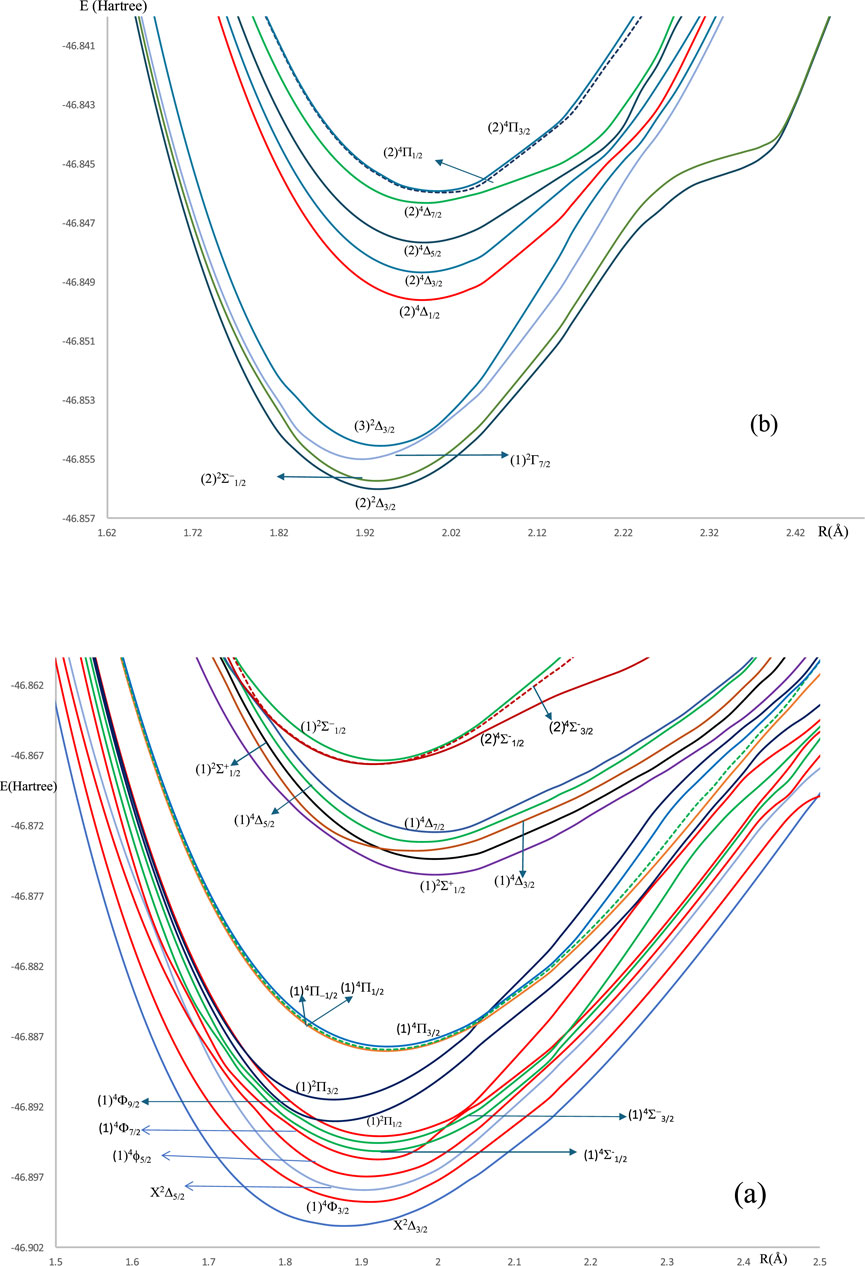
Figure 3. (a) The spin-orbit coupling potential energy curves in the range of −46.902 → −46.862 Hartree of ZrH molecule. (b) The spin-orbit coupling potential energy curves in the range of 46.857 → −46.841 Hartree of ZrH molecule.

3.1 Spectroscopic parameters

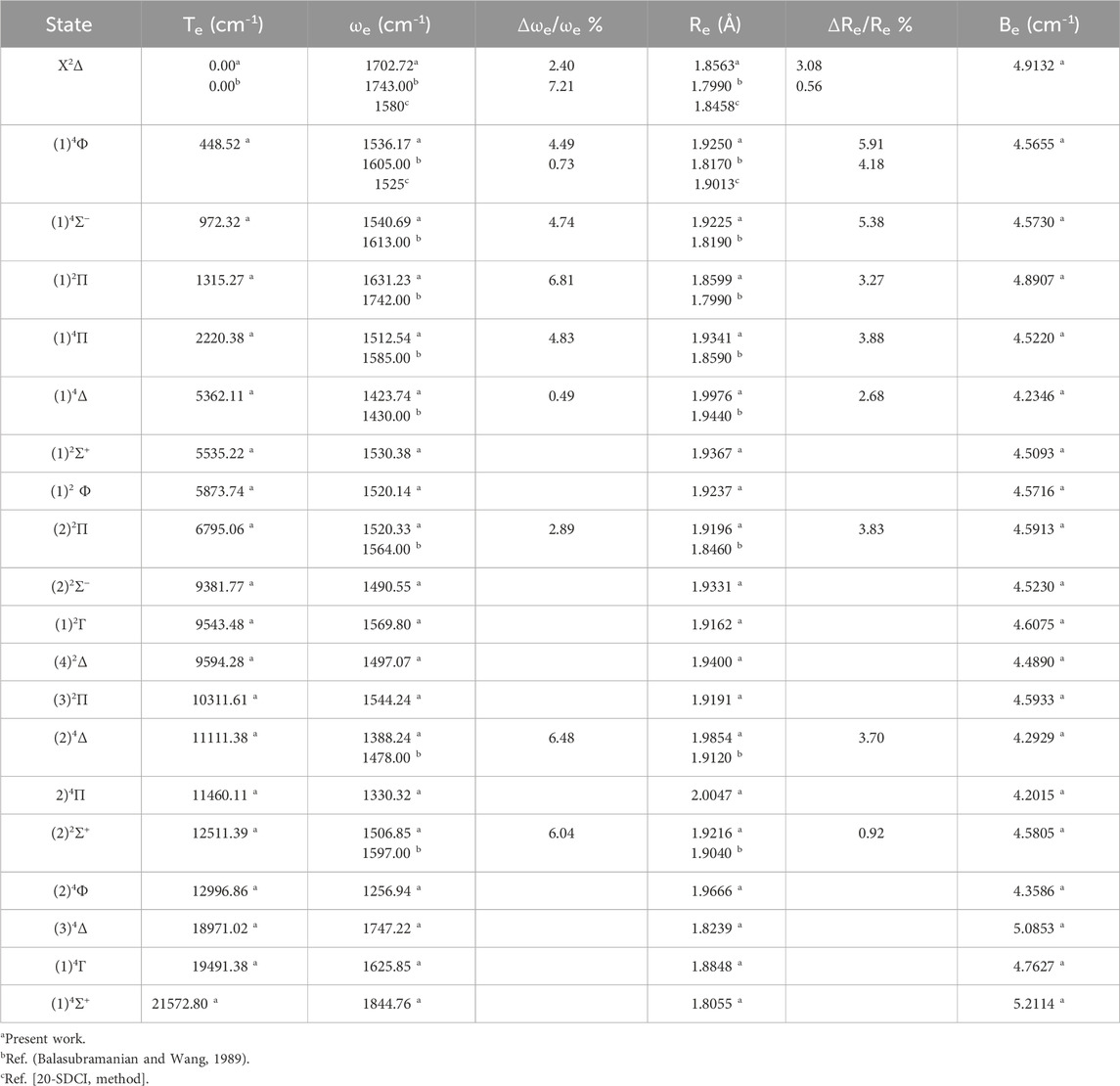
For the studied ZrH molecule, the spectroscopic constants have been calculated by adapting a polynomial of R around the internuclear distance at equilibrium R_e. These constants include the harmonic vibrational frequencies ω_e, the relative energy with respect to the ground state T_e, the internuclear distances R_e, and the rotational constants B_e. Tables 1, 2 provide these values for the various electronic states, along with those found in the literature for spin-orbital coupling and spin-free coupling. By comparing our outcomes of ω_e with those given in literature by Balasubramanian and Wang (1989), Langhoff et al. (1987b), we obtain a good accuracy with the relative differences Δω_e/ω_e = 2.4%, 4.5%, 4.7%, and 6.8% for the electronic states X²Δ, (1)⁴Φ, (1)⁴Σ⁻ and (1)²Π respectively. While the comparison of our calculated values of R_e with those given in the literature (Balasubramanian and Wang, 1989) also shows a good agreement with the relative differences 3.0%, 5.6%, 5.3%, and 3.8% for the electronic states X²Δ, (1)⁴ Φ, (1)⁴Σ⁻ and (1)²Π respectively.

Table 1

Table 1. The spin-free spectroscopic constants T_e, R_e, ω_e, and B_e of the molecule ZrH.

Table 2

Table 2. The spin-orbital coupling spectroscopic constants Te, Re, ωe, and Be of the molecule ZrH.

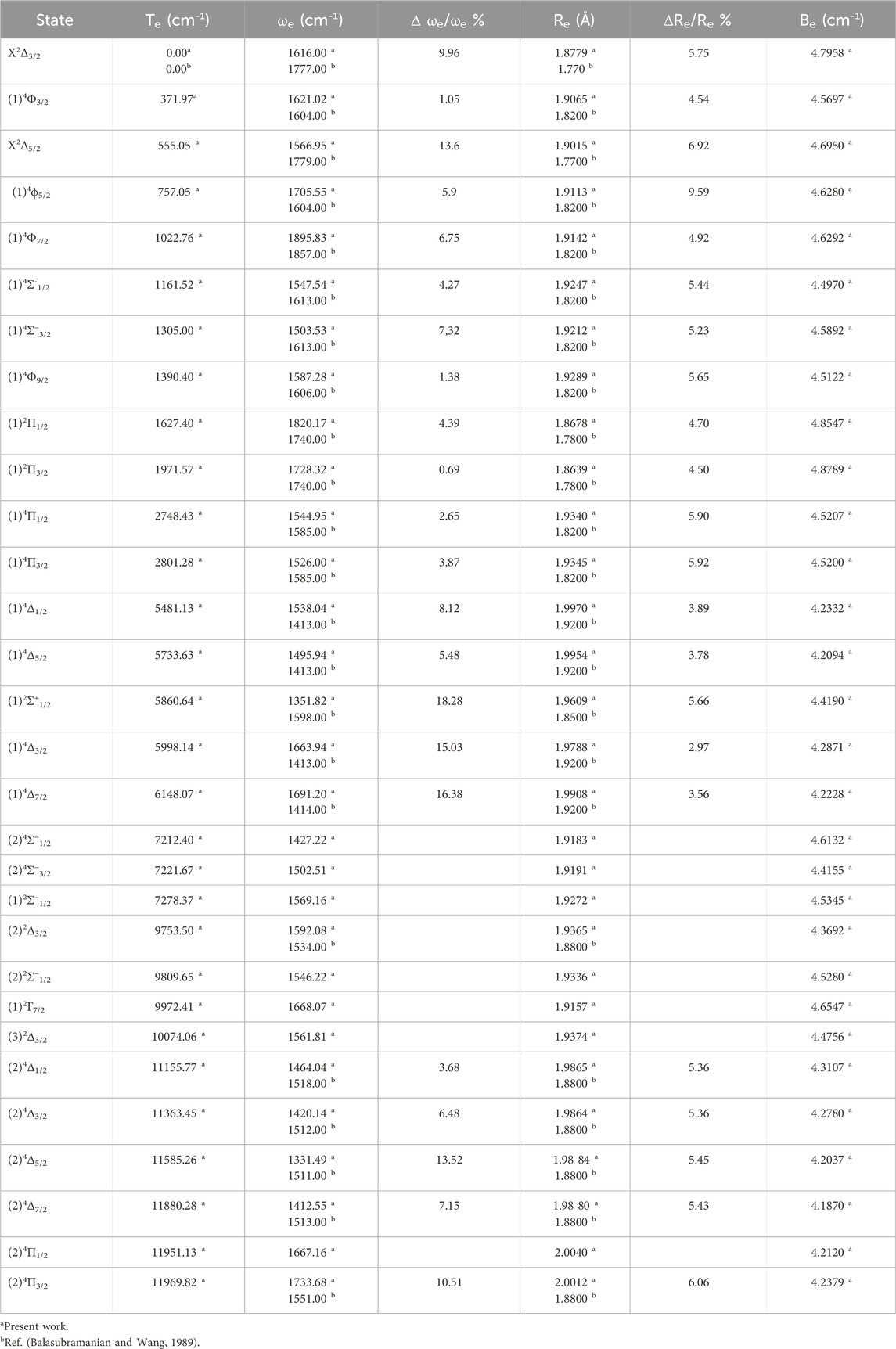
Similarly, for the spin-orbital coupling, our calculated data strongly matched with what had been published in the literature for ω_e with relative differences Δω_e/ω_e = 9.0%, 1.1%, 5.9% and 4.2% for the electronic states X²Δ_3/2, (1)⁴Φ_3/2, (1)⁴Φ_5/2 and (1)⁴Σ^-_1/2 respectively. Moreover, the relative difference in the internuclear distances R_e for the electronic states X²Δ_3/2, (1)⁴ Φ_3/2, (1)⁴Φ_5/2, and (1)⁴Σ⁻ also shows a very good agreement with relative differences of 4.6%, 4.4%, 4.7% and 5.2% for the states mentioned above respectively.

3.2 Ro-vibrational parameters

The rovibrational constants of the ZrH molecule, namely, the vibrational energy E_v, the rotational constant B_v, the centrifugal distortion constant D_v, and the abscissas of the turning point R_min and R_max have been determined up to v = 18 for the spin-free and up to v = 14 for the spin-orbital coupling, respectively, using the canonical function approach (Korek and El-Kork, 2018; Zeid et al., 2018; Chmaisani et al., 2019) with the cubic spline interpolation. Tables 3 provide the electronic states (X)²Δ and (1)²Σ⁺ for the spin-free ZrH molecule, while Tables 4 provide the spin-orbital electronic states X²Δ_3/2, X²Δ_3/2, and (1)²Φ_3/2. Additionally, 25 rovibrational spin-free electronic states have been studied with 26 spin-orbit coupling electronic states that are provided in Supplementary Tables TS1, TS2. The rovibrational constants of some electronic states are absent because of the crossing or avoided crossing of the corresponding potential energy curves. There is no comparison of these values with other results since they are calculated here for the first time.

Table 3

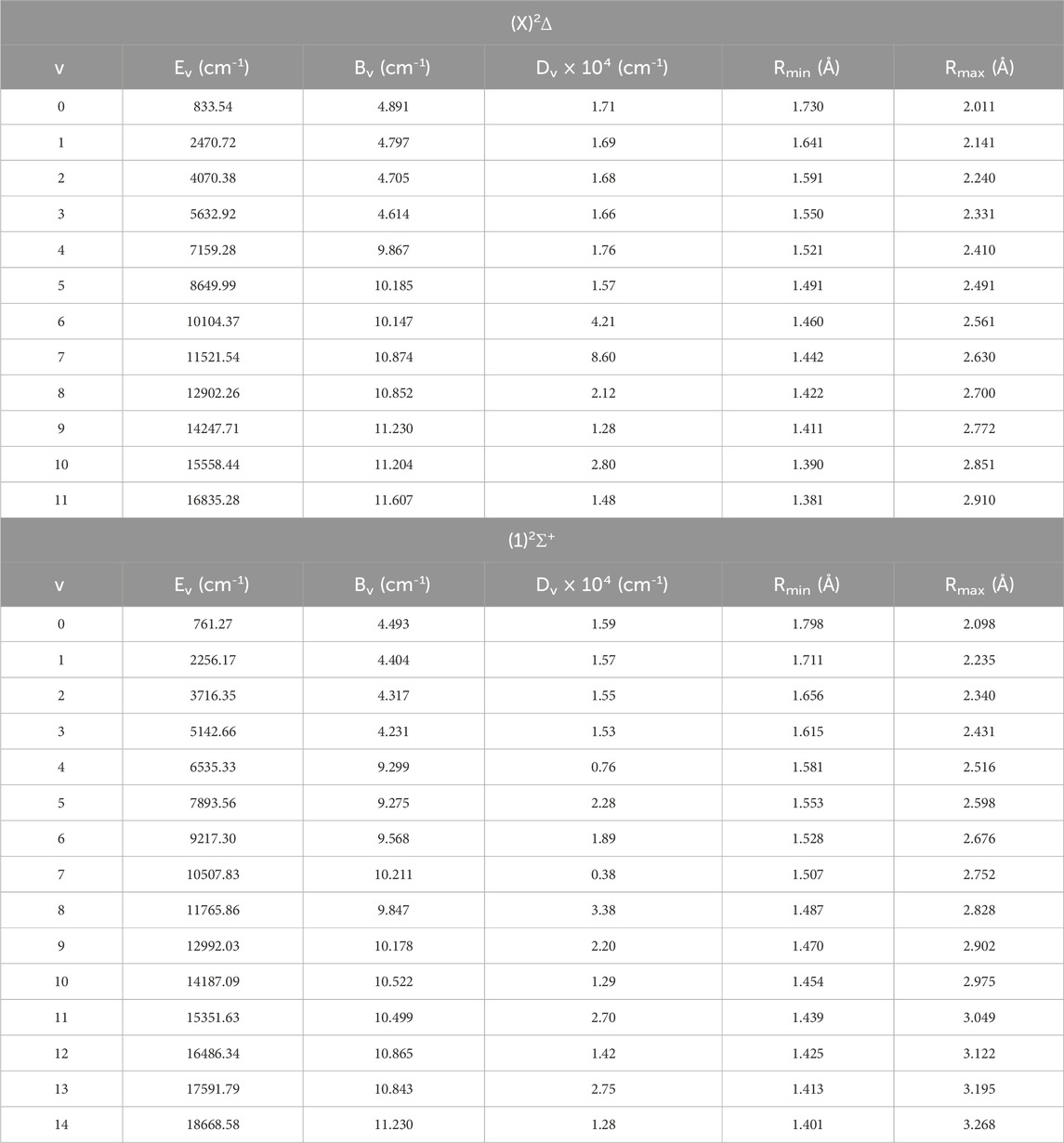
Table 3. The spin-free rovibrational constants for the different vibrational levels of (X)²Δ and (1)²Σ⁺ electronic states of ZrH molecule.

Table 4

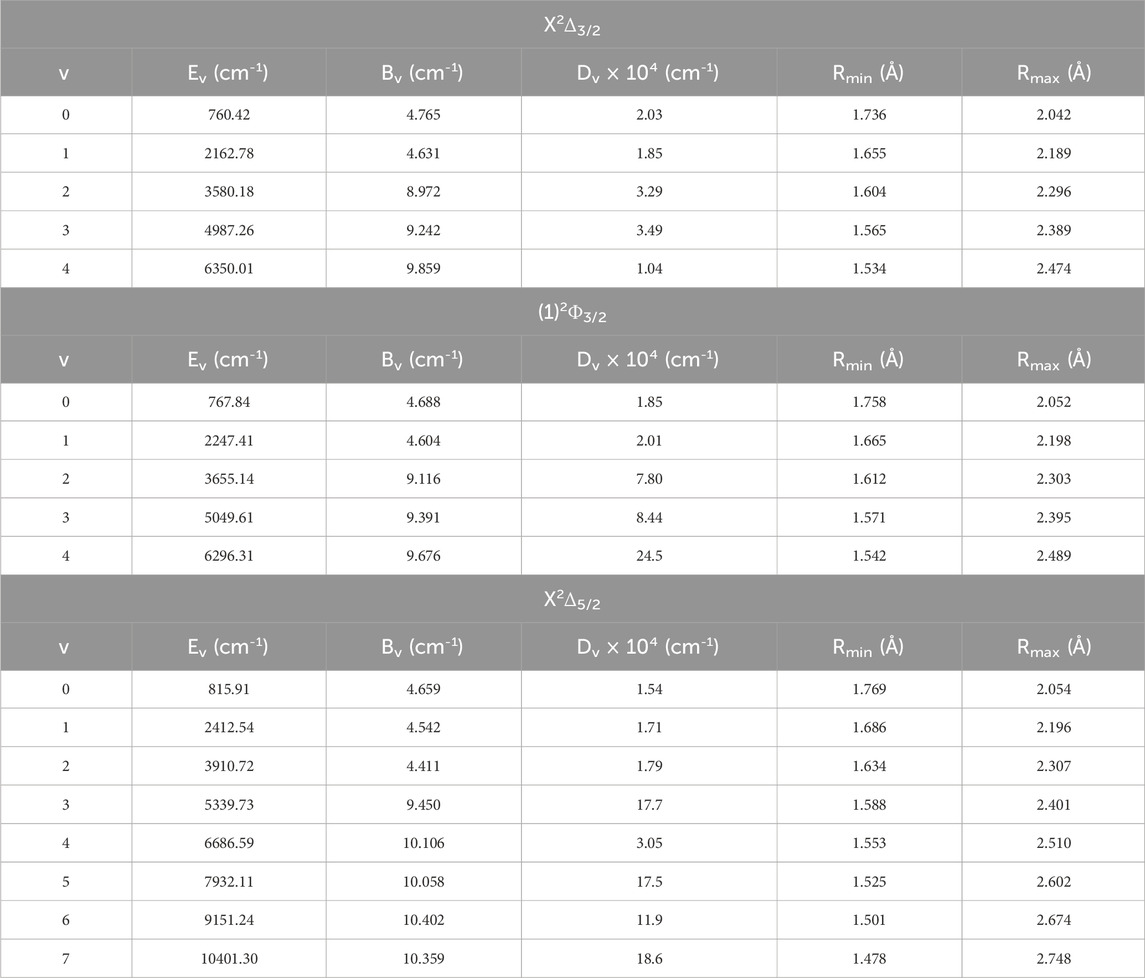
Table 4. The spin-orbit coupling rovibrational constants for the different vibrational levels of (X²)Δ_3/2, (1)²Φ_3/2, and X²Δ_5/2 electronic states of ZrH molecule.

3.3 Laser cooling and electronic transition dipole moment

The slight difference in the internuclear distance at equilibrium positions (Table 2) between the ground X²Δ_3/2 and the seven excited (1)⁴Φ_3/2, (1)⁴Φ_5/2, (1)²Π_1/2, (1)²Π_3/2, (1)⁴Π_-1/2, (1)⁴Π_1/2, and (1)⁴Π_3/2 states incited us to study the suitability of the molecule ZrH for laser cooling for the transition between the ground and these seven states. The transitions between the ground and the other low-lying excited states in Figure 3a are forbidden. The transition X²Δ_3/2 - (1)²Π_1/2 can not be considered for laser cooling because of the intersection of the PEC of state (1)²Π_1/2 with that of (1)⁴Φ_9/2 state at 22 cm^-1 from the ground, which can perturb the cooling cycling between these two states. Similarly, and because of the same reason, there is no cooling between the ground X²Δ_3/2 and the states (1)⁴Π_-1/2, (1)⁴Π_1/2, and (1)⁴Π_3/2 because of the intersections of their PEC with that of (1)²Π_3/2.

The three main conditions for laser cooling for a molecule are a diagonal Franck-Condon factor (FCF), a short radiative lifetime, and the absence of an intermediate state disturbing the cycling process between the two studied electronic states. Figure 4 shows the diagonality of the calculated FCF for the transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2 of the ZrH molecule by using the LEVEL 11 program (Le Roy, 2017). Having the diagonality of the FCF of this transition, we have to find the vibrational branching ratio loss R_v’v for these transitions between the two vibrational levels v' and v, which is given by (Equation 1)

$R_{\nu ’v}=\frac{A_{{\nu }^{\prime }\nu }}{{\sum }_{\nu }{A}_{{\nu }^{\prime }\nu }}(1)$

where $A_{{\nu }^{\prime }\nu }$ is the Einstein coefficients (Equation 2)

$A_{{\nu }^{\prime }\nu }=\left(\left(3.1361891\right)\left(10^{-7}\right){\left(\Delta E\right)}^3{\left(〈\left.{\psi }_{{\nu }^{\prime }}\right|M\left(r\right)\left|{\psi }_{\nu }\right.〉\right)}^2\right)(2)$

Figure 4

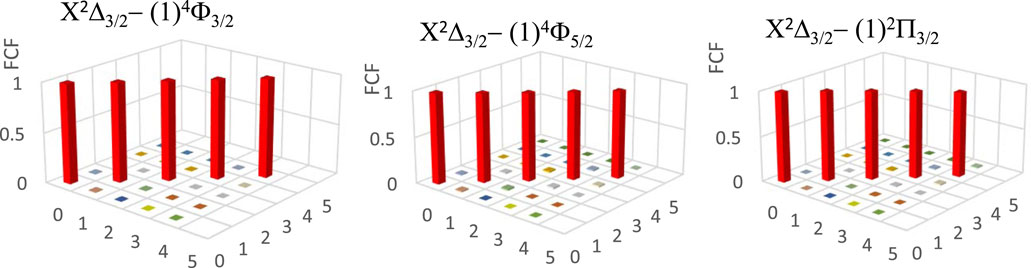
Figure 4. Franck-Condon factor for the transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2 of the ZrH molecule.

Between the two studied vibrational levels v and v', ΔE is the energy difference, and Μ(r) is the electronic transition dipole moment between the two electronic states that are considered (in Debye). By using the quantum chemistry program MOLPRO (Allouche, 2011), this transition dipole moment is calculated and plotted in Figure 5. The transition strength in electronic and other types of spectroscopy depends on the symmetry and orbital contributions. Generally, weak transitions occur between the same symmetries of the transitions, while strong transitions are obtained between different symmetries. From this Figure, one can notice that the transition dipole moment is larger for the higher spin than that of the lower one. The calculated values of the branching ratio loss R_v’v and the Einstein coefficients for the studied vibrational levels are given in Table 5 for the three transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 − (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2. Based on these calculated data, the investigated values of the radiative lifetime, which is given by τ (s) = 1/A_ν’ν for these transitions of the molecule ZrH, are given in Table 5. These large values of the radiative lifetime 0.094 ms˂τ˂13.651 ms show the non-availability of the molecule ZrH for laser cooling for these three transitions.

Figure 5

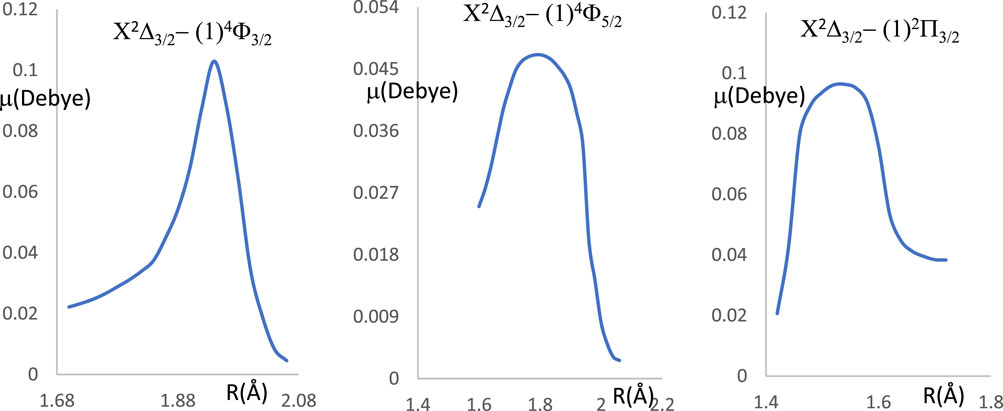
Figure 5. The transition dipole moment curves for the transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2 of the ZrH molecule.

Table 5

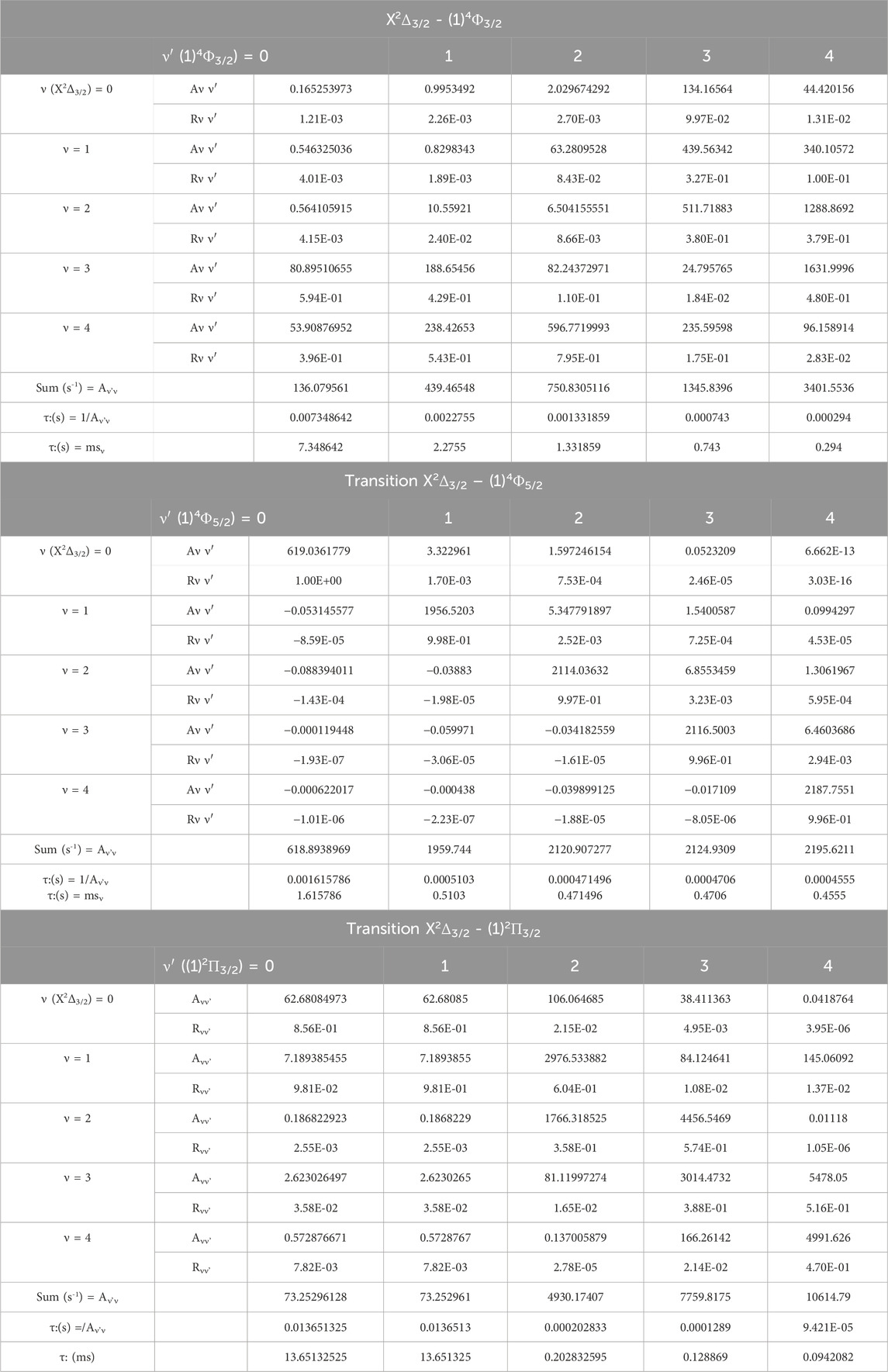
Table 5. The radiative lifetimes τ, and the vibrational branching ratio of the vibrational transitions X²Δ_3/2 - (1)⁴Φ_3/2, X²Δ_3/2 - (1)⁴Φ_5/2, X²Δ_3/2 - (1)²Π_3/2 of the molecule ZrH.

4 Conclusion

In the current work, an ab initio calculation using the Complete Active Space Self-Consistent Field/Multireference Configuration Interaction with Davidson corrective calculation (CASSCF/MRCI + Q) was carried out for doublet and quartet 53 low-lying electronic states of the ZrH molecule with and without spin-orbit coupling effect. The comparison of our calculated values of the spectroscopic constants R_e and ω_e with those available in the literature shows good accuracy with the average relative differences Δω_e/ω_e = 4.6% and ΔR_e/R_e = 5.05% for the free spin calculation and Δω_e/ω_e = 4.42% and ΔR_e/R_e = 4.72% for the spin-orbit coupling calculation for the states X²Δ, (1)⁴Φ, (1)⁴Σ⁻ and (1)²Π. By using the canonical function approach, the rovibrational calculation of the constants E_v, B_v, D_v, R_min, and R_max has been performed; there is no comparison of these values with other results since they are calculated here for the first time. The calculation of the Franck−Condon factors, the Einstein coefficients, the vibrational branching ratios, and the large values of the radiative lifetimes in (ms) for the transitions between the ground and the low-lying permitted transitions shows the non-availability of the molecule ZrH for direct laser cooling.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

GC: Writing – original draft, Data curation. LA: Writing – review and editing, Software, Resources. NE-K: Writing – review and editing, Formal Analysis, Funding acquisition. MK: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. 1. This publication is based upon work supported by the Khalifa University of Science and Technology under Award No. CIRA-2019-054. The authors would like to acknowledge the use of Al MISBAR High Power Computer to complete their work. 2. Faculty: NE.K (initials) is partly supported by the internal grant (8474000336-KU-SPSC).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2025.1603873/full#supplementary-material

References

Allouche, A. R. (2011). Gabedit: a graphical user interface for computational chemistry software. J. Comp. Chem. 174, 82. doi:10.1002/jcc.21600

CrossRef Full Text | Google Scholar

Balasubramanian, K., Feng, P. Y., and Liao, M. Z. (1987). Relativistic calculations of electronic states of PdH. J. Chem. Phys. 87, 3981–3985. doi:10.1063/1.452952

CrossRef Full Text | Google Scholar

Balasubramanian, K., and Liao, D. W. (1988). Electronic states and potential energy surfaces of RhH. J. Chem. Phys. 88, 317–321. doi:10.1063/1.454602

CrossRef Full Text | Google Scholar

Balasubramanian, K., and Wang, J. Z. (1989). Spectroscopic properties and potential energy curves of thirty-six electronic states of ZrH. Chem. Phys. Lett. 525, 30. doi:10.1016/0009-2614(89)87145-3

CrossRef Full Text | Google Scholar

Chmaisani, W., El-Kork, N., Elmoussaoui, S., and Korek, M. (2019). Electronic structure calculations with the spin-orbit effect of the low-lying electronic states of the YbBr molecule. ACS omega 14987, 14987–14995. doi:10.1021/acsomega.9b01759

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunning, J. , T. H. (1989). Gaussian basis sets for use in correlated molecular calculations. I. The atoms-boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Hay, P. J., and Martin, R. L. (1985). All-electron and valence-electron calculations on AgH, Ag2, and AgO. J. Chem. Phys. 83, 5174–5181. doi:10.1063/1.449729

CrossRef Full Text | Google Scholar

James, A. M., Fournier, R., Simard, B., and Campbell, M. D. (1993). Electronic spectroscopy of yttrium monosulfide: molecular beam studies and density functional calculations. Can. J. Chem. 71, 1598–1614. doi:10.1139/v93-200

CrossRef Full Text | Google Scholar

Korek, M., and El-Kork, N. (2018). Solution of the rovibrational schrödinger equation of a molecule using the volterra integral equation advances in. Phys. Chem., 1487982. doi:10.1155/2018/1487982

CrossRef Full Text | Google Scholar

Korek, M., and Hamdan, A. M. (2008). Theoretical electronic structure of the molecule ScBr. J. Quant. Chem. 108, 456–461. doi:10.1002/qua.21524

CrossRef Full Text | Google Scholar

Kraussand, S. W. J. (1985). Electronic structure of FeO and RuO. J. Chem. Phys. 8 (2), 5584–5596. doi:10.1063/1.448593

CrossRef Full Text | Google Scholar

Langhoff, S. R., and Bauschlicher, C. W. (1988). Theoretical studies of the monoxides and monosulfides of Y, Zr, and Nb. J. Chem. Phys. 89, 2160–2169. doi:10.1063/1.455060

CrossRef Full Text | Google Scholar

Langhoff, S. R., Pettersson, L. G. M., Bauschlicher, C. W., and Partridge, H. (1987b). Theoretical spectroscopic parameters for the low-lying states of the second-row transition metal hydrides. J. Chem. Phys. 86, 268–278.

CrossRef Full Text | Google Scholar

Langhoff, S. R., Pettersson, L. G. M., Bauschlicher, C. W., and Partridge, H. (1987a). Theoretical spectroscopic parameters for the low-lying states of the second-row transition metal hydrides. J. Chem. Phys. 86, 268–278. doi:10.1063/1.452617

CrossRef Full Text | Google Scholar

Le Roy, R. J. (2017). LEVEL: a computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Quat. Spectrosc. Radiat. Transf. 186, 167–178. doi:10.1016/j.jqsrt.2016.05.028

CrossRef Full Text | Google Scholar

McLean, A. D. (1983). Nonrelativistic all-electron SCF, MCSCF, and CI calculations on the AgH, AuH, and Ag2 molecules. J. Chem. Phys. 79, 3392–3403. doi:10.1063/1.446241

CrossRef Full Text | Google Scholar

Peterson, K. A., Figgen, D., Dolg, M., and Stoll, H. (2007). Energy-consistent relativistic pseudopotentials and correlation consistent basis sets for the 4d elements Y–Pd. J. Chem. Phys. 126, 124101. doi:10.1063/1.2647019

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, J. M., and Ziurys, L. M. (2001). Transition metal sulfide studies: the pure rotational spectrum of the CuS radical (X2Πi). Chem. Phys. Lett. 344, 75–84. doi:10.1016/s0009-2614(01)00693-5

CrossRef Full Text | Google Scholar

Werner, H. J., Knowles, P. J., Lindh, R., Manby, F. R., Schütz, M., Celani, P., et al. (2025). MOLPRO is a package of ab initio programs. Available online at: http://www.molpro.net/info/users.

Google Scholar

Zeid, I., Al Abdallah, R., El-Kork, N., and Korek, M. (2018). Ab-initio calculations of the electronic structure of the alkaline earth hydride anions XH− (X = Mg, Ca, Sr and Ba) toward laser cooling experiment. Acta Part A Mol. Biomol. Spectrosc. 224, 117461. doi:10.1016/j.saa.2019.117461

PubMed Abstract | CrossRef Full Text | Google Scholar