- Advanced Materials Group (AMG), Department of Mechanical Engineering, Koç University, Istanbul, Turkey
A multi-scale modeling approach was applied to predict the impact response of a strain rate sensitive high-manganese austenitic steel. The roles of texture, geometry, and strain rate sensitivity were successfully taken into account all at once by coupling crystal plasticity and finite element (FE) analysis. Specifically, crystal plasticity was utilized to obtain the multi-axial flow rule at different strain rates based on the experimental deformation response under uniaxial tensile loading. The equivalent stress – equivalent strain response was then incorporated into the FE model for the sake of a more representative hardening rule under impact loading. The current results demonstrate that reliable predictions can be obtained by proper coupling of crystal plasticity and FE analysis even if the experimental flow rule of the material is acquired under uniaxial loading and at moderate strain rates that are significantly slower than those attained during impact loading. Furthermore, the current findings also demonstrate the need for an experiment-based multi-scale modeling approach for the sake of reliable predictions of the impact response.
Introduction
Austenitic high-manganese (Mn) steels, a class of high strength steels, have received considerable attention since they offer a rare combination of exceptional work hardening capacity, high wear and abrasion resistance, high strength, and significant ductility (Owen and Grujicic, 1999; Bayraktar et al., 2004; Bouaziz et al., 2011). These extraordinary mechanical properties have been subject to several studies (Karaman et al., 2000, 2001; Bayraktar et al., 2004; Hutchinson and Ridley, 2006; Ueji et al., 2008; Niendorf et al., 2009, 2010), many of which revealed that the main mechanism underlying the observed mechanical behavior is the presence of twins in the microstructure accompanied by additional microstructural features, such as stacking faults, dynamic strain aging (DSA), and interaction of twins with dislocations (Karaman et al., 2000, 2001; Hutchinson and Ridley, 2006; Ueji et al., 2008). Simultaneous activity of all of the aforementioned micro-deformation mechanisms result in the improved strength and work hardening capacity of this class of steels, where all these mechanisms constitute obstacles against gliding dislocations (Karaman et al., 2000, 2001; Hutchinson and Ridley, 2006; Ueji et al., 2008). However, the complexity of the deformation behavior of these materials makes it difficult to clearly distinguish between the relative contributions of the hardening mechanisms.
A very good example to this complicated microstructure is that of Hadfield steel, high-Mn austenitic steel with a face-centered cubic (fcc) structure at room temperature (RT). Hadfield steel is well known for its deformation by both slip and twinning (Karaman et al., 2000; Toker et al., 2014), where the two mechanisms interact and further promote work hardening concomitant with increasing strain. To add further to the complexity of micro-deformation mechanisms, glide dislocations tend to form high-density dislocation walls (HDDWs), which effectively hinder active glide dislocations from moving further, contributing to the unusual strain hardening exhibited by this material (Canadinc et al., 2005, 2007). However, dislocations are prevented from gliding not by twin boundaries or HDDWs only, but also by carbon (C), which can diffuse within the matrix throughout the deformation, as it becomes easily excited by the energy provided by the applied stresses (Canadinc et al., 2008a).
The excited C atoms diffuse within the matrix, however; when they meet dislocations at interstitial zones, they prevent dislocations from gliding further, which is referred to as pinning of the dislocation by the C atom (Owen and Grujicic, 1999; Canadinc et al., 2008a). This, indeed, gives way to DSA (Owen and Grujicic, 1999; Canadinc et al., 2008a), which further adds to the complexity of the microstructure by promoting strain rate sensitivity (SRS) and negative strain rate sensitivity (NSRS) (Canadinc et al., 2008a). Specifically, as steel is deformed at a faster rate, the rate of generation of forest dislocations increases, also leading to an increased level of stress at the same strain value, which is known as the SRS (Canadinc et al., 2008a). In Hadfield steel, however; the diffusion velocity of C also increases concomitant with strain rate. At lower strain rates, the C atoms stay longer at an interstitial site, potentially pinning a dislocation for a longer period, which is a positive contribution in terms of strain hardening. However, as the deformation rate increases, C atoms start to diffuse much faster, and they cannot pin dislocations for extended periods, which indeed takes away an important contribution to the overall hardening: the result is softening, and even though the strain rate increases, the material attains lower levels of stress at the same strains, which is known as the NSRS (Canadinc et al., 2008a). The NSRS, however; is eliminated at very high strain rates, such that the missing contribution to the overall hardening due to the pinning of dislocations becomes negligible as compared to the significant forest hardening, which constitutes the major mechanism of hardening at elevated rates of deformation (Canadinc et al., 2008a).
Despite their complicated micro-deformation mechanisms, other high-Mn austenitic steels with similar microstructures, such as the twinning-induced plasticity (TWIP) steels, continue to attract attention and find use in applications, mainly owing to their superior mechanical properties (Hutchinson and Ridley, 2006; Jeong et al., 2012; Xu et al., 2013; Wen et al., 2014). Automotive industry and other load bearing applications utilize high-Mn steels at an increasing rate, and ballistic applications constitute another potential area that may utilize this class of steels. For all these applications, however, resistance to impact loading and understanding of the deformation response under impact becomes of utmost importance (Toker et al., 2014). Considering the design process of any commercial product, on the other hand, one realizes that the capability to realistically predict the impact response of these alloys by numerical modeling is warranted, which constitutes the motivation of the current work.
The impact performance of a material is governed by its microstructure, and the corresponding parameters, such as grain boundaries, grain size, precipitates, and delaminations, and the material’s ductile-to-brittle transition temperature (DBTT) altogether dictate the response to impact loading (Song et al., 2005; Kimura et al., 2008; Morris, 2008; Onal et al., 2014). Another important parameter affecting the impact response is the texture of the material, which defines the grain boundary–dislocation interactions, and thus, the crack propagation behavior under impact loading, as well as the degree of anisotropy, which dictates the relative slip activity in each grain (Onal et al., 2014), warranting incorporation of anisotropy effects into the design process.
The current study was undertaken with the motivation of addressing this issue, such that a combined experimental and numerical approach is proposed to predict the impact response of high-Mn austenitic steels in a realistic manner. For this purpose, uniaxial tensile deformation and impact responses of Hadfield steel were experimentally monitored, where the uniaxial deformation experiments featured four different strain rates ranging from moderate to high in order to also assess the role of NSRS exhibited by this material. Finite element (FE) simulations of the impact experiments were carried out, where the roles of texture, geometry, and SRS were successfully taken into account all at once by incorporating the proper multi-axial material flow rule obtained from crystal plasticity simulations into the FE analysis. Specifically, crystal plasticity was utilized to obtain the multi-axial flow rule at different strain rates based on the experimental deformation response under uniaxial tensile loading, and the equivalent stress – equivalent strain response was then incorporated into the FE model for the sake of a more representative hardening rule under impact loading. The current results demonstrate that reliable predictions can be obtained by proper coupling of crystal plasticity and FE analysis even if the experimental flow rule of the material is acquired under uniaxial loading and at moderate strain rates that are significantly slower than those attained during impact loading. Overall, the approach presented herein constitutes an important guideline for the design process of impact bearing applications utilizing high-Mn austenitic steels.
Materials and Methods
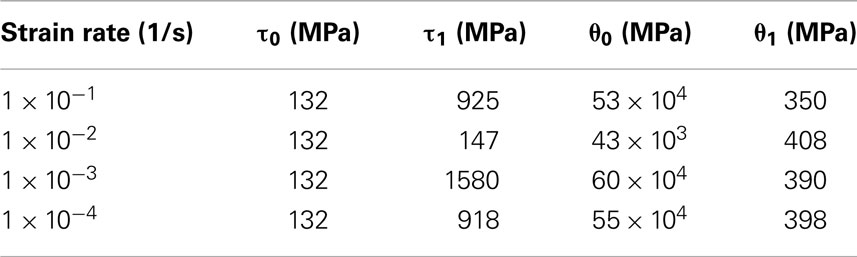
The material investigated in this study is Hadfield steel, high-Mn austenitic steel with an fcc structure, and has a chemical composition of 12.44 wt% Mn, 1.10 wt% C, and balance iron. Small-scale dog-bone shaped tension samples were extracted from railroad frogs taken from service with the aid of electro-discharge machining to avoid any process-induced residual stresses and strains on the samples. The RT monotonic tensile deformation experiments were carried out on a servo-hydraulic test frame equipped with a digital controller and a miniature extensometer of 3 mm gage length. The results revealed a significant SRS prevalent in Hadfield steel polycrystals within the strain rate range of 1 × 10−4 to 1 × 10−1 1/s (Figure 1). A serrated flow was exhibited by the material at all strain rates, however, the associated instability was much more prominent at 1 × 10−3 1/s, where NSRS was prevalent as evidenced by the lower stress levels attained despite the 10-fold increase in the strain rate from 1 × 10−4 to 1 × 10−3 1/s.
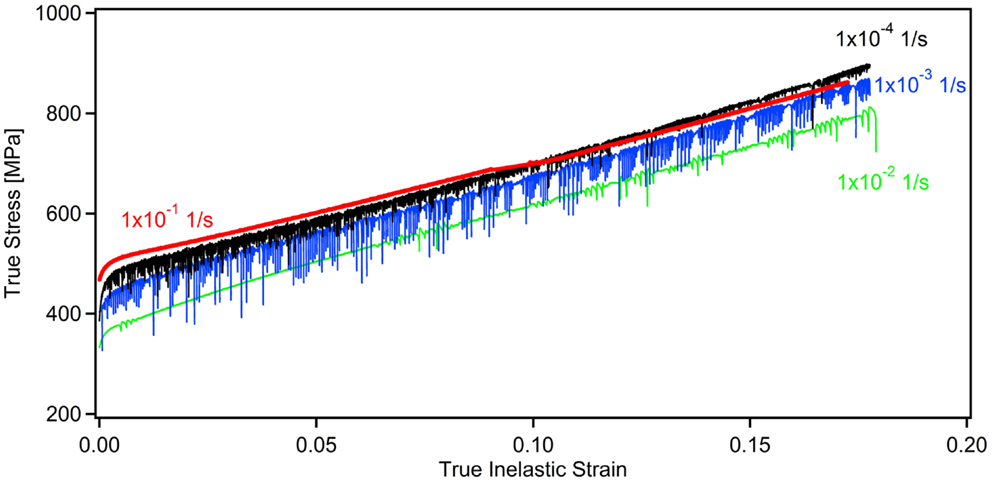
Figure 1. Room temperature uniaxial tensile deformation response of Hadfield steel obtained at different strain rates, demonstrating the NSRS. Data were recompiled from Canadinc et al. (2008a).
The impact samples were extracted from both the same Hadfield railroad frog with dimensions of 2.8 mm × 25 mm × 4 mm, featuring a 60° notch with a radius of 0.1 mm and a depth of 1 mm (Onal et al., 2014). The specimens were mechanically polished down to a 4000 grit size in order to minimize the detrimental effects of machined surfaces on the impact response. The impact experiments were conducted at RT, and the specimens were subjected to deformation with an impact energy of 50 J and at a velocity of 3.8 m/s, where 8000 data points were collected during each experiment with a data acquisition frequency of 2 MHz. For both uniaxial deformation and impact experiments, three companion samples were tested in each case in order to ensure repeatability. The initial textures of the samples prior to deformation were determined by X-ray diffraction.
Results and Discussion
Finite Element Simulations of Experimental Impact Response of Hadfield Steel
It is well known that very large deformations taking place within very short time periods constitute the major difficulty of FE simulations of impact loading (Kormi et al., 1997; Raykhere et al., 2010; Onal et al., 2014). Specifically, the available time period is insufficient for the stabilization of the computed displacements in the case of impact loading, such that the material’s behavior significantly deviates under this dynamic type of loading from that under normal conditions owing to the non-linear behavior under dynamic loading (Onal et al., 2014). The current FE simulations of the impact behavior were carried out utilizing the ANSYS® 15 commercial software and the FE analysis was based on an explicit dynamics system, where the LS-DYNA® solver was employed in computations for the sake of a reliable non-linear dynamic analysis.
The Lagrangian formulation and multilinear isotropic hardening were chosen to represent the non-linearity and the plastic flow, respectively. A fine “MultiZone” mesh was constructed with 13530 nodes and 11060 quadrilateral elements, where the geometry was automatically decomposed into a hex mesh, increasing both the accuracy and computational efficiency of the simulations. The notch region was meshed with an element size of 0.1 mm, and the mesh had an orthogonal quality of 0.98 (out of 1.0). All contact regions of the impact sample were assumed to be frictional, and the corresponding static and dynamic friction coefficients were set to 0.2 and 0.09, respectively (Onal et al., 2014). As for the boundary conditions, a nodal displacement was imposed on the top notch surface and fixed supports were placed at the right/left sides and on the bottom surface. Beyond the fracture point of the specimens, i.e., where the sample, hammer contact terminates, the equivalent plastic strain (EPS) criterion was utilized to define failure of the material, namely an EPS of 0.68 was preset as the failure initiation point. The Cartesian coordinate system was considered while designating the dimensions and constraints.
The first set of simulations made use of the experimental RT uniaxial tensile deformation response of Hadfield steel obtained at a strain rate of 1 × 10−4 1/s to define the multilinear isotropic hardening rule (Figure 2). This strain rate is rather a moderate strain rate typically utilized in laboratory experiments employed to characterize the material’s deformation response (Onal et al., 2014). It is evident that the corresponding simulation result significantly differs from the experimentally measured impact behavior, indicating that the flow rule of the material should be based on experiments featuring much higher strain rates as the impact deformation itself takes place very rapidly. Thus, in order to assess the role of strain rate, FE simulations considering higher rates of deformation, namely 1 × 10−1, 1 × 10−2, and 1 × 10−3 1/s, were carried out (Figure 3). As expected, a comparison of experimental and simulated impact responses (based on four different strain rates) expressed in terms of force–time data (Figures 2 and 3) indicates that the best predictions are made when the flow rule is based on the experimental deformation response obtained at the strain rate of 1 × 10−3 1/s. A further look at the results presented in Figures 2 and 3 reveal a more interesting fact: the second best prediction is obtained when the flow rule is defined based on the uniaxial tensile deformation response obtained at a strain rate of 1 × 10−4 1/s. This implies that the experimental data obtained within the NSRS range should not be utilized to define the hardening rule when constructing a FE model to predict impact response, regardless of the strain rate.
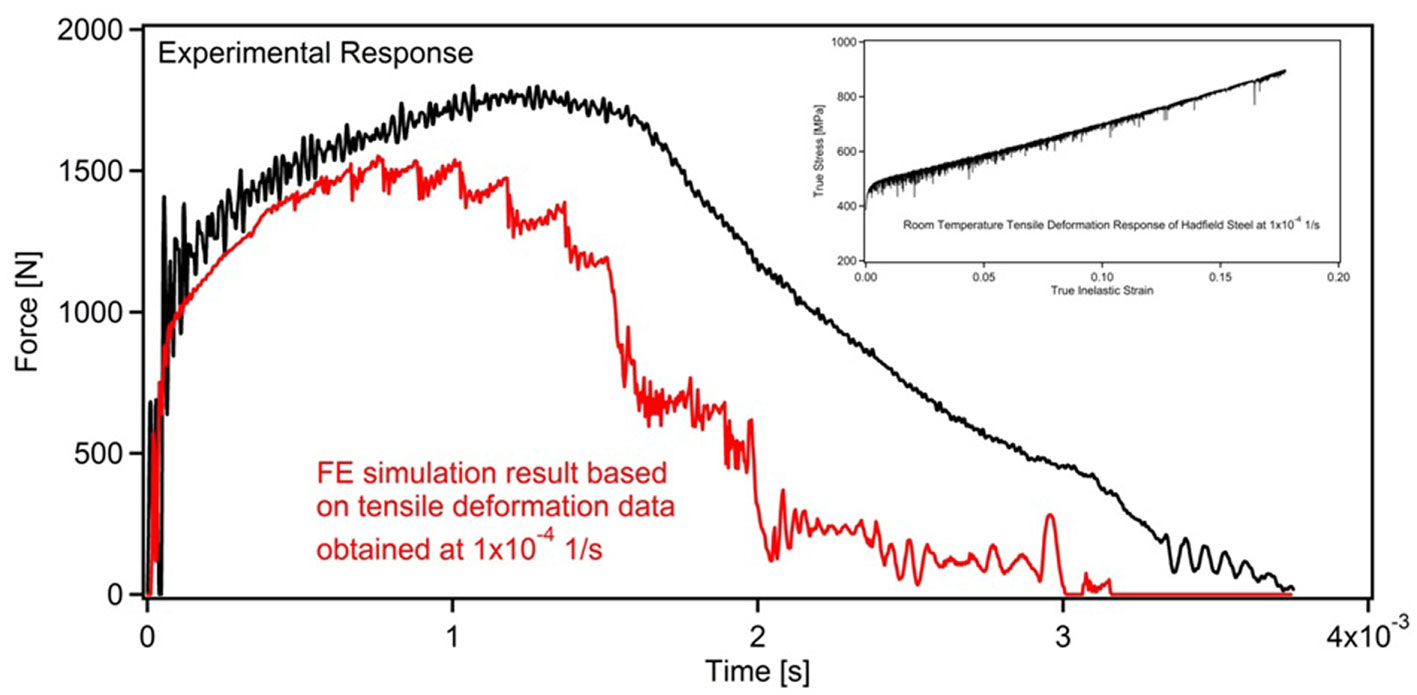
Figure 2. The RT experimental impact response of Hadfield steel and the corresponding FE simulation result, where the flow rule was defined based on the experimental uniaxial tensile deformation response obtained at a strain rate of 1 × 10−4 1/s.
Figure 3. A comparison of the RT experimental impact response of Hadfield steel and the corresponding FE simulation results, where the flow rule was defined based on the experimental uniaxial tensile deformation responses obtained at strain rates of 1 × 10−1, 1 × 10-2, and 1 × 10−3 1/s.
Overall, all of the FE simulation results presented in Figures 2 and 3 exhibited noticeable deviation from the experimental impact response, implying that the provided hardening response based on the experimental uniaxial tensile deformation data was not sufficiently representative of the material’s mechanical behavior under impact loading at any of the considered strain rates. Further simulations featuring a finer mesh were also carried out in order to question the numerical procedure; however, the same deviation from the experimental results persisted.
It has recently been demonstrated that a multi-axial stress–strain state is present in the critical region of the sample (Onal et al., 2014), and a comparison of normal and von Mises stress distributions reveals that employment of the uniaxial tensile deformation data as the input defining the material’s flow rule under impact loading is not appropriate (Figure 4). Even though this approach might be appropriate for an isotropic material, it falls far from being realistic for a textured material exhibiting a significant degree of anisotropy (Onal et al., 2014). The numerical analyses carried out until this point (Figures 2–4) clearly demonstrate the need for a proper representation of microstructure under impact loading, in addition to the strain rate effects.
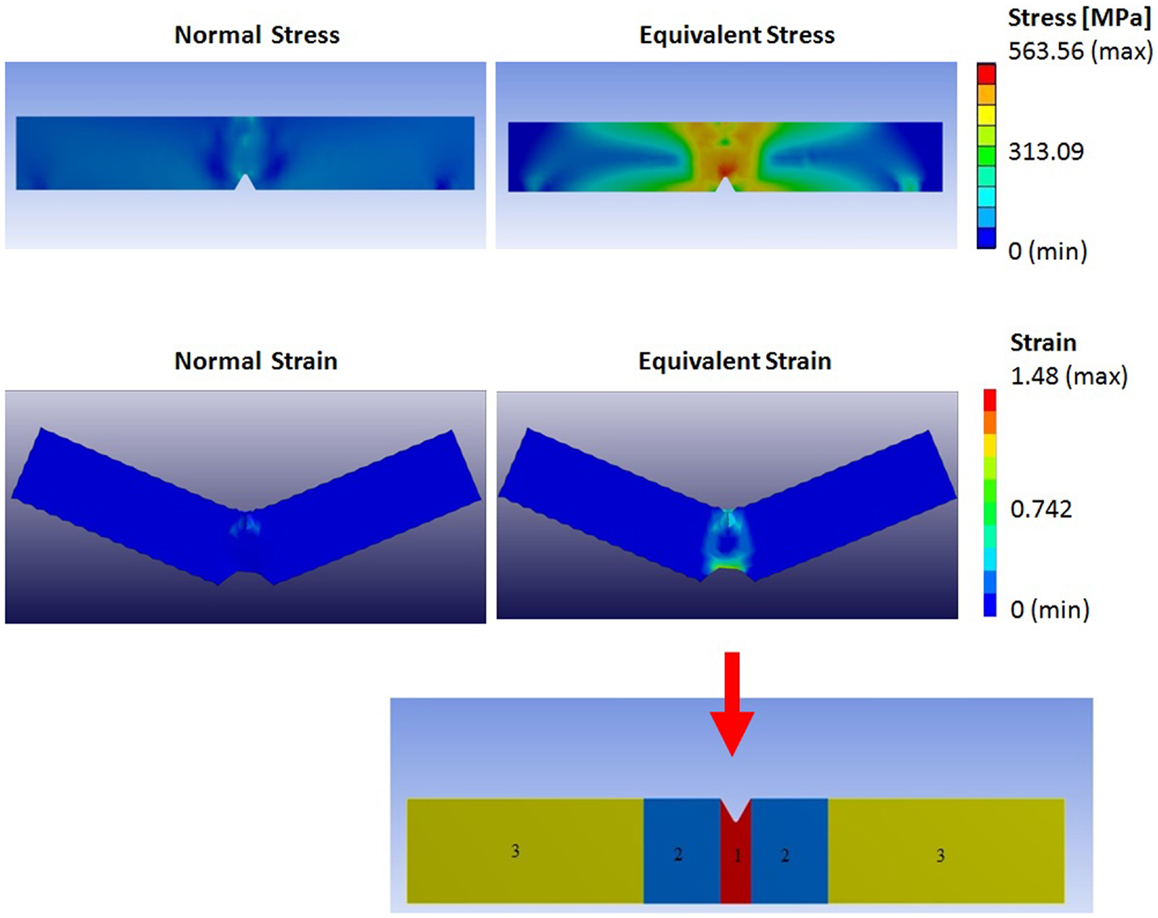
Figure 4. A material-independent FE simulation of impact loading demonstrating the typical distribution of normal and equivalent stress-strain fields (above the arrow), and the corresponding division of sample geometry based on stress intensities within the sample (Onal et al., 2014).
Incorporation of the Role of Microstructure into the Finite Element Simulations through Crystal Plasticity
In order to utilize a proper flow rule to define hardening of Hadfield steel during impact and account for the role of texture and the corresponding anisotropy, in addition to the strain rate effects, in the current FE simulations, a crystal plasticity approach was adopted. Specifically, based on the aforementioned analysis of stress–strain distributions upon impact loading (Figure 4), a flow rule based on equivalent stress–strain response was defined. In order to do so, a visco-plastic self-consistent (VPSC) algorithm was utilized to predict the von Mises stress–strain behavior of the material based on the experimental uniaxial tensile deformation data. Even though an alternative way of establishing the equivalent stress–strain response would have been carrying out multi-axial deformation experiments, the current methodology is much more efficient due to the impractical multi-axial experiments, especially in the case of high strain rates.
A successful crystal plasticity model should both predict the macroscopic deformation response and capture the deformation characteristics at the slip system level (Canadinc et al., 2011), such that the deformation response could be predicted under any type of loading (Canadinc et al., 2008b). With this motivation, the deformation of Hadfield steel was modeled at the microscopic level for each strain rate considered herein based on the corresponding experimentally obtained uniaxial deformation response (Figures 5–8). The VPSC model utilizes the initial texture of the material as an input, such that the loads on each grain, and thereby the slip activities in each grain, are dictated by the texture of the material (Lebensohn and Tomé, 1993; Kocks et al., 1998; Biyikli et al., 2010). Thereafter, the same micro level model established for each strain rate was utilized to predict the corresponding equivalent stress–strain response (Figures 5–8), which can be utilized as a proper flow rule for the impact simulations, as discussed before.
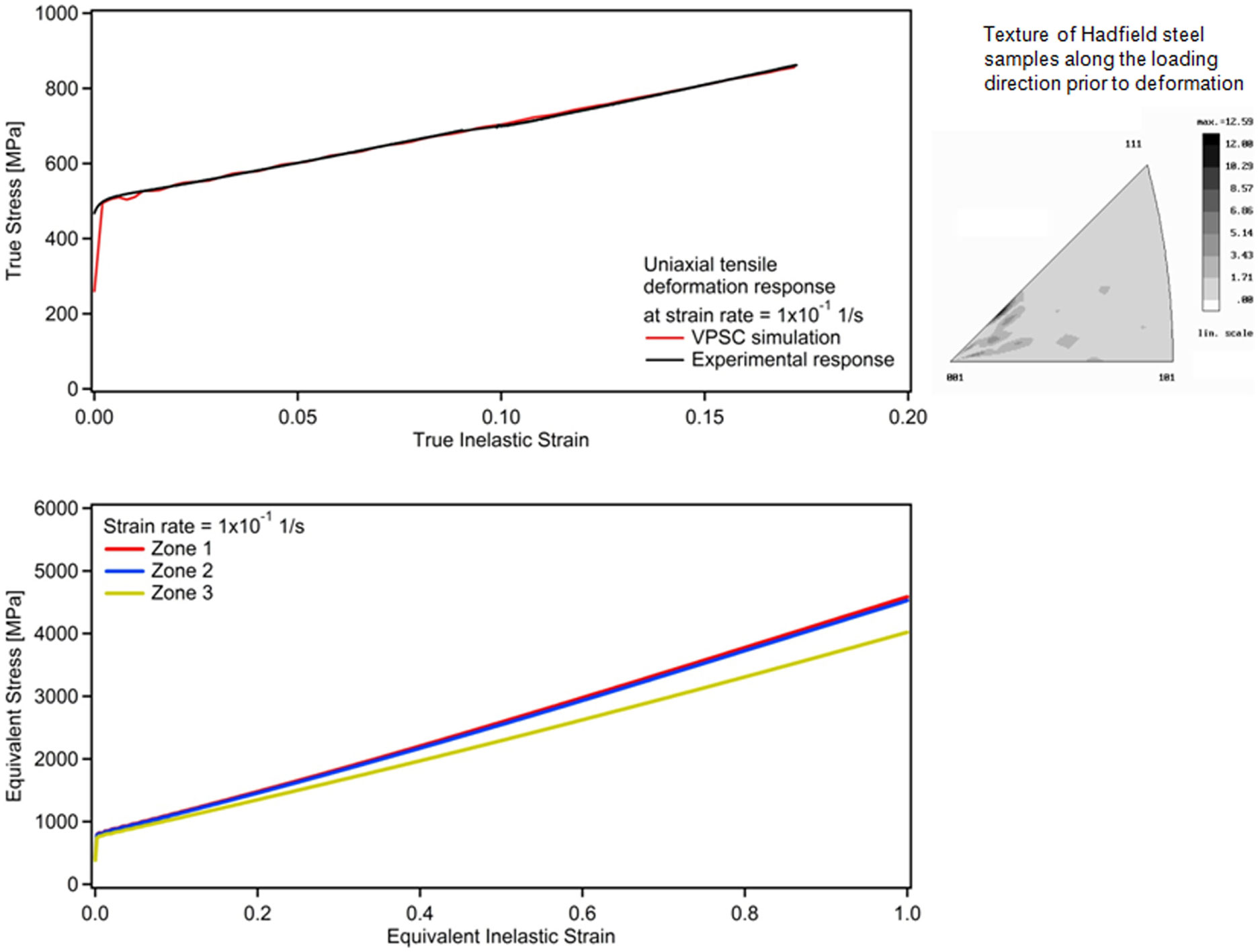
Figure 5. Top: VPSC simulation of the RT experimental uniaxial tensile deformation of Hadfield steel at a strain rate of 1 × 10−1 1/s, and the corresponding initial texture along the loading direction (representative of the texture of all companion samples). Bottom: the corresponding predicted equivalent stress–strain response for each zone within the impact sample based on the distribution of stress concentration (Figure 4).
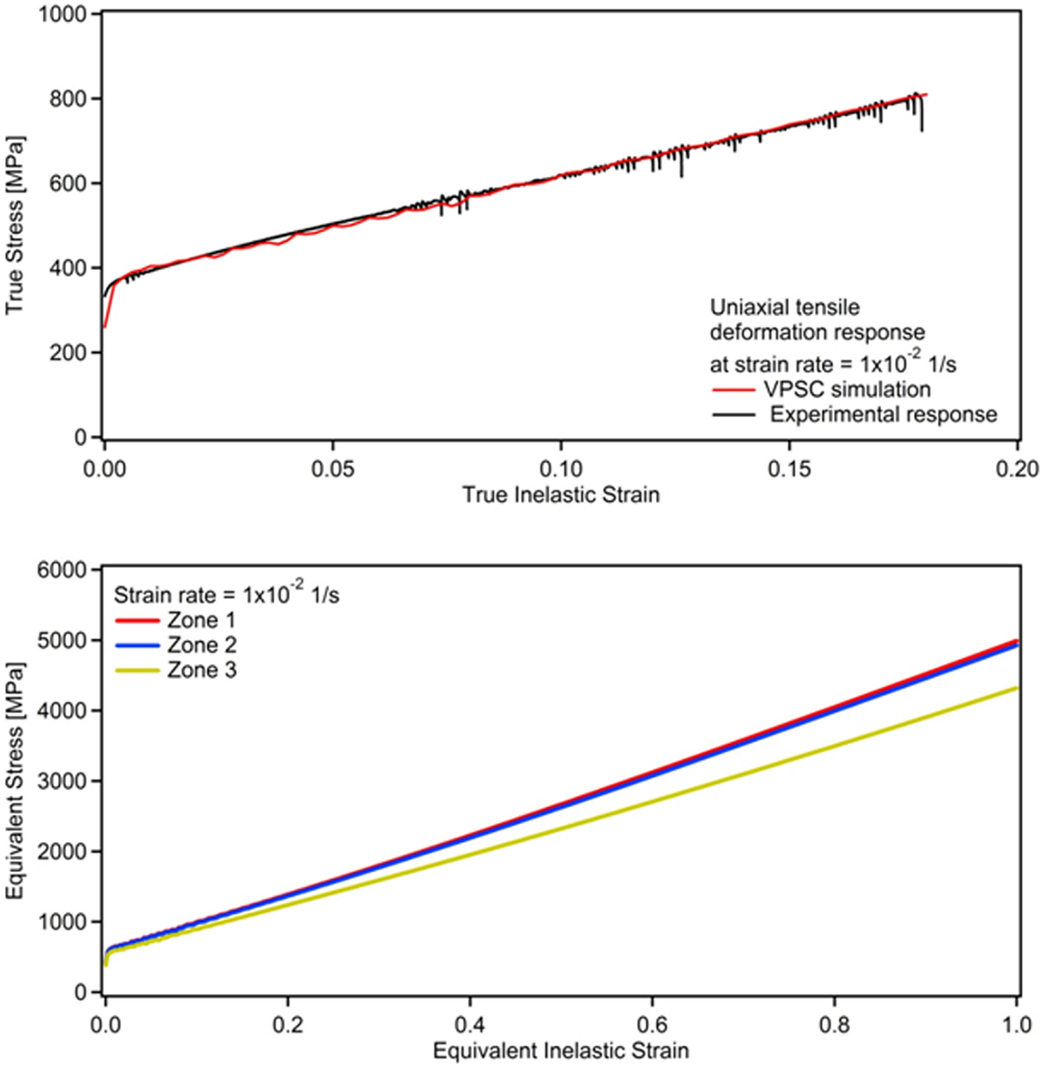
Figure 6. Top: VPSC simulation of the RT experimental uniaxial tensile deformation of Hadfield steel at a strain rate of 1 × 10−2 1/s. Bottom: the corresponding predicted equivalent stress–strain response for each zone within the impact sample based on the distribution of stress concentration (Figure 4).
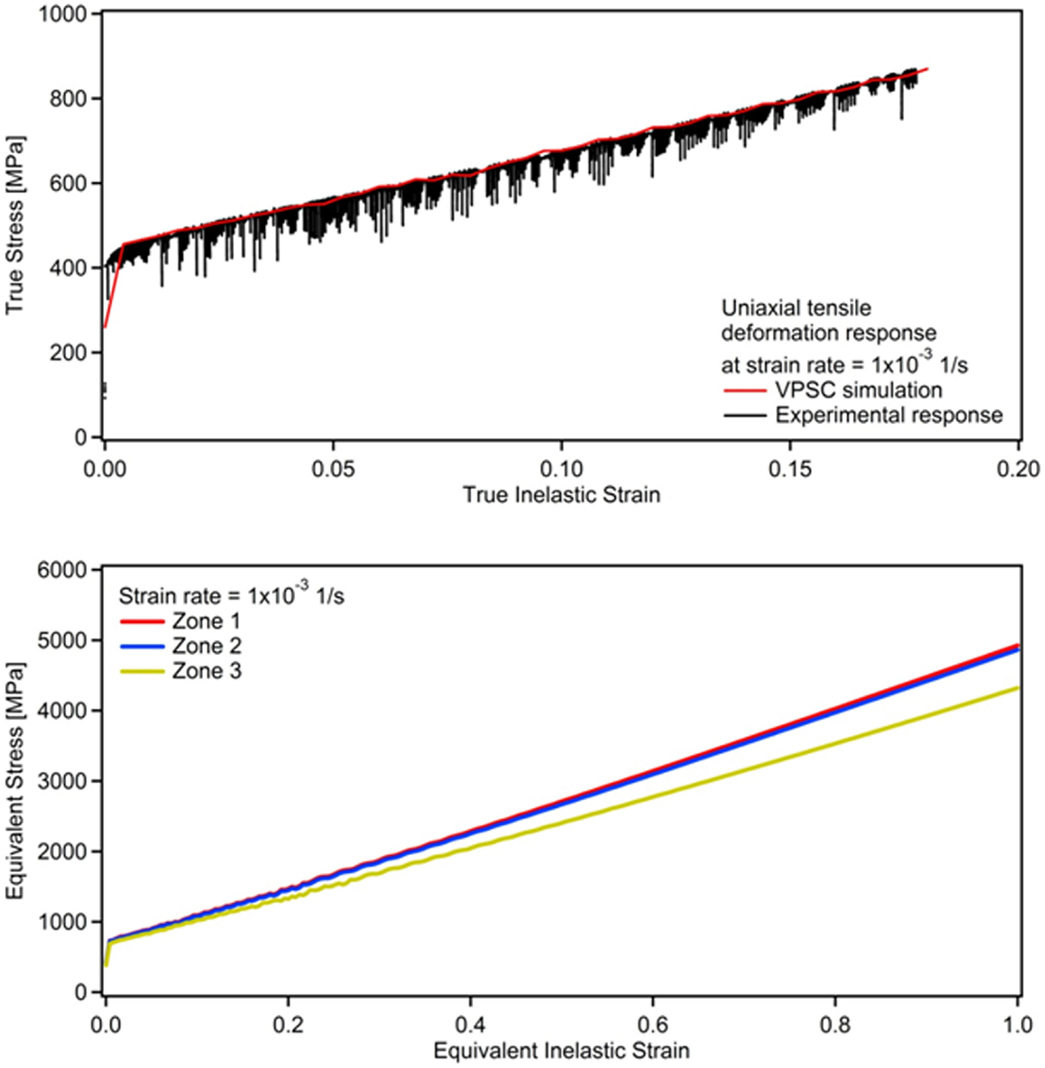
Figure 7. Top: VPSC simulation of the RT experimental uniaxial tensile deformation of Hadfield steel at a strain rate of 1 × 10−3 1/s. Bottom: the corresponding predicted equivalent stress–strain response for each zone within the impact sample based on the distribution of stress concentration (Figure 4).
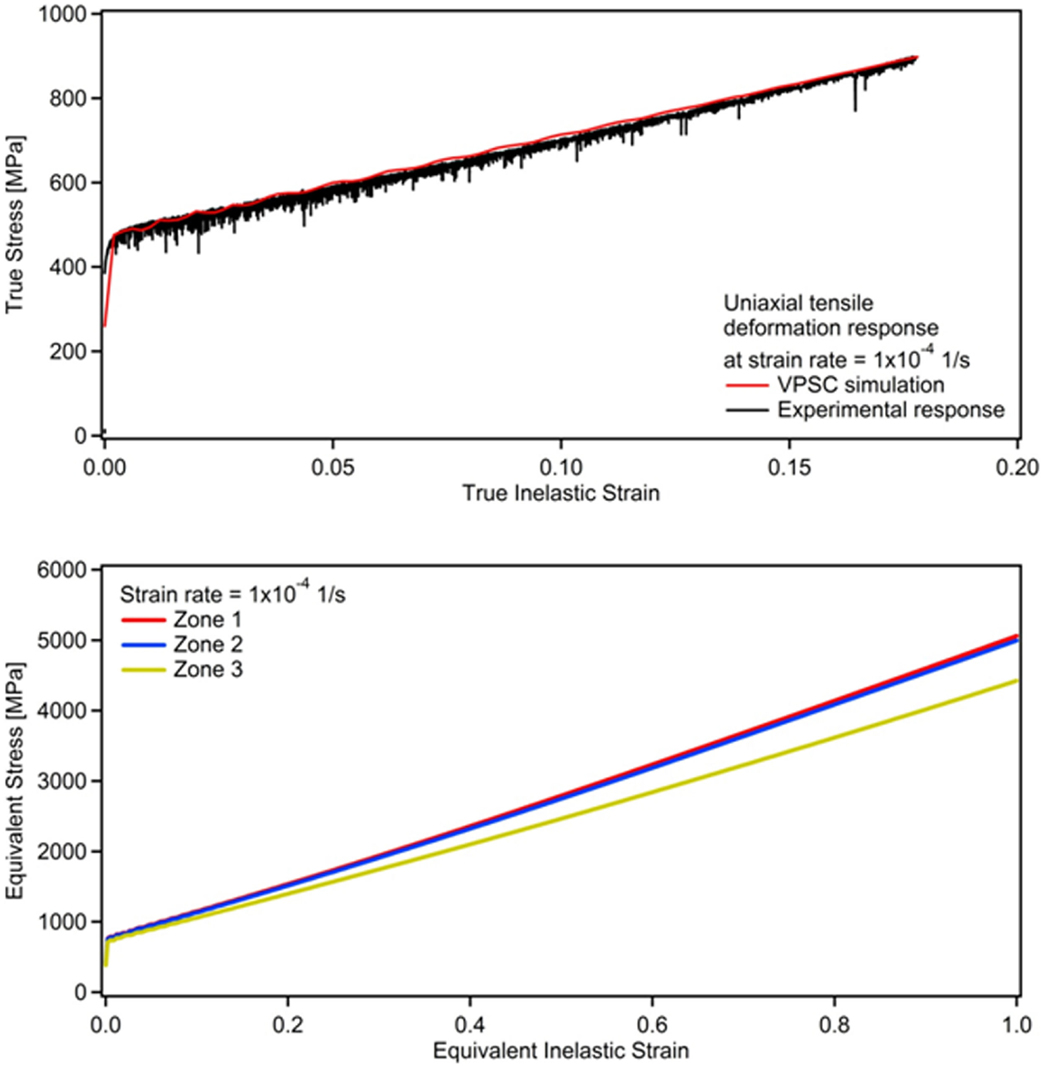
Figure 8. Top: VPSC simulation of the RT experimental uniaxial tensile deformation of Hadfield steel at a strain rate of 1 × 10−4 1/s. Bottom: the corresponding predicted equivalent stress–strain response for each zone within the impact sample based on the distribution of stress concentration (Figure 4).
The VPSC algorithm employed in the current study considers plastic deformation only, which takes place when one or more slip or twinning systems become active. For a slip system S, the corresponding resolved shear stress facilitating plastic deformation can be described in vector form based on the Schmid and the applied stress (σi) tensors:
The non-linear shear strain rate in the system S can be described as a function of :
where is a reference rate, is the threshold stress corresponding to this reference rate, and n is the inverse of the rate sensitivity index. When the contributions of all active systems in a single grain are superposed and pseudolinearized (Lebensohn and Tomé, 1993):
where is the secant visco-plastic compliance of the crystal, which gives the instantaneous relation between stress and strain rate. At the polycrystal level, this relationship assumes the following form (Lebensohn and Tomé, 1993):
where and Σ represent the polycrystal strain rate and applied stress, respectively.
In a continuum comprising a matrix and inclusions, the deviations in strain rate and stress of the inclusions from those of the matrix can be defined as:
where and σj stand for the local (grain level) strain rate and stress. When the Eshelby inclusion formulation is employed to solve the stress equilibrium, one can obtain (Kocks et al., 1998):
The interaction tensor is defined as:
where M(sec) is the secant compliance tensor for the polycrystal aggregate and S is the visco-plastic Eshelby tensor (Kocks et al., 1998). In Eq. 8, an effective value of n′ = 1 was used, which ensures a rigid interaction (Lebensohn and Tomé, 1993).
Substitution of Eqs 3 and 4 into Eq. 7 yields the macroscopic secant compliance, M(sec), and the macroscopic strain rate is evaluated by taking the weighted average of crystal strain rates over all the grains as in Eq. 9:
Iterative solution of the Eqs 3, 7, and 9 gives the stress in each grain, the crystal’s compliance tensor, and the polycrystal compliance consistent with the applied strain rate . In this work, the term n in Eq. 2 was chosen as 20, which makes the formulation rate insensitive (Lebensohn and Tomé, 1993). This sounds contradictory to the overall aim of incorporating the NSRS of Hadield steel into the simulations, however; it should be noted that the uniaxial deformation response at each strain rate was modeled separately rather than utilizing a single micro-deformation model accounting for the SRS. Therefore, the term n in Eq. 2 was assigned a value to ensure rate insensitivity within the same simulation, or in other words, for each case. One reason for this is that, to the best of the authors’ knowledge, a crystal plasticity model capable of predicting the NSRS exhibited by Hadfield steel has not been forwarded yet. Furthermore, the incorporation of NSRS requires coupling of crystal plasticity with atomistic simulations to properly account for the diffusivity of C and the corresponding consequences, which is beyond the scope of the current work.
The rate of overall dislocation density can be expressed as:
where k1 and k2 are geometric constants that define the athermal (statistical) storage of the moving dislocations (Kocks et al., 1998). The flow stress τ is defined in the traditional Taylor hardening format as:
where α is the dislocation interaction parameter and τ0 is a reference strength, which is related to deformation at the grain level. The reference strength value for Hadfield steel was determined as 132 MPa in previous work (Canadinc et al., 2007), where the 0.2% offset yield strength value is normalized by the Taylor factor. The Taylor factor for the current materials was determined based on the experimentally measured texture (Canadinc et al., 2008b), and it is about 3.11, which represents a slightly textured material as compared to the fully random texture case that has a Taylor factor of 3.06. From Eq. 11, with τ0 constant, the rate of the flow stress is obtained by taking the time derivative as,
Substituting Eq. 10 into Eq. 12 results in:
From Eq. 11, the following identity is obtained for the square root of the density of dislocations:
Once Eq. 14 is substituted into Eq. 13, the rate of flow stress evolution is given by:
One should note that the term in Eq. 15 is the linear Voce hardening term (Eq. 17). Having noted this, Eq. 15 can also be expressed as (Kocks et al., 1998):
where θ0 is the constant strain hardening rate, and τs represents the saturation stress in the absence of geometric effects, or the threshold stress. The hardening is defined by an extended Voce law (Kocks et al., 1998), which is characterized by the evolution of the threshold stress (τs) with accumulated shear strain (Γ) in each grain of the form
where τ0 is the reference strength, and τ1, θ0, and θ1 are the parameters that define the hardening behavior (Kocks et al., 1998). The hardening law defined by Eq. 17 characterizes the onset of plasticity and the saturation of threshold stress at larger strains.
The current VPSC model described by Eqs 1–17 was employed to solve for the stresses corresponding to the given strains throughout the deformation. The experimentally determined initial texture of Hadfield steel (inset of Figure 5) was utilized as input, and the macroscopic deformation responses were predicted as presented in Figures 5–8 for all the strain rates considered in this work. The corresponding Voce hardening parameters for each strain rate are provided in Table 1.
In order to define a proper hardening rule for the FE simulations of the impact deformation, the current VPSC model was employed to predict the equivalent stress–strain response of Hadfield steel based on the uniaxial deformation responses at all four strain rates considered herein (Figures 5–8). Specifically, the successful prediction of the experimental data (Figures 5–8) is a strong indication that the materials’ deformation was successfully modeled at the micro-deformation level, and therefore, the same VPSC model was utilized to predict the equivalent stress–strain response for each strain rate utilizing the same hardening parameters for each strain rate. Since the material-independent consideration of the stress–strain distribution under impact loading (Figure 4) had also demonstrated that the distribution of stresses and strains throughout the sample is heterogeneous, the FE mesh for each sample was divided into three different zones with three different flow rules (Figure 4), such that a more homogeneous stress–strain distribution can be obtained within each zone upon impact loading. Therefore, the VPSC model was utilized to predict the corresponding equivalent stress–strain state response for each zone at all four strain rates (Figures 5–8). Specifically, the same hardening parameters as in the VPSC model predicting the experimental uniaxial deformation response were employed in all three simulations for each strain rate. The corresponding deformation of the polycrystalline aggregate within each zone was defined to the VPSC algorithm through velocity gradient tensors, which were determined based on the material-independent strain distributions under impact loading (Figure 4). The corresponding velocity gradient tensors for each zone were computed as:
and
for zones 1, 2, and 3, respectively (Onal et al., 2014).
The corresponding VPSC simulation results demonstrating the equivalent for each zone are presented in Figures 5–8 for the strain rates of 1 × 10−1, 1 × 10−2, 1 × 10−3, and 1 × 10−4 1/s, respectively. It should be noted that the strength levels attained by the equivalent deformation curves for each strain rate follows the same trend as that of the experimental uniaxial curves. This is not surprising since both the plastic deformation and the hindering of dislocations by diffusing C atoms are considered at the slip system level, where the latter leads to NSRS in Hadfield steel. Moreover, for each strain rate, higher stresses were obtained for zone 1 as compared to zones 2 and 3, and zone 3 exhibited the lowest stress levels (Figures 5–8), which stands in good agreement with the stress intensities demonstrated in Figure 4, where the stresses decrease as one moves from zone 1 that contains the notch toward zone 3 with the least stress concentration factors.
The results of the FE simulations incorporating the roles of microstructure and NSRS texture through crystal plasticity are presented in Figure 9. Even though the predictions are much better for all strain rates as compared to those of the initial FE simulations that defined hardening based on the experimental uniaxial deformation response only (Figures 2 and 3), there is an important difference between the two cases in terms of strain rate dependence. Specifically, the results of the initial simulations revealed that the best predictions were obtained by defining the flow rule for Hadfield steel based on the uniaxial deformation response recorded at the highest strain rate (1 × 10−1 1/s in the current work), in addition to the fact that the worst predictions were based on the flow rules defined within the NSRS range. Upon incorporation of microstructure into the FE model through crystal plasticity, however, it was evident that the best prediction was obtained by defining the flow rule based on the VPSC predictions of the equivalent stress–strain response at 1 × 10−2 1/s (Figure 9), which is the second highest strain rate and within the NSRS range (Figure 1). This contradictory result clearly demonstrates that reliable predictions can be obtained by proper coupling of crystal plasticity and FE analysis even if the experimental flow rule of the material is acquired under uniaxial loading and at strain rates that fall within the NSRS range. This is especially important in terms of utilizing standard laboratory experiments to characterize a material’s fundamental properties, which are simple and may be restricted to strain rates within the NSRS owing to practical limitations, while predicting its deformation response under complicated loading scenarios, such as impact loading.
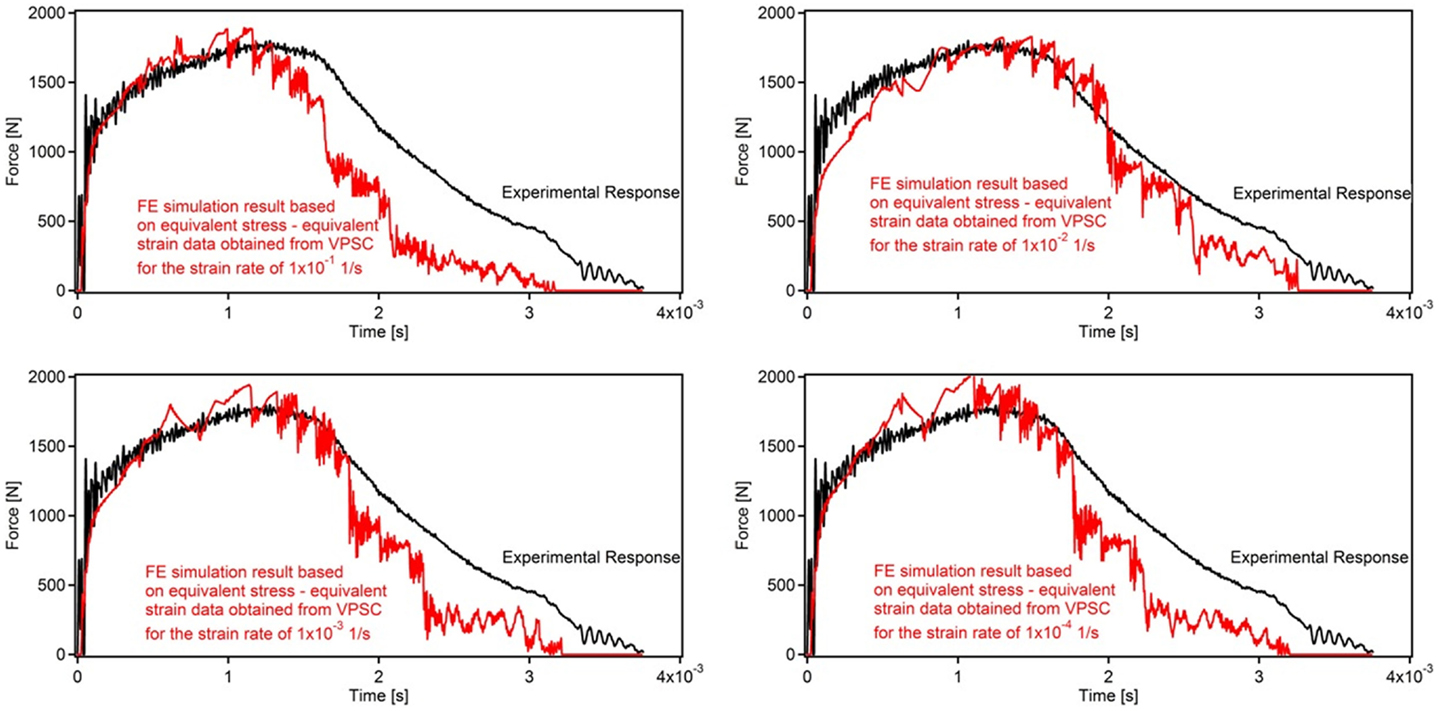
Figure 9. Comparison of the experimental impact response and results of the FE simulations incorporating equivalent stress–strain responses predicted by crystal plasticity for all strain rates considered.
Conclusion
The RT impact response Hadfield steel was studied with the aid of a multi-scale modeling approach coupling crystal plasticity and FE analysis. The roles of texture, geometry, and SRS were successfully taken into account all at once, where crystal plasticity was utilized to obtain the multi-axial flow rule at different strain rates based on the experimental deformation response under uniaxial tensile loading. The FE simulation results demonstrated that the utility of equivalent stress–equivalent strain response for defining the hardening rule under impact loading resulted in improved predictions. Interestingly, the simulation results indicated that a multi-axial definition of the material flow rule is the major parameter dictating the success of the predictions of impact loading deformation even in the presence of negative SRS, as in the case of Hadfield steel. Finally, the current set of results also demonstrated that reliable predictions can be obtained by proper coupling of crystal plasticity and FE analysis even if the experimental flow rule of the material is acquired under uniaxial loading and at moderate strain rates that are significantly slower than those attained during impact loading. This observation opens the venue for utilizing more practical and simpler laboratory experiments to characterize a material’s fundamental properties while predicting its deformation response under complicated loading scenarios, such as impact loading.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK) under grant 112M806.
References
Bayraktar, E., Khalid, F. A., and Levaillant, C. (2004). Deformation and fracture behaviour of high manganese austenitic steel. J. Mater. Process. Tech. 147, 145–154. doi: 10.1016/j.jmatprotec.2003.10.007
Biyikli, E., Canadinc, D., Maier, H. J., Niendorf, T., and Top, S. (2010). Three-dimensional modeling of the grain boundary misorientation angle distribution based on two-dimensional experimental texture measurements. Mater. Sci. Eng. A 527, 5604–5612. doi:10.1016/j.msea.2010.05.037
Bouaziz, O., Allain, S., Scott, C. P., Cugy, P., and Barbier, D. (2011). High manganese austenitic twinning induced plasticity steels: a review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 15, 141–168. doi:10.1016/j.cossms.2011.04.002
Canadinc, D., Biyikli, E., Niendorf, T., and Maier, H. J. (2011). Experimental and numerical investigation of the role of grain boundary misorientation angle on the dislocation–grain boundary interactions. Adv. Eng. Mater. 13, 281–287. doi:10.1002/adem.201000229
Canadinc, D., Efstathiou, C., and Sehitoglu, H. (2008a). On the negative strain rate sensitivity of hadfield steel polycrystals. Scripta Mater. 59, 1103–1106. doi:10.1016/j.scriptamat.2008.07.027
Canadinc, D., Sehitoglu, H., Maier, H. J., and Kurath, P. (2008b). On the incorporation of length scales associated with pearlitic and bainitic microstructures into a visco-plastic self-consistent model. Mater. Sci. Eng. A 485, 258–271. doi:10.1016/j.msea.2007.08.049
Canadinc, D., Sehitoglu, H., and Maier, H. J. (2007). The role of dense dislocation walls on the deformation response of aluminum alloyed hadfield steel polycrystals. Mater. Sci. Eng. A 454–455, 662–666. doi:10.1016/j.msea.2006.11.122
Canadinc, D., Sehitoglu, H., Maier, H. J., and Chumlyakov, Y. I. (2005). Strain hardening behavior of aluminum alloyed hadfield steel single crystals. Acta Mater. 53, 1831–1842. doi:10.1016/j.actamat.2004.12.033
Hutchinson, B., and Ridley, N. (2006). On dislocation accumulation and work hardening in Hadfield steel. Scripta Mater. 55, 299–302. doi:10.1016/j.scriptamat.2006.05.002
Jeong, J. S., Woo, W., Oh, K. H., Kwon, S. K., and Koo, Y. M. (2012). In situ neutron diffraction study of the microstructure and tensile deformation behavior in Al-added high manganese austenitic steels. Acta Mater. 60, 2290–2299. doi:10.1016/j.actamat.2011.12.043
Karaman, I., Sehitoglu, H., Chumlyakov, Y. I., Maier, H. J., and Kireeva, I. V. (2001). Extrinsic stacking faults and twinning in hadfield manganese steel single crystals. Scripta Mater. 44, 337–343.
Karaman, I., Sehitoglu, H., Gall, K., Chumlyakov, Y. I., and Maier, H. J. (2000). Deformation of single crystal Hadfield steel by twinning and slip. Acta Mater. 48, 1345–1359. doi:10.1016/S1359-6454(99)00383-3
Kimura, Y., Inoue, T., Yin, F., and Tsuzaki, K. (2008). Inverse temperature dependence of toughness in an ultrafine grain-structure steel. Science 320, 1057–1060. doi:10.1126/science.1156084
Kocks, U. F., Tomé, C. N., and Wenk, H. R. (1998). Texture and Anisotropy. New York: Cambridge University Press.
Kormi, K., Webb, D. C., and Johnson, W. (1997). The application of the FEM to determine the response of a pretorsioned pipe cluster to static or dynamic axial impact loading. Comp. Struct. 62, 353–368. doi:10.1016/S0045-7949(96)00176-9
Lebensohn, R. A., and Tomé, C. N. (1993). A self-consistent anisotropic approach for the simulation of plastic deformation and texture development of polycrystals: application to zirconium alloys. Acta Metall. Mater. 41, 2611–2624.
Niendorf, T., Lotze, C., Canadinc, D., Frehn, A., and Maier, H. J. (2009). The role of monotonic pre-deformation on the fatigue performance of a high-manganese austenitic TWIP steel. Mater. Sci. Eng. A 499, 518–524. doi:10.1016/j.msea.2008.09.033
Niendorf, T., Rubitschek, F., Maier, H. J., Niendorf, J., Richard, H. A., and Frehn, A. (2010). Fatigue crack growth–Microstructure relationships in a high-manganese austenitic TWIP steel. Mater. Sci. Eng. A 527, 2412–2417. doi:10.1016/j.msea.2009.12.012
Onal, O., Bal, B., Toker, S. M., Mirzajanzadeh, M., Canadinc, D., and Maier, H. J. (2014). Microstructure-based modeling of the impact response of a biomedical niobium-zirconium alloy. J Mater. Res. 29, 1123–1134. doi:10.1557/jmr.2014.105
Owen, W. S., and Grujicic, M. (1999). Strain aging of austenitic Hadfield manganese steel. Acta Mater. 47, 111–126. doi:10.1016/S1359-6454(98)00347-4
Raykhere, S. L., Kumar, P., Singh, R. K., and Parameswaran, V. (2010). Dynamic shear strength of adhesive joints made of metallic and composite adherents. Mater. Des. 31, 2102–2109. doi:10.1016/j.matdes.2009.10.043
Song, R., Ponge, D., and Raabe, D. (2005). Mechanical properties of an ultrafine grained C–Mn steelprocessed by warm deformation and annealing. Acta Mater. 53, 4881–4892. doi:10.1016/j.actamat.2005.07.009
Toker, S. M., Canadinc, D., Taube, A., Gerstein, G., and Maier, H. J. (2014). On the role of slip–twin interactions on the impact behavior of high-manganese austenitic steels. Mater. Sci. Eng. A 593, 120–126. doi:10.1016/j.msea.2013.11.033
Ueji, R., Tsuchida, N., Terada, D., Tsuji, N., Tanaka, Y., Takemura, A., et al. (2008). Tensile properties and twinning behavior of high manganese austenitic steel with fine-grained structure. Scripta Mater. 59, 963–966. doi:10.1016/j.scriptamat.2008.06.050
Wen, Y. H., Peng, H. B., Si, H. T., Xiong, R. L., and Raabe, D. (2014). A novel high manganese austenitic steel with higher work hardening capacity and much lower impact deformation than Hadfield manganese steel. Mater. Design 55, 798–804. doi:10.1016/j.matdes.2013.09.057
Keywords: high-manganese austenitic steel, crystal plasticity, finite element analysis, microstructure, strain rate sensitivity, impact
Citation: Onal O, Ozmenci C and Canadinc D (2014) Multi-scale modeling of the impact response of a strain-rate sensitive high-manganese austenitic steel. Front. Mater. 1:16. doi: 10.3389/fmats.2014.00016
Received: 16 July 2014; Accepted: 09 September 2014;
Published online: 30 September 2014.
Edited by:
Thomas Heine, Jacobs University Bremen gGmbH, GermanyReviewed by:
Atilim Eser, RWTH Aachen, GermanyReginald Felix Hamilton, The Pennsylvania State University, USA
Copyright: © 2014 Onal, Ozmenci and Canadinc. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Demircan Canadinc, Rumeli Feneri Yolu, Sariyer, Istanbul, Turkey e-mail:ZGNhbmFkaW5jQGt1LmVkdS50cg==
 Orkun Onal
Orkun Onal Cemre Ozmenci
Cemre Ozmenci Demircan Canadinc
Demircan Canadinc