Topological model for boroaluminosilicate glass hardness

Introduction

In many advanced applications of glasses, it is desirable to increase the hardness as much as possible to improve the scratch and damage resistance (Wondraczek et al., 2011). Hardness is a measure of the mean contact stress for the formation of a permanent deformation and it is typically quantified by permanently deforming the glass with a sharp indenter (e.g., Vickers diamond indenter), where hardness (H) is given by the load (P) divided by the project area (A) as H = P/A. Hardness is a function of chemical composition and different models and approaches have been proposed to predict the composition dependence of glass hardness (Georoff and Babcock, 1973; Yamane and Mackenzie, 1974; Calleja et al., 2002; Smedskjaer et al., 2010a). Relationships between H and various macroscopic properties have also been proposed (Liu and Cohen, 1989; Sehgal and Ito, 1999; Gao et al., 2003; Hand and Tadjiev, 2010), but there is an intrinsic difference in the scaling between hardness and, e.g., elastic moduli. Therefore, such efforts have not been successful at predicting the composition dependence of hardness (Teter, 1998; Kjeldsen et al., 2014).

Such predictions are particularly difficult for mixed network-former systems, since their complicated structural speciation (Zielniok et al., 2007; Manara et al., 2009; Zheng et al., 2012a) can lead to non-linear variations in hardness (Zheng et al., 2012b). Boroaluminosilicate glasses constitute an important class of mixed network-former glasses as they have found widespread applications in fields such as consumer electronics (Wondraczek et al., 2011), bioactive materials for regeneration of bone and tissue (Hench, 2006), fiberglass for composite applications (Li et al., 2014), and radioactive waste containment (Jantzen et al., 2010). The structure of boroaluminosilicate glasses is complicated due to the uncertainty of the extent and nature of mixing of the network-forming cations (Si, B, and Al) (Ollier et al., 2004; Du and Stebbins, 2005; Wu and Stebbins, 2009; Zheng et al., 2012a).

In this work, we attempt to apply the hardness model of Smedskjaer et al. (2010a) based on topological constraint theory (Gupta and Mauro, 2009; Mauro et al., 2009; Smedskjaer et al., 2010b; Bauchy and Micoulaut, 2011, 2013; Jiang et al., 2013; Rodrigues and Wondraczek, 2013) to predict the composition dependence of sodium boroaluminosilicate glass hardness. The model has been found to be quantitatively predictive for borate glasses (Smedskjaer et al., 2010a,c), borosilicate glasses (Smedskjaer et al., 2011), phosphosilicate glasses (Zeng et al., 2014), and calcium silicate hydrates (Bauchy et al., 2014), but has not yet been tested for a system with three network-forming oxides. Topological constraint theory originally developed by Phillips and Thorpe builds on an enumeration of the linear two-body bond-stretching (BS) and the angular three-body bond-bending (BB) constraints (Phillips, 1979; Thorpe, 1983; He and Thorpe, 1985; Phillips and Thorpe, 1985). The glassy network is classified as “flexible” with internal degrees of freedom (floppy modes) when the total number of BS and BB constraints per atom (n) is less than the number of degrees of freedom per atom (i.e., 3). When n > 3, the network is “stressed rigid” due to its high connectivity, whereas the isostatic state is achieved for n = 3. The theory has later been extended by Gupta and Mauro to account for the temperature dependence of the constraints (Gupta and Mauro, 2009; Mauro et al., 2009), allowing for a distinction of the individual constraints based on their chemistry via the constraint onset temperature. Here, we derive a topological hardness model for sodium boroaluminosilicate glasses and validate it against experimental measurements for three distinct series of glasses.

Experimental Section

The first investigated glass series has varying Si/Al ratio: (80 − x)SiO₂ − x Al₂O₃ − 5 B₂O₃ − 15 Na₂O with x = 0, 1, 2.5, 5, 7.5, 10, 12.5, 15, 17.5, and 20 (Zheng et al., 2012a,b). The second series also has varying Si/Al ratio but for a different Na/B ratio: (84.4 − x)SiO₂ − x Al₂O₃ − 11.6 B₂O₃ − 4.0 Na₂O with x = 0, 1.4, 2.7, 4, 5.3, and 6.6 (Smedskjaer et al., 2014). The third series has varying Na/B ratio: 83.0 SiO₂ − 1.4 Al₂O₃ − y B₂O₃ − (15.6 − y) Na₂O with y = 0, 2.3, 4.8, 7.1, 8.6, 10.1, and 11.6 (Smedskjaer et al., 2014). All compositions also included ≤0.15 mol% SnO₂ as a fining agent. Structural data from solid-state nuclear magnetic resonance (NMR) spectroscopy is already available for these glass series (Zheng et al., 2012a; Smedskjaer et al., 2014). In addition, the Vickers microhardness has previously been measured for the first series with varying Si/Al ratio (Zheng et al., 2012b). For the other two series, we have here determined it using the same method. This was done using a Duramin 5 indenter (Struers A/S). The measurements were performed in air atmosphere at room temperature. A load of 0.49 N for duration of 5 s was applied and 30 indentations were performed on each sample. The Vickers hardness was calculated from the lengths of the indentation diagonals.

Theory

To apply temperature-dependent constraint theory to calculate hardness, the first step is to obtain quantitative structural data on short length scales in the glass, i.e., the concentration of the network-forming species and their coordination number (r_i) should be known. The types and number of intact (rigid) constraints at room temperature (i.e., temperature of indentation measurement) must be identified and counted. The number of BS constraints is given by r_i/2 (each BS constraint is shared by two atoms) and the number of BB constraints is given by 2r_i − 3 (number of independent angles needed to define polyhedron). All of these linear and angular constraints are generally intact at room temperature for network-forming atoms in oxide glasses. The indentation hardness can then be calculated as (Smedskjaer et al., 2010a):

$H\left(x\right)=\left(\frac{dH}{dn}\right)\left[n\left(x\right)-n_{\mathrm{crit}}\right],$ (1)

where x is the composition variable, dH/dn is the proportionally constant, and n_crit is the critical number of constraints that must be present in order to produce a connected network that is required for the material to display mechanical resistance. We set n_crit = 2.5, since this gives a network that is rigid in two dimensions of the three-dimensional space (Smedskjaer et al., 2010a, 2011). The proportionality constant (dH/dn) is determined empirically and found to be dependent on the load of the indenter (Smedskjaer et al., 2010a). Additional work is required to understand the possible composition dependence of dH/dn (Smedskjaer et al., 2011).

Pure silicon dioxide glass under ambient conditions is composed exclusively of SiO₄ tetrahedra containing four bridging oxygens (BO) linking to neighboring Si atoms. Addition of sodium oxide causes BO to be converted to non-bridging oxygen (NBO), which do not bridge to other SiO₄ tetrahedra, but instead coordinate to the modifier cations. Pure boron oxide glass is composed of corner-sharing BO₃ triangles (B^III), a large fraction of which combine to form three-membered boroxol ring units (Jellison et al., 1977; Micoulaut et al., 1995; Youngman et al., 1995). Addition of sodium oxide to B₂O₃ causes either (i) the creation of a NBO, rupturing the linkage between two trigonally coordinated B^III groups, or (ii) conversion of boron from three-coordinated (trigonal boron, B^III) to a four-coordinated (tetrahedral boron, B^IV) state without the creation of an NBO. Aluminum mostly enters a glassy network in fourfold coordination (Al^IV) when there are sufficient network-modifier cations (e.g., Na₂O) available for charge compensation (Bottinga and Weill, 1972; Chan et al., 1999). Five- or sixfold coordination environment around Al is expected for compositions, where the amount of charge-balancing modifier cations (Na⁺) is insufficient to stabilize all Al in fourfold coordination. As a consequence, some higher coordination Al species are formed and believed to provide an additional source of charge compensation in these networks (Risbud et al., 1987; Sen and Youngman, 2004). Hence, the cation speciation in sodium boroaluminosilicate glasses is complex due to the inherent competition between Na₂O and three different glass-forming oxide constituents. When [Na₂O] < [Al₂O₃], all available sodium is used to charge compensate Al^IV, and deficiency in sodium concentration leads to fivefold coordinated aluminum (Al^V) groups. When [Na₂O] > [Al₂O₃], sodium first charge compensates Al^IV, and thus all aluminum is fourfold coordinated and unaffected by other compositional changes. Hence, there is preference in the formation of Al^IV over that of B^IV or NBOs (Zheng et al., 2012a).

In the topological constraint model of sodium boroaluminosilicate glass, we consider constraints arising from the boroaluminosilicate network backbone, as well as constraints related to the characteristic structures surrounding the sodium ions forming NBOs in the glass. The bond constraints are:

• α: Si–O, Al–O, B–O, and M^NB–O linear constraints. There are two α constraints at each oxygen.

• β_Si: O–Si–O angular constraints. There are five β_Si constraints per Si to form a rigid Si tetrahedron.

• β_Al: O–Al–O angular constraints. There are seven β_Al constraints per Al^V and five β_Al constraints per Al^IV.

• β_B: O–B–O angular constraints. There are five β_B constraints per B^IV and three β_B constraints per B^III.

• γ: Si–O–Si, Al–O–Al, B–O–B, Si–O–B, Si–O–Al, Al–O–B, Si–O–M^NB, Al–O–M^NB, and B–O-M^NB angular constraints. There is one γ constraint at each oxygen.

• μ: additional modifier rigidity due to clustering effects. Based on our previous findings for soda lime borate and borosilicate glasses (Smedskjaer et al., 2010b, 2011), we assign two μ constraints per NBO-forming Na atom.

Here, we have assigned all of the α constraints on the oxygen and none on the cations. It is assumed that all of these constraints are rigid at room temperature (∼300 K). It should be noted that the constraint counting is performed only over the nearest neighbors (i.e., constraints from intermediate- and long-range interactions have been approximated from the two- and three-body constraints). This is believed to be sufficient for the boroaluminosilicate glasses studied here, since the intermediate-range structures (e.g., boroxol rings) do not introduce any new independent constraints to the system.

The number of constraints per atom (n) for the glass (100 − x − y − z)SiO₂ − x Al₂O₃ − y B₂O₃ − z Na₂O can be calculated from the above analysis based on the fraction N of each network-forming species:

$\begin{array}{llll}\hfill n\left(x,y,z\right)& =3N\left(\mathrm{O}\right)+5N\left(\mathrm{Si}\right)+7N\left(\mathrm{A}{\mathrm{l}}^{\mathrm{V}}\right)+5N\left(\mathrm{A}{\mathrm{l}}^{\mathrm{IV}}\right)& \hfill & \\ \hfill & +5N\left({\mathrm{B}}^{\mathrm{IV}}\right)+3N\left({\mathrm{B}}^{\mathrm{III}}\right)+2N\left(\mathrm{Na\; -NBO}\right)\end{array}$ (2)

With this expression for n(x,y,z) inserted into Eq. 1, we can calculate the hardness of sodium boroaluminosilicate glasses, assuming that the necessary structural data are available and by taking dH/dn as a fitting parameter.

Results and Discussion

We first consider the series of glasses with varying Si/Al ratio [(80 − x)SiO₂ − x Al₂O₃ − 5 B₂O₃ − 15 Na₂O with x = 0, 1, 2.5, 5, 7.5, 10, 12.5, 15, 17.5, and 20], for which hardness data have already been reported (Zheng et al., 2012b). Figure 1 shows the composition dependence of the experimentally determined hardness values and those calculated based on Eqs 1 and 2 with the analyzed chemical compositions and ¹¹B and ²⁷Al magic angle spinning (MAS) NMR data as input (Zheng et al., 2012a). Hardness is plotted against the value [Al₂O₃] − [Na₂O], i.e., the excess concentration of Al³⁺ not being charge-balanced in tetrahedral configuration by Na⁺. dH/dn is found experimentally to be equal to 7.2 GPa. Using this value, we find good agreement between the predicted and measured values of hardness (Figure 1), even though the glasses cover a wide compositional regime from 0 to 20 mol% Al₂O₃. That is, the topological model is able to capture the increase in H with increasing [Al₂O₃] in the peralkaline regime until reaching its maximum value around [Al₂O₃] − [Na₂O] = −5 and the further increase in H with increasing [Al₂O₃] in the peraluminous regime is also captured.

FIGURE 1

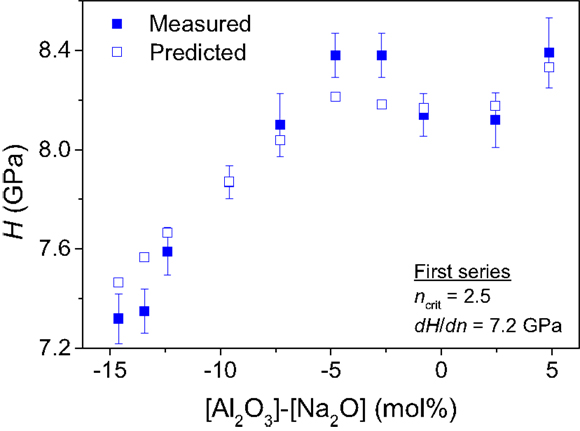
Figure 1. Composition dependence of Vickers hardness (H) for the first series of boroaluminosilicate glasses: (80 − x)SiO₂ − x Al₂O₃ − 5 B₂O₃ − 15 Na₂O with x = 0, 1, 2.5, 5, 7.5, 10, 12.5, 15, 17.5, and 20 (Zheng et al., 2012b). The filled squares represent the experimental data points, whereas the open squares represent the computed H(x) values with Eq. 1(dH/dn = 7.2 GPa) using the analyzed compositions and ¹¹B and ²⁷Al MAS NMR data (Zheng et al., 2012a).

In the second series of glasses also with varying Si/Al ratio but at different Na/B ratio, the experimentally determined hardness exhibits a minimum around the composition with [Al₂O₃] = [Na₂O] (Figure 2). As shown in the Figure, this compositional scaling of hardness can also be predicted by the topological model using the published structural data (Smedskjaer et al., 2014) and with dH/dn equal to 7.4 GPa. The decrease in hardness with increasing [Al₂O₃] in the peralkaline regime occurs due to the decrease in the fractions of the tetrahedral Si and B atoms, while the increase in hardness with increasing [Al₂O₃] in the peraluminous regime occurs due to the increase in the fraction of fivefold coordinated Al atoms.

FIGURE 2

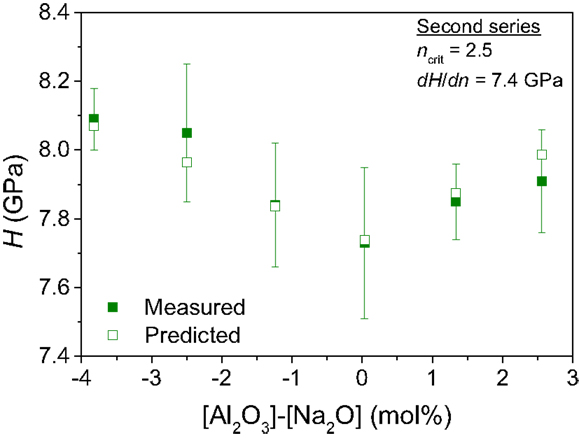
Figure 2. Composition dependence of Vickers hardness (H) for the second series of boroaluminosilicate glasses: (84.4 − x)SiO₂ − x Al₂O₃ − 11.6 B₂O₃ − 4.0 Na₂O with x = 0, 1.4, 2.7, 4, 5.3, and 6.6. The filled squares represent the experimental data points, whereas the open squares represent the computed H(x) values with Eq. 1 (dH/dn = 7.4 GPa) using the analyzed compositions and ¹¹B and ²⁷Al MAS NMR data (Smedskjaer et al., 2014).

For the third series of glasses with varying Na/B ratio, the experimentally determined hardness values are plotted in Figure 3 against the value [Na₂O] − [Al₂O₃] − [B₂O₃], i.e., the excess concentration of Na⁺ not being used for charge-balancing Al³⁺ and B³⁺ in tetrahedral configuration. Hardness increases with increasing modifier content (Na₂O) for [Na₂O] − [Al₂O₃] − [B₂O₃] < 0 due to the increase in the fractions of tetrahedral Si and B atoms, while hardness dramatically drops with increasing [Na₂O] for [Na₂O] − [Al₂O₃] − [B₂O₃] > 0 primarily due to the decrease in the fraction of tetrahedral B atoms. This trend can also be predicted by the model of Eq. 1 based on the published structural data (Smedskjaer et al., 2014) and with dH/dn equal to 7.4 GPa.

FIGURE 3

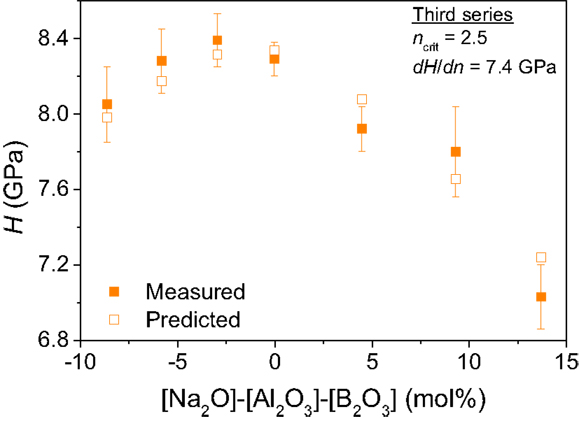
Figure 3. Composition dependence of Vickers hardness (H) for the third series of boroaluminosilicate glasses: 83.0 SiO₂ − 1.4 Al₂O₃ − y B₂O₃ − (15.6 − y) Na₂O with y = 0, 2.3, 4.8, 7.1, 8.6, 10.1, and 11.6. The filled squares represent the experimental data points, whereas the open squares represent the computed H(y) values with Eq. 1 (dH/dn = 7.4 GPa) using the analyzed compositions and ¹¹B and ²⁷Al MAS NMR data (Smedskjaer et al., 2014).

Our topological model is thus able to account for three distinct composition dependences of hardness of sodium boroaluminosilicate glasses with an approximate constant value of dH/dn equal to 7.3 GPa (Figures 1–3). Consequently, Figure 4 shows that the hardness values scale linearly with the number of room temperature constraints and n_crit = 2.5 appears to be a universal value valid also for these boroaluminosilicate glasses. Moreover, the results suggest that the proportionality constant dH/dn is a constant within a given glass family and for identical indentation conditions. We have previously found values of dH/dn equal to 9.9 GPa for borate glasses (Smedskjaer et al., 2010a,c) and 10.4 GPa for borosilicate glasses (Smedskjaer et al., 2011), but those indentations were performed at load of 0.25 N. For the borate glasses, we found dH/dn to be equal to 12.6 and 9.9 GPa for loads of 0.098 and 0.25 N, respectively, i.e., there appears to be a load dependence of the proportionality constant.

FIGURE 4

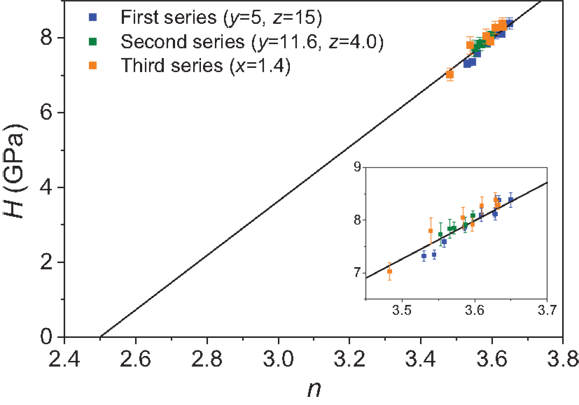
Figure 4. Measured Vickers hardness (H) at 0.49 N for the three series of sodium boroaluminosilicate glasses [(100 − x − y − z) SiO₂ − x Al₂O₃ − y B₂O₃ − z Na₂O)] as a function of the calculated average number of room temperature (T < T_γ) constraints n (Eq. 2). The solid line represents Eq. 1 with dH/dn = 7.3 GPa. The inset is an enlarged view of the H vs. n data.

We have shown that temperature-dependent constraint theory is a powerful tool for predicting the composition dependence of hardness for sodium boroaluminosilicate glasses. This can be applied to quantitatively design boroaluminosilicate glasses with desired hardness without having to melt a large number of glasses. However, to perform such model calculations, accurate structural models of boron and aluminum speciation are required. In the following, we apply the Yun–Bray model to predict the composition dependence of boron speciation (Yun and Bray, 1978), where we take [Na₂O] − [Al₂O₃] as the effective modifier concentration (Zheng et al., 2012a). According to this model, the concentration of fourfold coordinated boron atoms increases proportionally with the modifier content up to a maximum and then diminishes, since further modifier addition leads to NBO formation on the silica tetrahedra. To the best of our knowledge, no quantitative structural models of aluminum speciation in boroaluminosilicate glasses have been developed. We assume that the Al speciation is completely controlled by the sodium-to-aluminum ratio. For [Al₂O₃] < [Na₂O], we can simply subtract [Al₂O₃] from [Na₂O] to get the amount of modifier left to act in other roles. For [Al₂O₃] > [Na₂O], aluminum is assumed to consume all Na⁺ in charge-balancing Al tetrahedra, leading to formation of Al^V species, i.e., for simplicity, the possible formation of octahedral aluminum (Stebbins et al., 2000) or oxygen triclusters (Toplis et al., 1997) is neglected in the following model calculations.

With these assumptions, we can calculate the composition dependence of boron and aluminum speciation. These results are used as input to first calculate n(x,y,z) with Eq. 2 and then calculate H(x,y,z) with Eq. 1, where we set dH/dn equal to 7.3 GPa (i.e., the average value obtained for the three glass series). Figure 5 shows the model calculations for hardness of a sodium boroaluminosilicate system with [Na₂O] = 10% but varying ratios of the network-formers. For this system, high-hardness glasses are found in the low-B₂O₃, high-Al₂O₃ composition space due to the high concentration of fivefold Al atoms, each with seven angular O–Al–O constraints. Such simple analytical calculations can thus be used to identify compositional regions of high hardness and reveal the underlying structural and topological origins. We note that the glass-forming ability of the melts should also be considered when designing new glass compositions, since the entire composition space in Figure 5 cannot be turned into glasses using standard laboratory melt-quenching techniques.

FIGURE 5

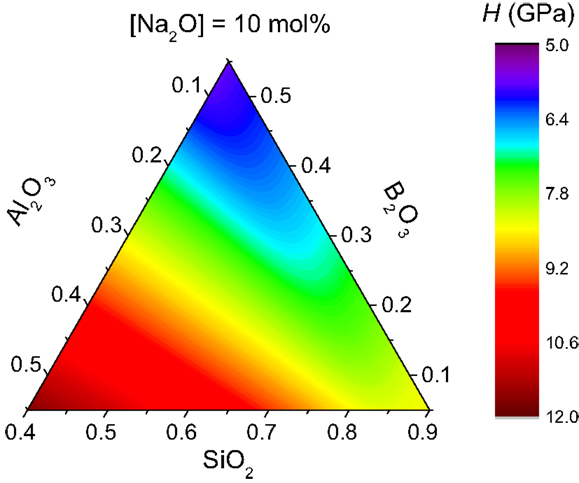
Figure 5. Model calculations of hardness (H) for sodium boroaluminosilicate glasses that all contain 10 mol% Na₂O, i.e., the fractions in the ternary diagram represent the relative concentrations of the network-formers (SiO₂, B₂O₃, and Al₂O₃). H is calculated using Eqs 1 and 2 with dH/dn = 7.3 GPa. Boron and aluminum speciation have been predicted as described in the text.

The hardness calculations performed in this study are all for sodium boroaluminosilicate glasses, but it would be interesting to extend the model to be applicable to boroaluminosilicate glasses with other network-modifier species. It is possible that the network-modifier cations could be distinguished based on their relative effect on the constraint onset temperatures. However, when calculating hardness, the constraints are counted at room temperature, where all constraints are assumed to be intact for boroaluminosilicate glasses. Therefore, the network-modifier cations with the same coordination number would be considered to have the same impact on the total number of constraints at room temperature. To account for the differences between different network-modifier cations, it could be possible to apply the recently introduced concept of constraint strength (Rodrigues and Wondraczek, 2014). Alternatively, the effect of the modifier cation on the hardness calculation could be accounted for through the value of the proportionality constant dH/dn, i.e., different dH/dn values might be obtained for lithium vs. sodium boroaluminosilicate glasses.

Conclusion

Using temperature-dependent constraint theory, a model has been developed to predict the composition dependence of indentation hardness of sodium boroaluminosilicate glasses. Applied to three distinct series of glasses, the predicted hardness values are in excellent agreement with experimental data. As this modeling approach is analytical, it can be applied to tailor new industrial glass compositions with maximized hardness given that accurate short-range structural data are available. For relatively low Na₂O concentrations, we show that high-hardness glasses are found in the low-B₂O₃, high-Al₂O₃ composition space. Our results also support the previous observation that a glass network must be rigid in at least two dimensions (n_crit = 2.5) to exhibit non-zero hardness. Finally, the proportionality constant dH/dn is found to be a constant for a given glass family when using identical indentation conditions.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks John C. Mauro and Randall E. Youngman for fruitful discussions. Financial support from the Danish Council for Independent Research under Sapere Aude: DFF-Starting Grant (1335-00051A) is acknowledged.

References

Bauchy, M., and Micoulaut, M. (2011). Atomic scale foundation of temperature-dependent bonding constraints in network glasses and liquids. J. Non-Cryst. Solids 357, 2530–2537. doi: 10.1016/j.jnoncrysol.2011.03.017

CrossRef Full Text | Google Scholar

Bauchy, M., and Micoulaut, M. (2013). Transport anomalies and adaptative pressure-dependent topological constraints in tetrahedral liquids: evidence for a reversibility window analogue. Phys. Rev. Lett. 110, 095501. doi:10.1103/PhysRevLett.110.095501

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bauchy, M., Qomi, M. J. A., Bichara, C., Ulm, F.-J., and Pellenq, R. J.-M. (2014). Nanoscale structure of cement: viewpoint of rigidity theory. J. Phys. Chem. C 118, 12485–12493. doi:10.1021/jp502550z

CrossRef Full Text | Google Scholar

Bottinga, Y., and Weill, D. F. (1972). The viscosity of magmatic silicate liquids; a model calculation. Am. J. Sci. 272, 438–475. doi:10.2475/ajs.272.5.438

CrossRef Full Text | Google Scholar

Calleja, F. J. B., Sanditov, D. S., and Privalko, V. P. (2002). Review: the microhardness of non-crystalline materials. J. Mater. Sci. 37, 4507–4516. doi:10.1023/A:1020648908142

CrossRef Full Text | Google Scholar

Chan, J. C. C., Bertmer, M., and Eckert, H. (1999). Site connectivities in amorphous materials studied by double-resonance NMR of quadrupolar nuclei:high-resolution ¹¹B ↔ ²⁷Al spectroscopy of aluminoborate glasses. J. Am. Chem. Soc. 121, 5238–5248. doi:10.1021/ja983385i

CrossRef Full Text | Google Scholar

Du, L. S., and Stebbins, J. F. (2005). Network connectivity in aluminoborosilicate glasses: a high-resolution ¹¹B, ¹⁷O, and ²⁷Al NMR study. J. Non-Cryst. Solids 351, 3508–3520. doi:10.1016/j.jnoncrysol.2005.08.033

CrossRef Full Text | Google Scholar

Gao, F. M., He, J. L., Wu, E. D., Liu, S. M., Yu, D. L., Li, D. C., et al. (2003). Hardness of covalent crystals. Phys. Rev. Lett. 91, 015502. doi:10.1103/PhysRevLett.91.015502

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Georoff, A. N., and Babcock, C. L. (1973). Relation of microindentation hardness to glass composition. J. Am. Ceram. Soc. 56, 97–99. doi:10.1111/j.1151-2916.1973.tb12366.x

CrossRef Full Text | Google Scholar

Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130, 094503. doi:10.1063/1.3077168

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hand, R. J., and Tadjiev, D. R. (2010). Mechanical properties of silicate glasses as a function of composition. J. Non-Cryst. Solids 356, 2417–2423. doi:10.1016/j.jnoncrysol.2010.05.007

CrossRef Full Text | Google Scholar

He, H., and Thorpe, M. F. (1985). Elastic properties of glasses. Phys. Rev. Lett. 54, 2107–2110. doi:10.1103/PhysRevLett.54.2107

CrossRef Full Text | Google Scholar

Hench, L. L. (2006). The story of bioglass^®. J. Mater. Sci. Mater. Med. 17, 967–978. doi:10.1007/s10856-006-0432-z

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jantzen, C. M., Brown, K. G., and Pickett, J. B. (2010). Durable glass for thousands of years. Int. J. Appl. Glass Sci. 1, 38–62. doi:10.1111/j.2041-1294.2010.00007.x

CrossRef Full Text | Google Scholar

Jellison, G. E., Panek, L. W., Bray, P. J., and Rouse, G. B. (1977). Determinations of structure and bonding in vitreous boron oxide by means of boron-10, -11, and oxygen-17 NMR. J. Chem. Phys. 66, 802–812. doi:10.1063/1.433959

CrossRef Full Text | Google Scholar

Jiang, Q., Zeng, H. D., Liu, Z., Ren, J., Chen, G. R., Wang, Z., et al. (2013). Glass transition temperature and topological constraints of sodium borophosphate glass-forming liquids. J. Chem. Phys. 139, 124502. doi:10.1063/1.4821617

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kjeldsen, J., Smedskjaer, M. M., Mauro, J. C., and Yue, Y. Z. (2014). Hardness and incipient plasticity in silicate glasses: origin of the mixed modifier effect. Appl. Phys. Lett. 104, 051913. doi:10.1063/1.4864400

CrossRef Full Text | Google Scholar

Li, H., Richards, C., and Watson, J. (2014). High-performance glass fiber development for composite applications. Int. J. Appl. Glass Sci. 5, 65–81. doi:10.1111/ijag.12053

CrossRef Full Text | Google Scholar

Liu, A. Y., and Cohen, M. L. (1989). Prediction of new low compressibility solids. Science 245, 841–842. doi:10.1126/science.245.4920.841

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Manara, D., Grandjean, A., and Neuville, D. R. (2009). Advances in understanding the structure of borosilicate glasses: a Raman spectroscopy study. Am. Mineral. 94, 777–784. doi:10.2138/am.2009.3027

CrossRef Full Text | Google Scholar

Mauro, J. C., Gupta, P. K., and Loucks, R. J. (2009). Composition dependence of glass transition temperature and fragility. II. A topological model of alkali borate liquids. J. Chem. Phys. 130, 234503. doi:10.1063/1.3152432

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Micoulaut, M., Kerner, R., and dos Santos-Loff, D. M. (1995). Statistical modeling of structural and thermodynamical properties of vitreous B₂O₃. J. Phys. Condens. Matter 7, 8035–8052. doi:10.1088/0953-8984/7/42/002

CrossRef Full Text | Google Scholar

Ollier, N., Charpentier, T., Boizot, B., Wallez, G., and Ghaleb, D. (2004). A Raman and MAS NMR study of mixed alkali Na-K and Na-Li aluminoborosilicate glasses. J. Non-Cryst. Solids 341, 26–34. doi:10.1016/j.jnoncrysol.2004.05.010

CrossRef Full Text | Google Scholar

Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: short-range order in chalcogenide alloys. J. Non-Cryst. Solids 34, 153–181. doi:10.1016/0022-3093(79)90033-4

CrossRef Full Text | Google Scholar

Phillips, J. C., and Thorpe, M. F. (1985). Constraint theory, vector percolation and glass formation. Solid State Commun. 53, 699–702. doi:10.1016/0038-1098(85)90381-3

CrossRef Full Text | Google Scholar

Risbud, S. H., Kirkpatrick, R. J., Taglialavore, A. P., and Montez, B. (1987). Solid-state NMR evidence of 4-, 5, and 6-fold aluminum sites in roller-quenched SiO₂-Al₂O₃ glasses. J. Am. Ceram. Soc. 70, C10–C12. doi:10.1111/j.1151-2916.1987.tb04859.x

CrossRef Full Text | Google Scholar

Rodrigues, B. P., and Wondraczek, L. (2013). Medium-range topological constraints in binary phosphate glasses. J. Chem. Phys. 138, 244507. doi:10.1063/1.4810868

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rodrigues, B. P., and Wondraczek, L. (2014). Cationic constraint effects in metaphosphate glasses. J. Chem. Phys. 140, 214501. doi:10.1063/1.4879559

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sehgal, J., and Ito, S. (1999). Brittleness of glass. J. Non-Cryst. Solids 253, 126–132. doi:10.1016/S0022-3093(99)00348-8

CrossRef Full Text | Google Scholar

Sen, S., and Youngman, R. E. (2004). High-resolution multinuclear NMR structural study of binary aluminosilicate and other related glasses. J. Phys. Chem. B 108, 7557–7564. doi:10.1021/jp031348u

CrossRef Full Text | Google Scholar

Smedskjaer, M. M., Mauro, J. C., Youngman, R. E., Hogue, C. L., Potuzak, M., and Yue, Y. Z. (2011). Topological principles of borosilicate glass chemistry. J. Phys. Chem. B 115, 12930–12946. doi:10.1021/jp208796b

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smedskjaer, M. M., Mauro, J. C., and Yue, Y. Z. (2010a). Prediction of glass hardness using temperature-dependent constraint theory. Phys. Rev. Lett. 105, 115503. doi:10.1103/PhysRevLett.105.115503

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smedskjaer, M. M., Mauro, J. C., Sen, S., and Yue, Y. Z. (2010b). Quantitative design of glassy materials using temperature-dependent constraint theory. Chem. Mater. 22, 5358–5365. doi:10.1021/cm1016799

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smedskjaer, M. M., Mauro, J. C., Sen, S., Deubener, J., and Yue, Y. Z. (2010c). Impact of network topology on cationic diffusion and hardness of borate glass surfaces. J. Chem. Phys. 133, 154509. doi:10.1063/1.3497036

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smedskjaer, M. M., Youngman, R. E., and Mauro, J. C. (2014). Principles of Pyrex^® glass chemistry: structure–property relationships. Appl. Phys. A 116, 491–504. doi:10.1007/s00339-014-8396-1

CrossRef Full Text | Google Scholar

Stebbins, J. F., Kroeker, S., Lee, S. K., and Kiczenski, T. J. (2000). Quantification of five- and six-coordinated aluminum ions in aluminosilicate and fluoride-containing glasses by high-field, high-resolution ²⁷Al NMR. J. Non-Cryst. Solids 275, 1–6. doi:10.1016/S0022-3093(00)00270-2

CrossRef Full Text | Google Scholar

Teter, D. M. (1998). Computational alchemy: the search for new superhard materials. Mater. Res. Bull. 23, 22–27. doi:10.1557/S0883769400031420

CrossRef Full Text | Google Scholar

Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non-Cryst. Solids 57, 355–370. doi:10.1016/0022-3093(83)90424-6

CrossRef Full Text | Google Scholar

Toplis, M. J., Dingwell, D. B., Hess, K. U., and Lenci, T. (1997). Peraluminous viscosity maxima in Na₂O-Al₂O₃-SiO₂ liquids: the role of triclusters in tectosilicate melts. Geochim. Cosmochim. Acta 61, 2605–2612. doi:10.1016/S0016-7037(97)00126-9

CrossRef Full Text | Google Scholar

Wondraczek, L., Mauro, J. C., Eckert, J., Kühn, U., Horbach, J., Deubener, J., et al. (2011). Towards ultrastrong glasses. Adv. Mater. 23, 4578–4586. doi:10.1002/adma.201102795

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wu, J. S., and Stebbins, J. F. (2009). Effects of cation field strength on the structure of aluminoborosilicate glasses: high-resolution ¹¹B, ²⁷Al and ²³Na MAS NMR. J. Non-Cryst. Solids 355, 556–562. doi:10.1016/j.jnoncrysol.2009.01.025

CrossRef Full Text | Google Scholar

Yamane, M., and Mackenzie, J. D. (1974). Vicker’s hardness of glass. J. Non-Cryst. Solids 15, 153–164. doi:10.1016/0022-3093(74)90044-1

CrossRef Full Text | Google Scholar

Youngman, R. E., Haubrich, S. T., Zwanziger, J. W., Janicke, M. T., and Chmelka, B. F. (1995). Short- and intermediate-range structural ordering in glassy boron oxide. Science 269, 1416–1420. doi:10.1126/science.269.5229.1416

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yun, Y. H., and Bray, P. J. (1978). Nuclear magnetic resonance studies of the glasses in the system sodium oxide-boron oxide-silicon dioxide. J. Non-Cryst. Solids 27, 363–380. doi:10.1016/0022-3093(78)90020-0

CrossRef Full Text | Google Scholar

Zeng, H. D., Jiang, Q., Liu, Z., Li, X., Ren, J., Chen, G. R., et al. (2014). Unique sodium phosphosilicate glasses designed through extended topological constraint theory. J. Phys. Chem. B 118, 5177–5183. doi:10.1021/jp5018357

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zheng, Q. J., Youngman, R. E., Hogue, C. L., Mauro, J. C., Potuzak, M., Smedskjaer, M. M., et al. (2012a). Structure of boroaluminosilicate glasses: impact of [Al₂O₃]/[SiO₂] ratio on structural role of sodium. Phys. Rev. B 86, 054203. doi:10.1103/PhysRevB.86.054203

CrossRef Full Text | Google Scholar

Zheng, Q. J., Potuzak, M., Mauro, J. C., Smedskjaer, M. M., Youngman, R. E., and Yue, Y. Z. (2012b). Composition-structure-property relationships in boroaluminosilicate glasses. J. Non-Cryst. Solids 358, 993–1002. doi:10.1016/j.jnoncrysol.2012.01.030

CrossRef Full Text | Google Scholar

Zielniok, D., Cramer, C., and Eckert, H. (2007). Structure/property correlations in ion-conducting mixed-network former glasses: solid-state NMR studies of the system Na₂O-B₂O₃-P₂O₅. Chem. Mater. 19, 3162–3170. doi:10.1021/cm0628092

CrossRef Full Text | Google Scholar