- Otto-Schott-Institute, University of Jena, Jena, Germany
The theory of temperature-dependent topological constraints has been used to successfully explain the compositional dependence of glass properties for oxide and non-oxide compositions. It relates the number of topological degrees of freedom with the glass transition temperature through the configurational entropy of the system. Based on this, we estimated the number of degrees of freedom directly from viscosity measurements of binary alkali borate and silicate glasses. Both approaches exhibit a strong decoupling, which we suggest can be traced to the presence of medium- and long-range constraints that are not taken into account by bond constraint counting. The observed variation of the energy barrier for structural rearrangement and floppy mode degeneracy also corroborate our interpretation. We provide evidence that the degeneracy of floppy modes changes with chemical composition and that the parameter K(x) of the MYEGA viscosity equation could be used to assess changes in the medium-range order.
Introduction
The theory of “topological constraints” has drawn significant attention for the prediction of specific properties of glassy materials (Phillips, 1979; Phillips and Thorpe, 1985; Gupta and Mauro, 2009; Mauro et al., 2009a; Smedskjaer et al., 2010; Wondraczek et al., 2011). It relates atomistic potentials and spatial relations between constituents of the glass to the ensemble’s degrees of freedom and the average number of atomic bond constraints, respectively. An estimate of the number of constraints can be obtained via the Adam–Gibbs equation (Adam and Gibbs, 1965), which relates the viscosity of a liquid with its configurational entropy:
where η∞(x) is the viscosity of the liquid at infinite temperature, B(x) corresponds to the energy barrier, which opposes the rearrangement of the melt structural units (Russell et al., 2003) and Sc(T,x) is the configurational entropy of the melt. The configurational entropy can, in principle, be determined from calorimetric (Richet et al., 1993) or electrochemical measurements (Jordanov et al., 2012) and is calculated from Eqs 2–4 (Richet, 1984, 2009; Richet et al., 1993).
where the difference in heat capacity between glassy state and super-cooled liquid state is typically taken as the configurational heat capacity (Richet et al., 1986). In reality, the experimental determination of Sc(T,x) is problematic at best (Sipp et al., 1997). So, while the Adam–Gibbs equation successfully links the thermodynamic state of a liquid with its dynamic properties, its practical application is restricted by the difficulties arising from the experimental determination of all required calorimetric data (Richet, 2009).
Recently, Mauro et al. (2009b) proposed a new equation to describe the viscosity of liquids, which is based on the Adam–Gibbs approach, the energy landscape analysis of Naumis (2006) and the temperature-dependent constraint model of Gupta and Mauro (2009) (Mauro et al., 2009a). The model states that temperature-induced changes in the glass topology are related to changes in the number of atomic constraints relative to the number of atomic degrees of freedom. The new equation postulates a link between the configurational entropy of the liquid and its topological degrees of freedom per atom, f (T,x):
where N is the number of atoms, k is Boltzmann’s constant, and Ω is the number of degenerate configurations per floppy mode (Mauro et al., 2009b). Furthermore, the authors consider that the network constraints exist in a simple two-state system: the constraints are either intact or broken. The energy difference between both states is given by H(x) (Mauro et al., 2009b):
Rearranging Eq. 1 with K(x) = B(x)/3NklnΩ and C(x) = H(x)/k, the MYEGA equation is obtained (Mauro et al., 2009b):
Equation 7 can be rewritten as a function of the glass transition temperature Tg(x) and the fragility index m(x) (Angell, 1995) assuming that logη∞(x) = −3 [log(Pa ⋅ s)] (Zheng et al., 2011):
This equation provides a versatile tool, which allows for the determination of the glass transition temperature, the kinetic fragility of the melt and the viscosity parameters K(x) and C(x) from viscosity data. Substituting C(x) in Eq. 6 one can calculate the number of degrees of freedom per atom from viscosity:
Number of Topological Degrees of Freedom
The temperature-dependent constraint theory of Gupta and Mauro (2009) provides another way of calculating the number of atomic degrees of freedom from experimental data (Mauro et al., 2009a). Starting with the Adam–Gibbs equation (Eq. 1), for two different but similar systems x and w at their glass transition temperature, the equilibrium viscosity should be equal to 1012 Pa ⋅ s, resulting in the following equality:
Assuming that the variation of the energy barrier is independent on chemical composition, B(x) ≈ B(w), and using Eq. 5 one gets:
In order to test if the number of atomic degrees of freedom calculated from viscosity (Eq. 9) and the Bond Constraint Theory (Eq. 11) coincide, we took viscosity data for B2O3, xNa2O × (1−x)B2O3, and xLi2O × (1−x)B2O3 glasses and fitted with Eqs 7 and 8 assuming logη∞(T,x) = −3. The results are shown in Table 1.
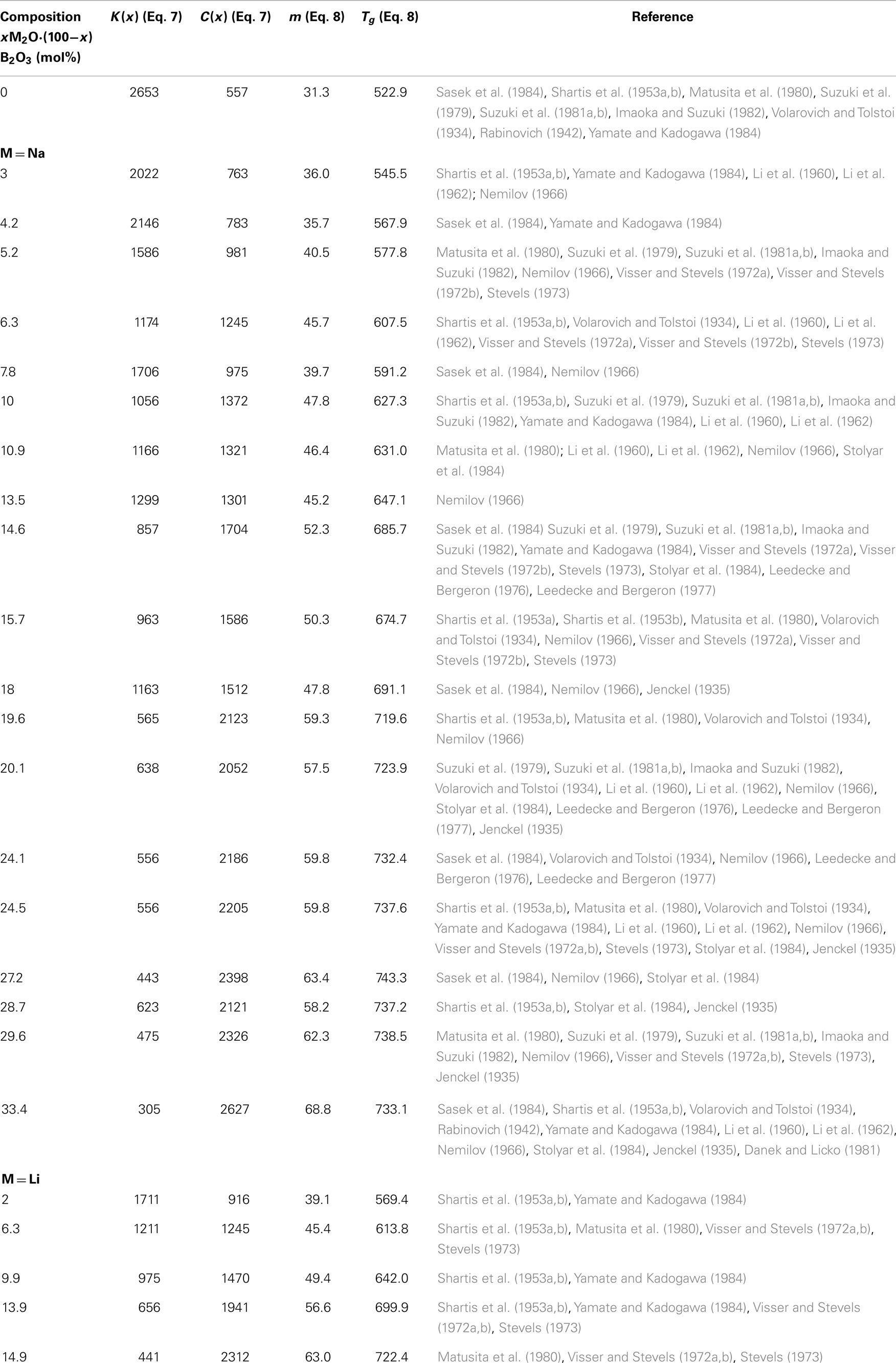
Table 1. Parameters of Eqs 7 and 8 as a function of chemical composition for binary xNa2O⋅(100−x)B2O3 and xLi2O⋅(100−x)B2O3.
Considering that the relative number of degrees of freedom [given by f (Tg(x), x)/f (Tg(w), w)] is the same for both approaches, Eqs 9 and 11 can then be combined as:
Taking vitreous B2O3 as a reference composition, Tg(w) = 522.9 K [see Table 1; this temperature is somewhat lower than the one reported by Mauro et al. (2009a)], C(w) = 557 K from Table 1 and f (Tg(w),w) = 3/5(Mauro et al., 2009a), then the comparison with the binary alkali glasses becomes straightforward and the results are found in Figures 1 and 2.
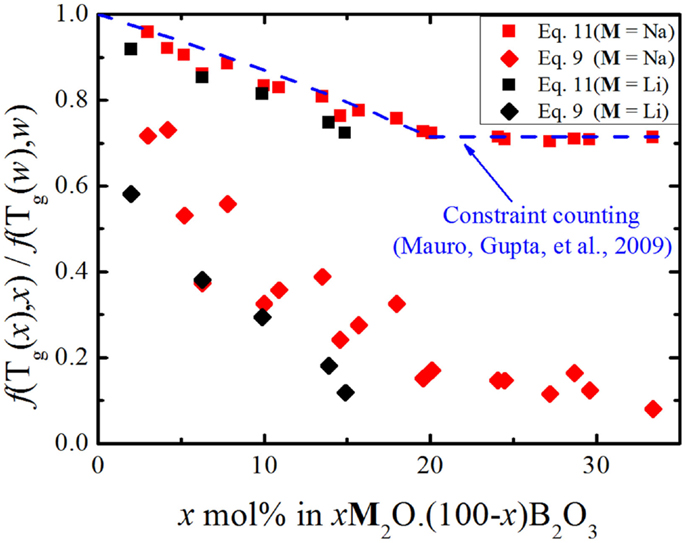
Figure 1. Relative number of topological degrees of freedom per atom as a function of glass composition for binary sodium borates according to Eqs 9 and 11. The dashed line shows the predicted variation obtained from the structural analysis of Mauro et al. (2009a).
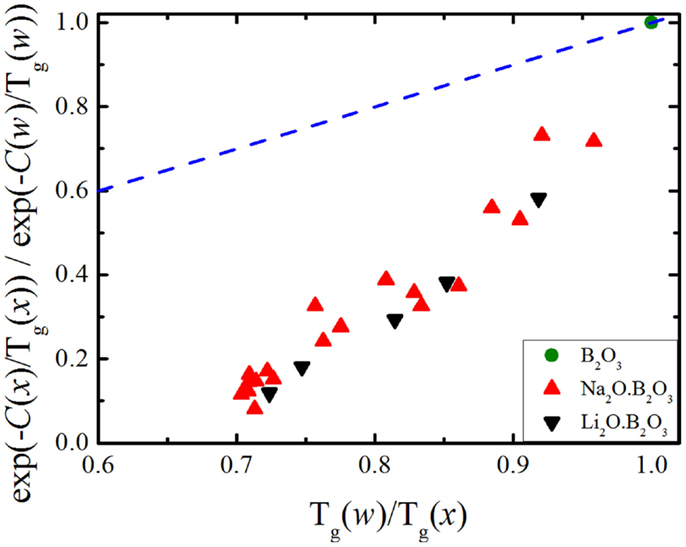
Figure 2. Relative number of atomic degrees of freedom according to Eqs 9 and 11. The dashed line represents a 1:1 correlation.
Interestingly, in Figure 1, we see that the number of floppy modes calculated from viscosity measurements has a stronger dependence on the chemical composition than the one calculated from glass transition temperature data. Figure 2 illustrates this mismatch very well and we see that both alkali borate glasses follow the same trend.
Degeneracy and Decoupling of Constraint Predictions
From Figures 1 and 2, the experimental data suggest that the number of degrees of freedom from viscosity and the BCT diverge significantly. Recalling Eq. 5, we see that the configurational entropy is a function of the atomic degrees of freedom, the number of atoms and the degeneracy of each floppy mode. Equation 11 assumes that the size of the system and the floppy mode degeneracy can be considered constant as the chemical composition changes. While the number of atoms in the system may vary slowly enough to be considered constant [as the molar volume of sodium borate glasses does not exhibit a strong compositional variation (Berkemeier et al., 2005)], the floppy mode degeneracy has to be analyzed more carefully. As stated above, Mauro et al. (2009a) modeled the bond constraints as a simple two-state system with the energy difference between the broken and intact constraints given by H(x) and the number of topological degrees of freedom given by Eq. 6. This simple system is represented schematically in Figure 3A.
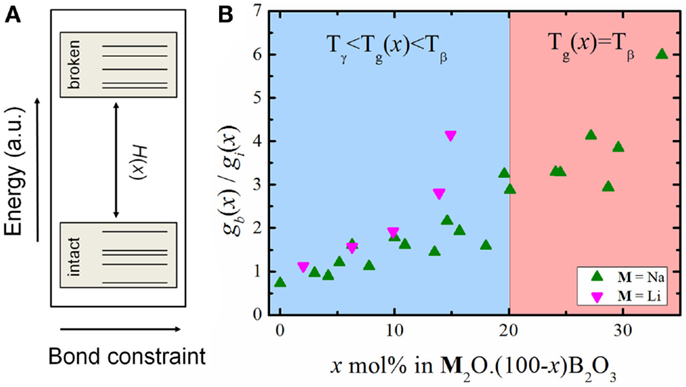
Figure 3. (A) Energy scheme of the bond constraint two-state system, where H(x) is the energy difference between both states. (B) Relative degeneracy of states as a function of chemical composition for binary lithium and sodium borates.
The fraction of bond constraints that are either broken or intact can then be calculated through the Boltzmann distribution (Landau and Lifshitz, 1980):
where Ni is the number of bond constraints with energy Ei, N is the total number of bond constraints, gi is the degeneracy of the state of energy Ei (or, in other words, the number of different states with the same energy Ei), and Z(T) is the partition function, given by:
It is important to note that this calculation of the fractions of intact and broken constraints requires that the constraint breakage to not be a step-function of the temperature, which is in line with recent MD simulations (Bauchy and Micoulaut, 2011). From Figure 3A, we have that the intact bond constraints have ground energy Eg(x) and the broken constraints have an energy of Eg(x) + H(x). Thus, the relation between the number of broken and intact constraints is given by:
where Nb(T,x) is the number of broken bond constraints, Ni(T,x) is the number of intact bond constraints, gb(T,x) is the degeneracy of the broken state, and gi(T,x) is the degeneracy of the intact state. Eq. 15 simplifies to:
The number of floppy modes is equal to the number of broken constraints, Nb(T,x) = f (T,x), and according to Gupta and Mauro (2009) the number of floppy modes is also given by f (T,x) = d − n(T,x), where d is the dimensionality of the network and n(T,x) is the number of intact bond constraints. In our case d = 3, resulting in n(T,x) = Ni(T,x) = 3 − f (T,x). As C(x) = H(x)/k, Eq. 16 can be rewritten as:
By taking values of C(x) and using Eq. 11 to calculate f (Tg(x),x), as it gives the best agreement with structural data, we can estimate the relative degeneracy of states as a function of chemical composition (Figure 3B).
As the glasses get richer in alkali (i.e., more polymerized), the floppy modes get more degenerate in relation to the intact bond constraints. This might provide an explanation for the transition in the type of floppy mode, which controls the glass transition temperature in these alkali borate glasses (Mauro et al., 2009a). The compositional changes might render the intact B–O–B angular constraints less degenerate and we interpret this as a reduction in the angular flexibility, meaning that as the degeneracy decreases these constraints become more rigid. At some compositional range, these transitions become so unlikely that it becomes more probable to break other constraints, in this case, the O–B–O angular constraint. The transition between floppy modes is very discernible independently of how the number of topological degrees of freedom is calculated (Figure 1). This also correlates with the variation of K(x) with the chemical composition, as can be seen in Figure 4.
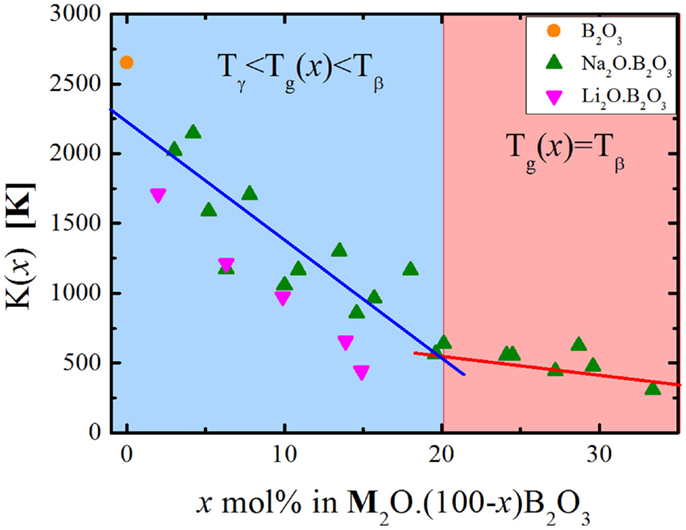
Figure 4. Compositional dependence of K(x) for the borate binary glasses. The lines represent linear fits of the data within the two distinct compositional regimes.
According to Mauro et al. (2009b), K(x) is written as:
Therefore, any change in K(x) means that either B(x) and/or Ω are changing. If the assumption that B(x) ≈ B(w) used in the derivation of Eq. 11 is correct, then plotting the values of K(x) as a function of 1/ln(Ω(x)) should result in a straight line passing through the origin, but as we can see from Figure 5 this is far from what we get. Therefore, not only the degeneracy is causing K(x) to change with composition but also the energy barrier of structural rearrangement, B(x). From Eqs 1 and 7 we get that, at T = Tg:
Thus, plotting K(x)exp(C(x)/Tg(x)) as a function of 1/Sc(Tg(x),x) should yield a straight line passing through the origin with a constant, positive slope of B(x) for all glasses of the same “family.” Analyzing the available thermodynamic and viscosity data for xNa2O ⋅ (1−x)SiO2 glasses (Knoche et al., 1994; Toplis, 2001) resulted in the graph in Figure 6, where one can see that even though B(x) appears to be constant for x ≥ 0.25, it increases as the glass compositions get richer in silica. The observed change in the behavior of B(x) at x ≈ 0.2 is consistent with the glass network transitioning from stressed-rigid to floppy. Such transition has already been reported in experimental (Vaills et al., 2005) and MD simulations (Bauchy and Micoulaut, 2011).
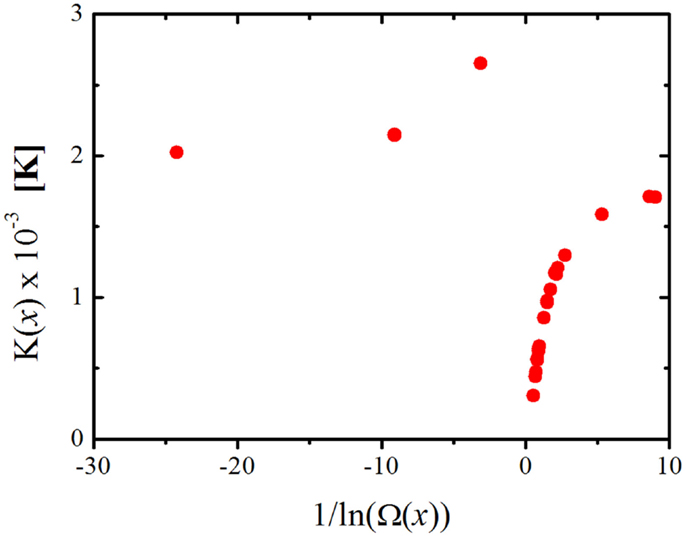
Figure 5. K(x) as a function of 1/ln(Ω(x)) for the lithium and sodium binary borate glasses. Ω(x) is calculated according to Equation 17.
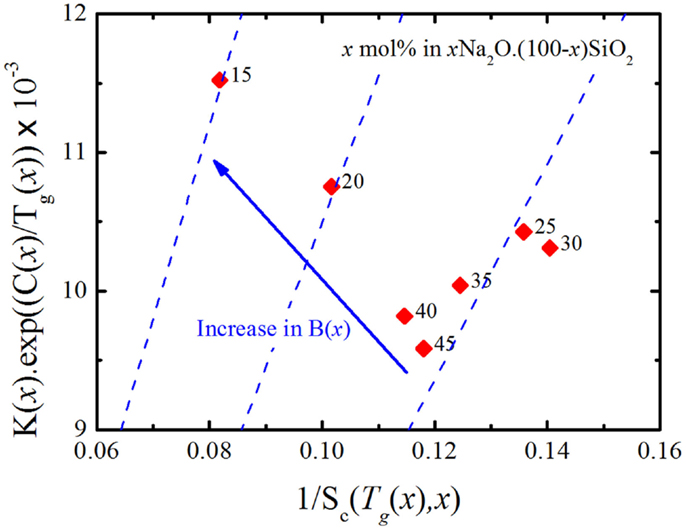
Figure 6. K(x)exp(C(x)/Tg(x)) as a function of 1/Sc(Tg(x),x) for binary sodium silicate (Knoche et al., 1994; Toplis, 2001) glasses. The labels indicate the value of x in mol% xNa2O ⋅ (100-x)SiO2.
Adam and Gibbs (1965) demonstrated that B(x) is given by:
where np is the number of particles in the system, Δμ(x) is the average energy barrier each rearranging region has to overcome during cooperative motion, and is the configurational entropy of the smallest rearranging region. As argued before, the number of particles in the system is considered to be constant, meaning that the observed variations in K(x) are due to changes in Δμ(x) and . These two parameters are sensitive to changes in the medium- and long-range orders, as they are associated with cooperative rearranging regions (CRRs); thus, we suggest that the observed variation of K(x) as a function of composition stems from the changes in the CRRs, which can only change if the floppy modes enable these regions to become more or less flexible. This line of reasoning suggests that the properties of the CRRs are deeply connected to the number and types of floppy modes in the glass network, as they should dictate the possible rearrangements a certain region can reach.
As B(x) ≠ B(w), one should observe a decoupling on the values of topological degrees of freedom per atom estimated from viscosity and bond constraint counting. We propose that the main reason for this decoupling is that while the viscosity reflects the behavior of the whole system, combining the responses of short-, medium-, and long-range interactions, the bond constraints are, by their own definition, restricted to short-range interactions. It is known that medium-range interactions affect the measured viscosity of polymers, with the molecular weight of side groups (Rogers and Mandelkern, 1957; Gargallo et al., 1987, 1988) and the shape of chains (Gonzalez et al., 1988; Hur et al., 2011; Khalyavina et al., 2012) having significant influence even though the covalent chemical bonds that make the backbone of the chains stay constant; and recent evidence points that the same effects may be present in inorganic oxide glasses (Rodrigues and Wondraczek, 2013). The coulombic interactions between the modifiers and the non-bridging oxygens extend beyond its first coordination shell, and it has been shown that they are a major part of the constraints present in phosphate glasses (Hermansen et al., 2014; Rodrigues and Wondraczek, 2014; Rodrigues et al., 2014), so they might also have an effect here. The apparent influence of the medium range also ties with the possible differentiability of the floppy modes. When counting, the constraints are either intact or broken and two floppy modes are considered the same even if their surroundings are very different. For example, in the binary alkali borate glasses, when considering the breakage of the angular constraints of the bridging oxygens, each trigonally coordinated boron has three floppy modes regardless of the fact that it may be bonded to three other trigonal borons or three tetragonal borons. But these two different configurations may very well have different configurational entropies associated, influencing the CRRs and, ultimately, the viscosity of the system. This may indicate that the parameter K(x) can be used to probe changes in the medium-range order of super-cooled liquids as a function of chemical composition.
Conclusion
In this paper, the viscosity of binary alkali borates and silicates was used to estimate the number of topological degrees of freedom as a function of glass composition. The number of floppy modes estimated from viscosity decouples from the values, which are obtained by bond constraint counting. We suggest that the origin of this decoupling is due to the difference in scale: while viscosity covers the whole system, bond constraint counting only handles short-range interactions; hence the observed inequality of B(x). We provide evidence that the degeneracy of floppy modes changes with chemical composition and that the parameter K(x) of the MYEGA viscosity equation could be used to assess changes in the medium-range order.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Financial support by the German Science Foundation through its priority program SPP 1594 (project no. WO 1220/10-1) is gratefully acknowledged.
References
Adam, G., and Gibbs, J. H. (1965). On the temperature dependence of cooperative relaxation properties in glass forming liquids. J. Chem. Phys. 43, 139–146. doi: 10.1063/1.1696442
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Angell, C. A. (1995). Formation of glasses from liquids and biopolymers. Science 267, 1924–1935. doi:10.1126/science.267.5206.1924
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Bauchy, M., and Micoulaut, M. (2011). Atomic scale foundation of temperature-dependent bonding constraints in network glasses and liquids. J. Non Cryst. Solids 357, 2530–2537. doi:10.1016/j.jnoncrysol.2011.03.017
Berkemeier, F., Voss, S., Imre, A. W., and Mehrer, H. (2005). Molar volume, glass-transition temperature, and ionic conductivity of Na- and Rb-borate glasses in comparison with mixed Na-Rb borate glasses. J. Non Cryst. Solids 351, 3816–3825. doi:10.1016/j.jnoncrysol.2005.10.010
Danek, V., and Licko, T. (1981). Apparatus for the measurement of physicochemical properties of oxide melts. Silikaty 25, 153–163.
Gargallo, L., Hamidi, N., and Radic, D. (1987). Effect of the side chain strucure on the glass transition temperature. Part 2. Poly(o-alkylphenyl methacrilate)s. Thermochim. Acta 114, 319–328. doi:10.1016/0040-6031(87)80054-0
Gargallo, L., Soto, E., Tagle, L. H., and Radic, D. (1988). Effect of side chain structure on the glass transition temperature. Part 3. Molecular weight dependence of Tg in some poly(thiocarbonates). Thermochim. Acta 130, 289–297. doi:10.1016/0040-6031(88)87075-8
Gonzalez, C. C., Perena, J. M., and Bello, A. (1988). Thermal analysis and molecular weight dependence on glass transition of poly(ditrimethylene terephtalate). Thermochim. Acta 134, 195–199. doi:10.1016/0040-6031(88)85236-5
Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130, 094503. doi:10.1063/1.3077168
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Hermansen, C., Mauro, J. C., and Yue, Y. (2014). A model for phosphate glass topology considering the modifying ion sub-network. J. Chem. Phys. 140, 154501. doi:10.1063/1.4870764
Hur, K., Jeong, C., Winkler, R. G., Lacevic, N., Gee, R. H., and Yoon, D. Y. (2011). Chain dynamics of ring and linear polyethylene melts from molecular dynamics simulations. Macromolecules 44, 2311–2315. doi:10.1021/ma102659x
Imaoka, M., and Suzuki, S. (1982). Retarded elasticity in SiO2-Na2O and B2O3-Na2O glasses. J. Ceram. Soc. Jpn 90, 440–447. doi:10.2109/jcersj1950.90.1044_440
Jenckel, E. (1935). Zur Konstitution der Gläser. Zeitschrift fuer Elektrochemie 41, 211–215. doi:10.1002/bbpc.19350410407
Jordanov, N., Wondraczek, L., and Gutzow, I. S. (2012). Thermodynamic properties of amorphous solids: the electrochemical approach. J. Non Cryst. Solids 358, 1239–1256. doi:10.1016/j.jnoncrysol.2012.02.031
Khalyavina, A., Häußler, L., and Lederer, A. (2012). Effect of the degree of branching on the glass transition temperature of polyesters. Polymer 53, 1049–1053. doi:10.1016/j.polymer.2012.01.020
Knoche, R., Dingwell, D. B., Seifert, F. A., and Webb, S. L. (1994). Non-linear properties of supercooled liquids in the system Na2O-SiO2. Chem. Geol. 116, 1–16. doi:10.1016/0009-2541(94)90154-6
Landau, L. D., and Lifshitz, E. M. (1980). Statistical Physics, Part 1, 3rd Edn. Oxford: Butterworth-Heinemann, 544.
Leedecke, C. J., and Bergeron, C. G. (1976). The growth of K2B8O13 in its stoichiometric melt. J. Cryst. Growth 32, 327–331. doi:10.1016/0022-0248(76)90113-5
Leedecke, C. J., and Bergeron, C. G. (1977). Crystallization of Na2B8O13 in selected Na2O-B2O3 melts. Phys. Chem. Glasses 18, 116–120.
Li, P.-Ch., Ghose, A. C., and Su, G.-J. (1960). Density of molten boron oxide, rubidium and caesium borates. Phys. Chem. Glasses 1, 198–200.
Li, P.-C., Ghose, A. C., and Su, G.-J. (1962). Viscosity determination of boron oxyde and binary borates. J. Am Ceram. Soc. 45, 83–88. doi:10.1111/j.1151-2916.1962.tb11085.x
Matusita, K., Watanabe, T., Kamiya, K., and Sakka, S. (1980). Viscosities of single and mixed alkali borate glasses. Phys. Chem. Glasses 21, 78–84.
Mauro, J. C., Gupta, P. K., and Loucks, R. J. (2009a). Composition dependence of glass transition temperature and fragility: II A topological model of alkali borate liquids. J. Chem. Phys. 130, 234503. doi:10.1063/1.3152432
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Mauro, J. C., Yue, Y., Ellison, A. J., Gupta, P. K., and Allan, D. C. (2009b). Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. U.S.A. 106, 19780–19784. doi:10.1073/pnas.0911705106
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Naumis, G. G. (2006). Glass transition phenomenology and flexibility: An approach using the energy landscape formalism. J. Non Cryst. Solids 352, 4865–4870. doi:10.1016/j.jnoncrysol.2006.01.160
Nemilov, S. V. (1966). Studies on the structure of glasses in B2O3-Na2O system by the viscosimetric method. Izvestiya Akademii Nauk SSSR, Neorganicheskie Materialy 2, 349–56.
Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: Short-range order in chacogenide alloys. J. Non Cryst. Solids 34, 153–181. doi:10.1016/0022-3093(79)90033-4
Phillips, J. C., and Thorpe, M. F. (1985). Constraint theory, vector percolation and glass formation. Solid State Commun. 53, 699–702. doi:10.1016/0038-1098(85)90381-3
Rabinovich, B. V. (1942). Viscosity of borax and boron oxide in the softening range. Zhurnal Fizicheskoi Khimii (USSR) 16, 23–6.
Richet, P. (1984). Viscosity and configurational entropy of silicate melts. Geochim. Cosmochim. Acta 48, 471–483. doi:10.1016/0016-7037(84)90275-8
Richet, P. (2009). Residual and configurational entropy: quantitative checks through applications of Adam–Gibbs theory to the viscosity of silicate melts. J. Non Cryst. Solids 355, 628–635. doi:10.1016/j.jnoncrysol.2009.01.027
Richet, P., Robie, R. A., and Hemingway, B. S. (1986). Low-temperature heat capacity of diopside glass (CaMgSi2O6): a calorimetric test of the configurational-entropy theory applied to the viscosity of liquid silicates. Geochim. Cosmochim. Acta 50, 1521–1533. doi:10.1016/0016-7037(86)90326-1
Richet, P., Robie, R. A., and Hemingway, B. S. (1993). Entropy and structure of silicate glasses and melts. Geochim. Cosmochim. Acta 57, 2751–2766. doi:10.1016/0016-7037(93)90388-D
Rodrigues, B. P., Mauro, J. C., Yue, Y., and Wondraczek, L. (2014). Modifier constraints in alkali ultraphosphate glasses. J. Non Cryst. Solids 405, 12–15. doi:10.1016/j.jnoncrysol.2014.08.035
Rodrigues, B. P., and Wondraczek, L. (2013). Medium-range topological constraints in binary phosphate glasses. J. Chem. Phys. 138, 244507. doi:10.1063/1.4810868
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rodrigues, B. P., and Wondraczek, L. (2014). Cationic constraint effects in metaphosphate glasses. J. Chem. Phys. 140, 214501. doi:10.1063/1.4879559
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Rogers, S. S., and Mandelkern, L. (1957). Glass formation in polymers. I. The glass trasitions of the poly(n-alkyl methacrylates). J. Phys. Chem. 61, 985–990. doi:10.1021/j150553a033
Russell, J. K., Giordano, D., and Dingwell, D. B. (2003). High-temperature limits on viscosity of non-Arrhenian silicate melts. Am. Mineral. 88, 1390–1394.
Sasek, L., Kovandova, J., and Drahonovski, M. (1984). Viscosity of soda-borate glasses and glass melts. Sb. Vys. Sk. Chem. Technol. Praze. Chem. Technol. Silik. L12, 47–72.
Shartis, L., Capps, W., and Spinner, S. (1953a). Density and expansivity of alkali borates and density characteristics of some other binary glasses. J. Am. Ceram. Soc. 36, 35–43. doi:10.1111/j.1151-2916.1953.tb12833.x
Shartis, L., Capps, W., and Spinner, S. (1953b). Viscosity and electrical resistivity of molten alkali borates. J. Am. Ceram. Soc. 36, 319–326. doi:10.1111/j.1151-2916.1953.tb12808.x
Sipp, A., Neuville, D. R., and Richet, P. (1997). Viscosity, configurational entropy and relaxation kinetics of borosilicate melts. J. Non Cryst. Solids 211, 281–293. doi:10.1016/S0022-3093(96)00648-5
Smedskjaer, M. M., Mauro, J. C., Sen, S., and Yue, Y. (2010). Quantitative design of glassy materials using temperature-dependent constraint theory. Chem. Mater. 22, 5358–5365. doi:10.1021/cm1016799
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Stevels, J. M. (1973). Rheological properties of alkali borate glasses. Rheol. Acta 12, 503–515. doi:10.1007/BF01525589
Stolyar, S. V., Klyuev, V. P., and Bulaeva, A. V. (1984). Viscosity and thermal expansion of sodium borate glasses in the glass transition range. Fizika i Khimiya Stekla 10, 447–457.
Suzuki, S., Takahashi, M., Kobayashi, T., and Imaoka, M. (1981a). Retarded elasticity in B2O3–GeO2 glasses. J. Non-Cryst. Solids 7, 163–169. doi:10.1016/0022-3093(81)90157-5
Suzuki, S., Kobayashi, T., Takahashi, M., and Imaoka, M. (1981b). Viscosity of some oxide glasses in the glass transition range. J. Ceram. Soc. Jpn 89, 252–259. doi:10.2109/jcersj1950.89.1029_252
Suzuki, S., Takahashi, M., and Kobayashi, T. (1979). No Title. Annu. Rep. Ceram. Eng. Res. Rep. Nagoya Inst. Technol. 6, 21.
Toplis, M. J. (2001). Quantitative links between microscopic properties and viscosity of liquids in the system SiO2-Na2O. Chem. Geol. 174, 321–331. doi:10.1016/S0009-2541(00)00323-5
Vaills, Y., Qu, T., Micoulaut, M., Chaimbault, F., and Boolchand, P. (2005). Direct evidence of rigidity loss and self-organization in silicate glasses. J. Phys. Condens. Matter 17, 4889–4896. doi:10.1088/0953-8984/17/32/003
Visser, T. J. M., and Stevels, J. M. (1972a). Rheological properties of boric oxide and alkali borate glasses. J. Non Cryst. Solids 7, 376–394. doi:10.1016/0022-3093(72)90272-4
Visser, T. J. M., and Stevels, J. M. (1972b). Influence of water on the rheological properties of alkali borate glasses. J. Non Cryst. Solids 7, 401–409. doi:10.1016/0022-3093(72)90274-8
Volarovich, M. P., and Tolstoi, D. M. (1934). The viscosity of the binary systems Na2B4O7-B2O3 and NaBO2-NaPO3 in the fused state. J. Soc. Glass Technol. 18, 209.
Wondraczek, L., Mauro, J. C., Eckert, J., Kühn, U., Horbach, J., Deubener, J., et al. (2011). Towards ultrastrong glasses. Adv. Mater. Weinheim 23, 4578–4586. doi:10.1002/adma.201102795
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Yamate, T., and Kadogawa, Y. (1984). Effect of glass composition on its viscosity. Viscosity of binary alkali borate glasses. Rep. Asahi Glass Found. Ind. Technol. 44, 15–24.
Keywords: glass, topological constraint theory, borates, silicates, viscosity
Citation: Rodrigues BP and Wondraczek L (2015) Floppy mode degeneracy and decoupling of constraint predictions in super-cooled borate and silicate liquids. Front. Mater. 1:32. doi: 10.3389/fmats.2014.00032
Received: 14 November 2014; Accepted: 01 December 2014;
Published online: 06 January 2015.
Edited by:
Morten M. Smedskjaer, Aalborg University, DenmarkReviewed by:
Mathieu Bauchy, University of California Los Angeles, USAJohn C. Mauro, Corning Incorporated, USA
Copyright: © 2015 Rodrigues and Wondraczek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lothar Wondraczek, Otto-Schott-Institute, University of Jena, Fraunhoferstrasse 6, Jena 07743, Germany e-mail:bG90aGFyLndvbmRyYWN6ZWtAdW5pLWplbmEuZGU=
 Bruno Poletto Rodrigues
Bruno Poletto Rodrigues Lothar Wondraczek
Lothar Wondraczek