- 1Istituto Nanoscienze, Consiglio Nazionale delle Ricerche, Pisa, Italy
- 2Laboratorio NEST: National Enterprise for nanoScience and nanoTechnology, Scuola Normale Superiore, Pisa, Italy
- 3Physics Department Enrico Fermi, University of Pisa, Pisa, Italy
- 4Graphene Labs, Istituto Italiano di Technologia (IIT), Genova, Italy
Exploring new perspectives for green technologies is one of the challenges of the third millennium, in which the need for non-polluting and renewable powering has become primary. In this context, the use of hydrogen as a fuel is promising, since the energy released in its oxidation per unit mass (~142 MJ/kg) is three times that released, on average, by hydrocarbons, and the combustion product is water (Ramage, 1983). Being hydrogen a vector of chemical energy, efficient conservation, and non-dispersive transportation are the main goals. Three issues must be considered to this respect: (i) storage capacity, (ii) storage stability, and (iii) kinetics of loading/release. Commercial technologies are currently based on cryo-compression or liquefaction of H2 in tanks. These ensure quite a high gravimetric density [GD, point (i)], namely 8–13% in weight of stored hydrogen, and a relatively low cost (Züttel, 2003). However, concerning points (ii) and (iii), these technologies pose problems of safety, mainly due to explosive flammability of hydrogen, and consequent unpractical conditions for transportation and use (Mori and Hirose, 2009). Therefore, research efforts are directed toward solid-state based storage systems (energy.gov, Bonaccorso et al., 2015).
Interactions of hydrogen with materials are classified as physisorption, occurring with H2 by means of van der Waals (vdW) forces, or chemisorption, i.e., chemical binding of H leading to the formation of hydrides (Mori and Hirose, 2009), requiring dissociative(associative) chemi(de)sorption of H2. Intermediate nature interactions, sometimes called “phenisorption,” can also occur between hydrogen electrons and the electrons of external orbital of metals. Indeed, stable and robust (light) metal hydrides (Sakintuna et al., 2007; Harder et al., 2011) are currently considered an alternative to tanks. Their main drawback is their high chemisorption and chemidesorption barrier, both many times the typical thermal energy, implying slow operational kinetics, which becomes acceptable only at very high temperature. Physisorption, conversely, generally results in barrierless and weak binding. It was considered as a storage mechanism in layered (Zhirko et al., 2007) or porous (Sastre, 2010) materials, and shown to be effective at low temperatures and/or high pressure. Therefore, it generally seems that if storage stability (ii) is improved then the loading/release kinetics (iii) is worsened.
Graphene shows good potential to be an efficient hydrogen-storage medium (Tozzini and Pellegrini, 2013): carbon is among the lightest elements forming layered and porous structures, and graphene is probably the material with the largest surface to mass ratio. These two conditions are in principle optimal to produce high GD [point (i)]. In addition, the chemical versatility of carbon allows it to interact with hydrogen both by physisorption (in sp2 hybridization) and chemisorption (Goler et al., 2013a) (in sp3 hybridization). [“Phenisorption is also obtained in graphene by functionalization with metals (Mashoff et al., 2013)].
On the other hand, concerning points (ii) and (iii), pure graphene does not perform dramatically better than other materials. H2 easily physisorbs onto graphene layers or within multilayers, but it was theoretically shown (Patchkovskiim et al., 2005) that large GD (6–8%) are reached within multi-layered graphene at cryogenic temperatures, while the room temperature value is at best ~2–3%. This was confirmed by measurements (Klechikov et al., private communication), which also indicate that graphene does not perform better than other carbon based bulk materials, such as nanoporous carbon or carbon nanotubes. In all cases, a key parameter determining GD is the specific surface to volume ratio. Theoretical works also show that stability can be improved (and GD optimized) at specific interlayer spacing (~7–8 Å), due to a cooperative effect of vdW forces (Patchkovskiim et al., 2005). A similar effect is responsible for the accumulation of physisorbed hydrogen within graphene troughs at low temperatures (~100 K) observed in simulations (Tozzini and Pellegrini, 2011). On the other hand, hydrogen chemisorption on graphene produces graphane (Sofo et al., 2007), its completely hydrated alkane counterpart, stable at room temperature [point (ii)] and with 8.2% GD [point (i)]. Graphane, however, shares with other hydrides high chemi(de)sorption barrier (~1.5 eV/atom). As in other materials, physisorption has good kinetics (iii), and bad storage capacity (i), and stability (ii), while chemisorption has good (i) and (ii), and bad (iii).
Graphene, however, displays extremely peculiar properties: a unique combination of strength and flexibility, and its bidimensionality. Therefore, it can be buckled on different scales down to nanometer (Fasolino et al., 2007; Wang et al., 2011), either statically, i.e., forming stable ripples as an effect of external constraints [i.e., compression or interaction with a substrate (Goler et al., 2013b)], or dynamically, sustaining traveling ripples, i.e., coherent transverse out-of-plane acoustic modes, also called ZA or flexural phonons (Lindsay and Broido, 2010; Xu et al., 2013). We explored the possibility of exploiting these properties in the context of hydrogen storage.
We first evaluated the dependence of chemisorbed H stability on the local curvature by means of a density functional theory (DFT) based study (Tozzini and Pellegrini, 2011). This revealed a linear dependency of the binding energy on the local curvature, leading to an over-stabilization of the adsorbate of up to 1–2 eV on crests and corresponding destabilization within troughs (Figure 1A), which is also modified by the presence of already chemisorbed hydrogen (Rossi et al., submitted). Theoretical evaluations were confirmed by Scanning Tunneling Microscopy performed on naturally corrugated graphene grown on SiC (Goler et al., 2013a), which demonstrated the presence of hydrogen prevalently on the convexities. These observations lead to the idea that an inversion of curvature (from concavity to convexity) could detach chemisorbed hydrogen. As a matter of fact, this mechanism was demonstrated in a simulation in which the curvature inversion was realized dynamically by the passage of a ZA coherent phonon of ~2 nm wavelength and ~THz frequency (Figure 1B). The simulation shows that hydrogen undergoes associative desorption at room temperature upon curvature inversion, which can be called a “mechanical catalysis”: the energy barrier is overcome by means of the energy provided by the traveling phonon.
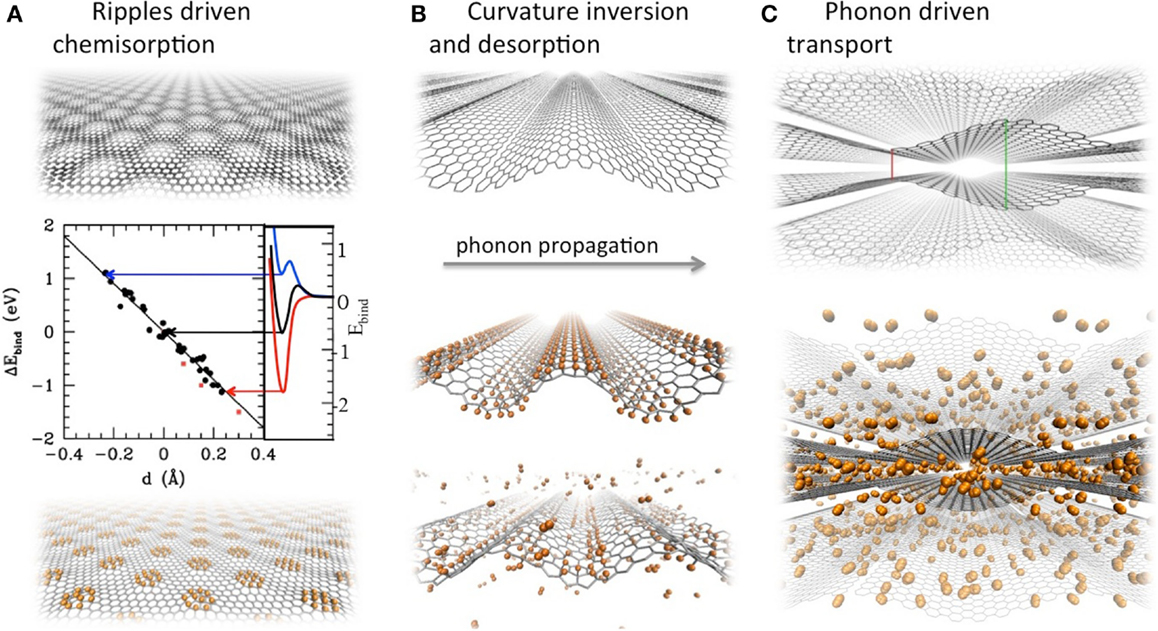
Figure 1. Graphene interaction with rippled and buckled graphene. (A) From top to bottom: graphene with buckling mimicking that of graphene on SiC; variation of stability vs. curvature, measured by means of the out of plane displacement of a C site with respect to the neighbors, d (blue and negative value of d = concave, red and positive value of d = convex); hydrogen (shown in orange) binds on concavities. (B) From top to bottom: coherent flexural phonon of nano-sized wavelength; hydrogen is initially attached on the crest of the ripples, but after half a period troughs replace crests, hydrogen destabilizes and desorbs in molecular form. (C) From top to bottom: flexural phonons excited in counterphase in subsequent multilayers generate traveling cavities; hydrogen is transported by phonons within those cavities.
Once detached, H2 finds itself in contact with a graphene sheet with traveling ripples. If sheets are at appropriate distances and if ZA phonons are excited with appropriate relative phases in subsequent sheets, the traveling ripples enclose traveling nano-cavities (Figure 1C). We showed by means of classical molecular dynamics (MD) simulations using empirical force fields (FF) (Camiola et al., 2014) that these nano-cavities can include and transport H2 at velocities near to the phase velocity of the phonon for almost micrometric distances before the phonon damps. This effect could be used to transport and pump hydrogen through multilayers, improving the GD of physisorbed hydrogen at room temperature and the kinetics of loading and release.
The existence of ripples and flexural phonons, therefore, offers specific strategies – unique to graphene – to overcome issues (i), (ii), and (iii). The proof of principle of the effectiveness of these strategies was given by means of a multi-scale approach, combining DFT and empirical FF based MD simulations, in order to couple high accuracy in the representation of interactions to the large time and size scales needed to represent the process. However, the realization of these processes relies on the practical possibility of finely manipulating the local curvature and generating and sustaining coherent flexural phonons. In fact, our current efforts are along that route: we are exploring several possibilities for static and dynamic curvature manipulation, including external electric fields (Cavallucci, 2014), functionalization with optically active molecular pillars (Burress et al., 2010), electro-mechanical pulling, coupling to piezo-electric substrates (Camiola et al., 2014). In this phase, a multi-scale simulation approach will be even more necessary: in the route toward the practical realization of possible devices, one must analyze also macroscopic effects of thermodynamic nature, in addition to the physical phenomena at the sub-nano scale and the dynamical behavior at the nano-to-micro scale. Therefore, we intend to add a continuum representation, where graphene is modeled as a membrane with mechano-elastic properties (Zang et al., 2013) to the DFT and to the MD with empirical FF. Consistency between the representations will be obtained by appropriate bottom-up parameterization and top-down transfer of macroscopic information, and will ensure a complete and accurate representation of the system properties and behavior.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledge financial support by the EU, 7th FP, Graphene Flagship (contract no. NECT-ICT-604391), the CINECA award “ISCRA C” IsC10_HBG, 2013 and PRACE “Tier0” award Pra07_1544, and IIT Compunet Platform for computational resources.
References
Bonaccorso, F., Colombo, L., Yu, G., Stoller, M., Tozzini, V., Ferrari, A. C., et al. (2015). Graphene, related two dimensional crystals, and hybrid systems for energy conversion and storage. Science 347, 1246501. doi: 10.1126/science.1246501
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Burress, J. W., Gadipelli, S., Ford, J., Simmons, J. M., Zhou, W., and Yildirim, T. (2010). Graphene oxide framework materials: theoretical predictions and experimental results. Angew. Chem. Int. Ed. Engl. 49, 8902–8904. doi:10.1002/anie.201003328
Camiola, V. D., Farchioni, R., Pellegrini, V., and Tozzini, V. (2014). Hydrogen transport within graphene multilayers by means of flexural phonons. arXiv:1412.0923.
Cavallucci, T. (2014). Density Functional Theory Simulations of Electro-Mechanical Properties of Naturally Corrugated Epitaxial Graphene. MS thesis. Pisa: University of Pisa.
Fasolino, A., Los, J. H., and Katsnelson, M. I. (2007). Intrinsic ripples in graphene. Nat. Mater. 6, 858–861. doi:10.1038/nmat2011
Goler, S., Coletti, C., Tozzini, V., Piazza, V., Mashoff, T., Beltram, F., et al. (2013a). The influence of graphene curvature on hydrogen adsorption: towards hydrogen storage devices. J. Phys. Chem. C 117, 11506–11513. doi:10.1021/jp4017536
Goler, S., Coletti, C., Piazza, V., Pingue, P., Colangelo, F., Pellegrini, V., et al. (2013b). Revealing the atomic structure of the buffer layer between SiC(0 0 0 1) and epitaxial graphene. Carbon 51, 249–254. doi:10.1016/j.carbon.2012.08.050
Harder, S., Spielmann, J., Intermann, J., and Bandmann, H. (2011). Hydrogen storage in magnesium hydride: the molecular approach. Angew. Chem. Int. Ed. Engl. 50, 4156–4160. doi:10.1002/anie.201101153
Lindsay, L., and Broido, D. A. (2010). Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 81, 205441. doi:10.1103/PhysRevB.81.205441
Mashoff, T., Takamura, M., Tanabe, S., Hibinio, H., Beltram, F., and Heun, S. (2013). Hydrogen storage with titanium-functionalized graphene. Appl. Phys. Lett. 103, 013903. doi:10.1063/1.4812830
Mori, D., and Hirose, K. (2009). Recent challenges of hydrogen storage technologies for fuel cell vehicles. Int. J. Hydrogen Energy 34, 4569–4574. doi:10.1016/j.ijhydene.2008.07.115
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Patchkovskiim, S., Tse, J. S., Yurchenko, S. N., Zhechkov, L., Heine, T., and Seifert, G. (2005). Graphene nanostructures as tunable storage media for molecular hydrogen. Proc. Natl. Acad. Sci. U.S.A. 102, 10439. doi:10.1073/pnas.0501030102
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Sakintuna, B., Lamari-Darkirim, F., and Hirscher, M. (2007). Metal hydride materials for solid hydrogen storage: a review. Int. J. Hydrogen Energy 32, 1121–1140. doi:10.1016/j.ijhydene.2006.11.022
Sastre, G. (2010). Hydrogen physisorption in metal-organic frameworks: concepts and quantum chemical calculations. Theor. Chem. Acc. 127, 259–270. doi:10.1007/s00214-010-0766-y
Sofo, J. O., Chaudhari, A. S., and Barber, G. D. (2007). Graphane: a two-dimensional hydrocarbon. Phys. Rev. B 75, 153401. doi:10.1103/PhysRevB.75.153401
Tozzini, V., and Pellegrini, V. (2011). Reversible hydrogen storage by controlled buckling of graphene layers. J. Phys. Chem. C 115, 25523–25528. doi:10.1021/jp208262r
Tozzini, V., and Pellegrini, V. (2013). Prospects for hydrogen storage in graphene. Phys. Chem. Chem. Phys. 15, 80. doi:10.1039/c2cp42538f
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Wang, Z. F., Zhang, Y., and Feng, L. F. (2011). Formation of hydrogenated graphene nanoripples by strain engineering and directed surface self-assembly. Phys. Rev. B 83, 041403(R). doi:10.1103/PhysRevB.83.041403
Xu, P., Neek-Amal, M., Barber, S. D., Schoelz, J. K., Ackerman, M. L., Thibado, P. M., et al. (2013). Unusual ultra-low-frequency fluctuations in freestanding graphene. Nat. Commun. 5, 3720. doi:10.1038/ncomms4720
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zang, J., Wang, Q., Tu, Q., Ryu, S., Pugno, N., Buehler, M., et al. (2013). Multifunctionality and control of the crumpling and unfolding of large-area graphene. Nat. Mater. 12, 321–325. doi:10.1038/nmat3542
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Zhirko, Y. I., Kovalyuk, Z. D., Pyrlja, M. M., and Boledzyuk, V. B. (2007). “Application of layered InSe and GaSe crystals and powders for solid state hydrogen storage,” in Hydrogen Materials Science and Chemistry of Carbon Nanomaterials Series: NATO Security Through Science Series A: Chemistry and Biology (Springer), 325–340. doi:10.1007/978-1-4020-5514-0_43
Keywords: density functional theory, classical molecular dynamics, rippled graphene, flexural phonons, hydrogen storage
Citation: Camiola VD, Farchioni R, Cavallucci T, Rossi A, Pellegrini V and Tozzini V (2015) Hydrogen storage in rippled graphene: perspectives from multi-scale simulations. Front. Mater. 2:3. doi: 10.3389/fmats.2015.00003
Received: 15 December 2014; Accepted: 08 January 2015;
Published online: 30 January 2015.
Edited by:
Simone Taioli, Bruno Kessler Foundation, ItalyReviewed by:
Silvio A. Beccara, Bruno Kessler Foundation, ItalyCopyright: © 2015 Camiola, Farchioni, Cavallucci, Rossi, Pellegrini and Tozzini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:dmFsZW50aW5hLnRvenppbmlAbmFuby5jbnIuaXQ=
 Vito Dario Camiola
Vito Dario Camiola Riccardo Farchioni
Riccardo Farchioni Tommaso Cavallucci
Tommaso Cavallucci Antonio Rossi
Antonio Rossi Vittorio Pellegrini
Vittorio Pellegrini Valentina Tozzini
Valentina Tozzini