- 1Department of Structural, Geotechnical and Building Engineering, Politecnico di Torino, Torino, Italy
- 2IMT Institute for Advanced Studies Lucca, Lucca, Italy
Where We are in Modeling Mechanical, Traffic, and Socio-Economical Discrete Systems
Discrete systems have been firstly introduced in physics (Fisher and Wiodm, 1969; Noor and Nemeth, 1980; Adhikari et al., 1996; Kornyak, 2009) to simulate materials at the micro- and nano-scales where a continuum description of matter breaks down. The constituents can be atoms or molecules and their interactions are usually modeled by force fields resulting from chemical potentials or weak van der Waals interactions, depending on the type of bonding. These models have been further exploited in mechanics with the aim of predicting macroscopic properties such as strength and toughness from the non-linear interactions taking place between the constituents at the different scales. Pioneering attempts in mechanics to model discrete mechanical systems are those using lattice models (van Mier et al., 1995; Schlangen and Garboczi, 1997) characterized by a network of nodes connected by links modeled by beams. Although proven to suffer from mesh-dependency, they have been broadly used for studying the non-linear fracture behavior of concrete at the meso-scale. Another line of research regards the generalized-Born approach (Pellegrini and Field, 2002; Marenich et al., 2013), firstly used in chemistry to model a solute represented as a set of three-dimensional spheres into a continuum medium solvent, then applied in molecular mechanics (called MM/GBSA) to investigate contact and fracture of bodies at the micro-scale.
The high-computational power and the development of powerful open source software allow nowadays the design of wide discrete scalable models composed of up to millions of particles or molecules whose equations of motions and mutual interactions are described by highly non-linear interatomic potential laws. This is the field of molecular dynamics (MD), which led to the development of specific explicit time integration schemes (like the velocity-verlet integration scheme) to solve large systems of equations with a reduced computational cost. Car and Parrinello (1985) proposed a minimization of the total energy of the system by applying a dynamical simulated annealing based on MD. MD computations can also be coupled with continuum simulations by multi-scale methods. Among the many strategies available in the literature, (Shenoy et al., 1999; Knap and Ortiz, 2001) developed an approach based on the Tadmor’s quasi-continuum method (Tadmor et al., 1996) operating on a representative atomistic zone with a reduced number of degrees of freedom. Local minima of the whole system potential energy are determined via the total energy from a cluster of atoms, avoiding the complete calculation of the full atomistic force field. The MD enriched continuum method by Belytschko and Xiao (2003) and Xiao and Belytschko (2003) was also another pioneering approach to couple a potential energy Hamiltonian calculation conducted on a fine scale MD domain with a Lagrangian calculation on a coarse scale continuum domain with an overlapped bridging domain among the two representations. Recently, an implementation of interatomic potential laws within a displacement-based finite element (FE) formulation has also been proposed in Nasdala et al. (2010), with a rigorous implicit solution scheme, aiming at generating models where non-linear discrete and continuous systems can be suitably combined.
Discrete systems made of nodes and links are also used in other disciplines than mechanics to model transport or socio-economical networks (Caldarelli and Vespignani, 2007; Whrittle, 2012). Based on a continuum version of traffic conservation along a link, Lighthill and Whitham (1955) and Whitham (1974) and independently Richards (1956) proposed the LWR model where the governing equation describing the dependency of the traffic flux on time and on location along a link is a non-linear hyperbolic partial differential equation (PDE) analogous to that describing the propagation of the front of a wave inside a medium. For a homogenous link where the velocity of traffic is the same at any location and no shocks on the traffic flow are present, the integration of the LWR PDE leads to a non-linear relation between the traffic flow and the density of vehicles, which fully represents the traffic state. Also, in economics, it is of great interest to quantify the effect of breaking a link over the whole network response by simulating the dynamics of flow redistribution. Again a flow model can be used as suggested in Zhou et al. (2010) to decode a huge human crowd without distinction between individuals, while small groups are better represented by an agent-based approach. Even if computationally demanding, the latter approach can be exploited in economics for competitive resource allocation (Chakraborti et al., 2015) with models characterized by strong heterogeneity and non-equilibrium dynamics among adaptive interacting agents. Similar problems are likewise of paramount importance in socio-economical systems, as, e.g., the prediction of the propagation of false news (trolling behavior) in the web, or the understanding of the socio-economic impact of removing a commercial or a web node (Caldarelli et al., 2008; Quattrociocchi et al., 2013). A graphical representation in Figure 1 of a mechanical system (Figure 1A) and a socio-economic network (Figure 1B) emphasizes also the visual similarity between them.
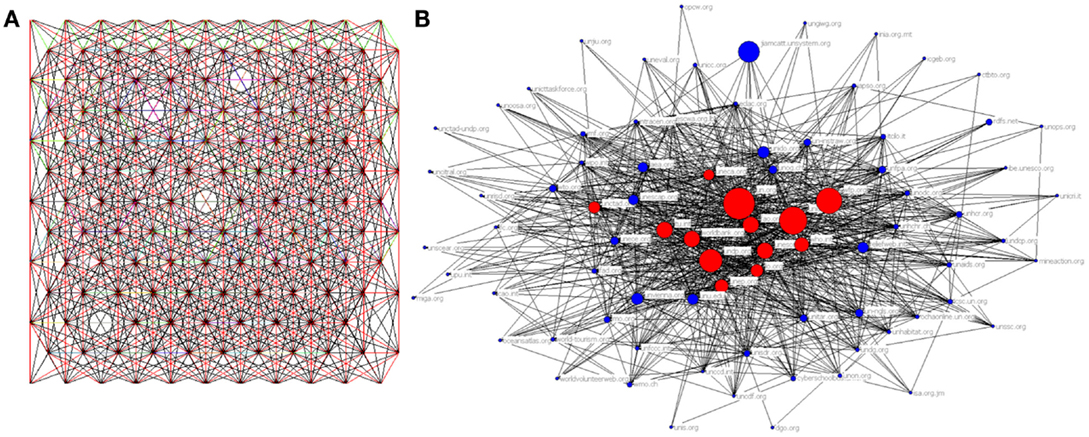
Figure 1. (A) A mechanical system with non-local interactions among atoms modeled by non-local links and with some randomly located vacancies inducing links removal. (B) A network of relationships between 87 mutually linked United Nations websites [adapted from Cugelman (2008)].
Where We are Going: Complexity of Discrete Systems, Analogies, and Differences
All the previous discrete systems and probably many others analyzed by the scientific Community share the common features of complex systems where the overall properties emerge from the non-local non-linear interactions between their basic network components and can only be predicted by numerically simulating the system response and the dynamic evolution of defects (cracks, node removal, link removal). Failure of the system is generally the result of a percolation of defects at different scales, which leads to complex redistribution of internal forces/flows. Understanding how the system is able to withstand perturbations, i.e., its resilience or flaw-tolerance, is a problem common to all of the disciplines mentioned in the previous section.
Hence, strong analogies and differences emerge from a deep analysis of network models if examined from a cross-disciplinary perspective. The integral formulation of LWR PDE leads to a non-linear relation between the flux and the vehicle density, which has an ascending branch up to a maximum and then decreased to 0 by further increasing the vehicle density. Interatomic potentials providing the constitutive behavior of a link are also relations between interaction forces and relative displacements of nodes with a similar non-linear trend. The equilibrium of each node is also a common concept: it can be the result of the net sum of the fluxes converging to a node or the net sum of the nodal forces. The removal of a link is typically the result of a propagation of a dislocation inside the material, whereas it represents an interruption of communication between nodes in traffic or in socio-economic systems. Non-local interactions can be considered both for mechanical and socio-economical systems and can be modeled as parallel links connecting nodes, in addition to serial links connecting only neighboring nodes. Therefore, given the elementary constitutive equations describing the link behavior that can be mechanically modeled as non-linear springs and the state variables characterizing the nodes, the basic dynamics of any discrete system can be in principle simulated according to the numerical techniques proper of non-linear mechanics. A non-locality index can also be used to classify and distinguish between different networks, as shown in Infuso and Paggi (2014) to interpret the response of a discrete system upon removal of nodes in different locations. From numerical simulations in Infuso and Paggi (2014), we observed that the higher the value of the non-locality index, the higher the total force supported by the network, for the same type of node removal.
Significant differences are also present among discrete systems in different disciplines. Links between atoms or molecules are always constructed on a deterministic basis, i.e., all the atoms are linked by a certain amount of links, just with different intensities depending on the spatial distance between the nodes. The situation in socio-economic systems is in reality much more complex, since the existence of links between nodes may depend on the reputation or the economic state of the nodes themselves, to cite two possible influencing state variables. Therefore, links are created dynamically and are probably the result of an optimization problem that should be modeled and solved at the local level. Although these differences may suggest that a unified theory for the simulation of complex networks is still to come and should be the result of a joint cross-disciplinary effort involving mathematicians, engineers, physicists, and economists, they also open interesting perspectives for mechanics. For instance, the fact that local optimization problems should take place at the local level, in mechanics they could be the result of the mechanical response of a constituent of a metamaterial, whose configuration is such that it can minimize or maximize certain properties depending on the intensity of diffusive external fields (temperature, humidity, electro-chemical potentials, etc.), as it happens in biomechanical applications. Within a bottom-up approach to model this cyber-physical system, given the links formed at the lower scale and their constitutive behavior that may depend on time, the global mechanical response of the network can then be simulated by minimizing the total energy of the system, using numerical methods proper of mechanics.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 306622 (ERC Starting Grant “Multi-field and Multi-scale Computational Approach to Design and Durability of PhotoVoltaic Modules” – CA2PVM).
References
Adhikari, S. K., Frederico, T., and Marinho, R. M. (1996). Lattice discretization in quantum scattering. J. Phys. A Math. Gen. 29, 7157. doi: 10.1088/0305-4470/29/22/015
Belytschko, T., and Xiao, S. P. (2003). Coupling methods for continuum model with molecular model. Int. J. Multiscale Comput. Eng. 1, 115–126. doi:10.1615/IntJMultCompEng.v1.i1.100
Caldarelli, G., Capocci, D., and Garlaschelli, A. (2008). A self-organized model for network evolution. Eur. Phys. J. B 64, 585–591. doi:10.1140/epjb/e2008-00243-5
Caldarelli, G., and Vespignani, A. (2007). Large Scale Structure and Dynamics of Complex Networks. Complex Systems and Interdisciplinary Science, Vol. 2. Singapore: World Scientific.
Car, R., and Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474. doi:10.1103/PhysRevLett.55.2471
Chakraborti, A., Challet, D., Chatterjee, A., Marsili, M., Zhang, Y.-C., and Chakrabarti, B. K. (2015). Statistical mechanics of competitive resource allocation using agent-based models. Phys. Rep. 552, 1–25. doi:10.1016/j.physrep.2014.09.006
Cugelman, B. (2008). The United Nations’ Web Network (July 2007). Available at: http://www.cugelman.com/online-research/united-nations-web-network/#sthash.QjNwZPQJ.dpuf
Fisher, M. E., and Wiodm, B. (1969). Decay of correlations in linear systems. J. Chem. Phys. 50, 3756. doi:10.1063/1.1671624
Infuso, A., and Paggi, M. (2014). Flaw-tolerance of nonlocal discrete systems and interpretation according to network theory. Fract. Struct. Integr. 29, 302–312. doi:10.3221/IGF-ESIS.29.26
Knap, J., and Ortiz, M. (2001). An analysis of the quasicontinuum method. J. Mech. Phys. Solids 49, 1899–1923. doi:10.1016/S0022-5096(01)00034-5
Kornyak, V. V. (2009). Discrete symmetry analysis of lattice systems. Phys. Part. Nuclei Lett. 6, 554–558. doi:10.1134/S1547477109070139
Lighthill, M. J., and Whitham, G. B. (1955). On kinematic waves II – a theory of traffic on long crowded roads. Proc. R. Soc. Lond. Ser. A 229, 317–345. doi:10.1098/rspa.1955.0089
Marenich, A. V., Cramer, C. J., and Truhlar, D. G. (2013). Generalized Born solvation model SM12. J. Chem. Theory Comput. 9, 609–620. doi:10.1021/ct300900e
Nasdala, L., Kempe, A., and Rolfes, R. (2010). The molecular dynamic finite element method (MDFEM). Comput. Mater. Con. 19, 57–104. doi:10.3970/cmc.2010.019.057
Noor, A. K., and Nemeth, M. P. (1980). Micropolar beams model for lattice grids with rigid joints. Comput. Methods Appl. Mech. Eng. 21, 249–263. doi:10.1016/0045-7825(80)90034-1
Pellegrini, E., and Field, M. J. (2002). A generalized-Born solvation model for macromolecular hybrid-potential calculations. J. Phys. Chem. A 106, 1316–1326. doi:10.1021/jp0135050
Quattrociocchi, W., Caldarelli, G., and Scala, A. (2013). Self-healing networks: redundancy and structure. PLoS ONE 9:e87986. doi:10.1371/journal.pone.0087986
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Schlangen, E., and Garboczi, E. J. (1997). Fracture simulations of concrete using lattice models: computational aspects. Eng. Fract. Mech. 57, 319–332. doi:10.1016/S0013-7944(97)00010-6
Shenoy, V. B., Miller, R., Tadmor, E. B., Rodney, D., Phillips, R., and Ortiz, M. (1999). An adaptive finite element approach to atomic-scale mechanics – the quasicontinuum method. J. Mech. Phys. Solids 47, 611–642. doi:10.1016/S0022-5096(98)00051-9
Tadmor, B. E., Ortiz, M., and Phillips, R. (1996). Quasicontinuum analysis of defects in solids. Philos. Mag. (Abingdon) 73, 1529–1563. doi:10.1080/01418619608243000
van Mier, J. G. M., Schlangen, E., and Vervuurt, A. (1995). “Lattice type fracture models for concrete,” in Continuum Models for Materials with Microstructure, ed. H. B. Mühlhaus (Chichester: John Wiley & Sons), 341–377.
Whrittle, P. (2012). “Networks – optimization and evolution,” in Cambridge Series in Statistical and Probabilistic Mathematics (Cambridge: Cambridge University Press).
Xiao, S. P., and Belytschko, T. (2003). A bridging domain method for coupling continua with molecular dynamics. Comput. Methods Appl. Mech. Eng. 193, 1645–1669. doi:10.1016/j.cma.2003.12.053
Keywords: discrete systems, molecular dynamics, networks theory, cross-disciplinary analogies
Citation: Infuso A and Paggi M (2015) Computational modeling of discrete mechanical systems and complex networks: where we are and where we are going. Front. Mater. 2:18. doi:10.3389/fmats.2015.00018
Received: 22 December 2014; Accepted: 21 February 2015;
Published online: 09 March 2015.
Edited by:
Maurizio Dapor, Bruno Kessler Foundation, ItalyReviewed by:
Stefano Mariani, Politecnico di Milano, ItalyCopyright: © 2015 Infuso and Paggi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:YW5kcmVhLmluZnVzb0Bwb2xpdG8uaXQ=
 Andrea Infuso
Andrea Infuso Marco Paggi
Marco Paggi