A bird’s eye view on the concept of multichannel scattering with applications to materials science, condensed matter, and nuclear astrophysics

The last few years have witnessed remarkable advances in two branches of condensed matter physics. The first deals with the experimental investigation by electron spectroscopy techniques of the laws governing the behavior of strongly correlated systems. This flourishing experimental area has been fueled most notably by potential applications of high-Tc superconductors (Kordyuk, 2012), graphene (Dresselhaus, 2014), graphene-like structures (Butler et al., 2013), and layered heterostructures (Novoselov et al., 2005) to device engineering. The most remarkable outcome of this analysis is the realization that electronic states other than simple Fermi liquids occur in several materials families. Consequently, a wealth of theoretical and computational methods have been developed to describe accurately the electronic correlation in these low-dimensional many-fermion systems and to investigate unusual physical phenomena that appear in the presence of charge confinement or strong interaction. These methodological developments can be branched in two categories: self-consistent mean-field approaches, such as Hartree-Fock (HF) and density functional, and approaches beyond mean-field, such as multi-configurational methods and many-body perturbation theory (MBPT) (Szabo and Ostlund, 1996; Onida et al., 2002). In this regard, the new “Fermi-Dirac” physics of graphene and its derivatives represents one of the most significant case studies of interlacing novel theories and experiments so far (Taioli et al., 2009a; Haberer et al., 2010, 2011; Umari et al., 2012; Taioli, 2014).

However, while these methods found extensive use in the specific research field for which they were tailored, mainly related to materials science, it is rather unusual to observe applications crossing the borders between different areas.

At variance, the goal of this opinion article is to provide a “bird’s eye view” on a recently developed ab initio method (Taioli et al., 2009b,c, 2010), firstly implemented to perform spectral analysis of solids at drastically reduced computational cost. This method has been further extended, as well as successfully used, in apparently distant applications, ranging from materials science to astrophysics. Hereby, after a description of the conceptual framework behind this approach we will prove its ability to span different research fields by interpreting a specific set of physical problems in the meV to MeV range. In particular, we will discuss the Auger effect in SiO₂ (Taioli et al., 2009b), the BEC-BCS crossover in ultracold Fermi gases (UFG) (Simonucci et al., 2011, 2012; Garberoglio et al., 2013), and finally the electron capture in stellar plasma (Simonucci et al., 2013).

The physical picture, under which all the previous phenomena can be framed, is the existence of one (or many) intermediate, quasi-bound state(s) produced by an initial scattering event, embedded in the continuum represented by one or more fragments of the system under investigation.

Depending on the initial kinetic energy of the impinging projectile, the dynamics of the excited target system may undergo a resonant state before decaying. Correlation between system’s many constituents in the intermediate state is the driving force to final decay, possibly leading to several outcomes characterized by a particular set of observables (“channels”). Multichannel outcomes are ultimately the fingerprint of the many-body nature of interactions. We stress that, while scattering events may be driven by different forces coupling the initial and final states, be it Coulomb as in the Auger decay or weak as in β-decay, nevertheless the common platform to all these processes is given by the discrete-continuum interaction, named after Fano-Fesbach (Fano, 1961). Scattering theory aims to find positive energy solutions (scattering states) of the following many-body Hamiltonian:

$\left(Ĥ-E\right){\mathrm{\Psi }}_{\mathrm{\alpha },\in }^{-}=0$ (1)

where the scattering wave function $|{\mathrm{\Psi }}_{\mathrm{\alpha },\in }^{-}⟩$ describes the motion of a particle asymptotically not interacting with kinetic energy ∈_α = E – E_α, while the scattering center is in the state classified by the quantum numbers α. The Hamiltonian in Eq. 1 usually contains kinetic and interaction terms. For example in condensed matter systems the electronic Hamiltonian within the Born–Oppenheimer approximation is:

$H=-\frac{{\hslash }^2}{2m}{\displaystyle \sum _{i=1}^N}{\nabla }_i^2+{\displaystyle \sum _{i<j}^N}\frac{e^2}{|r_i-r_j|}-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{k=1}^n}\frac{Z_k{e}^2}{|r_i-R_k|}$ (2)

where, in order of appearance, we find the electron kinetic energy, the electron–electron, and electron-nuclei Coulomb interaction terms, while N and n are, respectively, the total number of electrons of mass m at positions r_i and of nuclei with charge Z_k at positions R_k. Fano’s approach basically provides a useful way to write the scattering wavefunction by mixing the discrete quasi-bound spectrum $|\mathrm{\Phi }⟩$ of the Hamiltonian with N_c continuum channels $|{\mathrm{\chi }}_{\mathrm{\beta },\tau }^{-}⟩$ as follows:

$|{\mathrm{\Psi }}_{\mathrm{\alpha },\in }^{-}⟩=a_{\mathrm{\alpha }}\left(\in \right)|\mathrm{\Phi }⟩+{\displaystyle \sum _{\mathrm{\beta }\text{=1}}^{N_c}}{\displaystyle \underset{0}{\overset{\infty }{\int }}}|{\mathrm{\chi }}_{\mathrm{\beta },\mathrm{\tau }}^{-}⟩C_{\mathrm{\beta },\mathrm{\alpha }}\left(\mathrm{\tau },\in \right)d\mathrm{\tau }$ (3)

where a_α and C_β,α are the expansion coefficients. For example, in the case of the Auger process the final channel $|{\mathrm{\chi }}_{\mathrm{\beta },\tau }^{-}⟩$ represents an ionized target in the state β plus an electron in the continuum with kinetic energy τ.

In this regard, to determine the cross section for a given process is more suitable for implementations to write the many-body equation of motion for quantum particles (Eq. 1) in terms of the scattering T-matrix. The T-matrix is defined as (Taioli et al., 2010):

$\widehat{T}=\left(E-Ĥ\right)Ĝ\left(E\right)\widehat{V}+\widehat{V}Ĝ\left(E\right)\widehat{V}=\left(E-Ĥ+\widehat{V}\right)Ĝ\left(E\right)\widehat{V}=\left(E-{Ĥ}_0\right)Ĝ\left(E\right)\widehat{V}$ (4)

where $Ĝ\left(E\right)={\left(E-Ĥ+i\in \right)}^{-1}$ is the Green’s function of the full Hamiltonian, V is the interaction potential, H and H₀ are the full and non-interacting Hamiltonian (in Eq. 1 H₀ is the sum of kinetic energy and electron-nuclei potential) and E is the total energy.

This quantity calculated between initial (i) (usually free plane wave) and final (f) scattering states (Eq. 3) is a function of the possible ingoing and outgoing channels as well as of the many-body interaction potential within the scattering region. Furthermore, T is directly relatable to experiments via the scattering cross section as follows:

${\mathrm{\sigma }}_{\mathrm{if}}\propto |⟨f\left|T\right|i⟩{|}^2\mathrm{\delta }\left(E_{\mathrm{i}}-E_{\mathrm{f}}\right)$ (5)

and to other observables such as partial decay rates into reaction channels, transition life-times, and energy levels of the target (e.g., in the Korringa-Kohn-Rostoker multiple scattering scheme (Papanikolaou et al., 2002)).

A first example of application of this multichannel scattering approach is concerned with electron spectroscopies. These techniques are based on scattering processes in which the initial state consists of a projectile, typically represented by a photon or an electron, that collides with a target, and final decay states are characterized by the presence of a few fragments recorded by some spectrometers.

Depending on the beam incident energy, the target system may undergo several processes: (i) direct emission, whereby the electron is imparted sufficient energy to be emitted from the solid; (ii) absorption, which consists in the creation of an electron-hole pair to probe the unoccupied density of states; (iii) autoionization and Auger emission, which are the results of non-radiative transitions from neutrally excited (autoionization) or singly ionized (Auger process) systems as a consequence of the impact; (iv) energy loss, when monochromatic electron beams undergo inelastic interactions, change momentum and lose energy. In these processes, the system often goes through intermediate discrete quasi-bound states with lifetimes longer than the collision times, decaying by fragmentation afterward. In this case, the driving force leading to decay is the Coulomb interaction among system’s constituents. Observation of fragment types, as well as their angular and energy distribution, provides useful information on the many-particle system’s properties.

Historically, the most fruitful approach toward electron spectroscopy has been to understand measured spectra within a one-electron picture (Taioli et al., 2010). This amounts to hide electron–electron interactions by introducing the concept of quasi-particle, defined as a real particle dressed by its interaction with other electrons in the system. Whereby this picture holds, measured electron spectra and related observables (e.g., binding energies) are thus referred to quasi-particles; in this case, mean-field approaches, such as HF and DFT, are generally found in qualitative agreement with experiments.

Alternatively, one could also view electron spectra as a means to learn about electron–electron interactions. Electron correlation effects on spectral lineshapes are observed with respect to the one-electron picture through the appearance of:

• changes in spectrum profile (both line widths and intensities);

• shift in energy positions;

• appearance of satellites or secondary peaks;

• initial and final state effects.

Over the last few years, it has become possible to obtain electron spectra with a total energy resolution (monochromator plus electron spectrometer) considerably smaller than the linewidth of the core/valence-hole level investigated (Taioli et al., 2010). This fact allows accurate determination of the intensity distribution also for those transitions which are split into a large number of sub-levels due to the coupling of the emitted electrons with spectator electrons, nuclei and, collective excitations (plasmons). For a quantitative interpretation of electron spectra recorded on solids, problems mainly arise in the accurate treatment of the electronic correlation, in the localization of the electron emission, in the degree of localization over the valence band, and in the energy losses suffered by the electrons in their way out of the solid.

To take into account both extrinsic and intrinsic features on the same grounds, we proposed a unified method able to calculate electron spectra in solids (Taioli et al., 2009b,c, 2010) using beyond mean-field techniques. This method provides an extension of Fano’s resonant multichannel scattering, allowing several intermediate quasi bound states (see Eq. 3) and solving the scattering problem by calculating the T-matrix (see Eq. 4) with appropriate boundary conditions. Within this approach, the discrete-continuum interaction modifies the spectral lineshape by including the interchannel interaction between electronic orbitals calculated from beyond mean-field first-principles techniques, while Monte Carlo is used to simulate the effect of inelastic losses on the original line-shape.

With the last step, the theoretical intrinsic spectrum is convoluted with extrinsic losses, so that it can be directly compared to “as-acquired” experimental spectra (Shirley, 1972; Tougaard, 1986). Moreover, shake processes, electron-hole and hole-hole interactions can be considered without semiempirical parameters appearing in Hubbard-like models (Lander, 1953; Cini, 1976; Sawatzky, 1977).

An example of application of this method to the calculation of the Si K-LL Auger spectrum in SiO₂ is reported in Figure 1A. We stress that the effect of the multichannel nature of the scattering and of the continuum-discrete interaction are both visible respectively in the variety of transitions and in the asymmetric lineshape.

FIGURE 1

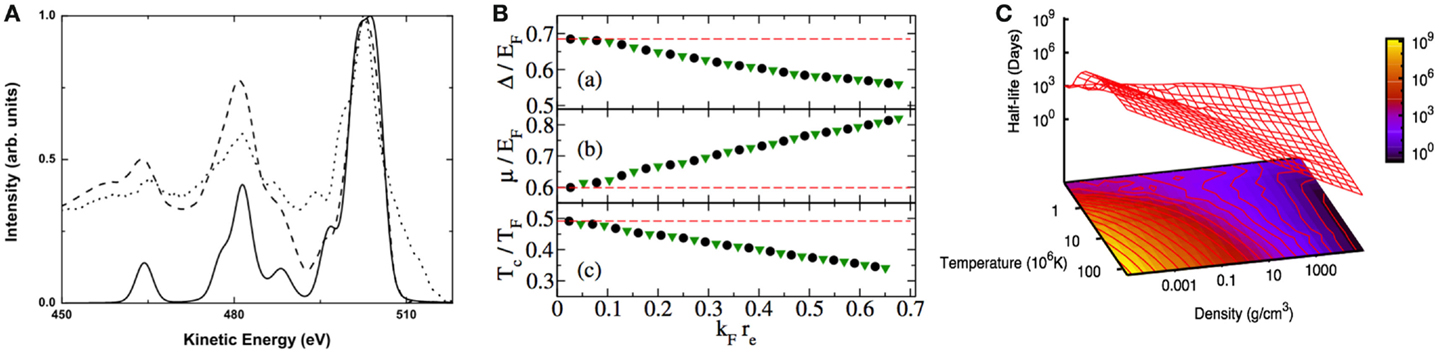
Figure 1. (A) Si K-LL Auger spectrum. Black line: ab initio spectrum. Dashed line: spectrum with added extrinsic features. Point line: experimental spectrum. (B) Pairing function Δ (A), chemical potential μ (B), and phase transition temperature T_c (C) for an ultracold Fermi gas of ⁶Li atoms at unitarity (BEC–BCS crossover) as a function of the Fermi momentum k_F times the effective range r_e. Dots and triangles refer to the narrow and broad resonances, respectively. The dashed horizontal lines report the same quantities calculated using the contact potential. (C) Electron-capture decay rate in days for ⁷Be as a function of ρ and T.

Related, but in some ways even more puzzling, are the properties of UFG (Giorgini et al., 2008), which represent the ideal playground for studying correlations within a scattering framework. Fermions repel each other due to the Pauli principle. However, recent experimental developments (Regal et al., 2003) have opened the possibility of tuning the interaction between fermionic atoms, typically alkali species, using external magnetic fields. In this way, the scattering length can be varied to values much larger than the mean interatomic distance, by forcing the system to undergo a Feshbach resonance. Under these conditions, resonant scattering between two particles may occur, in which the bound channel becomes energetically close to the continuum spectrum threshold, and may interact via discrete-continuum interaction. The theoretical methods used to describe this “unitary” regime, which is a crossover between the situation of weakly paired fermions in BCS theory and strongly coupled bosons in Bose–Einstein condensation, are mainly based on Quantum Monte Carlo and mean-field approaches (Giorgini et al., 2008), notably the Bogoliubov-de Gennes (BdG) equations.

There are two ways in which multichannel scattering theory can be applied to study this regime. The first is the calculation of the scattering length describing the interaction strength between alkali atoms. Secondly, we demonstrated (Simonucci et al., 2011, 2012; Garberoglio et al., 2013) that the BdG equations used to describe this system (and thus the pairing function Δ) can be naturally written in term of the T-matrix of the underlying potential. Many-body scattering techniques, as for the case of the Auger process, can thus be applied to the assessment of the UFG properties. In particular, using this T-matrix based approach one can avoid issues related to the divergence of the interaction arising from the contact potential and, moreover, assess the effect of the actual finite range of the potential on the observables in and out the universality regime (Simonucci et al., 2011, 2012; Garberoglio et al., 2013). In Figure 1B we show the application of our approach to the calculation of the main observables in a ⁶Li UFG as a function of the interaction effective range appearing in the second order expansion of the T-matrix (Simonucci et al., 2011).

To appreciate further more the general nature of our theoretical framework, we applied this multichannel scattering approach to bound-continuum interaction for determining the abundance of Li in evolved stars. This is a crucial problem to assess Big-Bang nucleosynthesis of Li and still an open issue in astrophysics (Adelberger et al., 2011). Indeed Li production and depletion in stars is not accounted for in details and is particularly hampered by poor knowledge of how β-decay rates are affected in the rapidly varying temperature and density conditions below the envelope of stars (Adelberger et al., 2011). Extrapolations from solar data are extremely uncertain and an accurate estimate of the electron capture on Be is needed. By applying our multichannel approach, we were able to demonstrate that the e^– capture is proportional to the weak force T-matrix, and, assuming the weak force as a contact interaction, to the electron density at the nucleus ρ₀ (Simonucci et al., 2013).

Due to the high temperatures and densities found in stellar plasma (ρ > 150 g/cm³ and T ≫ 10⁷ K), e^– capture may occur from both bound and continuum states. Our formalism allows one to calculate accurately the electron density at the nucleus by including bound, partially ionized, and continuum channels into the electron capture estimate on the same grounds and, thus, to go beyond the previous approaches relying on the Debye–Huckel approximation to the electronic screening (Bahcall, 1962).

We stress that the changes in the electron density at the nucleus with respect to previously used approximations (ρ₀ and, thus, half-life as different as 30% with respect to that obtained by Bachall (Bahcall, 1962) for high density, low temperature, i.e., quantum regime) and an enhanced electron screening, which helps thermonuclear fusion, might have rather wide astrophysical consequences (e.g., for p-captures on Li). In Figure 1C, we report the new β-decay rate as a function of T and ρ.

Summarizing, in this opinion article I discussed a recently developed many-body method, based on the concept of Fano’s interaction and the use of the scattering T-matrix, able to interpret a variety of physical phenomena, ranging from molecular and solid state physics to astrophysical scenarios.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work has received funding from the EU seventh Framework Programme under grant agreement n. 604391 Graphene Flagship. ST acknowledges support by Istituto Nazionale di Fisica Nucleare through the Supercalcolo agreement with Bruno Kessler Foundation, from the European Science Foundation under the INTELBIOMAT Exchange Grant and FBK for providing economical support through the “research mobility scheme”. Finally, ST acknowledges the Institute of Advanced Studies in Bologna for his ISA fellowship.

References

Adelberger, E. G., Garcia, A., and Robertson, R. G. H. (2011). Solar fusion cross sections. II. The pp chain and CNO cycles. Rev. Mod. Phys. 83, 195–245. doi: 10.1103/RevModPhys.83.195

CrossRef Full Text | Google Scholar

Bahcall, J. N. (1962). Beta decay in stellar interiors. Phys. Rev. 126, 1143–1149. doi:10.1103/PhysRev.126.1143

CrossRef Full Text | Google Scholar

Butler, S. Z., Hollen, S. M., Cao, L., Cui, Y., Gupta, J. A., Gutiérrez, H. R., et al. (2013). Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926. doi:10.1021/nn400280c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cini, M. (1976). Density of states of two interacting holes in a solid. Solid State Commun. 20, 605–607. doi:10.1016/0038-1098(76)91070-X

CrossRef Full Text | Google Scholar

Dresselhaus, M. S. (2014). What’s next for low-dimensional materials? Mater. Res. Lett. 2, 1–9. doi:10.1080/21663831.2013.838194

CrossRef Full Text | Google Scholar

Fano, U. (1961). Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 124, 1866–1878. doi:10.1103/PhysRev.124.1866

CrossRef Full Text | Google Scholar

Garberoglio, G., Taioli, S., and Simonucci, S. (2013). The BEC-BCS crossover in ultracold Fermi gases beyond the contact-potential approximation. Eur. Phys. J. D 67, 1–7. doi:10.1140/epjd/e2013-40114-6

CrossRef Full Text | Google Scholar

Giorgini, S., Pitaevskii, L. P., and Stringari, S. (2008). Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 80, 1215–1273. doi:10.1103/RevModPhys.80.1215

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Haberer, D., Petaccia, L., Farjam, M., Taioli, S., Jafari, S. A., Nefedov, A., et al. (2011). Direct observation of a dispersionless impurity band in hydrogenated graphene. Phys. Rev. B 83, 165433. doi:10.1103/PhysRevB.83.165433

CrossRef Full Text | Google Scholar

Haberer, D., Vyalikh, D. V., Taioli, S., Dora, B., Farjam, M., Fink, J., et al. (2010). Tunable band gap in hydrogenated quasi-free-standing graphene. Nanoletters 10, 3360–3366. doi:10.1021/nl101066m

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kordyuk, A. A. (2012). Iron-based superconductors: magnetism, superconductivity, and electronic structure. Low Temp. Phys. 38, 888–899. doi:10.1063/1.4752092

CrossRef Full Text | Google Scholar

Lander, J. J. (1953). Auger peaks in the energy spectra of secondary electrons from various materials. Phys. Rev. 91, 1382–1387. doi:10.1103/PhysRev.91.1382

CrossRef Full Text | Google Scholar

Novoselov, K. S., Jiang, D., Schedin, F., Booth, T. J., Khotkevich, V. V., Morozov, S. V., et al. (2005). Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. U.S.A. 102, 10451–10453. doi:10.1073/pnas.0502848102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Onida, G., Reining, L., and Rubio, A. (2002). Electronic excitations: density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659. doi:10.1103/RevModPhys.74.601

CrossRef Full Text | Google Scholar

Papanikolaou, N., Zeller, R., and Dederichs, P. H. (2002). Conceptual improvements of the KKR method. J. Phys. Condens. Matter 14, 2799–2823. doi:10.1088/0953-8984/14/11/304

CrossRef Full Text | Google Scholar

Regal, C. A., Ticknor, C., Bohn, J. L., and Jin, D. (2003). Creation of ultracold molecules from a Fermi gas of atoms. Nature 424, 47–50. doi:10.1038/nature01738

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sawatzky, G. A. (1977). Quasiatomic auger spectra in narrow-band metals. Phys. Rev. Lett. 39, 504–507. doi:10.1103/PhysRevLett.39.504

CrossRef Full Text | Google Scholar

Shirley, D. A. (1972). High-resolution X-ray photoemission spectrum of the valence bands of gold. Phys. Rev. B 5, 4709–4714. doi:10.1103/PhysRevB.5.4709

CrossRef Full Text | Google Scholar

Simonucci, S., Garberoglio, G., and Taioli, S. (2011). Finite-range effects in dilute Fermi gases at unitarity. Phys. Rev. A 84, 043639. doi:10.1103/PhysRevA.84.043639

CrossRef Full Text | Google Scholar

Simonucci, S., Garberoglio, G., and Taioli, S. (2012). A scattering view of the Bogoliubov-de Gennes equations. AIP Conf. Proc. 1485, 312–318. doi:10.1063/1.4755832

CrossRef Full Text | Google Scholar

Simonucci, S., Taioli, S., Palmerini, S., and Busso, M. (2013). Theoretical estimates of Stellar e–Captures. I. The half-life of ⁷Be in evolved stars. Astrophys. J. 764, 118–129. doi:10.1088/0004-637X/764/2/118

CrossRef Full Text | Google Scholar

Szabo, A., and Ostlund, N. S. (1996). Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Dover Books on Chemistry. Mineola, NY: Dover Publications.

Google Scholar

Taioli, S. (2014). Computational study of graphene growth on copper by first-principles and kinetic Monte Carlo calculations. J. Mol. Model. 20, 1–13. doi:10.1007/s00894-014-2260-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Taioli, S., Simonucci, S., Calliari, L., and Dapor, M. (2010). Electron spectroscopies and inelastic processes in nanoclusters and solids: theory and experiment. Phys. Rep. 493, 237–319. doi:10.1016/j.physrep.2010.04.003

CrossRef Full Text | Google Scholar

Taioli, S., Umari, P., and De Souza, M. M. (2009a). Electronic properties of extended graphene nanomaterials from GW calculations. Phys. Status Solidi B 246, 2572–2576. doi:10.1002/pssb.200982339

CrossRef Full Text | Google Scholar

Taioli, S., Simonucci, S., Calliari, L., Filippi, M., and Dapor, M. (2009b). Mixed ab initio quantum mechanical and Monte Carlo calculations of secondary emission from SiO₂ nanoclusters. Phys. Rev. B 79, 085432. doi:10.1103/PhysRevB.79.085432

CrossRef Full Text | Google Scholar

Taioli, S., Simonucci, S., and Dapor, M. (2009c). SURPRISES: when ab initio meets statistics in extended systems. Comput. Sci. Discov. 2, 015002. doi:10.1088/1749-4699/2/1/015002

CrossRef Full Text | Google Scholar

Tougaard, S. (1986). Background removal in x-ray photoelectron spectroscopy: relative importance of intrinsic and extrinsic processes. Phys. Rev. B 34, 6779–6783. doi:10.1103/PhysRevB.34.6779

CrossRef Full Text | Google Scholar

Umari, P., Petrenko, O., Taioli, S., and De Souza, M. M. (2012). Communication: electronic band gaps of semiconducting zig-zag carbon nanotubes from many-body perturbation theory calculations. J. Chem. Phys. 136, 181101. doi:10.1063/1.4716178

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar