- 1Departamento de Física-Química, Instituto de Física, Universidad Nacional Autónoma de México (UNAM), Mexico City, Mexico
- 2School of Physics Astronomy and Computational Sciences, George Mason University, Fairfax, VA, USA
Using rigidity (constraint) theory of glasses, the effects of low-frequency vibrational modes anomalies in the glass transition are studied. It is discussed how the possibility of tailoring by chemical doping the number of low-frequency modes gives clues about how to determine the glass transition temperature and glass formation ability. In particular, we present the effects of floppy modes in the specific heat, entropy, internal energy below glass transition, as well as a discussion of the thermodynamical effects above the glass transition. All the previous results can be extended to include the Boson peak, since it can also be understood from a rigidity point of view as a dilution of bonds in an over-constrained network. Finally, we discuss how a new subject is emerging: floppy modes effects in the electronic properties of flexible systems. Such relationship provides a natural connection with topological insulators and two dimensional materials like graphene.
Although in many senses, we have achieved several milestones in the understanding of glass transition (Jackle, 1984; Elliot, 1990), still there are many open questions and technological challenges to be tackled. At the same time, there are many competing theories looking for consensus among researchers (Debenedetti, 1998; Debenedetti and Stillinger, 2000; Egami et al., 2007), hence a vast amount of literature is devoted to provide a description of key experiments and relevant theories (Elliot, 1990; Debenedetti, 1998; Debenedetti and Stillinger, 2000). The aim of this article is to highlight the importance of topology in this field via rigidity theory. Thus, a map of the subject is provided. As a matter of fact, topology has an increased importance in solid state physics, since it is a powerful unifying concept that brings out robust and fundamental features of physical phenomena. For example, in the quantum Hall and spin quantum Hall effects, topologically protected states are immune to disorder. As a result, the conductance is universal even for different materials or degrees of disorder. Furthermore, topology brings out powerful analogies in fields that seem to be far away from glasses, increasing cross-fertilization between different disciplines. As an example, here we will discuss why the same exponents of the stretched exponentials observed in glass relaxation appear in the network of scientific citations.
In particular, there are several important questions to be solved by any suitable theory of glass transition,
1. What is fast enough? In other words, provide the minimal amount of cooling in order to form a glass.
2. What chemical factors determine glass transition?
3. How relaxation is achieved?
4. What is the origin of the low-frequency vibrational modes (LFVMs) anomalies, like the Boson peak, in glasses?
In a general sense, we have a partial understanding of all these questions (Elliot, 1990; Debenedetti, 1998; Debenedetti and Stillinger, 2000), yet we are not able to integrate all of them into a single, coherent, and solid body of knowledge. In this article, we will argue that rigidity, also known as rigidity (also known as constraint) theory (RT), introduced by Phillips (1979) to understand question number one, gives a remarkable key to integrate all of these questions into a single framework providing not only a nice concatenation of facts, but providing a powerful tool to develop real glasses (Gupta and Mauro, 2009; Mauro et al., 2009; Smedskjaer et al., 2010). Furthermore, it allows one to integrate many other open questions in the field of soft-matter, like in colloids, granular matter, and gels (Moukarzel, 1998; Huerta and Naumis, 2003a; Naumis, 2005b; Kraemer and Naumis, 2008).
The key provided by rigidity theory lies in the fact that, on the one hand, it gives a definitive answer to the origin of the floppy mode peak (Thorpe, 1983), which is a kind of low-frequency mode anomaly. By chemical doping, the fraction of floppy modes can be changed at will (Thorpe, 1983). At the same time, a huge amount of work has been made in order to determine the resulting physical properties as a function of chemical doping (Gupta and Mauro, 2009). Thus, we are able to compare how these anomalies affect the physical properties.
The outline of this paper is the following. In the first section, we present a brief introduction to rigidity theory (RT) and floppy modes. Then, we devote a section to show how the Boson peak can be included inside the same picture. In the last sections, we discuss the effects on the thermodynamical properties, glass transition, and relaxation of glasses when the Boson and floppy mode peaks are present. Finally, a section on electronic properties and floppy modes is presented, and the conclusions are given.
Rigidity (Constraint) Theory in a Nutshell
Rigidity theory was used first in glasses by Phillips (1979) to understand a general experimental observation: best network glass formers have an average coordination (< r > ) equal to < r > = 2.4. Here, best network glass formers means that the cooling speed is minimal in order to form the glass (Phillips, 1979). This special < r > = 2.4 coordination is obtained via chemical doping.
Why this magical number? The answer lies in a topological phase transition between a flexible to a rigid network (Thorpe, 1983). By considering each bond between any of the N atoms as a mechanical constraint, one can ask the question of how many bonds are needed to make the system rigid. If the number of constraints is bigger than the dimension of the configurational space, given by 3N, then the system is rigid. When the constraints are equal to 3N, the network is isostatic and has very special properties (Selvanathan et al., 2000; Wang et al., 2001). Otherwise is flexible.
When Nc is the number of constraints of a 3 dimensional system (3D), then a fraction (3N–Nc)/3N of the 3N configurational coordinates are cyclic, since the energy of the system does not depend on such variables (Thorpe, 1983). Thus, f is also the fraction of vibrational modes with zero frequency (f), called floppy modes.
Such fraction can be found using a mean-field approximation known as the Maxwell counting (Thorpe, 1983). This counting goes as follows: each of the r bonds in a site is shared by two sites. There are r/2 constraints due to distance fixing between neighbors. Angular forces also give constraints for directional bonding, and in 3D there are (2r − 3) constraints to give,
when f = 0 the network passes from a floppy network to a rigid one. In 3D, the mean-field approach predicts the transition at the critical value ⟨rc⟩ = 2.4 if all angular constraints are present.
Rigidity Theory at Finite Temperature
Notice that rigidity percolation theory was made for zero temperature (Thorpe, 1983). However, the original idea of Phillips’s RT was to explain the minimal cooling speeds to form glasses of a liquid supercooled melt (Phillips, 1979). Why a T = 0 theory works for the melt? This question is still in the process of being answered, and is a very active field of research. However, some preliminary conclusions are available, depending upon whether T is bigger or lower than Tg, where Tg is the glass transition temperature.
Below Tg
For T < Tg, the glass can be described as a harmonic solid when long-time relaxation can be neglected (Naumis, 2000a; Flores-Ruiz and Naumis, 2012). For long times, we need to average over meta-basins in the energy landscape, or consider stretched exponential relaxation in traps. Under the harmonic approximation, floppy modes present a blue-shifted peak due to residual Van deer Waals forces (Kamitakahara et al., 1991), around a frequency ω0 with weight f. Then, there is an important contribution to the entropy (S(T,V,N)) due to floppy modes, since they represent low-energy reaction coordinates in the energy landscape. If Van deer Waals forces are neglected, floppy modes provide channels in configurational spaces, giving lots of entropy (Naumis, 2000b, 2005a). In general, under the harmonic approximation, S(T,V,N) is given by Naumis (2005a, 2006c),
where ωj are the frequencies of the non-floppy normal modes. The last term is the contribution from floppy modes. Also, there is a source of extra entropy due to the different ways in which the constraints can be arranged in a lattice (Naumis, 2005a). Concerning other thermodynamical quantities, only for temperatures T < ℏω0/kB it is possible to obtain anomalous behaviors for the thermal conductivity (Romero-Arias et al., 2009; Naumis and Salazar, 2011) as well as for the internal energy and specific heat (Naumis, 2000a).
To understand this two last points, consider the internal energy per particle (U(T,N)/N) of the system, given in the harmonic approximation as a sum over all modes of the Bose–Einsten factor,
where ρ(ω) is the vibrational density of states. Let us make a simple model for ρ(ω) by using a combination of an Einstein model that puts a spectral weight f to the floppy mode peaks at frequencyω0. Notice that in ideal rigidity, ω0 = 0 since floppy modes do not store elastic energy. As explained before, in real systems, residual forces produce a blue shift with a non-zero ω0, as confirmed by neutron scattering (Kamitakahara et al., 1991). The rest (1–f) of the spectral weight is carried by a density ρR(ω),
where ωD is a cut-off frequency. Using this model for a flexible system, we get the internal heat as,
Now, we define a floppy-mode-temperature as Tf = ℏω0 /kB. Such temperature is akin to the Einstein or Debye temperature in those models. Basically, it defines a crossover between the classical limit, dominated by entropy via the thermal energy kBT, and quantum effects, determined by the energy of the floppy mode quantum, given by ℏω0. For low temperatures, i.e., below TD, there is a specific heat that is a combination of the Einstein one-frequency oscillator model, plus a T3 Debye contribution,
where the parameter TD is obtained by normalizing the non-floppy component. Notice that if the temperature is lowered below Tf, all floppy modes are frozen since the thermal energy is not enough to excite their quanta. As a result, cν follows the Debye model, but with a smaller value due to the reduced spectral weight of non-floppy modes. For high temperatures T > > TD, the Dulong-Petit law cν(T) = 3kB is recovered from equation (4). For this, the floppy-mode blue shift is paramount. A finite number of zero frequency modes will imply a violation since without this blue shift, cν(T) = 3(1–f)kB.
Above Tg
One of the most important questions in the field is why RT works to understand the supercooled liquid and non-equilibrium processes.
Initially, to answer this question, numerical simulations were performed on simple models of association leading to some preliminary conclusions (Huerta and Naumis, 2002a,b, 2003a,b). The advantage of these models is the possibility of defining in a clear-cut fashion the concept of active constraint, since short-range potentials are used. Then, if atoms are within a certain distance, the constraint is active. For example, it is clear that even in non-covalent bondings systems, like in disks and gels, dynamical arrest was related with a RT transition (Huerta and Naumis, 2002b, 2003a; Kraemer and Naumis, 2008).
The concept of temperature-broken constraints (Gupta and Mauro, 2009; Mauro et al., 2009; Bauchy and Micoulaut, 2015) has proved to be very important in the understanding of viscosity and relaxation, as has been confirmed in numerical simulations of real glasses (Smedskjaer et al., 2010; Bauchy and Micoulaut, 2011, 2015). The idea is that by heating, constraints are broken. The number of broken constants can be estimated through a Boltzmann factor (Gupta and Mauro, 2009). Notice that in a sense, the transition from a gas or liquid to a solid is just a problem of adding constraints. The problem is how to define an active constraint in realistic cases. However, recent work by Micoulaut’s group has provided a clear definition on how to determine active or broken constraints (Bauchy and Micoulaut, 2011, 2015), and thus solved a major open problem in the field.
From a more abstract point of view, the complexity of the energy landscape, determined by a distribution of metastable basins (Flores-Ruiz and Naumis, 2012), determines the minimal cooling speed, as can be explained by a simple solvable model that present a glass and a phase transition to a crystal depending on the cooling rate (Naumis, 2012). RT is, in fact, a clever way to estimate the fractal dimension of the “mountain” landscape (Naumis, 2005b).
Low-Frequency Mode Anomalies in Glasses: From Floppy Modes to the Boson Peak
All glasses present an excess of low-frequency vibrational modes (LVFMs) relative to the Debye crystal model, like the Boson peak (BP) or floppy modes (FM). They are in the THz range of frequencies (Buchenau et al., 1984; Elliot, 1990; Hehlen et al., 2000; Binder and Kob, 2005). Crystals can also present a Boson peak under pressure, like in SiO2 (Nakayama, 2002), where the rigid SiO4 tetrahedra units are connected by flexible bonds (Trachenko et al., 2004). In glasses, the nature of the Boson peak is still debated, while floppy modes are well understood.
During the last years, it has become clear that the Boson peak can also be explained as a consequence of rigidity. To understand this, suppose that we have an over-constrained network in which Nc > 3N, as shown in Figure 1. If bonds are removed at random, for example, by dilution, eventually Nc = 3N. At this point, the lattice becomes isostatic, see Figure 1. If we further dilute the lattice, eventually Nc < 3N and 3N–Nc zero frequency modes will appear. But what happens when we dilute the lattice starting from Nc < 3N?.
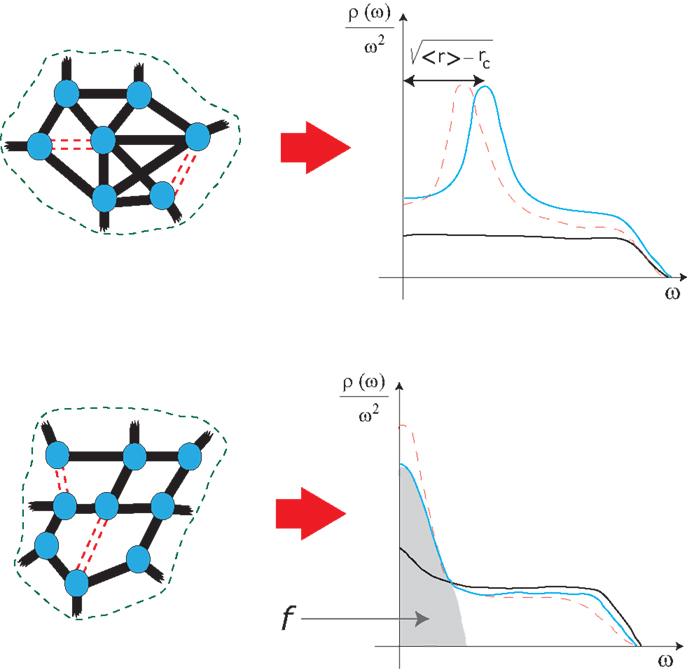
Figure 1. Evolution of the reduced density of states for a diluted bond network, starting from an over-constrained network (upper network) and from an isostatic lattice (lower network). The dotted lines indicate diluted bonds, while solid bars indicate intact bonds. The position of the Boson peak evolves as . For the isostatic lattice, < r > = rc and the Boson peak has zero frequency, i.e., it becomes a floppy mode. As dilution continues, the floppy peak, indicated by an f, has an increasing weight.
This question can be answered first by studying random bond dilution in periodic lattices (Flores-Ruiz and Naumis, 2011), then a Boson peak appears at a frequency ΩBP. It can appear at most at one-third of the Debye frequency (Flores-Ruiz and Naumis, 2011) ωD, while for example in almost all glasses (Rufflé et al., 2008) ΩBP = 0.1ωD. In addition, the position of the peak scales as (Flores-Ruiz and Naumis, 2011) , where < r > is the coordination of the network and rc is the critical coordination of the isostatic lattice. For disordered lattices, one can extend this approach by using perturbation theory or by performing numerical simulations (Flores-Ruiz et al., 2010).
Furthermore, the peak has an almost transverse mode nature and can be related with a Van Hove singularity occurring in the glass (Flores-Ruiz and Naumis, 2013). Recent evidence suggests that the Boson Peak in glasses is equivalent to the transverse acoustic van Hove singularity in crystals (Chumakov et al., 2011), supporting the analytical and computer model (Flores-Ruiz and Naumis, 2013). The shift of the Boson peak due to pressure effects (Monaco et al., 2006) can also be understood as an increase in the number of contacts (Flores-Ruiz and Naumis, 2013).
Thus, a new picture emerges by the process of bond dilution. The Boson peak is due to a diluted connectivity in an over-constrained network. As < r > goes to a critical rc, an isostatic lattice is reached. The Boson peaks reach a zero frequency and if dilution is performed again, floppy modes are obtained. Both low-frequency modes anomalies are due to a reduced connectivity of the network.
For example, in SiO2 under pressure a blue shift of the LFVM anomalies is observed (Trachenko et al., 2004). Such effect can be understood as a departure from isostaticity by an increased number of atomic contacts due to pressure. Below a pressure of 3GPa, constraint counting in SiO2 reveals an isostatic network due to the connection of rigid unit modes (RUM) made from SiO4 tetrahedra with flexible bonds. Pressure leads to the formation of defects with an increased coordination number (Trachenko et al., 2004).
Notice that in real glasses, floppy modes, and the Boson peak can coexist since regions with different elastic properties can coexist (Bhosle et al., 2011).
In the next section, we will discuss the importance of low-frequency modes for the glass transition.
Low-Frequency Modes and Glass Transition
Do low-frequency modes anomalies influence glass transition? There are several arguments against this. For example, within the energy landscape picture (Debenedetti and Stillinger, 2000), if a glass relax into a floppy mode channel reaction coordinate, eventually it will reach a new basin in which the floppy coordinates are different. Observe that floppy modes are important for fast relaxation. Long-time scale relaxation (α) does not retain memory of the almost instantaneous configuration of a floppy mode. However, energy landscape basins are in fact very similar (Flores-Ruiz and Naumis, 2012). Even in protein folding, an analysis of the landscape leads to the conclusion that the similarity of the minima is behind the remarkable phenomena of relaxation along soft coordinates (Pontiggia et al., 2007). For protein G, slow modes display a very mild dependence on the trajectory duration in the landscape. This originates from a striking self-similarity of the free-energy landscape embodied by the consistency of the principal directions of the local minima (Pontiggia et al., 2007), where the system dwells for several nanoseconds, and of the virtual jumps connecting them. Incidentally, proteins also have a boson peak (Ciliberti et al., 2006). Recently, a careful study of the short-time behavior distribution of normal modes on different meta-basins in Lennard-Jones binary glasses leads to the same conclusion (Flores-Ruiz and Naumis, 2012). In fact, such a remarkable result is behind another puzzling question, why short-time dynamics provides information about long-time dynamics in glasses (Dyre et al., 2006).
At the same time, there is a clear indication that low-frequency modes are paramount to the thermodynamical stability of a system. At this point, we will use an opposite approach to that used by most people. Instead of looking at melt cooling, here we assume that a glass was already formed, and has a temperature T lower than Tg. Then the glass is heated, until reach Tg.
Mechanical rigidity provides a clue on the thermodynamical stability of a system that contains a delicate balance between dimensionality and low-frequency vibrational modes. In particular, stability can be tested by looking at long-range correlations of the quadratic displacement u2(r j) of atom j at position r j,
where R ij is the vector R ij = r j – r i that joins atom i with j, and the bracket ⟨⟩ denotes average at temperature T and over all atoms. For a laboratory timescale, a glass is in a metastable state. Thus, we can suppose that the glass can be represented as an harmonic Hamiltonian in thermal equilibrium. Under this approximation, it is easy to prove that,
where < m > is the average mass. An excess of LFVM is enhanced by the 1/ω2 inside the integral in equation (5). LFVMs lead to an increased ⟨u2(T)⟩of the glass when compared with the crystal. Dimensionality (d) is also important for the crystal and glass. For crystals, the Debye model indicates that ρ(ω) = Cωd–1. Only for d = 3 the integral is convergent for non-zero T.
Summarizing, the stability of a solid is mainly contained in the factor ρ(ω)/ω2. Any excess of low-frequency modes will decrease the stability of the system.
Let us now further develop the previous arguments to show how LFVM can determine Tg. At low T, the system is trapped in an energy landscape basin (Debenedetti and Stillinger, 2000). As the system is heated, it can visit new basins. Following density functional theory, we look for transition states between basins, using the ansatz that atoms travel the least motion path between adjacent minima (Hall and Wolynes, 1987). The viscosity η(T) can be estimated as (Hall and Wolynes, 1987),
where η0 is the typical value of the melt viscosity, R0 is a constant related with the range of the inter-atomic potential. The mean quadratic displacement ⟨u2(T)⟩should be taken as measured by Mossbäuer scattering, since ⟨u2(T)⟩ will diverge for long-time scales. Since Tg corresponds to the temperature where η0 ≈1013 Poise, from equation (6) we get,
where y is an exponent defined by η = 10y Poise. For typical fluids (Hall and Wolynes, 1987) y ≈ 3. Also, for typical inter-atomic potentials (Hall and Wolynes, 1987) 0.3σ < R0 < 0.5σ (where σ is the atomic size). Thus, we obtain the following bounds,
The maximal quadratic displacement allowed for the system to be solid is determined by,
Since σ is of the order of the inter-atomic distance, it turns out that we just obtained for glasses the well known Lindemann criterion, i.e., for crystals melting occurs when the mean atomic displacement is around 10% of the atomic spacing a (Tabor, 1996). In fact, this criterion is valid for many glasses (Buchenau et al., 1984; Buchenau and Zorn, 1992). At this point, the fundamental role of low-frequency modes to determine Tg and Tm is clear, since we can separate the problem in two time scales.
Using equation (5) and that , Tg is given by,
The previous analysis can be combined with RT to estimate Tg as a function of chemical doping (Naumis, 2006a,b). Using the simple model of ρ(ω) described in equation (2) to feed equations (5) and (10), we get that
where γ a constant determined by ρR(ω) (the density of states when f = 0) and ω0,
This functional form deduced here for Tg as a function of ⟨r⟩ has been observed experimentally by many groups (Tatsumisago et al., 1990; Sreeram et al., 1991), and is called the empirically modified Gibbs-DiMarzio law (Naumis and Kerner, 1998; Kerner and Naumis, 2000).
Relaxation: From Glasses to Citations Networks and Turbulence
Here, we discuss recent progress in two fields: strain and thermal relaxation in glasses. In glasses, quenching produces defects with some residual internal stress. Such stress relaxation is known to be described experimentally by stretched exponentials (Phillips, 2006; Welch et al., 2013),
The relaxation parameters τ and β have been usually fitted from experimental data. Not so much work has been done on the theoretical side to understand a fundamental issue: how to get these parameters from a theory. Eventually, by considering defects as traps and a diffusion model, stretched relaxation theory (Phillips, 2006) (SER) was able to predict that in d dimensions β = d/(d + 2), giving the magic number β = 3/5 for d = 3. Later on, it was recognized that long-range forces can have an important effect in certain kind of glasses (Naumis and Phillips, 2012a,b), and the previous formula is modified by an effective dimensionality β = d*/(d* + 2), with d* = fd, and f = 1/2. This produces another magic number (Naumis and Phillips, 2012a,b), β = 3/7.
In real glasses, the accurate predictions of SER theory have been confirmed in a beautiful experiment by using a big homogeneous glass plate (Welch et al., 2013). Surprisingly, the same magic number appears in a study of twentieth century citations, involving 25 million papers (Wallace et al., 2009; Naumis and Phillips, 2012b). If papers are ranked by citations, then the ranking does not follow a power law. Instead, a stretched exponential is followed (Wallace et al., 2009). Before 1960, the number of citations has an exponent β = 3/5. After 1960, β = 3/7. The transition can be explained by the jet age, which increased the connectivity of the network (Naumis and Phillips, 2012b). The similarity with glasses is not coincidental, it is just the result of combining relaxation and topology, leading to a new exciting field. In fact, stretched exponentials lead to the modified beta rank law (Naumis and Cocho, 2008), which has many applications in biology, social sciences, soft-matter, physics, etc., i.e., when network topology matters (Naumis and Cocho, 2007).
Finally, we will discuss how thermal relaxation is modified by the rigid or flexible nature of the system. This is important for glass formation ability, since, for example, a fast relaxation will enhance crystallization. As an example, it has been observed that for metallic glasses, Tg is related with the chemical composition through the thermal conductivity (Louzguine-Luzgin et al., 2008). Also, the inclusion of group IV impurities leads to an enhanced glass formation ability (Reyes-Retana and Naumis, 2014, 2015).
The thermal conductivity for low temperatures of diluted flexible systems has been studied under the harmonic approximation, revealing also anomalies (Romero-Arias et al., 2009). For higher temperatures, the problem requires the study of non-linear Hamiltonians, which is a topic that even in one dimensional periodic case has many open questions (Campbell et al., 2004).
In fact, the study of thermal relaxation started with the well known Fermi–Pasta–Ulam (FPU) problem (Fermi et al., 1965; Campbell et al., 2004). They tried to solve the paradox that from a pure theoretical point of view, harmonic solids can never reach energy equipartition since there is no sharing of energy between normal modes. Fermi–Pasta–Ulam proposed a simple model to understand the problem. The model is a linear chain with equal masses and non-linear springs (Fermi et al., 1965; Campbell et al., 2004). The dynamical equations were solved using one of the first computers. The results were difficult to understand at that time, since equipartition did not appear as expected. After years of research, it is now clear that relaxation depends upon low-frequency vibrational modes (Ford, 1961; Reigada et al., 2001; Ponno, 2005), due to their quasi-resonant nature (Ford, 1961; Cerón et al., 2005; Ponno, 2005). As a result, they share energy in an efficient way (Ponno, 2005) when compared with high-frequency modes.
The FPU model can be modified to include rigidity (Romero-Arias and Naumis, 2008) by adding second-neighbor non-linear bonds in the original FPU model (Romero-Arias and Naumis, 2008). Constraints bonds are added at random or in a periodic way.
The relaxation from an initial temperature T to zero temperature can be studied in the following two steps (Reigada et al., 2002): a thermal bath is applied until thermal equilibrium is reached, then the bath is retired and a damping term is added at both ends of the chains. For long times, relaxation is always slower when the number of LFVMs is reduced. The relaxation of high-frequency modes requires a transference of energy to LFVMs (Reigada et al., 2001). Such a phenomenon is akin to turbulence (Ponno, 2005), in which energy is injected at large scales, and transferred via a cascade of self-similar eddies to a small scale, where energy is finally dissipated.
The study of relaxation in two and three dimensional systems using non-linear terms is still an open field since even for the original FPU model the work is scarce.
Electronic Properties and Floppy Modes: From Graphene to Topological Insulators
One of the less studied problems is how rigidity theory enters inside the electronic properties picture. At first sight, all vibrational modes affects electron scattering, and thus their effects are hidden inside the thermal noise. However, after the discovery of graphene and other pure bi-dimensional materials (Geim and Novoselov, 2007), there is a growing interest in the subject. Graphene, which is a 2D crystal with a one-atom thickness, can be considered as a flexible membrane. In such case, floppy modes are called flexural modes, since they correspond to vibrations in a perpendicular direction to the graphene’s plane (Geim and Novoselov, 2007). Note that there are predictions concerning the possibility of finding amorphous graphene, which is proposed to be as a simple realization of Zachariasen’s glass (Kumar et al., 2012).
Let us consider a simple example of the effects of floppy modes. For simplicity, we focus on a system described with a one-orbital nearest-neighbor tight-binding Hamiltonian, as happens in graphene (Geim and Novoselov, 2007),
where x′ runs over all sites of the distorted lattice due to a floppy mode. Here, is the creation operator for an electron at site x′ and is the annihilation operator at site . The vectors point in the direction of each nearest-neighbor for a given atom. The nearest-neighbor hopping parameters are usually modified by deformations, since they depend on the inter-atomic distances. For carbon, they fulfill an exponential decay (Oliva-Leyva and Naumis, 2013), , where t is the equilibrium hopping parameter.
Suppose the system is distorted by a floppy mode. Since bond lengths are not modified, the parameters are invariant (although in many systems, angular effects can induce changes depending of the orbital overlaps. For graphene, this effect is negligible for π orbitals). Under our approximation, the Hamiltonian matrix remains the same for floppy mode deformations. Thus, the eigenvalues are invariant under such distortion, and the electronic density of states also remains invariant. However, the electron’s speeds are modified. To see this in a simple way, consider a periodic system with an elastic deformation field u(x). The position of the atoms in the undeformed (x) and deformed lattices (x′) are related by,
with an associated strain tensor,
that here we assume that is uniform, i.e., without a spatial dependence. Replacing the creation/annihilation operators with their Fourier expansions, the Hamiltonian in momentum space is (Oliva-Leyva and Naumis, 2013)
and therefore, the dispersion relation is,
It is easy to see that the spectrum is the same as in the undeformed system, as expected from the eigenvalues of the Hamiltonian matrix. However, the dispersion relationship is distorted through a deformation of the reciprocal space. For strained or rippled graphene, this effect produces a deformation of the Dirac cone (Oliva-Leyva and Naumis, 2013).
Floppy modes in graphene are not only important for electron scattering. When boundaries or impurities appear, a fraction of the electronic modes have zero energy (with respect to the Fermi level). Such states are known as Dirac modes in graphene (Barrios-Vargas and Naumis, 2013), but appears in other bipartite lattices as confined states. For example, they have been observed in quasiperiodic systems (Naumis et al., 1994) and in random binary alloys (Naumis et al., 2002). Such modes can be described in terms of a mechanical instability when isostaticity appears (Kane and Lubensky, 2014). They are similar to the protected electronic boundary modes that occur in the quantum Hall effect and in topological insulators (Kane and Lubensky, 2014). Recently, Kane and Lubensky (2014) established the connection between the topological mechanical modes and the topological band theory of electronic systems, predicting new topological bulk mechanical phases.
These topological “floppy modes” are, in fact, behind the remarkable metal-insulator transition in doped graphene, which transforms graphene in a narrow-gap semiconductor with an enormous technological potential (Naumis, 2007; Barrios-Vargas and Naumis, 2011). They are also fundamental in graphene’s magnetic properties (Barrios-Vargas and Naumis, 2013).
Conclusion
Rigidity theory allows one to understand, via chemical modification, how low-frequency modes anomalies play an important role in glass transition. The Boson peak can also be included in the theory by considering bond dilution of over-constrained networks. When relaxation is combined with topology, stretched exponentials with magical β exponents are obtained. The ideas of rigidity can also be extended to study the electronic properties of solids, providing bridges between glasses and new topics in material science like graphene and quantum topological phases.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank DGAPA-UNAM project IN102513. This work was finished under the help of a sabatical leave program Estancias Sabaticas en el Extranjero, given by PASPA program in DGAPA-UNAM.
References
Barrios-Vargas, J. E., and Naumis, G. G. (2011). Doped graphene: the interplay between localization and frustration due to the underlying triangular symmetry. J. Phys. Condens. Matter. 23, 375501. doi: 10.1088/0953-8984/23/37/375501
Barrios-Vargas, J. E., and Naumis, G. G. (2013). Pseudo-gap opening and Dirac point confined states in doped graphene. Solid State Commun. 162, 23–27. doi:10.1016/j.ssc.2013.03.006
Bauchy, M., and Micoulaut, M. (2011). Atomic scale foundation of temperature-dependent bonding constraints in network glasses and liquids. J. Non Cryst. Solids 357, 2530–2537. doi:10.1016/j.jnoncrysol.2011.03.017
Bauchy, M., and Micoulaut, M. (2015). Densified network glasses and liquids with thermodynamically reversible and structurally adaptive behaviour. Nat. Commun. 6, 6398. doi:10.1038/ncomms7398
Bhosle, S., Gunasekera, K., Chen, P., Boolchand, P., Micoulaut, M., and Massobrio, C. (2011). Meeting experimental challenges to physics of network glasses: assessing the role of sample homogeneity. Solid State Commun. 151, 1851–1855. doi:10.1016/j.ssc.2011.10.016
Binder, K., and Kob, W. (2005). Glassy Materials and Disordered Solids. Singapore: World Scientific.
Buchenau, U., Nücker, N., and Dianoux, A. J. (1984). Neutron scattering study of the low-frequency vibrations in vitreous silica. Phys. Rev. Lett. 53, 2316–2319. doi:10.1103/PhysRevLett.53.2316
Buchenau, U., and Zorn, R. (1992). A relation between fast and slow motions in glassy and liquid selenium. Europhys. Lett. 18, 523. doi:10.1209/0295-5075/18/6/009
Campbell, D. K., Flach, S., and Kivshar, Y. S. (2004). Localizing energy through nonlinearity and discreteness. Phys. Today 43.
Cerón, I., Naumis, G. G., Salazar, F., and Wang, C. (2005). Efficient anharmonic phonon generation using a quasiperiodic lattice. Phys. Lett. A 337, 141. doi:10.1016/j.physleta.2005.01.054
Chumakov, A. I., Monaco, G., Monaco, A., Crichton, W. A., Bosak, A., Rüffer, R., et al. (2011). Equivalence of the boson peak in glasses to the transverse acoustic van hove singularity in crystals. Phys. Rev. Lett. 106, 225501. doi:10.1103/PhysRevLett.106.225501
Ciliberti, S., De Los Rios, P., and Piazza, F. (2006). Glasslike Structure of Globular Proteins and the Boson Peak. Phys. Rev. Lett. 96, 198103. doi:10.1103/PhysRevLett.96.198103
Debenedetti, P. G., and Stillinger, F. H. (2000). Supercooled liquids and the glass transition. Nature 240, 259. doi:10.1038/35065704
Dyre, J. C., Christensen, T., and Olsen, N. B. (2006). Elastic models for the non-Arrhenius viscosity of glass-forming liquids. J. Non Cryst. Solids 351, 4635. doi:10.1016/j.jnoncrysol.2006.02.173
Egami, T., Poon, S. J., Zhang, Z., and Keppens, V. (2007). Glass transition in metallic glasses: a microscopic model of topological fluctuations in the bonding network. Phys. Rev. B 76, 024203. doi:10.1103/PhysRevB.76.024203
Elliot, S. R. (1990). Physics of Amorphous Materials, 2nd Edn. London: Logman Scientific & Tecnical.
Fermi, E., Mohr, P. J., and Savageau, U. (1965). Los Alamos Report L. A., Enrico Fermi, Collected Papers II. Chicago, IL: Chicago Press.
Flores-Ruiz, H. M., and Naumis, G. G. (2011). Boson peak as a consequence of rigidity: a perturbation theory approach. Phys. Rev. B 83, 184204. doi:10.1103/PhysRevB.83.184204
Flores-Ruiz, H. M., and Naumis, G. G. (2012). Mean-square-displacement distribution in crystals and glasses: an analysis of the intrabasin dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 85, 041503. doi:10.1103/PhysRevE.85.041503
Flores-Ruiz, H. M., and Naumis, G. G. (2013). The transverse nature of the boson peak: a rigidity theory approach. Physica B Condens. Matter 418, 26. doi:10.1016/j.physb.2013.02.041
Flores-Ruiz, H. M., Naumis, G. G., and Phillips, J. C. (2010). Heating through the glass transition: a rigidity approach to the boson peak. Phys. Rev. B 82, 214201. doi:10.1103/PhysRevB.82.214201
Geim, A. K., and Novoselov, K. S. (2007). The rise of graphene. Nat. Mater. 6, 183–191. doi:10.1038/nmat1849
Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130, 094503. doi:10.1063/1.3077168
Hall, R. W., and Wolynes, P. G. (1987). The aperiodic crystal picture and free energy barriers in glasses. J. Chem. Phys. 86, 2943. doi:10.1063/1.452045
Hehlen, B., Courtens, E., Vacher, R., Yamanaka, A., Kataoka, M., and Inoue, K. (2000). Hyper-Raman scattering observation of the boson peak in vitreous silica. Phys. Rev. Lett. 84, 5355–5358. doi:10.1103/PhysRevLett.84.5355
Huerta, A., and Naumis, G. G. (2002a). Relationship between glass transition and rigidity in a binary associative fluid. Phys. Lett. A 299, 660. doi:10.1016/S0375-9601(02)00519-4
Huerta, A., and Naumis, G. G. (2002b). Evidence of a glass transition induced by rigidity self-organization in a network-forming fluid. Phys. Rev. B 66, 184204. doi:10.1103/PhysRevB.66.184204
Huerta, A., and Naumis, G. G. (2003a). Role of rigidity in the fluid-solid transition. Phys. Rev. Lett. 90, 145701. doi:10.1103/PhysRevLett.90.145701
Huerta, A., and Naumis, G. G. (2003b). Rigidity aspects of the glass transition. J. Non Cryst. Solids 329, 100. doi:10.1016/j.jnoncrysol.2003.08.020
Jackle, J. (1984). Models of the glass transition. Rep. Prog. Phys. 49, 171. doi:10.1088/0034-4885/49/2/002
Kamitakahara, W. A., Cappelletti, R. L., Boolchand, P., Halfpap, B., Gompf, F., Neumann, D. A., et al. (1991). Vibrational densities of states and network rigidity in chalcogenide glasses. Phys. Rev. B 44, 94. doi:10.1103/PhysRevB.44.94
Kane, C. L., and Lubensky, T. C. (2014). Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45. doi:10.1038/nphys2835
Kerner, R., and Naumis, G. G. (2000). Stochastic matrix description of the glass transition. J. Phys. Condens. Matter 12, 1641. doi:10.1088/0953-8984/12/8/306
Kraemer, A., and Naumis, G. G. (2008). Use of the cage formation probability for obtaining approximate phase diagram. J. Chem. Phys. 128, 134516. doi:10.1063/1.2899732
Kumar, A., Wilson, M., and Thorpe, M. F. (2012). Amorphous graphene: a realization of Zachariasen’s glass. J. Phys. Condens. Matter 24, doi:10.1088/0953-8984/24/48/485003
Louzguine-Luzgin, D. V., Saito, T., Yu, J. S., and Inoue, A. (2008). Influence of cooling rate on the structure and properties of a Cu-Zr-Ti-Ag glassy alloy. J. Mater. Res. 23, 515. doi:10.1557/JMR.2008.0066
Mauro, J. C., Yue, Y., Ellison, A. J., Gupta, P. K., and Allan, D. C. (2009). Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. U.S.A. 352, 19780–19784. doi:10.1073/pnas.0911705106
Monaco, A., Chumakov, A. I., Monaco, G., Crichton, W. A., Meyer, A., Comez, L., et al. (2006). Effect of densification on the density of vibrational states of glasses. Phys. Rev. Lett. 97, 135501. doi:10.1103/PhysRevLett.97.135501
Moukarzel, C. F. (1998). Isostatic phase transition and instability in stiff granular materials. Phys. Rev. Lett. 81, 1634. doi:10.1103/PhysRevLett.81.1634
Nakayama, T. (2002). Boson peak and terahertz frequency dynamics of vitreous silica. Rep. Prog. Phys. 65, 1195. doi:10.1088/0034-4885/65/8/203
Naumis, G., Barrio, R., and Wang, C. (1994). Effects of frustration and localization of states in the penrose lattice. Phys. Rev. B 50, 9834–9842. doi:10.1103/PhysRevB.50.9834
Naumis, G., and Phillips, J. (2012a). Bifurcation of stretched exponential relaxation in microscopically homogeneous glasses. J. Non Cryst. Solids 358, 893–897. doi:10.1016/j.jnoncrysol.2011.12.083
Naumis, G., and Phillips, J. (2012b). Diffusion of knowledge and globalization in the web of twentieth century science. Physica A 391, 3995–4003. doi:10.1016/j.physa.2012.02.005
Naumis, G., Wang, C., and Barrio, R. (2002). Frustration effects on the electronic density of states of a random binary alloy. Phys. Rev. B 65, doi:10.1103/PhysRevB.65.134203
Naumis, G. G. (2000a). Contribution of floppy modes to the heat capacity jump and fragility in chalcogenide glasses. Phys. Rev. B 61, R9205. doi:10.1103/PhysRevB.61.R9205
Naumis, G. G. (2000b). Contribution of floppy modes to the heat capacity jump and fragility in chalcogenide glasses. Phys. Rev. B 61, R9205–R9208. doi:10.1103/PhysRevB.61.R9205
Naumis, G. G. (2005a). Energy landscape and rigidity. Phys. Rev. E 71, 026114. doi:10.1103/PhysRevE.71.026114
Naumis, G. G. (2005b). Monte Carlo rejection as a tool for measuring the energy landscape scaling of simple fluids. Phys. Rev. E 71, 056132. doi:10.1103/PhysRevE.71.056132
Naumis, G. G. (2006a). Variation of the glass transition temperature with rigidity and chemical composition. Phys. Rev. B 73, 172202. doi:10.1103/PhysRevB.73.172202
Naumis, G. G. (2006b). Glass transition phenomenology and flexibility: An approach using the energy landscape formalism. J. Non Cryst. Solids 352, 4865–4870. doi:10.1016/j.jnoncrysol.2006.01.160
Naumis, G. G. (2006c). Glass transition phenomenology and flexibility: an approach using the energy landscape formalism. J. Non Cryst. Solids 352, 4865–4870; Proceedings of the 5th International Discussion Meeting on Relaxations in Complex Systems 5th International Discussion Meeting on Relaxations in Complex Systems. doi:10.1016/j.jnoncrysol.2006.01.160
Naumis, G. G. (2007). Internal mobility edge in doped graphene: frustration in a renormalized lattice. Phys. Rev. B 76, doi:10.1103/PhysRevB.76.153403
Naumis, G. G. (2012). Simple solvable energy-landscape model that shows a thermodynamic phase transition and a glass transition. Phys. Rev. E 85, 061505. doi:10.1103/PhysRevE.85.061505
Naumis, G. G., and Cocho, G. (2007). The tails of rank-size distributions due to multiplicative processes: from power laws to stretched exponentials and beta-like functions. New J. Phys. 9, 286. doi:10.1088/1367-2630/9/8/286
Naumis, G. G., and Cocho, G. (2008). Tail universalities in rank distributions as an algebraic problem: the beta-like function. Physica A 387, 84. doi:10.1016/j.physa.2007.08.002
Naumis, G. G., and Kerner, R. (1998). Stochastic matrix description of glass transition in ternary chalcogenide systems. J. Non Cryst. Solids 231, 111. doi:10.1016/S0022-3093(98)00417-7
Naumis, G. G., and Salazar, F. (2011). Thermal conductivity in a rigidity transition. Phys. Lett. A 375, 3483. doi:10.1021/jp8061042
Oliva-Leyva, M., and Naumis, G. G. (2013). Understanding electron behavior in strained graphene as a reciprocal space distortion. Phys. Rev. B 88, 085430, doi:10.1103/PhysRevB.88.085430
Phillips, J. (1979). Topology of covalent non-crystalline solids i: short-range order in chalcogenide alloys. J. Non Cryst. Solids 34, 153–181. doi:10.1016/0022-3093(79)90033-4
Phillips, J. (2006). Axiomatic theories of ideal stretched exponential relaxation (SER). J. Non Cryst. Solids 352, 4490–4494; Proceedings of the 5th International Discussion Meeting on Relaxations in Complex Systems 5th International Discussion Meeting on Relaxations in Complex Systems. doi:10.1016/j.jnoncrysol.2006.01.162
Ponno, A. (2005). Proceedings of the NATO Advanced Study Institute on International Summer School on Chaotic Dynamics and Transport in Classical and Quantum Systems Cargèse, Vol. 182. Corsica 431.
Pontiggia, F., Colombo, G., Micheletti, C., and Orland, H. (2007). Anharmonicity and self-similarity of the free energy landscape of protein G. Phys. Rev. Lett. 98, 048102. doi:10.1103/PhysRevLett.98.048102
Reigada, R., Sarmiento, A., and Lindenberg, K. (2001). Thermal resonance in signal transmission. Phys. Rev. E 64, 066113. doi:10.1103/PhysRevE.63.066113
Reigada, R., Sarmiento, A., and Lindenberg, K. (2002). Asymptotic dynamics of breathers in Fermi-Pasta-Ulam chains. Phys. Rev. E 66, 046607. doi:10.1103/PhysRevE.66.046607
Reyes-Retana, J., and Naumis, G. (2014). The effects of Si substitution on the glass forming ability of Ni–Pd–P system, a {DFT} study on crystalline related clusters. J. Non Cryst. Solids 387, 117–123. doi:10.1016/j.jnoncrysol.2014.01.001
Reyes-Retana, J., and Naumis, G. (2015). Ab initio study of Si doping effects in Pd–Ni–P bulk metallic glass. J. Non Cryst. Solids 409, 49–53. doi:10.1016/j.jnoncrysol.2014.11.011
Romero-Arias, J. R., and Naumis, G. G. (2008). Thermal relaxation and low-frequency vibrational anomalies in simple models of glasses: a study using nonlinear Hamiltonians. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 77(6 Pt 1), 061504. doi:10.1103/PhysRevE.77.061504
Romero-Arias, J. R., Salazar, F., Naumis, G. G., and Fernandez-Anaya, G. (2009). Thermal conductivity, relaxation and low-frequency vibrational mode anomalies in glasses: a model using the Fermi-Pasta-Ulam nonlinear Hamiltonian. Philos. Trans. A Math. Phys. Eng. Sci. 367, 3173–3181. doi:10.1098/rsta.2009.0069
Rufflé, B., Parshin, D. A., Courtens, E., and Vacher, R. (2008). Boson peak and its relation to acoustic attenuation in glasses. Phys. Rev. Lett. 100, 015501. doi:10.1103/PhysRevLett.100.015501
Selvanathan, D., Bresser, W. J., and Boolchand, P. (2000). Stiffness transitions in SixSe1-x glasses from Raman scattering and temperature-modulated differential scanning calorimetry. Phys. Rev. B 61, 15061. doi:10.1103/PhysRevB.61.15061
Smedskjaer, M. M., Mauro, J. C., Sen, S., and Yue, Y. (2010). Quantitative design of glassy materials using temperature-dependent constraint theory. Chem. Mater. 22, 5358–5365. doi:10.1021/cm1016799
Sreeram, A. N., Swiler, D. R., and Varshneya, A. K. (1991). Gibbs-DiMarzio equation to describe the glass transition temperature trends in multicomponent chalcogenide glasses. J. Non Cryst. Solids 127, 287. doi:10.1016/0022-3093(91)90481-K
Tatsumisago, M., Halfpap, B. L., Green, J. L., Lindsay, S. M., and Angell, C. A. (1990). Fragility of Ge-As-Se glass-forming liquids in relation to rigidity percolation, and the Kauzmann paradox. Phys. Rev. Lett. 64, 1549. doi:10.1103/PhysRevLett.64.1549
Thorpe, M. (1983). Continuous deformations in random networks. J. Non. Cryst. Solids 57, 355–370. doi:10.1016/0022-3093(83)90424-6
Trachenko, K., Dove, M. T., Brazhkin, V., and El’kin, F. S. (2004). Network rigidity and properties of sio2 and geo2 glasses under pressure. Phys. Rev. Lett. 93, 135502. doi:10.1103/PhysRevLett.93.135502
Wallace, M. L., Lariviere, V., and Gingras, Y. (2009). Modeling a century of citation distributions. J. Inform. 3, 296–303. doi:10.1016/j.joi.2009.03.010
Wang, Y., Wells, J., Georgiev, D. G., Boolchand, P., Jackson, K., and Micoulaut, M. (2001). Sharp rigid to floppy phase transition induced by dangling ends in a network glass. Phys. Rev. Lett. 87, 185503. doi:10.1103/PhysRevLett.87.185503
Keywords: glasses, boson peak, floppy modes
Citation: Naumis GG (2015) Low-frequency vibrational modes anomalies and rigidity: a key to understanding the glass and the electronic properties of flexible materials from a topological perspective. Front. Mater. 2:44. doi: 10.3389/fmats.2015.00044
Received: 05 March 2015; Accepted: 15 May 2015;
Published: 12 June 2015
Edited by:
Matthieu Micoulaut, Université Pierre et Marie Curie, FranceReviewed by:
Roger Jay Loucks, Alfred University, USAMathieu Bauchy, University of California Los Angeles, USA
Normand Mousseau, Université de Montréal, Canada
Copyright: © 2015 Naumis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gerardo G. Naumis, Circuito Exterior s/n, Mexico City, Mexico,bmF1bWlzQGZpc2ljYS51bmFtLm14
 Gerardo G. Naumis
Gerardo G. Naumis