- 1Center for Electrochemistry and Intelligent Materials (CEMI), Escuela Técnica Superior de Ingeniería Industrial, Universidad Politécnica de Cartagena, Cartagena, Spain
- 2Artificial Cell Research Group, Health Research Institute, National Institute of Advanced Industrial Science and Technology (AIST), Osaka, Japan
The nature of the electrochemical responses from carbon nanotubes (CNTs), capacitive (physical), or Faradaic (chemical, also named p-doping or n-doping) remain controversial. In this chapter, the literature is reviewed and discussed trying to elucidate if some of the two processes prevails, how the presence of chemical reactions can be elucidated and which properties, specific from the chemical processes, can be exploited. Different electrochemical responses and theories trying to explain those responses are discussed. The separation and quantification methodologies of the capacitive and Faradaic components involved in some electrochemical responses from CNTs are presented.
Introduction
When any material film based on carbon nanotubes (CNTs), as self-supported films or taking part of a device, are submitted in presence of liquid or solid electrolytes to potential steps, potential sweeps, or any other electrochemical methodology, an electrochemical response is obtained. The literature attributes the processes behind those responses to doping/de-doping processes, capacitive responses, oxidation and reduction processes, charge/discharge, and so on. So both, the name and the mechanism behind it are controversial (Li et al., 2002; Terrones, 2003; Rahman and Jeon, 2007; Zhai et al., 2011; Naoi et al., 2013; Ruiz et al., 2013; Simon and Gogotsi, 2013; Chopra et al., 2015; Ni et al., 2015). At the moment, it does not exist a widely accepted mechanism to explain the CNT electrochemical responses. It has been broadly accepted that they include mainly capacitive or physical effects, where balancing counter ions are oriented and disposed to compensate the excess of charges on their surface, but not changing the composition inside the CNTs bundles (Baughman et al., 1999; Riemenschneider et al., 2009a,b; Jiang et al., 2013). The almost square shape of the voltammetric responses in short potential ranges constitutes the main support of the claimed capacitive nature. At the same time, the authors accept that a uniform counter ions composition exists across the two films of CNTs acting as positive or negative pole of the capacitor. A uniform distribution of charges across the two constituent electrodes of a capacitor seems to contradict both, the Coulombic repulsion forces inside every capacitive electrode, and the attractive force from the second electrode translating most of the charges to the surface near the second electrode. A second issue offering technical difficulties is the long response time (seconds) required for the CNTs actuators to describe its maximum possible amplitude. The charge of the electrical double layer (EDL) of electrochemical capacitors in electrolyte concentrations higher that 10−3 M takes microseconds (Bard and Faulkner, 1980). Those supporters of the capacitive nature argue that CNT electrodes in electrolytes contain some electrolyte. So, when the electrodes are submitted to a potential gradient step, the response time depends on both, the capacitance of the CNT electrodes and the resistance to the ionic movement of the CNT electrodes and of the electrolyte between those CNT electrodes. The charge of EDL depends on the effective surface of the bundle of CNTs in the electrode layer. From a microscopic viewpoint, CNT bundles and pores full of electrolyte compose the CNT electrodes.
On the other side, an increasing number of scientists attribute electrochemical responses to actual insertion/extraction of ions in the CNTs film through redox processes, changing the double bond distribution along each CNT, and therefore, originating a new material for every different number of charges extracted from the electronic structure of the CNTs (Che et al., 1998; Gao et al., 1999; Claye et al., 2000; Ghosh et al., 2005; Chen et al., 2008; Eom and Kwon, 2008; Majeed et al., 2013). Some of them claim that these redox processes occur at the edges or at defects on the CNTs (Li et al., 2002; Banks et al., 2005; Hoefer and Bandaru, 2013; Wang et al., 2014). Some of such defects may be due to the presence of some catalysts remaining from the CNTs synthesis (Lyon and Stevenson, 2007; Chng et al., 2013; Remy et al., 2015). The processes are also named doping and de-doping. Whatever the amount of the involved charges, it generates new ionic chemical compounds, CNTn+(A−)n for p-doping (oxidation) or CNTn−(C+)n for n-doping (reduction). According to the main characteristic of a chemical compound, it must not only have a uniform chemical potential, which guarantees the uniform ionic distribution across the anodic, oxidized (p-doped or n-dedoped) CNT film and a different, but also uniform composition, across the cathodic, reduced (p-dedoped or n-doped) CNT film. In order to lodge the counterions, free volume must be generated and the film swells during insertion of ions and shrinks during ion’s ejection.
Clarifying the nature of the prevailing process taking place during electrochemical experiments from CNTs in electrolytic solutions, or its relative contribution, will provide valuable information to improve and optimize the design of new electrochemical devices based on CNTs. A prevalent capacitive process will allow the design of most efficient supercapacitors (Wildgoose et al., 2006; Endo et al., 2008; Liu et al., 2008; Zhang et al., 2009; Bondavalli et al., 2012; Kiamahalleh et al., 2012; Wang et al., 2012, 2015; Zheng et al., 2012; Li and Wei, 2013; Yan et al., 2014; Yiran et al., 2014; Abdalla et al., 2015); while a prevalent reactive, or faradic, process will allows the design of batteries for fast and ultrafast charge/discharge processes and multifunctional actuators having better control of the faradic movement (Dai et al., 2002; Landi et al., 2009; Du et al., 2011; Myung et al., 2015) acting, simultaneously, as sensor of the working and ambient conditions.
In this chapter, we will try to clarify the importance of faradic and capacitive processes in the electrochemical responses of CNTs, employing different electrochemical techniques and models.
Electrochemical Responses from CNTs
Voltammetric Responses
Most of the literature considers that the voltammetric responses from CNTs not showing any specific maxima and minima, thus, not showing any redox peaks, are uncontroversial evidences for the exclusive presence of capacitive processes in the electrochemical responses (Barisci et al., 2000a,b; Madden et al., 2006; Ruch et al., 2009; Hekmat et al., 2014).
When the voltammetric results are obtained from single walled CNTs (SWCNTs) and an ionic liquid glued by a non-active polymer, PVDF-HFP/Ionic liquid/SWCNTs, see Martinez et al. (2012) for the details on the construction of the film with those three components, in a narrow potential window in tetraethylammonium tetrafluoroborate (TEABF4) aqueous solution (between −100 and 600 mV versus Ag/AgCl), the voltammetric results show a capacitor-like response (Figure 1A). Repeating the experiments at different temperatures, the shape of the attained voltammograms does not change, but the involve charge, Q (obtained by integration of the voltammetric area below the anodic, or the cathodic current, , where I is the current flowing through the CNTs film, t is the flowing time, v is the scan rate, and E is the potential) increases for rising temperatures (Figure 1A). This fact points to an increasing fraction of CNTs from the film participating in those electrochemical responses at rising temperatures.
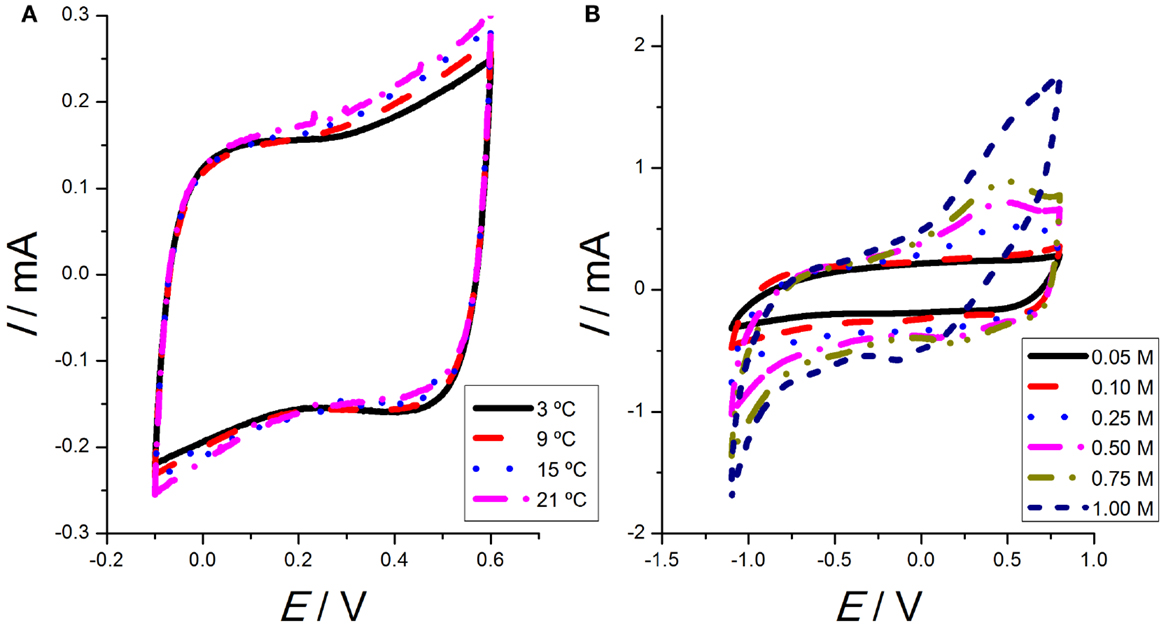
Figure 1. (A) Second voltammetric responses obtained from SWCNTs films cycled between −100 and 600 mV versus Ag/AgCl at 5 mV s−1, under different temperatures: 3, 9, 15, and 21°C in 0.1 M tetraethylammonium tetrafluoroborate (TEABF4) aqueous solution. (B) Second voltammetric responses obtained from SWCNTs films cycled between −1100 and 800 mV versus Ag/AgCl at 5 mV s−1 at room temperature in aqueous solution with different concentrations of TEABF4 (0.05, 0.10, 0.25, 0.50, 0.75, and 1.00M). Reproduced from Martinez et al. (2012), with permission from Wiley-VCH.
On the other hand, some works claim for an important redox component (Barisci et al., 2000a,b). When the potential limits are extended (to −1100 mV versus Ag/AgCl), the voltammetric responses present some peaks and shoulders, which are attributed now to actual redox processes (Figure 1B). For increasing concentrations of TEABF4, a well-defined anodic maximum is observed at 450 mV versus Ag/AgCl. On the cathodic branch, a minimum is observed at 250 mV and a shoulder at −300 mV versus Ag/AgCl. The involved anodic or cathodic charges also increase for rising electrolyte concentrations.
Thus, we can conclude that most of the CNTs’ voltammetric responses from the literature show a rectangular shape. Nevertheless, by changing the experimental conditions (the potential window, the working temperature, the electrolyte concentration, or the solvent) the voltammetric responses present well-defined peaks and shoulders. Those different results can support both, the capacitive nature of the involved processes (rectangular voltammograms) or their Faradaic nature (presence of peaks and shoulders on the voltammetric responses). So, the attained results and the prevailing model should result a function of the working conditions: further and complementary results from different electrochemical methodologies are required for a good clarification.
Chronoamperometric Responses
The presence of voltammetric maxima and the great influence of the electrolyte concentration suggest that the CNTs follow oxidation/reduction reactions. In that case, the reaction rate must follow those relationships stated by the chemical kinetics.
Experimental analytical results from CNTs point to a prevalent exchange of cations during redox reactions (Gupta et al., 2004; Yun et al., 2005). The electrochemical reaction responsible of the p-doping process could be expressed as Eq. 1:
where (CNT*)(C+A−) represents the active centers on the neutral CNTs in the film, understood as those C atoms of the CNT that will store a positive charge after oxidation (extraction of one electron and restructuration of the double bonds) becoming (CNTn+)(A−)n; (C+) represents the cation penetrating from the solution during reduction to compensate the charge of the A− anions trapped inside the film during its preparation.
The equilibrium for the transfer of one electron can be expressed as Eq. 2:
where K is the equilibrium constant and kox and kred are the oxidation and reduction, respectively, reaction kinetic constants or reaction coefficients, and α, β, and δ are the reaction orders for the concentration of the active centers in the CNTs film [(CNT*)(C+A−)], the oxidized CNTs, [(CNTn+)(A−)n] in the film, and the concentration of cations in solution (or in a solid electrolyte), [C+], respectively.
Considering the empirical oxidation reaction (p-doping) rate from reaction 1 (a similar procedure can be developed for the reduction reaction (p-de-doping) rate), it can be expressed (Martinez et al., 2012) as Eq. 3:
where r represents the oxidation rate, A exp(−Ea/RT) is the rate coefficient (k), A is the pre-exponential factor, Ea is the activation energy, R is the gas constant (8.314 J K−1 mol−1), T is the experimental temperature (K).
Any electrochemical reaction, as Eq. 1, is a Faradaic process. The reaction rate (moles of electrons, counterions, and active centers exchanged or transformed per unit of time and unit of volume) also can be expressed as a function of the charge involved per unit of time: the density current, i, A cm−2, flowing through the material, the film thickness, h, centimeters, and the Faraday constant, F = 96485 C mol−1 (Bard and Faulkner, 1980), Eq. 4:
By taking logarithms from Eq. 3, it is possible to get Eq. 5:
The concentration of oxidized centers in the CNTs can be calculated from the charge consumed to oxidize the material, Q; the material weight, w; its density, ρ, and the Faraday constant, F, using Eq. 6 (Otero and Garcia de Otazo, 2009):
Thus, if the relative influence of Faradaic processes in the film oxidation is important, the reaction rate must be influenced by the physical and chemical variables acting on Eqs 3 and 4.
The possible presence of an oxidation reaction of the CNTs can be followed by submitting the material to potential steps from the same reduced state, got by polarization at the same reduction potential for the same reduction time, and stepping then the potential to the oxidation potential to get the same final concentration of active centers. Following Eq. 4, the oxidation rate is determined by the current flowing after the potential step: the chronoamperometric response. Equation 5 also indicates the experimental methodology required to check whether or not the process occurs under chemical kinetic control: by changing one variable, keeping the rest, every time. A semilogarithmic relationship between 1/T and r (when [CNT*] and [C+] are kept constant) and a double-logarithmic relationship between [CNT*] and r (when k and [C+] are kept constant) indicate that the electrochemical reaction is the process controlling the electrochemical response from CNTs.
Figure 2A shows the anodic chronoamperometric responses got from a CNT based film (Martinez et al., 2012). In order to check the effect of the [CNT*], different potential steps are needed from the same initial reduced state (got by reduction at the same cathodic potential for the same reduction time for each experiment) until different final oxidation states (got at different anodic potentials: so different charges are extracted from the CNTs film every time, Eq. 1, getting a different final concentration of CNT*). The oxidation time must be enough to allow charging the EDL and the completion of the reaction. A very high-current flow through the system for long periods of time after the anodic potential step (>15 s). So, long time fact points to the presence of Faradaic processes: in a capacitive process the charge of the rigid EDL, when the ionic species is higher than 10−3M, only takes microseconds (Bard and Faulkner, 1980).
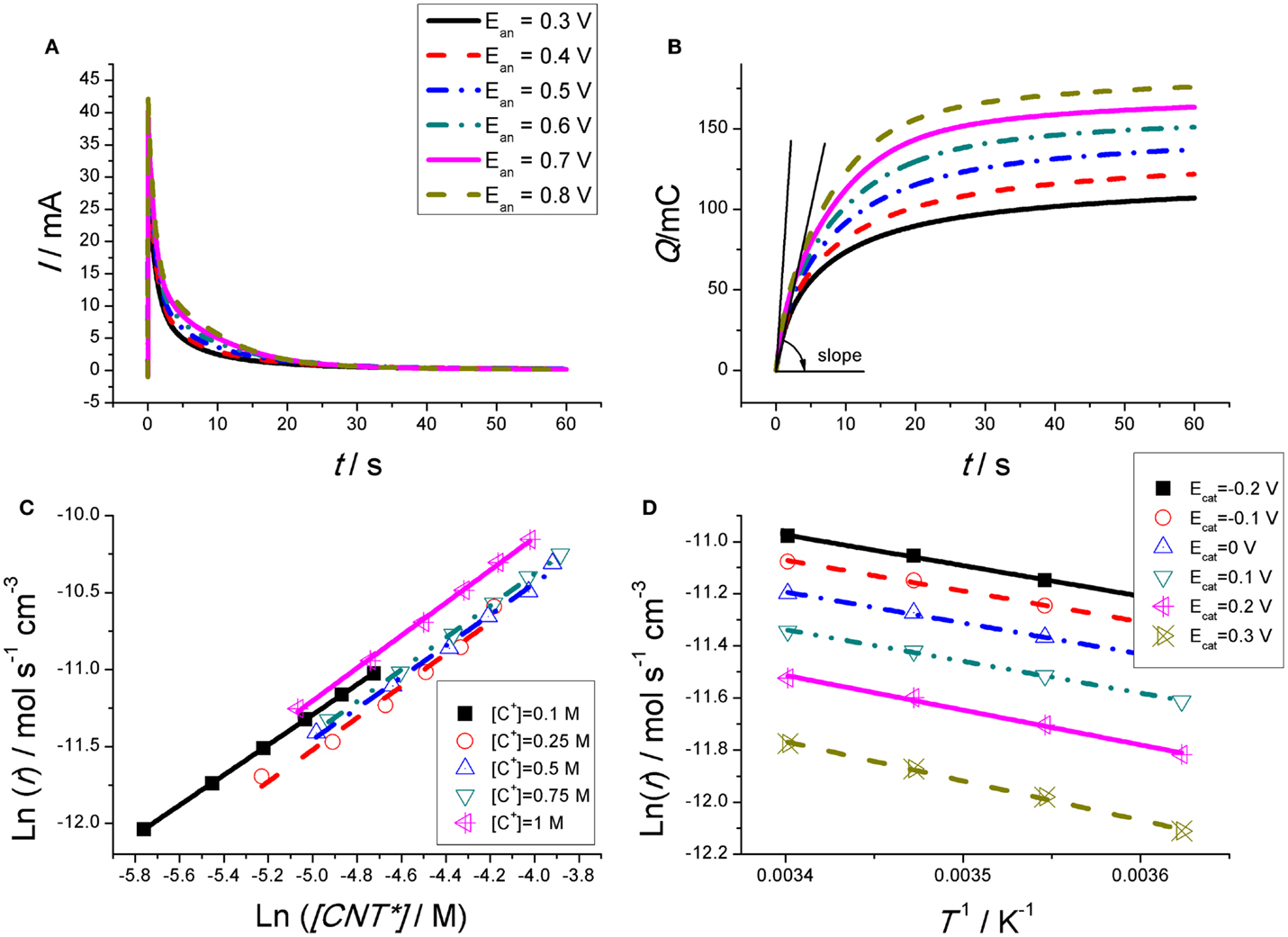
Figure 2. (A) Anodic chronoamperometric responses obtained from the second consecutive square potential wave at room temperature from CNT films submitted to consecutive square potential waves from −1100 mV (versus Ag/AgCl), kept for 60 s each time, to different potentials (300, 400, 500, 600, 700, and 800 mV), kept for 60 s every time in 0.1 M aqueous TEABF4 solution. (B) Consumed charge obtained by integration of the experimental chronoamperograms from (A). (C) Double-logarithmic plot of the experimental oxidation rates for different concentrations of active centers during oxidation of the CNT film, obtained from the initial slopes in (B). (D) Arrhenius plot for oxidation of the CNT film in 0.1 M TEABF4 aqueous solution at 3, 9, 15, and 21°C. The reaction rates were obtained by potential steps between different cathodic potentials and 600 mV. Reproduced from Martinez et al. (2012), with permission from Wiley-VCH.
By integration of the chronoamperometric responses the chronocoulograms (consumed charge versus time) can be obtained (Figure 2B). The slope of each chronocoulogram (dQ/dt = i) at the initial time (t → 0) gives the initial oxidation rate, r = (1/FV)(dQ/dt) = dc/dt being V the film volume and c = Q/FV the concentration of active centers, required for testing Eq. 5. The slopes from Figure 2B, at the initial time, are the initial reaction rates. Figure 2C shows the empirical double-logarithmic relationships, Eq. 3, between [CNT*] and the initial reaction rate r for different electrolyte concentrations. Figure 2D presents the expected, Eq. 3; semilogarithmic Arrhenius relationships between r and 1/T.
These empirical results fulfill the conditions stated by Eqs 2 and 3 and 5 for any chemical reaction. In conclusion, Figure 2 corroborates that the electrochemical response of the CNTs takes place under an electrochemical (Faradaic) kinetic control defined by Eqs 3 and 4 and 5.
The same methodology has been described and employed for the study of electrochemical kinetics in films of different conducting polymers: polythiophene (Otero and Santos, 2008), poly(3-methylthiophene) (Otero and Abadias, 2007, 2008), poly(3,4-ethylenedioxythiophene) (Otero and Caballero Romero, 2010), and polypyrrole (Otero and Garcia de Otazo, 2009; Otero and Martinez, 2011, 2013b).
Relaxation Processes in CNTs
In conducting polymers, oxidation/reduction reactions induce structural movements at the molecular and macroscopic scale: conformational relaxation, swelling, shrinking, and conformational packing. Under these conditions, the local concentration of the counterions inside and around a conformational packed region of the film is low. For concentrations lower than 10−3M, the charge required to charge the EDL during a potential step is a function of the ionic strength (Gouy–Chapman model) (Atkins and De Paula, 2002) and takes microseconds. Here, the oxidation of the CNTs and parallel charge of the EDL, of a packed structure of CNTs should take a long time (seconds) required for the reaction-driven structural relaxation.
Films of CNTs films taking part of three-layer actuators give unexpected chronoamperometric responses, when submitted to potential steps, showing two maxima (Figure 3A) (Mukai et al., 2011; Gimenez et al., 2012). Similar responses during the oxidation–reduction of conducting polymers were theoretically described from physical–chemical principles by a simultaneous presence of capacitive and reactive processes. The second maximum indicate that the rate of the electrochemical oxidation is controlled by structural (nucleation–relaxation) processes (Otero et al., 1995, 1997a, 2010; Otero and Grande, 1996; Otero and Abadias, 2007, 2008; Otero and Santos, 2008; Otero and Garcia de Otazo, 2009; Arias-Pardilla et al., 2010a,b; Otero and Caballero Romero, 2010; Otero and Martinez, 2011, 2013b). Each of the processes is described by a stretched exponential function. The two stretched exponential functions (capacitive and reaction-driven structural nucleation–relaxation) can be deduced for conducting polymers and CNTs from basic polymeric and electrochemical principles, not including any adjustable parameter.
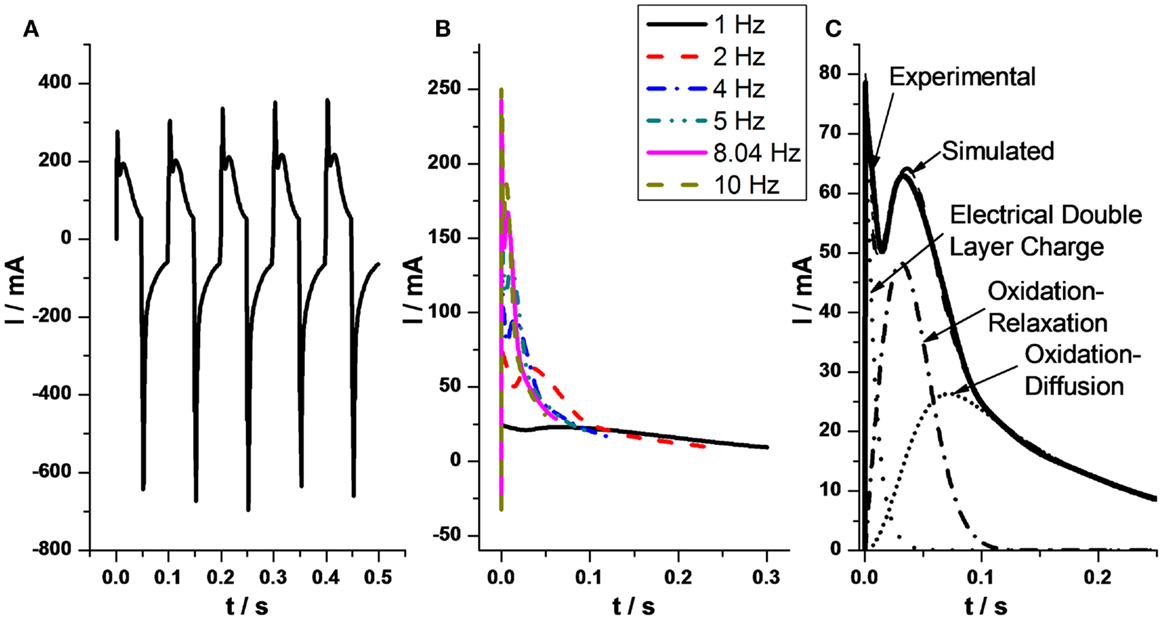
Figure 3. (A) Five consecutive anodic and cathodic chronoamperometric responses obtained from a SG–SWNT triple layer actuator submitted to ±2 V square potential waves at 10 Hz. (B) Anodic chronoamperometric responses from SG–SWNT actuator under different frequencies, from 1 to 10 Hz, of the square potential waves. (C) Experimental anodic chronoamperometric responses from SG–SWNT when the actuator was submitted to ±2 V square potential waves at a frequency of 2 Hz. Dotted line: capacitive charge of the electrical double layer (EDL). Dash-dotted line: oxidation under relaxation–nucleation kinetic control. Short dotted line: oxidation under diffusion kinetic control of the balancing counterions through the nanotube film. Dashed line: simulated responses obtained by addition of the three components. Reproduced from Gimenez et al. (2012), with permission from Elsevier.
The stretched exponential functions have been used for long time in physical and biological science to adjust responses from systems having a distribution of relaxation times due to different local environments, local orders, or comprising different molecular or structural lengths or dimensions (Lee et al., 2001; Otero and Boyano, 2003; Otero et al., 2004a; Funston et al., 2007; Lin et al., 2008; Otero and Martinez, 2011).
The initial sharp peak of the chronoamperometric responses from CNTs can be attributed to the charge of the EDL. This response is modeled by a stretched exponential function (Holzle et al., 1994). For electrochemical responses, the general stretched exponential function can be expressed as Eq. 7 (Funston et al., 2007; West et al., 2009):
where I is the current, I0 is the initial current, τ is the relaxation time, t is the elapsed time, and δ is the stretching coefficient.
When δ = 1, this equation corresponds to a Cottrell evolution of the current, occurring in absence of conformational relaxation control (Otero et al., 1997a). When the electrochemical response includes oxidation reactions, as Eq. 1, where the reaction rate is controlled by diffusion of the counterions through the CNTs film, the current passing through the electrode can be expressed as Eq. 8:
where Qd is the charge fraction consumed under reaction diffusion control. Compared with Eq. 7: I0 = bQd and τ = 1/b. Under those conditions (diffusion kinetic control), the empirical charge consumed at any reaction time, t, Q(t) after the potential step (obtained by integration of the chronoamperometric responses until that time) and the total charge of the electrochemical response are related by Eq. 9 (Otero et al., 1997a):
The apparent diffusion coefficient, D, of the counterions from the solution through the partially oxidized material is included by b through Eq. 10 (Otero et al., 2004b; Suarez et al., 2005):
where h is the thickness of the CNTs film.
The chronoamperometric responses obtained from CNTs shows, moreover, the first peak related to the charge of the EDL and the beginning of the oxidation under possible diffusion control, a second maximum (Figure 3B) related to the initial oxidation under nucleation–relaxation control of a packed structure of the film, followed by its oxidation completion under diffusion kinetic control. From basic physical–chemical principles, the two processes are described by Eq. 11, including two stretched functions (Otero et al., 1997a,b):
where Qr is the charge consumed by the oxidation–relaxation process (when the material is compacted, some additional energy is needed to relax the packed structure generating the free volume required to lodge balancing counterions coming from the solution by diffusion through the material). The coefficient a can be expressed as Eq. 12 (Otero et al., 1995):
where λ is the length of an elemental segment (average length of the CNTs here), N0 is the number of nuclei where the oxidation–relaxation is initiated after the anodic potential step under each defined experimental condition, τ0 is the pre-exponential factor of the relaxation time, A is the total film area, R is the universal gas constant (R = 8.314 J K−1 mol−1), T is the temperature and ΔH is given by Eq. 13:
with ΔH* is the conformational energy in the absence of any external electrical fields, zc is the cathodic polarization coefficient (charge consumed to compact by electrochemical reduction 1 mol of CNT segments), ηc is the cathodic overpotential, zr is the electrochemical relaxation coefficient (charge required to relax by electrochemical oxidation 1 mol of reduced and packed CNTs), and η is the anodic overpotential.
Equation 11 includes two different stretched exponential functions: the first term describes the oxidation under nucleation/relaxation kinetic control, Ir(t) = 2aQr texp(−at2); the second term describes the subsequent oxidation/swelling completion including counterion diffusion kinetic control. When the relaxation process is finished (the structure of the CNTs is swollen enough to allow the counterion’s diffusion), t′ becomes 0, and this second term can be expressed as Eq. 8.
Thus, the function describing all the full oxidation (chronoamperometric) response from the CNTs’ film is constituted by three stretched functions, as expressed by Eq. 14:
Each function quantifies (Figure 3C) a different process:
• Charge of the EDL: .
• Oxidation under nucleation/relaxation control:
• Oxidation-swelling completion under counterion’s diffusion kinetic control through the film of CNTs:
By addition of the three theoretical components the experimental response is overlapped.
At any oxidation time, each of the three components describes the fraction of current consumed to charge the EDL, by oxidation–relaxation of the compacted structure or for the oxidation of the relaxed material under diffusion kinetic control of the counterions, respectively. By integration of each of the functions the charge consumed by each of the simultaneous processes is attained. The total experimental charge, obtained by integration of the chronoamperometric response must be the addition of the theoretical (by integration of the three different attained functions) charge consumed by each of the three components.
In conclusion, the charge consumed by the capacitive component (the charge of the EDL) and the charge consumed by the two Faradaic components (oxidation–relaxation and oxidation–diffusion) of the electrochemical response can be identified and quantitatively separated (Gimenez et al., 2012). The capacitive percentage ranges, for the studied experimental conditions, between 8.6 and 12.2% and the faradic component between 91.4 and 87.8%.
Chronopotentiometric Results: Dual Actuating–Sensing Properties of CNTs
A unique characteristic of the chemical equilibrium is that after any perturbation (change of any experimental variable) responds trying to compensate its effect. This is the Le Chatelier principle (Smith, 2004). This principle has been translated outside the chemical equilibrium (Martinez and Otero, 2012, 2014; Otero et al., 2012b; Otero and Martinez, 2015): for films of CNTs including chemical reactions driven by a constant current (under constant reaction rate, Eq. 4) any external perturbation acting on the reaction rate shifts the potential evolution (the potential senses the perturbation) in order to adjust the new energetic requirements. Thus, if the electrochemical response of the CNTs includes a chemical component (Faradaic) the evolution of the material potential from the same initial (reduced or oxidized) state to the same final (oxidized or reduced, respectively) state must give quantitative information about the variables affecting the oxidation/reduction Eq. 1 rates: electrolyte concentration, temperature, or mechanical variables. This principle was checked for CNTs applying square current waves (chronopotentiometric responses), changing every time only one experimental variable, keeping the rest constant, as in the case of the kinetics experiments presented in the previous section.
Carbon nanotubes were subjected to consecutive square current waves (±0.5 mA) in aqueous solutions with different concentrations of TEABF4: 0.05, 0.1, 0.25, 0.5, 0.75, and 1M. The attained chronopotentiograms (evolution of the CNTs potential with time) show a strong influence of electrolyte concentration (Figure 4A). As expected for any chemical reaction, for a higher concentration of one of the reactants (electrolyte), the reaction becomes easier occurring at a lower potential under flow of the same current, that is, for the same reaction rate.
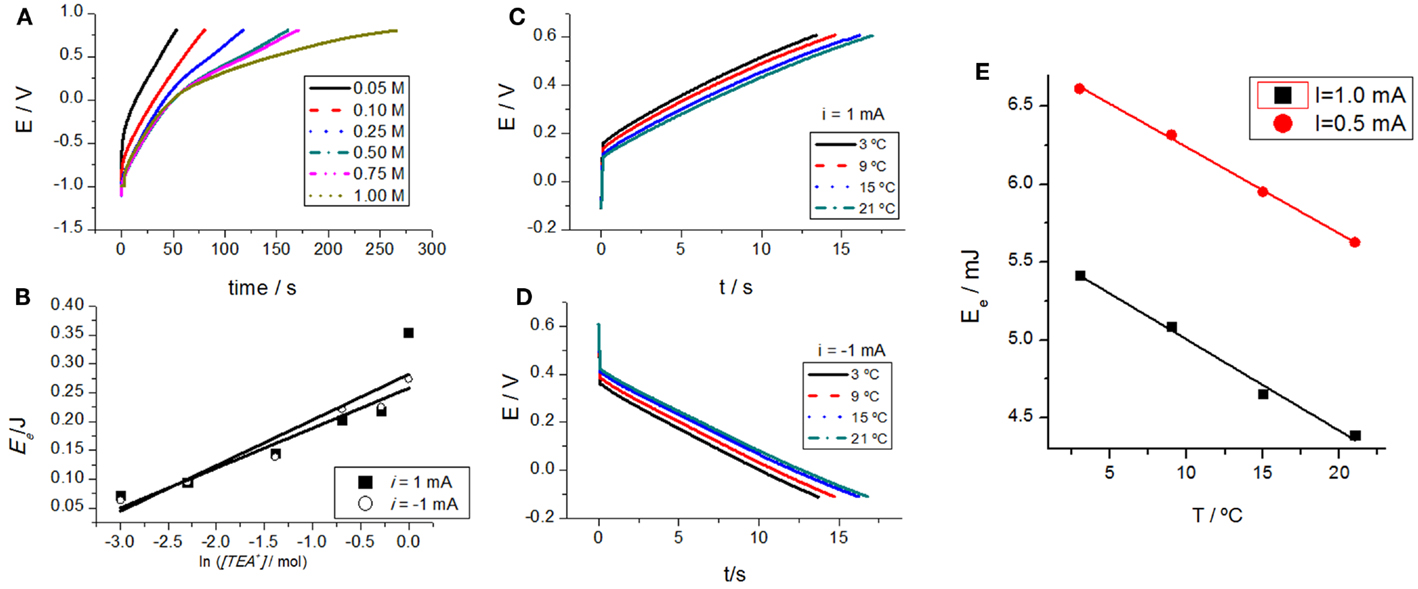
Figure 4. (A) Evolution of the CNT film potential in aqueous solutions with different concentrations of TEABF4: 0.05, 0.1, 0.25, 0.5, 0.75, and 1 M under flow of an anodic constant current of 0.5 mA. (B) Parallel evolution of the consumed electrical energy attained by integration of (A). (C) Chronopotentiometric responses in 0.1 M TEABF4 aqueous solution at different temperatures: 3, 9, 15, and 21°C under flow of 1 mA. (D) Chronopotentiometric responses in 0.1 M TEABF4 aqueous solution at different temperatures: 3, 9, 15, and 21°C under flow of −1 mA. (E) Consumed electrical energy after 13 s of current flow (after consumption of the same charge and for a constant concentration of active centers) at different temperatures under flow of different anodic constant currents: 1 or 0.5 mA. Reproduced from Martinez et al. (2012), with permission from Wiley-VCH.
The consumed electrical energy, U, is given by Eq. 15 (Beaty and Fink, 2013):
where E is the potential.
For chronopotentiometric experiments, Eq. 15 can be expressed as Eq. 16, where the applied current is constant:
where is the integral of each experimental chronopotentiometric response from the beginning of the current flow.
Thus, for the same oxidation state, after consumption of the same charge (Q = it), that is, after oxidation of the same number of active centers, the potential attained by the material, and the consumed electrical energy, follow a semilogarithmic dependence with the electrolyte concentration (Figure 4B). Figures 4A,B corroborate that the reactive material senses the electrolyte concentration while reacting.
The experimental procedure was repeated by changing the temperature for different experiments keeping the rest of experimental variables (consumed charges, applied currents, and electrolyte concentrations) constant. The material potential during oxidation and reduction changes with the experimental temperature, Figures 4C,D, respectively. The evolution of consumed electrical energy for a constant time (constant consumed charge) and different temperatures corroborates that the material, during reaction under flow of a constant current senses the working temperature (Figure 4E). The achieved potential or the consumed electrical energy, after a constant time of current flow, are the sensing magnitudes. The reacting material, and any device based on it, senses the working conditions. When CNTs take part, as active materials, of actuators, the actuator will sense working and surrounding conditions while working: this is a dual sensing–actuator system mimicking biological organs as haptic muscles. In summary, any electrochemical actuator based on CNTs and controlled by a constant current will sense through the device potential working temperature or electrolyte concentration variation: both sensing (potential or energy) and actuating (current) signals are present simultaneously in the two connecting wires while working.
Other Carbon-Based Materials
Similar electrochemical responses and subsequent conclusion to those here exposed were obtained from films of conducting polymers (Conzuelo et al., 2010; Otero et al., 2012a; Otero and Martinez, 2013a,b, 2015) or graphene (Martínez et al., 2012). The presence of chemical reactions gives for the empirical reaction rates the expected semilogarithmic or double-logarithmic relationships for the studied experimental variables. In addition, the potential, or the consumed electrical energy under flow of a constant current, senses any working conditions or external perturbation during the reaction, as it corresponds to any chemical or electrochemical reaction.
Capacitive, Reactive, and Structural Components: Final Remarks for Improving Electrochemical Devices and Products
We can conclude that electrochemical responses from films including CNTs change when the electrolyte concentration or the working temperature change, as expected for any chemical reaction. When the capacitive and the reactive component of the electrochemical response can be separated, as it occurs for chronoamperometric responses showing two maxima, the reactive component consumes over 80% of the involved charge. The electrochemical reaction drives swelling, shrinking, conformational relaxation, and conformational compaction structural changes in films of CNTs, or including CNTs. When any of those structural changes constitute the rate limiting process of the electrochemical reaction they also control the rate of the concomitant electrochemical application (actuator, supercapacitor, smart membrane, reactive conformational sensor, drug delivery, and so on).
On this way for the development of new devices based on the electrochemistry of CNTs, some preliminary optimization of the capacitive, Faradaic, and structural components of the electrochemical responses should be required. In particular, detecting which of the three components is the rate limiting process for each device will be useful for improving the response time, the energy efficiency, and the lifetime of the devices. Finally, the chemical nature of the electrochemical response should provide electrochemical devices based on CNTs with a unique biomimetic property: any of the devices will sense, while working, any physical or chemical property of the working or surrounding ambient variables acting on the reaction rate. This dual functionality is unique of the biological systems, as haptic muscles, without any parallel in present technological world.
Author Contributions
All authors have contributed to write the paper and revise it.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
Authors acknowledge financial support from the Spanish Government (MCINN) Project MAT2011-24973 and the Seneca Foundation project 19253/PI/14. JM acknowledges Spanish Education Ministry for a FPU grant (AP2010-3460).
References
Abdalla, S., Al-Marzouki, F., Al-Ghamdi, A. A., and Abdel-Daiem, A. (2015). Different technical applications of carbon nanotubes. Nanoscale Res. Lett. 10, 358. doi: 10.1186/s11671-015-1056-3
Arias-Pardilla, J., Otero, T. F., Blanco, R., and Segura, J. L. (2010a). Synthesis, electropolymerization and oxidation kinetics of an anthraquinone-functionalized poly(3,4-ethylenedioxythiophene). Electrochim. Acta 55, 1535–1542. doi:10.1016/j.electacta.2009.10.011
Arias-Pardilla, J., Walker, W., Wudl, F., and Otero, T. F. (2010b). Reduction and oxidation doping kinetics of an electropolymerized donor-acceptor low-bandgap conjugated copolymer. J. Phys. Chem. B 114, 12777–12784. doi:10.1021/jp1038865
Banks, C. E., Davies, T. J., Wildgoose, G. G., and Compton, R. G. (2005). Electrocatalysis at graphite and carbon nanotube modified electrodes: edge-plane sites and tube ends are the reactive sites. Chem. Commun. 829–841. doi:10.1039/b413177k
Bard, A. J., and Faulkner, L. R. (1980). Electrochemical Methods: Fundamentals and Applications. New York: Wiley.
Barisci, J. N., Wallace, G. G., and Baughman, R. H. (2000a). Electrochemical characterization of single-walled carbon nanotube electrodes. J. Electrochem. Soc. 147, 4580–4583. doi:10.1149/1.1394104
Barisci, J. N., Wallace, G. G., and Baughman, R. H. (2000b). Electrochemical studies of single-wall carbon nanotubes in aqueous solutions. J. Electroanal. Chem. 488, 92–98. doi:10.1016/S0022-0728(00)00179-0
Baughman, R. H., Cui, C. X., Zakhidov, A. A., Iqbal, Z., Barisci, J. N., Spinks, G. M., et al. (1999). Carbon nanotube actuators. Science 284, 1340–1344. doi:10.1126/science.284.5418.1340
Beaty, H. W., and Fink, D. G. (2013). Standard Handbook for Electrical Engineers, 16th Edn. New York: McGraw-Hill.
Bondavalli, P., Pribat, D., Schnell, J.-P., Delfaure, C., Gorintin, L., Legagneux, P., et al. (2012). Non-faradic carbon nanotube-based supercapacitors: state of the art analysis of all the main scientific contributions from 1997 to our days. Eur. Phys. J. Appl. Phys. 60, 10401. doi:10.1051/epjap/2012120242
Che, G. L., Lakshmi, B. B., Fisher, E. R., and Martin, C. R. (1998). Carbon nanotubule membranes for electrochemical energy storage and production. Nature 393, 346–349. doi:10.1038/30694
Chen, Y.-J., Zhu, C.-L., Xue, X.-Y., Shi, X.-L., and Cao, M.-S. (2008). High capacity and excellent cycling stability of single-walled carbon nanotube/SnO(2) core-shell structures as Li-insertion materials. Appl. Phys. Lett. 92, 223101. doi:10.1063/1.2937839
Chng, E. L. K., Poh, H. L., Sofer, Z., and Pumera, M. (2013). Purification of carbon nanotubes by high temperature chlorine gas treatment. Phys. Chem. Chem. Phys. 15, 5615–5619. doi:10.1039/c3cp50348h
Chopra, N., Wu, J., and Agrawal, P. (2015). Synthesis of nanoscale heterostructures comprised of metal nanowires, carbon nanotubes, and metal nanoparticles: investigation of their structure and electrochemical properties. J. Nanomater. 2015, 125970. doi:10.1155/2015/125970
Claye, A. S., Fischer, J. E., Huffman, C. B., Rinzler, A. G., and Smalley, R. E. (2000). Solid-state electrochemistry of the Li single wall carbon nanotube system. J. Electrochem. Soc. 147, 2845–2852. doi:10.1149/1.1393615
Conzuelo, L. V., Arias-Pardilla, J., Cauich-Rodríguez, J. V., Smit, M. A., and Otero, T. F. (2010). Sensing and tactile artificial muscles from reactive materials. Sensors 10, 2638–2674. doi:10.3390/s100402638
Dai, G. P., Liu, M., Wang, M. Z., and Cheng, H. M. (2002). Research progress of electrochemical hydrogen storage in carbon nanotubes. New Carbon Mater. 17, 70–74.
Du, H., Jiao, L., Wang, Q., Peng, W., Song, D., Wang, Y., et al. (2011). Structure and electrochemical properties of ball-milled co-carbon nanotube composites as negative electrode material of alkaline rechargeable batteries. J. Power Sources 196, 5751–5755. doi:10.1016/j.jpowsour.2010.11.145
Endo, M., Strano, M. S., and Ajayan, P. M. (2008). Potential applications of carbon nanotubes. Carbon Nanotubes 111, 13–61. doi:10.1007/978-3-540-72865-8_2
Eom, J., and Kwon, H. (2008). Improved lithium insertion/extraction properties of single-walled carbon nanotubes by high-energy ball milling. J. Mater. Res. 23, 2458–2466. doi:10.1557/JMR.2008.0291
Funston, A. M., Fadeeva, T. A., Wishart, J. F., and Castner, E. W. (2007). Fluorescence probing of temperature-dependent dynamics and friction in ionic liquid local environments. J. Phys. Chem. B 111, 4963–4977. doi:10.1021/jp068298o
Gao, B., Kleinhammes, A., Tang, X. P., Bower, C., Fleming, L., Wu, Y., et al. (1999). Electrochemical intercalation of single-walled carbon nanotubes with lithium. Chem. Phys. Lett. 307, 153–157. doi:10.1016/S0009-2614(99)00486-8
Ghosh, S., Gadagkar, V., and Sood, A. K. (2005). Strains induced in carbon nanotubes due to the presence of ions: Ab initio restricted Hatree-Fock calculations. Chem. Phys. Lett. 406, 10–14. doi:10.1016/j.cplett.2005.02.088
Gimenez, P., Mukai, K., Asaka, K., Hata, K., Oike, H., and Otero, T. F. (2012). Capacitive and faradic charge components in high-speed carbon nanotube actuator. Electrochim. Acta 60, 177–183. doi:10.1016/j.electacta.2011.11.032
Gupta, S., Hughes, M., Windle, A. H., and Robertson, J. (2004). Charge transfer in carbon nanotube actuators investigated using in situ Raman spectroscopy. J. Appl. Phys. 95, 2038–2048. doi:10.1063/1.1641518
Hekmat, F., Sohrabi, B., Rahmanifar, M. S., and Vaezi, M. R. (2014). Supercapacitive properties of coiled carbon nanotubes directly grown on nickel nanowires. J. Mater. Chem. A 2, 17446–17453. doi:10.1039/c4ta03022b
Hoefer, M., and Bandaru, P. (2013). Electrochemical characteristics of closely spaced defect tuned carbon nanotube arrays. J. Electrochem. Soc. 160, H360–H367. doi:10.1149/2.122306jes
Holzle, M., Retter, U., and Kolb, D. (1994). The kinetics of structural-changes in Cu and layers on Au(111). J. Electroanal. Chem. 371, 101–109. doi:10.1016/0022-0728(93)03235-H
Jiang, H., Lee, P. S., and Li, C. (2013). 3D carbon based nanostructures for advanced supercapacitors. Energy Environ. Sci. 6, 41–53. doi:10.1039/c2ee23284g
Kiamahalleh, M. V., Zein, S. H. S., Najafpour, G., Abd Sata, S., and Buniran, S. (2012). Multiwalled carbon nanotubes based nanocomposites for supercapacitors: a review of electrode materials. Nano 7, 1230002. doi:10.1142/S1793292012300022
Landi, B. J., Ganter, M. J., Cress, C. D., DiLeo, R. A., and Raffaelle, R. P. (2009). Carbon nanotubes for lithium ion batteries. Energy Environ. Sci. 2, 638–654. doi:10.1039/b904116h
Lee, K. C. B., Siegel, J., Webb, S. E. D., Leveque-Fort, S., Cole, M. J., Jones, R., et al. (2001). Application of the stretched exponential function to fluorescence lifetime imaging. Biophys. J. 81, 1265–1274. doi:10.1016/S0006-3495(01)75784-0
Li, J., Cassell, A., Delzeit, L., Han, J., and Meyyappan, M. (2002). Novel three-dimensional electrodes: electrochemical properties of carbon nanotube ensembles. J. Phys. Chem. B 106, 9299–9305. doi:10.1021/jp021201n
Li, X., and Wei, B. (2013). Supercapacitors based on nanostructured carbon. Nano Energy 2, 159–173. doi:10.1016/j.nanoen.2012.09.008
Lin, F., Wang, Y., and Lonergan, M. (2008). Ion transport in polyacetylene ionomers. J. Appl. Phys. 104, 103517. doi:10.1063/1.3026732
Liu, J., Cao, G., Yang, Z., Wang, D., Dubois, D., Zhou, X., et al. (2008). Oriented nanostructures for energy conversion and storage. ChemSusChem 1, 676–697. doi:10.1002/cssc.200800087
Lyon, J. L., and Stevenson, K. J. (2007). Anomalous electrochemical dissolution and passivation of iron growth catalysts in carbon nanotubes. Langmuir 23, 11311–11318. doi:10.1021/la7019186
Madden, J. D. W., Barisci, J. N., Anquetil, P. A., Spinks, G. M., Wallace, G. G., Baughman, R. H., et al. (2006). Fast carbon nanotube charging and actuation. Adv. Mater. 18, 870–873. doi:10.1002/adma.200502136
Majeed, S., Zhao, J., Zhang, L., Anjum, S., Liu, Z., and Xu, G. (2013). Synthesis and electrochemical applications of nitrogen-doped carbon nanomaterials. Nanotechnol. Rev. 2, 615–635. doi:10.1515/ntrev-2013-0007
Martinez, J. G., and Otero, T. F. (2012). Biomimetic dual sensing-actuators: theoretical description. Sensing electrolyte concentration and driving current. J. Phys. Chem. B 116, 9223–9230. doi:10.1021/jp302931k
Martinez, J. G., and Otero, T. F. (2014). Mechanical awareness from sensing artificial muscles: experiments and modeling. Sens. Actuators B Chem. 195, 365–372. doi:10.1016/j.snb.2013.12.099
Martínez, J. G., Otero, T. F., Bosch-Navarro, C., Coronado, E., Martí-Gastaldo, C., and Prima-Garcia, H. (2012). Graphene electrochemical responses sense surroundings. Electrochim. Acta 81, 49–57. doi:10.1016/j.electacta.2012.07.037
Martinez, J. G., Sugino, T., Asaka, K., and Otero, T. F. (2012). Electrochemistry of carbon nanotubes: reactive processes, dual sensing-actuating properties and devices. ChemPhysChem 13, 2108–2114. doi:10.1002/cphc.201100931
Mukai, K., Asaka, K., Hata, K., Fernandez Otero, T., and Oike, H. (2011). High-speed carbon nanotube actuators based on an oxidation/reduction reaction. Chem. Eur. J. 17, 10965–10971. doi:10.1002/chem.201003641
Myung, S.-T., Amine, K., and Sun, Y.-K. (2015). Nanostructured cathode materials for rechargeable lithium batteries. J. Power Sources 283, 219–236. doi:10.1016/j.jpowsour.2015.02.119
Naoi, K., Naoi, W., Aoyagi, S., Miyamoto, J., and Kamino, T. (2013). New generation “nanohybrid supercapacitor”. Acc. Chem. Res. 46, 1075–1083. doi:10.1021/ar200308h
Ni, J., Zhang, L., Fu, S., Savilov, S. V., Aldoshin, S. M., and Lu, L. (2015). A review on integrating nano-carbons into polyanion phosphates and silicates for rechargeable lithium batteries. Carbon 92, 15–25. doi:10.1016/j.carbon.2015.02.047
Otero, T., Boyano, I., Cortes, M., and Vazquez, G. (2004a). Nucleation, non-stoiquiometry and sensing muscles from conducting polymers. Electrochim. Acta 49, 3719–3726. doi:10.1016/j.electacta.2004.01.085
Otero, T. F., Marquez, M., and Suarez, I. J. (2004b). Polypyrrole: diffusion coefficients and degradation by overoxidation. J. Phys. Chem. B 108, 15429–15433. doi:10.1021/jp0490608
Otero, T., Grande, H., and Rodriguez, J. (1995). A new model for electrochemical oxidation of polypyrrole under conformational relaxation control. J. Electroanal. Chem. 394, 211–216. doi:10.1016/0022-0728(95)04033-K
Otero, T. F., and Abadias, R. (2007). Poly(3-methylthiophene) oxidation under chemical control. Rate coefficients change with prepolarization potentials of reduction. J. Electroanal. Chem. 610, 96–101. doi:10.1016/j.jelechem.2007.06.019
Otero, T. F., and Abadias, R. (2008). Potentiostatic oxidation of poly(3-methylthiophene): influence of the prepolarization time at cathodic potentials on the kinetics. J. Electroanal. Chem. 618, 39–44. doi:10.1016/j.jelechem.2008.02.019
Otero, T. F., Arias-Pardilla, J., and Chermak, E. (2010). Reactive polymer films polypyrrole oxidation kinetics in aqueous solution. Synth. Met. 160, 425–431. doi:10.1016/j.synthmet.2009.11.024
Otero, T. F., and Boyano, I. (2003). Nucleation and nonstoichiometry in electrochromic conducting polymers. ChemPhysChem 4, 868–872. doi:10.1002/cphc.200300640
Otero, T. F., and Caballero Romero, M. (2010). Conformational energy from the oxidation kinetics of poly(3,4-ethylenedioxythiophene) films. Polym. Int. 59, 329–336. doi:10.1002/pi.2774
Otero, T. F., and Garcia de Otazo, J. M. (2009). Polypyrrole oxidation: kinetic coefficients, activation energy and conformational energy. Synth. Met. 159, 681–688. doi:10.1016/j.synthmet.2008.12.017
Otero, T. F., and Grande, H. (1996). Thermally enhanced conformational relaxation during electrochemical oxidation of polypyrrole. J. Electroanal. Chem. 414, 171–176. doi:10.1016/0022-0728(96)04686-4
Otero, T. F., Grande, H. J., and Rodriguez, J. (1997a). Reinterpretation of polypyrrole electrochemistry after consideration of conformational relaxation processes. J. Phys. Chem. B 101, 3688–3697. doi:10.1021/jp9630277
Otero, T. F., Grande, H., and Rodriguez, J. (1997b). Role of conformational relaxation on the voltammetric behavior of polypyrrole. Experiments and mathematical model. J. Phys. Chem. B 101, 8525–8533. doi:10.1021/jp9714633
Otero, T. F., and Martinez, J. G. (2011). Activation energy for polypyrrole oxidation: film thickness influence. J. Solid State Electrochem. 15, 1169–1178. doi:10.1007/s10008-010-1170-1
Otero, T. F., and Martinez, J. G. (2013a). Biomimetic intracellular matrix (ICM) materials, properties and functions. Full integration of actuators and sensors. J. Mater. Chem. B 1, 26–38. doi:10.1039/C2TB00176D
Otero, T. F., and Martinez, J. G. (2013b). Structural and biomimetic chemical kinetics: kinetic magnitudes include structural information. Adv. Funct. Mater. 23, 404–416. doi:10.1002/adfm.201200719
Otero, T. F., and Martinez, J. G. (2015). Physical and chemical awareness from sensing polymeric artificial muscles. Experiments and modeling. Prog. Polym. Sci. 44, 62–78. doi:10.1016/j.progpolymsci.2014.09.002
Otero, T. F., Martinez, J. G., and Arias-Pardilla, J. (2012a). Biomimetic electrochemistry from conducting polymers. A review: artificial muscles, smart membranes, smart drug delivery and computer/neuron interfaces. Electrochim. Acta 84, 112–128. doi:10.1016/j.electacta.2012.03.097
Otero, T. F., Sanchez, J. J., and Martinez, J. G. (2012b). Biomimetic dual sensing-actuators based on conducting polymers. Galvanostatic theoretical model for actuators sensing temperature. J. Phys. Chem. B 116, 5279–5290. doi:10.1021/jp300290s
Otero, T. F., and Santos, F. (2008). Polythiophene oxidation: rate coefficients, activation energy and conformational energies. Electrochim. Acta 53, 3166–3174. doi:10.1016/j.electacta.2007.10.072
Rahman, M. M., and Jeon, I. C. (2007). Studies of electrochemical behavior of SWNT-film electrodes. J. Braz. Chem. Soc. 18, 1150–1157. doi:10.1590/S0103-50532007000600008
Remy, E., Cahen, S., Malaman, B., Ghanbaja, J., Bellouard, C., Medjahdi, G., et al. (2015). Quantitative investigation of mineral impurities of HiPco SWCNT samples: chemical mechanisms for purification and annealing treatments. Carbon N. Y. 93, 933–944. doi:10.1016/j.carbon.2015.06.015
Riemenschneider, J., Opitz, S., Sinapius, M., and Monner, H. P. (2009a). Modeling of carbon nanotube actuators: part II – mechanical properties, electro mechanical coupling and validation of the model. J. Intell. Mater. Syst. Struct. 20, 253–263. doi:10.1177/1045389X08092274
Riemenschneider, J., Opitz, S., Sinapius, M., and Monner, H. P. (2009b). Modeling of carbon nanotube actuators: part I – modeling and electrical properties. J. Intell. Mater. Syst. Struct. 20, 245–250. doi:10.1177/1045389X08092275
Ruch, P. W., Koetz, R., and Wokaun, A. (2009). Electrochemical characterization of single-walled carbon nanotubes for electrochemical double layer capacitors using non-aqueous electrolyte. Electrochim. Acta 54, 4451–4458. doi:10.1016/j.electacta.2009.03.022
Ruiz, V., Roldan, S., Villar, I., Blanco, C., and Santamaria, R. (2013). Voltage dependence of carbon-based supercapacitors for pseudocapacitance quantification. Electrochim. Acta 95, 225–229. doi:10.1016/j.electacta.2013.02.056
Simon, P., and Gogotsi, Y. (2013). Capacitive energy storage in nanostructured carbon-electrolyte systems. Acc. Chem. Res. 46, 1094–1103. doi:10.1021/ar200306b
Suarez, I. J., Otero, T. F., and Marquez, M. (2005). Diffusion coefficients in swelling polypyrrole: ESCR and Cottrell models. J. Phys. Chem. B 109, 1723–1729. doi:10.1021/jp046051q
Terrones, M. (2003). Science and technology of the twenty-first century: synthesis, properties and applications of carbon nanotubes. Annu. Rev. Mater. Res. 33, 419–501. doi:10.1146/annurev.matsci.33.012802.100255
Wang, G., Zhang, L., and Zhang, J. (2012). A review of electrode materials for electrochemical supercapacitors. Chem. Soc. Rev. 41, 797–828. doi:10.1039/c1cs15060j
Wang, X., Wang, K., Meng, Q., and Wang, D. (2014). Reactivity of the interior surface of (5,5) single-walled carbon nanotubes with and without a Stone-Wales defect. Comput. Theor. Chem. 1027, 160–164. doi:10.1016/j.comptc.2013.11.013
Wang, Y., Zeng, J., Li, J., Cui, X., Al-Enizi, A. M., Zhang, L., et al. (2015). One-dimensional nanostructures for flexible supercapacitors. J. Mater. Chem. A 3, 16382–16392. doi:10.1039/c5ta03467a
West, B. J., Otero, T. F., Shapiro, B., and Smela, E. (2009). Chronoamperometric study of conformational relaxation in PPy(DBS). J. Phys. Chem. B 113, 1277–1293. doi:10.1021/jp8058245
Wildgoose, G. G., Banks, C. E., Leventis, H. C., and Compton, R. G. (2006). Chemically modified carbon nanotubes for use in electroanalysis. Mikrochim Acta 152, 187–214. doi:10.1007/s00604-005-0449-x
Yan, J., Wang, Q., Wei, T., and Fan, Z. (2014). Recent advances in design and fabrication of electrochemical supercapacitors with high energy densities. Adv. Energy Mater. 4, 1300816. doi:10.1002/aenm.201300816
Yiran, K., Feng, C., Hongyuan, C., Minghai, C., Rui, Z., and Qingwen, L. (2014). Carbon nanotube/graphene hybrid nanostructures and their application in supercapacitors. Prog. Chem. 26, 1562–1569. doi:10.7536/PC140347
Yun, Y. H., Shanov, V., Schulz, M. J., Narasimhadevara, S., Subramaniam, S., Hurd, D., et al. (2005). Development of novel single-wall carbon nanotube-epoxy composite ply actuators. Smart Mater. Struct. 14, 1526–1532. doi:10.1088/0964-1726/14/6/045
Zhai, Y., Dou, Y., Zhao, D., Fulvio, P. F., Mayes, R. T., and Dai, S. (2011). Carbon materials for chemical capacitive energy storage. Adv. Mater. 23, 4828–4850. doi:10.1002/adma.201100984
Zhang, H., Cao, G., and Yang, Y. (2009). Carbon nanotube arrays and their composites for electrochemical capacitors and lithium-ion batteries. Energy Environ. Sci. 2, 932–943. doi:10.1039/b906812k
Keywords: carbon nanotubes, Faradaic processes, capacitive processes, carbonaceous materials, electrochemical responses
Citation: Otero TF, Martinez JG and Asaka K (2016) Faradaic and Capacitive Components of the CNT Electrochemical Responses. Front. Mater. 3:3. doi: 10.3389/fmats.2016.00003
Received: 22 October 2015; Accepted: 21 January 2016;
Published: 03 February 2016
Edited by:
David Gendron, Istituto Italiano di Tecnologia, ItalyReviewed by:
Thiagarajan Soundappan, Washington University in St. Louis, USAIlkwon Oh, Korea Advanced Institute of Science and Technology, South Korea
Copyright: © 2016 Otero, Martinez and Asaka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Toribio F. Otero, dG9yaWJpby5mb3Rlcm9AdXBjdC5lcw==
 Toribio F. Otero
Toribio F. Otero Jose G. Martinez
Jose G. Martinez Kinji Asaka
Kinji Asaka