- 1Otto Schott Institute of Materials Research, Friedrich Schiller University Jena, Jena, Germany
- 2Institute of Non-Metallic Materials, Clausthal University of Technology, Clausthal-Zellerfeld, Germany
Introducing an interaction parameter γ, we implement modifier interaction and the mixed-alkali effect into bond constraint theory and apply this extension for simplistic property prediction on ternary phosphate glasses. The severity of the mixed-alkali effect results from the interplay of two simultaneous contributions: bond constraints on the modifier species soften and stiffen with decreasing and increasing γ, respectively. When the modifier size is not too dissimilar, the decrease in γ reflects that the alkali ions can easily migrate between different sites, forcing the network to continuously reaccommodate for any subsequent distortions. With increasing size difference, migration becomes increasingly difficult without considerable network deformation. This holds even for smaller ions, where the sluggish dynamics of the larger constituent result in blocking of the fast ion movement, leading to the subsequent increase in γ. Beyond a certain size difference in the modifier pair, a value of γ exceeding unity may indicate the presence of steric hindrance due to the large surrounding modifiers impeding the phosphate network to reaccommodate deformation.
Introduction
The bond constraint theory (BCT), as originally formulated by Phillips (1979) and Phillips and Thorpe (1985), rationalizes the glass structure in terms of a simple “ball-and-stick” network. It uses topological relationships based on the number of linear and angular constraints found on the first coordination shell of each atom within the glass network. More recently, Gupta and Mauro (2009) and Mauro et al. (2009) introduced the concept of temperature-dependent constraints, based on previous work by Naumis (2005, 2006), taking into account the temperature dependence of configurational entropy and, hence, the number of bond constraints. This allowed for applying constraint counting to calculate the compositional trends of properties, such as the glass transition temperature (Gupta and Mauro, 2009; Mauro et al., 2009; Smedskjaer et al., 2010b, 2011; Fu and Mauro, 2013; Jiang et al., 2013; Rodrigues and Wondraczek, 2013, 2014; Hermansen et al., 2014a; Rodrigues et al., 2014), fragility (Gupta and Mauro, 2009; Mauro et al., 2009; Hermansen et al., 2014a), and surface hardness (Smedskjaer et al., 2010a,c, 2011; Wondraczek et al., 2011; Smedskjaer, 2014). While useful applications of the BCT need detailed structural information, the strength of this approach lies in its simplicity, as only the knowledge of the components’ first shell coordination number and a reasonable guess about the relative strength of the constraints considered are required for relatively accurate property prediction. However, the BCT is not without problems, which start already with its basic assumptions (Rodrigues and Wondraczek, 2015) as how to incorporate structural influences beyond the short range (Rodrigues and Wondraczek, 2013). In glass science, one such example is the so-called “mixed-alkali effect” (MAE), where the mixture of two alkali species results in a non-linear variation of several properties, such as ionic conductivity, glass transition temperature, internal friction, and volumetric relaxation (Bunde et al., 2004; Changstrom and Sidebottom, 2008). Here, we, therefore, aim to expand the current understanding of the BCT toward incorporation of such non-linear interaction terms, choosing the example of mixed-alkali phosphate glasses (Fu and Mauro, 2013; Hermansen et al., 2014a; Rodrigues and Wondraczek, 2014; Rodrigues et al., 2014). We demonstrate how appropriate interaction terms can be used to incorporate the MAE into BCT so as to enable accurate calculation of the glass transition temperature. However, we also show that in doing so, the empiricism of the approach is further highlighted, because the physical meaning of the required fitting parameters is presently not developed.
Modifier Constraints
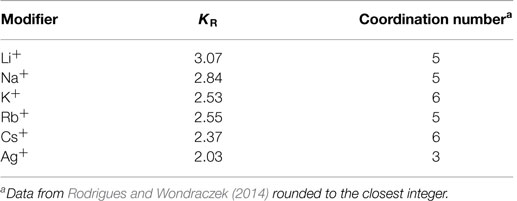
The BCT was originally developed and applied to chalcogenide glasses, which are particularly suitable to the “ball-and-stick” analogy, since the atoms are connected by predominantly covalent bonds with very well-defined first coordination shells, similar to the bonds between oxygen and the network formers in most oxide glasses. It was previously assumed that the number of constraints associated with each modifier atom within the glass network depends exclusively on its first coordination shell (Fu and Mauro, 2013). However, we have later shown that while the coordination number influences the number of constraints, the actual interaction strength is mainly a function of the electrostatic forces between the modifier and the non-bridging oxygens (Rodrigues and Wondraczek, 2014), in accordance with the observations of Eisenberg et al. (1966) several decades ago. The interactions between the non-bridging oxygens and the network modifiers have a strongly ionic character. This requires adaptations to the “ball-and-stick” model due to the lower directionality and longer ranges characteristic of the Coulombic interactions. This adaptation was achieved by the introduction of the characteristic “constraint strengths” to the model, for which there are now two ways of implementation: in our previous work (Rodrigues and Wondraczek, 2014; Rodrigues et al., 2014), we argue that the “constraint strength” defined as the ratio between the number of constraints each modifier R adds to the system (KR) and its coordination number (CNR) represents the number of constraints each modifier/non-bridging oxygen bond adds to the system, with the caveat that the numbers are relative to the absolute strength of all other constraints which are assumed to be equal to unity. Alternatively, Hermansen et al. (2014b) argue that the “constraint strength” (qγ in this notation) also represents the fraction of the modifier constraints that are still intact at the temperature in question. Both approaches result in equivalent glass transition temperature predictions for the studied binary phosphate glasses and both “constraint strength” values are linearly dependent on the Coulombic forces between the modifiers and non-bridging oxygens (Hermansen et al., 2014b; Rodrigues and Wondraczek, 2014). In this work, we will be using the former interpretation for two main reasons: first, it provides internal consistency on how the modifier constraints are treated, being considered either completely broken or completely intact, the same as all other constraints present in the system. Second, and more importantly, the distribution of modifier sites according to the calculations from Hermansen et al. (2014b) does not seem to correspond to experimental data. According to Hermansen et al. (2014b), the number of modifier constraints is given by 2 × XR(x) for x ≤ xcr and CNR × XR(x − xcrit) + 2 × XR(xcrit) for x > xcrit, where XR(x) is the modifier’s molar fraction, x is the compositional variable as in xR2O × (1 − x)P2O5 and xcrit is Hoppe’s critical composition (xcrit = ν/CNR, with the modifier valency ν) (Hoppe, 1996), above which the number of double-bonded oxygens is not enough to fully coordinate the modifier ions, which in consequence begin to share non-bridging oxygens and effectively repolymerize the phosphate network. One can see that according to these equations, even at the metaphosphate composition (x = 0.5), there would still be a finite number of modifiers that should be surrounded by double-bonded oxygens since 2 × R(xcrit) > 0, but from 31P NMR measurements, it is known that at the metaphosphate composition there are no (or almost no) Q3 groups and, therefore, double-bonded oxygens (Brow, 2000) and also NMR from the modifiers does not show evidence for more than one site (Schneider et al., 2013). On the other hand, for this study, the values of constraints per modifier (KR) as they are listed in Rodrigues and Wondraczek (2014) were recalculated, as the previous calculation used an inconsistent counting of the phosphate network constraints (Hermansen et al., 2014a). The final values of KR are shown in Table 1.
Bond Constraint Modeling of the Mixed-Alkali Metaphosphates
Continuous investigation on the nature of the MAE over the last 30 years has uncovered convincing evidence that the structural basis for this effect lies in the “mismatch effect” (Angell, 1990, 1992; Huang and Cormack, 1992; Hunt, 1997; Maass, 1999; Adams and Swenson, 2002; Fang et al., 2003; Bunde et al., 2004; Hall et al., 2004; Ingram et al., 2006; Puls and Eckert, 2006; Changstrom and Sidebottom, 2008; Dieterich and Maass, 2009; Dyre et al., 2009), as described by the dynamic structure model (DSM) of Bunde et al. (2004) and Ingram and Roling (2003). A simplified description of the model goes as follows: in a single alkali glass, the modifiers A reside in sites that match their requirements for coordination number and distance between the modifier and the non-bridging oxygens. The diffusion of such ions does not require large rearrangements from the glassy network, since all modifier sites are similar. However, the addition of a second modifier B to this same glass results in the presence of two different types of modifier sites, and while it remains possible for the modifiers to jump from similar to similar sites, there is also the possibility of jumps between dissimilar sites, especially as the ratio of A/B cations approaches unity. Ingram and Roling (2003) argue that the motion of cations to dissimilar sites causes the network to reconfigure itself so as to minimize the distortions caused by the presence of an A atom on a B site (or a B atom on a A site). If the cations are statistically distributed on the glass structure, one would expect that at the molar ratio of A/B of unity, the probability of the modifiers to jump to dissimilar sites is maximized, leading to an increased flexibility of the glassy network and the often observed depression of the glass transition temperature at compositions close or at A/B = 1.
From the mentioned concepts, we can assume that the number of constraints a modifier A adds to the glass network depends not only on its first coordination shell, comprised solely by non-bridging oxygens in the case of the phosphate glasses we are focusing on, but also on the neighboring sites the modifier can access. Therefore, the number of constraints depends not only on how strongly the modifiers are bonded to the non-bridging oxygens but also on how often they jump to surrounding modifier sites. This does not affect the calculated values shown in Table 1, because for binary metaphosphate glasses the number of constraints already takes into account the movement of the modifier to sites previously occupied by the same modifier (modifier A jumping from an A site to another A site).
Considering a mixed-alkali metaphosphate glass of composition yA2O × (0.5 − y)B2O × 0.5P2O5, the number of constraints that the modifiers add to the network (nM) can be written as:
where nA and nB are the number of constraints the cations A and B add to the network.
According to Rodrigues and Wondraczek (2014) and Rodrigues et al. (2014), nA and nB are a function of the number of constraints per modifier (KR) and their molar fraction (XR). The weakening of the modifier constraints due to the presence of cations in dissimilar sites is modeled with the addition of the term TR. One must note that this should only apply to the sites the modifier in question can effectively access, or, in other words, the term TR should only modify the number of constraints of cross-linking sites; therefore, the use of mixed-metaphosphate glasses simplifies the calculations, since, at this composition, all modifier sites are cross-linking or, alternatively, no modifier exists in isolated sites (Rodrigues et al., 2014), so Eq. 1 can be written as:
where TA is defined as:
CNA is the modifier’s coordination number (or closest integer), is the probability of finding an A site with CNA−i A atoms and i B atoms surrounding it and GCNA−i,i is defined as:
Here, γAA and γAB are factors that illustrate how the constraints are changed as the modifiers migrate to neighboring sites that are either the same as the original one, or different from the original one. γAA is fixed at unity, because there is no change to the constraint strength as the modifiers move to similar sites, as argued previously. If the modifiers are homogeneously distributed throughout the glassy network, then the probabilities of finding the different sites can be calculated via a simple binomial distribution (Eq. 5), akin connections between Q2 and Q3 groups (Alam and Brow, 1998; Alam et al., 2000).
So, the number of constraints the modifier A adds to the network can be written as:
As γAA = 1:
Rearranging Eq. 8, we get:
with
which can be rewritten as:
If
Substituting Eq. 12 for both A and B cations in Eq. 1 yields:
Assuming that γAB = γBA = γ, we have that:
or,
Equation 17 presents an important formulation, because it states that the number of constraints the modifiers add to the glassy network is linearly proportional to , the quantities that can be calculated with knowledge of the glass composition and the coordination number of the modifiers in question. In order to test the applicability of Eq. 17, we took glass transition temperature data for Li–Na, Li–Ag, Li–K, Li–Rb, and Li–Cs metaphosphate glasses from the literature (Eisenberg and Saito, 1966; Denoyelle et al., 1990; Doreau and Robert, 1991; Green et al., 1999; Sidebottom et al., 1999; Bandaranayake et al., 2002; Changstrom and Sidebottom, 2008; Hall et al., 2009; Tsuchida et al., 2012), since it has been shown by NMR measurements that there is no modifier clustering (Schneider et al., 2013), which we assumed in our derivation. Noteworthy, the present approach, therefore, cannot be used for analyzing glasses where the modifier distribution shows a pronounced divergence from random mixture, such as Na–K, Na–Rb, or Na–Cs mixed-metaphosphate glasses (Tsuchida et al., 2012).
Results and Discussion
Figure 1 shows the plots of as a function of for the five aforementioned glass systems, whereas Figure 2 shows the parameters from the linear regression of the data as a function of the difference in atomic radius between both modifiers. It should be noted that while the expected linear behavior is observed for all glasses, there is some scatter especially on Figures 1C,D, mainly because there are fewer datasets available for the Li–Rb and Li–Cs mixed metaphosphates, so that the number of constraints on Table 1 are not exactly representative.
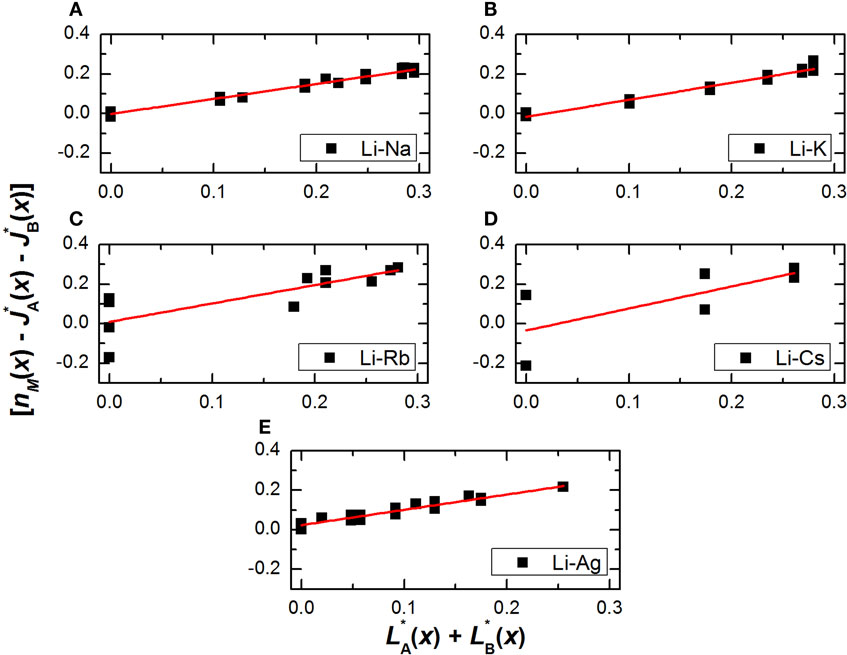
Figure 1. Plots of for mixed Li–Na (A), Li–K (B), Li–Rb (C), Li–Cs (D), and Li–Ag (E), metaphosphate glasses. The straight line shows the linear regression of the plotted data.
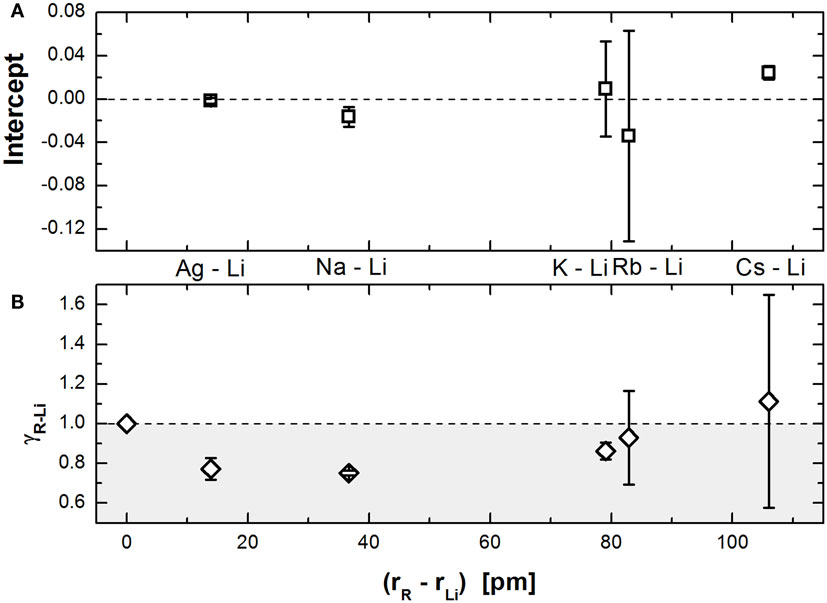
Figure 2. Parameters of the linear regressions [intercept (A) and slope γ (B)] shown in Figure 1 plotted as a function of the difference between the radius of the modifier R and Li.
Figure 2A shows that the intercept is very close to 0, practically independent of the pair of modifiers, while the value of γ (Figure 2B) shows an interesting dependence on the modifier size difference. The minimum present at size differences around 40 pm seems to indicate that the severity of the MAE results from the interplay of two simultaneous responses: one that softens the constrains on mixed sites and another that stiffens them (decreasing and increasing γ, respectively). When the modifier size is not too dissimilar, the net decrease in γ reflects that the alkali ions can easily move to different sites, forcing the network to continuously reaccommodate itself for the distortions caused by the presence of the modifiers in different sites. As the size difference increases, it becomes increasingly difficult for the modifiers to reach sites smaller than themselves without considerable network deformation, up to a point where the larger ions are bound to jump only to their own sites as they do not fit inside the others. So, even if the smaller ions can easily move between their own sites and the larger sites, the sluggish dynamics of the larger ions block the movement of the faster ions, decreasing the amount of reaccommodation the network suffers and subsequently increasing γ.
Another very interesting feature on Figure 2B is that beyond a certain size difference (roughly between 85 and 115 pm), the value of γ becomes greater than unity. This effectively means that the constraints would be stiffer in mixed sites, in contrast with what is expected from the current theoretical understanding. We suggest that this effect happens due to the larger ions sterically hindering the phosphate network. This is important because Ingram and Roling (2003) argue that the flexibility of the network, which allows for it to rearrange itself as the ions move in and out of dissimilar sites, is the rationale behind the observed decrease on the constraints.
These results highlight some of the advantages and disadvantages of using the BCT to model the glass transition temperature of oxide glasses. It is definitely advantageous that the theory is flexible enough to be easily modified to account for non-linear effects, such as the repolymerization of the phosphate network and the MAE. It is also simple enough so that almost any result can be adapted and remain self consistent. The analysis developed by Rodrigues et al. (2014) and this present paper can be used in conjunction to model the glass transition of a ternary phosphate system with knowledge of the coordination number of the two modifiers and the glass transition of only four compositions: vitreous phosphorus, both binary metaphosphates, and the A/B = 1 mixed metaphosphate (Figure 3 for the Li–Na metaphosphate system). This is a very quick and effortless way to generate the complete ternary diagram with a minimum of four glass transition temperature measurements. On the other hand, the BCT does not provide the tools to allow for the calculation of the values of constraint strength and γ, so, while they tie in reasonably well with some material properties, in order to use the correct values, one must always resort to use experimental data. Another open question is whether the trend observed in Figure 2 is valid for all modifier pairs and all other glass-forming oxides (such as silicates, borates, and germanates), or if the values of γ depend on the network, the modifiers are embedded within, much like the values of the constraint strength (Rodrigues and Wondraczek, 2015); or if they also depend on the pair of modifiers in question, meaning that the data points for mixed Na–R metaphosphate glasses would be shifted from the Li–R and so on.
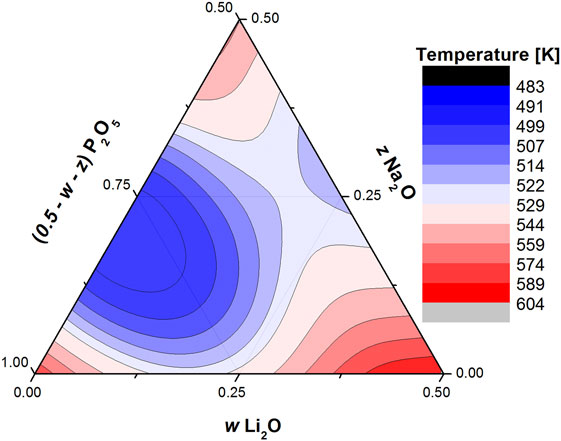
Figure 3. Ternary diagram showing the calculated glass transition temperatures glasses within the wLi2O × zNa2O × (1 − w − z)P2O5 with 0 ≤ (w + z) ≤ 0.5 using the proper values of constraint strength and γ.
Conclusion
We showed that the BCT can be extended to model the glass transition temperature of mixed-alkali metaphosphates and that the “mixed-alkali effect” can be parameterized with the addition of a single variable γ, which can be calculated with the knowledge of the coordination numbers of the two modifiers and the glass transition temperatures of the two binary metaphosphate glasses and the A/B = 1 composition. The reported results follow the same pattern of other BCT applications, showing good agreement between model and experimental data with few fitting parameters. But BCT does not present a way of estimating the fitting parameters ab initio, and their physical meaning is presently not developed.
Author Contributions
This manuscript was written through the contributions of all authors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
Financial support by the German Science Foundation through its priority program SPP 1594 (project no. WO 1220/10-1) is gratefully acknowledged.
References
Adams, S., and Swenson, J. (2002). Bond valence analysis of transport pathways in RMC models of fast ion conducting glasses. Phys. Chem. Chem. Phys. 4, 3179–3184. doi:10.1039/b111310k
Alam, T. M., and Brow, R. K. (1998). Local structure and connectivity in lithium phosphate glasses: a solid-state 31P MAS NMR and 2D exchange investigation. J. Non Cryst. Solids 223, 1–20. doi:10.1016/S0022-3093(97)00345-1
Alam, T. M., Liang, J.-J., and Cygan, R. T. (2000). Molecular dynamics simulations of the lithium coordination environment in phosphate glasses. Phys. Chem. Chem. Phys. 2, 4427–4432. doi:10.1039/b004627m
Angell, C. A. (1990). Dynamic processes in ionic glasses. Chem. Rev. 90, 523–542. doi:10.1021/cr00101a006
Angell, C. A. (1992). Mobile ions in amorphous solids. Annu. Rev. Phys. Chem. 43, 693–717. doi:10.1146/annurev.pc.43.100192.003401
Bandaranayake, P. W. S. K., Imrie, C. T., and Ingram, M. D. (2002). Pressure dependent conductivities and activation volumes in LixNa(1-x)PO3 glasses: evidence for a new matrix-mediated coupling mechanism in mixed-cation glasses? Phys. Chem. Chem. Phys. 4, 3209–3213. doi:10.1039/b201215d
Brow, R. K. (2000). Review: the structure of simple phosphate glasses. J. Non Cryst. Solids 26, 1–28. doi:10.1016/S0022-3093(99)00620-1
Bunde, A., Ingram, M. D., and Russ, S. (2004). A new interpretation of the dynamic structure model of ion transport in molten and solid glassesy. Phys. Chem. Chem. Phys. 6, 3663–3668. doi:10.1039/B316738K
Changstrom, J. R., and Sidebottom, D. L. (2008). Study of the mixed alkali effect in lithium and sodium metaphosphate glass-forming liquids by photon correlation spectroscopy. J. Phys. Condens. Matter 20, 285103. doi:10.1088/0953-8984/20/28/285103
Denoyelle, A., Duclot, M., and Souquet, J.-L. (1990). Charge carrier concentration and mobility from the mixed alkali effect and ionic hall effect in phosphate based glasses. Phys. Chem. Glasses 31, 98.
Dieterich, W., and Maass, P. (2009). Models for ion transport in amorphous materials: recent advances. Z. Phys. Chem. 223, 1187–1200. doi:10.1524/zpch.2009.6073
Doreau, M., and Robert, G. (1991). Effet de cations mixtes et effet d’halogenure conjugues dans le verres de metaphosphate. Conductivite et structure. Mater. Res. Bull. 26, 959–969. doi:10.1016/0025-5408(91)90178-O
Dyre, J. C., Maass, P., Roling, B., and Sidebottom, D. L. (2009). Fundamental questions relating to ion conduction in disordered solids. Rep. Prog. Phys. 72, 046501. doi:10.1088/0034-4885/72/4/046501
Eisenberg, A., Farb, H., and Cool, L. G. (1966). Glass transitions in ionic polymers. J. Polym. Sci. 4, 855–868. doi:10.1002/pol.1966.160040603
Eisenberg, A., and Saito, S. (1966). Possible experimental equivalence of the Gibbs-DiMarzio and free volume theories of the glass transition. J. Chem. Phys. 45, 1673–1678. doi:10.1063/1.1727813
Fang, X., Ray, C. S., and Day, D. E. (2003). Glass transition and fragility of iron phosphate glasses. II. Effect of mixed-alkali. J. Non Cryst. Solids 319, 314–321. doi:10.1016/S0022-3093(02)01965-8
Fu, A. I., and Mauro, J. C. (2013). Topology of alkali phosphate glass networks. J. Non Cryst. Solids 361, 57–62. doi:10.1016/j.jnoncrysol.2012.11.001
Green, P. F., Brown, E. F., and Brow, R. K. (1999). Dynamics of mixed alkali metaphosphate glasses and liquids. J. Non Cryst. Solids 255, 87–96. doi:10.1016/S0022-3093(99)00427-5
Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130, 094503. doi:10.1063/1.3077168
Hall, A., Adams, S., and Swenson, J. (2004). The nature of conduction pathways in mixed alkali phosphate glasses. Ionics 10, 396–404. doi:10.1007/BF02378000
Hall, A., Swenson, J., Bowron, D. T., and Adams, S. (2009). Structure of LixRb1-xPO3 glasses near the glass transition. J. Phys. Condens. Matter 21, 245106. doi:10.1088/0953-8984/21/24/245106
Hermansen, C., Mauro, J. C., and Yue, Y. (2014a). A model for phosphate glass topology considering the modifying ion sub-network. J. Chem. Phys. 140, 154501. doi:10.1063/1.4870764
Hermansen, C., Rodrigues, B. P., Wondraczek, L., and Yue, Y. (2014b). An extended topological model for binary phosphate glasses. J. Chem. Phys. 141, 244502. doi:10.1063/1.4904287
Hoppe, U. (1996). A structural model for phosphate glasses. J. Non Cryst. Solids 195, 138–147. doi:10.1016/0022-3093(95)00524-2
Huang, C., and Cormack, A. N. (1992). Structure and energetics in mixed-alkali-metal silicate glasses from molecular dynamics. J. Mater. Chem. 2, 281–287. doi:10.1039/jm9920200281
Hunt, A. (1997). The mixed-alkali effect discussed within the context of percolative transport. J. Non Cryst. Solids 220, 1–16. doi:10.1016/S0022-3093(97)00191-9
Ingram, M. D., Imrie, C. T., and Konidakis, I. (2006). Activation volumes and site relaxation in mixed alkali glasses. J. Non Cryst. Solids 352, 3200–3209. doi:10.1016/j.jnoncrysol.2006.05.009
Ingram, M. D., and Roling, B. (2003). The concept of matrix-mediated coupling: a new interpretation of mixed-cation effects in glass. J. Phys. Condens. Matter 15, S1595–S1605. doi:10.1088/0953-8984/15/16/309
Jiang, Q., Zeng, H., Liu, Z., Ren, J., Chen, G., Wang, Z., et al. (2013). Glass transition temperature and topological constraints of sodium borophosphate glass-forming liquids. J. Chem. Phys. 139, 124502. doi:10.1063/1.4821617
Maass, P. (1999). Towards a theory for the mixed alkali effect in glasses. J. Non Cryst. Solids 255, 35–46. doi:10.1016/S0022-3093(99)00422-6
Mauro, J. C., Gupta, P. K., and Loucks, R. J. (2009). Composition dependence of glass transition temperature and fragility: II a topological model of alkali borate liquids. J. Chem. Phys. 130, 234503. doi:10.1063/1.3152432
Naumis, G. G. (2005). Energy landscape and rigidity. Phys. Rev. E 71, 026114. doi:10.1103/PhysRevE.71.026114
Naumis, G. G. (2006). Glass transition phenomenology and flexibility: an approach using the energy landscape formalism. J. Non Cryst. Solids 352, 4865–4870. doi:10.1016/j.jnoncrysol.2006.01.160
Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: short-range order in chacogenide alloys. J. Non Cryst. Solids 34, 153–181. doi:10.1016/0022-3093(79)90033-4
Phillips, J. C., and Thorpe, M. F. (1985). Constraint theory, vector percolation and glass formation. Solid State Commun. 53, 699–702. doi:10.1016/0038-1098(85)90381-3
Puls, S. P., and Eckert, H. (2006). Site discrimination in mixed-alkali glasses studied by cross-polarization NMR. J. Phys. Chem. B 110, 14253–14261. doi:10.1021/jp062251l
Rodrigues, B. P., Mauro, J. C., Yue, Y., and Wondraczek, L. (2014). Modifier constraints in alkali ultraphosphate glasses. J. Non Cryst. Solids 405, 12–15. doi:10.1016/j.jnoncrysol.2014.08.035
Rodrigues, B. P., and Wondraczek, L. (2013). Medium-range topological constraints in binary phosphate glasses. J. Chem. Phys. 138, 244507. doi:10.1063/1.4810868
Rodrigues, B. P., and Wondraczek, L. (2014). Cationic constraint effects in metaphosphate glasses. J. Chem. Phys. 140, 214501. doi:10.1063/1.4879559
Rodrigues, B. P., and Wondraczek, L. (2015). Floppy mode degeneracy and decoupling of constraint predictions in supercooled borate and silicate liquids. Front. Mater. 1:32. doi:10.3389/fmats.2014.00032
Schneider, J., Tsuchida, J. E., and Eckert, H. (2013). Cation size effects in mixed-ion metaphosphate glasses: structural characterization by multinuclear solid state NMR spectroscopy. Phys. Chem. Chem. Phys. 15, 14328–14339. doi:10.1039/c3cp51421h
Sidebottom, D. L., Green, P. F., and Brow, R. K. (1999). Brillouin scattering in alkali metaphosphate glasses and melts. J. Mol. Struct. 479, 219–226. doi:10.1016/S0022-2860(98)00872-2
Smedskjaer, M. M. (2014). Topological model for boroaluminosilicate glass hardness. Front. Mater. 1:23. doi:10.3389/fmats.2014.00023
Smedskjaer, M. M., Mauro, J. C., Sen, S., Deubener, J., and Yue, Y. (2010a). Impact of network topology on cationic diffusion and hardness of borate glass surfaces. J. Chem. Phys. 133, 1–6. doi:10.1063/1.3497036
Smedskjaer, M. M., Mauro, J. C., Sen, S., and Yue, Y. (2010b). Quantitative design of glassy materials using temperature-dependent constraint theory. Chem. Mater. 22, 5358–5365. doi:10.1021/cm1016799
Smedskjaer, M. M., Mauro, J. C., and Yue, Y. (2010c). Prediction of glass hardness using temperature-dependent constraint theory. Phys. Rev. Lett. 115, 10–13. doi:10.1103/PhysRevLett.105.115503
Smedskjaer, M. M., Mauro, J. C., Youngman, R. E., Hogue, C. L., Potuzak, M., and Yue, Y. (2011). Topological principles of borosilicate glass chemistry. J. Phys. Chem. B 115, 12930–12946. doi:10.1021/jp208796b
Tsuchida, J. E., Schneider, J., Deshpande, R. R., and Eckert, H. (2012). Cation distribution and local order in mixed sodium metaphosphate glasses. J. Phys. Chem. C 116, 24449–24461. doi:10.1021/jp308268h
Keywords: mixed-alkali effect, glass transition temperature, bond constraint theory, phosphate glasses, topological constraints
Citation: Rodrigues BP, Deubener J and Wondraczek L (2016) Modifier Interaction and Mixed-Alkali Effect in Bond Constraint Theory Applied to Ternary Alkali Metaphosphate Glasses. Front. Mater. 3:25. doi: 10.3389/fmats.2016.00025
Received: 22 March 2016; Accepted: 04 May 2016;
Published: 20 May 2016
Edited by:
Matthieu Micoulaut, Université Pierre et Marie Curie, FranceReviewed by:
Sylwester Janusz Rzoska, Institute of High Pressure Physics Academy of Sciences, PolandFrancisco Muñoz, Consejo Superior de Investigaciones Científicas, Spain
Copyright: © 2016 Rodrigues, Deubener and Wondraczek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lothar Wondraczek, bG90aGFyLndvbmRyYWN6ZWtAdW5pLWplbmEuZGU=
 Bruno Poletto Rodrigues
Bruno Poletto Rodrigues Joachim Deubener
Joachim Deubener Lothar Wondraczek
Lothar Wondraczek