Shape Transitions in Anisotropic Multicomponent Lipid Tubules

Ternary mixtures of saturated and unsaturated lipids together with cholesterol can be induced to phase separate by photo-peroxidation into lipid-ordered (l_o) and lipid-disordered (l_d) domains. Because these have different mechanical properties, the phase separation is accompanied by dramatic changes in morphology. This work considers a tubule composed of l_d phase with l_o phase inclusions that possess greater rigidity; this system has been shown experimentally by Yuan and coworkers to spontaneously adopt either banded or disk configurations following phase separation. The static behavior of inter-domain interactions is analyzed in each of these geometries by solving the linearized shape equations. These calculations suggest a possible mechanism by which the two structures form.

1. Introduction

Lipid membranes exhibit a remarkable variety of stable configurations, including bilayers, vesicles, and tubules. Generically, these equilibrium shapes minimize the energy (Helfrich, 1973; Lipowsky, 1991),

$U={\mathit{\int }}_C\sigma \mathit{\text{dA}}+4{\mathit{\int }}_C\kappa {\left(H-H_0\right)}^2\mathit{dA}+{\kappa }_G{\mathit{\int }}_C\mathit{KdA}+\mathrm{\lambda }{\mathit{\int }}_{\mathrm{\partial C}}\mathit{dl}.$ (1)

This expression has many terms, reflecting the rich physics of these systems. The first three terms occur in a single component structure: the first term penalizes area with prefactor σ the surface tension; the second resists mean-squared curvature with elastic constant κ, H the mean curvature, and H₀ the spontaneous curvature; the third term resists Gaussian curvature K with associated elastic constant κ_G. The space of possible equilibrium shapes is increased further if multiple immiscible lipid types with different mechanical properties coexist in the same structure. In such a case, the energy must be supplemented by the final term in equation (1), which tries to minimize the contact line ∂C between immiscible domains, with λ the line tension. In equation (1), numerical prefactors have been chosen to simplify expressions in the remainder of the paper.

With many terms in the energy equation (1), the equilibrium shape represents a compromise between these different effects and can include features disfavored by one term if it leads to a net reduction in the energy because of some other term. For example, a multidomain vesicle deforms into a bispherical shape (Baumgart et al., 2003), or a spherical shape with multiple inclusions (Gutlederer et al., 2009), reducing the line tension between the domains at the expense of introducing additional curvature. Changes in any of the mechanical properties, for example, the membrane tension (Shi and Baumgart, 2015), are accompanied by dramatic shape changes, such as budding or tubulation (Shi and Baumgart, 2015). Interplay between curvature and phase separation may lead to modulated phases (Sunil Kumar et al., 1999).

Despite the importance of these systems, the complexity of the energy functional equation (1) and the high order of the corresponding Euler–Langrange equations makes theoretical work challenging. Only nanometer-sized patches of membrane, with inclusions and solvent molecules, can be simulated with atomistic resolution (Tieleman et al., 2010). Pioneering work on budding (Julicher and Lipowsky, 1993) focused on axisymmetric solutions. Similar methods were used to study the shape of extruded tubules and lipid bridges between membranes (Powers et al., 2002). Computational differential geometry tools, such as the Surface Evolver (Brakke, 1992), are useful for single-component systems. Other mesh-based tools have identified a large number of stable configurations with more than two domains (Gutlederer et al., 2009). Coarse-grained models, such as Dissipative Particle Dynamics have proven successful at modeling processes involving a topological change, such as the adhesion and fusion of a vesicle to a membrane (Shillcock and Lipowsky, 2005). Phase separation has been studied using Monte Carlo sampling (Weikl and Lipowsky, 2001). Phase field modeling is another promising approach (Lowengrub et al., 2009).

Experimental results on vesicles provide biologically relevant models of processes, such as raft formation (Veatch and Keller, 2005). Experiments with varying curvature reveal the dynamics of lipid sorting (Heinrich et al., 2010). Another pertinent morphology is multicomponent lipid tubules, which were investigated by Yuan et al. (2008) using a ternary mixture of a two lipids of different melting temperatures and cholesterol. Photoinduced peroxidation of one of the lipids drives phase separation into regions of liquid-ordered (l_o) and liquid-disordered (l_d) phase (Yeagle, 2011). Since these have different material properties, including elastic constants, the phase separation is accompanied by a spontaneous shape change into one of two structures shown in Figure 1. The first possibility is a banded structure, illustrated in Figure 1A, where the tubule is divided along its length into cylindrically symmetric regions of l₀ and l_d phase, and the l_o regions tend to bulge out from the cylindrical l_d regions. In the second configuration, shown in Figure 1B, the l_d tubules are interrupted by disk structures that comprise two opposite relatively flat regions of l_o with a band of l_d phase around the rim. Yuan et al. (2008) hypothesize that these morphologies arise from the l₀ phase’s higher κ, which explains the tendency of the l_o domains to promote and occupy regions of lower curvature; this is consistent with the flattened vesicles observed in computer simulations (Gutlederer et al., 2009) with anisotropic curvature elastic constants. The physics determining which structure occurs in a particular situation, however, remains incompletely understood and requires knowledge of their energetics, the dynamical process by which they form and the chemistry of the phase separation.

FIGURE 1

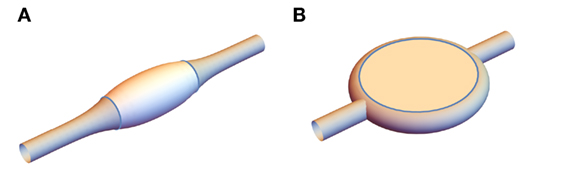
Figure 1. Experimentally observed possible structures for a multicomponent lipid tubule. (A) banded structure and (B) disk structure.

In this paper, we perform a theoretical analysis of the statics of the banded and disk structures, which illuminates the influences leading the system to adopt one structure or the other. The analysis is performed in a linearized regime applicable to small domains, as would be observed in the early stages of the phase separation, or equivalently small differences in curvature elastic constants κ between domains. The paper is organized as follows: in section 2, we derive the equations to be solved; results are presented in section 3 with discussion in section 4. Finally, conclusions are drawn in section 5.

2. Materials and Methods

2.1. Uniform Tubules

Cylindrical tubules are a well-known equilibrium configuration that minimizes equation (1) for homogeneous membranes. The radius ρ is found by substituting a cylindrical solution into equation (1), obtaining an energy per length,

$\frac{U}{L}=\mathrm{2\pi }\rho \left[\mathit{\sigma }+4\kappa {\left(\frac{1}{2\rho }-C\right)}^2\right],$ (2)

that is minimized by setting,

$\frac{\mathit{dU}}{d\rho }=C^2\kappa -\frac{\kappa }{\rho }+\mathit{\sigma }=0,$ (3)

yielding,

$\rho =\frac{\sqrt{\kappa }}{\sqrt{2C^2\kappa +\mathit{\sigma }}}.$ (4)

Hence, the tubule radius represents a balance between curvature elasticity, surface tension, and spontaneous curvature. In this paper, we assume that it is the difference in mean curvature elasticity that is primarily responsible for the difference in radii and that the spontaneous curvature C can be neglected in both phases. Assuming that κ_G is the same in each phase allows the Gaussian term to be eliminated from equation (1) using the Gauss–Bonnet theorem, so we will focus on the mean-squared curvature and the line tension terms for the remainder of this work.

2.2. Approximate Analysis of Multidomain Tubules

The experimentally observed banded and disk structures depicted in Figure 1 are significantly more challenging to analyze than the uniform structure, not least because they arise from a complex dynamical process. Before phase separation, the tubules are uniform cylinders; upon photo-induced peroxidation, domains are nucleated randomly along these tubules which then grow. If the elastic constants κ_o and κ_d are equal, the shape of the tubule would be unperturbed and the domains would simply grow with approximately circular shape and radius a(t) (Figures 2A,B). Since the l_d phase is fluidic, l_o domains may diffuse, collide with other domains, and coalesce. Once the size of a single domain reaches a ~ 2πρ, the domain reconnects and forms a continuous band (Figure 2C). These bands can grow further if they absorb nearby domains and this process will continue up to the limit of available l_o material once the phase separation is complete. After this, bands can only grow if the l_d phase is able to pass through the l_o phase, leading to Ostwald ripening of larger domains at the expense of smaller domains. The fact that the banded structures are stable over at least hours suggests that this latter mechanism is suppressed.

FIGURE 2

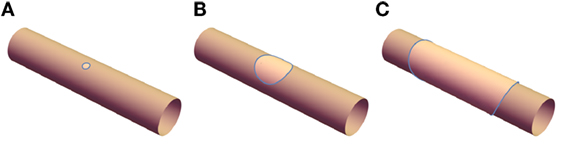
Figure 2. (A) A small domain of l_o phase is nucleated and (B) grows; once it reaches a sufficient size, opposite sides connect, leading to (C) the banded structure.

If the elastic constants are not equal, then the process is modified. Specifically, l_o domains will gradually deform the tubule as they grow; they may additionally exert a force on one another through capillary interactions. It is the purpose of the present paper to understand these interactions, because the disk structure must be stabilized, at least in its early stages, by some mechanism that prevents recombination of the two flattened l_o domains.

It is instructive to compare the asymptotic contributions to the energy of the two structures for very large or very small l_o domains. To do so, suppose that the disk structure comprises two circular patches of radius a and that the separation between the disks remains the same as the thickness of the l_d tubule to which it is connected. Contrast this with a banded structure with l_o domain of length b and suppose that the radius of that domain has reached the equilibrium value ${\rho }_o=\sqrt{\kappa ∕\mathit{\sigma }}$. The local mean curvature is, therefore, $H\approx \frac{1}{2{\rho }_o}$.

First, consider the mean-squared curvature contribution to the energy. For the disk structure, the curvature of the l_o phase is 0; the only contribution comes from the l_d phase around the edge, which is approximately the outer portion of a torus. The local mean curvature of the l_d section is, therefore, approximately $H=\left(R^{-1}+{\rho }_d^{-1}\right)∕2$ if R ≫ ρ_d, which converges on the mean curvature of a cylinder as R/ρ_d → ∞; from this, we conclude that the curvature of the l_d phase is essentially unchanged by forming the disk structure relative to uniform tubules for sufficiently large domain sizes. Additional curvature exists at the point where the tubule meets the disk, but this depends on ρ_d not R. We, therefore, conclude that, at least asymptotically, the mean-squared curvature contribution to the energy for the disk structure converges on a constant with increasing R. By contrast, the banded structure does not completely relieve the curvature of the l_o phase; it must grow linearly with the domain length L. The mean-squared curvature term, therefore, favors the disk structure.

The line tension of the disk structure grows ~λ4πR accounting for the circular patch on either side; in contrast for the banded structure, the line tension term lies between λ4πρ_d and λ4πρ_o, i.e., independent of the domain size. Line tension, therefore, favors the banded structure for large domains. Line tension and mean-squared curvature, therefore, favor opposing structures: for smaller domains, the banded structure has lower energy; for sufficiently large domains, the disk structure has lower energy.

We now consider very small R. For κ_o = κ_d, bands have a higher line tension that a single circular domain unless 2πR ≿ 2 × 2πρ_d. For κ_o > κ_d, small bands and individual circular domains do not permit much reduction of the curvature energy to avoid the mismatch, so we assume that both these configurations have roughly the same mean-squared curvature energy. These together suggest that bands below a certain critical size will tend to be unstable with respect to reorganization into a circular domain. The disk structure, on the other hand, requires a mechanism to stabilize the position of two growing domains relative to one another and preventing them from coalescence during the growth process.

The approximate argument above has shown that, depending on the material parameters and domain sizes, either the band or disk structure could be stable and that, moreover, the band structure requires a minimum size to be stable. This helps to explain why both structures are observed in the same experiment. Depending on the growth dynamics, either structure might form; moreover, the activation energy to convert a metastable structure to the stable structure might be prohibitively expensive. To convert a band to a disk, for example, requires a topological change, i.e., the separation of domains. This incurs a large increase in line tension and likely involves intermediate highly distorted structures.

The purpose of the remainder of the paper is to examine the equilibrium shape of the two structures and determine the capillary interactions between different domains; these results will enable us to build a picture of the energy landscape occupied by l_o domains in the initial stages of the phase separation process, and thereby propose a mechanism for their formation. Since the disk structures are observed to be stable, we infer that the line tension between the l_o and l_d phases is not the important effect and that the process is driven primarily by mean-squared curvature elasticity in accordance with the claims of Yuan et al. (2008).

2.3. Band Configuration

First, we examine the banded configuration shown schematically in Figure 1A and in Figures 2(e) and 2(f) of Yuan et al. (2008). Looking carefully at the experimental images, we note that the observed bands in Yuan et al. (2008) are approximately cylindrical, particularly for the larger bands. As discussed above, this implies that some or all of these parameters in equation (4) are different in the two domains.

To find the equilibrium configuration of a single band of higher elastic constant κ embedded on an infinite cylinder, the surface is first parameterized by a cylindrical Monge form,

$\mathbf{\text{X}}=\left\{r\left(z\right)\cos \varphi ,r\left(z\right)\sin \varphi ,z\right\},$ (5)

where r(z) = ρ + αR(z). Here ρ is the equilibrium radius of the cylinder in the absence of the patches, R(z) is the deformation profile from cylindrical shape, and α is an expansion parameter that will be used to linearize the problem.

To calculate the energy, it is necessary to calculate the coefficients of the first fundamental form,

$\begin{array}{l}E={\mathbf{\text{X}}}_z\cdot {\mathbf{\text{X}}}_z=1+{\mathrm{\alpha }}^2{R\prime }^2\\ F={\mathbf{\text{X}}}_z\cdot \mathbf{\text{X}}\varphi =0\\ G={\mathbf{\text{X}}}_{\varphi }\cdot {\mathbf{\text{X}}}_{\varphi }={\left(\rho +\alpha R\right)}^2,\end{array}$ (6)

the surface normal,

$\mathbf{\text{N}}={\mathbf{\text{X}}}_z\times {\mathbf{\text{X}}}_{\varphi }∕\left|{\mathbf{\text{X}}}_z\times {\mathbf{\text{X}}}_{\varphi }\right|,$ (7)

and the second fundamental form,

$\begin{array}{ll}\hfill e& ={\mathbf{\text{X}}}_{\mathit{zz}}\cdot \mathbf{\text{N}}=-\alpha \mathit{rR}″∕s\\ \hfill f& ={\mathbf{\text{X}}}_{z\varphi }\cdot \mathbf{\text{N}}=0\\ \hfill g& ={\mathbf{\text{X}}}_{\mathit{\varphi \varphi }}\cdot \mathbf{\text{N}}=r^2∕s.\end{array}$ (8)

where $s^2=r^2\left(1+\alpha {R\prime }^2\right)$. These quantities together are sufficient to determine the area element,

$\mathit{dA}=\sqrt{\mathit{EG}-F^2}d\varphi \mathit{dz}$ (9)

and the mean curvature,

$H=\frac{1}{2}\frac{\mathit{eG}+\mathit{gE}-2\mathit{Ff}}{\mathit{EG}-F^2}$ (10)

as required. Using these formulae, the energy is

$\frac{U}{2\pi }={\mathit{\int }}_{-L}^L\sqrt{r^2\left(1+\alpha {R\prime }^2\right)}\left[\mathit{\sigma }+\frac{\kappa \left(z\right){\left(1+\alpha {R\prime }^2-\alpha \mathit{rR}″\right)}^2}{r^2{\left(1+\alpha {R\prime }^2\right)}^3}\right]\mathit{dz}$ (11)

where we assumed that the elastic parameter κ is a function of position z. To obtain linearized Euler–Lagrange equations, equation (11) must be expanded to quadratic order in α yielding,

$\begin{array}{ll}\hfill \frac{U}{2\pi }& ={\mathit{\int }}_{-L}^L{R}^2\kappa -R\left(\kappa -1\right)+\frac{1}{2}\left\{2+{R\prime }^2-\kappa \left[{R\prime }^2-2\left(R″-1\right)\right]\right\}\mathit{dz}\end{array}$ (12)

where the other constants were removed by setting them to σ = 1 and ρ = 1. An ansatz form for κ(z) of

$\kappa =\frac{{\kappa }_o+{\kappa }_d}{2}-\frac{1}{2}\left({\kappa }_o-{\kappa }_d\right)\text{\hspace{0.17em}tanh\hspace{0.17em}}\left[\mathrm{\lambda }\left(z-z_0\right)\right]$ (13)

was adopted, where κ_o is the curvature elastic constant in the l_o domain and κ_d is the equivalent constant in the l_d domain. The parameter λ is the width over which κ varies from κ_o to κ_d, and z₀ is the location of the boundary between the two phases. Taking variations of equation (22) with respect to R yields the following Euler–Lagrange shape equation,

$\begin{array}{l}\kappa \left(2R″″+R″+2R-1\right)+\kappa \prime \left(R\prime +4R″\prime \right)+\left(R″-1\right)\left(2\kappa ″-1\right)=0.\end{array}$ (14)

We solved this equation numerically; results are presented in section 3.

2.4. Disk Configuration

To study the disk structure, similar approximations to the previous section must be made. Neglecting the spontaneous curvature and line tension, the shape of the lipid tubule minimizes the energy,

$U={\displaystyle \sum _i}{\mathit{\int }}_{C_i}\left({\mathit{\sigma }}_i+4{\kappa }_i{H}^2\right)\mathit{dA}$ (15)

where C_i represents the domain enclosed by the ith patch that has surface tension and elastic constant σ_i and κ_i, respectively. The surface is parameterized in cylindrical coordinates as above, but the radius r(z, ϕ) = ρ + αR(z, ϕ) is now a function of both z and ϕ,

$\mathbf{\text{X}}=\left\{r\left(z,\varphi \right)\cos \varphi ,r\left(z,\varphi \right)\sin \varphi ,z\right\}.$ (16)

With this parameterization, the tangent vectors lie parallel to X_z and X_ϕ where subscripts indicate derivatives with respect to the stated coordinates. The coefficients of the first fundamental form are

$\begin{array}{l}E={\mathbf{\text{X}}}_z\cdot {\mathbf{\text{X}}}_z=1+{\alpha }^2{R}_z^2\\ F={\mathbf{\text{X}}}_z\cdot {\mathbf{\text{X}}}_{\varphi }={\alpha }^2{R}_{\varphi }{R}_z\\ G={\mathbf{\text{X}}}_{\varphi }\cdot {\mathbf{\text{X}}}_{\varphi }={\rho }^2+2\alpha R_{z\varphi }+{\alpha }^2\left(R^2+R_{\varphi }^2\right)\end{array}$ (17)

where subscripts are used to denote the respective derivatives and the surface normal is

$\mathbf{\text{N}}={\mathbf{\text{X}}}_z\times {\mathbf{\text{X}}}_{\varphi }∕\left|{\mathbf{\text{X}}}_z\times {\mathbf{\text{X}}}_{\varphi }\right|,$ (18)

where $\left|{\mathbf{\text{X}}}_z\times {\mathbf{\text{X}}}_{\varphi }\right|=s^2=r^2+{\alpha }^2\left(r^2{R}_z^2+R_{\varphi }^2\right)$. The coefficients of the second fundamental form are

$\begin{array}{l}e=\alpha r{R}_{\mathit{zz}}∕s\\ f=\alpha \left(\alpha R_z{R}_{\varphi }-r{R}_{z\varphi }\right)∕s\\ g=\left[{\rho }^2+\alpha \left(2\rho R+\alpha R^2+\alpha R_{\varphi }^2+\alpha r^2{R}_{\mathit{\varphi \varphi }}^2\right)\right]∕s.\end{array}$ (19)

The energy functional is readily obtained by inserting the coefficients in equations (17) and (19) into the expressions in equations (9) and (10), and, thence, into the energy equation (15); it is not displayed here due to its length. The Euler–Lagrange equations are constructed as usual,

$\frac{\mathit{\partial U}}{\mathit{\partial R}}-{\partial }_i\frac{\mathit{\partial U}}{\partial R_i}+{\partial }_{\mathit{ij}}\frac{\mathit{\partial U}}{\partial R_{\mathit{ij}}}=0,i,j\in \left\{z,\varphi \right\}.$ (20)

Having constructed these equations, they are linearized as above by Taylor expansion in powers of α about α = 0 and retaining terms only up to quadratic order. At first order in α is an equation representing the equilibrium cylindrical shape,

$\left({\mathit{\sigma }}_i-\frac{{\kappa }_i}{{\rho }^2}\right)=0,$ (21)

which has a positive solution if $\rho =\sqrt{{\kappa }_i∕{\mathit{\sigma }}_i}$. At second order in α is the desired linearized equation for R(z, ϕ),

$\begin{array}{l}0=2{\kappa }_i\left(R_{\mathit{\varphi \varphi \varphi \varphi }}+2{\rho }^2{R}_{\mathit{zz}\mathit{\varphi \varphi }}+{\rho }^4{R}_{\mathit{zzzz}}\right)\hfill \\ +\left(5{\kappa }_i-{\rho }^2{\mathit{\sigma }}_i\right)R_{\mathit{\varphi \varphi }}+\left({\kappa }_i{\rho }^2-{\mathit{\sigma }}_i{\rho }^4\right)R_{\mathit{zz}}+2{\kappa }_{i}R\end{array}$ (22)

which is an anisotropic biharmonic equation. To avoid a specialist finite element discretization, equation (22) may be separated into two coupled PDEs of quadratic order,

$\begin{array}{ll}\hfill {\nabla }^{2}R& =S\\ \hfill 2\left(1-S\right)+2\kappa \left(S+2R-1\right)+4\kappa {\nabla }^{2}S+8\kappa R_{\mathit{\varphi \varphi }}& =0\end{array}$ (23)

where ∇² = ∂_ϕϕ + ∂_zz and where we have also set ρ = 1 and σ = 1 as before. Results are presented in section 3 below.

3. Results

3.1. Band Configuration

Equation (22) was solved numerically on the domain [0, L] subject to mirror boundary conditions R^″ = 0 and R^″″ = 0 at z = 0, and R = 0, R′ = 0 at z = L. The parameter L was chosen to be much greater than the position of the domain interface z₀. Results are shown for different values of z_o in Figure 3. Clearly, as the l_o domain gets bigger, its radius approaches that of a single domain l_o tubule.

FIGURE 3

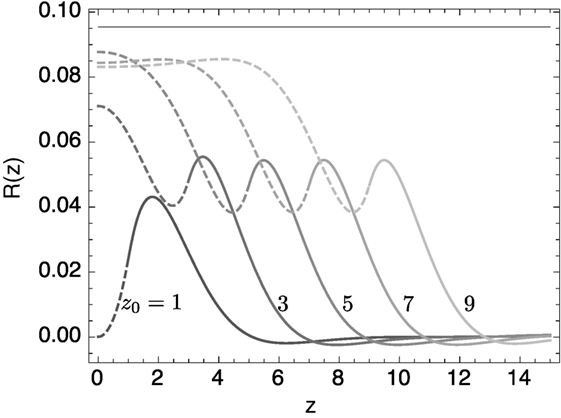
Figure 3. Equilibrium solutions of the linearized shape equation for the banded structure. The lipid membrane between 0 < z < z₀, composed of l_o phase, has κ = 1.2; the remaining l_d lipid has κ = 1. Only one half of the parity symmetric R(−z) = R(z) shape is shown. The solid horizontal line represents the equilibrium radius of the l_o phase with these parameters if it formed a uniform cylinder.

3.2. Disk Configuration

The computational domain used to solve equation (22) consists of a rectangle defined by ϕ ∈ [−π, π] and z ∈ [−L, L] where L ≫ π. Two interior circular patches labeled i ∈ {1, 2} are located at $\left(z,\varphi \right)=\left(z_0^i,{\varphi }_0^i\right)$ with radius aⁱ. Periodic boundary conditions are enforced on the top and bottom edges, and the left and right boundaries are intended to be sufficiently remote from the patches that R and all derivatives vanish upon them, i.e., the natural boundary conditions of the Euler–Lagrange equations are enforced.

A commercial finite element solver, FlexPDE 6 (PDE Solutions), is used to solve the Euler–Lagrange equation (23). Typical results are shown in Figure 4A: notice that the distortion in height function R bridges the two domains if they are relatively close. The surfaces corresponding to this solution are reconstructed in Figure 4B and shown with R magnified by a factor of 4 in Figure 4C to aid visualization. Corresponding plots for several other domain positions are shown in Figures 4D–I.

FIGURE 4

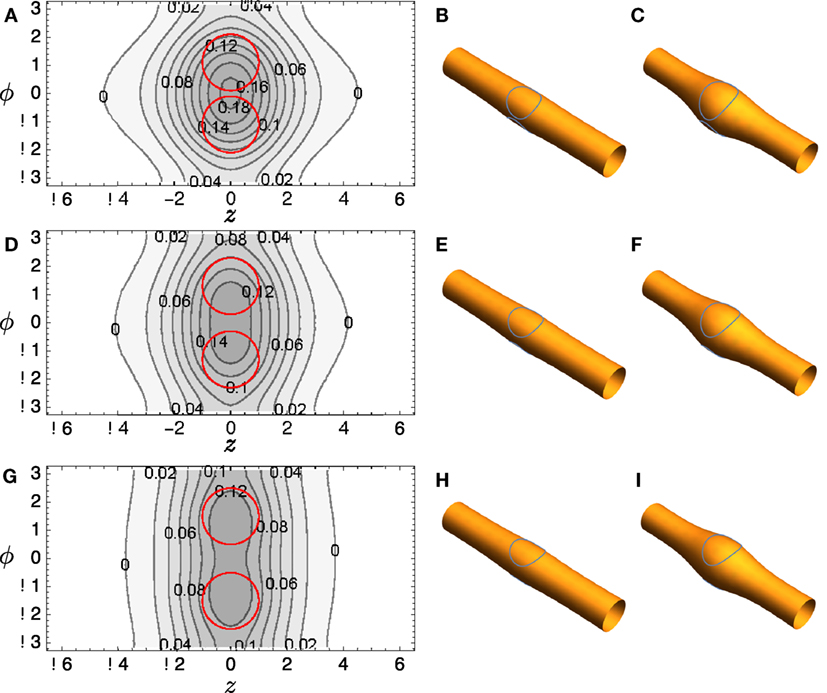
Figure 4. (A) Contour plot of R(z, ϕ) for tubule with two included circular domains and κ_o = 2. (B) It depicts the surface reconstructed from the solution; (C) It shows the same solution, but the radial variation R is magnified by a factor of 4 to aid visualization. (D–F) and (G–I) show corresponding plots for different domain locations.

The energy of the surface obtained by solving the Euler–Lagrange equations can readily be computed from the solution. It is helpful to separate the terms in the energy functional in powers of α,

$\begin{array}{llll}\hfill 1& :1+\kappa & \hfill & \\ \hfill \alpha & :2\kappa S-R\left(\kappa -1\right)& \hfill & \\ \hfill {\alpha }^2& :2\kappa R^2+\left(1+\kappa \right)R_z^2+\left(3\kappa +1\right)R_{\varphi }^2+8\kappa R{R}_{\mathit{\varphi \varphi }}-\kappa S^2,\end{array}$ (24)

because the quadratic term is found, as expected, to be substantially smaller than the linear term; this separation allows the adaptive refinement algorithm to strategically place additional mesh points to resolve this contribution accurately.

By shifting around the position of the domains, solving the Euler–Lagrange equations and calculating the corresponding energy, it is possible to reconstruct the energy landscape experienced by two l_o domains on the surface of the l_d tubule. The landscape for two equal sized domains is shown in Figure 5, where the energy is plotted as a function of the Δz and Δϕ separation of the centers of the domains; note that some regions of the parameter space are excluded as they would imply domain overlap. Two important features are observed: first, the global minimum is located at (Δz, Δϕ) = (0, π), i.e., the two domains located on opposite sides of the tubule. As the domains are pushed apart, either along the tubule or azimuthally, the energy increases. The energy landscape becomes flat as |z| ≫ 2π, corresponding to a longitudinal separation much greater than the radius of the tubule.

FIGURE 5

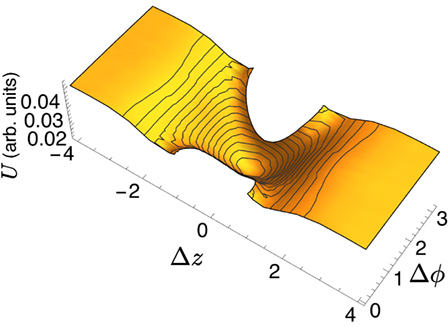
Figure 5. Energy landscape for multidomain interactions; Δz and Δϕ represent the separation between the domain centers; some regions of (Δz, Δϕ) space are excluded because they imply domain overlap.

We also considered the interaction between a small l_o domain and the edge of a band. Sample results shown in Figure 6; the left-hand side of the domain is all l_o phase, and a single circular l_o domain is placed with center at (z₀, 0). The energy of the equilibrium solution for different values of z₀ is plotted in Figure 7; clearly the l_o domain is attracted to the band at distances z₀ < 2π. It appears that there may be a small repulsion as the l_o domain gets very close to the edge, the contribution coming from the α² term in equation (24).

FIGURE 6

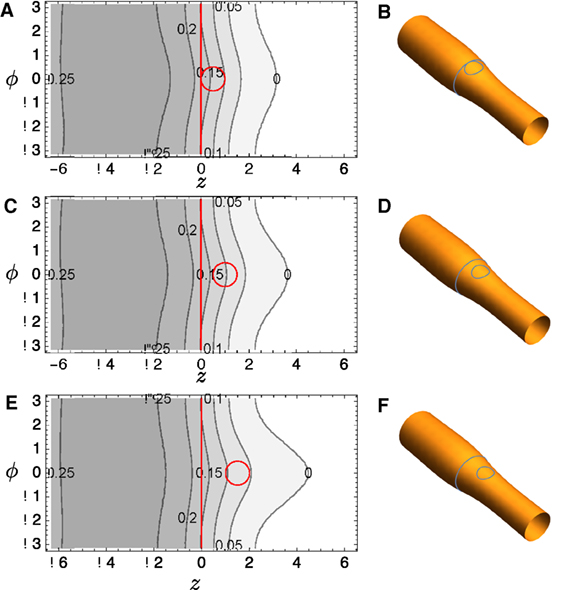
Figure 6. (A) Contour plot of R(z, ϕ) for tubule with a circular domain and part of a band structure, both with κ_o = 2; (B) corresponding reconstructed surface where R is magnified by a factor of 2 to aid visualization. (C–F) show corresponding plots for different locations of the circular domain relative to the band edge.

FIGURE 7

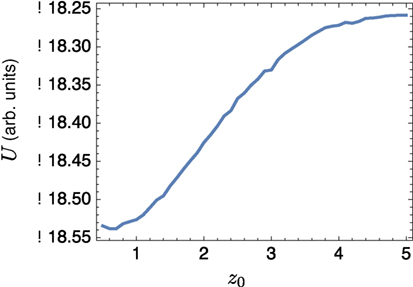
Figure 7. Energy landscape for a small circular domain of radius 1/2 centered at z₀ to the right of a band edge.

4. Discussion

These energy landscapes provide information on the forces experienced by l_o domains embedded in the tubule, as allow us to propose a mechanism behind the formation of the two structures illustrated in Figure 8. For disks, suppose two l_o domains are simultaneously nucleated by photo-induced peroxidation, and subsequently grow (Figure 8A). If they are separated by a longitudinal distance less than approximately 2πρ, they will be attracted toward one another. Depending on kinetic effects, they may collide and merge, leading to a larger domain, or be pushed to the opposite sides of the tubule by the capillary interaction characterized above (Figure 8B). As the two domains grow from the opposite sides of the tubule the disk structure emerges (Figure 8C). Band formation requires one initial domain that grows (Figure 8D) deforming the tubule and self-intersect (Figures 8E,F), forming the banded structure. As the band structure is forming, additional domains that are nucleated nearby will tend to be attracted to the band and will merge with it, progressively increasing its area. We assume in both cases that the more flexible and fluid l_d phase changes conformation to accommodate either structure. The maximum size of the domains is ultimately limited when all of free molecules of the relevant lipid from the ternary mixture has migrated into the l_o domains.

FIGURE 8

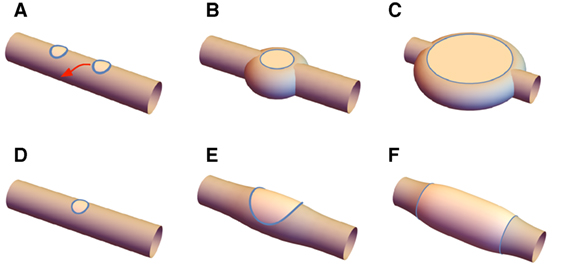
Figure 8. Disks form when (A) two nearby l_o domains migrate to opposite sides of the tubule and are stabilized by capillary forces; (B) these then grow, and the inter-disk structure being filled in by l_d resulting in the final disk state (C). Bands form by (D) growth of an initial l_o domain that (E) wraps around the tubule, and (F) finally connecting and creating the banded structure.

In this view, the discriminant between disk and banded structures is controlled by the rate of growth of l_o phase: if it is sufficiently slow that l_o domains are able to migrate to their equilibrium position on opposite sides of the tubule, the disk structure will emerge; on the other hand, a faster growth rate – at least locally – will lead to the band structure as single, isolated domains of l_o phase grow to the point that they self-intersect.

5. Conclusion

We have investigated the energy landscape experiences by lipid patches embedded in a tubule geometry. If these components have a different curvature elastic constant than the surrounding structure, they deform the tubule and attract one another through capillary interactions. Depending on the growth rate, they may self-intersect as they grow around the tubule, forming the band structure, or settle into a stable configuration with domains on opposite sides of the tubule that then grow to form the disk structure. This prediction is experimentally testable by dynamic imaging of the early stages of the phase separation process.

In order to construct this model, we have neglected many effects, such as line tension and anisotropy in the resistance to Gaussian curvature; moreover, we have only studied linear equations describing the static process. A full non-linear study of these shapes should be conducted to gain a more quantitatively accurate picture of the energy landscape, although we expect that even with the approximations made, our model should accurately capture the qualitative features present in early stages of the growth. Moreover, the emergence of the structures is the result of a growth process, and so a dynamic model is needed to test whether the mechanism proposed is kinetically feasible.

Author Contributions

The author TA is the sole contributor to this work; he performed the research and wrote the paper.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

TA wishes to thank the Kavli Institute for Theoretical Physics and the organizers of the SHEETS’16 program at KITP during which this work was performed, as well as the Research Corporation for Science Advancement for a Cottrell Award. This research was supported in part by the National Science Foundation under Grant No. NSF PHY11-25915.

References

Baumgart, T., Hess, S. T., and Webb, W. W. (2003). Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature 425, 821–824. doi: 10.1038/nature02013

PubMed Abstract | CrossRef Full Text | Google Scholar

Brakke, K. A. (1992). The surface evolver. Exp. Math. 1, 141–165. doi:10.1080/10586458.1992.10504253

CrossRef Full Text | Google Scholar

Gutlederer, E., Gruhn, T., and Lipowsky, R. (2009). Polymorphism of vesicles with multi-domain patterns. Soft Matter 5, 3303–3311. doi:10.1039/b902388g

CrossRef Full Text | Google Scholar

Heinrich, M., Tian, A., Esposito, C., and Baumgart, T. (2010). Dynamic sorting of lipids and proteins in membrane tubes with a moving phase boundary. Proc Natl Acad Sci U.S.A. 107, 7208–7213. doi:10.1073/pnas.0913997107

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28, 693–703.

Google Scholar

Julicher, F., and Lipowsky, R. (1993). Domain-induced budding of vesicles. Phys. Rev. Lett. 70, 2964–2967. doi:10.1103/PhysRevLett.70.2964

CrossRef Full Text | Google Scholar

Lipowsky, R. (1991). The conformation of membranes. Nature 349, 475–481. doi:10.1038/349475a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lowengrub, J. S., Rätz, A., and Voigt, A. (2009). Phase-field modeling of the dynamics of multicomponent vesicles: spinodal decomposition, coarsening, budding, and fission. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 79, 031926. doi:10.1103/PhysRevE.79.031926

PubMed Abstract | CrossRef Full Text | Google Scholar

Powers, T. R., Huber, G., and Goldstein, R. E. (2002). Fluid-membrane tethers: minimal surfaces and elastic boundary layers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65(4 Pt 1), 041901. doi:10.1103/PhysRevE.65.041901

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, Z., and Baumgart, T. (2015). Membrane tension and peripheral protein density mediate membrane shape transitions. Nat. Commun. 6, 5974. doi:10.1038/ncomms6974

PubMed Abstract | CrossRef Full Text | Google Scholar

Shillcock, J. C., and Lipowsky, R. (2005). Tension-induced fusion of bilayer membranes and vesicles. Nat. Mater. 4, 225–228. doi:10.1038/nmat1333

PubMed Abstract | CrossRef Full Text | Google Scholar

Sunil Kumar, P. B., Gompper, G., and Lipowsky, R. (1999). Modulated phases in multicomponent fluid membranes. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 60(4 Pt B), 4610–4618.

PubMed Abstract | Google Scholar

Tieleman, P., Vattulainen, I., Tajkhorshid, E., Essex, J. W., Ulmschneider, M. B., Schulten, K., et al. (2010). Molecular Simulations and Biomembranes. RSC Biomolecular Sciences. London: The Royal Society of Chemistry.

Google Scholar

Veatch, S. L., and Keller, S. L. (2005). Miscibility phase diagrams of giant vesicles containing sphingomyelin. Phys. Rev. Lett. 94, 148101. doi:10.1103/PhysRevLett.94.148101

PubMed Abstract | CrossRef Full Text | Google Scholar

Weikl, T. R., and Lipowsky, R. (2001). Adhesion-induced phase behavior of multicomponent membranes. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 64(1 Pt 1), 011903. doi:10.1103/PhysRevE.64.011903

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeagle, P. (2011). The Structure of Biological Membranes, Third Edition. Boca Raton, FL: CRC Press.

Google Scholar

Yuan, J., Hira, S. M., Strouse, G. F., and Hirst, L. S. (2008). Lipid bilayer discs and banded tubules: photoinduced lipid sorting in ternary mixtures. J. Am. Chem. Soc. 130, 2067–2072. doi:10.1021/ja710305c

PubMed Abstract | CrossRef Full Text | Google Scholar