The TTT Curves of the Heterogeneous and Homogeneous Crystallization of Lithium Disilicate – A Stochastic Approach to Crystal Nucleation

The present study explores the temperature and time dependence of heterogeneous (HET) crystal nucleation in a lithium disilicate glass using the stochastic approach. In particular, a single lithium disilicate sample was repeatedly (284 runs) undercooled to 1173 K in a PtRh-crucible and the crystallization onset time during an isothermal hold was detected in each run. The statistical distribution of the times elapsed before crystallization is described by a first-order reaction with a HET crystal nucleation rate of (9.19 ± 0.04) × 10⁻⁴ s⁻¹ while individually shaped crystallization exotherms of each run were recorded, which indicate growth of a single or only few crystals during crystallization of the entire volume. The data were used together with results of previous stochastic experiments and those of double-stage heat treatments to calculate the crystallization time of a fraction of 10⁻⁴ percent for all temperatures between glass transition and melting. The derived TTT diagram shows a double-nose of crystallization in the volume at large undercoolings (0.53–0.61 T_m) and crystallization at the surface at small undercoolings (0.62–0.92 T_m) initiated by homogeneous and HET crystal nucleation, respectively. The critical cooling rate at the HET nose is approximately 73 K s⁻¹.

Introduction

In the last 40 years, crystal nucleation in silicate glasses has been addressed by counting crystal number densities in the volume of glass specimens subjected to double-stage heat treatments (Fokin et al., 2006). The techniques bears the advantage of direct determination of the crystal nucleation rate from calculating the first time derivative of the number density curve but has the drawback that it is limited to a narrow temperature range near the glass transformation temperature (T_g ≤ T ≤ 1.2 T_g) where driving forces are high and crystal nucleation is occurring frequently in the volume. Another drawback is the dissolution of nuclei that are critical at the first stage but subcritical at the second stage. In the case of surface crystallization, the accessible temperature range becomes broader but the time period of crystal nucleation is mostly limited due to fast saturation of active sites. A short nucleation period merely allows for an indirect determination of the crystal nucleation rate. Thus, birth- (from crystal size distribution) (Müller et al., 2000) and impingement-times (Krüger and Deubener, 2015a) of crystals at the surface have been analyzed to deduce their rates of nucleation. In each of these methods (and also for analyzing high-temperature X-ray diffraction data (Dressler et al., 2011, 2014), an ensemble of crystals is analyzed in order to derive nucleation parameters. The criterion applies for large undercoolings but becomes ineffective at higher temperatures where crystal grow rates are generally high and the entire liquid volume is shortly consumed by the first nucleated crystal. In consequence, nucleation data for temperatures T > 1.2 T_g are lacking for both binary/ternary model glasses and for technical multi-component glass systems. The occurrence of a substantial gap in the reported nucleation data is surprising and unexpected if one recalls the large number of glasses produced in industrial practice by forming during quench. Furthermore, the analysis of a crystal ensemble does not allow to prove randomness in the nucleation events, a necessary condition in the framework of CNT. By contrast, the observation of single crystal events helps in discriminating partition of long-range diffusion fluxes (Kelton, 2000).

In the light of the above, this study aims at establishing nucleation kinetics by its time average of repeated single crystal nucleation events rather than using the ensemble average of crystals of double-stage heat treatments. The so-called stochastic approach to crystal nucleation has been introduced for undercooled low viscous (mPa s) liquids, such as metals and hydrous suspensions (Toschev and Markov, 1967; Toschev and Gutzow, 1972; Toschev et al., 1972; Toschev, 1973; Morton et al., 1994; Barlow and Haymet, 1995; Uttormark et al., 1997; Heneghan et al., 2001, 2002; Heneghan and Haymet, 2002; Wilson et al., 2005; Wilde et al., 2006, 2009; Yang et al., 2009, 2011, 2013). Our results show that it is applicable to high viscous (kPa s) silicate melts and it results in heterogeneous (HET) crystal nucleation rates from which TTT representations and critical cooling rates can be derived.

The formation of supercritical nuclei is a stochastic process. Nucleation events occur randomly and independent from each other. Already in the 1960s, Toschev and Markov (1967) showed that the electrolytic deposition of cadmium on platinum single crystal electrodes follows a Poisson distribution. Thereby, both the number of nuclei in a given time interval and the time necessary to form a certain number of nuclei are linked to probability distributions (Toschev and Gutzow, 1972; Toschev et al., 1972; Toschev, 1973).

Later probability distribution functions in the formation of the first supercritical nucleus have been studied for other liquid metals, such as niobium and zirconium (Morton et al., 1994), aluminum (Uttormark et al., 1997), gold and copper (Wilde et al., 2006, 2009), and tin (Yang et al., 2009, 2011, 2013) but also in water (pure and seeded) (Barlow and Haymet, 1995; Heneghan et al., 2001, 2002; Heneghan and Haymet, 2002; Wilson et al., 2005) and in gas hydrates (Maeda et al., 2011, 2012). In all these experiments, a single sample was repeatedly undercooled from above the melting temperature, while either the time (at an isothermal hold) or the temperature (at an isochronal cooling) of crystallization was detected. These experiments provided primary information on the average lag time and the mean undercooling, from which the crystal nucleation rate and the critical cooling rate can be derived. Secondary information include the activity of seeds and the purification of the liquid upon thermal cycling. Especially the ALTA (“automated lag time apparatus”) concept developed for studying the freezing behavior of water (Barlow and Haymet, 1995) is acknowledged since it has been designed to permit time-saving through a feed-back control that heats the sample immediately upon freezing.

In the past years, non-adiabatic fast scanning calorimetry has been developed to in situ measure the response of single metallic drops to temperature changes in a large range of cooling rate spanning four orders of magnitude (Yang et al., 2009, 2011, 2013). In these experiments, a small drop (volume ≈ 10⁻⁶ mm³) is repeatedly heated and cooled on a thin film sensor with rates up to 10⁴ K s⁻¹. Unfortunately, current technology of the so-called flash- or chip-calorimeters is limited to a maximum sensor temperature of about 700 K, which is much lower than the liquidus temperature of lithium disilicate glass [1306 K (Kracek, 1930)].

Glasses in the binary Li₂O–SiO₂ system, such as lithium disilicate (Li₂Si₂O₅) have been the object of extensive research (see, for example, Tomozawa, 1972, 1973; Matusita and Tashiro, 1973; James, 1974, 1985; Fokin et al., 1981; Weinberg and Neilson, 1985; Barker et al., 1988; Deubener et al., 1993; Ota et al., 1997; Burgner and Weinberg, 2001; Nascimento et al., 2011) since their crystal nucleation and growth rates are relatively low at high undercoolings (T < 1.2 T_g) and thus conveniently measurable from crystal number densities and crystal sizes of optical microscopy images (James, 1974, 1989; Rowlands and James, 1979). Furthermore, detailed thermodynamic data are available for this system (Takahashi and Yoshio, 1973) which allow to test the validity of basic nucleation models from comparisons of predicted rates with measured data (Neilson and Weinberg, 1979; Rowlands and James, 1979; Zanotto and James, 1985; Weinberg and Zanotto, 1989; Fokin et al., 2010a).

Li₂Si₂O₅ crystals nucleate homogeneously in the volume (James et al., 1978; James, 1985; Zanotto and James, 1985; Zanotto, 1987; Barker et al., 1988) disregarding the controversy of metastable phase formation prior to the crystallization of stable Li₂Si₂O₅ crystals (Hench et al., 1971; Tomozawa, 1972; Barker et al., 1988; Deubener et al., 1993; Zanotto, 1997; Burgner et al., 1999; Iqbal et al., 1999) but also heterogeneously at suspended particles, such as platinum (Cronin and Pye, 1986; Narayan et al., 1996; Ray and Day, 1996; Ray et al., 1996; Mishima et al., 2006; Ranasinghe et al., 2007) and at the surfaces with the surrounding gas atmosphere (James, 1989; Ray and Day, 1996; Ray et al., 1996; Ranasinghe et al., 2007; Fokin et al., 2010b). Ranasinghe et al. (2007) performed heat treatments on pure and platinum doped Li₂Si₂O₅ glasses and found that the critical cooling rate increases and the activation energy of crystallization decreases when Li₂Si₂O₅ glass is heated in a container as compared to containerless processing (levitation) and that in both cases platinum promotes the crystallization of lithium disilicate glasses. However, the temperature dependence of preferred HET crystal nucleation leading to observable “coast-island” microstructures [see Fig. 1C in Krüger and Deubener (2015a) and Fig. 14 in Fokin et al. (2010b)] is not well understood with respect to isothermal heat treatments and for ramping at constant rates from above melting temperature and below glass transformation temperature, respectively.

The present paper reports on novel experiments of HET crystal nucleation, which have been performed by the stochastic approach under isothermal conditions at small undercooling (1.6 T_g). In particular, the time elapsed before the formation of the first supercritical nucleus is detected from repeated measurements in a PtRh-crucible and the HET steady-state nucleation rate is derived from the first-order kinetics of the probability distribution function. Using previous data (Krüger and Deubener, 2014, 2015a), a TTT diagram is produced from which the HET and homogeneous (HOM) crystallization can be clearly distinguished. The TTT curves of lithium disilicate help in understanding the development of coast-island microstructures observed in practice during cooling from above the liquidus temperature. We assume that the here established method is able to clarify also the crystallization mechanisms in other glass-forming systems.

Experimental

A glass of nominal composition Li₂Si₂O₅ was prepared by melting a batch of the raw materials SiO₂ and Li₂CO₃ (both of analytical grade). The batch was mixed and melted three times in a platinum crucible at 1673 K for 1 h under ambient conditions. The melt was subsequently quenched between two steel plates, which resulted in cooling rates of ~150–250 K min⁻¹. The glass was analyzed by X-ray fluorescence (S4 Pioneer; Bruker AXS, Karlsruhe, Germany) while the Li₂O content was determined by atomic emission spectroscopy (ICP-OES Vista MPX; Varian). The analyzed chemical composition was 77.4 SiO₂, 21.0 Li₂O, and 1.6 impurities (all in percent by weight), which slightly deviates from the nominal stoichiometry of Li₂Si₂O₅.

A chip (= 21.4 mg) of the glass was inserted in a lidded PtRh-crucible and subjected to high-temperature differential scanning calorimetry (DSC 404 F3 Pegasus; Netzsch, Selb, Germany) under nitrogen atmosphere. A scheme of the operating mode of the DSC with the characteristic repeatedly performed heating-dwelling–cooling-dwelling cycles (red dashed-dotted line) is shown in Figure 1. In particular, the glass chip was heated at 0.167 K s⁻¹ to a temperature of 1353 K, which is 47 K above T_m [T_m = 1306 K (Kracek, 1930)], dwelled for 300 s to ensure fully melting of the sample, cooled by ~1.25 K s⁻¹ to the dwell temperature of 1173 K (undercooling ΔT = 133 K) and dwelled for 3360 s [the dwell time was set to ca. 1 h, a reasonable time in accordance with the results of Krüger and Deubener (2014)]. After dwelling the sample was immediately heated again to start the next run. In total 284 (= N₀) runs were performed. In each run, the time elapsed before the first supercritical nucleus is formed (δ_N and δ_N+1) was calculated by subtracting the beginning of the isothermal hold (t_b(N) and t_b(N+1)) from the crystallization onset time (t_N and t_N+1) of the isothermal exothermal DSC signal (blue solid line in Figure 1). We assume that the recorded crystallization onset times follow the same distribution as δ_N and δ_N+1 since the time for crystal growth is negligible at this high temperature.

FIGURE 1

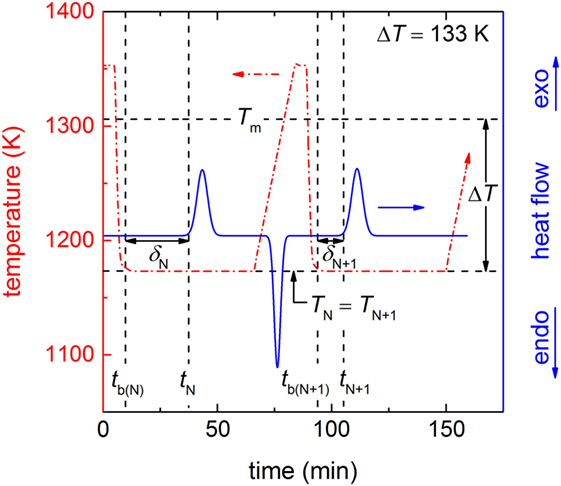
Figure 1. Scheme of the DSC protocol for two subsequent cooling-dwelling runs (N and N + 1) in the isothermal operating mode (ΔT = 133 K). The red dashed-dotted line shows the progression of the temperature of the heating-dwelling–cooling-dwelling cycles. The black horizontal dashed lines are T_m and the nucleation temperature of the runs N and N + 1 with T_N = T_N+1 = 1173 K, thus ΔT = 133 K (black double arrow). The black vertical dashed lines show the times of the beginning of the isothermal hold of the runs N and N + 1 with t_{b (N)} and t_{b (N+1)}, respectively and the times of the start of the crystallization of both runs with t_N and t_N+1. Herein, the beginning of the crystallization equals the onset of the exothermal peak in the DSC signal (blue solid line). The time of the formation of the first supercritical nucleus in each run (black horizontal double arrows) δ_N (for run N) and δ_{N + 1} (for run N + 1) is calculated by t_N − t_{b (N)} and t_N+1 − t_{b (N+1)}, respectively.

Results

The basic result of our experiment is a histogram of the time of the formation of the first supercritical nucleus for each run δ_N in dependence of the run number N (Figure 2). This histogram provides the following information: first, 26 runs were crystallized before the dwell temperature at ΔT = 133 K was reached (δ_N < 0 s, blue dashed-dotted line of Figure 2) and 21 runs remained uncrystallized due to the programmed maximum dwell time of 3360 s (δ_N > 3360 s, red dashed-dotted line of Figure 2). Second, the histogram shows a random distribution of δ_N which indicates that the preferred HET nucleation site is continuously active during the entire experiment. A fast Fourier transformation (not shown) proved absence of any diurnal or other periodic behavior. One may assume that the crystal nucleates at the three-phase boundary between the silicate melt, the crucible wall, and the nitrogen atmosphere, but this is not known. Furthermore, the silhouette of Figure 2 (black outline of the time elapsed before the first supercritical nucleus is formed) seems to be horizontal, which indicates that compositional changes of the melt due to possible nitrogen dissolution and lithium evaporation at the surface are negligible. Furthermore, no shift in the integrated signal values was observed (not shown) which confirms the absence of any traceable mass loss during the entire period of the experiment.

FIGURE 2

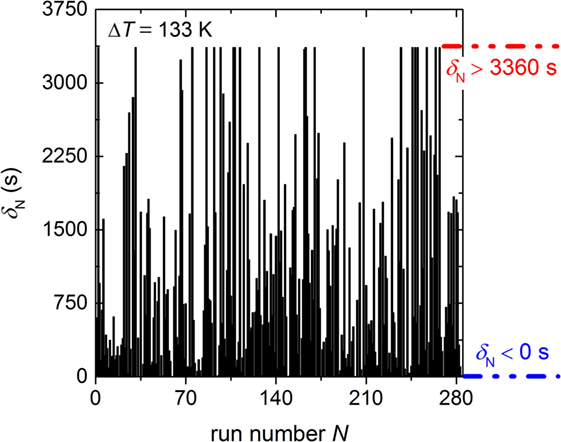
Figure 2. Time of formation of the first supercritical nucleus δ_N in dependence of the run number for the undercooling of 133 K. It has to be noted that 26 runs crystallized during cooling to the dwell temperature (δ_N < 0 s; blue dashed-dotted line) and 21 runs were not crystallizing within the dwell time 3360 s (δ_N > 3360 s; red dashed-dotted line).

In order to determine the HET steady-state nucleation rate I_{0 (HET)} from this isothermal experiment, the relative frequencies of the number of runs remained unfrozen after a certain time are calculated. The procedure is similar to the calculation of the survival curve in Barlow and Haymet (1995) and Krüger and Deubener (2014). The δ_N data of Figure 2 are first arranged according to their length. At the shortest δ_N (= 0 s), there are 258 runs uncrystallized (26 runs crystallized during cooling to the dwell temperature). In all other runs, crystallization occurred at larger δ_N. For δ_N = 0, the uncrystallized fraction is N(δ_N = 0)/N₀ = 258/284 = 0.908. For the second shortest δ_N, the fraction uncrystallized is 257/284 = 0.905 and so on. The last N(δ_N)/N₀ fraction calculated in that way is 21/284 = 0.074 at δ_N = 3342 s since 21 runs were still uncrystallized at the end of the programmed isothermal hold. This fraction is set to 0. The calculated fractions N(δ_N)/N₀ are plotted as a function of δ_N (Figure 3). The distribution curve shows a simple exponential decay that illustrates an increase in the nucleation probability with longer δ_N. The nucleation probability can be described by a simple first-order rate equation

$\frac{N\left({\mathrm{\delta }}_{\text{N}}\right)}{N_0}=A\exp \left(-I_{0\left(\text{HET}\right)}{\mathrm{\delta }}_{\text{N}}\right)$ (1)

and its logarithmic form

$\ln \left(\frac{N\left({\mathrm{\delta }}_{\text{N}}\right)}{N_0}\right)=\ln \left(A\right)-I_{0\left(\text{HET}\right)}{\mathrm{\delta }}_{\text{N}}$ (2)

where the constant A accounts for the initially crystallized fraction at δ_N = 0. Equation 2 is shown by the insert of Figure 3. The apparently linear dependence of the data on δ_N confirmed first-order reaction kinetics, and fitting the data (green solid line in Figure 3) results in a HET crystal nucleation rate of I_{0 (HET)} = (9.19 ± 0.04) × 10⁻⁴ s⁻¹. We note that exclusion of the 26 runs crystallized before the isothermal hold is reached results in the same value of I_{0 (HET)} but the parameter A of Eq. 1 will become unity. However, we think that the consideration of all data points in the probability distribution as shown in Figure 3 is the most appropriate linking to the stochastic experiment.

FIGURE 3

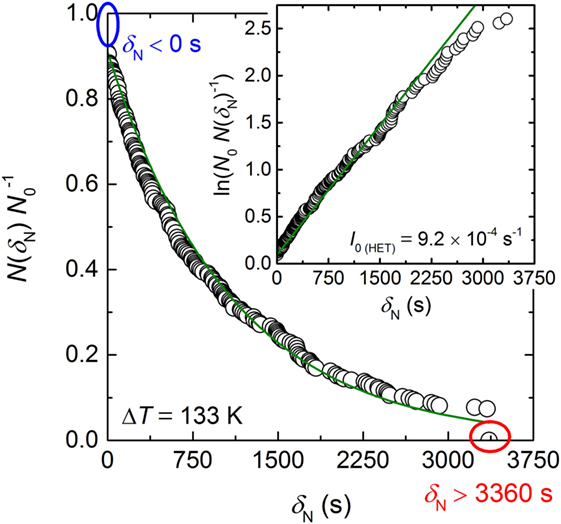
Figure 3. Probability distribution of the fraction of runs uncrystallized (N(δ_N) N₀⁻¹) in dependence of δ_N. The ovals (blue and red) correspond to the dashed-dotted lines of Figure 2. The insert shows the logarithmic Eq. 2. I_{0 (HET)} is given as the slope of the linear dependence. The green solid line is the best linear fit through the data with a regression coefficient R² = 0.995.

Discussion

The most striking feature of the results is that the found exponential decay of Figure 3 is similar to those reported for seeded water (Barlow and Haymet, 1995; Heneghan et al., 2001, 2002). This underlines the fundamental character of crystal nucleation as a stochastic process obeying first-order reaction kinetics. However, one should note that due to the experimental constraints, such as the limited cooling rate to reach the dwell temperature and the restricted dwell time of 3360 s, 47 of the 248 runs are not captured by the probability distribution. Thus, a second crystal nucleation mechanism might be active with characteristic time scales t_N < t_{b (N)} and t_N > δ_N (3360 s). This assumption is supported by the fact that the long time fractions of Figure 3 show a negative deviation from the proposed linearity. On the other hand, the negative deviation can also arise from an insufficient number of cooling runs preventing good statistics and, therefore, underestimating N(δ_N)/N₀ at long times.

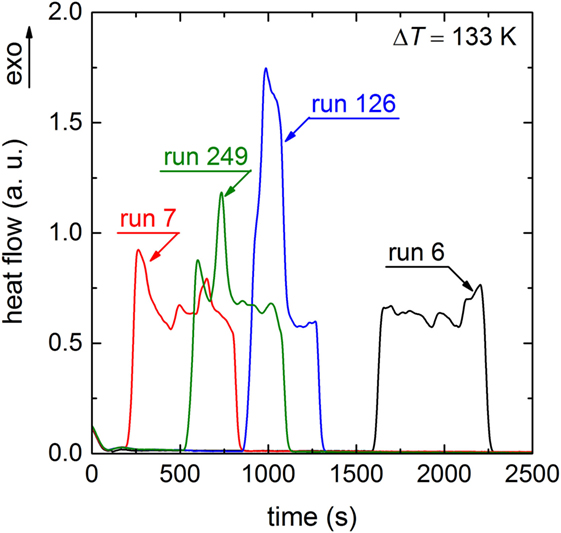
In order to exclude memory effects between adjacent runs of the histogram (Figure 2), a Pearson correlation test (Barlow and Haymet, 1995; Heneghan et al., 2001) was performed (not shown). A Pearson correlation coefficient r = 0.01 was obtained, which confirms that the probability of having correlation between adjacent runs is close to 0. The exclusion of memory effects is illustrated by different onset times of adjacent runs (Figure 4). Herein, the runs 6 and 7 exhibit significantly different crystallization onset times. Moreover, the individual evolution of the heat release of each run of Figure 4 reveals growth of one or only few crystals (Krüger and Deubener, 2014). A larger ensemble of growing crystals would lead to an averaged signal shape (Gaussian) as it is typical for heating lithium disilicate glasses in DTA/DSC experiments from temperatures below glass transformation (Krüger et al., 2013).

FIGURE 4

Figure 4. DSC crystallization peaks of runs 6, 7, 126, and 249 during dwelling at ΔT = 133 K.

Additionally to the visual inspection of the signal’s shape the broadness is analyzed. As an example, the signal of run 249 exhibits a broadness of 600 s (Figure 4). Assuming only one growing crystal and a crystal size that corresponds to the circumference of the crucible (the final geometry of the crystal after 284 runs is ring-shaped due to wetting of the crucible walls by the Li₂Si₂O₅ melt) leads to a crystal growth rate of 3.4 × 10⁻⁵ m s⁻¹. The approximated growth rate from the signal’s length is very close to the reported value (5.1 × 10⁻⁵ m s⁻¹) of Burgner and Weinberg (2001) for the same temperature that supports the assumption that the entire liquid volume is consumed by only one or few crystals. Few crystals would result in a somewhat smaller broadness (see, e.g., run 126 of Figure 4). A low number of crystals growing simultaneously at the surface are further supported by the observations of Ranasinghe et al. (2007). They found that only up to two crystals were simultaneously growing at the surface of levitated Li₂Si₂O₅ drops. Thus, in accordance with our DSC protocol (Figure 1), assigning the onset time of the crystallization peak to the time of the formation of the first supercritical nucleus seems to be reasonable.

In order to link I_{0 (HET)} to our previous stochastic experiment (Krüger and Deubener, 2014), which was run under constant cooling conditions (cooling rate = 0.083 K s⁻¹), nucleation rate data have to be derived from the undercooling-dependent N(ΔT)/N₀ vs. ΔT distribution curve (Figure 5). In this case, the probability curve with the fractions of runs remaining unfrozen N(ΔT)/N₀ at a certain undercooling is deconvoluted considering the temperature-dependent I_{0 (HET)}:

$I_{0\left(\text{HET}\right)}=\frac{C_1}{\mathrm{\eta }}\exp \left(-\frac{C_2}{T\mathrm{\Delta }{T}^2}\right)$ (3)

where C₁ and C₂ are temperature-independent constants and η is the viscosity of the Li₂Si₂O₅ melt. In order to determine C₁ and C₂ from the isochronal experiment, Eq. 3 is inserted in Eq. 1 and the parameter A is set to unity. By doing so, we assume that the crystal nucleation process is independent on the cooling rate. Rearranging the equation and taking the logarithm results in:

$\ln \left[\frac{\mathrm{\eta }}{{\mathrm{\delta }}_{\text{N}}}\ln \left(\frac{N_0}{N\left(\mathrm{\Delta }T\right)}\right)\right]=\ln \left(C_1\right)-\frac{C_2}{T\mathrm{\Delta }{T}^2}.$ (4)

FIGURE 5

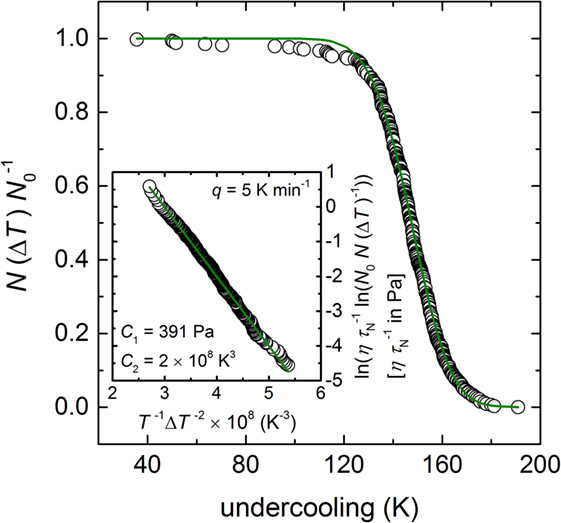
Figure 5. Probability distribution of the fraction of runs uncrystallized (N(ΔT) N₀⁻¹) in dependence of the undercooling taken from Krüger and Deubener (2014) and deconvoluted to determine the temperature-dependent nucleation rate curve (insert). The green solid line of the insert shows the best fit of Eq. 4 through the data points using the adjustable parameters C₁ = 391 Pa and C₂ = 2 × 10⁸ K³. Note the renaming τ_N ≡ δ_N.

By applying Eq. 4 to the already published data of Krüger and Deubener (2014) and the temperature-dependent viscosity of Krüger and Deubener (2015b), the adjustable parameter C₁ = 391 Pa and C₂ = 2 × 10⁸ K³ were determined (green solid line in the insert of Figure 5). We note the small deviation from the fitted trend of the runs of ΔT < 120 K that is either an artifact of an insufficient number of cooling runs or an indication of a second crystal nucleation mechanism as already discussed in case of the isothermal experiment.

Plotting together the HET nucleation rate curve of the above calculation in the range 0.62–0.92 T_m (red solid line), I_{0 (HET)} of the isothermal experiment at T = 0.898 T_m (red circle), I_{0 (HET)} of single-stage experiments in the range 0.64–0.68 T_m (Krüger and Deubener, 2015a) (red squares), and the HOM nucleation rates of double-stage experiments in the range 0.53–0.61 T_m (James, 1974; Zanotto and James, 1985; Barker et al., 1988; Deubener et al., 1993) (blue circles) on the reduced temperature scale T/T_m reveals that the HET nucleation rate curve is well separated from the HOM one. Maximum nucleation rates are found at T_{max (HOM)} = 0.55 T_m and T_{max (HET)} = 0.82 T_m for the HOM and the HET crystal nucleation, respectively (Figure 6). The equations of the classical nucleation theory and the material-specific input parameters listed in Tables 1 and 2 were used to fit these experimental data (OriginPro 9.0.0G; OriginLab Corp.). In order to calculate crystal nucleation rates (blue and red dashed-dotted lines in Figure 6) in the dimension of a frequency, HOM and HET nucleation rates were multiplied by the sample volume and the surface area, respectively. The liquid–crystal interfacial energy was treated as an adjustable parameter for which a linear temperature dependence in accordance with James (1985) was anticipated (Tables 1 and 2). The coordination number of the moving particle (CN = 2) and the number of atoms in a structural unit (n = 9) both entering the Eyring equation to adopt diffusivity to viscous flow where utilized from a previous study (Krüger and Deubener, 2015b). In case of the HET nucleation rate curve, additionally the number of active nucleation sites n_S = (0.023 ± 0.001) m⁻² and the wetting angle θ = (26.4 ± 0.1)° were adjusted to fit the data best. The resulting curves emphasize that at T_max the HET crystal nucleation rate is about two orders of magnitude smaller than the HOM one. The sum of both rates is the effective crystal nucleation rate that is highlighted by the black solid line in Figure 6. We note that possible sources of the small deviation between I_{0 (HET)} of the isothermal and the isochronal statistical experiment are differences in the glass composition and changes in the quality of the crucible used in the two studies.

FIGURE 6

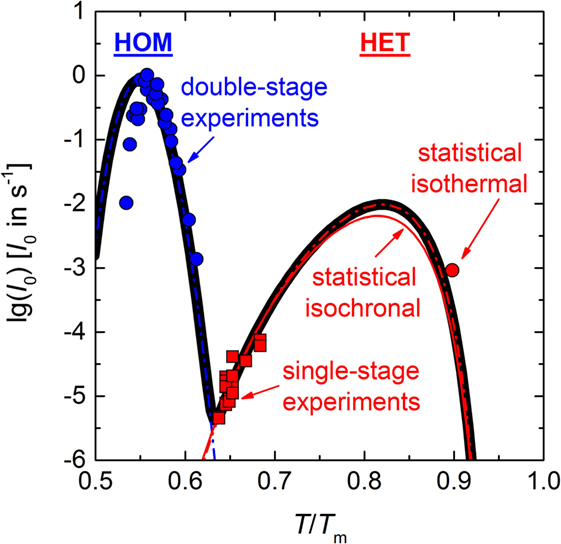
Figure 6. Temperature-dependent homogeneous (HOM) and heterogeneous (HET) nucleation rate curves (blue and red dashed-dotted lines, respectively) and the effective nucleation rate curve (black solid line). Data: surface nucleation rate calculated by Eq. 3 and using the constants C₁ and C₂ as determined in Figure 5 (red solid line), I_{0 (HET)} of the isothermal experiment of Figure 3 (red circle), I_{0 (HET)} as determined from impingement times of single-stage experiments (Krüger and Deubener, 2015a) (red squares). Homogeneous nucleation rates of double-stage experiments (James, 1974; Zanotto and James, 1985; Barker et al., 1988; Deubener et al., 1993) (blue circles).

TABLE 1

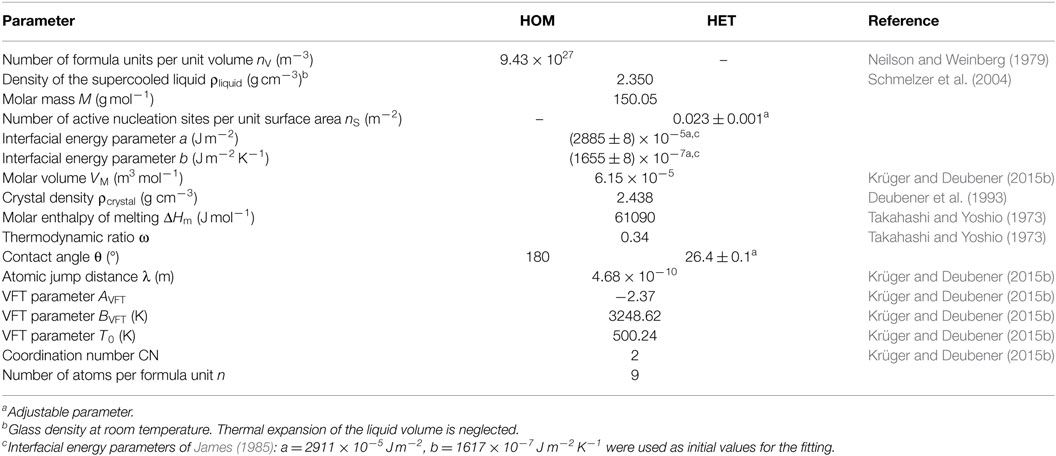
Table 1. Parameters of the calculation of the homogeneous (HOM) and heterogeneous (HET) nucleation rate of Li₂Si₂O₅ crystals in lithium disilicate melt.

TABLE 2

Table 2. Equations of the calculation of the homogeneous (HOM) and heterogeneous (HET) crystal nucleation rate.

With regard to the large difference in T_max between surface and volume crystal nucleation in lithium disilicate, it is interesting to compute a TTT diagram for the crystalline fraction α = 10⁻⁶ (Uhlmann, 1972) using the following two equations (Zanotto, 1996):

$t_{\text{V}}={\left(-\frac{3\ln \left(1-\mathrm{\alpha }\right)}{\mathrm{\pi }{I}_{0\left(\text{HOM}\right)}{U}^3}\right)}^{\frac{1}{4}}$ (5)

and

$t_{\text{S}}={\left(-\frac{\ln \left(1-\mathrm{\alpha }\right)}{I_{0\left(\text{HET}\right)}{U}^2}\right)}^{\frac{1}{3}}.$ (6)

In Equations 5 and 6, t_V and t_S are the times necessary to crystallize 10⁻⁴ percent of the glass in the volume and at the surface, respectively. U is the crystal growth rate that is utilized from the data compilation of Burgner and Weinberg (2001). Figure 7 shows that crystallization initiated by HET surface nucleation (red dashed-dotted line) and HOM volume nucleation (blue dashed-dotted line) overlap only partially. In order to calculate the overall crystallization time, Eq. 6 was used, while I_{0 (HOM)} was converted to a surface nucleation rate [I_{0 (HOM, S)} = I_{0 (HOM, V)}^2/3 × t_V^−1/3 (Krüger and Deubener, 2015a), the uncertainty of the conversion is less than 1%] and added to the HET nucleation rate. The shape of the overall time with a “double-nose” (black solid line) resembles those of an aqueous lithium chloride solution (MacFarlane et al., 1983) and of polybutylene terephthalate (Androsch et al., 2015). The double-nose diagram helps to explain the formation of a coast-island microstructure if lithium disilicate glass is heated at low rates from below T_g in practice. In agreement with the microstructures shown for different heating rates in Krüger and Deubener (2015a), larger heating rates suppress HOM volume nucleation of crystals and allow for surface crystallization only. By contrast, if a lithium disilicate glass sample is subjected at the first stage of the double-stage heat treatment to a temperature in the HOM nucleation range dwelling will form initially crystal nuclei in the volume (James, 1974). Additionally, the distinct HET nose of the TTT diagram emphasizes that cooling a lithium disilicate melt from above T_m always leads to a crystallized surface and dictates the critical cooling rate in this system. The latter is estimated by the so-called nose method using the simple calculus R_c = (T_n − T_m)/t_n (Uhlmann, 1972). With the coordinates of the nose T_n = 1122 K and t_n = 2.51 s, the critical cooling rate is ca. 73 K s⁻¹ (green dotted line in Figure 7).

FIGURE 7

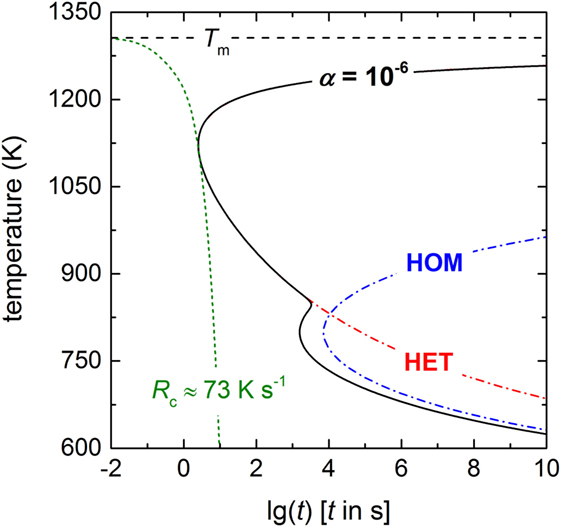
Figure 7. TTT diagram of lithium disilicate for a crystallized fraction of α = 10⁻⁶ (black solid line), including both homogeneous crystallization in the volume (blue dashed-dotted line, HOM) and heterogeneous crystallization at the surface (red dashed-dotted line, HET) using Equations 5 and 6. The critical cooling rate R_c is ~73 K s⁻¹ (green dotted line).

We are fully aware that R_c is overestimated by the TTT representation (Xu et al., 2013). A TTT diagram has to be converted to a CCT diagram to calculate the critical cooling rate more exactly (Grange and Kiefer, 1941; Zhu et al., 2006). However, it was shown by Davies (1976), Ramachandrarao et al. (1977), Uhlmann and Yinnon (1983), and Scherer (1991) that R_c calculated from a TTT diagram meets the experimental result within one order of magnitude. A first attempt to determine TTT and CCT diagrams in lithium disilicate was performed by Zhu et al. (2006) 10 years ago. They spotted a small glass volume on the tip of a Pt-thermocouple and measured the onset temperature and time of the crystallization peak in isochronal and isothermal mode of operation. By comparison to Figure 7, their single nose can be clearly identified as the HET part of the overall crystallization leading to exclusively surface crystallization.

Conclusion

The most striking outcome of the present study is the “double-nose” TTT diagram of lithium disilicate due to a decoupling of the nucleation mechanisms of HOM volume nucleation of crystals at large undercoolings (0.53–0.61 T_m) and HET surface nucleation of crystals at smaller undercoolings (0.62–0.92 T_m). This behavior is the origin for the evolution of coast-island microstructures of lithium disilicate in practice. Due to the stochastic experiments at small undercoolings HET nucleation is measurable and the corresponding rate with a maximum at 1071 K is quantified for the first time. Based on the calculated TTT diagram the critical cooling rate is about 73 K s⁻¹.

The results emphasize that exploring the time average of nucleation events by thermal cycling is a novel and highly attractive route to study HET crystal nucleation in silicate glasses. In particular, they point out that the rare data on HET nucleation rates and critical cooling rates that are based on one-time cooling experiments have to be reconsidered to include statistical certainty.

Author Contributions

SK performed experiments. SK and JD prepared manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge support by Open Access Publishing Fund of Clausthal University of Technology.

References

Androsch, R., Rhoades, A. M., Stolte, I., and Schick, C. (2015). Density of heterogeneous and homogeneous crystal nuclei in poly (butylene terephthalate). Eur. Polym. J. 66, 180–189. doi: 10.1016/j.eurpolymj.2015.02.013

CrossRef Full Text | Google Scholar

Barker, M. F., Wang, T.-H., and James, P. F. (1988). Nucleation and growth kinetics of lithium disilicate and lithium metasilicate in lithia-silica glasses. Phys. Chem. Glasses 29, 240–248.

Google Scholar

Barlow, T. W., and Haymet, A. D. J. (1995). ALTA: an automated lag-time apparatus for studying the nucleation of supercooled liquids. Rev. Sci. Instrum. 66, 2996–3007. doi:10.1063/1.1145586

CrossRef Full Text | Google Scholar

Burgner, L. L., and Weinberg, M. C. (2001). An assessment of crystal growth behavior in lithium disilicate glass. J. Non-Cryst. Solids 279, 28–43. doi:10.1016/S0022-3093(00)00325-2

CrossRef Full Text | Google Scholar

Burgner, L. L., Weinberg, M. C., Lucas, P., Soares, P. C. Jr., and Zanotto, E. D. (1999). XRD investigation of metastable phase formation in Li₂O-2SiO₂ glass. J. Non-Cryst. Solids 255, 264–268. doi:10.1016/S0022-3093(99)00376-2

CrossRef Full Text | Google Scholar

Cronin, D., and Pye, L. D. (1986). Platinum catalyzed crystallization of Li₂O⋅2SiO₂ glass. J. Non-Cryst. Solids 84, 196–205. doi:10.1016/0022-3093(86)90778-7

CrossRef Full Text | Google Scholar

Davies, H. A. (1976). Formation of metallic glasses. Phys. Chem. Glasses 17, 159–173.

Google Scholar

Deubener, J., Brückner, R., and Sternitzke, M. (1993). Induction time analysis of nucleation and crystal growth in di- and metasilicate glasses. J. Non-Cryst. Solids 163, 1–12. doi:10.1016/0022-3093(93)90638-E

CrossRef Full Text | Google Scholar

Dressler, M., Rüdinger, B., and Deubener, J. (2011). An in situ high-temperature X-ray diffraction study of early-stage crystallization in lithium alumosilicate glass-ceramics. J. Am. Ceram. Soc. 94, 1421–1426. doi:10.1111/j.1551-2916.2010.04252.x

CrossRef Full Text | Google Scholar

Dressler, M., Rüdinger, B., and Deubener, J. (2014). Crystallization kinetics in a lithium alumosilicate glass using SnO₂ and ZrO₂ additives. J. Non-Cryst. Solids 389, 60–65. doi:10.1016/j.jnoncrysol.2014.02.008

CrossRef Full Text | Google Scholar

Eyring, H., Henderson, D., Stover, B. J., and Eyring, E. M. (1982). Statistical Mechanics and Dynamics, 2nd Edn. New York, NY: Wiley.

Google Scholar

Fokin, V. M., Kalinina, A. M., and Filipovich, V. N. (1981). Nucleation in silicate glasses and effect of preliminary heat treatment on it. J. Cryst. Growth 52, 115–121. doi:10.1016/0022-0248(81)90178-0

CrossRef Full Text | Google Scholar

Fokin, V. M., Zanotto, E. D., and Schmelzer, J. W. P. (2010a). On the thermodynamic driving force for interpretation of nucleation experiments. J. Non-Cryst. Solids 356, 2185–2191. doi:10.1016/j.jnoncrysol.2010.07.040

CrossRef Full Text | Google Scholar

Fokin, V. M., Cabral, A. A., Reis, R. M. C. V., Nascimento, M. L. F., and Zanotto, E. D. (2010b). Critical assessment of DTA-DSC methods for the study of nucleation kinetics in glasses. J. Non-Cryst. Solids 356, 358–367. doi:10.1016/j.jnoncrysol.2009.11.038

CrossRef Full Text | Google Scholar

Fokin, V. M., Zanotto, E. D., Yuritsyn, N. S., and Schmelzer, J. W. P. (2006). Homogeneous crystal nucleation in silicate glasses: a 40 years perspective. J. Non-Cryst. Solids 352, 2681–2714. doi:10.1016/j.jnoncrysol.2006.02.074

CrossRef Full Text | Google Scholar

Fulcher, G. S. (1925). Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 8, 789–794. doi:10.1111/j.1151-2916.1925.tb16731.x

CrossRef Full Text | Google Scholar

Grange, R. A., and Kiefer, J. M. (1941). Transformation of austenite on continuous cooling and its relation to transformation at constant temperature. Trans. ASM 29, 85.

Google Scholar

Gutzow, I., and Schmelzer, J. (1995). Nucleation in Glass-Forming Systems, The Vitreous State. Berlin: Springer, 218–281.

Google Scholar

Hench, L. L., Frieman, S. W., and Kinser, D. L. (1971). Early stages of crystallisation in a Li₂O-2SiO₂ Glass. Phys. Chem. Glasses 12, 58–63.

Google Scholar

Heneghan, A. F., and Haymet, A. D. J. (2002). Liquid-to-crystal nucleation: a new generation lag-time apparatus. J. Chem. Phys. 117, 5319–5327. doi:10.1063/1.1497635

CrossRef Full Text | Google Scholar

Heneghan, A. F., Wilson, P. W., and Haymet, A. D. J. (2002). Heterogeneous nucleation of supercooled water, and the effect of an added catalyst. Procs. Nat. Acad. Sci. U.S.A. 99, 9631–9634. doi:10.1073/pnas.152253399

PubMed Abstract | CrossRef Full Text | Google Scholar

Heneghan, A. F., Wilson, P. W., Wang, G., and Haymet, A. D. J. (2001). Liquid-to-crystal nucleation: automated lag-time apparatus to study supercooled liquids. J. Chem. Phys. 115, 7599–7608. doi:10.1063/1.1407290

CrossRef Full Text | Google Scholar

Iqbal, Y., Lee, W. E., Holland, D., and James, P. F. (1999). Crystal nucleation in P₂O₅-doped lithium disilicate glasses. J. Mater. Sci. 34, 4399–4411. doi:10.1023/A:1004668701163

CrossRef Full Text | Google Scholar

James, P. F. (1974). Kinetics of crystal nucleation in lithium silicate-glasses. Phys. Chem. Glasses 15, 95–105.

Google Scholar

James, P. F. (1985). Kinetics of crystal nucleation in silicate glasses. J. Non-Cryst. Solids 73, 517–540. doi:10.1016/0022-3093(85)90372-2

CrossRef Full Text | Google Scholar

James, P. F. (1989). “Volume nucleation in silicate glasses,” in Glasses and Glass-Ceramics, ed. M. H. Lewis (New York: Chapman and Hall), 59–105.

Google Scholar

James, P. F., Scott, B., and Armstrong, P. (1978). Kinetics of crystal nucleation in lithium disilicate glass. A comparison between melts prepared in platinum and silica crucibles and between melts prepared from ordinary and high purity starting materials. Phys. Chem. Glasses 19, 24–27.

Google Scholar

Kelton, K. F. (2000). Kinetic model for nucleation in partitioning systems. J. Non-Cryst. Solids 274, 147–154. doi:10.1016/S0022-3093(00)00185-X

CrossRef Full Text | Google Scholar

Kracek, F. C. (1930). The binary system Li₂O-SiO₂. J. Phys. Chem. 34, 2641–2650. doi:10.1021/j150318a001

CrossRef Full Text | Google Scholar

Krüger, S., and Deubener, J. (2014). Stochastic nature of the liquid-to-crystal heterogeneous nucleation of supercooled lithium disilicate liquid. J. Non-Cryst. Solids 388, 6–9. doi:10.1016/j.jnoncrysol.2014.01.036

CrossRef Full Text | Google Scholar

Krüger, S., and Deubener, J. (2015a). Heterogeneous surface nucleation of lithium disilicate glass: an isothermal DSC study. J. Non-Cryst. Solids 417, 45–51. doi:10.1016/j.jnoncrysol.2015.03.013

CrossRef Full Text | Google Scholar

Krüger, S., and Deubener, J. (2015b). Lag time to crystal nucleation of supercooled lithium disilicate melts: a test of the classical nucleation theory. J. Non-Cryst. Solids 426, 1–6. doi:10.1016/j.jnoncrysol.2015.06.023

CrossRef Full Text | Google Scholar

Krüger, S., Deubener, J., Ritzberger, C., and Höland, W. (2013). Nucleation kinetics of lithium metasilicate in ZrO₂-bearing lithium disilicate glasses for dental application. Int. J. Appl. Glass Sci. 4, 9–19. doi:10.1111/ijag.12011

CrossRef Full Text | Google Scholar

MacFarlane, D. R., Kadiyala, R. K., and Angell, C. A. (1983). Homogeneous nucleation and growth of ice from solutions. TTT curves, the nucleation rate, and the stable glass criterion. J. Chem. Phys. 79, 3921–3927. doi:10.1063/1.446260

CrossRef Full Text | Google Scholar

Maeda, N., Wells, D., Becker, N. C., Hartley, P. G., Wilson, P. W., Haymet, A. D. J., et al. (2011). Development of a high pressure automated lag time apparatus for experimental studies and statistical analyses of nucleation and growth of gas hydrates. Rev. Sci. Instrum. 82, 065109. doi:10.1063/1.3602926

PubMed Abstract | CrossRef Full Text | Google Scholar

Maeda, N., Wells, D., Hartley, P. G., and Kozielski, K. A. (2012). Statistical analysis of supercooling in fuel gas hydrate systems. Energy Fuels 26, 1820–1827. doi:10.1021/ef201965z

CrossRef Full Text | Google Scholar

Matusita, K., and Tashiro, M. (1973). Rate of homogeneous nucleation in alkali disilicate glasses. J. Non-Cryst. Solids 11, 471–484. doi:10.1016/0022-3093(73)90092-6

CrossRef Full Text | Google Scholar

Mishima, N., Wakasugi, T., and Ota, R. (2006). Bulk crystallisation in mixed alkali disilicate glasses doped with a nucleating agent. Phys. Chem. Glasses 47, 259–265.

Google Scholar

Morton, C. W., Hofmeister, W. H., Bayuzick, R. J., and Robinson, M. B. (1994). A statistical approach to understanding nucleation phenomena. Mater. Sci. Eng. A 178, 209–215. doi:10.1016/0921-5093(94)90545-2

CrossRef Full Text | Google Scholar

Müller, R., Zanotto, E. D., and Fokin, V. M. (2000). Surface crystallization of silicate glasses: nucleation sites and kinetics. J. Non-Cryst. Solids 274, 208–231. doi:10.1016/S0022-3093(00)00214-3

CrossRef Full Text | Google Scholar

Narayan, K. L., Kelton, K. F., and Ray, C. S. (1996). Effect of Pt doping on nucleation and crystallization in Li₂O⋅2SiO₂ glass: experimental measurements and computer modeling. J. Non-Cryst. Solids 195, 148–157. doi:10.1016/0022-3093(95)00526-9

CrossRef Full Text | Google Scholar

Nascimento, M. L. F., Fokin, V. M., Zanotto, E. D., and Abyzov, A. S. (2011). Dynamic processes in a silicate liquid from above melting to below the glass transition. J. Chem. Phys. 135, 194703. doi:10.1063/1.3656696

PubMed Abstract | CrossRef Full Text | Google Scholar

Neilson, G. F., and Weinberg, M. C. (1979). A test of classical nucleation theory: crystal nucleation of lithium disilicate glass. J. Non-Cryst. Solids 34, 137–147. doi:10.1016/0022-3093(79)90013-9

CrossRef Full Text | Google Scholar

Ota, R., Mishima, N., Wakasugi, T., and Fukunaga, J. (1997). Nucleation of Li₂O-SiO₂ glass and its interpretation based on a new liquid model. J. Non-Cryst. Solids 219, 70–74. doi:10.1016/S0022-3093(97)00253-6

CrossRef Full Text | Google Scholar

Ramachandrarao, P., Cantor, B., and Cahn, R. W. (1977). Viscous behaviour of undercooled metallic melts. J. Non-Cryst. Solids 24, 109–120. doi:10.1016/0022-3093(77)90065-5

CrossRef Full Text | Google Scholar

Ranasinghe, K. S., Ray, C. S., Day, D. E., Rogers, J. R., Hyers, R. W., and Rathz, T. (2007). Containerless processing of a lithium disilicate glass. J. Mater. Sci. 42, 4291–4297. doi:10.1007/s10853-006-1232-z

CrossRef Full Text | Google Scholar

Ray, C. S., and Day, D. E. (1996). Identifying internal and surface crystallization by differential thermal analysis for the glass-to-crystal transformations. Thermochim. Acta 280/281, 163–174. doi:10.1016/0040-6031(95)02640-1

CrossRef Full Text | Google Scholar

Ray, C. S., Day, D. E., Huang, W., Narayan, K. L., Cull, T. S., and Kelton, K. F. (1996). Non-isothermal calorimetric studies of the crystallization of lithium disilicate glass. J. Non-Cryst. Solids 204, 1–12. doi:10.1016/0022-3093(96)00401-2

CrossRef Full Text | Google Scholar

Rowlands, E. G., and James, P. F. (1979). Analysis of steady state crystal nucleation rates in glasses. Part 1. Methods of analysis and application to lithium disilicate glass., Part 2. Further comparison between theory and experiment for lithium disilicate glass. Phys. Chem. Glasses 20, 9–14.

Google Scholar

Scherer, G. W. (1991). “Glass formation and relaxation,” in Materials Science and Technology – A Comprehensive Treatment, Vol. 9: Glasses and Amorphous Materials, eds R. W. Cahn, P. Haasen, E. J. Kramer, and J. Zarzycki (Weinheim: VCH Verlagsgesellschaft mbH), 119–173.

Google Scholar

Schmelzer, J. W. P., Potapov, O. V., Fokin, V. M., Müller, R., and Reinsch, S. (2004). The effect of elastic stress and relaxation on crystal nucleation in lithium disilicate glass. J. Non-Cryst. Solids 333, 150–160. doi:10.1016/j.jnoncrysol.2003.10.002

CrossRef Full Text | Google Scholar

Takahashi, K., and Yoshio, T. (1973). Thermodynamic quantities of alkali silicates in the temperature range from 25°C to melting point. Yogyo Kyokai Shi 81, 524–533. doi:10.2109/jcersj1950.81.940_524

CrossRef Full Text | Google Scholar

Tammann, G., and Hesse, W. (1926). Die Abhängigkeit der Viscosität von der Temperatur bei unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 156, 245–257. doi:10.1002/zaac.19261560121

CrossRef Full Text | Google Scholar

Tomozawa, M. (1972). Liquid phase separation and crystal nucleation in Li₂O–SiO₂ glasses. Phys. Chem. Glasses 13, 161–166.

Google Scholar

Tomozawa, M. (1973). Liquid phase separation and crystal growth in Li₂O-SiO₂ glass. Phys. Chem. Glasses 14, 112–115.

Google Scholar

Toschev, S. (1973). “Homogeneous nucleation,” in Crystal Growth: An Introduction, ed. P. Hartman (Amsterdam: North-Holland Publishing Co.), 1–49.

Google Scholar

Toschev, S., and Gutzow, I. (1972). Nichtstationäre Keimbildung: Theorie und Experiment. Krist. Tech. 7, 43–73. doi:10.1002/crat.19720070108

CrossRef Full Text | Google Scholar

Toschev, S., and Markov, I. (1967). Electrolytic nucleation of cadmium. Electrochim. Acta 12, 281–286. doi:10.1016/0013-4686(67)80006-9

CrossRef Full Text | Google Scholar

Toschev, S., Milchev, A., and Stoyanov, S. (1972). On some probabilistic aspects of the nucleation process. J. Cryst. Growth 1, 123–127. doi:10.1016/0022-0248(72)90073-5

CrossRef Full Text | Google Scholar

Turnbull, D. (1956). “Phase changes,” in Solid State Physics, Vol. 3, eds F. Seitz and D. Turnbull (New York: Academic Press), 225–306.

Google Scholar

Uhlmann, D. R. (1972). A kinetic treatment of glass formation. J. Non-Cryst. Solids 7, 337–348. doi:10.1016/0022-3093(72)90269-4

CrossRef Full Text | Google Scholar

Uhlmann, D. R., and Yinnon, H. (1983). “The formation of glasses,” in Glass: Science and Technology, Vol. 1: Glass-Forming Systems, eds D. R. Uhlmann and N. J. Kreidl (New York, London, Paris, San Diego, San Francisco, Sao Paulo, Sydney, Tokyo, Toronto: Academic Press, Inc.), 1–47.

Google Scholar

Uttormark, M. J., Zanter, J. W., and Perepezko, J. H. (1997). Repeated nucleation in an undercooled aluminum droplet. J. Cryst. Growth 177, 258–264. doi:10.1016/S0022-0248(96)01121-9

CrossRef Full Text | Google Scholar

Vogel, H. (1921). The law of the relation between the viscosity of liquids and the temperature. Phys. Z. 22, 645–646.

Google Scholar

Weinberg, M. C., and Neilson, G. F. (1985). On the possibility of critical radius measurements in the homogeneous crystal nucleation of glass. J. Non-Cryst. Solids 74, 177–179. doi:10.1016/0022-3093(85)90412-0

CrossRef Full Text | Google Scholar

Weinberg, M. C., and Zanotto, E. D. (1989). Re-examination of the temperature dependence of the classical nucleation rate: homogeneous crystal nucleation in glass. J. Non-Cryst. Solids 108, 99–108. doi:10.1016/0022-3093(89)90337-2

CrossRef Full Text | Google Scholar

Wilde, G., Santhaweesuk, C., Sebright, J. L., Bokeloh, J., and Perepezko, J. H. (2009). Kinetics of heterogeneous nucleation on intrinsic nucleants in pure fcc transition metals. J. Phys. Condens. Matter 21, 464113. doi:10.1088/0953-8984/21/46/464113

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilde, G., Sebright, J. L., and Perepezko, J. H. (2006). Bulk liquid undercooling and nucleation in gold. Acta Mater. 54, 4759–4769. doi:10.1016/j.actamat.2006.06.007

CrossRef Full Text | Google Scholar

Wilson, P. W., Lester, D., and Haymet, A. D. J. (2005). Heterogeneous nucleation of clathrates from supercooled tetrahydrofuran (THF)/water mixtures, and the effect of an added catalyst. Chem. Eng. Sci. 60, 2937–2941. doi:10.1016/j.ces.2004.12.047

CrossRef Full Text | Google Scholar

Xu, K., Wang, Y., Li, J., and Li, Q. (2013). Critical cooling rate for the glass formation of ferromagnetic Fe80P13C7 alloy. Acta Metall. Sin. (Engl. Lett.). 26, 56–62. doi:10.1007/s40195-012-0117-1

CrossRef Full Text | Google Scholar

Yang, B., Abyzov, A. S., Zhuravlev, E., Gao, Y., Schmelzer, J. W. P., and Schick, C. (2013). Size and rate dependence of crystal nucleation in single tin drops by fast scanning calorimetry. J. Chem. Phys. 138, 054501. doi:10.1063/1.4789447

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, B., Gao, Y., Zou, C., Zhai, Q., Abyzov, A. S., Zhuravlev, E., et al. (2011). Cooling rate dependence of undercooling of pure Sn single drop by fast scanning calorimetry. Appl. Phys. A 104, 189–196. doi:10.1007/s00339-010-6100-7

CrossRef Full Text | Google Scholar

Yang, B., Gao, Y. L., Zou, C. D., Zhai, Q. J., Zhuravlev, E., and Schick, C. (2009). Repeated nucleation in an undercooled tin droplet by fast scanning calorimetry. Mater. Lett. 63, 2476–2478. doi:10.1016/j.matlet.2009.08.041

CrossRef Full Text | Google Scholar

Zanotto, E. D. (1987). Isothermal and adiabatic nucleation in glass. J. Non-Cryst. Solids 89, 361–370. doi:10.1016/S0022-3093(87)80278-8

CrossRef Full Text | Google Scholar

Zanotto, E. D. (1996). The applicability of the general theory of phase transformations to glass crystallization. Thermochim. Acta 28, 73–82. doi:10.1016/0040-6031(95)02636-3

CrossRef Full Text | Google Scholar

Zanotto, E. D. (1997). Metastable phases in lithium disilicate glasses. J. Non-Cryst. Solids 219, 42–48. doi:10.1016/S0022-3093(97)00249-4

CrossRef Full Text | Google Scholar

Zanotto, E. D., and James, P. F. (1985). Experimental tests of the classical nucleation theory for glasses. J. Non-Cryst. Solids 74, 373–394. doi:10.1016/0022-3093(85)90080-8

CrossRef Full Text | Google Scholar

Zhu, D., Zhou, W., Ray, C. S., and Day, D. E. (2006). Method for estimating continuous cooling transformation curves of glasses. Phys. Chem. Glasses 47, 271–277.

Google Scholar