- 1Center of Micro-BioRobotics, Istituto Italiano di Tecnologia, Pontedera, Italy
- 2Laboratory of Bio-Inspired and Graphene Nanomechanics, Department of Civil, Environmental and Mechanical Engineering, University of Trento, Trento, Italy
- 3School of Engineering and Materials Science, Queen Mary University of London, London, UK
- 4Italian Space Agency, Rome, Italy
Today, soft materials (e.g., elastomers, polymers, fabrics, etc.), with compliances and extensibilities not allowed by rigid components, are investigated in order to develop artificial tactile sensors that can emulate the adaptability of the natural tissues to objects and environment in general. This research is fueled by the increasing demand for conformable, yet functional and robust, systems in many fields from soft robotics to wearable systems and biomedical devices (Kim et al., 2013).
In the past decades, remarkable results were obtained in the design and fabrication of tactile sensors and, more in general, of electronic skins (e-skins) (Someya et al., 2004; Sekitani et al., 2008; Kim et al., 2011; Park et al., 2014; Xu et al., 2014; Zhang et al., 2015). These achievements were fundamental for a plethora of new applications, such as human–machine interfaces, body-integrated electronics, and medical/health-monitoring devices. Also, they offered very advanced technological solutions for robotics and wearable systems. From a mechanical point of view, flexible and stretchable substrates were chosen, while the integrated components went from rigid (Yang et al., 2010; Kim et al., 2011; Xu et al., 2014) to semi-rigid (Engel et al., 2005; Yang et al., 2008) and finally to flexible (Tien et al., 2014; Park et al., 2015; Zhang et al., 2015) and stretchable (Someya et al., 2004; Sekitani et al., 2008; Park et al., 2014; Chou et al., 2015) devices.
In particular, pressure sensors are widely applied in classical robotics, i.e., where the materials of the robot body are rigid. Thus, when positioning the sensors on the hosting structures, the sensors’ functionality is not affected by the mechanical characteristics of the robot itself, since the rigid and elastic materials do not store any mechanical energy. Hence, tactile sensors were developed and characterized as independent components that were integrated in the robot at a later stage. On the other hand, especially for integrating pressure sensors in a soft robot or in a wearable system, this approach would not give the desired results. Indeed, the mechanical characteristics of the soft robots or the natural skin, which act as hosting substrates, could reduce or even totally impair the correct functionality of such mechanical sensors. In particular, due to the substrate softness, the largest compression can occur in the substrate rather than in the sensing device. The abovementioned weaknesses can be overcome with an integrated approach (i.e., considering the mechanical characteristics of both sensing device and substrate) in the modeling, fabrication, and characterization of such systems. For instance, in the case of wearable systems, the properties of human skin, and underlying tissues and bones, should be taken into account; whereas in soft robotics, the materials used for fabricating them [e.g., mainly elastomers such as polydimethylsiloxane (PDMS) and Ecoflex® (Shepherd et al., 2011; Morin et al., 2012)] must be included as part of the working system. From the mechanical point of view, human skin can be approximated as a bilayer tissue standing on a soft substrate, with non-linear and viscoelastic properties (Hendriks et al., 2003) depending on several factors, such as the age, the sex, or the body region (Escoffier et al., 1989). The lower layer (hypodermis) has an average thickness around 0.8 mm, with a Young’s modulus around 2 kPa. Otherwise, the upper (dermis) has a thickness between 1.2 and 1.5 mm, with a Young’s modulus around 35 kPa, while the most superficial layer (epidermis) can be neglected from a mechanical point of view, due to its very low thickness (around 80 µm). Finally, the subcutaneous tissue (muscle) has an average Young’s modulus of 80 kPa (Pailler-Mattei et al., 2008). Looking at the soft robotics side, PDMS and Ecoflex® present non-linear and viscoelastic behaviors for high strain rates, while the stress–strain relationships are almost linear for strain under 40% (Case et al., 2015). In particular, PDMS is a transparent silicone with a Young’s modulus varying from 100 kPa to 4 MPa, mainly due to its curing temperature and to the mix ratio of prepolymers. Also, Ecoflex® has a Young’s modulus around 30–40 kPa (Case et al., 2015), and it is one of the very few materials available for mimicking the human skin mechanical behavior (Amjadi et al., 2015).
Hence, modeling the behavior of a soft pressure sensor on a multilayer soft substrate can be not trivial. In our opinion, analyzing the correlation between the mechanical and functional (e.g., electrical) behavior of sensors made of soft materials is mandatory. In particular, it is important to understand how the mechanical properties of the constituent materials of sensors affect the electrical response and to evaluate the influence of the soft structures and substrates in which they will be embedded. Then, these characteristics can be exploited to encode tactile cues more efficiently and with simpler designs. This requires the development of non-linear mechanical models, also considering the way the mechanical response of such materials is typically described in literature, i.e., with hyperelastic models like the Mooney–Rivlin, Ogden, or Fung (Fung, 1993; Holzapfel, 2000).
In the overall vision of designing innovative smart devices for soft robotics and wearable applications in the near future, here we present a case study evaluating the behavior of a skin-like soft pressure sensor when stimulated by external loads quasi-statically (i.e., the indentation velocity is low). This way, some theoretical insights can be given for future analyses of more complex stimuli. The sensor, shown in Figure 1A, is made of different soft layers. It is highly sensitive and can detect normal forces in the 20 N range. Since the sensor area is 8 mm × 8 mm, the pressure range is around 300 kPa. The device structure, sketched in Figure 1B, is built by integrating in between them two non-stretchable conductive textile electrodes (Zelt fabric, Mindsets Ltd., Whaltam Abbey, UK) and a thin film of Ecoflex®. It is a super soft silicone elastomer (Smooth-On 0010, USA), which acts as a deformable dielectric layer. The whole structure is embedded between two PDMS (Sylgard 184, Dow Corning, Midland, TX, USA) layers that insulate the textile electrodes while providing a soft and compliant surface to outer stimuli. In our case, we used a 1:10 mix ratio, with the films cured at room temperature for at least 24 h before the use. Regarding elastomeric layers, the corresponding Young’s modulus is around 3 MPa for PDMS and 30 kPa for Ecoflex. Both values have been measured by means of indentation tests. Moreover, a particular aspect that affects sensor response is given by the textile electrodes: they consist of copper/tin-coated woven fabric. The architecture of a woven fabric is such that small air volumes (i.e., sheds) are embedded among the warp and weft that confer unique properties to the tactile sensor. Indeed, a microporous structure is obtained in the active region of the device. When a pressure is applied, together with the compression of elastomeric layers, the sheds’ volume in the stimulated area is reduced relevantly, thereby resulting in an enhanced sensor response for a wider pressure range (Viry et al., 2014).
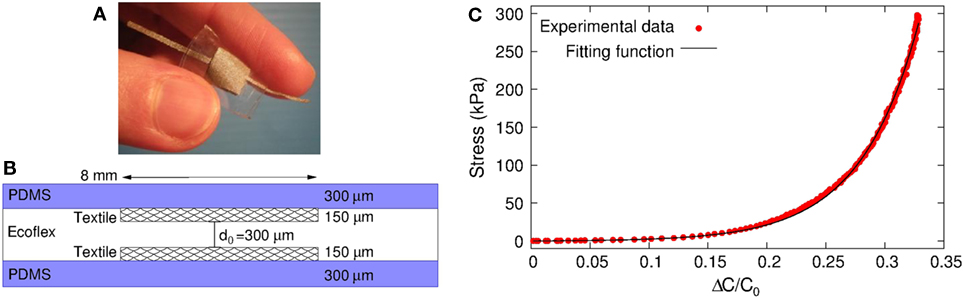
Figure 1. Picture (A) and schematic structure (B) of the soft capacitive pressure sensor based on conductive textile electrodes and silicone elastomers. (C) Stress vs. ΔC/C0 experimental data (red circles), compared to the fitting curve (black solid line) considering the Ecoflex dielectric layer as a Fung non-linear material.
A pressure applied on the sensor surface causes the variation of the dielectric layer thickness d, with respect to d0 = 300 μm, giving
being C0 = kA0/d0 the capacitance for null pressure, k and A0 the permittivity and the sensor area, respectively, and εc = (d0 − d)/d0 the compressive strain of the dielectric layer. The best fitting of the compressive stress (σc)–strain (εc) experimental curve of the multilayer film is given by the Fung model, with an exponential stress–strain constitutive equation (Fung, 1993), valid for uniaxial response
with c1 and c2 two material constants.
Then, combining Eqs 1 and 2, we obtain
where x = ΔC/C0.
Equation 3 is exploited for the evaluation of experimental data obtained by indentation tests. In particular, a flat Delrin 8 mm × 8 mm probe was connected to a 6-axis load cell (ATI Nano 17, ATI Industrial Automation Inc., Apex, NC, USA), which acquired force data during the tests. The indentations were made at constant low velocity (10 µm/s) by means of a servo-controlled micrometric translation stage (M111.DG, Physik Instruments, Karlsruhe, Germany), while the capacitive output signals were acquired simultaneously with a custom made printed circuit board based on 24-bits resolution capacitance-to-digital converter (CDC) (AD7747, Analog Devices Inc., Nordwood, MA, USA) and PIC32 microcontroller that sends data to a control PC via USB interface. The CDC resolution is 1 fF, while the RMS noise is reduced to around 2 fF by implementing a differential capacitance reading strategy and using coaxial cables. Thus, the minimum detectable signal is around 6 fF (three times the RMS noise), which allows a readout force resolution at the millinewton scale.
In Figure 1C, the σc − ΔC/C0 curve, averaged over 12 tests, is fitted using Eq. 3, showing a very good agreement. We obtain c1 = 0.0660 and c2 = 33.847 kPa.
To study the influence of each different layer, a first approach could be to limit the analysis to small deformations. In this case, linearizing Eq. 2, , and the product c1c2 represents the Young’s modulus for small deformations. Then, for small strain, the apparent Young’s modulus of the whole structure is Ea = c1c2 = 2.24 kPa, well below the nominal value of Ecoflex E0 = 30–40 kPa. A direct measurement of the Young modulus of textile by means of indentation tests is not trivial, since the experimental errors can affect the results considerably. Thus, we made tests on a multilayer composed of Ecoflex embedded between two textile films (which correspond to the active region of the sensor), obtaining a multilayer modulus Em = 4 kPa. Finally, comparing the stiffness of the whole structure to the series of three layers, the Young’s modulus Et of the textile electrodes can be estimated. Indeed, considering
where dt = 150 μm is the textile thickness, we obtain Et = 2.22 kPa, almost equal to Ea. This demonstrates the relevance of the textile material in the mechanical behavior of the sensor. Also, as already shown in Viry et al. (2014), the air sheds enhance the sensor response at low pressure ranges and considerably enlarge its operating range. Moreover, it is noteworthy to mention that, even if during compression all different layers are subjected to deformation, the capacitance variation is due mainly to the thickness variation of the central sensor region. Therefore, due to the strong non-linear behavior of the whole structure, it is not possible to relate directly the total compressive strain to the measured capacitance. Indeed, the output signal is due to the compression of the central region only. By contrast, this example suggests that such electrical measurements could also be exploited as a tool to evaluate the effective deformation of a single layer embedded in a composite structure, even in the presence of several non-linear materials.
In conclusion, we provided some insight about the kind of complexity introduced by the presence of soft materials in modeling and designing a tactile sensor. Starting from this analysis, future work will be dedicated to quantitatively describe the effect of mechanical behavior of the constituent materials (especially textile) on the sensor response, by using stimuli with different stiffness and shape. In addition, the effect of the soft substrates, such as human skin for wearable systems or elastomers (i.e., PDMS, Ecoflex®) for soft robotic applications, should be included, as mentioned above. In this way, it will be possible to better understand how to encode different tactile features, thus not only force but also, e.g., shape and hardness, with improved but simple sensor designs.
Author Contributions
MT, NP, and LB developed and discussed the model. MT performed experiments. LB supervised the work. All the authors discussed the results and wrote the manuscript preparation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past coauthorship with one of the authors (NP) and states that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
NP is supported by the European Research Council PoC 2015 “Silkene” No. 693670 and by the European Commission H2020 under the Graphene Flagship Core 1 No. 696656 (WP14 “Polymer Nanocomposites”) and under the FET Proactive “Neurofibres” No. 732344.
References
Amjadi, M., Yoon, Y. J., and Park, I. (2015). Ultra-stretchable and skin-mountable strain sensors using carbon nanotubes–Ecoflex nanocomposites. Nanotechnology 26, 375501. doi:10.1088/0957-4484/26/37/375501
Case, J. C., White, E. L., and Kramer, R. K. (2015). Soft material characterization for robotic applications. Soft Rob. 2, 80–87. doi:10.1089/soro.2015.0002
Chou, H.-H., Nguyen, A., Chortos, A., To, J. W. F., Lu, C., Mei, J., et al. (2015). A chameleon-inspired stretchable electronic skin with interactive colour changing controlled by tactile sensing. Nat. Commun. 6, 8011. doi:10.1038/ncomms9011
Engel, J., Chen, J., Fan, Z. F., and Chang, L. (2005). Polymer micromachined multimodal tactile sensors. Sens. Actuators Phys. 117, 50–61. doi:10.1016/j.sna.2004.05.037
Escoffier, C., de Rigal, J., Rochefort, A., Vasselet, R., Leveque, J.-L., and Agache, P. G. (1989). Age-related mechanical properties of human skin: an in vivo study. J. Invest. Dermatol. 93, 353–357. doi:10.1111/1523-1747.ep12280259
Hendriks, F. M., Brokken, D., Van Eemeren, J. T. W. M., Oomens, C. W. J., Baaijens, F. P. T., and Horsten, J. B. A. M. (2003). A numerical-experimental method to characterize the non-linear mechanical behaviour of human skin. Skin Res. Technol. 9, 274–283. doi:10.1034/j.1600-0846.2003.00019.x
Kim, D.-H., Lu, N., Ma, R., Kim, Y.-S., Kim, R.-H., Wang, S., et al. (2011). Epidermal electronics. Science 333, 838–843. doi:10.1126/science.1206157
Kim, S., Laschi, C., and Trimmer, B. (2013). Soft robotics: a bioinspired evolution in robotics. Trends Biotechnol. 31, 23–30. doi:10.1016/j.tibtech.2013.03.002
Morin, S. A., Shepherd, R. F., Kwok, S. W., Stokes, A. A., Nemiroski, A., and Whitesides, G. M. (2012). Camouflage and display for soft machines. Science 337, 828–832. doi:10.1126/science.1222149
Pailler-Mattei, C., Bec, S., and Zahouani, H. (2008). In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med. Eng. Phys. 30, 599–606. doi:10.1016/j.medengphy.2007.06.011
Park, J., Kim, M., Lee, Y., Lee, H. S., and Ko, H. (2015). Fingertip skin–inspired microstructured ferroelectric skins discriminate static/dynamic pressure and temperature stimuli. Sci. Adv. 1, e1500661. doi:10.1126/sciadv.1500661
Park, S., Kim, H., Vosgueritchian, M., Cheon, S., Kim, H., Koo, J. H., et al. (2014). Stretchable energy-harvesting tactile electronic skin capable of differentiating multiple mechanical stimuli modes. Adv. Mater. Weinheim 26, 7324–7332. doi:10.1002/adma.201402574
Sekitani, T., Noguchi, Y., Hata, K., Fukushima, T., Aida, T., and Someya, T. (2008). A rubberlike stretchable active matrix using elastic conductors. Science 321, 1468–1472. doi:10.1126/science.1160309
Shepherd, R. F., Ilievski, F., Choi, W., Morin, S. A., Stokes, A. A., Mazzeo, A. D., et al. (2011). Multigait soft robot. Proc. Natl. Acad. Sci. U.S.A. 108, 20400–20403. doi:10.1073/pnas.1116564108
Someya, T., Sekitani, T., Iba, S., Kato, Y., Kawaguchi, H., and Sakurai, T. (2004). A large-area, flexible pressure sensor matrix with organic field-effect transistors for artificial skin applications. Proc. Natl. Acad. Sci. U.S.A. 101, 9966–9970. doi:10.1073/pnas.0401918101
Tien, N. T., Jeon, S., Kim, D.-I., Trung, T. Q., Jang, M., Hwang, B.-U., et al. (2014). A flexible bimodal sensor array for simultaneous sensing of pressure and temperature. Adv. Mater. Weinheim 26, 796–804. doi:10.1002/adma.201302869
Viry, L., Levi, A., Totaro, M., Mondini, A., Mattoli, V., Mazzolai, B., et al. (2014). Flexible three-axial force sensor for soft and highly sensitive artificial touch. Adv. Mater. Weinheim 26, 2659–2664. doi:10.1002/adma.201305064
Xu, S., Zhang, Y. H., Jia, L., Mathewson, K. E., Jang, K. I., Kim, J., et al. (2014). Soft microfluidic assemblies of sensors, circuits, and radios for the skin. Science 344, 70–74. doi:10.1126/science.1250169
Yang, Y. J., Cheng, M. Y., Chang, W. Y., Tsao, L. C., Yang, S. A., Shih, W. P., et al. (2008). An integrated flexible temperature and tactile sensing array using PI-copper films. Sens. Actuators Phys. 143, 143–153. doi:10.1016/j.sna.2007.10.077
Yang, Y. J., Cheng, M. Y., Shih, S. C., Huang, X. H., Tsao, C. M., Chang, F. Y., et al. (2010). A 32 × 32 temperature and tactile sensing array using PI-copper films. Int. J. Adv. Manuf. Technol. 46, 945–956. doi:10.1007/s00170-009-1940-z
Keywords: non-linear mechanics, tactile sensors, hyperelastic materials, soft robotics, wearable systems
Citation: Totaro M, Pugno NM, Mazzolai B and Beccai L (2017) Micromechanical Analysis of Soft Tactile Sensors. Front. Mater. 4:3. doi: 10.3389/fmats.2017.00003
Received: 30 November 2015; Accepted: 03 February 2017;
Published: 21 February 2017
Edited by:
Asa Barber, University of Portsmouth, UKReviewed by:
Alberto Salvadori, University of Brescia, ItalyMassimiliano Gei, Cardiff University, UK
Copyright: © 2017 Totaro, Pugno, Mazzolai and Beccai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Massimo Totaro, bWFzc2ltby50b3Rhcm9AaWl0Lml0
 Massimo Totaro
Massimo Totaro Nicola Maria Pugno
Nicola Maria Pugno Barbara Mazzolai
Barbara Mazzolai Lucia Beccai
Lucia Beccai