Strain and Thermally Induced Magnetic Dynamics and Spin Current in Magnetic Insulators Subject to Transient Optical Grating

We analyze the magnetic dynamics and particularly the spin current in an open-circuit ferromagnetic insulator irradiated by two intense, phase-locked laser pulses. The interference of the laser beams generates a transient optical grating and a transient spatiotemporal temperature distribution. Both effects lead to elastic and heat waves at the surface and into the bulk of the sample. The strain induced spin current as well as the thermally induced magnonic spin current are evaluated numerically on the basis of micromagnetic simulations using solutions of the heat equation. We observe that the thermo-elastically induced magnonic spin current propagates on a distance larger than the characteristic size of thermal profile, an effect useful for applications in remote detection of spin caloritronics phenomena. Our findings point out that exploiting strain adds a new twist to heat-assisted magnetic switching and spin-current generation for spintronic applications.

1. Introduction

Magneto-elastic coupling (Kittel, 1958; Akhiezer et al., 1959) enables the manipulation of the magnetization via elastic means. Fueled by potential applications in spintronics and sensorics thermal and magnetoelastic driven magnetic dynamics is attacking a great deal of research (Davis et al., 2010; Scherbakov et al., 2010; Roy et al., 2011; Uchida et al., 2011a; Weiler et al., 2011; Azovtsev and Pertsev, 2016). Elastic excitations might be triggered in a variety of ways, for instance via acoustic transducers (Davis et al., 2010; Uchida et al., 2011b; Weiler et al., 2011, 2012; Thevenard et al., 2013) or by optical methods (Scherbakov et al., 2010; Kim et al., 2012; Jäger et al., 2013; Kovalenko et al., 2013; Afanasiev et al., 2014). Optical methods mainly generate elastic excitations via laser heating and thermoelastic effects. As compared to transducers, laser pulses achieve larger amplitude thermoelastic deformations (Saito et al., 2003; Scherbakov et al., 2010; Kim et al., 2012; Jäger et al., 2013; Kovalenko et al., 2013; Afanasiev et al., 2014). A further interesting method to induce magneto-elastic excitations via electric fields is to use multiferroics materials, particularly heterostructures of coupled piezoelectric or ferroelectric and ferromagnetic layers (Vaz, 2012; Cherepov et al., 2014; Jia et al., 2014, 2016; Gilbert et al., 2016). In recent experiments (Janušonis et al., 2015, 2016), a transient optical grating is generated on the surface of a ferromagnet by two phase-locked interfering laser pulses. On the length scale of the interference pattern, a frequency tunable elastic wave is generated. By virtue of magneto-elastic coupling, a magnetization precession in the ferromagnetic film is launched. This method bridges the transducer and the optical approaches. Hitherto, these experiments were interpreted on the basis of elastically driven magnetic precession without thermal fluctuations. Obviously, for the laser intensities generating efficient optical grating heating effects are unavoidable and may affect the magnetization dynamics. In fact, the thermal magnetization dynamics generated by a single laser pump has been studied recently. It has been found that the laser-induced thermal gradient generates a propagating thermal magnonic spin current (magnonic spin Seebeck effect) (Schreier et al., 2013; Roschewsky et al., 2014; Etesami et al., 2015; Giles et al., 2015). Hence, we expect that a transient optical grating may bring about new phenomena in addition to the aforementioned magneto-elastic waves, particularly the magnonic spin Seebeck effect will be inspected below. For the magnetization simulations, we use classical micromagnetic theory. The magnonic spin Seebeck is studied under the influence of the transient optical grating and in the preence of magneto-elastic excitations triggered by the elastic waves. At the surface of the ferromagnetic film, we analyze the effects of thermal gradient and surface elastic wave excitation on the magnonic spin current. The elastic wave excites resonantly the magnetization dynamics and magnonic spin current near the ferromagnetic resonance frequency. This prediction is in line with the recent experiments reported by Janušonis et al. (2015, 2016). Furthermore, we identify a magnonic spin current flowing perpendicular to the film surface plane, i.e., perpendicular to the propagation direction of the elastic waves. The spin current is induced by the thermal gradient away from the laser spots into the depth of the sample. The elastic wave excitation is shown to be very weak in this direction. In addition, changing the magnetization direction the effect of the magneto-elastic coupling can be suppressed. The diffusion length of the magnonic spin current and the effect of the pulse length are discussed in light of the obtained results.

2. Results and Discussions

2.1. Materials and Methods

We consider an experimental situation consisting of a transient optical grating generated by the interference of two laser beams impinging on the surface plane (x − y plane) of an insulating ferromagnet (cf. Figure 1). The laser heating results in a time-dependent non-uniform temperature profile [T(x, y, z, t)]. Due to thermoelastic effects, the laser heating triggers an elastic wave at the surface of the thick ferromagnetic film. The thermal fluctuations and the elastic excitations cooperatively contribute to the magnetization dynamics and generate a propagating magnon flow. To study the magnetization dynamics, we utilize the stochastic Landau–Lifshitz–Gilbert equation including thermal fluctuations and magneto-elastic coupling effects

$\frac{\partial \mathbf{\text{M}}}{\mathrm{\partial t}}=-\mathrm{\gamma }\mathbf{\text{M}}\times \left({\mathbf{\text{H}}}_{\mathit{eff}}+\mathbf{\text{h}}\right)+\frac{\mathrm{\alpha }}{M_s}\mathbf{\text{M}}\times \frac{\partial \mathbf{\text{M}}}{\mathrm{\partial t}}$ (1)

where M is the magnetization of the sample, M_s is the saturation magnetization, γ is the gyro-magnetic ratio, and α is the phenomenological Gilbert damping constant. The total effective field H_eff consists of the exchange field $\frac{2A_{\mathit{ex}}}{{\mathrm{\mu }}_0{M}_s^2}\mathrm{\Delta }\mathbf{\text{M}}$, the external field H_ext aligned along x axis, and the magneto-elastic coupling field H_me. The random field h stems from thermal fluctuations (García-Palacios and Lázaro, 1998)

$〈h_i\left(t,\mathbf{\text{r}}\right)h_j\left(t\prime ,\mathbf{\text{r}}\prime \right)〉=\frac{2k_{B}T\mathrm{\alpha }}{\mathrm{\gamma }{M}_{\text{S}}V}{\mathrm{\delta }}_{\mathit{ij}}\mathrm{\delta }\left(\mathbf{\text{r}}-\mathbf{\text{r}}\prime \right)\mathrm{\delta }\left(t-t\prime \right)$ (2)

here, T(r, t) is the temperature profile formed due to laser heating, k_B is the Boltzmann constant and V is the volume of the sample.

FIGURE 1

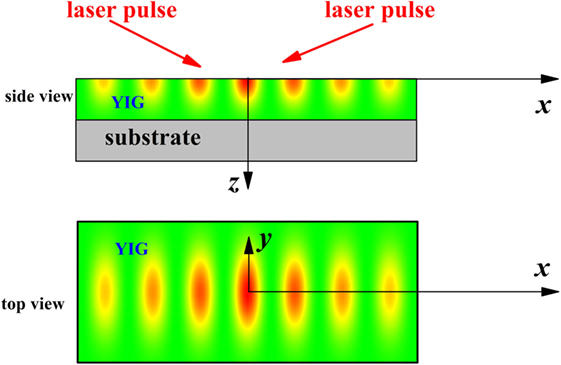
Figure 1. Schematics of the simulated setup. The optical grating at the surface is generated by two crossed laser pulses triggering to a spatially oscillating temperature profile in the top layer (here it is the insulating ferromagnet YIG) which defines the x–y plane.

[T(x, y, z, t)] derives from the solution of the heat equation (Etesami et al., 2015):

$\frac{\mathrm{\partial T}\left(x,y,z,t\right)}{\mathrm{\partial t}}=\frac{k_{\mathit{ph}}}{\mathrm{\rho }C}{\nabla }^{2}T\left(x,y,z,t\right)+I\left(x,y,z,t\right)$ (3)

k_ph is the thermal conductivity, ρ is the mass density, and C is the heat capacity. The source term I(x, y, z, t) signifies a spatially periodic laser intensity generated by the transient grating, i.e.,

$I\left(x,y,z,t\right)=I_0\left(t\right){\text{cos}}^2\left(\mathrm{2\pi }x∕r_l\right)e^{-{\mathrm{\delta }}_T\left|z\right|}{e}^{-{\mathrm{\lambda }}^2\left(x^2+y^2\right)}$ (4)

δ_T is the laser penetration depth and λ is the inverse radius of the radial beam. We implement periodic series of the rectangular laser pulses S(2πf_modet) with the modulation frequency f_mode = 0.1 GHz. Here, $I_0\left(t\right)=\frac{{\mathrm{\delta }}_T}{\mathrm{\rho }C}{I}_{00}S\left(\mathrm{2\pi }{f}_{\mathit{mode}}t\right)$, and I₀₀ is the intensity of the pulse. The periodic function cos²(2πx/r_l) describes the effect of the transient grating. The grating period r_l/2 is tunable by the phase difference between the two laser beams (Etesami et al., 2015; Janušonis et al., 2015, 2016). The profile of laser intensity I is shown in Figure 2 for r_l = 2.8 μm. The oscillating behavior of I along the x axis is related the transient grating. Apparently I decays exponentially along the z axis (perpendicular to the surface).

FIGURE 2

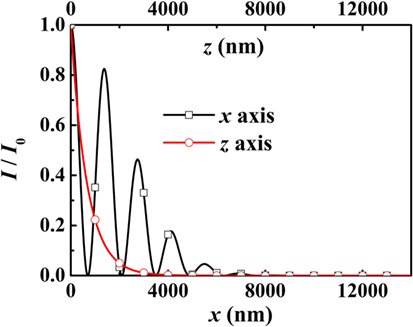
Figure 2. Profiles of the normalized laser intensity I/I₀ along x axis (y = 0 and z = 0) and z axis (x = 0 and y = 0).

The laser beams are such that they generate a transient grating which is oscillating along the x direction. The temperature profile T along the x axis is also spatially oscillating (numerical results are shown below), and decays along the z axis (which is perpendicular to the surface) into the bulk of the sample. The oscillating heat profile generates a periodic elastic deformation and a propagating elastic wave along the x axis. For simplicity, we use the propagating wave solution u_amp sin(ωt − kx) to describe the excited elastic waves in our simulation, and u_amp is the amplitude. Here, ω = 2πf is the wave frequency, and k is the wave vector. The wave is only located in the film surface due to the form of the temperature profile (Janušonis et al., 2015, 2016). The wave-vector is determined by the period of the transmitted grating k = 4π/r_l, and the frequency is a function of the wave-vector f = v Λ with v ≈ 5,600 m/s. The elastic amplitude u_amp increases linearly with the laser intensity I₀₀.

The magneto-elastic coupling term ${\mathbf{\text{H}}}_{\mathit{me}}=-\frac{1}{{\mathrm{\mu }}_0{M}_s}\mathrm{\delta }{F}_{\mathit{me}}∕\mathrm{\delta }\mathbf{\text{m}}$ derives from the magneto-elastic energy F_me (Akhiezer et al., 1959; Azovtsev and Pertsev, 2016),

$F_{\mathit{me}}=b_1\left(e_{\mathit{xx}}{m}_x^2+e_{\mathit{yy}}{m}_y^2+e_{\mathit{zz}}{m}_z^2\right)+b_2\left(e_{\mathit{xy}}{m}_x{m}_y+e_{\mathit{xz}}{m}_x{m}_z+e_{\mathit{yz}}{m}_y{m}_z\right)$ (5)

here, b₁ and b₂ are material dependent magneto-elastic coupling constants, and e_xx, e_xy… are the components of the strain tensor. For simplicity, only the e_xz component is considered. Although e_xx is found to be large (Janušonis et al., 2015, 2016), it does not contribute to the magnetization dynamics for the equilibrium magnetization along the x axis (a strong enough external field H_ext is applied along the x axis).

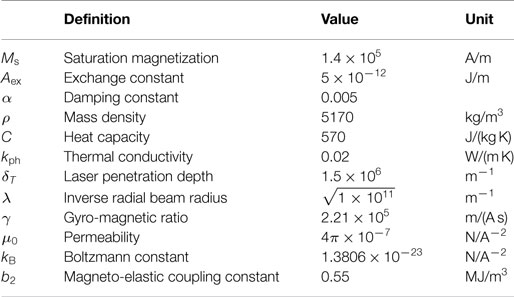
In the modeling of the magnetization dynamics in the ferromagnet, we use the material parameters of YIG (Table 1). For simplicity, two one-dimensional models are considered for two cases: (i) the magnetization dynamics in the film surface is solved in a model along x axis for y = 0 and z = 0 with the surface propagating elastic wave. Here, the component $e_{\mathit{xz}}=\frac{1}{2}\frac{U_z}{x}=\epsilon \text{sin}\left(\mathrm{\omega }t-\mathit{kx}\right)$ is calculated as the spatial derivative of the displacement U_z in the z direction, where ε is a constant. For b₂ε = 200 J/m³, the amplitude of U_z is about 0.15 nm. (ii) in the direction perpendicular to the surface, the model along z axis for x = 0 and y = 0 is calculated without elastic wave. The external field H_ext = 1.14 × 10⁵ A/m is applied along the x axis and the equilibrium magnetization m₀ is in the +x direction. For the laser profile (Eq. 4), we use f_mode = 0.1 GHz and I₀₀ = 2 × 10¹⁰ W/m².

TABLE 1

Table 1. Parameters for YIG.

2.2. Model (i) Along x Axis

In the film surface, the spatially oscillating temperature profile for r_l = 2.8 μm is generated as shown in Figure 3. The temperature T increases linearly with time when S(2πf_modet) ≠ 0, and it remains nearly unchanged in the region of a zero laser intensity (S(2πf_modet) = 0). For 0 < t < 50 ns, the spatial profile of T(x) is always spatially oscillating. We note that in reality the temperature increase by laser heating is limited. With heating up the sample the thermal losses due to the environment increases. As the time span of our simulations is limited to only 50 ns, this limiting factor of temperature increase is not accounted for. The elastic wave has the wave-vector k = 4 π/r_l and the frequency f = 4 GHz. Solving Eq. 1, the magnonic spin current $J_x=\frac{\mathrm{2\gamma }{A}_{\mathit{ex}}}{{\mathrm{\mu }}_0{M}_s^2}\left(M_y{\partial }_x{M}_z-M_z{\partial }_x{M}_y\right)$ propagating along the x axis is calculated. Here, M_y and M_z are the y and z components of the local magnetization, respectively. The numerical results are statistically averaged over 1,000 realizations of the noise. Apart from boundary effects, the spatial profile of J_x(x) is always constant, as shown in Figure 4A, signifying a steady current. In the time domain (Figure 4B), after an initial increase and oscillations, J_x(t) attains the steady state constant value. Varying the grating period r_l, the features of the magnonic spin current J_x change, as shown in Figure 5 (r_l = 3.7 μm and f = 3 GHz). The value of J_x becomes much smaller compared to that for f = 4 GHz. Also, the spatial profile of J_x(x) turns spatially oscillating after t = 1 ns, and it approaches 0 at x = 0 due to the free boundary conditions. Besides, similar to the time-dependent temperature T(t), the current J_x(t) increases gradually with time t, and oscillates with a frequency of 0.1 GHz.

FIGURE 3

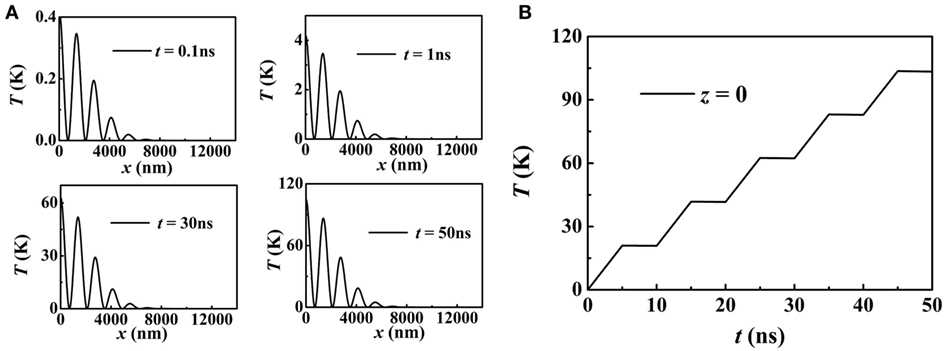
Figure 3. (A) The spatiotemporal temperature profiles of T(x, t) at t = 0.1, 1, 30, and 50 ns. (B) At x = 0, temperature T as a function of time t.

FIGURE 4

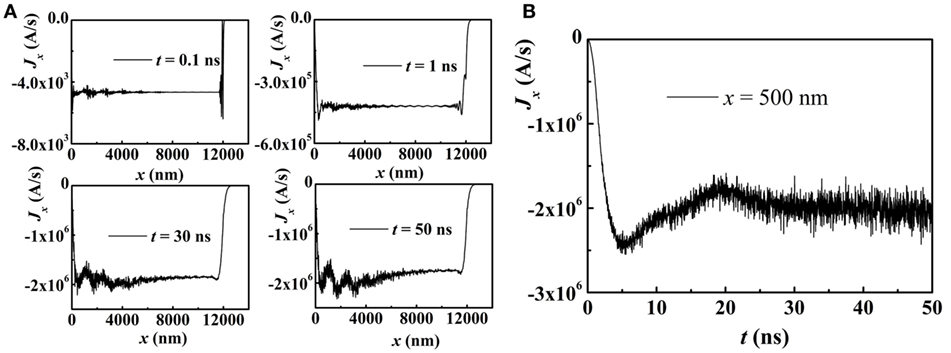
Figure 4. For r_l = 2.8 μm and f = 4 GHz, (A) the profiles of the magnonic spin current J_x(x) at t = 0.1, 1, 30, and 50 ns. (B) At x = 500 nm, J_x as a function of time t. The equilibrium magnetization is in the +x direction.

FIGURE 5

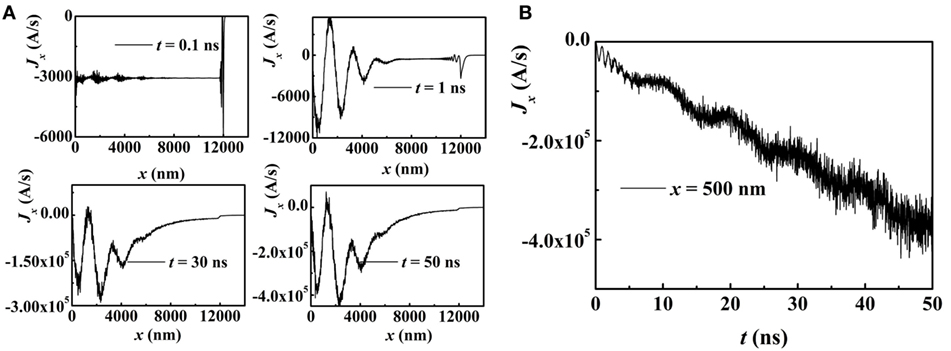
Figure 5. For r_l = 3.7 μm and f = 3 GHz, (A) the profiles of the magnonic spin current J_x(x) at t = 0.1, 1, 30, and 50 ns. (B) At x = 500 nm, J_x as a function of time t. The equilibrium magnetization m₀ is in the +x direction.

The r_l-dependent phenomena above are ascribed to a magnetization resonance behavior. Based on the spin-wave dispersion relation $\mathrm{2\pi }{f}_{\mathit{sw}}=\frac{\mathrm{2\gamma }{A}_{\mathit{ex}}}{{\mathrm{\mu }}_0{M}_s}{k}_{\mathit{sw}}^2+\mathrm{\gamma }{H}_{\mathit{ext}}$, the resonance frequency is estimated to be 4 GHz when the spin wave vector k_sw is equal to the wave vector 2πΛ of the propagating elastic wave, i.e., the resonance condition. Here, we note that the influence of the dynamic magneto-elastic coupling on the spin-wave dispersion relation is weak enough to be neglected. At the resonance frequency f = 4 GHz, the spin-wave amplitude excited by the elastic wave is very large, and dominates the value of J_x. As the time independent amplitude of the elastic wave is not spatially varying, J_x is independent of distance x and time t (Figure 4). For a different frequency (f = 3 GHz) away from the resonance condition, the spin-wave amplitude excited by the elastic wave becomes smaller than the thermal effect. The thermal gradient dominates the value of J_x, and J_x varies with x and time t.

To detect the effect of a thermal gradient, we apply an external field H_ext = 1.14 × 10⁵ A/m along y axis. The equilibrium magnetization m₀ is in the +y direction. In this case, the magneto-elastic coupling field H_me is very small, and the magnonic spin current J_x is dominated by the thermal gradient. As shown in Figure 6, $J_x=\frac{\mathrm{2\gamma }{A}_{\mathit{ex}}}{{\mathrm{\mu }}_0{M}_s^2}\left(M_z{\partial }_x{M}_x-M_x{\partial }_x{M}_z\right)$ gradually increases with the temperature and has an oscillatory profile along the x axis.

FIGURE 6

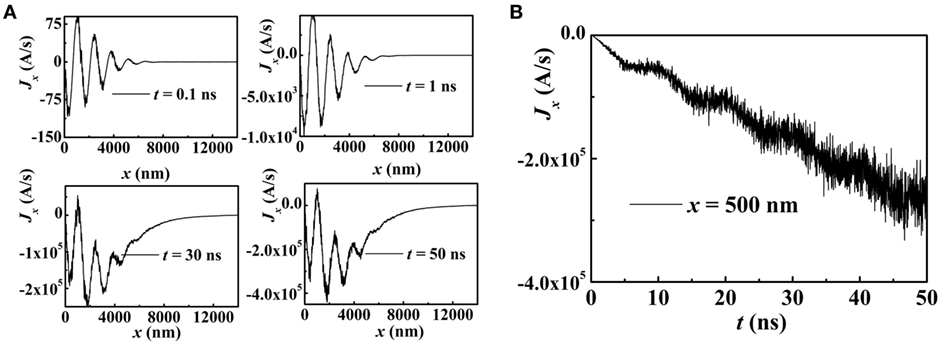
Figure 6. For r_l = 2.8 μm and f = 4 GHz, (A) the profiles of the magnonic spin current J_x(x) at t = 0.1, 1, 30, and 50 ns. (B) At x = 500 nm, J_x as a function of time t. The equilibrium magnetization m₀ is in the +y direction.

2.3. Model (ii) Along z Axis

The optical grating is periodic in the x direction only. For the effects on the spin dynamics along the z direction (perpendicular to the surface), we solve Eq. 3 with the laser intensity being I decaying with z (Figure 2). The temperature profile T(z) is similar to I(z), as shown in Figure 7A. Also, in Figure 7B, the temperature increases linearly with t in the region of I ≠ 0. In this model, the generated magnonic spin current $J_z=\frac{\mathrm{2\gamma }{A}_{\mathit{ex}}}{{\mathrm{\mu }}_0{M}_s^2}\left(M_y{\partial }_z{M}_z-M_z{\partial }_z{M}_y\right)$ propagates along the z axis and is shown in Figure 8. Here, the equilibrium magnetization is in the +x direction. Excited by the thermal gradient, J_z(z) reaches its maximum near the boundary. The zero spin current density at x = 0 is caused by the boundary effect. With time, J_z(t) has a similar profile with T(t) increasing gradually in the oscillation frequency of 0.1 GHz. Moreover, the above features are independent of the equilibrium magnetization m₀. By changing the equilibrium magnetization m₀ to the +y direction, the values of magnonic spin current remain unchanged (not shown).

FIGURE 7

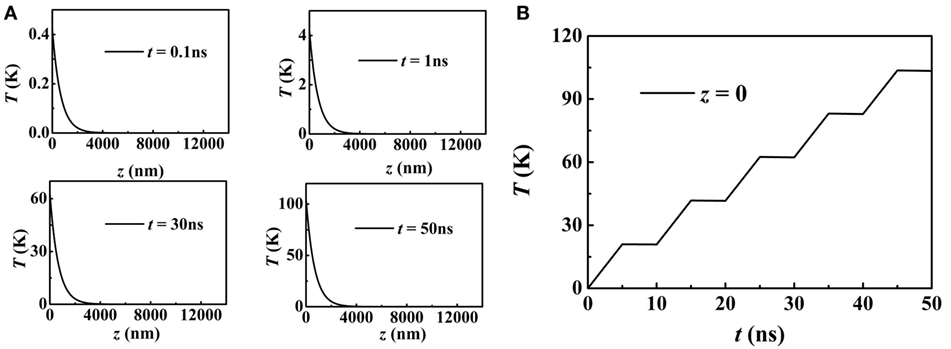
Figure 7. (A) The profiles of T(z, t) at t = 0.1, 1, 30, and 50 ns. (B) At z = 0, temperature T as a function of time t.

FIGURE 8

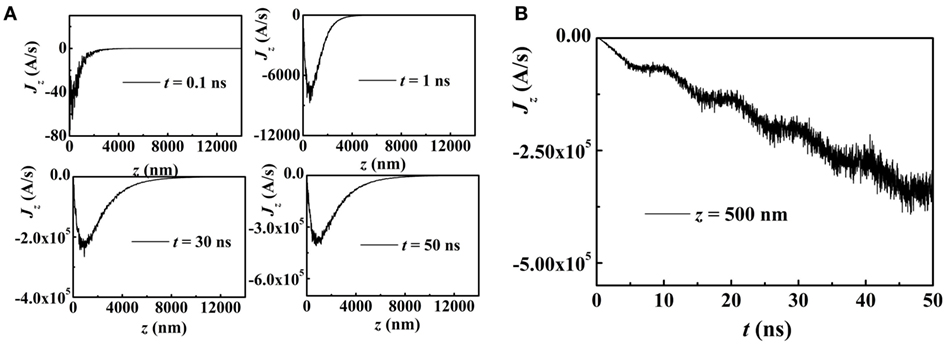
Figure 8. (A) The profiles of the magnonic spin current J_z(z) at t = 0.1, 1, 30, and 50 ns. (B) At z = 500 nm, J_z as a function of time t. The equilibrium magnetization m₀ is in the +x direction.

2.4. Spin Current As a Surface Heat Sensor

Our numerical results indicate that the diffusion length of thermal magnonic spin current can be larger than that of the thermal profile. To show this effect, the thermal magnonic spin current J_x(x), the thermal profile T(x) and the laser profile I/I₀ are shown together in Figure 9A. Here, the model (i) is adopted, and the equilibrium magnetization m₀ in the +y direction is used to remove the effect of elastic waves. The features of the thermal profile T(x) are completely determined by I/I₀ but J_x(x) is different. Apart from boundary effects, J_x(x) decays exponentially with x, together with the oscillations caused by I/I₀. We use a non-linear function $J_0{\text{cos}}^2\left(\mathrm{2\pi }x∕r_l\right)e^{-{\mathrm{\lambda }}^2{x}^2}+J_1{e}^{-{\mathrm{\delta }}_S^x\left|x\right|}$ for fitting the curve of J_x in x > 1000 nm (Figure 9A), and ${\mathrm{\delta }}_S^x$ = 2.45 × 10⁵ m⁻¹ is obtained. Obviously, the thermal magnonic spin current J_x(x) diffuses longer than the region where the temperature T(x) changing. The same effect exists also for the model (ii) along z axis, as shown in Figure 9B. Here, the non-linear fitting function $J_0{e}^{-{\mathrm{\delta }}_T\left|z\right|}+J_1{e}^{-{\mathrm{\delta }}_S^z\left|z\right|}$ is adopted, and ${\mathrm{\delta }}_S^z$ = 5.9 × 10⁵ m⁻¹ is obtained. ${\mathrm{\delta }}_S^z$ is obviously smaller than δ_T, indicating a larger diffusion length $1∕{\mathrm{\delta }}_S^z$ of J_z. This difference in the range of the heat current and the spin current can be utilized to sense a temperature increase at the surface by measuring the associated spin current, e.g., via the inverse spin Hall effect.

FIGURE 9

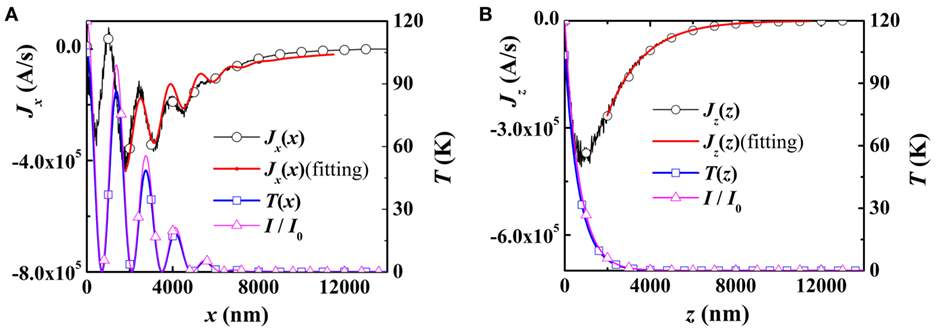
Figure 9. At t = 50 ns, (A) profiles of the magnonic spin current J_x (simulations and fitting curves), temperature T(x), and laser intensity I/I₀. (B) Profiles of the magnonic spin current J_z (simulations and fitting curves), the temperature T(z), and the laser intensity I/I₀.

2.5. Duration of the Laser Pulse

The effect of the duration of the laser pulse in a single period is also of relevance. The duration 5 ns is used in the above simulations, as demonstrated by the periodic rectangular pulse S(2πf_modet) in Figure 10A. By setting f_mode = 0.1 GHz and changing the duration to 2.5 ns, we find that the temperature increase in a single period is unchanged. Here, the amplitude of S is twice larger than that for duration of 5 ns, to keep the energy pumped in a period unchanged. Finally, at t = 50 ns, the temperature profiles for a duration of 2.5 ns are still the same as for the curves shown in Figures 3A and 7A. The corresponding magnonic spin current has the same feature, as shown in Figure 10B.

FIGURE 10

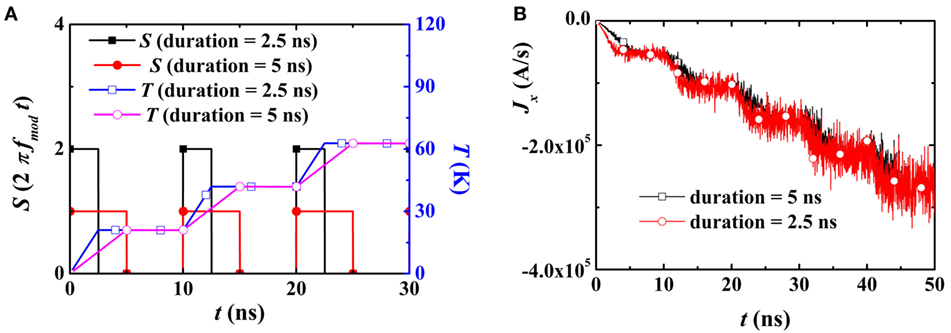
Figure 10. (A) Time-varying periodic rectangular pulses S(2πf_modet) and T(x = 0, t). The duration of non-zero S in a single period is 2.5 ns (squares) and 5 ns (circles). (B) At x = 500 nm, J_x as a function of time t for the duration of 2.5 and 5 ns.

2.6. Conclusion

To conclude, for a magnetic film surface, we considered the magnonic spin current excited by thermal effects and by elastic waves generated by an optical transient grating is studied. Approaching the ferromagnetic resonance, the magnonic spin current is triggered dominantly by the laser-generated elastic wave. Away from resonance, thermal effects dominate. By manipulating the equilibrium magnetization, one can totally suppress the effects of elastic waves. The magnonic spin current excitation perpendicular to the film surface is also studied and found to be determined by thermal effects only. Besides, we find the thermal magnonic spin current to diffuse to regions well beyond the spatial extension of the temperature gradient generated by the laser pulse. This effect provides a new method to detect thermal effects remotely on a long range scale.

Author Contributions

X-GW conducted all numerical calculations and provided the initial draft of the manuscript. LC performed the analytical part. JB conceived and supervised the project. All authors contributed to the interpretation and writing of the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. S. R. Etesami for useful discussions and consultations.

Funding

This research was funded by the German Science Foundation (DFG) under SFB 762.

References

Afanasiev, D., Razdolski, I., Skibinsky, K. M., Bolotin, D., Yagupov, S. V., Strugatsky, M. B., et al. (2014). Laser excitation of lattice-driven anharmonic magnetization dynamics in dielectric FeBo₃. Phys. Rev. Lett. 112, 147403. doi: 10.1103/PhysRevLett.112.147403

PubMed Abstract | CrossRef Full Text | Google Scholar

Akhiezer, A., Bar’iakhtar, V., and Peletminskii, S. (1959). Coupled magnetoelastic waves in ferromagnetic media and ferroacoustic resonance. J. Exp. Theor. Phys. 8, 157.

Google Scholar

Azovtsev, A. V., and Pertsev, N. A. (2016). Magnetization dynamics and spin pumping induced by standing elastic waves. Phys. Rev. B 94, 184401. doi:10.1103/PhysRevB.94.184401

CrossRef Full Text | Google Scholar

Cherepov, S., Amiri, P. K., Alzate, J. G., Wong, K., Lewis, M., Upadhyaya, P., et al. (2014). Electric-field-induced spin wave generation using multiferroic magnetoelectric cells. Appl. Phys. Lett. 104, 082403. doi:10.1063/1.4865916

CrossRef Full Text | Google Scholar

Davis, S., Baruth, A., and Adenwalla, S. (2010). Magnetization dynamics triggered by surface acoustic waves. Appl. Phys. Lett. 97, 232507. doi:10.1063/1.3521289

CrossRef Full Text | Google Scholar

Etesami, S. R., Chotorlishvili, L., and Berakdar, J. (2015). Spectral characteristics of time resolved magnonic spin Seebeck effect. Appl. Phys. Lett. 107, 132402. doi:10.1063/1.4931701

CrossRef Full Text | Google Scholar

García-Palacios, J. L., and Lázaro, F. J. (1998). Langevin-dynamics study of the dynamical properties of small magnetic particles. Phys. Rev. B 58, 14937–14958. doi:10.1103/PhysRevB.58.14937

CrossRef Full Text | Google Scholar

Gilbert, I., Chavez, A. C., Pierce, D. T., Unguris, J., Sun, W.-Y., Liang, C.-Y., et al. (2016). Magnetic microscopy and simulation of strain-mediated control of magnetization in PMN-PT/Ni nanostructures. Appl. Phys. Lett. 109, 162404. doi:10.1063/1.4965028

CrossRef Full Text | Google Scholar

Giles, B. L., Yang, Z., Jamison, J. S., and Myers, R. C. (2015). Long-range pure magnon spin diffusion observed in a nonlocal spin-Seebeck geometry. Phys. Rev. B 92, 224415. doi:10.1103/PhysRevB.92.224415

CrossRef Full Text | Google Scholar

Jäger, J. V., Scherbakov, A. V., Linnik, T. L., Yakovlev, D. R., Wang, M., Wadley, P., et al. (2013). Picosecond inverse magnetostriction in galfenol thin films. Appl. Phys. Lett. 103, 032409. doi:10.1063/1.4816014

CrossRef Full Text | Google Scholar

Janušonis, J., Chang, C. L., Jansma, T., Gatilova, A., Vlasov, V. S., Lomonosov, A. M., et al. (2016). Ultrafast magnetoelastic probing of surface acoustic transients. Phys. Rev. B 94, 024415. doi:10.1103/PhysRevB.94.024415

CrossRef Full Text | Google Scholar

Janušonis, J., Chang, C. L., van Loosdrecht, P. H. M., and Tobey, R. I. (2015). Frequency tunable surface magneto elastic waves. Appl. Phys. Lett. 106, 181601. doi:10.1063/1.4919882

CrossRef Full Text | Google Scholar

Jia, C., Zhang, N., Sukhov, A., and Berakdar, J. (2016). Ultrafast transient dynamics in composite multiferroics. New J. Phys. 18, 023002. doi:10.1088/1367-2630/18/2/023002

CrossRef Full Text | Google Scholar

Jia, C.-L., Wei, T.-L., Jiang, C.-J., Xue, D.-S., Sukhov, A., and Berakdar, J. (2014). Mechanism of interfacial magnetoelectric coupling in composite multiferroics. Phys. Rev. B 90, 054423. doi:10.1103/PhysRevB.90.054423

CrossRef Full Text | Google Scholar

Kim, J.-W., Vomir, M., and Bigot, J.-Y. (2012). Ultrafast magnetoacoustics in nickel films. Phys. Rev. Lett. 109, 166601. doi:10.1103/PhysRevLett.109.166601

PubMed Abstract | CrossRef Full Text | Google Scholar

Kittel, C. (1958). Interaction of spin waves and ultrasonic waves in ferromagnetic crystals. Phys. Rev. J. Arch. 110, 836–841. doi:10.1103/PhysRev.110.836

CrossRef Full Text | Google Scholar

Kovalenko, O., Pezeril, T., and Temnov, V. V. (2013). New concept for magnetization switching by ultrafast acoustic pulses. Phys. Rev. Lett. 110, 266602. doi:10.1103/PhysRevLett.110.266602

PubMed Abstract | CrossRef Full Text | Google Scholar

Roschewsky, N., Schreier, M., Kamra, A., Schade, F., Ganzhorn, K., Meyer, S., et al. (2014). Time resolved spin Seebeck effect experiments. Appl. Phys. Lett. 104, 202410. doi:10.1063/1.4879462

CrossRef Full Text | Google Scholar

Roy, K., Bandyopadhyay, S., and Atulasimha, J. (2011). Hybrid spintronics and straintronics: a magnetic technology for ultra low energy computing and signal processing. Appl. Phys. Lett. 99, 063108. doi:10.1063/1.3624900

CrossRef Full Text | Google Scholar

Saito, T., Matsuda, O., and Wright, O. B. (2003). Picosecond acoustic phonon pulse generation in nickel and chromium. Phys. Rev. B 67, 205421. doi:10.1103/PhysRevB.67.205421

CrossRef Full Text | Google Scholar

Scherbakov, A. V., Salasyuk, A. S., Akimov, A. V., Liu, X., Bombeck, M., Brüggemann, C., et al. (2010). Coherent magnetization precession in ferromagnetic (Ga,Mn)As induced by picosecond acoustic pulses. Phys. Rev. Lett. 105, 117204. doi:10.1103/PhysRevLett.105.117204

PubMed Abstract | CrossRef Full Text | Google Scholar

Schreier, M., Kamra, A., Weiler, M., Xiao, J., Bauer, G. E. W., Gross, R., et al. (2013). Magnon, phonon, and electron temperature profiles and the spin Seebeck effect in magnetic insulator/normal metal hybrid structures. Phys. Rev. B 88, 094410. doi:10.1103/PhysRevB.88.094410

CrossRef Full Text | Google Scholar

Thevenard, L., Duquesne, J.-Y., Peronne, E., von Bardeleben, H. J., Jaffres, H., Ruttala, S., et al. (2013). Irreversible magnetization switching using surface acoustic waves. Phys. Rev. B 87, 144402. doi:10.1103/PhysRevB.87.144402

CrossRef Full Text | Google Scholar

Uchida, K., Adachi, H., An, T., Ota, T., Toda, M., Hillebrands, B., et al. (2011a). Long-range spin Seebeck effect and acoustic spin pumping. Nat. Mater. 10, 737–741. doi:10.1038/nmat3099

CrossRef Full Text | Google Scholar

Uchida, K., An, T., Kajiwara, Y., Toda, M., and Saitoh, E. (2011b). Surface-acoustic-wave-driven spin pumping in Y₃Fe₅O₁₂/Pt hybrid structure. Appl. Phys. Lett. 99, 212501. doi:10.1063/1.3662032

CrossRef Full Text | Google Scholar

Vaz, C. A. F. (2012). Electric field control of magnetism in multiferroic heterostructures. J. Phys. Condens. Matter 24, 333201. doi:10.1088/0953-8984/24/33/333201

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiler, M., Dreher, L., Heeg, C., Huebl, H., Gross, R., Brandt, M. S., et al. (2011). Elastically driven ferromagnetic resonance in nickel thin films. Phys. Rev. Lett. 106, 117601. doi:10.1103/PhysRevLett.106.117601

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiler, M., Huebl, H., Goerg, F. S., Czeschka, F. D., Gross, R., and Goennenwein, S. T. B. (2012). Spin pumping with coherent elastic waves. Phys. Rev. Lett. 108, 176601. doi:10.1103/PhysRevLett.108.176601

PubMed Abstract | CrossRef Full Text | Google Scholar