A Review of Solid-Solution Models of High-Entropy Alloys Based on Ab Initio Calculations

Similar to the importance of XRD in experiments, ab initio calculations, as a powerful tool, have been applied to predict the new potential materials and investigate the intrinsic properties of materials in theory. As a typical solid-solution material, the large degree of uncertainty of high-entropy alloys (HEAs) results in the difficulty of ab initio calculations application to HEAs. The present review focuses on the available ab initio based solid-solution models (virtual lattice approximation, coherent potential approximation, special quasirandom structure, similar local atomic environment, maximum-entropy method, and hybrid Monte Carlo/molecular dynamics) and their applications and limits in single phase HEAs.

Introduction

High-entropy alloys (HEAs) have received significant research attention in the last decades (Cantor et al., 2004; Yeh et al., 2004), due to the excellent mechanical behaviors and potential industrial applications. HEAs are the solid solutions composed of at least five four equimolar or near-equimolar alloying elements. Depending on the process of heat treatment and the change of the content of dopant elements, the microstructures in the family of HEAs are found from the single phase solid solutions to double phase solid solutions to multiphase microstructure containing the solid-solution phase and inter-metallic compounds (Zhang et al., 2013; Tsai and Yeh, 2014; Lu et al., 2015; Jyothi, 2016; Miracle and Senkov, 2016). Whereas the single phase solid solutions are an ideal sample which is used to study the formation mechanism and intrinsic mechanism responsible for the excellent performance in the family of HEAs. To date, a good number of single phase HEAs have been collected and reviewed (Guo and Liu, 2011; Yang and Zhang, 2012; Kozak et al., 2015; Tian et al., 2015a).

The single-phase HEAs have a simple lattice crystal structure, for example, face centered cubic (fcc) (Yeh et al., 2004), body centered cubic (bcc) (Senkov et al., 2010), hexagonal close packed (hcp) (Takeuchi et al., 2014; Feuerbacher et al., 2015; Gao et al., 2015), and sodium chloride (Fan et al., 2016) structures, etc. Whereas their alloying elements in from of the substitutional solid solutions are randomly distributed on the lattice sites, different types of atoms can substitute each other. Namely the long range order of the crystal lattice sites is broken. One names the random distribution of the atoms on the lattice sites as the chemical disorder. Considering the alloying elements of some HEAs are composed of Cr, Mn, Fe, Co, or Ni, we introduce the magnetic disorder in the solid-solution alloys. With increase of temperature, the magnetic interaction energy is overtaken by the magnetic entropy contribution, and as a result, the individual magnetic moments of alloying elements become randomly oriented, and total vector moment is vanished. The paramagnetic (PM) state is a disordered phase formed by randomly distributed atomic magnetic moments, which indicates that some alloying elements may have local atomic magnetic moments.

Due to the chemical and magnetic disorders, HEAs present a great fundamental challenge to the conventional ab initio calculations, and the few availably theoretical predictions, based on ab initio calculations, involve a large degree of uncertainty. Until now, in the framework of ab initio calculations based on density functional theory (DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965), the available approximations are the virtual crystal approximation (VCA) (Bellaiche and Vanderbilt, 2000), the coherent potential approximation (CPA) (Soven, 1967), the simple supercell with random atomic distribution (SC), the special quasirandom structure (SQS) (Zunger et al., 1990), and the similar local atomic environment (SLAE) method (Song et al., 2017) as well as the maximum entropy (MaxEnt) (Wang, 2013) and the hybrid Monte Carlo/molecular dynamics (MC/MD) method (Widom et al., 2013). Based on these models, one studied the electronic density of state (DOS) (Zhang et al., 2015), the equilibrium bulk properties (Tian et al., 2013b, 2014), the phase transformation (Tian et al., 2013a; Ma et al., 2015; Rogal et al., 2017), the elastic properties, the local lattice distortion (Okamoto et al., 2016; Song et al., 2017), and stacking fault energy (SFE) of HEAs (Huang et al., 2015; Zhao et al., 2017). At the same time, the alloy is very sensitive to the temperature. The accuracy calculations of phonon DOS are extremely lack for HEAs. The temperature dependent thermal-physical properties were studied based on the quasiharmonic approximation (QHA) in ab initio calculations (Ge et al., 2017; Tian et al., 2017).

The following sections are arranged as follows: In Sec. II, ab initio based method is presented, including DFT, ab initio molecular dynamics (AIMD), QHA, and elastic theory for cubic and hexagonal crystal structures. The solid-solution models (effective medium and supercell method) and their applications are and discussed in Sec. III, and the review ends with conclusions.

Ab Initio-Based Method

Density Functional Theory

Today, DFT is one of the most popular ab initio methods and is extensively applied to calculate the electronic properties of molecules and solids. According to the theorem of Hohenberg and Kohn (1964), the ground state of a system is described via the energy functional

$E_e\left[n\right]=F\left[n\right]+\int v_e\left(r\right)n\left(r\right)\mathit{dr},$ (1)

where F[n] is a universal functional of the electron density n(r), $\int v_e\left(r\right)n\left(r\right)\mathit{dr}$ is the interaction energy with the external potential. One can prove that the minimum of E_e[n] is equal to the total energy of electronic system via the equilibrium electron density. The F[n] is often represented as

$F\left[n\right]=T_s\left[n\right]+E_H\left[n\right]+E_{\mathit{xc}}\left[n\right],$ (2)

where T_s[n] is the kinetic energy of non-interacting particles, E_H[n] is the Hartree energy $\int \frac{n\left(r^{\prime }\right)}{\left|r-r^{\prime }\right|}\mathit{dr}$. The last term E_xc[n] is the exchange-correlation functional. Although it contributes small energy for total energy, E_xc[n] is a key term to predict correctly the equilibrium bulk properties of a material.

Within the Kohn-Sham scheme (Kohn and Sham, 1965), the effective one-electron Schrödinger equation is defined as

$\left[-{\nabla }^2+V_{\text{ext}}+2\int \frac{n\left(r^{\prime }\right)}{\left|r-r^{\prime }\right|}\mathit{dr}+{\mu }_{\mathit{xc}}\right]{\psi }_i={\epsilon }_i{\psi }_i,$ (3)

where μ_xc = δE_xc(n)/δn(r), ε_i is the one electron energy, and ψ_i is the corresponding Kohn-Sham orbitals. Due to the unknown exact form of μ_xc, one has to adopt different approximations. The local density approximation and the generalized gradient approximation are the two most widely applied approximations for the exchange-correlation terms. There exist several methods for solving the Kohn-Sham equations, of which the pseudopotential and muffin-tin methods are extensively applied in the calculations of materials.

Ab Initio Molecular Dynamics

In fact, the Kohn-Sham scheme is to solve the time-independent Schrödinger equation of electrons. So we can obtain the electronic eigenvalue. Because the electrons respond instantaneously to the nuclear motion, on the electronic surface from the electronic eigenvalue, the nuclear dynamics can be determined by a time-dependent Schrödinger equation for the nuclear wave function.

When the non-adiabatic effects are neglected and the motion only on the ground electronic surface is considered, we may further approximate and arrive at the classical nuclear evolution. The classical motion on the ground-state surface, E₀(R) = ε₀(R) + V_NN(R) is given by

${\stackrel{\cdot }{R}}_I=\frac{P_I}{M_I},$ (4)

${\stackrel{\cdot }{P}}_I={\nabla }_I{E}_0\left(R\right).$ (5)

The force −∇_IE₀(R) contains a term from the nuclear–nuclear repulsion and a term from the derivative of the electronic eigenvalue, ε₀(R) According to the Hellman-Feynman theorem, ε₀(R) can be expressed as

$-{\nabla }_I{\mathrm{\epsilon }}_0\left(R\right)=⟨{\mathrm{\varphi }}_0\left(R\right)\left|{\nabla }_I{H}_e\left(R\right)\right|{\mathrm{\varphi }}_0\left(R\right)⟩.$ (6)

The Eqs. 4–6 form the theoretical basis of the AIMD approach.

Ab initio molecular dynamics method combines the finite temperature dynamics with forces obtained from electronic structure calculations performed “on the fly” as the simulation proceeds of molecular dynamics. Considering that the electronic structure is treated explicitly in AIMD calculations, the electronic polarization, bond-breaking and many-body forces can be described in principle with the calculated accuracy of the electronic structure. More detailed discussions of AIMD are found in Ref. (Tuckerman, 2002).

Ab initio molecular dynamics simulations can be used to predict individual atomic trajectories of solid or liquids held at a constant elevated temperature. However, the drawback is the computational demanding, limited to a small system (several hundred (< 500) atoms) and a short period of time (~10–100 ps).

The QHA

In the harmonic model, the vibrations in a crystal are treated as a gas of 3nN non-interacting phonons with volume independent frequencies, where n is the number of atoms per primitive cell and N is the number of cells in the macroscopic solid. To avoid the unphysical behaviors in harmonic model and rightly describe the thermodynamic properties, the anharmonic effect should be considered. Although the phonon DOS can be used to accurately calculate the lattice vibrations and estimate the thermodynamic quantities, the quasi-harmonic approximation (QHA) is still the simplest way of accounting for anharmonic effects. In QHA, we assume the harmonic approximation at any given crystal structure, even if it does not correspond to the equilibrium structure. The quasi-harmonic Debye–Grüneisen model (Blanco et al., 2004) allows us to investigate the thermodynamic properties with thermal effects. The vibrational contribution A_vib is written as

$A_{\mathit{vib}}\left(\mathrm{\Theta };T\right)=\mathit{nkT}\left[\frac{9}{8}\frac{\mathrm{\Theta }}{T}+3\mathit{ln}\left(1-e^{-\mathrm{\Theta }/T}\right)-D\left(\mathrm{\Theta }/T\right)\right],$ (7)

where n is the number of atoms per primitive cell, k is the Boltzmann constant, Θ is the Debye temperature, and D(y) is the Debye integral which is defined as

$D\left(y\right)=\frac{3}{y^3}{\displaystyle \underset{0}{\overset{y}{\int }}}\frac{x^3}{e^x-1}\mathit{dx}.$ (8)

For an isotropic crystal with Poisson ratio ν, Θ can be expressed as

$\mathrm{\Theta }=\frac{h}{k}{\left[6{\mathrm{\pi }}^2{V}^{1/2}n\right]}^{1/3}f\left(\mathrm{\nu }\right)\sqrt{\frac{B_S}{M}},$ (9)

where M is the molecular mass per primitive cell, and the adiabatic bulk modulus B_S is simplified as

$B_S\simeq B\left(V\right)=V\left(\frac{d^{2}E\left(V\right)}{{\mathit{dV}}^2}\right).$ (10)

The function f (ν) in Eq. 9 is given by

$f\left(\mathrm{\nu }\right)={\left\{3{\left[2{\left(\frac{2}{3}\frac{1+\mathrm{\nu }}{1-\mathrm{2\nu }}\right)}^{3/2}+{\left(\frac{1}{3}\frac{1+\mathrm{\nu }}{1-\mathrm{\nu }}\right)}^{3/2}\right]}^{-1}\right\}}^{1/3}.$ (11)

Using the density function theory based ab initio calculations, we can extract the bulk modulus B and the volume V from the curves of total energy vs. volume of crystal cell. The Poisson ratio v is often set to be 0.25 or obtained from the calculations of elastic constants.

The magnetic entropy $S_{\text{mag}}=k_B{\displaystyle \sum _{\text{i}=1}^n}\text{ln}\left(1+{\mathrm{\mu }}_i\right)$, where c_i is the concentration and μ_i the magnetic moment of the ith alloying element.

The electronic entropy is estimated via the Sommerfeld form at the low-temperature limit

$S_{\mathit{el}}=\left(\frac{2{\mathrm{\pi }}^2}{3}\right)N\left(E_F\right)\left(1+{\mathrm{\gamma }}_{\text{el}-\text{phon}}\right)k_B^{2}T,$ (12)

where N(E_F) is the DOS at the Fermi energy and γ_el-phon is the constant of electron–phonon interactions, which becomes small at high temperatures. Using another estimated method, the electronic entropy contribution at temperatures above the Debye temperature may be expressed as

$S_{\mathit{el}}=-\int \mathit{dE}N\left(E\right)\left[f\left(E\right)\mathit{lnf}\left(E\right)+\left(1-f\left(E\right)\right)\ln \left(1-f\left(E\right)\right)\right],$ (13)

where N(E) is the electron DOS, f (E) is the electronic excitations. In the Kohn-Sham scheme, f (E) is taken into account by using the Fermi-Dirac distribution function.

According the above entropy contributions, the Gibbs free energy can be written as

$G\approx E-{\mathit{TS}}_{\text{vib}}-{\mathit{TS}}_{\text{el}}-{\mathit{TS}}_{\text{mix}}-{\mathit{TS}}_{\text{mag}},$ (14)

where E is the statistic energy at 0 K using ab initio calculations, S_mix is the mixing entropy. According to the Gibbs free energy G, the thermodynamic stability a function of temperature can be estimated for different phases. The phase transformation further can be predicted.

Elastic Constants Calculations from Energy vs. Strain

For ab initio calculated elastic constants, one of available methods is based on the energy-strain relations. Considering the crystal structures of single phase HEAs found in experiments, we only discuss how to derive the elastic constants of the cubic and hexagonal structures from the structural deformation and the equation of state.

According to the elastic theory, the cubic lattice has three independent elastic constants c₁₁, c₁₂, and c₄₄. Two of the cubic elastic constants can be derived from the bulk modulus B = (c₁₁ + 2c₁₂)/3 and the tetragonal shear modulus $c^{\prime }=\left(c_{11}-c_{12}\right)/2$. The bulk modulus can be obtained from the equation of state with the Morse or forth-order Birch-Murnaghan function. The two shear moduli c′ and c₄₄ may be obtained from the orthorhombic and monoclinic distortions (Vitos, 2007)

$\left(\begin{array}{ccc}\hfill 1+{\mathrm{\delta }}_o\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1-{\mathrm{\delta }}_o\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{1-{\mathrm{\delta }}_o^2}\hfill \end{array}\right)\text{ and }\left(\begin{array}{ccc}\hfill 1\hfill & \hfill {\mathrm{\delta }}_m\hfill & \hfill 0\hfill \\ \hfill {\mathrm{\delta }}_m\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{1-{\mathrm{\delta }}_m^2}\hfill \end{array}\right),$ (15)

which result in the energy change $\mathrm{\Delta }E\left({\mathrm{\delta }}_o\right)=2V{c}^{\prime }{\mathrm{\delta }}_o^2+\mathcal{O}\left({\mathrm{\delta }}_o^4\right)$ and $\mathrm{\Delta }E\left({\mathrm{\delta }}_m\right)=2V{c}_{44}{\mathrm{\delta }}_m^2+\mathcal{O}\left({\mathrm{\delta }}_m^4\right)$.

The hexagonal lattice has five independent elastic constants c₁₁, c₁₂, c₁₃, c₃₃, and c₄₄. The bulk modulus can be calculated from B = c²/c_s, where $c^2\equiv c_{33}\left(c_{11}+c_{12}\right)-2c_{13}^2$, and c_s ≡c₁₁ + c₁₂ + 2c₃₃ − 4c₁₃. The dimensionless quantity R = − dln(c/a)₀(V)/dlnV has relationship with hexagonal elastic constants which can be described as R = (c₃₃ − c₁₁ − c₁₂ + c₁₃)/c_s. The three elastic constants c_s, c₆₆, and c₄₄ may be obtained from the isochoric, orthorhombic, and monoclinic distortions (Vitos, 2007)

$\left(\begin{array}{ccc}\hfill 1+{\mathrm{\delta }}_h\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1+{\mathrm{\delta }}_h\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{{\left(1+{\mathrm{\delta }}_h\right)}^2}\hfill \end{array}\right),\left(\begin{array}{ccc}\hfill 1+{\mathrm{\delta }}_o\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1-{\mathrm{\delta }}_o\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{1-{\mathrm{\delta }}_o^2}\hfill \end{array}\right),\text{and}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill {\mathrm{\delta }}_m\hfill \\ \hfill 0\hfill & \hfill \frac{1}{1-{\mathrm{\delta }}_m^2}\hfill & \hfill 0\hfill \\ \hfill {\mathrm{\delta }}_m\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),$ (16)

which result in the energy change $\mathrm{\Delta }E\left({\mathrm{\delta }}_h\right)=V{c}_s{\mathrm{\delta }}_h^2+\mathcal{O}\left({\mathrm{\delta }}_o^3\right)$, $\mathrm{\Delta }E\left({\mathrm{\delta }}_o\right)=2V{c}_{66}{\mathrm{\delta }}_o^2+\mathcal{O}\left({\mathrm{\delta }}_o^4\right)$, and $\mathrm{\Delta }E\left({\mathrm{\delta }}_m\right)=2V{c}_{44}{\mathrm{\delta }}_m^2+\mathcal{O}\left({\mathrm{\delta }}_m^4\right)$, where c₆₆ = (c₁₁ − c₁₂)/2. All of the above energy calculations were computed for six deformations δ = 0.00, 0.01,…,0.05.

For the isotropic polycrystalline system, the polycrystalline elastic moduli, for example Young’s modulus E, shear modulus, G, and Poisson ratio v can be derived from the elastic constants c_ij.

Solid-Solution Models

For the theoretically calculated study of solid-solution alloys, the approximation is necessary in the framework of ab initio based on DFT. One direct approach is the supercell approximation, i.e., the periodic boundary condition is artificially imposed on the supercell to study the disordered configuration, the size of supercell strongly depends on the chemical disorder. Another way is the effective medium, in which, one only uses a primitive periodicity cell to study the arbitrary chemical disorder. In the following subsections, we will introduce the effective mediums and supercell methods and their applications.

The Effective Medium

The single phase HEAs are usually composed of the equimolar multicomponent solid solutions, i.e., HEAs have many elemental components at high concentrations and have the local structural distortions and chemical and magnetic disorders. The traditionally analytical theories of solute strengthening for dilute alloys with non-interacting solutes would not seem to apply. Whereas each alloying element can be seen as a “solute” embedded in the average effective medium “matrix” of the surrounding material. Such an effective medium approximation is well-established in the DFT, such as the virtual crystal approximation (VCA) based on the electronic band structure calculations and the CPA based on the multiple dispersion method.

The Virtual Crystal Approximation

As a convenient way to simulate the solid-solution alloys, the VCA is usually applicable and effective if the alloying elements are neighbors in the periodic table of element (i.e., atoms in the neighboring rows or columns). The concept of VCA is to replace the true alloy with a “virtual” metal that consists of a weighted average between the different alloying elements in the parent compounds. For example, according to the VCA, the bcc TiVZrNb HEA is considered as a monoatomic metal with a nuclear number of 31.5 and a total of 31.5 core and valence electrons (see Figure 1). Although the VCA is considered as an overly simplified approach to substitutional solid solutions, many examples have shown that the VCA can be reliably used to study the alloys composed of refractory elements (Li et al., 2007; Qi and Chrzan, 2014).

FIGURE 1

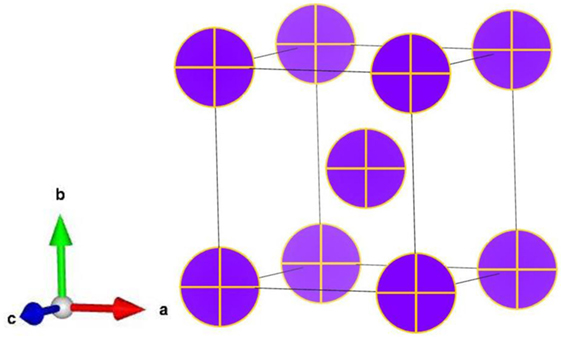
Figure 1. (Color online) Using virtual crystal approximation (VCA), virtual metal M^31.5 for the body centered cubic (bcc) TiVZrNb high-entropy alloy (HEA).

Mu et al. (2017) used the VCA to study the electronic DOS of the single phase Ti-Zr-V-Mo-Ta-Nb-Cr-W refractory HEAs. The total DOS suggests that the typical metallic bond in refractory HEAs and the change of DOS at Fermi level implies that the dynamical stability against tetragonal deformation strengthens with increase of the number of alloying elements (from TiZrVMo to TiZrVMoNbCrW). The relatively small DOS of Mo (Nb) suggests that Mo may be a strong (weak) bcc stabilizer, compared to other alloying elements.

Both ideal tensile strength and shear strength are the intrinsic mechanical properties of materials. The VCA calculations indicated that the tensile strength σ of TiVNbMo is about 10 GPa at the strain ε = 0.14 along the face centered orthorhombic (fco) path, while σ = 19 GPa at the strain ε = 0.18 along the body centered tetragonal path (bct), i.e., the Bain path. The ideal shear strength is σ = 8.5 GPa at ε = 0.20 under {110} < 111 > shear, while σ = 2.5 GPa at strain ε = 0.10 for {211} < 111 > shear (Tian et al., 2016b).

When the disorder has no large effect on the crystal-field Hamiltonian, the VCA may be used to describe the magnetic state of HEA. The angular momentum at each lattice site can be replaced with a compositional average $\overrightarrow{J}=\frac{1}{n}{\displaystyle \sum _{m=1}^n}\overrightarrow{J_m}$, where the sum is for all alloying elements of HEAs. Within the VCA, the disorder-induced pinning potential is neglected due to fast thermal fluctuations of the spins and the spin system behaves as a pure system of compositionally averaged spins coupled via the exchange and interacting with the crystalline electric fields and external magnetic field. Readers are referred to more details in Ref. (Lužnik et al., 2015).

The CPA

The CPA is based on the assumption that HEA may be replaced by an ordered effective medium, the parameters of which are determined self-consistently. The impurity problem is usually treated within the single-site approximation. No information is provided about the charge redistribution around the impurities.

Figure 2 shows the illustration of the CPA to HEAs. The quinary HEA, composed of the alloying elements A, B, C, D, and E, is replaced by an effective medium. Within the CPA there exists two main approximations, one is to assume the local potentials (P_A, P_B, P_C, P_D, P_E) around a certain type of atom from the alloy are the same, which results in the ignorance of local environment effect. Another approximation is that the system is replaced by a monoatomic medium described by the site independent coherent potential $\tilde{P}$.

FIGURE 2

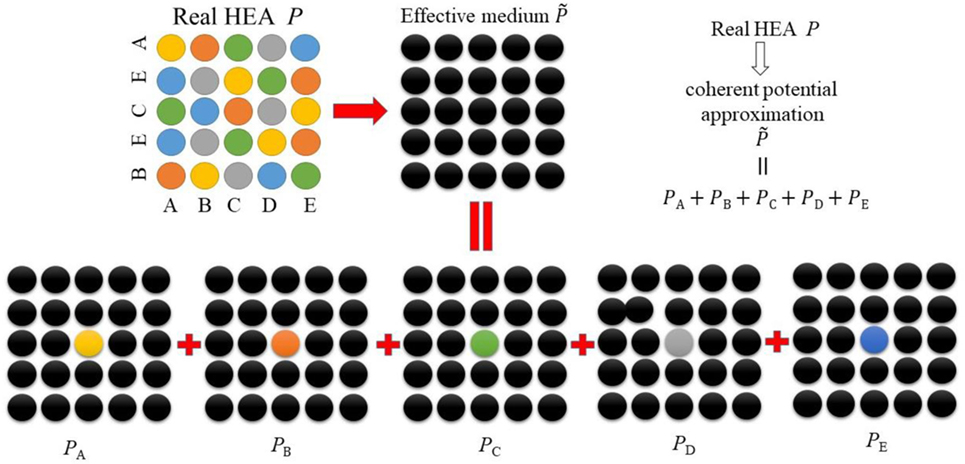
Figure 2. (Color online) Two-dimensional illustration of the coherent potential approximation (CPA) for the equimolar ABCDE high-entropy alloys (HEAs). The symbol P represents the real alloy potential, $\tilde{P}$ for coherent potential, P_A, P_B, P_C, P_D, P_E are the potentials of the alloying elements.

Using the CPA in combination with the exact muffin-tin orbitals (EMTOs) method (Vitos, 2007), ab initio calculations can properly describe the fundamental properties of HEA, for instance, the equilibrium lattice parameters, elastic modulus, simple crystal phase transformation and magnetic transformation from ferromagnetic (FM) to PM state (T_c). Table 1 lists the elastic constants (c₁₁, c₁₂, c₄₄) and Young’s moduli from theoretical calculations and experiments for some typical fcc and bcc HEAs. For a mechanically stable material, the single-crystal elastic constants satisfy the dynamical stability conditions (c₄₄ > 0, c₁₁ > c₁₂, and c₁₁ + 2c₁₂ > 0). The ab initio calculations listed in Table 1 suggest the mechanical stability of the available HEAs in experiments. We can see that the theoretical predictions are in good agreement with the experimental measures for Co-Cr-Fe-Mn-Ni 3d HEAs and Ti-Zr-Hf-V-Nb-Ta-Mo-W refractory HEAs.

TABLE 1

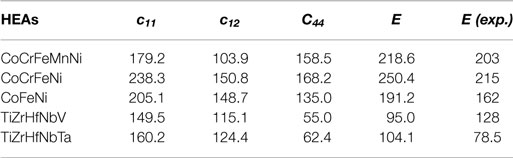
Table 1. Theoretical calculated elastic constants c_ij (GPa), Young’s modulus E (GPa), and available experiments (GPa) for HEAs (Fazakas et al., 2014; Tian et al., 2016a).

The temperature-dependent phase stability is usually determined via the Gibbs free energy including the static energy and the contribution from vibrational entropy, magnetic entropy, mixing entropy and electronic entropy. Based on ab initio (EMTO-CPA) calculations of the equation of state (total energy vs. volume), one can use the QHA to estimate the vibrational entropy and then estimate the Gibb free energy. The temperature of hcp-fcc phase transformation is about 450 and 350 K for the FM and PM CoCrFeMnNi HEAs, respectively (Ma et al., 2015).

The Supercell Method

In the supercell method, the key points are how to mimic the distribution of local chemical environment in random solid solutions and to reduce the demanding of computations. Due to the random distribution of alloying elements, short-range order, long-range order, possible partial order, etc. in solid-solution HEAs, the effective supercell models are expected to consider the above configurations.

The Simple Supercell with Random Distributed Atoms

In this method, one first constructs the large supercell based on the unit cell of crystal structure, then makes the alloying elements randomly distribute on the lattice sites. Based on the hcp (two lattice sites) and Pmma symmetry (six lattice sites) unit cells, the modeled systems including 54 and 48 atom supercells for the fully disordered and partial-order hexagonal Mo-Pd-Rh-Ru-Tc HEAs, respectively. King et al. (2017) showed that these sizes are sufficient to achieve convergence in total energy. Results suggested that single phase solid solutions are predicted to transform to a partial-order structure (Middleburgh et al., 2014; King et al., 2017).

Due to the large number of possible arrangements, Middleburgh et al. (2014) constructed the 20 2 × 2 × 2 fcc supercells (32 atoms) to study the segregation and migration of species in the CoCrFeNi HEA. For each supercell, the equimolar Co, Cr, Fe, and Ni alloying elements were randomly assigned to the 32 lattice sites. Via the geometrical optimization based on ab initio calculations, the energy per CoCrFeNi unit varied by ±0.06 eV for most of configurations, but the energy per CoCrFeNi unit for three configurations varied by >0.15 eV. The average energies are acceptable considering the variation in arrangement between each supercell, whereas both vacancy formation energy and defect energy strongly depend on the alloying elements (Middleburgh et al., 2014).

Based on 200-atom cubic supercells with random distributed atoms, AIMD simulated partial correlation functions show that the chemical interaction and atomic diffusivities can be used to assist in identifying single phase solid-solution composition. The selected partial pair correlation functions in the 200-atom liquid phase indicated that some atomic pairs (for example, Al-Ni, Cr-Fe, and Cu-Cu) are much more likely to be found as the nearest neighbors in all atomic pairs (for example, Al-Al and Cr-Ni) in Al_1.3CoCrCuFeNi. Such preferred nearest-neighbor pairs in the liquid phase are consistent with the formation of a B2-ordered solid solution primary phase (Santodonato et al., 2015).

The low SFE may be responsible for the good ductility of HEAs. To calculate the realistic statistical mean of SFE, Zhang et al. constructed the 80 supercell structures containing 300–500 atoms to study the SFE for each HEA. In these SC structures, atom are randomly assigned to the lattice sites of the corresponding crystal structure, Via the geometrical optimization, the ground state configurations are obtained for each SC structure. Although the computation is very demanding, the supercell allows to evaluate the stacking-fault energies and their formation energy barriers (Zhang et al., 2017). Interestingly the SC stacking faulty energy prediction for CoCrNi is in good agreement with the CPA calculations. Note that Zhang et al.’s calculations were performed on non-magnetic structures based on non-spin-polarized set. The good agreement may be due to the very small local magnetic moments for alloying elements.

For the simple supercell method, one may not guarantee the real random distribution of alloying elements on the lattice sites in one configuration. The large number of configurational samples may result in the high demanding of computations, besides that the predicted properties depend on the configurations.

The SQS

Based on the effective cluster expansion, the objective correlation function in SQS method is defined to determine the degree of mimic the atomic pairs, triplets and quadruplets correlations. At present, as two popular algorithms, the MC and genetic algorithms are often used to accelerate the production of the SQS model. For binary or ternary substitutional alloys, the SQS approach is to identify specially designed small-unit-cell periodic structures that closely mimic the local pair and multisite correlation functions of a random alloy under the constraint of a given unit cell size. Note that the product SQS does not keep the cubic or hcp configuration in case of the type alloys, whereas in HEAs, due to too many objection correlation functions, the pair correlation is often mimicked (Gao et al., 2016).

Rogal et al. (2017) used the SQS method in combination with VASP calculated tool (Kresse and Joubert, 1999) to predict the temperature-dependent stability of hcp D0₁₉ and hcp A3. The 216-atom SQSs were generated, corresponding to 6 × 6 × 3 times the primitive hcp cell. Due to many possible configurations satisfying the pair correction functions in SQS, two SQS configurations are used to estimate the energy vs. volume for hcp D0₁₉ and hcp A3. Both SQS’ results suggest that hcp D0₁₉ is more stable than bcc A2 and hcp A3. With increase of temperature, the hcp A3 becomes more stable. The temperature of phase formation is 1,230 K when the contributions to Gibbs free energy are considered from the vibrational, electronic, and configuration entropy.

It is well known that SQS can well represent the random solid solutions of alloys and allows one to use many convenient subsequent methods. To study the effect of defects in HEAs (for example, calculating SFE), one constructs the solid-solution configurations with the planar defects. The introduction of the planar defect may break the perfect-matched SQS correlation functions. It may induce that atomic arrangements near the planar defect do not satisfy the random solid solutions. This challenge is also for the SLAE solid-solution model. For refractory alloys and HEAs, Tian et al. (2015b, 2017) compared the elastic constants from the SQS and CPA calculations. Results showed that both SQS and CPA calculations predict the consistent equilibrium bulk properties with experiments, whereas the elastic constants are slightly dependent on the size of SQS. As far as I am concerned, SQS is not be used to simulate the PM HEAs due to the limit of size.

For multicomponent HEAs, with increasing number of alloying elements, the correlation functions quickly increase, it becomes very difficult to find a small-sized SQS that can still adequately mimic the statistics of a random alloy. Jiang and Uberuaga (2016) propose a novel small set of ordered structures (SSOS) method. Different from the single large supercell to mimic the random state, within SSOS method, the real solid-solution HEA is replaced by using a set of small ordered structures with the weight-averaged properties approximate.

The SLAE

Different from SQS, which is obtained by optimizing the correlation functions of the supercell to match those of the perfectly random alloys, the SLAE model for the random alloys proposed is constructed by setting the local atomic environments of all the lattice sites similar to each other (Song et al., 2017). The local atomic environment is defined according to the radial distribution functions (RDFs) and three-body correction functions similar to three-body potential,

$g_2\left(r\right)=\frac{1}{N}⟨{\displaystyle \sum _{i=1}^{N_{\mathrm{\alpha }}}}{\displaystyle \sum _{j=1}^{N_{\mathrm{\beta }}}}\left(\mathrm{\delta }\left(r-r_i+r_j\right)\right)⟩/\left(c_{\mathrm{\alpha }}{c}_{\mathrm{\beta }}p\right),$ (17)

$g_3\left(r_{\mathit{ij}},r_{\mathit{ik}},\mathrm{\theta }\right)=\frac{1}{N}⟨{\displaystyle \sum _i^{N_{\mathrm{\alpha }}}}{\displaystyle \sum _j^{N_{\mathrm{\beta }}}}{\displaystyle \sum _k^{N_{\mathrm{\gamma }}}}R\left(r_{\mathit{ij}},r_{\mathit{ik}}\right)\mathrm{\delta }\left(\mathrm{\theta }-{\mathrm{\theta }}_{\mathit{jik}}\right)⟩/\left(c_{\mathrm{\alpha }}{c}_{\mathrm{\beta }}{c}_{\mathrm{\gamma }}p\right),$ (18)

where N is the total number of atoms, N_α(N_β, N_γ) is the number of atoms of alloy component α(β,γ). c_α(c_β, c_γ) is the molar fraction of alloy component α(β,γ). p stands for the overall numbers density. r is the interatomic distance while θ(θ_jik) is the angle among the three neighboring atoms (j-i-k).

In order to intuitively describe the radial distribution and the three-body correlation, we use the standard deviation to determine the disorder degree. The SLAE supercell for each lattice site may be obtained via random search. The number of atomic pairs on the boundary is equally divided by the two neighboring supercells to treat the periodic boundary condition.

Figure 3 shows the 150-atom bcc, fcc, and hcp SLAE configurations and their radial distribution as a function of the near neighboring atomic pairs for the equimolar sequary HEA. Note that for the 150-atom fcc SLAE structure, the primitive cell along fcc (111) crystal direction (three crystal sites) is adopted.

FIGURE 3

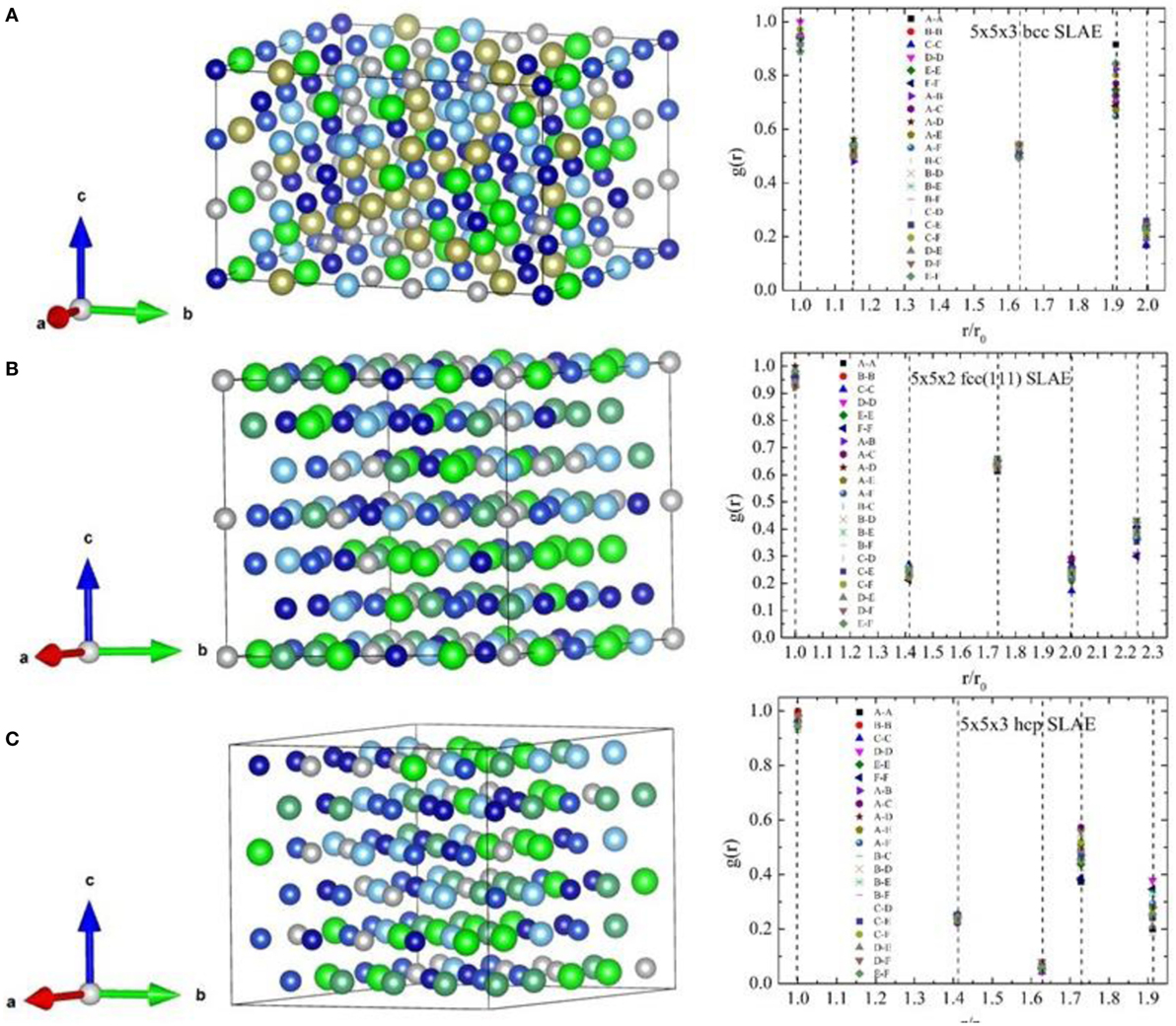
Figure 3. (Color online) Structural illustration (left panels) and the radial distribution g(r) (right panels) of the 150-atom similar local atomic environment (SLAE) for the sequary body centered cubic (bcc) (A), face centered cubic (fcc) (B), and hexagonal close packed (hcp) (C) A-B-C-D-E-F high-entropy alloys (HEAs).

Based on the relatively large-size SLAE cubic or orthogonal structures for Co-Cr-Fe-Mn-Ni alloys, Song et al. (2017) used the disorder local moment approximation to simulate the PM state. The predicted Curie temperatures (718.8 K for CoFeNi, 81.3 K for CoCrFeNi, and 31.4 K for CoCrFeMnNi) are acceptable comparing with experiments (868, 81.3, and 23 K for three HEAs) (Körmann et al., 2015).

The Maximum-Entropy Method

According to the second rule of thermodynamics, the particle distribution of MaxEnt corresponds to the most micro-states. The principle of MaxEnt (Carlsson and Fedders, 1986) is the combination of the Shannon’s entropy in informatics with the Boltzmann-Gibbs entropy in statistical mechanics for estimating probability distribution from a few limited pieces of information. Although the entropy of a solid-solution system mainly consists of zero point entropy, electronic entropy, magnetic entropy, vibrational entropy, and configurational entropy (entropy of mixing), in the MaxEnt method (Carlsson and Fedders, 1986), the configurational entropy is only considered. The configurational entropy depends on the number of possible configurations of a system. Because the configurational entropy of melt alloy is similar to the mixing entropy of ideal gases, the configurational entropy of the melt n-component alloy is defined by $S_{\text{conf}}=-R{\displaystyle \sum _{i=1}^n}{x}_i\mathit{ln}\left(x_i\right).$ Here x_i is the molar concentration of the ith alloying element which satisfies ${\displaystyle \sum _{i=1}^n}{x}_i$, R is the ideal gas constant. Note that the equation is only valid for randomly solid-solution alloys.

The free space of a particle is defined as its maximum non-overlapping space with the other particles. We can define v_i as the free space of the particle i for a system with N identical particles in space V. v_i = V/N is under the MaxEnt condition, i.e., the identical particles have the equal maximum free space V/N within the limitation of MaxEnt. It is corresponding to a state of uniform spatial distribution of particles. So, the MaxEnt state has the configuration with a uniform particles distribution over the system (Wang, 2013).

According to the MaxEnt principle, every particle is striving for the maximum free space in the system. The driving force for this trend is called as the entropic force. The entropic force is defined as

$F\left(X\right)=T{\mathrm{\Delta }}_{X}S\left(X\right),$ (19)

where T is temperature, S(X) is the entropy under the system configuration X. Since there is a proportional relationship between entropy and the particle’s free space for a closed particle system with a fixed volume V, the contribution of particle i to the system entropy is s_i(r) = kv_i(r), where v_i(r) is the free space of particle i at position r, k is a constant. Further, the entropic force f_i(r) on particle i is obtained as

$f_i\left(r\right)=\mathit{kT}{\mathrm{\Delta }}_r{v}_i\left(r\right).$ (20)

Equation 20 indicates that the entropic force f_i(r) is pointed to the increase of v_i(r). So the MaxEnt configuration can be gotten through minimizing f_i(r) for each particle in the system.

To generate the MaxEnt configurations, the MC method is used to generate periodic models guided by the principle that all same-element atoms should disperse homogeneously in the model, hundreds of MaxEnt structures can be generated at the same time. According to the defined screening criterion which is the same-element atoms have the same neighbors, the ideal MaxEnt configurations are chosen.

The Hybrid MC/MD

The hybrid MC/MD has been used to construct the configurations of HEAs (Widom et al., 2013; Brink et al., 2016). In ab initio framework, the hybrid MC/MD has been estimated by Widom et al. The feasibility of the MC/MD method depends on adequate acceptance rates for attempted species swaps.

Generally speaking, molecular dynamics can be used to well reproduce the small amplitude oscillations of atoms in the vicinity of crystal lattice sites. The probability of an atom crossing the barrier from one lattice site to another is prohibitively low and will rarely occur on the time scale of a molecular dynamics run at low temperature. Whereas MC swaps of atomic species on different sites occur with a probability P = exp (ΔE/k_BT) related to the net energy difference ΔE = E_swap − E_ini of swapped and initial configurations. In particular, it is independent of the energy barrier separating the states.

In the Multi-Cell Monte Carlo [(MC)² Relaxation] relaxation method proposed by Ghazisaeidi et al. (Niu et al., 2017), the atom swaps between/within the two supercells are allowed. Combining with the ab initio energy optimizations, one can predict the ordering or phase separation in HEAs. Niu et al. (2017) used the (MC)² Relaxation to predict the phase stability of HfNbTaZr refractory HEA. Results reproduce the separation into HfZr and TaNb phases found in experiments (Otto et al., 2016).

The hybrid MD/MC calculations are implemented by alternating molecular dynamics with MC swaps. Based on the calculations of AIMD, Widom et al. performed the species swap in between every 10 MD steps at a given temperature. The 16-atom 2 × 2 × 2 bcc supercell was first constructed, where the atomic species are random distributed. The configuration was thoroughly annealed under MC/MD at a given temperature. Then the annealed structures are used to generate successively larger supercells, of size 32, 64, and 128 atoms, thoroughly annealing at each size. The partial RDFs g_αβ at room temperature, we may find the maximizing the number of Ta-Mo atomic pairs is correspond to the large enthalpy of Ta-Mo pairwise interactions, whereas the weak peak of Nb-W atomic pairs suggest the weak inter-group bonds.

Due to the adopted ab initio calculations instead of empirical potentials, the computational demanding is necessary to both (MC)² Relaxations and hybrid MC/MD simulations. Meanwhile the involved supercell limits the application of (MC)² Relaxations and hybrid MC/MC to the selected-stoichiometry HEAs.

Conclusion

In ab initio or classical molecular dynamics calculations, the available solid-solution models are necessary for HEAs.

The effective medium is an efficient method to simulate the arbitrary-stoichiometry alloys. Both virtual lattice approximation and CPA can used to properly predict the equilibrium bulk properties, especially the elastic constants, simple phase transformation, and the magnetic disorder (PM state) can be reproduced via the EMTO-CPA method. Whereas that the local environment is ignored in CPA and VCA. One is expecting the further implements of no-local CPA, in which the near-range environment can be effectively considered. Note that the limit of VCA is HEAs composed of the alloying element having similar chemical property, for example, refractory HEAs.

To mimic the random distribution of atoms in HEAs, in the supercell framework, different solid-solution models are proposed. The local atomic distributions can be determined via the radial correlation function. Meanwhile these solid-solution models allow to use many convenient subsequent methods. Due to the many number of alloying elements, the size of supercell has to be enlarged to satisfy the random distribution of atoms, short range order, partial order, etc. different atomic environments, resulting in demanding computations and the calculated energy differences between different configurations. Due to the size limits, it is slightly difficult for the supercell method to simulate the off-stoichiometry HEAs and the PM HEAs.

In all, based on the ab initio calculations, both effective medium and supercell model are available methods to investigate the properties of HEAs, where we have to be careful of their limits.

Author Contributions

FT finished this review, including wiriting, figures, and tables.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Work was supported by the Science Challenge Project (grant no. JCKY2016212A502) and the National Natural Science Foundation of China (grant nos. 51771015 and 51401014).

References

Bellaiche, L., and Vanderbilt, D. (2000). Virtual crystal approximation revisited: application to dielectric and piezoelectric properties of perovskites. Phys. Rev. B 61, 7877–7882. doi: 10.1103/PhysRevB.61.7877

CrossRef Full Text | Google Scholar

Blanco, M. A., Francisco, E., and Luaña, V. (2004). GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Comput. Phys. Commun. 158, 57–72. doi:10.1016/j.comphy.2003.12.001

CrossRef Full Text | Google Scholar

Brink, T., Koch, L., and Albe, K. (2016). Structural origins of the boson peak in metals: from high-entropy alloys to metallic glasses. Phys. Rev. B 94, 1–9. doi:10.1103/PhysRevB.94.224203

CrossRef Full Text | Google Scholar

Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 375–377, 213–218. doi:10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Carlsson, A. E., and Fedders, P. A. (1986). Maximum-entropy method for electronic properties of alloys. Phys. Rev. B 34, 3567–3571. doi:10.1103/PhysRevB.34.3567

CrossRef Full Text | Google Scholar

Fan, Z., Wang, H., Wu, Y., Liu, X., and Lu, Z. (2016). Thermoelectric performance of PbSnTeSe high-entropy alloys. Mater. Res. Lett. 5, 187–194. doi:10.1080/21663831.2016.1244116

CrossRef Full Text | Google Scholar

Fazakas, É, Zadorozhnyy, V., Varga, L. K., Inoue, A., Louzguine-Luzgin, D. V., Tian, F., et al. (2014). Experimental and theoretical study of Ti20Zr20Hf20Nb20X20 (X=V or Cr) refractory high-entropy alloys. Int. J. Refract. Met. Hard Mater. 47, 131–138. doi:10.1016/j.ijrmhm.2014.07.009

CrossRef Full Text | Google Scholar

Feuerbacher, M., Heidelmann, M., and Thomas, C. (2015). Hexagonal high-entropy alloys. Mater. Res. Lett. 3, 1–6. doi:10.1080/21663831.2014.951493

CrossRef Full Text | Google Scholar

Gao, M. C., Niu, C., Jiang, C., and Irving, D. L. (2016). “Applications of special quasi-random structures to high-entropy alloys,” in High-Entropy Alloys: Fundamentals and Applications, eds M. C. Gao, J.-W. Yeh, P. K. Liaw, and Y. Zhang (Cham: Springer International Publishing), 333–368. doi:10.1007/978-3-319-27013-5_10

CrossRef Full Text | Google Scholar

Gao, M. C., Zhang, B., Guo, S. M., Qiao, J. W., and Hawk, J. A. (2015). High-entropy alloys in hexagonal close-packed structure. Metall. Mater. Trans. A 47, 3322–3332. doi:10.1007/s11661-015-3091-1

CrossRef Full Text | Google Scholar

Ge, H., Tian, F., and Wang, Y. (2017). Elastic and thermal properties of refractory high-entropy alloys from first-principles calculations. Comput. Mater. Sci. 128, 185–190. doi:10.1016/j.commatsci.2016.11.035

CrossRef Full Text | Google Scholar

Guo, S., and Liu, C. T. (2011). Phase stability in high entropy alloys: formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 21, 433–446. doi:10.1016/S1002-0071(12)60080-X

CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

Huang, S., Li, W., Lu, S., Tian, F., Shen, J., Holmström, E., et al. (2015). Temperature dependent stacking fault energy of FeCrCoNiMn high entropy alloy. Scr. Mater. 108, 44–47. doi:10.1016/j.scriptamat.2015.05.041

CrossRef Full Text | Google Scholar

Jiang, C., and Uberuaga, B. P. (2016). Efficient Ab initio modeling of random multicomponent alloys. Phys. Rev. Lett. 116, 105501. doi:10.1103/PhysRevLett.116.105501

CrossRef Full Text | Google Scholar

Jyothi, V. (2016). High-Entropy Alloys: A Review. International Research Journal of Engineering and Technology (IRJET), 3, 1563–1566.

Google Scholar

King, D. J. M., Burr, P. A., Obbard, E. G., and Middleburgh, S. C. (2017). DFT study of the hexagonal high-entropy alloy fission product system. J. Nucl. Mater. 488, 70–74. doi:10.1016/j.jnucmat.2017.02.042

CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Körmann, F., Ma, D., Belyea, D. D., Lucas, M. S., Miller, C. W., Grabowski, B., et al. (2015). “Treasure maps” for magnetic high-entropy-alloys from theory and experiment. Appl. Phys. Lett. 107, 142404. doi:10.1063/1.4932571

CrossRef Full Text | Google Scholar

Kozak, R., Sologubenko, A., and Steurer, W. (2015). Single-phase high-entropy alloys – an overview. Zeitschrift für Krist. Mater. 230, 55–68. doi:10.1515/zkri-2014-1739

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B, 59, 1758. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Li, T., Morris, J. W., Nagasako, N., Kuramoto, S., and Chrzan, D. C. (2007). “Ideal” engineering alloys. Phys. Rev. Lett. 98, 105503. doi:10.1103/PhysRevLett.98.105503

CrossRef Full Text | Google Scholar

Lu, Z. P., Wang, H., Chen, M. W., Baker, I., Yeh, J. W., Liu, C. T., et al. (2015). An assessment on the future development of high-entropy alloys: summary from a recent workshop. Intermetallics 66, 67–76. doi:10.1016/j.intermet.2015.06.021

CrossRef Full Text | Google Scholar

Lužnik, J., Koželj, P., Vrtnik, S., Jelen, A., Jagličić, Z., Meden, A., et al. (2015). Complex magnetism of Ho-Dy-Y-Gd-Tb hexagonal high-entropy alloy. Phys. Rev. B 92, 224201. doi:10.1103/PhysRevB.92.224201

CrossRef Full Text | Google Scholar

Ma, D., Grabowski, B., Körmann, F., Neugebauer, J., and Raabe, D. (2015). Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: importance of entropy contributions beyond the configurational one. Acta Mater. 100, 90–97. doi:10.1016/j.actamat.2015.08.050

CrossRef Full Text | Google Scholar

Middleburgh, S. C., King, D. M., Lumpkin, G. R., Cortie, M., and Edwards, L. (2014). Segregation and migration of species in the CrCoFeNi high entropy alloy. J. Alloys Compd. 599, 179–182. doi:10.1016/j.jallcom.2014.01.135

CrossRef Full Text | Google Scholar

Miracle, D. B., and Senkov, O. N. (2016). A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511. doi:10.1016/j.actamat.2016.08.081

CrossRef Full Text | Google Scholar

Mu, Y., Liu, H., Liu, Y., Zhang, X., Jiang, Y., and Dong, T. (2017). An ab initio and experimental studies of the structure, mechanical parameters and state density on the refractory high-entropy alloy systems. J. Alloys Compd. 714, 668–680. doi:10.1016/j.jallcom.2017.04.237

CrossRef Full Text | Google Scholar

Niu, C., Windl, W., and Ghazisaeidi, M. (2017). Multi-cell Monte Carlo relaxation method for predicting phase stability of alloys. Scr. Mater. 132, 9–12. doi:10.1016/j.scriptamat.2017.01.001

CrossRef Full Text | Google Scholar

Okamoto, N. L., Yuge, K., Tanaka, K., Inui, H., and George, E. P. (2016). Atomic displacement in the CrMnFeCoNi high-entropy alloy – a scaling factor to predict solid solution strengthening. AIP Adv. 6, 125008. doi:10.1063/1.4971371

CrossRef Full Text | Google Scholar

Otto, F., Dlouhý, A., Pradeep, K. G., Kubenová, M., Raabe, D., Eggeler, G., et al. (2016). Decomposition of the single-phase high-entropy alloy CrMnFeCoNi after prolonged anneals at intermediate temperatures. Acta Mater. 112, 40–52. doi:10.1016/j.actamat.2016.04.005

CrossRef Full Text | Google Scholar

Qi, L., and Chrzan, D. C. (2014). Tuning ideal tensile strengths and intrinsic ductility of bcc refractory alloys. Phys. Rev. Lett. 112, 115503. doi:10.1103/PhysRevLett.112.115503

PubMed Abstract | CrossRef Full Text | Google Scholar

Rogal, L., Bobrowski, P., Koermann, F., Divinski, S., Stein, F., and Grabowski, B. (2017). Computational engineering of sublattice ordering in a hexagonal AlHfScTiZr high entropy alloy. Sci. Rep. 7, 25. doi:10.1038/s41598-017-02385-w

CrossRef Full Text | Google Scholar

Santodonato, L. J., Zhang, Y., Feygenson, M., Parish, C. M., Gao, M. C., Weber, R. J. K., et al. (2015). Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy. Nat. Commun. 6, 5964. doi:10.1038/ncomms6964

PubMed Abstract | CrossRef Full Text | Google Scholar

Senkov, O. N., Wilks, G. B., Miracle, D. B., Chuang, C. P., and Liaw, P. K. (2010). Refractory high-entropy alloys. Intermetallics 18, 1758–1765. doi:10.1016/j.intermet.2010.05.014

CrossRef Full Text | Google Scholar

Song, H., Tian, F., Hu, Q., Vitos, L., Wang, Y., Shen, J., et al. (2017). Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 1, 23404. doi:10.1103/PhysRevMaterials.1.023404

CrossRef Full Text | Google Scholar

Soven, P. (1967). Coherent-potential model of substitutional disordered alloys. Phys. Rev. 156, 809–813. doi:10.1103/PhysRev.156.809

CrossRef Full Text | Google Scholar

Takeuchi, A., Amiya, K., Wada, T., Yubuta, K., and Zhang, W. (2014). High-entropy alloys with a hexagonal close-packed structure designed by equi-atomic alloy strategy and binary phase diagrams. JOM 66, 1984–1992. doi:10.1007/s11837-014-1085-x

CrossRef Full Text | Google Scholar

Tian, F., Delczeg, L., Chen, N., Varga, L. K., Shen, J., and Vitos, L. (2013a). Structural stability of NiCoFeCrAlx high-entropy alloy from ab initio theory. Phys. Rev. B 88, 85128. doi:10.1103/PhysRevB.88.085128

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., Chen, N., Delczeg, L., and Vitos, L. (2013b). Ab initio investigation of high-entropy alloys of 3d elements. Phys. Rev. B 87, 75144. doi:10.1103/PhysRevB.87.075144

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., Chen, N., Shen, J., and Vitos, L. (2014). Ab initio design of elastically isotropic TiZrNbMoVx high-entropy alloys. J. Alloys Compd. 599, 19–25. doi:10.1016/j.jallcom.2014.01.237

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., Chen, N., Shen, J., and Vitos, L. (2015a). Empirical design of single phase high-entropy alloys with high hardness. Intermetallics 58, 1–6. doi:10.1016/j.intermet.2014.10.010

CrossRef Full Text | Google Scholar

Tian, L.-Y., Hu, Q.-M., Yang, R., Zhao, J., Johansson, B., and Vitos, L. (2015b). Elastic constants of random solid solutions by SQS and CPA approaches: the case of fcc Ti-Al. J. Phys. Condens. Matter 27, 315702. doi:10.1088/0953-8984/27/31/315702

CrossRef Full Text | Google Scholar

Tian, F., Varga, L. K., Shen, J., and Vitos, L. (2016a). Calculating elastic constants in high-entropy alloys using the coherent potential approximation: current issues and errors. Comput. Mater. Sci. 111, 350–358. doi:10.1016/j.commatsci.2015.09.058

CrossRef Full Text | Google Scholar

Tian, F., Wang, D., Shen, J., and Wang, Y. (2016b). An ab initio investigation of ideal tensile and shear strength of TiVNbMo high-entropy alloy. Mater. Lett. 166, 271–275. doi:10.1016/j.matlet.2015.12.064

CrossRef Full Text | Google Scholar

Tian, F., Wang, Y., and Vitos, L. (2017). Impact of aluminum doping on the thermo-physical properties of refractory medium-entropy alloys. J. Appl. Phys. 121, 15105. doi:10.1063/1.4973489

CrossRef Full Text | Google Scholar

Tsai, M.-H., and Yeh, J.-W. (2014). High-entropy alloys: a critical review. Mater. Res. Lett. 2, 107–123. doi:10.1080/21663831.2014.912690

CrossRef Full Text | Google Scholar

Tuckerman, M. E. (2002). Ab initio molecular dynamics: basic concepts, current. J. Phys. Condens. Matter 14, R1297–R1355. doi:10.1088/0953-8984/14/50/202

CrossRef Full Text | Google Scholar

Vitos, L. (2007). Computational Quantum Mechanics for Materials Engineers: The EMTO Method and Applications. London, UK: Springer-Verlag.

Google Scholar

Wang, S. (2013). Atomic structure modeling of multi-principal-element alloys by the principle of maximum entropy. Entropy 15, 5536–5548. doi:10.3390/e15125536

CrossRef Full Text | Google Scholar

Widom, M., Huhn, W. P., Maiti, S., and Steurer, W. (2013). Hybrid Monte Carlo/molecular dynamics simulation of a refractory metal high entropy alloy. Metall. Mater. Trans. A 45, 196–200. doi:10.1007/s11661-013-2000-8

CrossRef Full Text | Google Scholar

Yang, X., and Zhang, Y. (2012). Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 132, 233–238. doi:10.1016/j.matchemphys.2011.11.021

CrossRef Full Text | Google Scholar

Yeh, J., Chen, S., Gan, J., Lin, S., and Chin, T. (2004). Communications: formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements. Metall. Mater. Trans 35, 2533–2536. doi:10.1007/s11661-006-0234-4

CrossRef Full Text | Google Scholar

Zhang, Y., Stocks, G. M., Jin, K., Lu, C., Bei, H., Sales, B. C., et al. (2015). Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat. Commun. 6, 8736. doi:10.1038/ncomms9736

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2013). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001

CrossRef Full Text | Google Scholar

Zhang, Z., Sheng, H., Wang, Z., Gludovatz, B., Zhang, Z., George, E. P., et al. (2017). Dislocation mechanisms and 3D twin architectures generate exceptional strength-ductility-toughness combination in CrCoNi medium-entropy alloy. Nat. Commun. 8, 14390. doi:10.1038/ncomms14390

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, S., Stocks, G. M., and Zhang, Y. (2017). Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 134, e839–e843. doi:10.1016/j.actamat.2017.05.001

CrossRef Full Text | Google Scholar

Zunger, A., Wei, S.-H., Ferreira, L. G., and Bernard, J. E. (1990). Special quasirandom structures. Phys. Rev. Lett. 65, 353–356. doi:10.1103/PhysRevLett.65.353

CrossRef Full Text | Google Scholar