- 1Department of Structures for Engineering and Architecture, University of Naples Federico II, Naples, Italy
- 2Department of Civil Engineering, University of Salerno, Fisciano, Italy
- 3Faculty of Civil and Environmental Engineering and Architecture, Rzeszów University of Technology, Rzeszów, Poland
This study formulates numerical and analytical approaches to the self-equilibrium problem of novel units of tensegrity metamaterials composed of class θ = 1 tensegrity prisms. The freestanding configurations of the examined structures are determined for varying geometries, and it is shown that such configurations exhibit a large number of infinitesimal mechanisms. The latter can be effectively stabilized by applying self-equilibrated systems of internal forces induced by cable prestretching. The equilibrium equations of class θ = 1 tensegrity prisms are studied for varying values of two aspect parameters, and local solutions to the self-equilibrium problem are determined by recourse to Newton–Raphson iterations. Such a numerical approach to the form-finding problem can be easily generalized to arbitrary tensegrity systems. An analytical approach is also proposed for the class θ = 1 units analyzed in the present work. The potential of such structures for development of novel mechanical metamaterials is discussed, in the light of recent findings concerned with structural lattices alternating lumped masses and tensegrity units.
1. Introduction
Recent research in the area of mechanical metamaterials has revealed several distinctive features of lattice materials formed by tensegrity units and lumped masses, which originate from the peculiar, nonlinear mechanical response of such units. Ordinary engineering materials typically exhibit either elastic stiffening (e.g., crystalline solids) or elastic softening (e.g., foams). More puzzling is the geometrically nonlinear response of structural lattices based on tensegrity units (e.g., tensegrity prisms), which may gradually change their elastic response from stiffening to softening through the modification of mechanical, geometrical, and prestress variables (tensegrity metamaterials (Skelton and de Oliveira, 2010; Fraternali et al., 2012, 2014, 2015a; Amendola et al., 2014; Davini et al., 2016; Rimoli and Pal, 2017)). Tensegrity structures are prestressable truss structures, which are obtained by connecting compressive members (bars or struts) through the use of pre-stretched tensile elements (cables or strings). Several studies have shown that it is possible to modulate the properties of tensegrity units by playing with local (or internal) and global (or external) prestress variables, so as to match arbitrary, user-defined nonlinear constitutive laws at the mesoscale, such as, e.g., power-law responses with arbitrary exponents (refer, e.g., to Skelton and de Oliveira (2010); Fraternali et al. (2012, 2014, 2015a); Amendola et al. (2014); Davini et al. (2016); Rimoli and Pal (2017) and references therein). For what concerns the wave dynamics of tensegrity metamaterials, it has been shown that elastically hardening systems support compressive solitary waves and the unusual reflection of waves on material interfaces (Fraternali et al., 2012; Davini et al., 2016), while elastically softening systems support the propagation of rarefaction solitary waves under initially compressive impact loading (Amendola et al., 2014; Fraternali et al., 2014, 2015a). Solitary wave dynamics has been proven to be useful for the construction of a variety of novel acoustic devices. These include effective impact mitigation systems based on tensegrity metamaterials with softening-type response, which are able to transform compressive disturbances into solitary rarefaction waves with progressively vanishing oscillatory tail (Herbold and Nesterenko, 2013; Fraternali et al., 2015a), as well as tunable focus acoustic lenses, which are based on systems featuring elastically stiffening response and compression solitary wave dynamics (Spadoni and Daraio, 2010; Fraternali et al., 2012; Theocharis et al., 2013; Donahue et al., 2014).
The tensegrity metamaterials studied in Fraternali et al. (2012, 2014, 2015a) and Amendola et al. (2014) make use of tensegrity prisms (or T-prisms) acting as nonlinear springs that connect disks (or plates) providing supplementary stiffness and lumped masses. The present work studies a new type of tensegrity unit consisting of the so-called class θ = 1 tensegrity prism (Bieniek, 2017a,b). The class θ tensegrity systems are formed by two different sets of strings, one of which connects the external nodes of the structure (i.e., the boundary nodes), while the other one connects a group of internal nodes (refer, e.g., to Ref. (Bieniek, 2017a) and references therein for an extensive description of such systems). Even if the original nomenclature relative to these structures makes use of the capital letter Θ, whose symbol graphically illustrates the concept of a structure endowed with outer and inner cables, the present work relaxes such a notation through the use of the lower-case symbol θ. Class θ = 1 systems exhibit only one compressive member (or bar) attached to the generic node of the structure, and provide a special subset of the class k = 1 tensegrity systems introduced in Skelton and de Oliveira (2010). Class θ > 1 systems instead feature a maximum number of bars attached to the nodes of the structure that is greater than one (Bieniek, 2017a).
A primary goal of this work is the study the existence of self-equilibrium configurations of class θ = 1 tensegrity prisms for varying values of two aspect parameters, which characterize the twisting angle between the terminal bases, and the coplanarity of the inner nodes (cf. Sect. 2). Self-equilibrium placements are configurations in which the structure is in equilibrium under 0 external forces and non-zero (self-balanced) internal forces. Displacement fields from such configurations that do not change the lengths of all members, according to the small deformation theory, are hereafter named infinitesimal mechanisms. The equilibrium equations of the examined structure are studied for arbitrary values of the design parameters within suitable search intervals, with the aim of finding freestanding configurations in absence of external loads (cf. Sect. 3). Local solutions of the self-equilibrium problem are numerically obtained through Newton–Raphson iterations. Sect. 4 presents an alternative, analytical approach to the form-finding problem, by inspecting the equilibrium equations of selected nodes. The internal mechanisms of the self-stressed configuration and their stabilization through prestress forces are illustrated in Sect. 5. Concluding remarks and a discussion about potential uses of the examined unit for the construction of novel tensegrity metamaterials are given in Sect. 6.
2. Geometry of a Class θ = 1 Tensegrity Prism
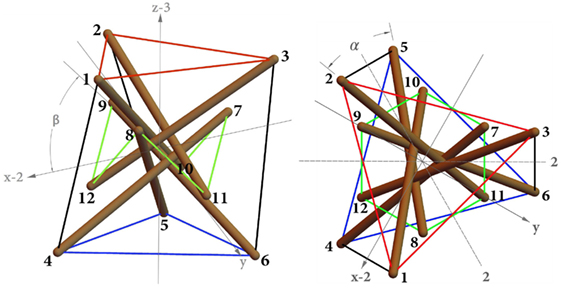
Let us consider the class θ = 1 triangular tensegrity prisms shown in Figure 1. Such systems consist of a network of nn = 12 nodes, nb = 6 compressed members (bars) with equal length b, and ns = 15 tensile members (cables) of different lengths. The cable elements include: two sets of horizontal cables labeled 1–2–3 and 4–5–6 in Figure 1 with equal length ℓ; one set of inner cables 7–8–9–10–11–12 with equal length c; and three cross cables 1–4, 2–5, 3–6 with equal length v. The bars are labeled 1–10, 2–11, 3–12 (top bars) and 7–4, 8–5, 9–6 (bottom bars) in Figure 1. The color code used in Figure 1 employs red and blue lines to mark the top and bottom cables, respectively; green lines for the inner cables; black lines for the cross cables; and brown-colored tubes for the bars.
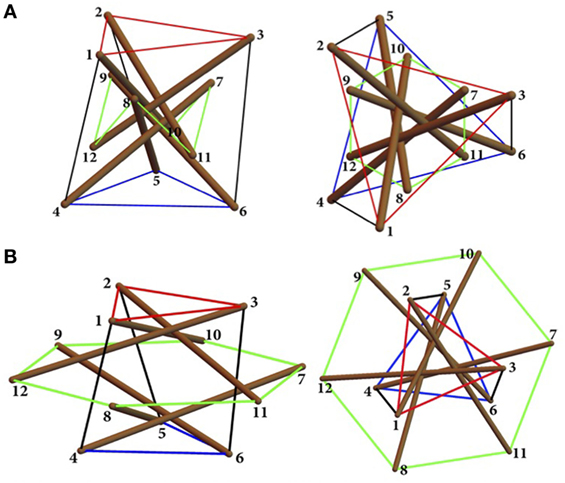
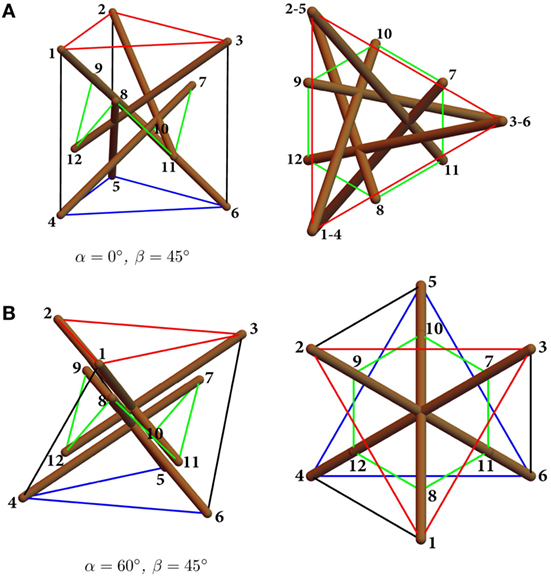
Figure 1. Reference configurations of class θ = 1 tensegrity prisms for α = 30°, β = 45° and different values of the member lengths (arbitrary units). Here and in what follows, red, blue, green, and black lines, respectively, mark top, bottom, inner, and cross cables, while brown tubes mark the bars. (A) System 1: axonometric (left) and top (right) views of the standard configuration corresponding to l = v = 100, c = 50. (B) System 2: axonometric (left) and top (right) views of the expanded configuration corresponding to l = v = c = 100.
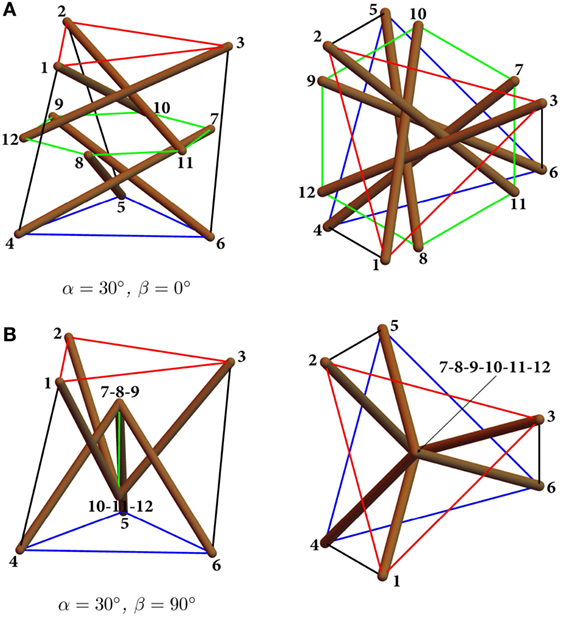
With the aim of comparing the results of this study with those available in Bieniek (2017a,b), our next developments will examine the two configurations depicted in Figure 1, which correspond l = v = 100, c = 50 (standard configuration or System 1) and l = v = c = 100 (expanded configuration or System 2) in arbitrary units. Such systems will be studied for varying values of two aspect angles α and β. The first angle α describes the geometry of the system in the top view and measures the twisting angle that the top and bottom bases form with respect to each other (Figure 2). Following Bieniek (2017a,b), we let such an angle range between the two extreme values α = 0° (bases parallel to each other) and α = 60° (top and bottom bars touching each other, cf. Figure 3). The second angle β describes the geometry in the front view and is related to the slope of the internal strings with respect to the horizontal plane (Figure 2). We let β range between β = 0° (coplanar inner nodes), and β = 90° (inner nodes collapsing on two single nodes, cf. Figure 4) (Bieniek, 2017a,b).
By introducing a Cartesian reference frame with the origin at the centroid of the prism, and letting the superscript T denote the transpose of a matrix or vector, the vectors collecting the node coordinates can be expressed in terms of the aspect parameters ℓ, v, c, α, and β as follows (Bieniek, 2017a,b):
Following the notation presented in Skelton and de Oliveira (2010), we introduce the matrix of the node coordinates N, whose ith column is given by vector ni defined above, and let M be the matrix of member vectors, whose kth column is given by , where and are the position vectors of the nodes i and j attached to the kth member. It is convenient to write M in the following form:
where B and S are the matrices that describe bar and string elements, respectively (Skelton and de Oliveira, 2010). The matrix notation employed in Skelton and de Oliveira (2010) also uses the connectivity matrix C = [CB CS]T, whose (i, j) entry is set equal to −1 if the ith member (bar or string) vector is directed away from the jth node, equal to 1 if it is directed toward the jth node, equal to 0 if it does not touch the jth node. By using such a matrix, it is straightforward to verify that one can write,
3. A Numerical Approach to the Search for Freestanding Configurations
The state of stress acting on the structure under examination can be characterized through the force densities acting in all the members (i.e., the members’ forces divided by their current length). We collect such quantities into the following matrix (Donahue et al., 2014):
where Λ and Γ are the diagonal matrices whose non-zero elements are the forces densities λi, γi acting in the bars and strings, respectively. Since the bars and strings are supposed to carry compressive and tensile forces, respectively, we assume Λ ≥ 0, Γ ≥ 0. We also introduce the vector of the external forces w, which collects all the Cartesian components of the forces acting on the nodes of the structure. Under the above notation, the equilibrium equations of the nodes are written as follows:
where
is the equilibrium matrix of the structure, and x is the vector with m = nb + ns entries that collects all the force densities λi and γi.
Our current goal is to formulate a numerical approach to the search for solutions of the equilibrium problem (8) under 0 external forces (i.e., when w = 0), in correspondence with fixed values of ℓ, v and c (cf. Figure 1), and arbitrary values of the aspect angles α and β. Such solutions will allow us to find the freestanding configurations of a class θ = 1 tensegrity prism for varying geometries (form-finding problem), which we also name prestressable configurations (Skelton and de Oliveira, 2010; Tilbert and Pellegrino, 2011). We start by multiplying both sides of equation (8) by the matrix obtaining the following equation:
where is the Gramian matrix of (Gentle, 2017). We search for states of freestanding or prestressable configurations, by looking for the 0 points of the following objective function (Gentle, 2017):
Let’s start first by examining System 1 in Figure 1, by picking l = v = 100, and c = 50. Figure 5 shows the map of f(α, β), which was numerically obtained for such a system through MathematicaⓇ (Version 11), over the whole search domain α ∈ [0, 60]° × β ∈ [0, 90]° (Figure 5A), which corresponds to the feasibility range of the variables α and β (cf. Sect. 2), and over the restricted domain α ∈ [24.0, 26.5]° × β ∈ [14.0, 15.5]° (Figure 5B), which encompasses the local minimum of f(α, β) observed in panel (Figure 5A). The quantity f in Figures 5A,B has been normalized with respect to the maximum value observed over the plotting interval. The results shown in the above figures highlight that the objective function f exhibits a 0 point in correspondence with the local search interval shown in Figure 5B, and is uniformly equal to 0 in correspondence with β = 90° (degenerate configurations with the inner nodes collapsing into two single nodes, cf., e.g., Figure 4), independently of the current value of α (Figure 1A).
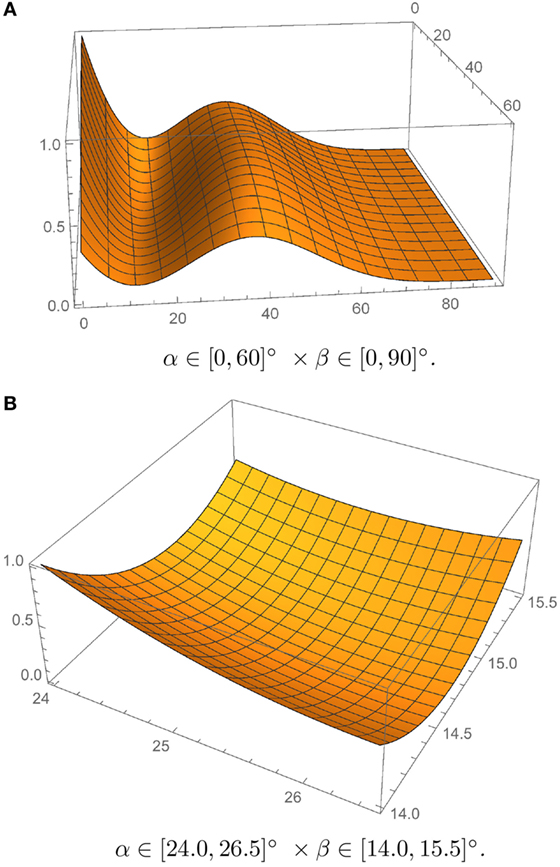
Figure 5. Plots of f(α, β) normalized to the maximum value for different search intervals. (A) α ∈ [0,60]° × β ∈ [0,90]°. (B) α ∈ [24.0, 26.5]° × β ∈ [14.0,15.5]°.
We are interested in the local minimum of f(α, β) that corresponds to a non-degenerate prestressable configuration. By sampling such a function over the domain α ∈ [24.0, 26.5]° × β ∈ [14.0, 15.5]°, we obtain a first estimate of such a local minimum (0) point at α ≈ 26°, β ≈ 15°. Upon setting y = [α, β]T, we refine such an initial guess y0 = [α0, β0]T by recourse to Newton–Raphson iterations,
where ▽ f denotes the gradient of f with respect to y = [α, β]T. We numerically estimate ▽ f by computing difference quotients of f from y0 with increments equal to 10−7 of the amplitude of the search interval. In addition, we iteratively solve equation (12) for Δ y, and recursively update the initial guess through y0 = y0 + Δy, until we match the termination condition.
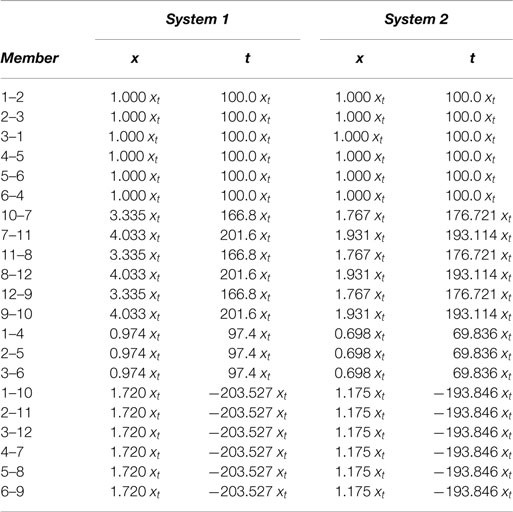
where we set tol = 10−7. The use of the above iterative procedure led us to detect a (non-degenerate) prestressable configuration of System 1 (cf. Figure 1) at α = 25°47ʹ(0.450 rad) and β = 14°48ʹ (0.258 rad). The same procedure gives a (non-degenerate) prestressable configuration of System 2 in Figure 1 at α = 36°13ʹ(0.632 rad) and β = 10°09ʹ (0.177 rad). Such configurations are coincident with those found in Ref. Bieniek (2017b), via a different approach, and are graphically illustrated in Figure 6.
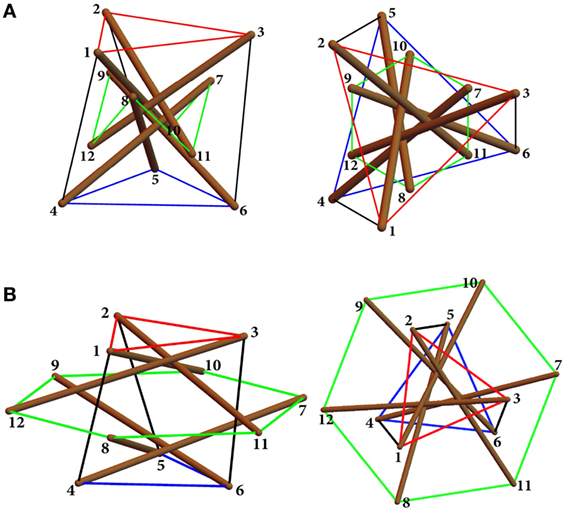
Figure 6. Freestanding configurations obtained for System 1 and System 2 in Figure 1. (A) System 1: standard configuration corresponding to l = v = 100, c = 50. (B) System 2: expanded configuration corresponding to l = v = c = 100.
4. Analytic Formulation of the Self-Equilibrium Problem
The numerical approach to the self-equilibrium problem of class θ = 1 tensegrity prisms, which has been presented in the previous section, can be easily generalized to arbitrary tensegrity systems whose geometry is parametrized as a function of suitable aspect variables.
We now aim at formulating an alternative analytic approach to the same problem that makes use of the symmetry properties of the system under consideration and examines the equilibrium equations of the two nodes attached to an arbitrary bar. Let us examine, e.g., the bar that connects the nodes 2 and 11 (cf. Figure 1). The special symmetry of the structure illustrated in Figure 1 leads us to recognize that its state of self-stress involves equal force densities xt in all the top and base strings, and equal force densities xb in all the bars. For the sake of example, let us refer to System 1 assuming l = v = 100, c = 50. The three self-equilibrium equations of node 2, i.e., the equilibrium equation of node 2 in absence of an external force, involve the forces densities x2–1, x2–3, x2–11, and x2–3. One can use such equations to obtain x2–1, x2–3, and x2–3 as a function of x2–11 ≡ xb. On invoking the above symmetry ansatz, one can next enforce the equation x2–1 = x2–3 ≡ xt, which leads us to the following relationship between α and β:
which must hold for any arbitrary value of xb.
For what concerns the self-equilibrium equations of node 11, we observe that such equations involve only the three force densities x2−11 ≡ xb, x7−11 ≡ xc, and x8−11 ≡ xc. It is immediate to verify that such equations require that the resultant of the forces acting in the strings 7–11 and 8–11 must be parallel to the bar 2–11. This implies in turn that the vector product of the string vectors n7 − n11 and n8 − n11 must be orthogonal to the bar vector n2 − n11, i.e., it results,
Making use of equations (1)–(4), we rewrite equation (15) as follows:
By grouping equation (14) for xb = 1 and equation (16), we obtain a system of two equations for α and β, which can be solved with the help of MathematicaⓇ to get the same result obtained in the previous section, i.e., α = 25°47ʹ, β = 14°48ʹ. It is also easy to apply the analytic approach above to System 2 (l = v = c = 100) obtaining α = 36°13ʹ, β = 10°09ʹ, as it was already found in Sect. 3. We close the present section by computing the states of self-stress that characterize the freestanding configurations of Systems 1 and 2. The solution of equation (8) through MathematicaⓇ in correspondence to w = 0 and the values of α and β given above leads us to the results shown in Table 1, where t = ± xl denotes the force acting in the member with length l (the + sign holding in the case of a string member, and the − sign holding in the case of a bar). The results in Table 1 assume the force density in the top and bottom strings xt as the independent prestress variable.
5. Prestress Stabilization
The kinematic problem conjugate to equation (8) rules the existence of infinitesimal mechanisms of the structure from the freestanding configuration, that is, displacement fields from such a configuration that do not change the lengths of all members (inextensional incremental displacements forming the nullspace of the kinematic matrix). Such a problem is analytically formulated in the Appendix in Supplementary Material, by making use of the approach presented in Fraternali et al. (2015b). As shown in Pellegrino and Calladine (1986), the number of such mechanisms nm of a spatial lattice is related to the rank of the equilibrium matrix r() through
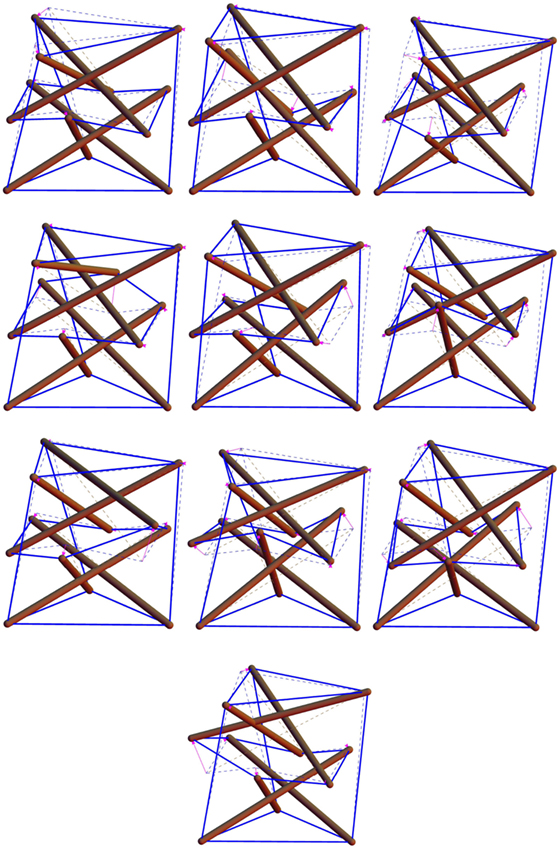
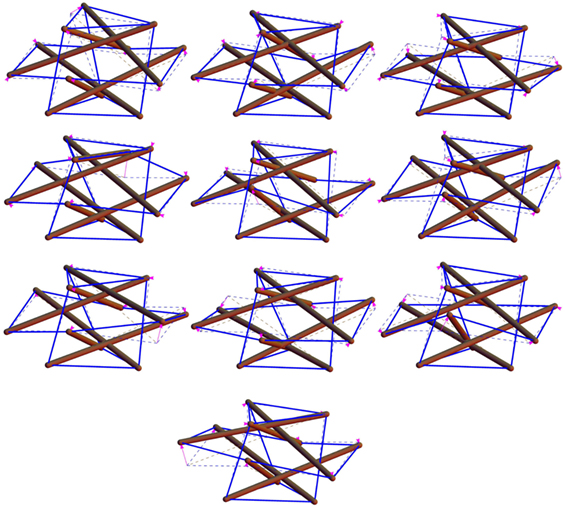
where ndof denotes the total number of degrees of freedom of the structure. By making use of the kinematic problem presented in Appendix in Supplementary Material, we obtain that the freestanding configurations shown in Figure 6 exhibit nm = 10 infinitesimal (internal) mechanisms (excluding rigid body motions), which are graphically illustrated in Figures 7 and 8.
Let’s now assume that all the members of the structure under consideration behave as linear elastic springs governed by the following constitutive equations:
where denotes the rest length of the ith member in the stress-free (or natural) configuration, and ki denotes the stiffness constant characterizing the response of such a member. Our current goal is to determine the tangent stiffness matrix of the systems in Figure 6, and to study the possibility to stabilize the mechanisms shown in Figures 7 and 8 through the application of nontrivial states of prestress. We refer the reader to Guest (2006) and Fraternali et al. (2015b), for the notions of prestress-stabilty and superstability of tensegrity systems, and Skelton et al. (2015) and De Tommasi et al. (2017) (with references therein) for the analysis of the global stability of such systems. Following Guest (2006) and Fraternali et al. (2015b), we start rewriting the equilibrium problem equation (8) into the following scalar form:
where m = nb + ns; ndof = 3nn; li is the length of the generic member in the freestanding configuration; denotes the Cartesian component of the global, nodal displacement vector from the freestanding configuration, which is associated with the jth degree of freedom (dof); the quantities give the cosine directors of the members’ axes; and fj denotes the nodal force component associated with the jth dof (Fraternali et al., 2015b). The generic (j, k) entry of the tangent stiffness matrix in the freestanding configuration is given by Fraternali et al. (2015b),
Such a matrix can be decomposed as follows:
where KM is the material stiffness matrix of lattice, which depends on the axial stiffness and the cosine directors of the members, and is defined through (Fraternali et al., 2015b)
while KG is the geometric matrix that depends on the prestress forces ti acting in all members in the freestanding configuration, and the changes in the cosine directors of the members’ axes due to an arbitrary incremental deformation of the structure from such a configuration. The (j, k) entry of KG is given by Fraternali et al. (2015b).
According to the nomenclature given in Guest (2006), Schenk et al. (2007), Micheletti (2013) and Fraternali et al. (2015b), the structure is said to be prestress-stable if the geometric stiffness KG matrix is positive-definite in correspondence with any nontrivial mechanism , i.e., it results,
for any that represents the vector of nodal displacements associated with an infinitesimal mechanism of the structure. In the Appendix in Supplementary Material, we give the analytic expressions of (m = 1, …, 10), KM and KG for the analyzed systems, which are rather cumbersome. It is easily verified that equation (24) holds true in correspondence to each of the mechanisms illustrated in Figures 7 and 8, which implies that the freestanding configurations of the systems under examination are prestress-stable, since the prestress forces given in Table 1 act against any infinitesimal mechanism of the structure from such configurations (assuming xt > 0, see Sects. Appendix SA3 and SA4 in Supplementary Material).
6. Concluding Remarks
We have formulated numerical and analytical approaches to the search for freestanding configurations of class θ = 1 tensegrity prisms, by parameterizing the geometry of such systems in terms of two aspect angles. The numerical approach given in Sect. 3 can be easily generalized to arbitrary tensegrity systems whose geometry is described through suitable design variables, since it is based on the study of the 0s of the Gramian of the static matrix of the structure, as a function of the chosen design parameters.
The results obtained in Sects. 4 and 5 lead us to conclude that the freestanding configurations of class θ = 1 tensegrity prisms have static indeterminacy equal to 1 (see Sect. 4), and kinematic indeterminacy equal to 10 (Sect. 5). They can be effectively stabilized through the application of pre-tensioning forces to the string members, which act against the infinitesimal mechanisms allowed by such structures (Sect. 5).
The presence of a high number of infinitesimal mechanisms from the freestanding configurations suggests that the examined systems can be usefully employed as novel units of mechanical metamaterials, which exhibit geometrically nonlinear response, support solitary wave dynamics, and offer a valid alternative to the standard tensegrity prisms studied in Fraternali et al. (2012, 2014) (see Figure 9 for a one-dimensional chain alternating lumped masses and class θ = 1 tensegrity prisms). The remarkable influence of infinitesimal mechanisms on the geometrically nonlinear constitutive response and wave dynamics of tensegrity metamaterials has been highlighted in Fraternali et al. (2012, 2014). Analytic, numerical, and experimental studies on the implementation of the units studied in the present work within novel tensegrity metamaterials, including, e.g., impact protection gear (Fraternali et al., 2014) and vibration isolation devices (Fraternali and Amendola, 2017), are addressed to future work.
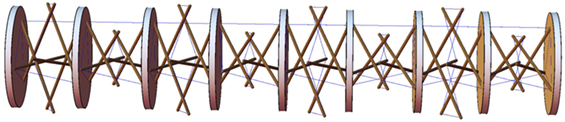
Figure 9. One-dimensional tensegrity metamaterial alternating lumped masses with regular and expanded class θ = 1 tensegrity prisms.
Author Contributions
MM has developed the numerical conditions and has taken care of the writing together with IM. IM has employed the numerical codes developed within the project and has contributed to the writing. FF has supervised the work carried out by all the authors. ZB has provided the topic and the motivation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
IM gratefully acknowledges financial support from the Ph.D. School in Civil Engineering at the University of Salerno.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/articles/10.3389/fmats.2018.00005/full#supplementary-material.
References
Amendola, A., Carpentieri, G., de Oliveira, M. C., Skelton, R. E., and Fraternali, F. (2014). Experimental investigation of the softening-stiffening response of tensegrity prisms under compressive loading. Compos. Struct. 117, 234–243. doi: 10.1016/j.compstruct.2014.06.022
Bieniek, Z. W. (2017a). The self-equilibrium problem of the class-theta tetrahedral tensegrity module. Compos. B Eng. 115, 21–29. doi:10.1016/j.compositesb.2016.10.054
Bieniek, Z. W. (2017b). “The self-equilibrium configurations for the class-theta triangular tensegrity prism,” in Proceedings of the XXIII Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno, IT, Vol. 3, 1103–1109.
Davini, C., Micheletti, A., and Podio-Guidugli, P. (2016). On the impulsive dynamics of T3 tensegrity chains. Meccanica 51, 2763–2776. doi:10.1007/s11012-016-0495-y
De Tommasi, D., Maddalena, F., Puglisi, G., and Trentadue, F. (2017). Fractality in selfsimilar minimal mass structures. J. Mech. Phys. Solids 107, 433–450. doi:10.1016/j.jmps.2017.07.002
Donahue, C., Anzel, P. W. J., Bonanomi, L., Keller, T. A., and Daraio, C. (2014). Experimental realization of a nonlinear acoustic lens with a tunable focus. Appl. Phys. Lett. 104, 014103. doi:10.1063/1.4857635
Fraternali, F., and Amendola, A. (2017). Mechanical modeling of innovative metamaterials alternating pentamode lattices and confinement plates. J. Mech. Phys. Solids 99, 259–271. doi:10.1016/j.jmps.2016.11.010
Fraternali, F., Carpentieri, G., and Amendola, A. (2015a). On the mechanical modeling of the extreme softening/stiffening response of axially loaded tensegrity prisms. J. Mech. Phys. Solids 74, 136–157. doi:10.1016/j.jmps.2014.10.010
Fraternali, F., De Chiara, E., and Skelton, R. E. (2015b). On the use of tensegrity structures for kinetic solar facades of smart buildings. Smart Mater. Struct. 24, 1–10. doi:10.1088/0964-1726/24/10/105032
Fraternali, F., Carpentieri, G., Amendola, A., Skelton, R. E., and Nesterenko, V. F. (2014). Multiscale tunability of solitary wave dynamics in tensegrity metamaterials. Appl. Phys. Lett. 105, 201903. doi:10.1063/1.4902071
Fraternali, F., Senatore, L., and Daraio, C. (2012). Solitary waves on tensegrity lattices. J. Mech. Phys. Solids 60, 1137–1144. doi:10.1016/j.jmps.2012.02.007
Gentle, J. E. (2017). Matrix Algebra: Theory, Computations and Applications in Statistics. Faifax, VA: Springer, XXIX.
Guest, S. D. (2006). The stiffness of prestressed frameworks: a unifying approach. Int. J. Solids Struct. 43, 842–854. doi:10.1016/j.ijsolstr.2005.03.008
Herbold, E. B., and Nesterenko, V. F. (2013). Propagation of rarefaction pulses in discrete materials with strain-softening behavior. Phys. Rev. Lett. 110, 144101. doi:10.1103/PhysRevLett.110.144101
Micheletti, A. (2013). Bistable regimes in an elastic tensegrity system. Proc. R. Soc. A 469:20130052. doi:10.1098/rspa.2013.0052
Pellegrino, S., and Calladine, C. R. (1986). Matrix analysis of statically and kinematically indeterminate frameworks. Int. J. Solids Struct. 22, 409–428. doi:10.1016/0020-7683(86)90014-4
Rimoli, J. J., and Pal, R. K. (2017). Mechanical response of 3-dimensional tensegrity lattices. Compos. B Eng. 115, 30–42. doi:10.1016/j.compositesb.2016.10.046
Schenk, M., Guest, S. D., and Hender, J. L. (2007). Zero stiffness tensegrity structure. Int. J. Solids Struct. 44, 6569–6583. doi:10.1016/j.ijsolstr.2007.02.041
Skelton, R. E., Montuori, R., and Pecoraro, V. (2015). Globally stable minimal mass compressive structures. Compos. Struct. 141, 346–354. doi:10.1016/j.compstruct.2016.01.105
Spadoni, A., and Daraio, C. (2010). Generation and control of sound bullets with a nonlinear acoustic lens. Proc. Natl. Acad. Sci. U.S.A. 107, 7230–7234. doi:10.1073/pnas.1001514107
Theocharis, G., Boechler, N., and Daraio, C. (2013). “Nonlinear phononic structures and metamaterials,” in Acoustic Metamaterials and Phononic Crystals. Springer Series in Solid State Sciences, Vol. 173, ed. P. A. Deymier (Berlin: Springer), 217–251.
Keywords: lattice metamaterials, class θ tensegrity prisms, self-stress, prestress stabilization, freestanding configurations
Citation: Modano M, Mascolo I, Fraternali F and Bieniek Z (2018) Numerical and Analytical Approaches to the Self-Equilibrium Problem of Class θ = 1 Tensegrity Metamaterials. Front. Mater. 5:5. doi: 10.3389/fmats.2018.00005
Received: 24 November 2017; Accepted: 23 January 2018;
Published: 21 February 2018
Edited by:
Federico Bosia, Università degli Studi di Torino, ItalyReviewed by:
Massimiliano Zingales, Università degli Studi di Palermo, ItalyGiuseppe Puglisi, Politecnico di Bari, Italy
Copyright: © 2018 Modano, Mascolo, Fraternali and Bieniek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mariano Modano, bW9kYW5vQHVuaW5hLml0;
Fernando Fraternali, Zi5mcmF0ZXJuYWxpQHVuaXNhLml0
 Mariano Modano
Mariano Modano