- 1Barcelona Centre for New Medical Technologies (BCN MedTech), Pompeu Fabra University, Barcelona, Spain
- 2School of Engineering, University of Portsmouth, Portsmouth, United Kingdom
- 3Institució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona, Spain
Trabecular bone fracture is a traumatic and localized event studied worldwide in order to predict it. During the years, researchers focused over the mechanical characterization of the trabecular tissue to understand its mechanics. Several studies pointed out the very local nature of the trabecular failure, finally identifying the fracture zone with the aim to study it separately. The complexity of the three-dimensional trabecular framework and the local nature of the fracture event do not allow the direct evaluation of a single trabecula’s behavior within its natural environment. For this reason, micro-Finite Element Modeling has been seen as the best way to investigate this biomechanical issue. Mechanical strain analysis is adopted in the literature for the identification of micro fracture using criteria based on principal strains. However, it was never verified if the fracture zone is actually the zone where principal strains are concentrated. Here, we show how the maximum strain of the tissue might not be directly correlated to the fracture. In the present work, a previously validated technique was used to identify the fracture zone of 10 trabecular specimen mechanically tested in compression and scanned in micro-CT before and after the mechanical test. Before-compression datasets were used to develop 10 micro-FE models were the same boundary conditions of the mechanical test were reproduced. Our results show how the known linear behavior of the trabecular framework might not be directly related to the development of the fracture suggesting other non-linear phenomenon, like buckling or microdamage, as actual cause of the traumatic event. This result might have several implications both in micro-modeling and in clinical applications for the study of fracture related pathology, like osteoporosis.
Introduction
Mechanical characterization of trabecular bone is an issue studied since several years due to its relationship with several musculo-skeletal pathologies (Crane et al., 1990; Aerssens et al., 1997; Silva and Gibson, 1997; Goldring, 2009; Kijowski et al., 2012; Milovanovic et al., 2012; Djuric et al., 2013).
The principal way to investigate trabecular bone biomechanics is the mechanical testing of tissue specimens (Helgason et al., 2008). The most common procedure includes the extraction of the specimens from different anatomical sites, embedment in endcaps to avoid toe-artifacts during the measurement, and finally mechanical test in compression using an axial testing machine. Even if this introduced procedure is still today considered the golden standard for mechanical studies of trabecular bone behavior, it clearly presents several limitations.
First of all, the test described is a destructive one; therefore, it can only be applied once for each specimen. This limits also the number of measurements that can be taken for each specimen; typically, Young modulus, yield, and ultimate stress. Moreover, these values can be related only to global characteristics of the specimen without any insight of the internal and local behavior of the tissue. This is a strong limitation since the trabecular framework is a complex structure, and its failure passes through local damage of the structure followed by the development of the fracture. In this process, the local morphology of the bone plays a relevant role.
The 3-dimensional morphology of trabecular microstructure can nowadays be investigated by means of micro-tomography (micro-CT). Micro-CT allows visualizing and studying the trabecular framework performing non-destructive analysis. Following this procedure, correlation studies of the framework morphology with the mechanical behavior can be carried out (Ohman et al., 2007; Nazarian et al., 2009). The combination of the two techniques soon showed the importance of trabecular framework heterogeneity in the evaluation of the mechanical behavior of bone. Local analyses were suggested by several authors with different methodologies in order to take into consideration the variability of the structure in analysis (Nazarian et al., 2006; Perilli et al., 2008; Tassani et al., 2010). The study of local morphology leads to the study of the trabecular fracture zone itself, aiming to investigate the specific morphology that could explain the development of the trabecular framework failure. A method for the identification of the trabecular fracture zone was proposed (Tassani et al., 2012) and validated (Tassani and Matsopoulos, 2014). Results again underlined the local and three-dimensional nature of the fracture event identifying full 3D fracture zone having a volumetric broken fraction of about 9% (average). The morphometry identified with this procedure allowed to successfully describe (a posteriori classification, 95.5% accuracy) (Tassani and Matsopoulos, 2014) and predict (a priori classification, 91.8% AUC) (Korfiatis et al., 2017) the fracture zone of each trabecular specimen.
In this scenario, micro-Finite Element Modeling (micro-FEM) has the potentiality to play an important role to study the local and internal behavior of the trabecular bone. Several works were already presented suggesting different approaches (Pistoia et al., 2002; Nagaraja et al., 2005; Verhulp et al., 2008a; Sidorenko et al., 2011; Zysset et al., 2013).
The most common approach of micro-FEM simulation is probably the linear one. Even if this is clearly valid only in the elastic stress-strain zone and cannot describe the fractures themselves, the resulting values are often used as predictive value of the bone strength as reaction to external loads. Using this technique strain and stresses of the 3D framework can be plotted and used as estimator of the fracture initiation.
Micro-FEM models have been widely used to study the mechanical behavior of trabecular bone at tissue level. Most of the studies reported in the literature adopted linear elastic constitutive law (Hara et al., 2002; Verhulp et al., 2006; Kim et al., 2007; Bevill and Keaveny, 2009; Wolfram et al., 2010; Vilayphiou et al., 2011; Torcasio et al., 2012; Gross et al., 2013; Harrison et al., 2013; Bauer et al., 2014) to assess elastic modulus at tissue level, to retrieve overall mechanical behavior at apparent level or finally to study the strain distribution. A number of non-linear models are reported in the literature, adopting both different constitutive law and failure criteria to try to replicate the force–displacement curve as experimentally measured at apparent level (Niebur et al., 2000; Bayraktar and Keaveny, 2004; Verhulp et al., 2008b; Sanyal et al., 2012; Wolfram et al., 2012; Harrison et al., 2013; Bauer et al., 2014; Baumann et al., 2016). However, there is lack of a clear consensus of the literature over which non-linear approach is the most suitable and reliable in identifying the overall failure in terms of both ultimate strain and loading curve. On the other hand, models based on purely linear elastic constitutive laws have been successfully proposed at both organ level [homogenized CT based models (Schileo et al., 2008; Falcinelli et al., 2014)] and tissue level [micro-CT based models (Pistoia et al., 2002; Hosseini et al., 2017)]: these models adopted a principal strain based failure criteria and identified the failure load by simply scaling the linear model in order to reach the yielding condition in a given portion of the model volume. The idea behind this approach is that fracture is a strain driven mechanical event that can be modeled adopting a maximum principal strain criterion.
Aim of non-linear models was mainly the identification of the mechanical behavior of the bone tissue rather than the prediction of the sites of fracture. It is worth here to mention that for the purposes of the latter aim, an independent method to identify the fracture is required. In many studies, fracture zones are identified by visual inspection over the complex three-dimensional trabecular framework. Consequently, the whole procedure is time-consuming and operator-dependent, possibly inducing a considerable bias in the analysis and, therefore, not applicable to large scale analysis. Damage localization has been proposed by Nagaraja et al. (2005) who studied the occurrence of microdamage events in quasi-static uniaxial compression of trabecular bone using linear elastic micro-CT finite element models and registered histological sections. On the other hand, Hambli (2013) proposed an isotropic micro-FEM coupled to a damage law to predict apparent failure properties of human trabecular bone under quasi-static uniaxial compression. The results were visually validated against the micro-CT images of the same specimen mechanically tested showing good correspondence. The work presented an interesting tool for the description of the fracture propagation leaving an open question: are linear micro-FEM good tools for the identification of fracture regions?
It is clear that micro-FEM cannot describe the propagation of trabecular fracture without the aid of the damage law; nonetheless, the identification of a good correlation between stiffness and bone strength can be considered a reasonable basis to predict the mechanical behavior of the trabecular framework and to identify the initiation of the fracture event.
Aim of the present study is to check whether a correspondence exists between the regions where fracture has been identified and regions where principal strains values are higher in linear finite element models. This correspondence will be validated using a full3D and user-independent automatic technique. In other words, aim of the study is to verify the consistency of the basic assumption (i.e., principal strain concentration as indicator of bone failure initiation) made by many studies that identified bone fracture by means of principal strain analysis based on linear elastic models.
Materials and Methods
This study is partially based on the analysis of data previously collected during the European projects Living Human Digital Library (LHDL; IST-2004-026932) and MOSAIC (PIEF-GA-2009-253924), and none of the authors had access to identifiable patient information. For this reason, an ethics approval for the present study was not required as per institutional and national guidelines and regulations. Micro-CT images were produced by Laboratorio di Tecnologia Medica, Istituto Ortopedico Rizzoli, Bologna, Italy, with the financial support of the EU project LHDL (IST-2004-026932). The authors only had access to anonymized images.
The whole data collection procedure is here briefly summarized. Four femora and four tibiae were obtained from two female cadavers (72 and 78 years old) without skeletal disorders by means of a donor program during the LHDL European project. The samples had been embalmed using the modified Dankmeyer’s method (Van Sint Jan and Rooze, 1992; Ohman et al., 2008). Tibiae and femora were cut into slices perpendicular to the longitudinal axis of the bone. The epiphyses were cut into 26-mm slices. A number of cylindrical trabecular specimens, with a diameter of 10 mm, were then extracted (Tassani et al., 2011). All specimens were scanned by means of a micro-CT (model Skyscan 1072, Bruker microCT, Kontich, Belgium) with an isotropic voxel size of 19.5 µm, using a previously published protocol (Perilli et al., 2007a,b). All specimens were loaded to failure (displacement control, strain rate 0.01 s−1, model Mini bionix 858, MTS Systems Corp., Minneapolis, MN, USA). Each specimen was cemented directly onto the testing machine. The free length of each specimen was 20 mm (Ohman et al., 2007; Perilli et al., 2008; Tassani et al., 2010). The same acquisition procedure was performed both before (pre-failure dataset) and after the mechanical testing (post-failure dataset). In each set, the final analyzed volume of interest (VOI) was a cylinder of 991 micro-CT cross sections (slices) equal to 19.3 mm height and 9 mm in diameter (Perilli et al., 2008). A fixed threshold was used for the segmentation of trabecular structure from marrow [GV = 143, established in a previous comparison between segmented dataset analyses and histological sections, on trabecular bone specimens adopting the same micro-CT settings (Ohman et al., 2007; Perilli et al., 2007b)]. The fracture zone was identified using a two-step registration method already described in the literature (Tassani et al., 2012; Tassani and Matsopoulos, 2014). The trabecular fracture zone was defined as the region presenting brittle fracture or plastic deformation of at least one trabecula. Briefly, the two steps 3D registration was implemented with the aim to highlight differences between the pre- and post-failure datasets due to mechanical testing. For each slice, each disconnected trabecula lying on the slice in the pre-failure dataset is compared to the same trabecula in the post-failure dataset. Each trabecula of each slice of each dataset was classified as broken if the trabecula of the pre- and post-failure datasets had an overlap inferior of a threshold of 30% [the value of the threshold was identified during the validation study reported in Tassani et al. (2012)]. In order to identify a “full 3D” fracture zone, a morphological 3D dilation procedure was used to calculate a VOI around each broken trabecula. Each VOI was dilated in every direction by 25 px [about 0.50 mm in radius, according to Nazarian et al. (2006)]; thus, an ellipsoidal VOI centered on the broken trabecula was obtained. When trabeculae were closer than 50 px in any direction (25 for each ROI), the VOIs fused creating a single VOI.
In the present study, 10 specimens were selected and for each of them a micro-FEM was developed. The specimens were selected based on the dimension of the identified fracture zone to explore its relation to the deformation of the trabecular framework. Specifically, five specimens with a fracture zone larger than 10% and five with a fracture zone smaller than 1% of total specimen volume were selected.
Micro-FEM Development
A voxel-based Finite Element model was built from segmented micro-CT datasets by direct conversion of voxels in hexahedral Finite Elements. Fixed global threshold was adopted.
Boundary conditions were imposed to replicate the uniaxial compression test: all the nodes lying on the lower surface were fully constrained; all the nodes belongings to the top slices were imposed vertical displacement corresponding to 0.5% of apparent axial strain for the whole specimen and no transverse displacement were allowed.
The material of the trabecular structure was assumed homogeneous and isotropic with a linear elastic constitutive law. Thanks to the linearity of the model and to the purely cinematic nature of the studied problem (essential boundary conditions imposed studying the output strains), a conventional value for the Young’s modulus (1 GPa) was considered. Poisson’s ratio was assumed 0.3.
The solution of each model was obtained using the fully parallel micro-FE linear solver based on octree ParOSol (Flaig and Arbenz, 2012) using 20 parallel processes on Sciama HPC cluster of the Institute of Cosmology and Gravitation of the University of Portsmouth. Compression and tension principal strains were then computed at the centroid of each voxel.
Principal Strains Analysis: Maximum Strain Identification
To remove artifacts related to single high-strain voxels and in the boundary elements of the rough voxel-based surfaces, an erosion procedure (1 px), followed by a 3D median filter (kernel 3 px × 3 px × 3 px) were applied to all the generated datasets (ImageJ 15.1n Wayne Rasband National Institutes of Health, USA). The new datasets were mapped back on a 256 gray values colormap of a typical 8-bit micro-CT dataset reconstruction.
Maximum strains were identified in both compression and tension datasets as the maximum 5% of strain range in each specimen (95% to maximum strain). For each dataset, all the voxels included in the maximum strain criteria were labeled. Starting from these voxels, a procedure similar to the one described for the identification of the full 3D fracture zone, was applied for the identification of the maximum strain zone (CtAn, Bruker microCT, Kontich, Belgium).
For each slice, each disconnected trabecula lying on the slice was analyzed. The whole trabecula including the maximum strain pixel was identified as “maximum strain tissue.” In order to identify a “full 3D” max strain zone, a morphological 3D dilation procedure was used to calculate a VOI around each max strain trabecula. Each VOI was dilated in every direction by 25 px [about 0.50 mm in radius, according to Nazarian et al. (2006)]; thus an ellipsoidal VOI centered on the broken trabecular was obtained. When trabeculae were closer than 50 px in any direction (25 for each ROI), the VOIs fused creating a single VOI.
Finally, three zones were identified and compared to each other, in each specimen: whole specimen, fracture zone, and maximum strain. The analysis was performed over both compression and tension strains. However, while fracture zone was a constant region, independent of the kind of strain, maximum compression and maximum tension led to the identification of two different regions. Once identified, the maximum strain zones were visually compared to the fracture zone.
Principal Strains Analysis: Comparison of Strains
A two-way ANOVA for repeated measurements was implemented to test the influence of both “within” and “between” factors over the strain distribution. The identified region was defined as within factor to analyze since each specimen was compared against itself. The region factor presented three categorical levels; whole specimen, fracture zone, and maximum strain zone. The “between” factor was the kind of stress generated with two levels defined; compression and tension. Kind of stress was not a within factor since the regions of tension and compression were different in each specimen. A post hoc test with Bonferroni correction for multiple testing was used to evaluate the statistical differences among the three levels of the region factor.
The whole statistical model was used to evaluate the effect of the two defined factors and their interaction on the absolute values of the strains.
Results
Global strains showed to be generally homogenous with fluctuations given by the complexity of the trabecular framework (Figure 1). Fracture regions and maximum strain regions, both compression and tension, are shown in Figure 2 for low fracture volume specimen and in Figure 3 for high fracture volume specimens. The location of the maximum strain regions show no direct relation to the fracture zone.
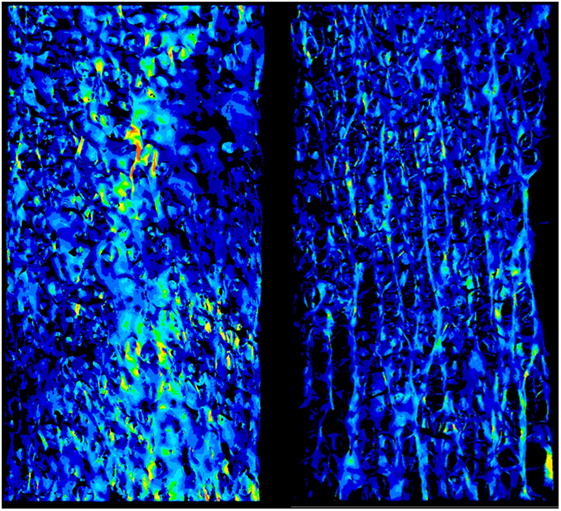
Figure 1. The strain field of two specimens is shown. It appears to be essentially homogeneous with punctual strain variations related to the complexity to the geometry.

Figure 2. Zones of maximum compression (left) and maximum tension (right), are reported in comparison to the fracture zone (center) for the five low fracture volume specimens.
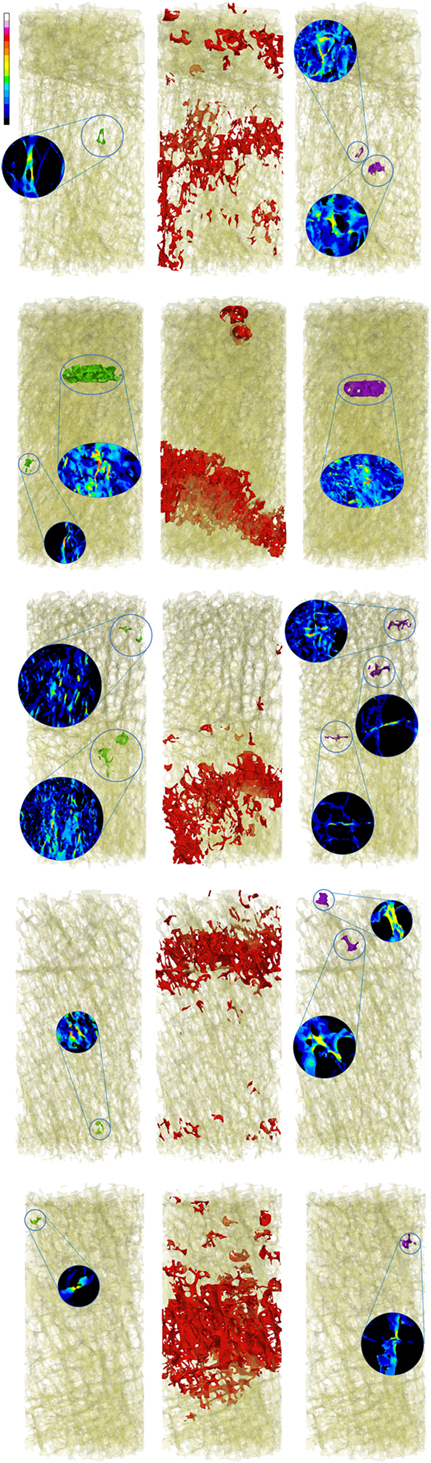
Figure 3. Zones of maximum compression (left), fracture (center), and maximum tension (right) are reported in comparison to the fracture zone (center) for the five high fracture volume specimens.
The strain distributions in the whole specimen and in the fracture region shown to be statistically different from the strain in the maximum strain region. Strain in the fracture region was also found higher than the average strain of the whole specimen but lower than the ones in the maximum strain region. Average compression and tension values for each region and kind of strain are shown in Figure 4. No interaction between region and type of strain was detected (p-value = 0.056, Greenhouse–Geisser sphericity correction).
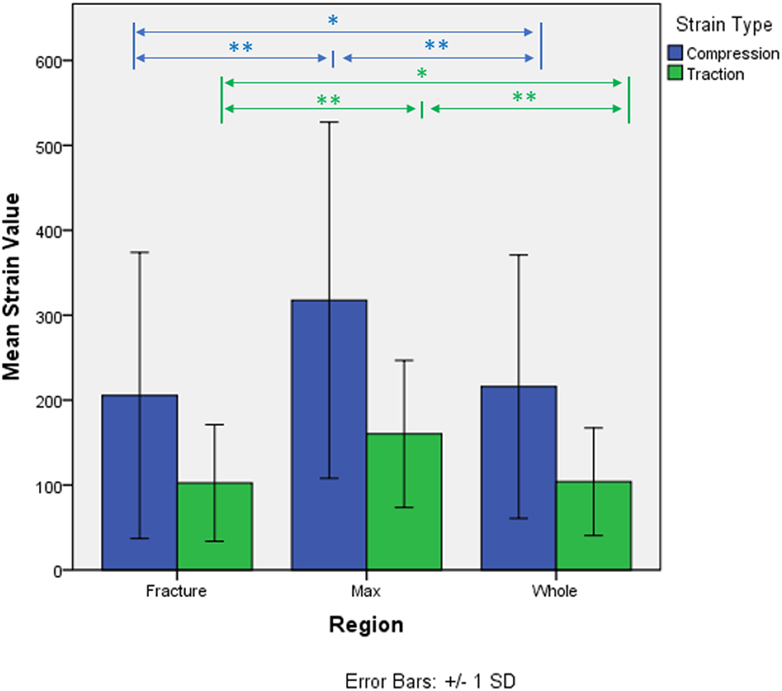
Figure 4. Micro-strains in compression and traction in the three identified regions of analysis. *p-value < 0.05. **p-value < 0.005.
There seems to be no relation between the dimension of the fracture zone and the dimension and distribution of the maximum strain regions.
Discussion
The presented work led to two main results. First, the visual analysis underlined the local nature of maximum strain. Figure 1 shows how the distribution of the strain is essentially homogeneous. Since the numerical model assumes the material to be homogeneous (a strong assumption widely adopted in the high majority of such kind of models), strain fluctuations are uniquely related to the complexity to the geometry. Figures 2 and 3 are collecting fracture and maximum strain zones for all the specimens. It is easy to see how the maximum strain regions identified by the proposed criterion, both in compression and in tension, are extremely localized, very often related to few, or even one single trabecula. In the same figures, the detail of the strain distribution underline that often the trabecula showing maximum strain is isolated. This result could support the hypothesis that maximum strain can identify the specific point in which the fracture can start and propagate. However, the same visual results allow to compare maximum strain zones to the fracture zone of the same specimen. The identification of the fracture zone was automatic and completely described the 3D framework. This approach allowed to fully compare the distribution of the strain to the fracture zone of several specimens, without the limitation of visual identification. The reported relation appears to be poor. In more than half of the cases, the maximum strain zones appeared unrelated to the identified fracture zone, therefore, rejecting the hypothesis that maximum strain can identify the initiation point of the fracture. Maximum strain regions seem also unrelated to the final dimension of the fracture.
Second, the paired analysis showed how in each specimen the maximum strain region, both in compression and in tension, consisted of statistically higher strain, compared to both the fracture region and the average of the whole specimen. Particularly, the strains of the maximum strain region showed to be almost double the ones of the fracture region; 413 ± 211 μstrain max strain region and 256 ± 131 μstrain fracture region in compression, 179 ± 53 μstrain max strain region and 120 ± 50 μstrain fracture region in tension. Again, this result suggests how the whole fracture zone might not develop simply following the laws of higher strain, since the strains localized in the fracture are much lower. On the other hand, fracture regions also showed slightly higher strain compared to the average of the whole specimen (209 ± 83 μstrain compression and 98 ± 29 μstrain tension) letting open the possibility that strain can actually play a role in the development of the fracture. The interaction between the two factors was rejected; however, the p-value was very close to the threshold of 5% (p-value = 0.056). Considering the fact that only 10 specimens were analyzed, the possibility that the structure might behave differently in compression and tension, in relation to the fracture and max strain zone, should be further explored.
After the failure of the first trabecula the work of the whole trabecular framework is far from over. Loads can be redistributed and let the structure strong enough to sustain the global load. If not, compaction of the trabecular bone creates a new shape of the structure that can again sustain the load. Following the concept that the biggest amount of bone can ensure a stronger tissue, bone volume fraction has been used for several years for bone strength prediction (Helgason et al., 2008). Nonetheless, BV/TV was recently suggested to be a poor descriptor (Tassani and Matsopoulos, 2014) and predictor (Korfiatis et al., 2017) of the trabecular fracture zone. The trabecular tissue seems to behave following the distribution of the bone in the elastic region; however, this does not describe the event of the fracture where non-linear events might play an important role. In the same way, maximum strain can describe the elastic behavior of the structure; however, failure of the framework, or even of a single trabecula, cannot be explained by this feature.
From Kopperdahl and Keaveny (1998), non-linear behavior in compression in slender trabeculae is dominated by buckling instead of yielding. At least for lower bone volume fraction, failure seems to be related to buckling occurring in regions of trabeculae aligned with the applied load. On the other hand, Snyder et al. (1991) demonstrated how trabecular slenderness is negatively correlated with bone volume fraction. Müller et al. (1998) observed as in a rod-like architecture failure was initiate by buckling of trabeculae followed by the collapse of the overloaded structure. It is worth to highlight as this collapse can results in a ductile apparent behavior due to individual response of individual trabeculae to buckling in wet condition (Townsend et al., 1975). On the theoretical side, Ramtani and Abdi (2005) formalized the framework to experimentally assess buckling in plate-like trabeculae, focusing the relevance of this instability also in wider structural elements. These assumptions are supported by the results showed in the literature (Tassani and Matsopoulos, 2014), where BV/TV was shown to be lower and structure model index higher, indicating more rod-like trabeculae, in the fracture zone.
According to Stölken and Gibson (Gibson, 1985; Stölken and Kinney, 2003), buckling might occur in individual trabeculae that are not necessarily the most highly strained ones (especially if highly slender). What is more, Eswaran et al. (2007) highlighted how in trabecular bone initial failure may occur in regions that result different from the regions where subsequent failure is located.
Clearly, non-linear behavior of the trabecular framework can also be related to the heterogeneity of the extracellular matrix (Fantner et al., 2004; Gao, 2006; Viguet-Carrin et al., 2006). Microdamage could accumulate and lead to structure failure. According to Blanchard et al. (2013), plasticity prior to fracture may involve nanoscale processes that in terms depend on the nano-to-micro composition and ultrastructure of bone. In this sense, considering homogeneous elastic modulus might limit the here presented results. However, in previous works the tissue mineral density was proved to be fairly constant in trabecular bone (Tassani et al., 2011), reducing the effect of extracellular matrix heterogeneity, and in more recent studies morphometrical characteristics alone were enough to correctly describe (Tassani and Matsopoulos, 2014) and predict (Korfiatis et al., 2017) in more than 90% of the cases, the trabecular fracture zone. These results suggest that the key to understand the mechanics of trabecular fracture might be more related to the micro-level of the structure than to the nanoscale of the tissue.
Moreover, in a recently published paper, Goff et al. (2015) studied the correlation between microdamage localization and local strains as identified by linear micro-FE models. Even though microdamage appears more likely to occur at the greatest tissue level, they did not identify principal strains as a reliable predictor of microdamage occurrence. What is more, the locations with the greatest tissue strains appeared rarely near site of microdamage. Once again, even if heterogeneity of the nano-structure might play a relevant role in the definition of trabecular failure, principal strains seems to be unrelated even at that scale.
Some limitations must be taken into consideration before to conclude this discussion. First of all, the study takes into consideration only 10 specimens from two donors. Even if the specimens were selected in order to study the variety of the trabecular fracture zone, more specimens might be required in order to have a more complete description. Moreover, the definition of the maximum strain region might be considered somehow arbitrary, even if it was chosen to be consistent with the process for the identification of the fracture region. For convenience of the analysis, a single value per voxel was computed at the centroid instead of using and averaging the values at the integration points. The imposed apparent strain was fixed at only 0.5%. Nonetheless, thanks to the linearity of the model, even if the absolute values of the strains would change, the relative distribution of strain is independent from the imposed apparent strain, and therefore, the identification of the maximum strain region would not change. Because of the proposed linearity, the model lacks the capability to capture geometric and constitutive non-linearities that might alter the strain evolution pattern. Buckling it is an example of non-linearity and is exactly what we pointed out as the most probable origin of collapse mechanism that occurred in all the studied specimens. Non-linear constitutive law might be the key to the description of the trabecular fracture zone. Finally, even though nobody seems to be worried about this point, we acknowledge that results might exhibit some sort of dependency on the segmentation technique implemented, since smaller and slender trabeculae might be reduced or completely disappear if the wrong segmentation is applied.
In conclusion, the present study shows not direct correspondence between the regions where fracture have been identified and regions where strains values are higher. Not only the identified maximum strain regions are extremely small but also often not related to the fracture zone, therefore, excluding the possibility to be directly associated to the initiation zone of the fracture. This output does not corroborate the assumption on which some work reported in the literature based their analyses (i.e., the consistency between strain concentration and fracture initiation, particularly for those models that assumed a linear elastic constitutive law). This “negative” result does not provide further insight to the comprehension of bone mechanic while consolidate the claim that a modeling procedure more complex must be considered when approaching the fracture identification on bony structures. Authors consider their outcomes to be significant mostly for their meaning of stressing open questions, in the belief of the importance of negative results, which are more and more difficult to find in modern literature while they should be much more present (Knight, 2003; Ioannidis, 2005; Fanelli, 2012).
Author Contributions
ST and MP were principal investigators and conceived together the main study’s aim. ST and JN designed and performed measurements, while MP developed all the micro-FEM models. JN and MB supervised the study. All authors discussed the results and implications, performed the data analysis, and reviewed the manuscript at all stages.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The micro-CT datasets were produced by Laboratorio di Tecnologia Medica, Istituto Ortopedico Rizzoli, Bologna, Italy, with the financial support of the EU project LHDL (IST-2004-026932). This work was partially supported by the Spanish Government (project number RYC—2015-18888) and by Chair QUAES-UPF Computational Technologies for Healthcare.
Supplementary Material
The Supplementary Material for this article can be found online at http://www.frontiersin.org/articles/10.3389/fmats.2018.00006/full#supplementary-material.
References
Aerssens, J., Boonen, S., Joly, J., and Dequeker, J. (1997). Variations in trabecular bone composition with anatomical site and age: potential implications for bone quality assessment. J. Endocrinol. 155, 411–421. doi: 10.1677/joe.0.1550411
Bauer, J. S., Sidorenko, I., Mueller, D., Baum, T., Issever, A. S., Eckstein, F., et al. (2014). Prediction of bone strength by micro-CT and MDCT-based finite-element-models: how much spatial resolution is needed? Eur. J. Radiol. 83, e36–e42. doi:10.1016/j.ejrad.2013.10.024
Baumann, A. P., Shi, X., Roeder, R. K., and Niebur, G. L. (2016). The sensitivity of nonlinear computational models of trabecular bone to tissue level constitutive model. Comput. Methods Biomech. Biomed. Engin. 19, 465–473. doi:10.1080/10255842.2015.1041022
Bayraktar, H. H., and Keaveny, T. M. (2004). Mechanisms of uniformity of yield strains for trabecular bone. J. Biomech. 37, 1671–1678. doi:10.1016/j.jbiomech.2004.02.045
Bevill, G., and Keaveny, T. M. (2009). Trabecular bone strength predictions using finite element analysis of micro-scale images at limited spatial resolution. Bone 44, 579–584. doi:10.1016/j.bone.2008.11.020
Blanchard, R., Dejaco, A., Bongaers, E., and Hellmich, C. (2013). Intravoxel bone micromechanics for microCT-based finite element simulations. J. Biomech. 46, 2710–2721. doi:10.1016/j.jbiomech.2013.06.036
Crane, G. J., Fazzalari, N. L., Parkinson, I. H., and Vernon-Roberts, B. (1990). Age-related changes in femoral trabecular bone in arthrosis. Acta Orthop. Scand. 61, 421–426. doi:10.3109/17453679008993554
Djuric, M., Zagorac, S., Milovanovic, P., Djonic, D., Nikolic, S., Hahn, M., et al. (2013). Enhanced trabecular micro-architecture of the femoral neck in hip osteoarthritis vs. healthy controls: a micro-computer tomography study in postmenopausal women. Int. Orthop. 37, 21–26. doi:10.1007/s00264-012-1713-4
Eswaran, S. K., Gupta, A., and Keaveny, T. M. (2007). Locations of bone tissue at high risk of initial failure during compressive loading of the human vertebral body. Bone 41, 733–739. doi:10.1016/j.bone.2007.05.017
Falcinelli, C., Schileo, E., Balistreri, L., Baruffaldi, F., Bordini, B., Viceconti, M., et al. (2014). Multiple loading conditions analysis can improve the association between finite element bone strength estimates and proximal femur fractures: a preliminary study in elderly women. Bone 67, 71–80. doi:10.1016/j.bone.2014.06.038
Fanelli, D. (2012). Negative results are disappearing from most disciplines and countries. Scientometrics 90, 891–904. doi:10.1007/s11192-011-0494-7
Fantner, G. E., Birkedal, H., Kindt, J. H., Hassenkam, T., Weaver, J. C., Cutroni, J. A., et al. (2004). Influence of the degradation of the organic matrix on the microscopic fracture behavior of trabecular bone. Bone 35, 1013–1022. doi:10.1016/j.bone.2004.05.027
Flaig, C., and Arbenz, P. (2012). “A highly scalable matrix-free multigrid solver for µFE analysis based on a pointer-less octree,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Vol. 7116, 498–506. doi:10.1007/978-3-642-29843-1_56
Gao, H. (2006). Application of fracture mechanics concepts to hierarchical biomechanics of bone and bone-like materials. Int. J. Fract. 138, 101–137. doi:10.1007/s10704-006-7156-4
Gibson, L. J. (1985). The mechanical behaviour of cancellous bone. J. Biomech. 18, 317–328. doi:10.1016/0021-9290(85)90287-8
Goff, M. G., Lambers, F. M., Sorna, R. M., Keaveny, T. M., and Hernandez, C. J. (2015). Finite element models predict the location of microdamage in cancellous bone following uniaxial loading. J. Biomech. 48, 4142–4148. doi:10.1016/j.jbiomech.2015.10.023
Goldring, S. R. (2009). Role of bone in osteoarthritis pathogenesis. Med. Clin. North Am. 93, 25–35,xv. doi:10.1016/j.mcna.2008.09.006
Gross, T., Pahr, D. H., and Zysset, P. K. (2013). Morphology-elasticity relationships using decreasing fabric information of human trabecular bone from three major anatomical locations. Biomech. Model. Mechanobiol. 12, 793–800. doi:10.1007/s10237-012-0443-2
Hambli, R. (2013). Micro-CT finite element model and experimental validation of trabecular bone damage and fracture. Bone 56, 363–374. doi:10.1016/j.bone.2013.06.028
Hara, T., Tanck, E., Homminga, J., and Huiskes, R. (2002). The influence of microcomputed tomography threshold variations on the assessment of structural and mechanical trabecular bone properties. Bone 31, 107–109. doi:10.1016/S8756-3282(02)00782-2
Harrison, N. M., McDonnell, P., Mullins, L., Wilson, N., O’Mahoney, D., and McHugh, P. E. (2013). Failure modelling of trabecular bone using a non-linear combined damage and fracture voxel finite element approach. Biomech. Model. Mechanobiol. 12, 225–241. doi:10.1007/s10237-012-0394-7
Helgason, B., Perilli, E., Schileo, E., Taddei, F., Brynjólfsson, S., and Viceconti, M. (2008). Mathematical relationships between bone density and mechanical properties: a literature review. Clin. Biomech. (Bristol, Avon) 23, 135–146. doi:10.1016/j.clinbiomech.2007.08.024
Hosseini, H. S., Dünki, A., Fabech, J., Stauber, M., Vilayphiou, N., Pahr, D., et al. (2017). Fast estimation of Colles’ fracture load of the distal section of the radius by homogenized finite element analysis based on HR-pQCT. Bone 97, 65–75. doi:10.1016/j.bone.2017.01.003
Ioannidis, J. P. (2005). Why most published research findings are false. PLoS Med. 2:e124. doi:10.1371/journal.pmed.0020124
Kijowski, R., Tuite, M., Kruger, D., Munoz Del Rio, A., Kleerekoper, M., and Binkley, N. (2012). Evaluation of trabecular microarchitecture in nonosteoporotic postmenopausal women with and without fracture. J. Bone Miner. Res. 27, 1494–1500. doi:10.1002/jbmr.1595
Kim, C. H., Zhang, H., Mikhail, G., von Stechow, D., Müller, R., Kim, H. S., et al. (2007). Effects of thresholding techniques on microCT-based finite element models of trabecular bone. J. Biomech. Eng. 129, 481–486. doi:10.1115/1.2746368
Kopperdahl, D. L., and Keaveny, T. M. (1998). Yield strain behavior of trabecular bone. J. Biomech. 31, 601–608. doi:10.1016/S0021-9290(98)00057-8
Korfiatis, V. C., Tassani, S., and Matsopoulos, G. K. (2017). A new Ensemble Classification System for fracture zone prediction using imbalanced micro-CT bone morphometrical data. IEEE J. Biomed. Health Inform. doi:10.1109/JBHI.2017.2723463
Milovanovic, P., Djonic, D., Marshall, R. P., Hahn, M., Nikolic, S., Zivkovic, V., et al. (2012). Micro-structural basis for particular vulnerability of the superolateral neck trabecular bone in the postmenopausal women with hip fractures. Bone 50, 63–68. doi:10.1016/j.bone.2011.09.044
Müller, R., Gerber, S. C., and Hayes, W. C. (1998). Micro-compression: a novel technique for the nondestructive assessment of local bone failure. Technol. Health Care 6, 433–444. doi:10.1016/S0021-9290(98)80302-3
Nagaraja, S., Couse, T. L., and Guldberg, R. E. (2005). Trabecular bone microdamage and microstructural stresses under uniaxial compression. J. Biomech. 38, 707–716. doi:10.1016/j.jbiomech.2004.05.013
Nazarian, A., Meier, D., Müller, R., and Snyder, B. D. (2009). Functional dependence of cancellous bone shear properties on trabecular microstructure evaluated using time-lapsed micro-computed tomographic imaging and torsion testing. J. Orthop. Res. 27, 1667–1674. doi:10.1002/jor.20931
Nazarian, A., Stauber, M., Zurakowski, D., Snyder, B. D., and Müller, R. (2006). The interaction of microstructure and volume fraction in predicting failure in cancellous bone. Bone 39, 1196–1202. doi:10.1016/j.bone.2006.06.013
Niebur, G. L., Feldstein, M. J., Yuen, J. C., Chen, T. J., and Keaveny, T. M. (2000). High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J. Biomech. 33, 1575–1583. doi:10.1016/S0021-9290(00)00149-4
Ohman, C., Baleani, M., Perilli, E., Dall’Ara, E., Tassani, S., Baruffaldi, F., et al. (2007). Mechanical testing of cancellous bone from the femoral head: experimental errors due to off-axis measurements. J. Biomech. 40, 2426–2433. doi:10.1016/j.jbiomech.2006.11.020
Ohman, C., Dall’Ara, E., Baleani, M., Van Sint Jan, S., and Viceconti, M. (2008). The effects of embalming using a 4% formalin solution on the compressive mechanical properties of human cortical bone. Clin. Biomech. (Bristol, Avon) 23, 1294–1298. doi:10.1016/j.clinbiomech.2008.07.007
Perilli, E., Baleani, M., Ohman, C., Baruffaldi, F., and Viceconti, M. (2007a). Structural parameters and mechanical strength of cancellous bone in the femoral head in osteoarthritis do not depend on age. Bone 41, 760–768. doi:10.1016/j.bone.2007.07.014
Perilli, E., Baruffaldi, F., Visentin, M., Bordini, B., Traina, F., Cappello, A., et al. (2007b). MicroCT examination of human bone specimens: effects of polymethylmethacrylate embedding on structural parameters. J. Microsc. 225, 192–200. doi:10.1111/j.1365-2818.2007.01731.x
Perilli, E., Baleani, M., Ohman, C., Fognani, R., Baruffaldi, F., and Viceconti, M. (2008). Dependence of mechanical compressive strength on local variations in microarchitecture in cancellous bone of proximal human femur. J. Biomech. 41, 438–446. doi:10.1016/j.jbiomech.2007.08.003
Pistoia, W., van Rietbergen, B., Lochmüller, E.-M., Lill, C. A., Eckstein, F., and Rüegsegger, P. (2002). Estimation of distal radius failure load with micro-finite element analysis models based on three-dimensional peripheral quantitative computed tomography images. Bone 30, 842–848. doi:10.1016/S8756-3282(02)00736-6
Ramtani, S., and Abdi, M. (2005). Buckling of adaptive elastic bone-plate: theoretical and numerical investigation. Biomech. Model. Mechanobiol. 3, 200–208. doi:10.1007/s10237-004-0056-5
Sanyal, A., Gupta, A., Bayraktar, H. H., Kwon, R. Y., and Keaveny, T. M. (2012). Shear strength behavior of human trabecular bone. J. Biomech. 45, 2513–2519. doi:10.1016/j.jbiomech.2012.07.023
Schileo, E., Taddei, F., Cristofolini, L., and Viceconti, M. (2008). Subject-specific finite element models implementing a maximum principal strain criterion are able to estimate failure risk and fracture location on human femurs tested in vitro. J. Biomech. 41, 356–367. doi:10.1016/j.jbiomech.2007.09.009
Sidorenko, I., Monetti, R., Bauer, J., Mueller, D., Rummeny, E., Eckstein, F., et al. (2011). Assessing methods for characterising local and global structural and biomechanical properties of the trabecular bone network. Curr. Med. Chem. 18, 3402–3409. doi:10.2174/092986711796504754
Silva, M., and Gibson, L. (1997). Modeling the mechanical behavior of vertebral trabecular bone: effects of age-related changes in microstructure. Bone 21, 191–199. doi:10.1016/S8756-3282(97)00100-2
Snyder, B. D., Piazza, S. J., and Hayes, W. C. (1991). “Mechanisms of trabecular bone failure in the osteoporotic lumbar vertebral body,” in Transactions of the Orthopaedic Research Society, Vol. 16 (Anaheim, CA), 132.
Stölken, J. S., and Kinney, J. H. (2003). On the importance of geometric nonlinearity in finite-element simulations of trabecular bone failure. Bone 33, 494–504. doi:10.1016/S8756-3282(03)00214-X
Tassani, S., Matsopoulos, G., and Baruffaldi, F. (2012). 3D identification of trabecular bone fracture zone using an automatic image registration scheme: a validation study. J. Biomech. 45, 2035–2040. doi:10.1016/j.jbiomech.2012.05.019
Tassani, S., and Matsopoulos, G. K. (2014). The micro-structure of bone trabecular fracture: an inter-site study. Bone 60, 78–86. doi:10.1016/j.bone.2013.12.007
Tassani, S., Ohman, C., Baleani, M., Baruffaldi, F., and Viceconti, M. (2010). Anisotropy and inhomogeneity of the trabecular structure can describe the mechanical strength of osteoarthritic cancellous bone. J. Biomech. 43, 1160–1166. doi:10.1016/j.jbiomech.2009.11.034
Tassani, S., Ohman, C., Baruffaldi, F., Baleani, M., and Viceconti, M. (2011). Volume to density relation in adult human bone tissue. J. Biomech. 44, 103–108. doi:10.1016/j.jbiomech.2010.08.032
Torcasio, A., Zhang, X., Duyck, J., and Van Lenthe, G. H. (2012). 3D characterization of bone strains in the rat tibia loading model. Biomech. Model. Mechanobiol. 11, 403–410. doi:10.1007/s10237-011-0320-4
Townsend, P. R., Rose, R. M., and Radin, E. L. (1975). Buckling studies of single human trabeculae. J. Biomech. 8, 199–200. doi:10.1016/0021-9290(75)90025-1
Van Sint Jan, S., and Rooze, M. (1992). The thenar muscles – new findings. Surg. Radiol. Anat. 14, 325–329. doi:10.1007/BF01794759
Verhulp, E., van Rietbergen, B., and Huiskes, R. (2006). Comparison of micro-level and continuum-level voxel models of the proximal femur. J. Biomech. 39, 2951–2957. doi:10.1016/j.jbiomech.2005.10.027
Verhulp, E., Van Rietbergen, B., Muller, R., and Huiskes, R. (2008a). Micro-finite element simulation of trabecular-bone post-yield behaviour – effects of material model, element size and type. Comput. Methods Biomech. Biomed. Engin. 11, 389–395. doi:10.1080/10255840701848756
Verhulp, E., van Rietbergen, B., Müller, R., and Huiskes, R. (2008b). Indirect determination of trabecular bone effective tissue failure properties using micro-finite element simulations. J. Biomech. 41, 1479–1485. doi:10.1016/j.jbiomech.2008.02.032
Viguet-Carrin, S., Garnero, P., and Delmas, P. D. (2006). The role of collagen in bone strength. Osteoporos. Int. 17, 319–336. doi:10.1007/s00198-005-2035-9
Vilayphiou, N., Boutroy, S., Szulc, P., Van Rietbergen, B., Munoz, F., Delmas, P. D., et al. (2011). Finite element analysis performed on radius and tibia HR-pQCT images and fragility fractures at all sites in men. J. Bone Miner. Res. 26, 965–973. doi:10.1002/jbmr.297
Wolfram, U., Gross, T., Pahr, D. H., Schwiedrzik, J., Wilke, H. J., and Zysset, P. K. (2012). Fabric-based Tsai-Wu yield criteria for vertebral trabecular bone in stress and strain space. J. Mech. Behav. Biomed. Mater. 15, 218–228. doi:10.1016/j.jmbbm.2012.07.005
Wolfram, U., Wilke, H. J., and Zysset, P. K. (2010). Valid micro finite element models of vertebral trabecular bone can be obtained using tissue properties measured with nanoindentation under wet conditions. J. Biomech. 43, 1731–1737. doi:10.1016/j.jbiomech.2010.02.026
Keywords: micro-CT, micro-FEM, trabecular bone, fractures, bone, micro strain
Citation: Tassani S, Pani M, Noailly J and Gonzalez Ballester MA (2018) Trabecular Fracture Zone Might Not Be the Higher Strain Region of the Trabecular Framework. Front. Mater. 5:6. doi: 10.3389/fmats.2018.00006
Received: 31 August 2017; Accepted: 25 January 2018;
Published: 16 February 2018
Edited by:
Alberto Corigliano, Politecnico di Milano, ItalyReviewed by:
Stefano Vidoli, Sapienza Università di Roma, ItalyEnrico Radi, University of Modena and Reggio Emilia, Italy
Copyright: © 2018 Tassani, Pani, Noailly and Gonzalez Ballester. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simone Tassani, c2ltb25lLnRhc3NhbmlAdXBmLmVkdQ==
 Simone Tassani
Simone Tassani Martino Pani
Martino Pani Jerome Noailly
Jerome Noailly Miguel Angel Gonzalez Ballester
Miguel Angel Gonzalez Ballester