Experimental Observation of a Large Low-Frequency Band Gap in a Polymer Waveguide

1. Introduction

One of the main problems facing physicists and engineers working in the field of metamaterials is to achieve vibration damping and control over large, low-frequency ranges. This is true in fields ranging from noise absorption (Aurégan et al., 2016; Jiménez et al., 2016; Li and Assouar, 2016; Morandi et al., 2016) to seismic wave abatement (Colombi et al., 2016; Miniaci et al., 2016). Phononic crystals (PCs) and acoustic metamaterials (AMMs), generally made of periodically distributed inclusions in a matrix (or hosting material), are of particular interest because of their ability to act as stop-band filters, i.e., attenuate mechanical waves over entire frequency bands, commonly known as band gaps (BGs) (Pennec et al., 2010; Craster and Guenneau, 2012; Hussein et al., 2014).

Bragg scattering and local resonance are the mechanisms mainly exploited for BG nucleation. BGs due to Bragg scattering arise from the wave diffraction by periodic inclusions and thus occur at wavelengths of the order of the unit cell size (Platts et al., 2002), while local resonance is related to the vibration of individual elements within the medium and is thus independent of the spatial periodicity of the lattice (Baravelli and Ruzzene, 2013; Bigoni et al., 2013). In some cases, Bragg BGs can be coupled with hybridization BGs (Croënne et al., 2011; Kaina et al., 2013), due to resonating “inhomogeneities” (Fano interference effects (Kosevich et al., 2006), electrical resonances (Bergamini et al., 2015; Kherraz et al., 2016), etc.).

The concept of a BG naturally lends itself to applications involving vibration damping, acoustic filtering, and wave attenuation, as well as waveguiding (Khelif et al., 2005; Pennec et al., 2010). Applications at high frequencies include wave filters, couplers, sensing devices, wave splitters, demultiplexers, etc. (Pennec et al., 2004; Sukhovich et al., 2009). A non-exhaustive list of low-frequency applications includes acoustic absorption, vibration shielding, subwavelength imaging, cloaking, etc (Craster and Guenneau, 2012; Deymier, 2013).

With these applications in mind, a plethora of different architectures (including multiphase materials) and multiphysics approaches have been proposed in recent years (Bavencoffe et al., 2009; Pennec et al., 2010; Wang and Wang, 2013; Andreassen et al., 2015), but many involve considerable practical difficulties in their realization due to their inherent complexity.

Recently, particular attention has been focused on phononic plates because of their potential technological applications, ranging from microelectromechanical systems to non-destructive evaluation (Hsu and Wu, 2007; He et al., 2010; Mohammadi et al., 2011; Wu et al., 2011; Celli and Gonella, 2014; Gliozzi et al., 2015; Miniaci et al., 2017). Among others, phononic plates made of periodic distributions of studs or gratings on the surface (Wu et al., 2009; Casadei et al., 2012; Yu et al., 2013) as well as those realized by a periodic distribution of empty cavities perpendicular or parallel to the propagation plane (Hsu and Wu, 2007; Wu et al., 2011; Chen et al., 2012; Wang and Wang, 2013) have been studied.

In addition to theoretical predictions, experimental measurements of BGs in phononic plates have been performed. In this context, Brunet et al. (2008) reported BGs for Lamb waves propagating in rectangular and square arrays of holes drilled in a silicon phononic plate, while Bonello et al. (2007) proved the existence of BGs for Lamb waves in silicon plates coated by a very thin phononic film. Publications dealing with BGs for Lamb waves generated in a plate with a periodic grating on the surface have also appeared (Bavencoffe et al., 2009, 2013) with the aim of quantitatively verifying the relation between the width of the BG and the depth of the grooves. Finally, several studies have considered and shown that filtering and waveguiding properties are achievable in plates with stubs, including biphase materials (Hsiao et al., 2007; Hsu and Wu, 2007; Wu et al., 2009, 2011; Oudich et al., 2011; Casadei et al., 2012).

In these approaches, geometrical/physical complexity is often inevitable, leading to considerable complications in their practical realization. This requires unit cells capable of providing the desired dynamic performance while simultaneously being compact, lightweight, and easy to manufacture. In this work, we propose a phononic plate that is simple to fabricate and is capable of opening large, low-frequency complete Lamb BGs, exploiting the resulting equivalent arrangement of masses and stiffnesses produced by cavities in a monolithic material. This simple but efficient design is capable of generating large and low-frequency Lamb BGs when cross-like holes are considered, showing that a sort of “mass centrifugation” process is beneficial. The idea is supported by numerical calculations and experimental scanning laser Doppler vibrometer (SLDV) measurements on an isotropic polyvinyl chloride (PVC) plate with a square ring region of cross-like holes. The full wave field reconstruction below, within and above the BG frequencies clearly confirms the ability of the proposed design to reflect Lamb waves in the desired frequency range.

The article is organized as follows: first, we present extensive numerical simulations aimed at finding suitable plate configurations capable of nucleating large BGs within the optimal operative frequency range of the SLDV using finite element simulations (FEMs). Through-the-thickness cavities with different geometries are considered as scatterers (inclusions). Next, finite element time-transient analysis is performed to study the influence of the phononic region length (number of unit cells) on wave propagation. Finally, SLDV measurements on ad hoc machined phononic PVC plates are presented and compared to the numerically predicted results. The calculated BGs are verified experimentally, and the direct observation of scattering phenomena below, within, and above the BGs is described.

2. Design and Numerical Analysis

In this section, the description of the phononic plate design is provided. Different geometries of the scatterers, made of through-the-thickness cavities, are considered to find Bragg-type BGs in the frequency range 0–45 kHz.

In view of the experimental phase, PVC was chosen as the material matrix since it can be easily machined. The PVC mechanical properties are the density ρ_PVC = 1,430 kg/m³, the Young’s modulus E_PVC = 3 GPa, and the Poisson’s ratio v_PVC = 0.4 (Miniaci et al., 2014).

A lattice parameter of a = 20 mm is chosen for the unit cell and a plate thickness H = 0.4 a, so that the lowest Bragg BGs relative A0 mode are expected at around 14 and 36 kHz, corresponding to the half and full wavelength of the A0 propagating mode, respectively. The A0 mode is chosen as it is easy to excite using piezoelectric (PZT) sensors and to measure with SLDV. Once the lattice parameter has been set, band structures for different types of structures are computed. The unit cells are shown in Figure 1 relative to (a) circular, (b) square, and (c) rounded cross-like cavities. Geometrical parameters (see Table 1) are chosen so as to guarantee a constant filling fraction f_f = 41% for all three models.

FIGURE 1

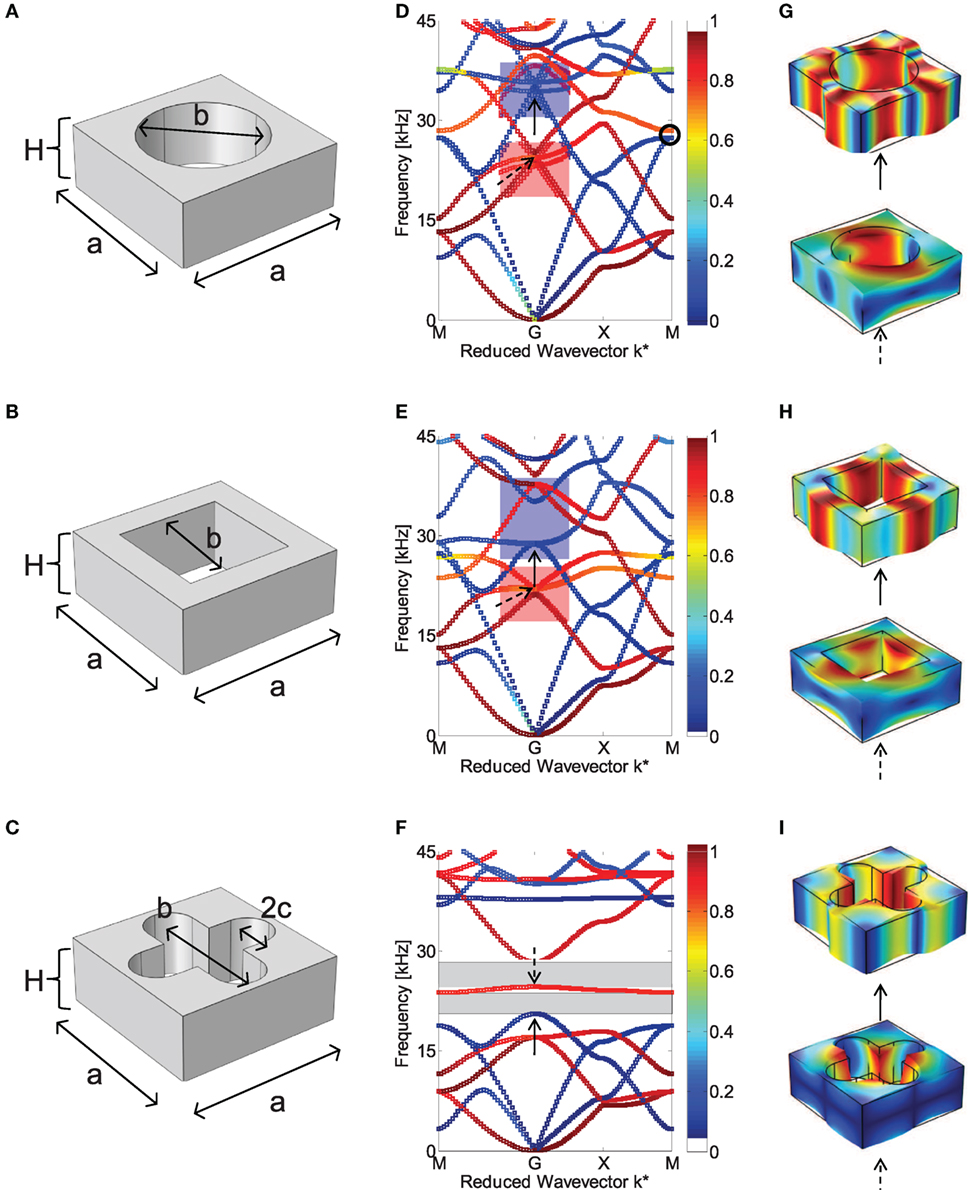
Figure 1. Unit cells made of (A) circular, (B) square, and (C) cross-like cavities in a PVC matrix and their corresponding band structures (D–F) and mode shapes (G–I). The color of the curves indicates the mode polarization, ranging from pure in-plane (blue) to pure out-of-plane (red). On the other hand, blue and red in the mode shapes represent the zero and maximum displacement, respectively. Geometrical parameters are given in Table 1 and guarantee the same filling fraction of f_f = 41% for all the three models.

TABLE 1

Table 1. Geometrical parameters for unit cells shown in Figures 1A–C, characterized by (i) circular, (ii) square, and (iii) cross-like cavities, respectively. The parameters are chosen so as to guarantee the same filling fraction for all the three designs.

The corresponding band structures are shown in Figures 1D–F along with the mode shapes for some specific branches (Figures 1G–I). The dispersion diagram is computed along the three high symmetry directions of the first irreducible Brillouin zone (Figure 2), exploiting the Bloch-Floquet theorem by using COMSOL MultyPhysics. Band structures are reported in terms of reduced wavevector k* with wavenumber components k* = [k_xa/π; k_ya/π]. A detailed description of the finite element procedure can be found in Ref. (Miniaci et al., 2014).

FIGURE 2

Figure 2. Schematic representation of the first irreducible Brillouin zone for a square lattice.

Phononic plates with circular and square holes do not nucleate any BGs, whereas the unit cell with a rounded cross-like hole exhibits two complete BGs (highlighted as light gray regions). To shed light on this different behavior, we highlight the in-plane or out-of-plane polarization of the modes in the dispersion diagrams by defining a polarization factor:

$p=\frac{{\displaystyle {\int }_V}{(|u_z|)}^{2}dV}{{\displaystyle {\int }_V}(\mathrm{|}{u}_x{\mathrm{|}}^2+\mathrm{|}{u}_y{\mathrm{|}}^2+\mathrm{|}{u}_z{\mathrm{|}}^2)dV},$ (1)

where V is the volume of the unit cell and u_x, u_y, and u_z are the displacement components along x, y, and z axes, respectively. The points of the dispersion curves are shaded accordingly, with colors varying from p = 0 (blue) to p = 1 (red). Thus, colors close to red indicate vibration modes that are predominantly polarized out-of-plane, while colors close to blue are predominantly polarized in-plane.

This allows us to infer that the different arrangement of the cavities is responsible for the shift of some dispersion bands while leaving others unaltered. For instance, Figures 1D,E highlight the shift occurring for two modes: one with a mainly in-plane deformation mechanism (blue rectangle) and another one with a mainly out-of-plane deformation mechanism (red rectangle). The shift is clearly due to the equivalent stiffness variations occurring due to the cavity geometry (see Figures 1G,H). Introducing a cross-like cavity can accentuate this process and lead to the opening of two BGs (Figure 1F) with a smaller deformation of the unit cell for the same branches (Figure 1I).

Results hold true for varying plate thickness with the same type of mechanical effects. Figure 3 shows a parametric analysis in which band structures for the unit cell with a cross-like cavity have been computed increasing the thicknesses from H = 0.2 a to H = 1.2 a in steps of 0.2 a. Results show that the plate thickness plays a critical role for (i) the nucleation of BGs, (ii) the frequency shift of the curves, and thus of the upper and/or lower BG boundaries, as well as (iii) polarization of the unit cell modes (as for the previous case, the color scale denotes here the in-plane/out-of-plane contribution to the total modal displacement). If the thickness of the plate is relatively small (see Figure 3A for H ≤ 0.4 a), the modes are characterized by mainly in-plane or out-of-plane deformation (curves are either red or blue), whereas for thicknesses H ≥ 0.8, a (see Figure 3B) deformation modes with non-negligible in-plane and out-of plane components are present.

FIGURE 3

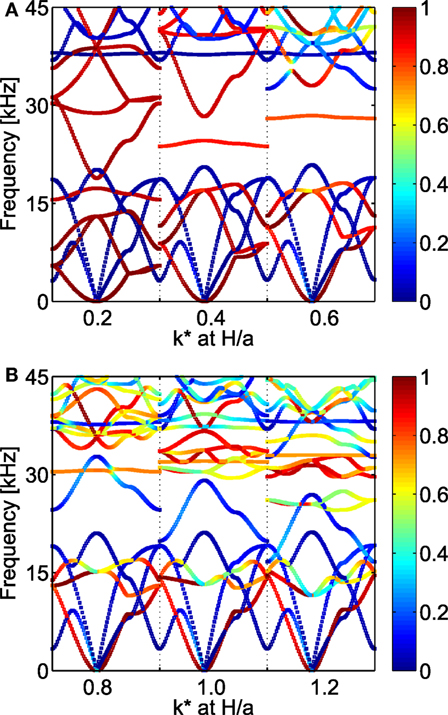
Figure 3. Parametric study showing the influence of the height to lattice parameter ratio H/a on the band structure for the case study of a unit cell with a cross-like cavity. Dispersion diagrams for (A) H/a = 0.2–0.6 and (B) H/a = 0.6–1.2 are reported. The color of the curves indicates the mode polarization, ranging from pure in-plane (blue) to pure out-of-plane (red).

The dependence of the BGs with respect to the plate thickness is summarized in Figure 4 where the lower and upper bounds and width of the BGs are reported as a function of H/a (in steps of 0.1 a). No BG appears in the system when H/a = 0.2, whereas a single large BG from approximately 20.70 to 28.00 kHz is present when H/a = 0.7. In all the other cases, two total BGs are present. The plate thickness giving rise to the widest total BG is for H/a = 0.6, corresponding to a relative width of 36% ($f_{B{G}_L}\in$[20.60–27.95] kHz and $f_{B{G}_U}\in$[28.42–32.52] kHz), highlighted in red in Figure 4. In this case, the two BGs are connected, except for an almost flat band between them.

FIGURE 4

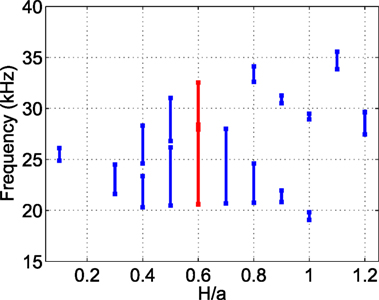
Figure 4. BG frequencies versus the unit cell thickness to lattice parameter ratio H/a. The ratio leading to the widest total BG is highlighted in red.

Thus results show that as the plate thickness increases, the frequency range covered by BGs increases up to the largest value at H/a = 0.6, which is therefore the chosen thickness for the manufacturing of experimental samples. To determine the necessary number of repeated unit cells to obtain efficient signal damping in experiments, finite element time transient analysis are performed (using ABAQUS). Numerical models with unit cells such as the one presented in Figure 1C, arranged in concentric square rings with 1, 2, 3, and 4 rows in a specific portion of the PVC plate, as shown in Figure 5, are considered.

FIGURE 5

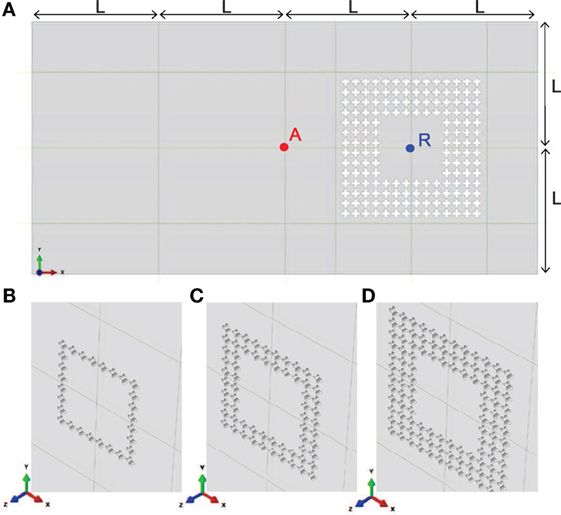
Figure 5. (A) Schematic representation of the numerical model of a plate including a four-row “ring-like” area in the right part of the plate. A zoom of the same structure with the “ring-like” zone made of (B) 1 row, (C) 2 rows, and (D) 3 rows of unit cells is provided. A and R denote the Lamb wave excitation and receiving points, respectively. L = 250 mm.

First, wave propagation analysis is performed to evaluate the screening power of the phononic region as a function of the number of rows of unit cells over a large frequency range. Guided waves are excited by means of an imposed orthogonally displacement (1 × 10⁻⁶ mm in the z-direction) at point A (see Figure 5A). A pulse of 2 sinusoidal cycles centered at 50 kHz and modulated by a Hanning window (Figure 6A) is chosen since it generates Lamb waves over a large frequency spectrum.

FIGURE 6

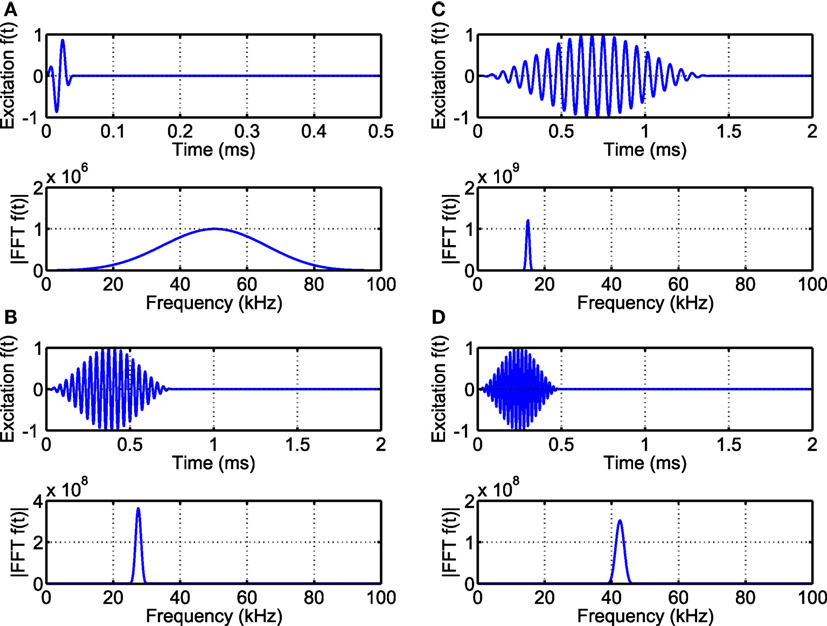
Figure 6. Excitation pulses: (A) 2 sine cycles at 50 kHz modulated by a Hanning window and 21 sine cycles at (B) 27.5 kHz, (C) 15 kHz, and (D) 42.5 kHz modulated by a Hanning window.

The out-of-plane displacement detected at point R for the four considered cases along with their Fourier transforms are shown in Figure 7. The system is modeled as linear elastic, so that the signal attenuation is totally due to the Bragg scattering mechanism. The results clearly show that waves with a frequency content falling outside the BG (gray rectangle) propagate through the phononic region reaching the monitoring point R without substantial attenuation as the number of cross-like cavities increases, while when the frequency content of the propagating waves falls inside the BG, the phononic crystal ring region inhibits the wave propagation so that the displacement at point R is much smaller as the number of cross-like cavities increases. Results show that the destructive interference mechanism starts taking place when two unit cell rows are present and that as the number of unit cell rows increases the edges of the attenuation frequency regions become sharper. The results are presented in semi-logarithmic scale and prove that each additional row of unit cells introduces an attenuation factor of about 4, allowing to infer that a plate with four rows of unit cells can reduce incident wave amplitudes by more than one order of magnitude.

FIGURE 7

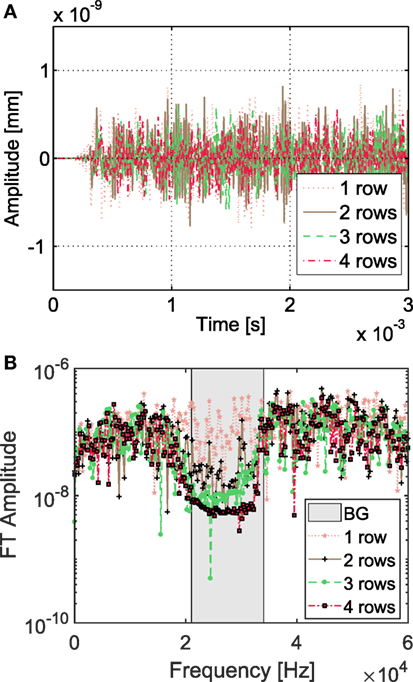
Figure 7. (A) Out-of-plane displacement for the phononic plate with 1, 2, 3, and 4 rows and (B) its Fourier Transform (FT) amplitude. The gray region denotes the calculated BG.

The dynamics of the plate is further investigated assigning as excitation pulse 21 sinusoidal cycles centered at 27.5 kHz (i.e., inside the BG) and modulated by a Hanning window (Figure 6B). The full wavefield reconstruction of the Von Mises stress after 780 µs from the excitation is reported in Figure 8. Green and red colors correspond to zero and maximum stresses, respectively, induced in the plate. The area surrounded by four rows of cross-like cavities is practically free from stresses. For this reason, the phononic plate with four rows of cross-like cavities is chosen for the experimental phase of the study. In particular, the cavities are distributed over a square frame of width 4 × a = 80 mm. A homogeneous area of 120 × 120 mm² is enclosed by the annular phononic crystal region.

FIGURE 8

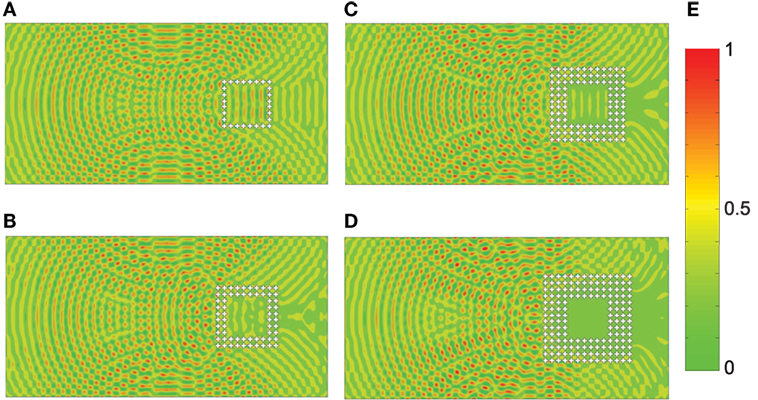
Figure 8. Von Mises stress for the phononic plate with (A) 1 row, (B) 2 rows, (C) 3 rows, and (D) 4 rows. Displacement fields are recorded at 780 µs from the excitation time. (E) Colors from green to red denote zero and maximum stress, respectively.

3. Experimental Measurements and Full Wavefield Reconstruction

The sample used for experimental analysis consists of a standard 1,000 mm × 500 mm × 12 mm (PVC) plate subjected to a machining process whereby 160 hollow rounded cross-cylinder inclusions were drilled, as shown in Figure 9A. The cavities cover a total area of 64 cm² and are arranged in 4 concentric rings, which leave a homogeneous 120 mm × 120 mm PVC region at the center. The manufacturing process requires a tolerance of 0.1 mm, which slightly modifies the band structure of the system (Miniaci et al., 2014).

FIGURE 9

Figure 9. (A) In-plane view of the SLDV scanning grid point superimposed on the PVC phononic plate and (B) positioning of the SLDV measurement head.

The adopted experimental setup consists of a scanning laser Doppler vibrometer (SLDV) PSV 400 3D by Polytec (see Figure 9B) allowing waveform digitization up to 70 kHz, which is sufficient for detecting and visualizing ultrasonic waves in the frequency range of interest since the probe beam size is small enough to detect the motion at a single point on the surface of the phononic plate (Ostachowicz et al., 2012; Kudela et al., 2015). Elastic guided waves are induced by means of a ceramic piezoelectric disk of diameter 10 mm made of Sonox^® by CeramTec^® bonded to the surface of the investigated sample (point A in Figure 9A) using commercial super glue. The pulse is excited by a TGA1241 generator by Thurlby Thandar Instruments through an EPA-104 amplifier by Piezo Systems^® Inc, inducing a 200 V_pp signal. To improve measurement accuracy, the investigated specimen is covered with self-adhesive retroreflective film by ORALITE^® enhancing the laser vibrometer signal level in each measurement point regardless of the incidence angle of the measurement beam.

The investigated spatial grid covers the entire phononic surface (see Figure 9A) and consists of 500 × 500 equally spaced grid points. The laser vibrometer is perpendicularly positioned 1 m away from the investigated surface, and only one SLDV head is used to perform the out-of-plane measurements of the velocity amplitudes over the target area (Figure 9B). Multiple (512) measurements are performed and averaged for each node, to filter out part of the noise.

A set of verification experiments is conducted to evaluate the elastic wavefield of the phononic plate at some frequencies of interest highlighted by the numerical study. Based on this analysis, sine functions with 21 Hanning modulated sine cycles with central frequencies of 15, 27.5, and 42.5 kHz are used as input signals (Figures 6B–D) to reconstruct the wavefield for excitations below, within, and above the BGs, respectively.

The excitation signal is used to trigger the data acquisition process. Out-of-plane velocity time histories are acquired starting from laser beam reflections back to the scanning head and their Doppler frequency shift detected by interferometers. Upon completion of measurements at all grid points, the recorded responses are postprocessed to obtain full images of the propagating wavefield aggregating single-point measurements within the region of inspection. The knowledge of the velocity time histories at all grid points (which can be integrated to obtain displacement time histories) allows the reconstruction of the time-evolving wavefields established in the scanning domain (Ostachowicz et al., 2012).

Figure 10 shows the comparison of the experimental wavefield reconstruction and the corresponding calculated displacements for the three aforementioned excitations (Figures 6B–D). At frequencies below the BGs (Figures 10A,B), Lamb waves travel through the periodic lattice relatively undisturbed. Limited reflection, scattering, or other losses can be observed, indicating that the phononic region does not interfere significantly with the wave motion.

FIGURE 10

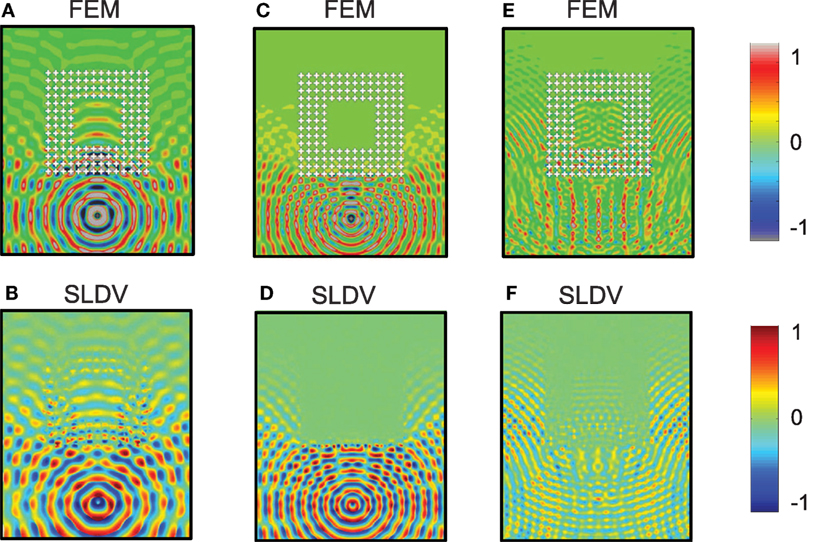
Figure 10. Computed and experimental out-of-plane displacement, respectively, for excitations below (A,B), inside (C,D), and above (E,F) the BGs. Numerical results are computed by means of ABAQUS, and measurements are performed by means of a PSV 400 3D SLDV by Polytec.

When operating at a frequency within the BGs, instead, the destructive interferences due to the Bragg scattering occurring within this region become large. Figures 10C,D clearly show that waves are reflected in the plate portion around the phononic region, mainly between the transmitting PZT and the lower edge of the unit cell ring. This behavior is accompanied by an extremely low transmission due to the absence of detectable wave amplitudes inside the phononic region.

Above the BG frequencies, the SLDV again registers transmission inside the phononic region, allowing the wavefield reconstruction at the same intensity scale. However, in this case, unit cells scatter the wave field, resulting in an observable delay in the wave propagation (Figures 10E,F). In this case, despite the scattering, the phononic region does not cause significant attenuation of the wave field.

Thus, numerical and experimental results show qualitative agreement. In particular, the clear attenuation of the wave field in the phononic region due to Bragg scattering can be observed in the case of a pulse centered within the BG, i.e., at 27.5 kHz, confirming the presence of the numerically calculated BG. It is worth highlighting that as the excitation is provided at a single point, the waves impinge on the phononic region from a wide range of angles proving the “complete” nature of the BG.

4. Conclusion

In this article, the existence of a complete BG for Lamb waves propagating in a phononic plate is provided by means of full wave field measurements. Extensive numerical simulations are presented to optimize the attenuating performance of a 12-mm thick PVC plate with 4 rows of unit cells of lattice parameter a = 20 mm, characterized by through-the-thickness cross-like cavities arranged in a square ring. Ultrasonic measurements on an ad hoc machined phononic PVC plate are performed via SLDV measurements and compared to the numerical results. Excellent agreement between the numerical predictions and experimental measurements is found both in terms of the BG frequency range and the decreasing trend of the transmission power spectrum. Besides confirming the existence of the numerically predicted complete BGs, measurements provide a direct observation of the scattering phenomena observed for waves characterized by frequency content below, within, and above the BG.

This design shows promise due to its simplicity and effectiveness and could be exploited at different size scales, e.g., at large scales for seismic shielding applications. In the study by Miniaci et al. (2016), we have shown that for sandy type soils, similar structures in the range of about 10 m are sufficient for effective shielding at frequencies below 5 Hz. Experimental verification remains to be performed on scaled models of these shields. In future, it would be interesting to extend the experiments to other geometries of practical interest, and especially to weakly disordered phononic materials or stubbed phononic plates, to further extend the study of metamaterial geometries providing efficient attenuation over wide low-frequency ranges.

Author Contributions

M. Miniaci performed most of the simulations. M. Miniaci and MR performed most of the experiments. M. Mazzotti, NK, PK, and BM helped with simulations. WO supervised the work and FB and NMP contributed to the writing of the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

M. Miniaci acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement no. 658483. NMP is supported by the European Commission H2020 under the Graphene Flagship Core 1 No. 696656 (WP14 “227 Polymer composites”) and FET Proactive “Neurofibres” grant No. 732344. FB is supported by H2020 FET Proactive “Neurofibres” grant No. 732344. FB and NK have been funded by Progetto d’Ateneo/Fondazione San Paolo “Metapp”, n. CSTO160004.

References

Andreassen, E., Manktelow, K., and Ruzzene, M. (2015). Directional bending wave propagation in periodically perforated plates. J. Sound Vibr. 335, 187–203. doi: 10.1016/j.jsv.2014.09.035

CrossRef Full Text | Google Scholar

Aurégan, Y., Farooqui, M., and Groby, J.-P. (2016). Low frequency sound attenuation in a flow duct using a thin slow sound material. J. Acoust. Soc. Am. 139, EL149–EL153. doi:10.1121/1.4951028

PubMed Abstract | CrossRef Full Text | Google Scholar

Baravelli, E., and Ruzzene, M. (2013). Internally resonating lattices for bandgap generation and low-frequency vibration control. J. Sound Vibr. 332, 6562–6579. doi:10.1016/j.jsv.2013.08.014

CrossRef Full Text | Google Scholar

Bavencoffe, M., Hladky-Hennion, A.-C., Morvan, B., and Izbicki, J.-L. (2009). Attenuation of Lamb waves in the vicinity of a forbidden band in a phononic crystal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 1960–1967. doi:10.1109/TUFFC.2009.1272

PubMed Abstract | CrossRef Full Text | Google Scholar

Bavencoffe, M., Morvan, B., Hladky-Hennion, A.-C., and Izbicki, J.-L. (2013). Experimental and numerical study of evanescent waves in the mini stopband of a 1D phononic crystal. Ultrasonics 53, 313–319. doi:10.1016/j.ultras.2012.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergamini, A., Zündel, M., Parra, E. A. F., Delpero, T., Ruzzene, M., and Ermanni, P. (2015). Hybrid dispersive media with controllable wave propagation: a new take on smart materials. J. Appl. Phys. 118, 154310. doi:10.1063/1.4934202

CrossRef Full Text | Google Scholar

Bigoni, D., Guenneau, S., Movchan, A. B., and Brun, M. (2013). Elastic metamaterials with inertial locally resonant structures: application to lensing and localization. Phys. Rev. B 87, 174303. doi:10.1103/PhysRevB.87.174303

CrossRef Full Text | Google Scholar

Bonello, B., Charles, C., and Ganot, F. (2007). Lamb waves in plates covered by a two-dimensional phononic film. Appl. Phys. Lett. 90, 021909. doi:10.1063/1.2431569

CrossRef Full Text | Google Scholar

Brunet, T., Vasseur, J. O., Bonello, B., Djafari-Rouhani, B., and Hladky-Hennion, A.-C. (2008). Lamb waves in phononic crystal slabs with square or rectangular symmetries. J. Appl. Phys. 104, 043506. doi:10.1063/1.2970067

CrossRef Full Text | Google Scholar

Casadei, F., Delpero, T., Bergamini, A., Ermanni, P., and Ruzzene, M. (2012). Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials. J. Appl. Phys. 112, 064902. doi:10.1063/1.4752468

CrossRef Full Text | Google Scholar

Celli, P., and Gonella, S. (2014). Laser-enabled experimental wavefield reconstruction in two-dimensional phononic crystals. J. Sound Vibr. 333, 114–123. doi:10.1016/j.jsv.2013.09.001

CrossRef Full Text | Google Scholar

Chen, J., Xia, Y., Han, X., and Zhang, H. (2012). Lamb waves in phononic crystal slabs: truncated plane parallels to the axis of periodicity. Ultrasonics 52, 920–924. doi:10.1016/j.ultras.2012.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Colquitt, D., Roux, P., Guenneau, S., and Craster, R. V. (2016). A seismic metamaterial: the resonant metawedge. Sci. Rep. 6, 27717. doi:10.1038/srep27717

PubMed Abstract | CrossRef Full Text | Google Scholar

Craster, R. V., and Guenneau, S. (2012). Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking. Springer Series in Materials Science. London: Springer.

Google Scholar

Croënne, C., Lee, E. J. S., Hu, H., and Page, J. H. (2011). Band gaps in phononic crystals: generation mechanisms and interaction effects. AIP Adv. 1, 041401. doi:10.1063/1.3675797

CrossRef Full Text | Google Scholar

Deymier, P. A. (2013). Acoustic Metamaterials and Phononic Crystals. Springer Series in Solid-State Sciences. Berlin, Heidelberg: Springer.

Google Scholar

Gliozzi, A. S., Miniaci, M., Bosia, F., Pugno, N. M., and Scalerandi, M. (2015). Metamaterials-based sensor to detect and locate nonlinear elastic sources. Appl. Phys. Lett. 107, 161902. doi:10.1063/1.4934493

CrossRef Full Text | Google Scholar

He, Z., Jia, H., Qiu, C., Peng, S., Mei, X., Cai, F., et al. (2010). Acoustic transmission enhancement through a periodically structured stiff plate without any opening. Phys. Rev. Lett. 105, 074301–074304. doi:10.1103/PhysRevLett.105.074301

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsiao, F.-L., Khelif, A., Moubchir, H., Choujaa, A., Chen, C.-C., and Laude, V. (2007). Waveguiding inside the complete band gap of a phononic crystal slab. Phys. Rev. E 76, 056601. doi:10.1103/PhysRevE.76.056601

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, J.-C., and Wu, T.-T. (2007). Propagation of Lamb waves in phononic-crystal plates. J. Mech. 23, 223–228. doi:10.1017/S1727719100001258

CrossRef Full Text | Google Scholar

Hussein, M. I., Leamy, M. J., and Ruzzene, M. (2014). Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66, 40802–40838. doi:10.1115/1.4026911

CrossRef Full Text | Google Scholar

Jiménez, N., Huang, W., Romero-García, V., Pagneux, V., and Groby, J.-P. (2016). Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 109, 121902. doi:10.1063/1.4962328

CrossRef Full Text | Google Scholar

Kaina, N., Fink, M., and Lerosey, G. (2013). Composite media mixing Bragg and local resonances for highly attenuating and broad bandgaps. Sci. Rep 3, 3240. doi:10.1038/srep03240

PubMed Abstract | CrossRef Full Text | Google Scholar

Khelif, A., Choujaa, A., Benchabane, S., Djafari-Rouhani, B., and Laude, V. (2005). Experimental study of guiding and filtering of acoustic waves in a two dimensional ultrasonic crystal. Zeitschrift für Kristallographie 220, 836–840. doi:10.1524/zkri.2005.220.9-10.836

CrossRef Full Text | Google Scholar

Kherraz, N., Haumesser, L., Levassort, F., Benard, P., and Morvan, B. (2016). Controlling Bragg gaps induced by electric boundary conditions in phononic piezoelectric plates. Appl. Phys. Lett. 108, 093503. doi:10.1063/1.4943138

CrossRef Full Text | Google Scholar

Kosevich, Y. A., Goffaux, C., and Sánchez-Dehesa, J. (2006). Fano-like resonance phenomena by flexural shell modes in sound transmission through two-dimensional periodic arrays of thin-walled hollow cylinders. Phys. Rev. B 74, 012301. doi:10.1103/PhysRevB.74.012301

CrossRef Full Text | Google Scholar

Kudela, P., Radzieński, M., and Ostachowicz, W. (2015). Identification of cracks in thin-walled structures by means of wavenumber filtering. Mech. Syst. Sig. Process. 5051, 456–466. doi:10.1016/j.ymssp.2014.05.041

CrossRef Full Text | Google Scholar

Li, Y., and Assouar, B. M. (2016). Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 108, 063502. doi:10.1063/1.4941338

CrossRef Full Text | Google Scholar

Miniaci, M., Gliozzi, A. S., Morvan, B., Krushynska, A., Bosia, F., Scalerandi, M., et al. (2017). Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys. Rev. Lett. 118, 214301. doi:10.1103/PhysRevLett.118.214301

PubMed Abstract | CrossRef Full Text | Google Scholar

Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016). Large scale mechanical metamaterials as seismic shields. New J. Phys. 18, 083041. doi:10.1088/1367-2630/18/8/083041

CrossRef Full Text | Google Scholar

Miniaci, M., Marzani, A., Testoni, N., and Marchi, L. D. (2014). Complete band gaps in a polyvinyl chloride (PVC) phononic plate with cross-like holes: numerical design and experimental verification. Ultrasonics 56(Suppl. C), 251–259. doi:10.1016/j.ultras.2014.07.016

CrossRef Full Text | Google Scholar

Mohammadi, S., Eftekhar, A. A., Pourabolghasem, R., and Adibi, A. (2011). Simultaneous high-Q confinement and selective direct piezoelectric excitation of flexural and extensional lateral vibrations in a silicon phononic crystal slab resonator. Sens. Actuat. A 167, 524–530. doi:10.1016/j.sna.2011.03.014

CrossRef Full Text | Google Scholar

Morandi, F., Miniaci, M., Marzani, A., Barbaresi, L., and Garai, M. (2016). Standardised acoustic characterisation of sonic crystals noise barriers: sound insulation and reflection properties. Appl. Acoust. 114(Suppl. C), 294–306. doi:10.1016/j.apacoust.2016.07.028

CrossRef Full Text | Google Scholar

Ostachowicz, W., Kudela, P., Krawczuk, M., and Zak, A. (2012). Guided Waves in Structures for SHM: The Time – Domain Spectral Element Method. West Sussex: John Wiley & Sons, Ltd.

Google Scholar

Oudich, M., Senesi, M., Assouar, M. B., Ruzenne, M., Sun, J.-H., Vincent, B., et al. (2011). Experimental evidence of locally resonant sonic band gap in two-dimensional phononic stubbed plates. Phys. Rev. B 84, 165136. doi:10.1103/PhysRevB.84.165136

CrossRef Full Text | Google Scholar

Pennec, Y., Djafari-Rouhani, B., Vasseur, J. O., Khelif, A., and Deymier, P. A. (2004). Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 69, 046608. doi:10.1103/PhysRevE.69.046608

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennec, Y., Vasseur, J. O., Djafari-Rouhani, B., Dobrzyśki, L., and Deymier, P. A. (2010). Two-dimensional phononic crystals: examples and applications. Surf. Sci. Rep. 65, 229–291. doi:10.1016/j.surfrep.2010.08.002

CrossRef Full Text | Google Scholar

Platts, S. B., Movchan, N. V., McPhedran, R. C., and Movchan, A. B. (2002). Two-dimensional phononic crystals and scattering of elastic waves by an array of voids. Proc. R. Soc. London A 458, 2327–2347. doi:10.1098/rspa.2002.0960

CrossRef Full Text | Google Scholar

Sukhovich, A., Merheb, B., Muralidharan, K., Vasseur, J. O., Pennec, Y., Deymier, P. A., et al. (2009). Experimental and theoretical evidence for subwavelength imaging in phononic crystals. Phys. Rev. Lett. 102, 154301. doi:10.1103/PhysRevLett.102.154301

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y.-F., and Wang, Y.-S. (2013). Multiple wide complete bandgaps of two-dimensional phononic crystal slabs with cross-like holes. J. Sound Vibr. 332, 2019–2037. doi:10.1016/j.jsv.2012.11.031

CrossRef Full Text | Google Scholar

Wu, T.-C., Wu, T.-T., and Hsu, J.-C. (2009). Waveguiding and frequency selection of Lamb waves in a plate with a periodic stubbed surface. Phys. Rev. B 79, 104306. doi:10.1103/PhysRevB.79.104306

CrossRef Full Text | Google Scholar

Wu, T.-T., Hsu, J.-C., and Sun, J.-H. (2011). Phononic plate waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58, 2146–2161. doi:10.1109/TUFFC.2011.2064

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, K., Chen, T., and Wang, X. (2013). Band gaps in the low-frequency range based on the two-dimensional phononic crystal plates composed of rubber matrix with periodic steel stubs. Phys. B 416, 12–16. doi:10.1016/j.physb.2013.02.011

CrossRef Full Text | Google Scholar