Effect of Length, Diameter, Chirality, Deformation, and Strain on Contact Thermal Conductance Between Single-Wall Carbon Nanotubes

Thermal energy transfer across physically interacting single-wall carbon nanotube interconnects has been investigated using non-equilibrium molecular dynamics simulations. The role of various geometrical and structural (length, diameter, chirality) as well as external (deformation and strain) carbon nanotube (CNT) parameters has been explored to estimate total as well as area-normalized thermal conductance across cross-contact interconnects. It is shown that the CNT aspect ratio and degree of lateral as well as tensile deformation play a significant role in determining the extent of thermal energy exchange across CNT contacts, while CNT chirality has a negligible influence on thermal transport. Depending on the CNT diameter, aspect ratio, and degree of deformation at the contact interface, the thermal conductance values can vary significantly—by more than an order of magnitude for total conductance and a factor of 3 to 4 for area-normalized conductance. The observed trends are discussed from the perspective of modulation in number of low-frequency out-of-plane (transverse, flexural, and radial) phonons that transmit thermal energy across the contact and govern the conductance across the interface. The established general dependencies for phonon-governed thermal transport at CNT contacts are anticipated to help design and performance prediction of CNT-based flexible nanoelectronic devices, where CNT–CNT contact deformation and strain are routinely encountered during device operations.

Introduction

Carbon nanotubes (CNTs) have shown tremendous potential of their applicability in a wide gamut of fields such as nanoelectronics, field emission, chemical and physical sensing, bio-sensing, nanocomposites, etc. (Meyyappan, 2004). Within the specialized field of nanoelectronics, fabrication as well as modeling of the novel carbon-based nanoelectronic devices, such as thin-film transistors, flexible traces, conductive solders, and adhesives, etc., have gained a lot of momentum in recent years (Artukovic et al., 2005; Allen et al., 2006; Engel et al., 2008; Ishikawa et al., 2008; Behnam et al., 2013; Cao et al., 2013; Park et al., 2013; Rao et al., 2013; Wang et al., 2013; Schiessl et al., 2014; Liu et al., 2015; Chortos et al., 2016), because of their excellent thermal and electrical properties, which are two key characteristics required for nanoelectronics device applications. These properties can be further tuned through chemical and structural modifications (such as functionalization, dopants, defects, contact/interface characteristics, etc.), thus providing device designers/fabricators additional dimensions toward tailoring nanoelectronics device characteristics (Saito et al., 1998; Avouris and Xia, 2012; Pop et al., 2012; Marconnet et al., 2013).

As device dimensions shrink, power dissipation at device interconnects often becomes a performance-limiting issue because of the large surface-area to volume ratio. Equally important are the specifics of the material contact configurations within the device where dominant heating is expected to occur. The energy transfer through these contacts occurs via conduction electrons and thermal vibrations as well as their mutual interactions. These are often characterized as electrical contact resistance (for electrons), interface thermal resistance (for heat), and electron–phonon coupling, respectively. In an operating CNT-based device, these resistances collectively govern the current, thermal energy flow and the temperature distribution within the device, identify detrimental hot spots, and thus, dictate its performance. Despite the large number of potential nanoelectronics applications, the use of CNT devices is limited by their unknown reliability and variations in performance (possibly originating from purity concerns associated with mixing of semi-conducting and metallic CNTs, inefficient removal of adsorbed surfactants required for CNT dispersion, diameter and length distribution, mixed chiral nature, junction morphology of CNTs in contact, etc.), thus advocating the necessity of understanding the energy transfer and the loss at device interconnects (Cao and Han, 2013). Of particular interest to this study is the issue of thermal conductance at the physically interacting single-wall CNT–CNT contacts, which is associated with vibrational energy transfer (its inverse is often termed thermal resistance). Within the framework of carbon materials, such interfaces are often realized in CNT-mesh based nanoelectronic devices (Kumar et al., 2007; Chandra et al., 2011; Behnam et al., 2013; Cao et al., 2013; Lau et al., 2013; Park et al., 2013; Wang et al., 2013; Schiessl et al., 2014; Liu et al., 2015; Chortos et al., 2016), 3D CNT foams (Hashim et al., 2012; Kim et al., 2012; Yang et al., 2014b; Ozden et al., 2015a,b), CNT-based polymeric nanocomposites (Ma et al., 2010; Kim et al., 2014), etc.

Several groups, both experimentally [predominantly multiwall carbon nanotubes (MWCNTs)] (Cola et al., 2007; Prasher, 2008; Ma et al., 2010; Yang et al., 2010, 2014a; Yamada et al., 2012) and through simulations [predominantly single-wall carbon nanotubes (SWCNTs)] (Maruyama et al., 2006; Zhong and Lukes, 2006; Chalopin et al., 2009; Prasher et al., 2009; Xu and Buehler, 2009; Evans and Keblinski, 2010; Varshney et al., 2010; Bui et al., 2011, 2012; Evans et al., 2012; Gharib-Zahedi et al., 2013; Hu and Cao, 2013; Volkov et al., 2013; Hu and McGaughey, 2014; Chen et al., 2016, 2017; Salaway and Zhigilei, 2016; Liao et al., 2017), have investigated the thermal conductance across CNT contacts over the past decade. Recently, a few studies focusing on diameter dependence and number of walls in MWCNTs on the behavior of interface thermal conductance has also been reported (Rong et al., 2017; Varshney et al., 2017). Overall, these studies have offered significant insights into the conduction mechanism, and how it can be tailored using different modifications such as alignment (Prasher et al., 2009), surrounding environment (Maruyama et al., 2006; Xu and Buehler, 2009), possible metallization (Gengler et al., 2012), functionalization (Bui et al., 2012; Roy et al., 2012; Gharib-Zahedi et al., 2013), tensile strain (Chen et al., 2017), etc. The reported conductance values (or ranges) for the different studied SWCNT–SWCNT interfaces, as retrieved from experimental and modeling literature, are tabulated in Table 1 along with the brief comments on their estimation. The table shows a considerable scatter in both predicted and measured values of conductance (~10 of pW/K to ~1,000 pW/K; ~4 MW/m²-K to ~10³ MW/m²-K), which could be attributed to differences in CNT parameters (diameter, length), type of simulation methodology adopted, interpretation of surface-area for cylindrical contacts, and surrounding environment, among other factors.

TABLE 1

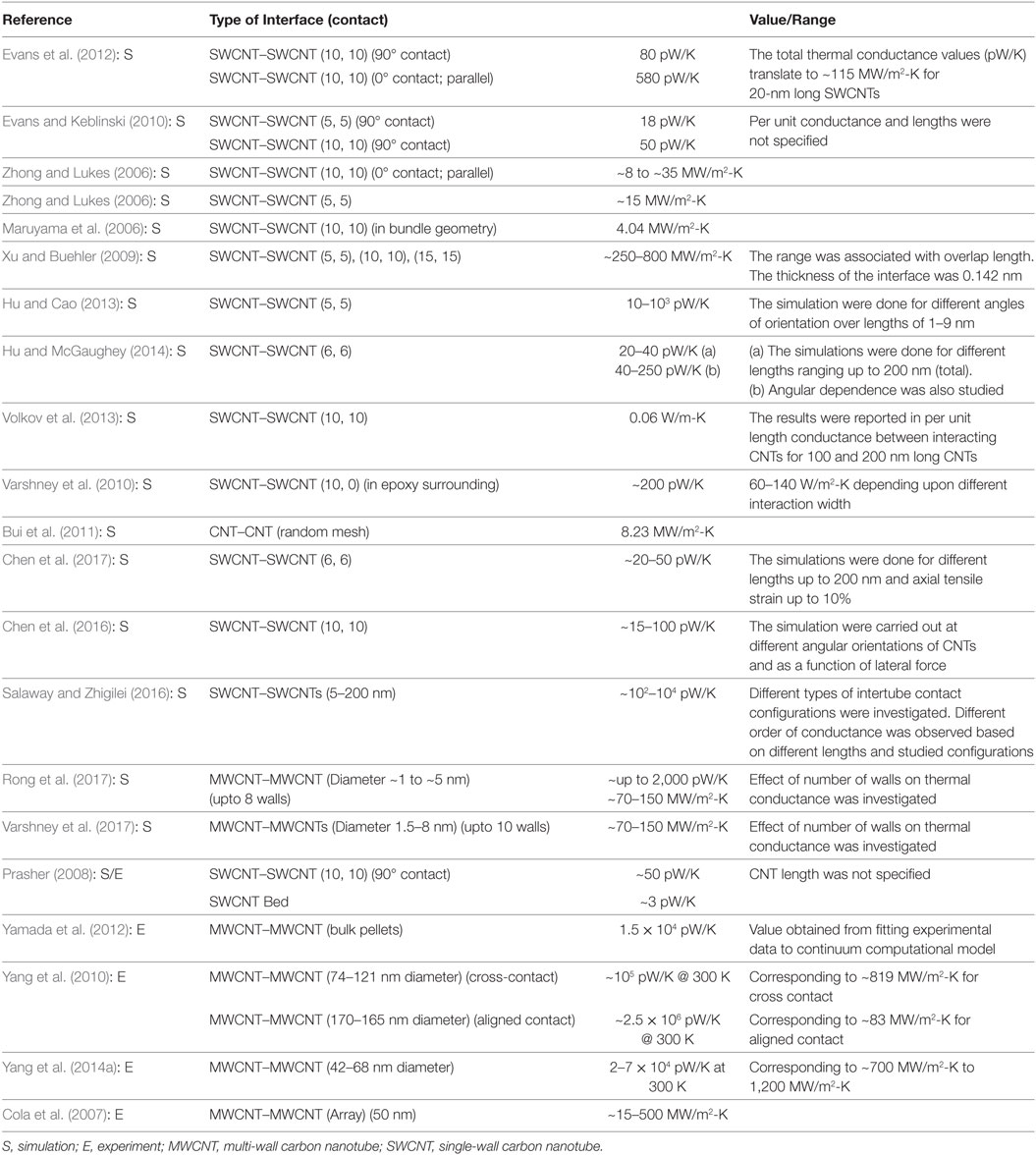
Table 1. Interface thermal conductance values of CNT–CNT interfaces as retrieved from previous literature.

Barring a few studies mentioned above (Rong et al., 2017; Varshney et al., 2017), most of the computational literature to date has investigated the thermal conductance across very thin SWCNTs (~1–2 nm in diameter) contacts, with a few focusing on the effects of CNT length (Zhong and Lukes, 2006; Evans et al., 2012; Hu and Cao, 2013; Hu and McGaughey, 2014), and their angular orientation (at the contact) on thermal energy transfer (Evans et al., 2012; Hu and McGaughey, 2014; Chen et al., 2016). Other CNT characteristics such as varying diameter, aspect ratio, chirality, mechanical modulation (tensile and radial deformation), number of walls (for multiwall CNTs), which could also play an important role toward determining thermal energy transfer have not been investigated to a similar details except few recent studies (Chen et al., 2017; Rong et al., 2017; Varshney et al., 2017). In this study, we attempt to address a few of these parameters of interest and provide further insights into the behavior of thermal conductance. Specifically, we investigate how the conductance across a SWCNT–SWCNT contact interface is modified with nanotube length and diameter (and thus aspect ratio, by corollary), degree of radial deformation, chirality, and tensile strain. For example, the understanding of thermal conductance as a function of the CNT–CNT junction shape (circular vs. radially deformed vs. collapsed) as well as number of CNT walls in multiwall CNT contacts, is essential as these specifications will determine the thermal dissipative characteristics of flexible and stretchable device junctions and thus, its performance. In fact, mechanical contact perturbations with tensile or compressive strain, deformation or even a potential radial collapse of CNTs constitute very realistic circumstances that could occur in flexible and stretchable CNT-based nanoelectronics such as printed traces, solders, thin-film transistors, etc. (Artukovic et al., 2005; Allen et al., 2006; Engel et al., 2008; Ishikawa et al., 2008; Park et al., 2013; Rao et al., 2013; Wang et al., 2013; Schiessl et al., 2014; Liu et al., 2015; Chortos et al., 2016).

Simulation Methodology

Simulation Setup

Figure 1 shows a representative system of a physically interacting SWCNT pair contact in a cross-contact geometry. Initially, several SWCNTs with diameters (D) and lengths (L) ranging from ~1.5 − ~8 nm and 10 − 100 nm, respectively, with varying chirality (also shown in the Figure 1) were generated using Materials Studio^®. We should point out that (a) in this study, we focused on SWCNTs with diameter >1.5 nm as SWCNTs with diameter <1 nm are well investigated in literature; and (b) while larger diameter SWCNTs are not thermodynamically stable in cylindrical or tubular form, we modeled large diameter SWCNTs to explore the dependency of contact area (larger diameter CNTs are expected to have larger contact area) and aspect ratio on normalized thermal conductance across the SWCNT-SWCNT contacts. As the size of CNT unit-cell (repeat unit along axial direction) varies for different chiral CNTs, the initial generation of CNTs with length L (between 10 and 100 nm) was done by replicating the unit-cell to reach a longer length L′ (L′ > L), followed by clipping atoms at the edges to retain the desired length, L as discussed in detail elsewhere (Varshney et al., 2017). In order to create the cross-contact, an in-house script was used to replicate second identical CNT, rotate (90°) and translate it such that inter-CNT surface to surface spacing is 3.4 Å. Non-periodic boundary conditions were used in all three-directions, in which the cross-contact SWCNT system resides in a relatively larger simulation box as shown in the Figure 1 schematic.

FIGURE 1

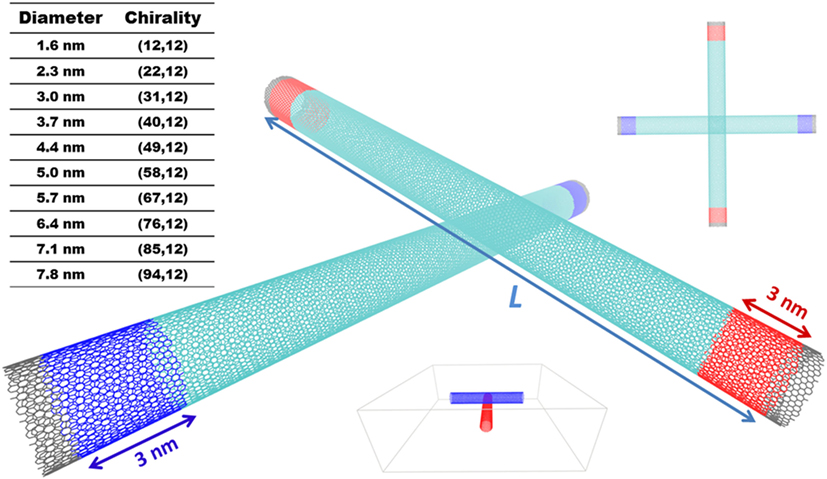
Figure 1. Schematic of a representative 3.7 nm diameter physically interacting SWCNT pair in a cross-contact geometry (perspective view: main figure; top view: top-right corner) as considered in this study for calculation of contact thermal conductance. L represents the length of the SWCNT. Color scheme: fixed carbon atoms (black); hot thermostated carbon atoms (red); cold thermostated carbon atoms (blue); unthermostated carbon atoms (cyan). The specifics of studied SWCNTs’ chirality are also shown in top-left corner. The overall geometry of the system in a large slab is shown at the bottom; red and blue colors are shown to differentiate the SWCNTs.

All simulations were performed with LAMMPS molecular dynamics simulation package (Plimpton, 1995) using the PCFF force field (Sun et al., 1994). This force field has been successfully employed for the investigation of thermal conductance/conductivity in several CNT related studies (Huxtable et al., 2003; Shenogin et al., 2004; Clancy and Gates, 2006; Hu et al., 2008; Lee et al., 2011; Varshney et al., 2011, 2014; Liu et al., 2012). After an initial minimization, all systems were subjected to NVT (canonical ensemble) simulations for equilibration for 200–500 ps (depending upon the system size) where the edges of the SWCNTs were fixed (see Figure 1). During equilibration stage, a timestep of 1 fs was used for all simulations. As the length of the SWCNTs was fixed (because of fixed edges), the initial C–C bond lengths were equilibrated to make sure that there was no residual tensile/compressive stress/strain within the CNTs during equilibration. It is shown later that tensile stress/strain have noticeable effect on contact thermal conductance between SWCNTs. Furthermore, as the edges were constrained (fixed) to be circular, the SWCNTs retained their shape of circular cross-section along the symmetry axis during equilibration (a schematic is shown later). We will refer them as un-deformed CNTs.

In order to generate and model radially deformed CNTs, two fictitious repulsive walls were introduced at the top and bottom of the cross-contact CNT system and were slowly pressed toward each other during an NVT simulation. Because of the wall compression, the CNTs were forced to radially deform due to the repulsive interaction with walls and flatten out (but not fully collapsed). These simulations were carried out for several chiral nanotube pairs, where the CNTs’ coordinates were stored at different stages of the simulation corresponding to different degrees (or stages) of deformation. Subsequently, the stored deformed CNT datasets were used as a starting point for a new set of simulations without fictitious walls. Here, further NVT equilibration (200 ps) was performed for each case in the deformed state, where the deformed edge atoms were fixed (similar to un-deformed CNTs) to maintain the overall deformed shape of the CNTs.

Thermal Transport Simulations

After equilibration, non-equilibrium molecular dynamics (NEMD) simulations were used to calculate thermal conductance across the physically interacting contacts of the different studied CNT pairs. For these simulations as well, the edges (~1 nm) on both ends of the CNTs were kept fixed during the course of the NEMD simulations. To introduce a temperature drop (or discontinuity) at the interface, 3 nm sections near both edges were thermostated at 350 (hot CNT) and 250 K (cold CNT) for all systems of interest as shown in Figure 1. All simulations were performed with the timestep of 0.5 fs under NVE (microcanonical) ensemble. To investigate possible artifacts caused by the choice of thermostat, several thermostats were tested (heating/cooling either at the boundaries or across the whole CNTs, using either Nose–Hoover or temperature rescaling thermostats with different updating time intervals). However, negligible differences were observed with no statistically significant trends as also reported previously (Varshney et al., 2012). For all the results presented further, the temperature rescaling approach was used in the thermostated regions with a rescaling time-interval of 100 timesteps (50 fs). Once a steady-state was reached (~500 ps), the interface thermal conductance(s) were calculated using the following set of equations:

${\Lambda }_1=\frac{Q}{\mathrm{\Delta }T};{\Lambda }_2=\frac{Q}{A\mathrm{\Delta }T},$ (1)

where Λ₁ (pW/K) and Λ₂ (MW/m²-K) are the total and area-normalized thermal conductance (we will also refer the latter as the interface thermal conductance), respectively, Q is the heat flow rate, ΔT is the temperature drop at the interface, and A is the effective area of interaction between the interacting SWCNTs which is discussed next.

At nano/sub-micron length scales, the thermal conductance values for CNTs are generally reported either in units of pW/K or MW/m²-K as also depicted in Table 1. For the latter, as the CNTs are intrinsically cylindrical, but flexible, the effective contact area for thermal energy transfer is not trivial to calculate and several methodologies have been employed in the past for estimating the contact area (Zhong and Lukes, 2006; Xu and Buehler, 2009; Liao et al., 2010; Varshney et al., 2010; Bui et al., 2012; Evans et al., 2012). In order to have a measure of the effective interaction area, a methodology similar to Evans et al. (2012) was employed, in which the van-der Waals interaction energy between two layers of flat graphene sheets is calculated for a known area and then used to calculate the effective area of CNT interaction using the following relation:

$A_{\text{CNT}}=\frac{E_{\text{CNT}}}{E_{\text{G}}}{A}_{\text{G}},$ (2)

where E_G and E_CNT are the interaction energies between graphene layers and cylindrical SWCNTs, respectively, and A_G is the known area for graphene interaction.

Results and Discussion

Effect of CNT Length, Diameter, and Aspect Ratio on Thermal Conductance

Figure 2A plots the total thermal conductance (Λ₁) as a function of length for the different diameter SWCNTs on a log–log scale. Few points in Figure 2A are shown as partly transparent colors. These points represent additional simulations (to what is discussed in simulation setup) and were performed to observe and estimate the trends over the range spanning an order of magnitude in CNT length. The figure shows two noticeable trends. First, the total thermal conductance (and thus thermal energy transfer) is increasing with increase in CNT length as well as CNT diameter. Here, we should also point out that predicted values of Λ₁ (especially for shorter CNTs) in this study are consistent with the increasing trend when compared to the reported values for shorter (<1 nm) and thinner CNTs (see Table 1) (Evans and Keblinski, 2010; Evans et al., 2012; Hu and Cao, 2013; Hu and McGaughey, 2014). Second, similar to previous studies, Λ₁ appears to be increasing, but saturating in few cases with CNT length (up to 100 nm).

FIGURE 2

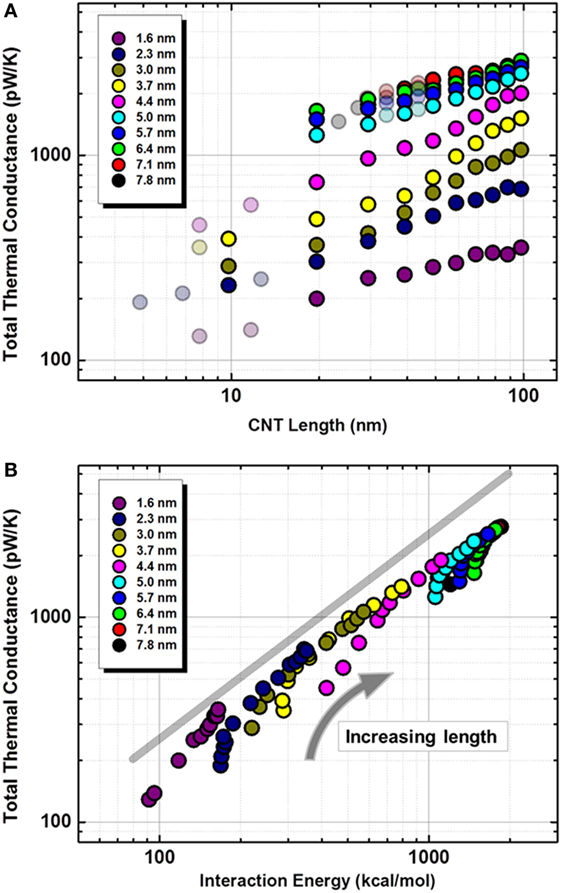
Figure 2. Log–log plots of total thermal conductance (pW/K) as a function of (A) SWCNT length and (B) interaction energy between SWCNT pair for different diameter CNTs. Data color scheme for different diameter SWCNTs is shown in legends. Please refer to the main text for the discussion of lightly shaded data points. In (B), a power-law scaling of unity is shown as a guide for the eye.

It is imperative to assume that contact interaction region should directly correlate to total thermal energy transfer, i.e., the larger contact interaction region should induce the larger total thermal conductance. In our simulations, we associate this region with interaction energy (E) between the cross-contact SWCNT pair. In this context, the same data set of Λ₁ is re-plotted with respect to E in Figure 2B and sheds more insights on the length and diameter trends. Also depicted in the figure is the power-law scaling of unity as a guideline for a quantitative interpretation of the dependence of Λ₁ on interaction energy. The shown scaling power of unity corresponds to the situation when Λ₁ is linearly proportional to the increase in contact region, characterized by interaction energy.

First, for all sets of same diameter CNTs, an increase in interaction energy is observed with the increase in CNT length. CNTs become more flexible with length, thus they can locally deform and flatten near the interface due to attractive van-der Waals forces, also increasing the interaction energy between them. For shorter CNTs, however, the increase in interaction energy with CNT length is much less evident because of their difficulty (intrinsic stiffness) toward local deformation in Figure 2B (for example, blue data points near ~E = 200 kcal/mol). Second, the figure shows that for shorter CNTs, a small increase in interaction energy (thus interaction area) leads to an over-proportional (>unity power-law scaling) increase in Λ₁. However, after a certain CNT length, the data points align along the unity power-law guideline, suggesting a proportionate relationship between E and Λ₁ for longer CNTs. These observations suggest that, in addition to interaction area, the length of the CNTs plays an important role in determining thermal conductance across CNTs interfaces (Zhong and Lukes, 2006; Evans et al., 2012; Hu and Cao, 2013; Hu and McGaughey, 2014). Chalopin and co-authors have suggested that only low-frequency modes (<few tens of THz) contribute toward thermal transmission between physical interacting CNTs’ contact (Chalopin et al., 2009). With increasing length, we suggest that both factors, i.e., the greater number of low-frequency modes (lowering of external resistance as noted previously) (Hu and McGaughey, 2014; Chen et al., 2017) as well as the increase in contact area, contribute to the observed increase in the thermal conductance. Third, Figure 2 also shows that for constant length, large diameter CNTs have a higher interaction energy (due to larger overlap area) and higher total thermal conductance.

The effect of the interaction energy (and thus overlap area) is implicitly included in Figure 3 which shows area-normalized interface thermal conductance (Λ₂) as a function of length for different diameter SWCNTs. Due to a large data set (~100 data points), we have only emphasized the regions (in different transparent colors) with different statistical variation in predicted interfacial thermal conductance instead of showing error bars on each data point as it would have cluttered the figure significantly. The figure highlights several trends worth noting. At first, one would expect that thermal conductance—when normalized by the interaction area—should be independent of CNT geometric parameters. However, we propose that the observed trends in Λ₂ in Figure 3 can be appreciated using the argument of effectiveness of non-longitudinal low-frequency modes (i.e., transverse radial and flexural modes) toward transferring thermal energy across the interface. We define a term, number of low-frequency modes per unit contact area (χ_LM) and postulate that modulation in this term modulates the normalized thermal energy exchange across the contact. Below, the observed trends in normalized thermal conductance with respect to SWCNT length and diameter are discussed from the perspective of possible reasons behind the modulation of χ_LM. It is to be pointed out that “low-frequency modes per unit area” concept is introduced to gain insights into “per unit area” thermal transfer. The total thermal transport (in terms of pW/K) has been shown to increase with both length and diameter as also reported in previous studies.

FIGURE 3

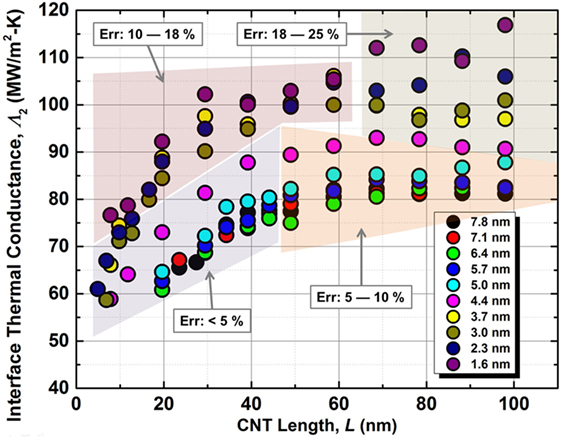
Figure 3. Plot of interface thermal conductance (MW/m²-K) as a function of SWCNT length for different diameter CNTs. Data color scheme for different diameter SWCNTs is shown in legends. Due to number of data points, the regions with different standard error are shown in different semi-transparent colors.

First, Figure 3 shows that the normalized conductance increases with CNT length and asymptotically saturates around ~60 nm, irrespective of CNT diameter. We attributed the observed increase to increase in χ_LM (longer CNTs would have greater number of low-frequency phonon microstates) in SWCNTs that can couple via van-der Waals interactions and lead to increased thermal transport across the contact. We also argue that after certain length, the effect of these modes gets saturated. For example, the energy of transverse acoustic and flexural optical phonon modes decay in quadratic function as wave number decreases. Under such circumstances, the total thermal energy exchange becomes proportional to the contact area, leading to a converged value of normalized thermal conductance.

Second, it is observed that for a fixed length, normalized thermal conductance decreases with the increase in diameter. Such a behavior has also been reported recently by Rong et al. where they investigated the diameter dependence of thermal conductance in SWCNTs and MWCNTs (Rong et al., 2017). Although, the observation seems counter-intuitive at first glance as larger diameter CNTs have more number of phonon modes (for constant length), we attribute this decrease to lessening of χ_LM that can couple via van-der Waals interactions toward thermal transmission. While larger diameter CNTs do consist of more phonon modes, most of these modes are optical in nature that need to be scattered to low-frequency radial, flexural or transverse modes in order to effectively transfer vibrational energy across the junction. We argue that with increasing fraction of optical modes, the “overall probability” for their transfer to low-frequency modes is reduced, thus resulting in the reduction in χ_LM (number low-frequency modes per unit area), which can effectively transport thermal energy across the interface leading to the observed decrease in the “normalized” thermal conductance, although “total” number of such modes (when accumulated over the whole contact area) will increase with diameter.

It is to be noted that while previous studies have either investigated thermal transport in terms of CNT length or in terms of CNT diameter, investigation of thermal transport as a function of both in a single study allowed us to appreciate the thermal transport in terms of CNT aspect ratio via combining both length and diameter dependence into a single parameter. In this context, after observing a systematic variation in Λ₂ with length and diameter, we incorporated both dependencies in a single parameter as aspect ratio, η which is highlighted in Figure 4. For the sake of comparison as well as completeness, two aspect ratios are defined as follows.

FIGURE 4

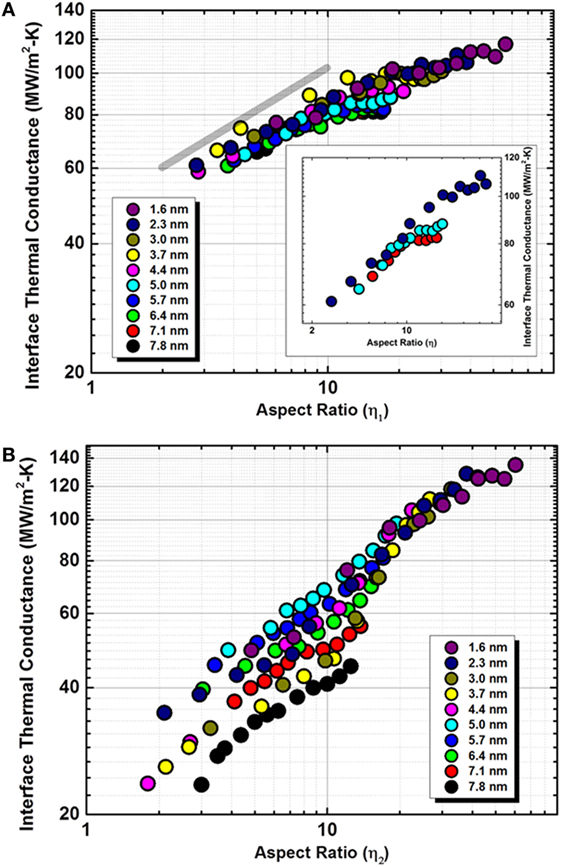
Figure 4. Log–log plots of SWCNTs interface thermal conductance (MW/m²-K) as a function of (A) interaction energy-based aspect ratio (η₁) and (B) geometrical aspect ratio (η₂) for different diameter CNTs. Data color scheme for different diameter SWCNTs is shown in legends. In (A), a power-law scaling of 1/3 is shown as a guide for the eye.

${\mathrm{\eta }}_1=\frac{L}{\sqrt{A_{\text{CNT}}}};{\mathrm{\eta }}_2=\frac{\text{L}}{\text{D}},$ (3)

where η₁ and η₂ are the aspect ratios calculated from the interaction energy derived area and simple geometric considerations, respectively. For η₁, $\sqrt{A_{\text{CNT}}}$ signifies a lateral length scale (a.k.a. effective diameter) of interaction for the aspect ratio calculation. Figure 4A shows the interface thermal conductance (Λ₂), calculated using an effective area (A_CNT), as a function of interaction area based aspect ratio η₁. On the contrary, Figure 4B shows the noticeably different interface thermal conductance $\left({\Lambda }_2^{\text{'}}\right)$, calculated using geometric area (πD²/4), as a function of geometric aspect ratio η₂. In order to show a fair comparison in calculated values of thermal conductance, both figures are plotted on the same ordinate and abscissa scales in Figure 4.

It is fascinating to note the collapse of all data points onto a single master curve in Figure 4A. For SWCNTs, we postulate that the aspect ratio manifests itself as a measure of the ability of low-frequency phonon modes to transport thermal energy across the junction. It is the combination of (a) more number of non-longitudinal low-frequency phonon microstates with increase in length (χ_LM↑) and (b) lower probability of effective coupling between high-frequency optical and low-frequency non-longitudinal modes with increase in diameter (χ_LM↓), which leads to observed dependence of normalized thermal conductance with respect to aspect ratio. Figure 4A also shows a power-law scaling guideline of 1/3. While at low aspect ratios, the scaling seems fitting, the inset of Figure 4A clearly shows the deviation and eventual Λ₂ saturation at higher aspect ratios, suggesting that after a certain aspect ratio, longer CNT lengths do not modify interface thermal conductance. In contrast, when the same data is plotted in terms of geometrically calculated values of ${\Lambda }_2^{\text{'}}$ and η₂ in Figure 4B, considerable scatter in the data is observed. This further validates that thermal conductance values and aspect ratios calculated using η₁ should be more appropriate than those based on η₂ as local deformation in the interacting region plays a significant role in thermal energy exchange, which is neglected in calculation of ${\Lambda }_2^{\text{'}}$ and η₂.

Effect of Chirality on Thermal Conductance

Given the variation in modeling different diameter SWCNTs with varying chiral angles (~6–30°) and noting the correlated trends in thermal conductance, the effects of chirality toward van-der Waals interactions-driven thermal conductance are expected to be minor. In order to confirm this, we performed additional simulations to investigate if SWCNTs have any chiral bias toward interface thermal conductance. Figure 5 plots the interface thermal conductance (Λ₂) for a series of simulations for SWCNTs with similar diameter (~2.7 nm) and the same length (~30 nm) but different chiral angles, varying from 0° (zigzag) to 30° (armchair). The figure does not put forward any clear trend or bias based on observed values of Λ₂ (and the associated standard error). Hence, it is interpreted that the chirality does not have any substantial effect on the interface thermal conductance in SWCNTs as long as the temperature discontinuity at the overlapped region is governed by phonons. Such a behavior concurs with the observation that the SWCNTs are only interacting through van-der Waals interactions which intrinsically do not have any directional character and are predominantly governed by a number of interacting atomic-pairs and the associated distances. We reiterate that our analysis is only focused on vibrational energy transfer due to the classical nature of MD simulations and does not consider contributions from electronic thermal transport. In metallic CNTs, however, (where n − m is a factor of 3; n and m being the chiral vectors), if electronic conduction is included, electron contribution to the thermal transport and the possible occurrence of electron–phonon coupling at the interface are expected to alter the thermal conductance behavior from Figure 5.

FIGURE 5

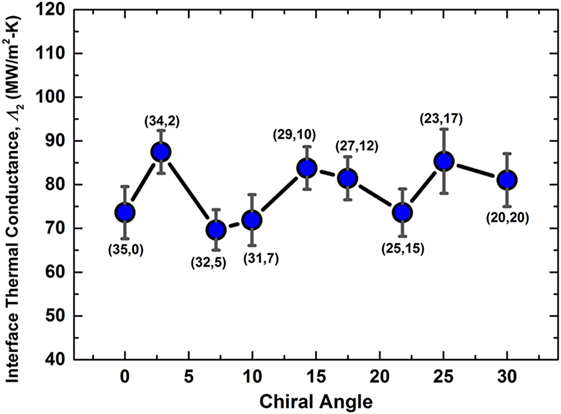
Figure 5. Plot of interface thermal conductance (MW/m²-K) showing the effect of chirality for several studied different chiral physically interacting SWCNTs (diameter ~2.7 nm). The specific chirality of SWCNTs is represented alongside the data points.

Effect of CNT Lateral Deformation on Thermal Conductance

The study of the lateral deformation of SWCNTs on the thermal energy exchange across the cross-contact requires a much larger parameter space (deformation provides an additional dimension in addition to CNT length and diameter). Thus, for all deformation simulations, the length of the CNTs was fixed to be 30 nm. Figure 6 shows the calculated thermal conductance (Λ₂) values as a function of interaction energy for 7.8 nm diameter CNT for different deformed shapes, which are also shown for visualization purposes. From the deformed shapes, it is evident that interaction energy increases with higher deformation. Since the interaction energy is reflective of the effective area of interaction (Eq. 2), it is appropriately chosen as abscissa to quantify the degree of deformation. The figure clearly shows that for CNTs under different degrees of deformation, Λ₂ decreases with increase in interaction area, suggesting that as the interface gets flatter, the increase in thermal energy exchange is less than proportional to the increase in interaction area.

FIGURE 6

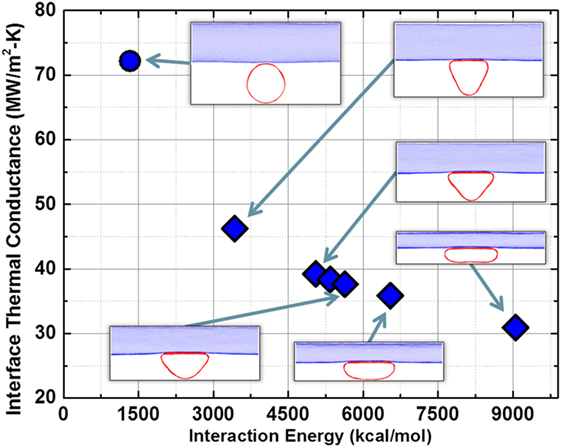
Figure 6. Plot of interface thermal conductance (MW/m²-K) as a function of interaction energy between physically interacting 7.8 nm SWCNT pair for different degrees of deformation. Schematics of CNTs’ deformed shapes in equilibrium are also shown alongside data points for better visualization. The deformed shape of the blue CNT looks similar to red CNT when looked along “its” axial direction. The circle data point corresponds to un-deformed CNT while diamonds correspond to deformed CNTs to be consistent with legends of Figures 7–9.

This important observation is further validated in Figure 7 which plots the Λ₁ (main figure) and Λ₂ (inset) vs. interaction energy (E) for all studied deformed CNTs’ contacts. The guideline in the main figure shows that for deformed cases, Λ₁ ∝ ~E^α where α ~ 2/3. Figure 8 re-plots the data for both Λ₁ and Λ₂ as a function of aspect ratio, η₁ with respective power-law guidelines. For both figures, it is fascinating to observe the collapse of all data for CNTs with different diameters for both Λ₁ and Λ₂ (in the inset) onto a single master-curve, signifying a possible correlation between the interaction energy, degree of deformation and the thermal conductance. Given α being ~2/3, different power-law scaling values as shown in Figures 7 and 8 can be easily deduced through the relationship between Λ₁, Λ₂, E, and η₁. We should point out that the power-law guidelines are only shown for highlighting the data trends and should not be treated as predicted power-law scaling. In fact, in both figures, it is not difficult to observe the deviations of the data points from the power-law guidelines at higher E and η₁.

FIGURE 7

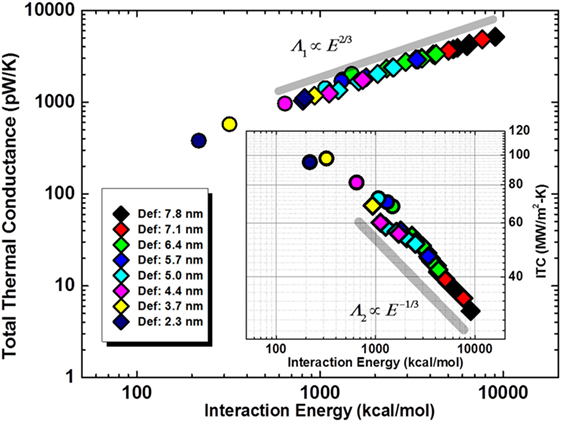
Figure 7. Plots of total thermal conductance (pW/K) and interface thermal conductance (MW/m²-K) (in inset) as a function of interaction energy between physically interacting SWCNTs. Data color scheme for different diameter SWCNTs is shown in legends. The circular data points represent corresponding SWCNTs in their un-deformed state. As a guide for the eye, a power-law scaling guidelines of 2/3 and −1/3 are shown in main figure and inset figure, respectively.

FIGURE 8

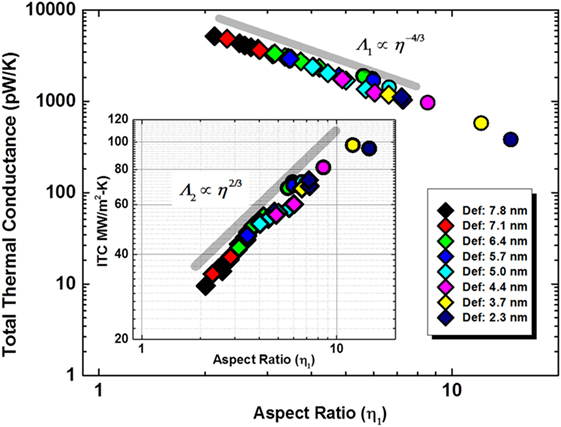
Figure 8. Plots of total thermal conductance (pW/K) and interface thermal conductance (MW/m²-K) (in inset) as a function of interaction energy-based SWCNT aspect ratio. Data color scheme for different diameter SWCNTs is shown in legends. The circular data points represent corresponding SWCNTs in their deformed state. As a guide for the eye, a power-law scaling guidelines of −4/3 and 2/3 are shown in main figure and inset figure, respectively.

The trends in Figures 6–8 clearly suggest that under deformation at fixed CNT length, the increase in interaction energy does not increase proportionally with thermal energy exchange (i.e., α < 1). We argue that this trend is indicative of decrease in effectiveness of χ_LM toward the thermal energy exchange across CNT contact. As previously discussed, the effectiveness of χ_LM is determined by three factors; (a) number density of low-frequency transverse and radial phonons; (b) total number of phonon modes; and (c) the conversion probability (or effectiveness) of high energy optical modes to low energy transverse, radial, and flexural modes. We argue that for CNT contacts with constant length and diameter, the non-symmetrical deformation of CNT tubule (with respect to axis) notably hinders the conversion efficiency (factor c as noted above) of optical phonons to be scattered to low-frequency non-longitudinal modes that carry thermal energy from hot to cold CNT, which in turn results in decrease of χ_LM and lead to the observed behavior of α < 1.

Figure 9 plots the Λ₂ as a function of η₁ for the studied un-deformed as well as deformed SWCNTs cases to compare relative Λ₂ values and the corresponding aspect ratio dependence. In addition, it also plots similar data for planar graphene nano-ribbons interface thermal conductance, studied previously (Varshney et al., 2014). The figure highlights several important findings in addition to what has been discussed previously. First, it is fascinating to observe that regardless of the carbon nanostructure being studied (deformed or un-deformed CNTs, graphene nano-ribbons), there exists a master-curve for Λ₂ as a function of η₁ for each of them. It shows the importance of aspect ratio as well as interaction energy-based interaction area in determining Λ₂. Second, the Λ₂ dependence on η₁ is notably sharper for deformed CNTs than un-deformed CNTs. Third, for a given aspect ratio, Λ₂ is always higher for CNTs than that of graphene nano-ribbons. Finally, as the CNTs are deformed and become flatter (graphene-like) near the interacting zone (see Figure 6), they are also approaching graphene nano-ribbon Λ₂ values, especially when the aspect ratio is small.

FIGURE 9

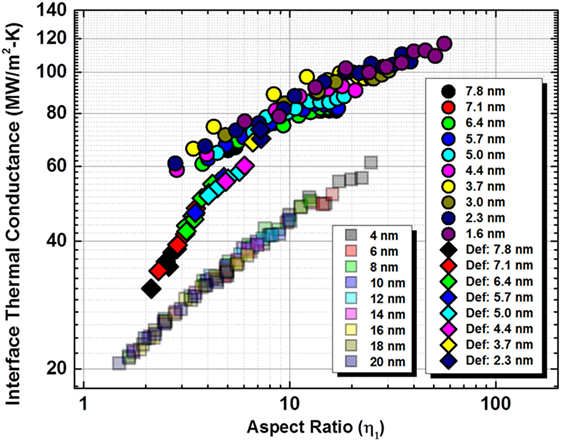
Figure 9. Plots of SWCNT interface thermal conductance (MW/m²-K) as a function of interaction energy-based aspect ratio for deformed SWCNTs (diamonds), un-deformed SWCNTs (circles), and graphene nano-ribbons (squares) (Varshney et al., 2014). Data color scheme for different diameter un-deformed and deformed SWCNTs as well as graphene nano-ribbons (ribbon width) are shown in legends.

Effect of Tensile Strain on Thermal Conductance

Figure 10 shows the predicted interface thermal conductance values (Λ₂) for different degrees of tensile strain along CNT’s axial direction with respect to unstrained CNTs. Also depicted in the figure are a couple of schematic snapshots of strained systems in the equilibrated geometry for visualization purposes. It is expected that CNTs become significantly stiffer with tensile strain due to stiffening of C–C bonds. It was recently shown that graphene ZO (out-of-plane) optical mode (~20 THz) gets shifted to higher frequency while applying in-plane tensile strain (Varshney et al., 2014). We foresee a similar increase in frequency of low energy modes for CNTs under applied strain. Recently, Chen et al. also showed similar trends in decrease in interface thermal conductance across axially stretched very thin (6, 6) SWCNT pair. They suggested that blue shifted phonons (higher frequency) phonon must be scattered to lower frequency phonons (<25 THz) in order to effectively transport thermal energy (Chen et al., 2017). In addition, we also suggest that the stiffening due to axial stretching is expected to increase the group velocity of the phonons and increase their effective mean free path. This, in turn, relatively lessens the number of anharmonic phonon–phonon scattering events (because of higher mean free path and reduce the overall scattering probability of high energy modes to low-frequency modes), also lowering the effective phonon interaction time (because of higher group velocity) across the junction. We argue that both factors contribute toward observed lowering of normalized thermal conductance with increasing tensile strain. We should point out that while testing compressive simulations for thermal transport simulations, a collapse of a SWCNT pair near the interaction zone was observed during equilibration (please see additional schematic). Hence, Λ₂ calculations were not pursued for compressive strain cases.

FIGURE 10

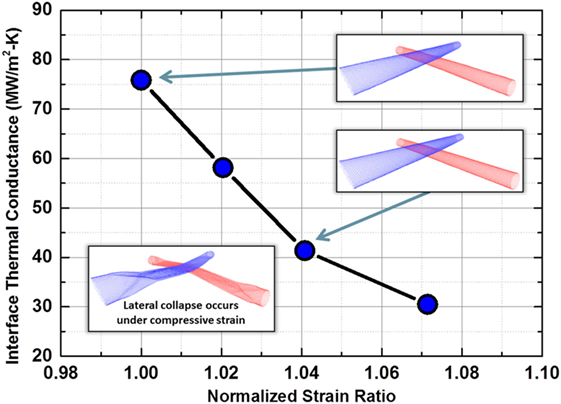
Figure 10. Plot of interface thermal conductance (MW/m²-K) as a function of tensile and compressive strain in physically interacting SWCNTs (diameter ~5.0 nm). Schematic equilibrium geometries are also shown for a few data points for better visualization.

Summary and Conclusion

This study showcases several contact thermal conductance trends which can be effectively employed for thermal contact behavior analysis in CNT-based nanoelectronic device designs as well as predicting effective thermal properties of SWCNT-based nanocomposites. While the absolute values of interface thermal conductance in MD simulations are an evident function of the force field employed, the observed trends and master-curves in the current study do demonstrate a few important points. When the interconnects/contact dimensions are of a few nanometer length scales, a single value of thermal conductance for CNTs appears to be an improper term. As seen from the different simulations, several factors—diameter, length, strain, as well as degree of deformation—play significant roles toward the determination of both total and area-normalized thermal conductance across the CNT contact. Among several parameters, SWCNT aspect ratio (based on interaction energy calculation), number of low-frequency phonons interacting across the interface and effectiveness of their generation from high energy optical modes emerge as the governing parameters toward determining thermal conductance values for both deformed and un-deformed interfaces. Other parameters such as their orientation with respect to the contact and their equilibrium geometry at the temperature region of interest (higher temperature may lead to more deformed SWCNTs due to higher fluctuations) should be considered as well while measuring device performance. At the same time, CNT chirality is shown to have a negligible effect on the phonon-governed thermal conductance at the contact.

Finally, it is important to note that from the standpoint of nanoelectronic device designs, single contacts between SWCNTs are more often to be encountered where it is impossible to accurately define the constriction area of CNT contact through which thermal energy exchange is occurring. In such cases, although it is theoretically possible to estimate the area-normalized thermal conductance values (Λ₂) across physically interacting SWCNT contacts for understanding fundamental mechanisms, total thermal conductance (Λ₁) should be of primary consideration when comparing data between experimental measurements and simulation predictions.

Author Contributions

VV and AR conceived the problem. VV and JB conducted the research. VV, JL, JB, and AR prepared the manuscript. AV and BF provided their guidance during the course of the study as well as provided significantly valuable comments during the preparation of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful to Department of Defense Supercomputing Research Center (AFRL-DSRC) for the computational resources to carry out the simulations.

Funding

US Air Force Office of Scientific Research (AFOSR): Task 15RXCOR140 (Program Manager: Dr. Jamie Tiley) Task 14RW02COR (Program Manager: Dr. Byung-Lip (Les) Lee).

References

Allen, A. C., Sunden, E., Cannon, A., Graham, S., and King, W. (2006). Nanomaterial transfer using hot embossing for flexible electronic devices. Appl. Phys. Lett. 88, 083112. doi: 10.1063/1.2178414

CrossRef Full Text | Google Scholar

Artukovic, E., Kaempgen, M., Hecht, D. S., Roth, S., and Grüner, G. (2005). Transparent and flexible carbon nanotube transistors. Nano Lett. 5, 757–760. doi:10.1021/nl050254o

PubMed Abstract | CrossRef Full Text | Google Scholar

Avouris, P., and Xia, F. (2012). Graphene applications in electronics and photonics. MRS Bull. 37, 1225–1234. doi:10.1557/mrs.2012.206

CrossRef Full Text | Google Scholar

Behnam, A., Sangwan, V. K., Zhong, X., Lian, F., Estrada, D., Jariwala, D., et al. (2013). High-field transport and thermal reliability of sorted carbon nanotube network devices. ACS Nano 7, 482–490. doi:10.1021/nn304570u

PubMed Abstract | CrossRef Full Text | Google Scholar

Bui, K., Grady, B. P., and Papavassiliou, D. V. (2011). Heat transfer in high volume fraction CNT nanocomposites: effects of inter-nanotube thermal resistance. Chem. Phys. Lett. 508, 248–251. doi:10.1016/j.cplett.2011.04.005

CrossRef Full Text | Google Scholar

Bui, K., Nguyen, H., Cousin, C., Striolo, A., and Papavassiliou, D. V. (2012). Thermal behavior of double-walled carbon nanotubes and evidence of thermal rectification. J. Phys. Chem. C 116, 4449–4454. doi:10.1021/jp2107878

CrossRef Full Text | Google Scholar

Cao, Q., and Han, S.-J. (2013). Single-walled carbon nanotubes for high-performance electronics. Nanoscale 5, 8852–8863. doi:10.1039/C3NR02966B

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Q., Han, S. J., Tulevski, G. S., Zhu, Y., Lu, D. D., and Haensch, W. (2013). Arrays of single-walled carbon nanotubes with full surface coverage for high-performance electronics. Nat. Nanotechnol. 8, 180–186. doi:10.1038/nnano.2012.257

PubMed Abstract | CrossRef Full Text | Google Scholar

Chalopin, Y., Volz, S., and Mingo, N. (2009). Upper bound to the thermal conductivity of carbon nanotube pellets. J. Appl. Phys. 105, 084301. doi:10.1063/1.3088924

CrossRef Full Text | Google Scholar

Chandra, B., Park, H., Maarouf, A., Martyna, G. J., and Tulevski, G. S. (2011). Carbon nanotube thin film transistors on flexible substrates. Appl. Phys. Lett. 99, 072110. doi:10.1063/1.3622767

CrossRef Full Text | Google Scholar

Chen, W., Yang, J., Wei, Z., Liu, C., Bi, K., and Chen, Y. (2017). Axial tensile strain effects on the contact thermal conductance between cross contacted single-walled carbon nanotubes. J. Appl. Phys. 121, 054310. doi:10.1063/1.4975466

CrossRef Full Text | Google Scholar

Chen, W., Zhang, J., and Yue, Y. (2016). Molecular dynamics study on thermal transport at carbon nanotube interface junctions: effects of mechanical force and chemical functionalization. Int. J. Heat Mass Transfer 103, 1058–1064. doi:10.1016/j.ijheatmasstransfer.2016.08.016

CrossRef Full Text | Google Scholar

Chortos, A., Koleilat, G. I., Pfattner, R., Kong, D., Lin, P., Nur, R., et al. (2016). Mechanically durable and highly stretchable transistors employing carbon nanotube semiconductor and electrodes. Adv. Mater. 28, 4441–4448. doi:10.1002/adma.201501828

CrossRef Full Text | Google Scholar

Clancy, T. C., and Gates, T. S. (2006). Modeling of interfacial modification effects on thermal conductivity of carbon nanotube composites. Polymer 47, 5990–5996. doi:10.1016/j.polymer.2006.05.062

CrossRef Full Text | Google Scholar

Cola, B. A., Xu, J., Cheng, C., Xu, X., Fisher, T. S., and Hu, H. (2007). Photoacoustic characterization of carbon nanotube array thermal interfaces. J. Appl. Phys. 101, 054313. doi:10.1063/1.2510998

CrossRef Full Text | Google Scholar

Engel, M., Small, J. P., Steiner, M., Freitag, M., Green, A. A., Hersam, M. C., et al. (2008). Thin film nanotube transistors based on self-assembled, aligned, semiconducting carbon nanotube arrays. ACS Nano 2, 2445–2452. doi:10.1021/nn800708w

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, W. J., and Keblinski, P. (2010). Thermal conductivity of carbon nanotube cross-bar structures. Nanotechnology 21, 475704. doi:10.1088/0957-4484/21/47/475704

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, W. J., Shen, M., and Keblinski, P. (2012). Inter-tube thermal conductance in carbon nanotubes arrays and bundles: effects of contact area and pressure. Appl. Phys. Lett. 100, 261908. doi:10.1063/1.4732100

CrossRef Full Text | Google Scholar

Gengler, J. J., Shenogin, S. V., Bultman, J. E., Roy, A. K., Voevodin, A. A., and Muratore, C. (2012). Limited thermal conductance of metal-carbon interfaces. J. Appl. Phys. 112, 094904. doi:10.1063/1.4764006

CrossRef Full Text | Google Scholar

Gharib-Zahedi, M. R., Tafazzoli, M., Bohm, M. C., and Alaghemandi, M. (2013). Transversal thermal transport in single-walled carbon nanotube bundles: influence of axial stretching and intertube bonding. J. Chem. Phys. 139, 184704. doi:10.1063/1.4828942

PubMed Abstract | CrossRef Full Text | Google Scholar

Hashim, D. P., Narayanan, N. T., Romo-Herrera, J. M., Cullen, D. A., Hahm, M. G., Lezzi, P., et al. (2012). Covalently bonded three-dimensional carbon nanotube solids via boron induced nanojunctions. Sci. Rep. 2, 363. doi:10.1038/srep00363

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, G.-J., and Cao, B.-Y. (2013). Thermal resistance between crossed carbon nanotubes: molecular dynamics simulations and analytical modeling. J. Appl. Phys. 114, 224308. doi:10.1063/1.4842896

CrossRef Full Text | Google Scholar

Hu, L., and McGaughey, A. J. H. (2014). Thermal conductance of the junction between single-walled carbon nanotubes. Appl. Phys. Lett. 105, 193104. doi:10.1063/1.4902074

CrossRef Full Text | Google Scholar

Hu, M., Keblinski, P., Wang, J.-S., and Raravikar, N. (2008). Interfacial thermal conductance between silicon and a vertical carbon nanotube. J. Appl. Phys. 104, 083503. doi:10.1063/1.3000441

CrossRef Full Text | Google Scholar

Huxtable, S. T., Cahill, D. G., Shenogin, S., Xue, L., Ozisik, R., Barone, P., et al. (2003). Interfacial heat flow in carbon nanotube suspensions. Nat. Mater. 2, 731–734. doi:10.1038/nmat996

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishikawa, F. N., Chang, H.-K., Ryu, K., Chen, P.-C., Badmaev, A., Gomez De Arco, L., et al. (2008). Transparent electronics based on transfer printed aligned carbon nanotubes on rigid and flexible substrates. ACS Nano 3, 73–79. doi:10.1021/nn800434d

CrossRef Full Text | Google Scholar

Kim, J. W., Sauti, G., Siochi, E. J., Smith, J. G., Wincheski, R. A., Cano, R. J., et al. (2014). Toward high performance thermoset/carbon nanotube sheet nanocomposites via resistive heating assisted infiltration and cure. ACS Appl. Mater. Interfaces 6, 18832–18843. doi:10.1021/am5046718

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, K. H., Oh, Y., and Islam, M. F. (2012). Graphene coating makes carbon nanotube aerogels superelastic and resistant to fatigue. Nat. Nanotechnol. 7, 562–566. doi:10.1038/nnano.2012.118

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S., Murthy, J. Y., and Alam, M. A. (2007). Computational model for transport in nanotube-based composites with applications to flexible electronics. J. Heat Transfer 129, 500–508. doi:10.1115/1.2709969

CrossRef Full Text | Google Scholar

Lau, P. H., Takei, K., Wang, C., Ju, Y., Kim, J., Yu, Z., et al. (2013). Fully printed, high performance carbon nanotube thin-film transistors on flexible substrates. Nano Lett. 13, 3864–3869. doi:10.1021/nl401934a

CrossRef Full Text | Google Scholar

Lee, J., Varshney, V., Roy, A. K., and Farmer, B. L. (2011). Single mode phonon energy transmission in functionalized carbon nanotubes. J. Chem. Phys. 135, 104109. doi:10.1063/1.3633514

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, A., Alizadegan, R., Ong, Z.-Y., Dutta, S., Xiong, F., Hsia, K. J., et al. (2010). Thermal dissipation and variability in electrical breakdown of carbon nanotube devices. Phys. Rev. B 82, 205406. doi:10.1103/PhysRevB.82.205406

CrossRef Full Text | Google Scholar

Liao, D., Chen, W., Zhang, J., and Yue, Y. (2017). Tuning thermal conductance of CNT interface junction via stretching and atomic bonding. J. Phys. D Appl. Phys. 50, 475302. doi:10.1088/1361-6463/aa8ff8

CrossRef Full Text | Google Scholar

Liu, J., Alhashme, M., and Yang, R. (2012). Thermal transport across carbon nanotubes connected by molecular linkers. Carbon N. Y. 50, 1063–1070. doi:10.1016/j.carbon.2011.10.014

CrossRef Full Text | Google Scholar

Liu, N., Yun, K. N., Yu, H.-Y., Shim, J. H., and Lee, C. J. (2015). High-performance carbon nanotube thin-film transistors on flexible paper substrates. Appl. Phys. Lett. 106, 103106. doi:10.1063/1.4914400

CrossRef Full Text | Google Scholar

Ma, P.-C., Siddiqui, N. A., Marom, G., and Kim, J.-K. (2010). Dispersion and functionalization of carbon nanotubes for polymer-based nanocomposites: a review. Compos. A Appl. S. 41, 1345–1367. doi:10.1016/j.compositesa.2010.07.003

CrossRef Full Text | Google Scholar

Marconnet, A. M., Panzer, M. A., and Goodson, K. E. (2013). Thermal conduction phenomena in carbon nanotubes and related nanostructured materials. Rev. Mod. Phys. 85, 1295–1326. doi:10.1103/RevModPhys.85.1295

CrossRef Full Text | Google Scholar

Maruyama, S., Igarashi, Y., Taniguchi, Y., and Shiomi, J. (2006). Anisotropic heat transfer of single-walled carbon nanotubes. J. Therm. Sci. Tech. 1, 138–148. doi:10.1299/jtst.1.138

CrossRef Full Text | Google Scholar

Meyyappan, M. (2004). Carbon Nanotubes: Science and Applications. New York: CRC Press.

Google Scholar

Ozden, S., Narayanan, T. N., Tiwary, C. S., Dong, P., Hart, A. H., Vajtai, R., et al. (2015a). 3D macroporous solids from chemically cross-linked carbon nanotubes. Small 11, 688–693. doi:10.1002/smll.201402127

CrossRef Full Text | Google Scholar

Ozden, S., Tiwary, C. S., Hart, A. H., Chipara, A. C., Romero-Aburto, R., Rodrigues, M. T., et al. (2015b). Density variant carbon nanotube interconnected solids. Adv. Mater. 27, 1842–1850. doi:10.1002/adma.201404995

CrossRef Full Text | Google Scholar

Park, S., Vosguerichian, M., and Bao, Z. (2013). A review of fabrication and applications of carbon nanotube film-based flexible electronics. Nanoscale 5, 1727–1752. doi:10.1039/c3nr33560g

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Pop, E., Varshney, V., and Roy, A. K. (2012). Thermal properties of graphene: fundamentals and applications. MRS Bull. 37, 1273–1281. doi:10.1557/mrs.2012.203

CrossRef Full Text | Google Scholar

Prasher, R. (2008). Thermal boundary resistance and thermal conductivity of multiwalled carbon nanotubes. Phys. Rev. B 77, 075424. doi:10.1103/PhysRevB.77.075424

CrossRef Full Text | Google Scholar

Prasher, R. S., Hu, X. J., Chalopin, Y., Mingo, N., Lofgreen, K., Volz, S., et al. (2009). Turning carbon nanotubes from exceptional heat conductors into insulators. Phys. Rev. Lett. 102, 105901. doi:10.1103/PhysRevLett.102.105901

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, K., Radha, B., Smith, K. C., Fisher, T. S., and Kulkarni, G. (2013). Solution-processed soldering of carbon nanotubes for flexible electronics. Nanotechnology 24, 075301. doi:10.1088/0957-4484/24/7/075301

PubMed Abstract | CrossRef Full Text | Google Scholar

Rong, Q., Shao, C., and Bao, H. (2017). Molecular dynamics study of the interfacial thermal conductance of multi-walled carbon nanotubes and van der Waals force induced deformation. J. Appl. Phys. 121, 054302. doi:10.1063/1.4975032

CrossRef Full Text | Google Scholar

Roy, A. K., Farmer, B. L., Varshney, V., Sihn, S., Lee, J., and Ganguli, S. (2012). Importance of interfaces in governing thermal transport in composite materials: modeling and experimental perspectives. ACS Appl. Mater. Interfaces 4, 545–563. doi:10.1021/am201496z

PubMed Abstract | CrossRef Full Text | Google Scholar

Saito, R., Dresselhaus, G., and Dresselhaus, M. S. (1998). Physical Properties of Carbon Nanotubes. London: Imperial College Press.

Google Scholar

Salaway, R. N., and Zhigilei, L. V. (2016). Thermal conductance of carbon nanotube contacts: molecular dynamics simulations and general description of the contact conductance. Phys. Rev. B 94, 014308. doi:10.1103/PhysRevB.94.014308

CrossRef Full Text | Google Scholar

Schiessl, S. P., Frohlich, N., Held, M., Gannott, F., Schweiger, M., Forster, M., et al. (2014). Polymer-sorted semiconducting carbon nanotube networks for high-performance ambipolar field-effect transistors. ACS Appl. Mater. Interfaces 7, 682–689. doi:10.1021/am506971b

CrossRef Full Text | Google Scholar

Shenogin, S., Xue, L., Ozisik, R., Keblinski, P., and Cahill, D. G. (2004). Role of thermal boundary resistance on the heat flow in carbon-nanotube composites. J. Appl. Phys. 95, 8136–8144. doi:10.1063/1.1736328

CrossRef Full Text | Google Scholar

Sun, H., Mumby, S. J., Maple, J. R., and Hagler, A. T. (1994). An ab initio CFF93 all-atom force field for polycarbonates. J. Am. Chem. Soc. 116, 2978–2987. doi:10.1021/ja00086a030

CrossRef Full Text | Google Scholar

Varshney, V., Lee, J., Farmer, B. L., Voevodin, A. A., and Roy, A. K. (2014). Modeling of cross-plane interface thermal conductance between graphene nano-ribbons. 2D Mater. 1, 025005. doi:10.1088/2053-1583/1/2/025005

CrossRef Full Text | Google Scholar

Varshney, V., Lee, J., Li, D., Brown, J. S., Farmer, B. L., Voevodin, A. A., et al. (2017). Understanding thermal conductance across multi-wall carbon nanotube contacts: role of nanotube curvature. Carbon N. Y. 114, 15–22. doi:10.1016/j.carbon.2016.11.056

CrossRef Full Text | Google Scholar

Varshney, V., Lee, J., Roy, A. K., and Farmer, B. L. (2011). Modeling of interface thermal conductance in longitudinally connected carbon nanotube junctions. J. Appl. Phys. 109, 084913. doi:10.1063/1.3560914

CrossRef Full Text | Google Scholar

Varshney, V., Patnaik, S. S., Roy, A. K., and Farmer, B. L. (2010). Modeling of thermal conductance at transverse CNT−CNT interfaces. J. Phys. Chem. C 114, 16223–16228. doi:10.1021/jp104139x

CrossRef Full Text | Google Scholar

Varshney, V., Roy, A. K., Dudis, D. S., Lee, J., and Farmer, B. L. (2012). A novel nano-configuration for thermoelectrics: helicity induced thermal conductivity reduction in nanowires. Nanoscale 4, 5009–5016. doi:10.1039/C2NR30602F

PubMed Abstract | CrossRef Full Text | Google Scholar

Volkov, A. N., Salaway, R. N., and Zhigilei, L. V. (2013). Atomistic simulations, mesoscopic modeling, and theoretical analysis of thermal conductivity of bundles composed of carbon nanotubes. J. Appl. Phys. 114, 104301. doi:10.1063/1.4819911

CrossRef Full Text | Google Scholar

Wang, C., Takei, K., Takahashi, T., and Javey, A. (2013). Carbon nanotube electronics – moving forward. Chem. Soc. Rev. 42, 2592–2609. doi:10.1039/c2cs35325c

CrossRef Full Text | Google Scholar

Xu, Z., and Buehler, M. J. (2009). Nanoengineering heat transfer performance at carbon nanotube interfaces. ACS Nano 3, 2767–2775. doi:10.1021/nn9006237

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, Y., Nishiyama, T., Yasuhara, T., and Takahashi, K. (2012). Thermal boundary conductance between multi-walled carbon nanotubes. J. Therm. Sci. Tech. 7, 190–198. doi:10.1299/jtst.7.190

CrossRef Full Text | Google Scholar

Yang, J., Shen, M., Yang, Y., Evans, W. J., Wei, Z., Chen, W., et al. (2014a). Phonon transport through point contacts between graphitic nanomaterials. Phys. Rev. Lett. 112, 205901. doi:10.1103/PhysRevLett.112.205901

CrossRef Full Text | Google Scholar

Yang, X., Chen, D., Han, Z., Ma, X., and To, A. C. (2014b). Effects of welding on thermal conductivity of randomly oriented carbon nanotube networks. Int. J. Heat Mass Transfer 70, 803–810. doi:10.1016/j.ijheatmasstransfer.2013.11.071

CrossRef Full Text | Google Scholar

Yang, J., Waltermire, S., Chen, Y., Zinn, A. A., Xu, T. T., and Li, D. (2010). Contact thermal resistance between individual multiwall carbon nanotubes. Appl. Phys. Lett. 96, 023109. doi:10.1063/1.3292203

CrossRef Full Text | Google Scholar

Zhong, H., and Lukes, J. R. (2006). Interfacial thermal resistance between carbon nanotubes: molecular dynamics simulations and analytical thermal modeling. Phys. Rev. B 74, 125403. doi:10.1103/PhysRevB.74.125403

CrossRef Full Text | Google Scholar