- Department of Mechanical Engineering, Centre for Advanced Structural Materials, City University of Hong Kong, Kowloon Tong, Hong Kong
Lattice distortion in high entropy alloys (HEAs) is an issue of fundamental importance but yet to be fully understood. In this article, we first focus on the recent research dedicated to lattice distortion in HEAs with an emphasis on the basic understanding derived from theoretical modeling and atomistic simulations. After that, we discuss the implications of the recent research findings on lattice distortion, which can be related to the phase transformation, dislocation dynamics and yielding in HEAs.
Introduction
Since first proposed in 2004, high entropy alloys (HEAs) or multicomponent complex alloys, which comprise at least five different elements in an equal or near-equal atomic fraction, have been attracting a great deal of research interest (Cantor et al., 2004; Yeh et al., 2004; Ye et al., 2016b; Miracle and Senkov, 2017). Many attractive mechanical and physical properties were reported from various HEAs, such as the combined high strength and ductility from CoCrFeMnNi (Li et al., 2016), the exceptional damage tolerance from CoCrNi and CoCrFeMnNi at cryogenic temperatures (Gludovatz et al., 2014, 2016; Zhang et al., 2015b), high ion irradiation resistance (Zhang et al., 2015a; Yang et al., 2016), and the superb specific hardness from Al20Li20Mg10Sc20Ti30 (Youssef et al., 2015). At the fundamental level, these promising properties could be attributed to the unique local atomic structure of HEAs. Due to the mixing of different sized elements in a concentrated solution, it was once speculated that the constituent atoms in HEAs will be displaced away from the ideal lattice sites, resulting in an atomic scale distorted lattice or an intrinsic elastic residual stress field which fluctuates from one atom to another. As a result, local lattice distortion will raise the energy barrier against dislocation movement, giving rise to solid-solution typed strengthening in HEAs (Cižek et al., 1974; Gypen and Deruyttere, 1977; Ma et al., 2015). Likewise, local lattice distortion may also cause sluggish atom diffusion, thereby promoting the thermodynamic stability of HEAs. In spite of the fundamental importance, however, lattice distortion in HEAs still remains as an open issue, yet to be fully understood (Pickering and Jones, 2016; Miracle and Senkov, 2017).
To validate the idea about lattice distortion, a number of experiments were proposed to characterize lattice distortion in HEAs (Yeh et al., 2007; Guo et al., 2013; Tsai and Yeh, 2014; Yeh, 2015; Owen et al., 2017; Tong et al., 2017). At the first attempt, X-Ray diffraction was used as the means of characterization (Yeh et al., 2007; Tsai and Yeh, 2014; Yeh, 2015) with the basic assumption that large lattice distortion would reduce the intensity of diffraction peaks. Although it was shown experimentally that the diffraction peak intensities did decrease with the increasing number of constituent elements in particular HEAs (Yeh et al., 2007; Tsai and Yeh, 2014; Yeh, 2015), the proof of lattice distortion so obtained was later disputed because of the confounding effects from thermal vibration and crystallographic texture on the diffraction peak intensity (Pickering and Jones, 2016). High resolution transmission electron microscopy (HRTEM) was also utilized to characterize lattice distortion (Zou et al., 2014). However, one should be cautious about the interpretation of a HRTEM image because a curved atomic plane on it may not be associated with lattice distortion, which could be also caused by a strain field around crystalline defects, such as dislocations. Recently, Owen et al. systematically studied lattice distortion in Ni, CrNi, CoCrNi, and CoCrFeMnNi through neutron diffraction (Owen et al., 2017). Although it was shown that the lattice strain in CoCrFeMnNi is larger than in pure Ni, however, the magnitude of the lattice strain is not significant and similar to that in CrNi and CoCrNi. Similarly, Tong et al. also carried out a quantitatively analysis of the local lattice distortion in CoCrFeNi, CoCrFeMnNi, CoCrFeNiPd HEAs using the X-ray total scattering and extended X-ray absorption fine structure methods (Tong et al., 2017). According to Tong et al. (Tong et al., 2017), the lattice distortion in CoCrFeNi and CoCrFeMnNi is very small but becomes larger in CoCrFeNiPd owing to the relatively large size of Pd. Besides, Guo et al. characterized the local atomic structure of ZrNbHf using high-energy synchrotron X-ray and neutron scattering. Interestingly, they found that the ZrNbHf lattice is strongly distorted (Guo et al., 2013).
Apart from the above experimental efforts, a number of lattice distortion models (Zhang et al., 2008; Ye et al., 2015, 2016a, 2018) were also developed either on a semi-empirical basis or in the light of atomistic simulations (Toda-Caraballo et al., 2015; Oh et al., 2016; Ye et al., 2018) and ab initio calculations (Song et al., 2017). In conventional alloys or dilute solid solution, lattice distortion and the resultant residual strain field can be derived by treating solute atoms as “inclusions” embedded into a “matrix” made up of solvent atoms (Eshelby, 1956, 1957, 1959). However, this approach finds difficulties when it is applied to HEAs as there is no clear distinction between solutes and solvents. As the first attempt, Zhang et al. proposed to use an atomic size difference parameter δ to characterize lattice distortion in HEAs, although only on a qualitative basis (Zhang et al., 2008). In theory, Zhang's proposal is based on the notion of the hard sphere model in which the atomic size of the constituent elements remains to be constant during alloying. Alternatively, Ye et al. developed a geometric model to account for the intrinsic residual strains in HEAs by treating their constituent atoms as soft or deformable spheres which could be stretched out or squeezed in a common lattice in order to reach a uniform packing efficiency (Ye et al., 2015, 2016a). As a result, a local volumetric strain field arises due to the change of the atom size. Recently, Ye et al. refined the geometric model by taking account of atomic displacement (Ye et al., 2018). In this new model, both volumetric and shear strains are derived and the model predictions agree quite well with the results of the first principles calculations. In this work, we would like to provide a brief overview of the recent advancement with respect to our understanding of lattice distortion in HEAs and discuss the implications of these research findings.
Discussion
Hard Sphere Model
In the early HEA literature, the idea of “severely distorted lattice” was proposed as one of the “four core effects” for HEAs (Yeh, 2015; Macdonald et al., 2017). This idea may be rooted into the hard sphere model, as schematically shown in Figure 1, i.e., if all constituent elements keep their original size and are forced into a common lattice, a severely distorted lattice may result if a large atom size difference is present. To characterize such an atomic size effect in HEAs, Zhang et al. proposed to use the following δ parameter (Zhang et al., 2008):
in which ci is the atomic fraction of element i, ri the atomic radius of element i and n the total number of constituent elements. Later, the δ parameter was widely accepted as one of the empirical parameters to guide the design of HEAs because of the apparently good correlation between the value of the δ parameter and the general character of the phases formed in HEAs (Zhang et al., 2008; Guo and Liu, 2011; Ye et al., 2016b; He et al., 2017), seen Figure 2. However, the δ parameter fails when it comes to an accurate estimation of local lattice distortions. According to the simulation work of Song et al. (2017), the δ parameter tends to overestimate the lattice distortion in refractory HEAs while underestimate those in HEAs with 3d valence electrons. This may be partly due to the empirical nature of the δ parameter. Nevertheless, when it comes to ranking different HEAs, it is somewhat a surprise that the δ parameter performs very well as it is generally correlated with the HEA alloys of different phases (see Figure 2).
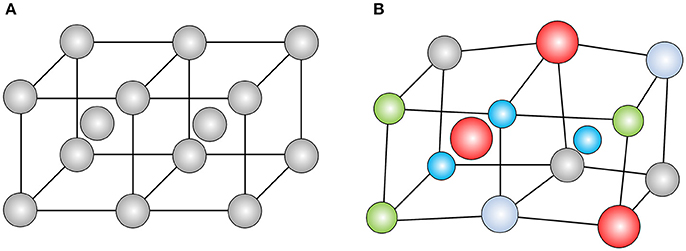
Figure 1. The illustrations of (A) a perfect BCC lattice in pure metals and (B) a distorted BCC lattice in multicomponent alloys.
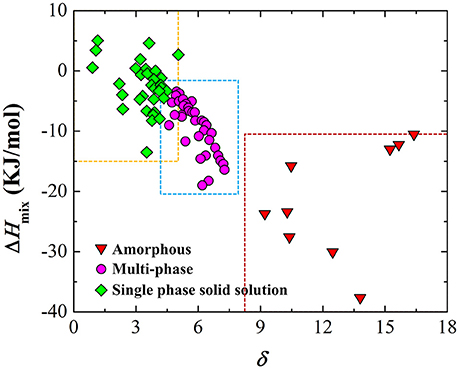
Figure 2. The atom size difference parameter δ vs. the mixing enthalpy ΔHmix for a variety of as-cast HEAs with different phases.
Soft Sphere Model
In principle, atoms in alloys are deformable in the sense that charge can transfer among the constituent atoms, leading to the change in their atomic radii (Magnaterra and Mezzetti, 1971) and therefore the residual strain field inside the alloys. On a phenomenological basis, such a residual strain field in conventional alloys can be derived with the classic mean field model (Eshelby, 1956, 1957, 1959). According to the mean field approach, residual strains result after “forcing” a solute atom into a homogeneous elastic “matrix” made up of solvent atoms. However, this mean field approach is not applicable directly to HEAs because of the lack of a clear distinction between solute and solvent atoms in them. Different from the classic mean field approach, Ye et al. proposed that different sized atoms should be stretched or squeezed into the lattice of HEAs in order to achieve a uniform packing efficiency, as illustrated in Figure 3A. As a result, there is a change in the atomic radii of the constituent elements relative to their original sizes, leading to a volumetric residual strain field. This physical picture differs fundamentally from the hard sphere model (Figure 1). According to Ye et al. (2015), the lattice in HEAs is not distorted but well behaved as implied by the sharp diffraction peaks exhibited by HEAs. However, residual volumetric strains are developed because of the change in the atomic radii even through the average residual strain is about zero. Assuming that the overall packing efficiency of an alloy is , the radial residual strain εi surrounding the ith element can be derived as:
where ωij is the solid angle subtended by an atom j around atom i, ci the atomic fraction of element i, Ni the coordinate number of atom i and Aij= where xij=ri/rj. Since the average volumetric strain , the local residual strain fluctuation can be quantified as εRMS=, where εRMS is the root-mean-square residual strain and scales with the density of the elastic strain energy storage. Theoretically, it can be proved that the lattice of FCC alloys becomes unstable and could turn into an amorphous structure by fully relaxing the stored elastic energy if or into another crystalline lattice by partially relaxing the stored elastic energy if . Through the analyses of hundreds of HEAs, Ye et al. found that single phase solid solution HEAs tend to form for εRMS < 5%, multi-phase HEAs to form for 5% < εRMS < 10% while amorphous alloys to for εRMS > 10% (see Figure 4), which agrees fairly well with the theory. Interestingly, it was also found that εRMS is correlated very well with the δ parameter, as seen in Figure 5, which may explain why the δ parameter is so useful in alloy ranking despite its empirical nature.
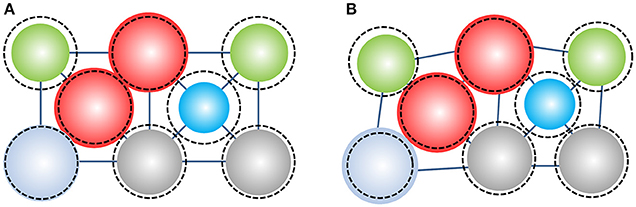
Figure 3. The schematics of (A) close packed atoms in a well-defined lattice with volumetric strain (B) close packed atoms in a distorted lattice with volumetric and shear strains. Note that the color balls represent the original constituent atoms while the dashed circles donate the profile of atoms with residual strains.
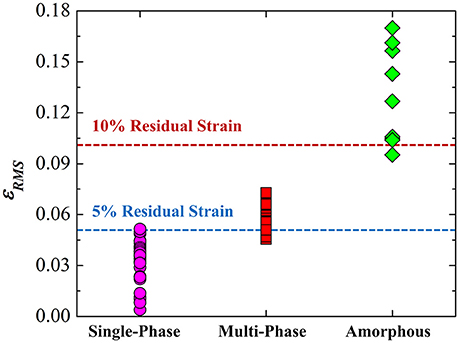
Figure 4. The root-mean-square residual strain εRMS for a variety of as-cast HEAs with difference phases.
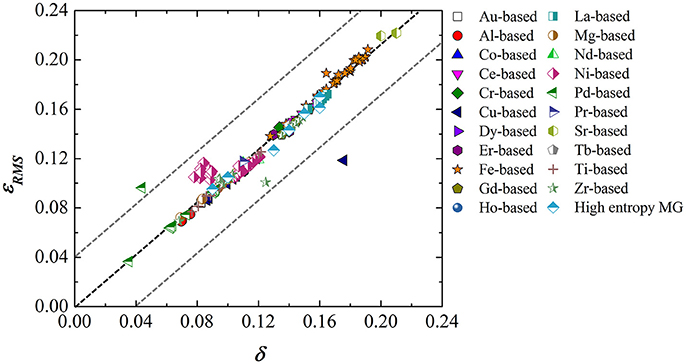
Figure 5. The correlation between the root-mean-square residual strain εRMS and atomic size difference δ for a variety of metallic glass (MG)-forming alloys.
In the soft sphere model developed by Ye et al. (2015), only atomic size change is considered by assuming that the individual atoms sit exactly on an ideal lattice. Next, the question is what if we allow the atoms to move from their ideal position. This atom movement is a reflection of lattice distortion, as shown in Figure 1B, which could generate both shear and dilatational strains, therefore raising the total elastic energy by an amount ΔE1; however, the same atom movement could also release part of the elastic energy caused by the atomic size change as previously discussed, say, by ΔE2, as seen in Figure 3B. Physically, one can reason that lattice distortion becomes generically favorable if ΔE1 < ΔE2 or unfavorable if ΔE1 > ΔE2. To validate the above thinking, Ye et al. very recently carried out extensive density functional theory (DFT) calculations on a series of equal-molar binary to quinary chemical complex alloys (Ye et al., 2018). An ideal FCC lattice without distortion was firstly constructed by allowing the atoms to expand or contract in order to reach a local energy minimum. This lattice is designated as the pristine lattice and serves as a reference to study lattice distortion. After that, the “pristine” lattice was allowed to further relax through the atomic displacement, leading to a distorted lattice as schematically shown in Figure 3B. Figure 6 displays the simulated atomic structure of the CoCrFeNi alloy before and after lattice distortion. As indicate by the red arrows in Figures 6A,B, the “pristine” lattice exhibit a well-defined FCC structure while notable local atomic-scale distortions can be seen in the distorted lattice (Figure 6B). To quantify the local lattice distortion, the strain tensors at each atomic site can be calculated via the atomic displacement field, which show considerably fluctuating local strains in various HEAs even though their average values are close to zero (Ye et al., 2018). To capture the overall effect of such local strain fluctuations, an effective shear strain was defined as:
where C11, C12, C44 are elastic constants, the local hydrostatic strain and the von Mises local shear strain invariant, , , the shear strain components at different directions. The effective shear strain is closely related to the local atomic environment and varies from one atom to another. As a result, the elastic strain energy change ΔEp induced by shear displacement can be derived as:
where n is the total number of atoms; is defined as the average equivalent strain. As such, we obtain ΔE1= and ΔE2=, in which and εRMS represent the root-mean-square residual strain in the distorted and pristine lattice respectively. In theory, lattice distortion is energetically favorable if the following condition is met:
For a first order approximation, one can assume that is correlated linearly with εRMS via , where α is a parameter to be determined. By minimizing the energy difference (Equation 5), one can obtain the following formula for the critical effective shear strain for an isotropic system:
where υ is the Poisson ratio. Equation (6) is important, which correlates the effective shear strain, which measures the degree of lattice distortion, with the atomic size difference (the δ parameter) that can be easily calculated for HEAs. Furthermore, it delivers a strong message that the critical effective shear strain γth depends not only on the magnitude of atomic size difference but also on the Poisson ratio of an alloy. Before moving to the next section, it is worth pointing out that the pristine lattice structures all display sharp FCC diffraction peaks, as seen in Figure 7. By comparison, the diffraction peaks of the distorted lattices look similar to those of the pristine lattices (Figures 7A,B). However, as lattice distortion, or the value of the effective strain, increases, the diffraction peak profile of the distorted lattice exhibits peak broadening and even peak splitting, particularly so for the high angle peaks (Figures 7C,D). Furthermore, a careful examination of the diffraction peaks of both pristine and distorted lattice shows that both lattices share a similar lattice constant, which is consistent with the recent finding reported by Song et al. (2017).
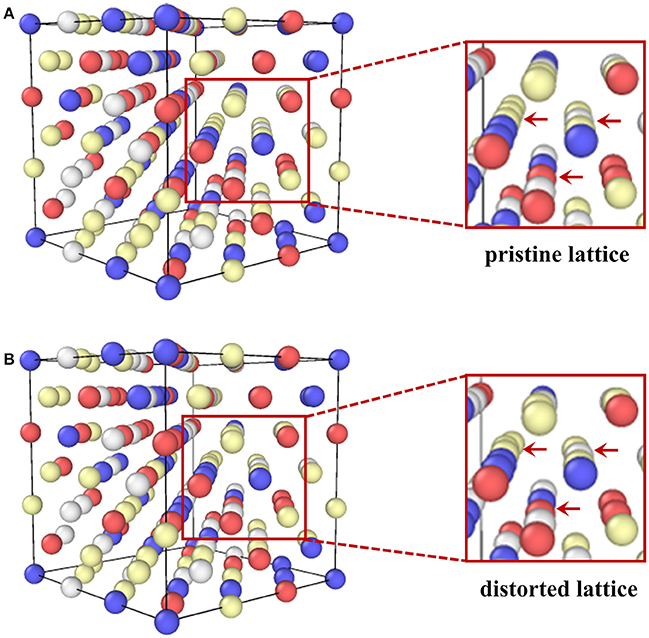
Figure 6. The DFT simulation results of (A) the pristine lattice with an ideal FCC structure and (B) the distorted lattice of the CoCrFeNi alloy.
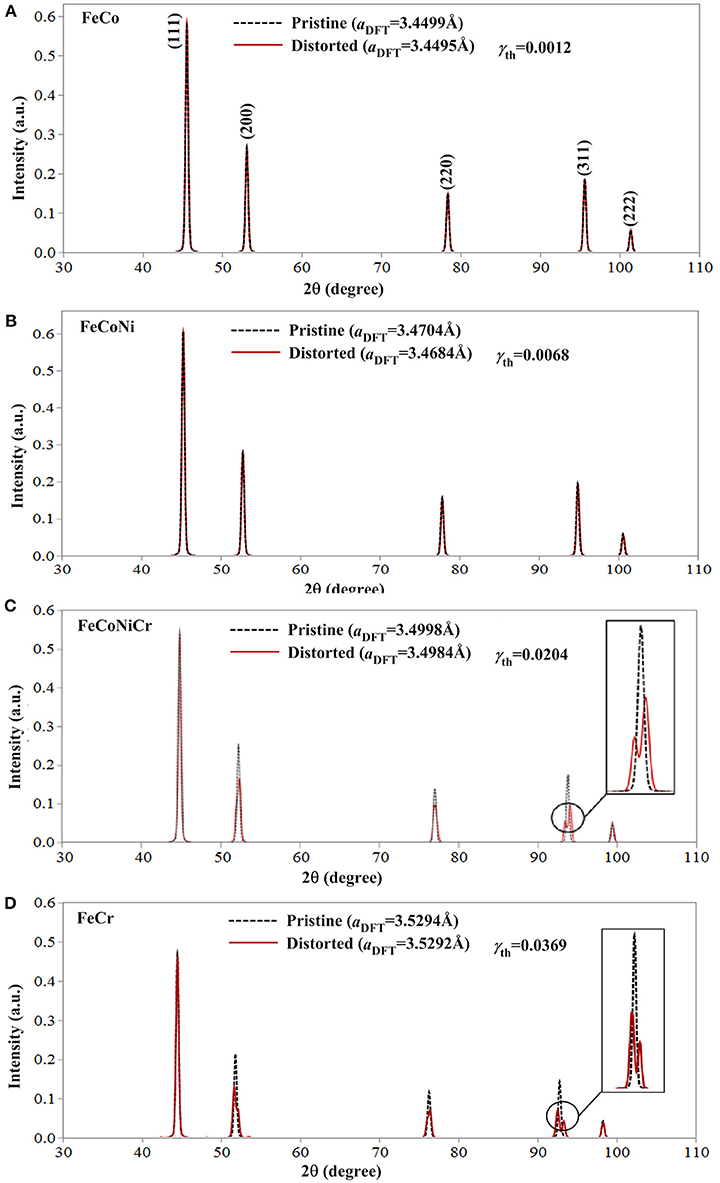
Figure 7. The simulated XRD results of pristine (black dash line) and distorted lattice (red solid line) of (A) FeCo, (B) FeCoNi, (C) FeCoNiCr, and (D) FeCr with a FCC structure. With the increasing of the average effective shear strain, diffraction peak splitting occurs implicative of lattice distortion.
Implication
Now let us discuss the possible influence of lattice distortion on the mechanical and physical properties of HEAs. In principle, lattice distortion and the resultant residual stress field can interact with dislocations, thereby leading to significant strengthening (Oh et al., 2016; Varvenne et al., 2016; Owen et al., 2017). In conventional alloys with a regular lattice, dislocation movements need to overcome the Peierls friction or the lattice stress through a kink-pair mechanism (Hirth and Lothe, 1982), as illustrated in Figure 8A. In general, this leads to a rather small activation volume, on the order of several b3, where b is the magnitude of burgers vector. However, the dislocation line in a distorted lattice could be tortuous and wavy because of the presence of an intrinsic stress field. This is similar to dislocation pinning as it moves through a forest of obstacles (Figure 8B). According to Wu et al. (Wu et al., 2016), such a pinning effect is weak and should appeal to the classic Labusch model, which was developed for the weak pinning effect of a “forest” of solute atoms on gliding dislocations (Labusch, 1970, 1972). Compared to the kink-pair mechanism, dislocation gliding in a highly distorted lattice may involve a large activation volume, as schematically shown in Figure 8B, which may affect the strain rate sensitivity and the high temperature performance of these alloys.
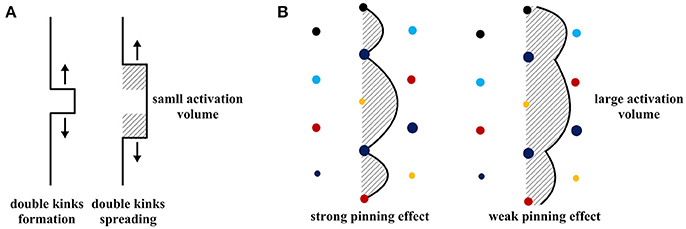
Figure 8. (A) Dislocation gliding via kink-pair mechanisms in an ideal lattice. (B) Wavy dislocation gliding in a distorted lattice in chemical complex alloys.
Summary
To summarize, a brief overview of lattice distortion in HEAs was provided in this work. When alloying different sized elements into a common lattice, a residual strain field with atomic scale fluctuation will be induced by the atomic size difference and the elastic modulus misfit of the constituent elements. The residual strain field comprises both volumetric and shear components, which exhibit a large spreading as captured by the recently developed theoretical model. However, the average value of the residual strains is very small, resulting in almost a same lattice constant for both pristine and distorted lattices. The magnitude of the fluctuation of the residual strains, which can be deemed as a measure of the lattice distortion, depends on not only the atomic size but also the Poisson ratio of an alloy.
Author Contributions
QH and YY discussed and wrote the paper together.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor is currently co-organizing a Research Topic with one of the authors, YY, and confirms the absence of any other collaboration.
Acknowledgments
The research of YY is supported by the City University of Hong Kong with the project Nos 9610366 and 7004597.
References
Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. 375–377, 213–218. doi: 10.1016/j.msea.2003.10.257
Cižek, L., Kratochvíl, P., and Smola, B. (1974). Solid solution hardening of copper crystals. J. Mater. Sci. 9, 1517–1520. doi: 10.1007/BF00552938
Eshelby, J. D. (1956). “The continuum theory of lattice defects,” in Solid State Physics, eds F. Seitz and D. Turnbull (Cambridge, MA: Academic Press), 79–144.
Eshelby, J. D. (1957). The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. 241:376. doi: 10.1098/rspa.1957.0133
Eshelby, J. D. (1959). The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. Ser. 252, 561–569. doi: 10.1098/rspa.1959.0173
Gludovatz, B., Hohenwarter, A., Catoor, D., Chang, E. H., George, E. P., and Ritchie, R. O. (2014). A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158. doi: 10.1126/science.1254581
Gludovatz, B., Hohenwarter, A., Thurston, K. V., Bei, H., Wu, Z., George, E. P., et al. (2016). Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat. Commun. 7:10602. doi: 10.1038/ncomms10602
Guo, S., and Liu, C. T. (2011). Phase stability in high entropy alloys: formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. 21, 433–446. doi: 10.1016/S1002-0071(12)60080-X
Guo, W., Dmowski, W., Noh, J.-Y., Rack, P., Liaw, P. K., and Egami, T. (2013). Local atomic structure of a high-entropy alloy: an X-ray and neutron scattering study. Metal. Mater. Trans. 44, 1994–1997. doi: 10.1007/s11661-012-1474-0
Gypen, L. A., and Deruyttere, A. (1977). Multi-component solid solution hardening. J. Mater. Sci. 12, 1028–1033. doi: 10.1007/BF00540987
He, Q. F., Ding, Z. Y., Ye, Y. F., and Yang, Y. (2017). Design of high-entropy alloy: a perspective from nonideal mixing. JOM 69, 2092–2098. doi: 10.1007/s11837-017-2452-1
Labusch, R. (1970). A statistical theory of solid solution hardening. Phys. Stat. Solid 41, 659–669. doi: 10.1002/pssb.19700410221
Labusch, R. (1972). Statistische theorien der mischkristallhärtung. Acta Metallurg. 20, 917–927. doi: 10.1016/0001-6160(72)90085-5
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D., and Tasan, C. C. (2016). Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 534:227. doi: 10.1038/nature17981
Ma, D., Friák, M., Von Pezold, J., Raabe, D., and Neugebauer, J. (2015). Computationally efficient and quantitatively accurate multiscale simulation of solid-solution strengthening by ab initio calculation. Acta Mater. 85, 53–66. doi: 10.1016/j.actamat.2014.10.044
Macdonald, B. E., Fu, Z., Zheng, B., Chen, W., Lin, Y., Chen, F., et al. (2017). Recent progress in high entropy alloy research. JOM 69, 2024–2031. doi: 10.1007/s11837-017-2484-6
Magnaterra, A., and Mezzetti, F. (1971). Charge transfer in binary alloys. Il Nuovo Cimento B 6, 206–213. doi: 10.1007/BF02735386
Miracle, D. B., and Senkov, O. N. (2017). A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511. doi: 10.1016/j.actamat.2016.08.081
Oh, H., Ma, D., Leyson, G., Grabowski, B., Park, E., Körmann, F., et al. (2016). Lattice distortions in the FeCoNiCrMn high entropy alloy studied by theory and experiment. Entropy 18:321. doi: 10.3390/e18090321
Owen, L. R., Pickering, E. J., Playford, H. Y., Stone, H. J., Tucker, M. G., and Jones, N. G. (2017). An assessment of the lattice strain in the CrMnFeCoNi high-entropy alloy. Acta Mater. 122, 11–18. doi: 10.1016/j.actamat.2016.09.032
Pickering, E. J., and Jones, N. G. (2016). High-entropy alloys: a critical assessment of their founding principles and future prospects. Int. Mater. Rev. 61, 183–202. doi: 10.1080/09506608.2016.1180020
Song, H., Tian, F., Hu, Q.-M., Vitos, L., Wang, Y., Shen, J., et al. (2017). Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 1:023404. doi: 10.1103/PhysRevMaterials.1.023404
Toda-Caraballo, I., Wróbel, J. S., Dudarev, S. L., Nguyen-Manh, D., and Rivera-Díaz-Del-Castillo, P. E. J. (2015). Interatomic spacing distribution in multicomponent alloys. Acta Mater. 97, 156–169. doi: 10.1016/j.actamat.2015.07.010
Tong, Y., Velisa, G., Yang, T., Jin, K., Lu, C., Bei, H., et al. (2017). Probing local lattice distortion in medium-and high-entropy alloys. arXiv [preprint] arXiv:1707.07745.
Tsai, M.-H., and Yeh, J.-W. (2014). High-entropy alloys: a critical review. Mater. Res. Lett. 2, 107–123. doi: 10.1080/21663831.2014.912690
Varvenne, C., Luque, A., and Curtin, W. A. (2016). Theory of strengthening in fcc high entropy alloys. Acta Mater. 118, 164–176. doi: 10.1016/j.actamat.2016.07.040
Wu, Z., Gao, Y., and Bei, H. (2016). Thermal activation mechanisms and Labusch-type strengthening analysis for a family of high-entropy and equiatomic solid-solution alloys. Acta Mater. 120, 108–119. doi: 10.1016/j.actamat.2016.08.047
Yang, T., Xia, S., Liu, S., Wang, C., Liu, S., Fang, Y., et al. (2016). Precipitation behavior of AlxCoCrFeNi high entropy alloys under ion irradiation. Sci. Rep. 6:32146. doi: 10.1038/srep32146
Ye, Y. F., Liu, C. T., and Yang, Y. (2015). A geometric model for intrinsic residual strain and phase stability in high entropy alloys. Acta Mater. 94, 152–161. doi: 10.1016/j.actamat.2015.04.051
Ye, Y. F., Liu, X. D., Wang, S., Liu, C. T., and Yang, Y. (2016a). The general effect of atomic size misfit on glass formation in conventional and high-entropy alloys. Intermetallics 78, 30–41. doi: 10.1016/j.intermet.2016.08.005
Ye, Y. F., Wang, Q., Lu, J., Liu, C. T., and Yang, Y. (2016b). High-entropy alloy: challenges and prospects. Mater. Today 19, 349–362. doi: 10.1016/j.mattod.2015.11.026
Ye, Y. F., Zhang, Y. H., He, Q. F., Zhuang, Y., Wang, S., Shi, S. Q., et al. (2018). Atomic-scale distorted lattice in chemically disordered equimolar complex alloys. Acta Mater. 150, 182–194. doi: 10.1016/j.actamat.2018.03.008
Yeh, J.-W. (2015). Physical metallurgy of high-entropy alloys. JOM 67, 2254–2261. doi: 10.1007/s11837-015-1583-5
Yeh, J.-W., Chang, S.-Y., Hong, Y.-D., Chen, S.-K., and Lin, S.-J. (2007). Anomalous decrease in X-ray diffraction intensities of Cu–Ni–Al–Co–Cr–Fe–Si alloy systems with multi-principal elements. Mater. Chem. Phys. 103, 41–46. doi: 10.1016/j.matchemphys.2007.01.003
Yeh, J. W., Chen, S. K., Lin, S. J., Gan, J. Y., Chin, T. S., Shun, T. T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303. doi: 10.1002/adem.200300567
Youssef, K. M., Zaddach, A. J., Niu, C., Irving, D. L., and Koch, C. C. (2015). A novel low-density, high-hardness, high-entropy alloy with close-packed single-phase nanocrystalline structures. Mater. Res. Lett. 3, 95–99. doi: 10.1080/21663831.2014.985855
Zhang, Y., Sachan, R., Pakarinen, O. H., Chisholm, M. F., Liu, P., Xue, H., et al. (2015a). Ionization-induced annealing of pre-existing defects in silicon carbide. Nat. Commun. 6:8049. doi: 10.1038/ncomms9049
Zhang, Y., Zhou, Y. J., Lin, J. P., Chen, G. L., and Liaw, P. K. (2008). Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 10, 534–538. doi: 10.1002/adem.200700240
Zhang, Z., Mao, M. M., Wang, J., Gludovatz, B., Zhang, Z., Mao, S. X., et al. (2015b). Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi. Nat. Commun. 6:10143. doi: 10.1038/ncomms10143
Keywords: high entropy alloy, lattice distortion, theoretical modeling, first principles calculation, solid solution strengthening
Citation: He Q and Yang Y (2018) On Lattice Distortion in High Entropy Alloys. Front. Mater. 5:42. doi: 10.3389/fmats.2018.00042
Received: 10 April 2018; Accepted: 04 July 2018;
Published: 24 July 2018.
Edited by:
Sheng Guo, Chalmers University of Technology, SwedenReviewed by:
Fuyang Tian, University of Science and Technology Beijing, ChinaFuxiang Zhang, Oak Ridge National Laboratory (DOE), United States
Copyright © 2018 He and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Quanfeng He, cXVhbmZlbmhlMi1jQG15LmNpdHl1LmVkdS5oaw==
Yong Yang, eW9ueWFuZ0BjaXR5dS5lZHUuaGs=
 Quanfeng He
Quanfeng He Yong Yang
Yong Yang