- School of Minerals and Energy Resources Engineering, The University of New South Wales, Sydney, NSW, Australia
Analytical solutions of limit analysis design for the simple problem of plane strain expansion of a cylindrical cavity are derived and generalized into entropic extremum principles that allow a fundamental assessment of coupled thermal/hydro/mechanical/chemical (THMC) material instabilities and their effect on the upper and lower bounds of dissipation. The proposed approach integrates a thermodynamically based estimation of uncertainties in coupled deformation processes and an identification of the intrinsic material length/time scales that appear as energy eigenstates of the localization problem. Analytical limit analysis design solutions of the cavity expansion are obtained and upper and lower bound estimates are shown to coincide. This provides a robust framework for adding multiphysics feedbacks. Isothermal conditions are first relaxed and the feedback between shear heating, thermal weakening and thermal diffusion is analyzed. Then the analysis is extended to a full range of THMC localization phenomena which are described with a cascade of characteristic time/length scales derived from instabilities in the governing reaction-diffusion equations. Entropic uncertainties are estimated by alternating system constraints between thermodynamic flux and thermodynamic force on the boundaries.
1. Introduction
In this paper we extend the classical upper and lower bound principle of plastic work (“limit analysis design”) into an uncertainty framework for multiphysics coupling. We propose that in such problems the same method can be extended through assessing the steady state limit of the deformation process and evaluating the upper and lower bounds of entropy production. In order to demonstrate the extended limit analysis design we choose the simple problem of cavity expansion, which is widespread through all disciplines. Its universal nature is encountered in geomechanics, metal forming processes, tunneling, soil mechanics with many other applications in geotechnical, petroleum, civil, mining, material, energy, mechanical and manufacturing engineering (Johnson et al., 1983; Papamichos et al., 2001; Haimson, 2007; Fjar et al., 2008; Meier et al., 2013; François et al., 2014; Hu et al., 2017). Figure 1 shows an example of borehole breakout in hollow-cylinder tests for black shale where the area around the hole is damaged through an application of internal pressure (Meier et al., 2013). Meanwhile, radial expansion of a round cavity is mathematically appealing as closed form solutions can be derived due to its cylindrical symmetry (Johnson et al., 1983; Hu et al., 2017).
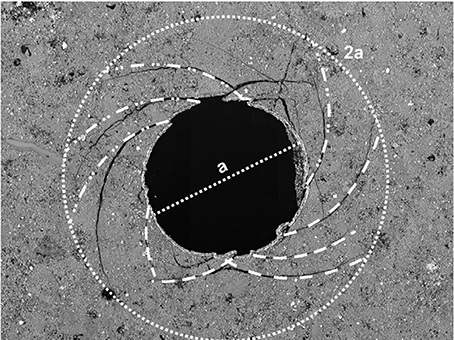
Figure 1. Shear localization pattern in the form of logarithmic spirals observed in hole enlargement experiments on black shale (Meier et al., 2013).
Slip-line field theory of plasticity, as an upper bound solution of limit analysis design, has been extensively studied since the rise of the second industrial revolution (featuring mass production and manufacturing) in early twentieth century, due to its convenience in yield estimation for metals (e.g., punching, extrusion, indentation) and its neatness in graphical presentation. Nadai (1950) systematically studied the theory of plastic flow in solids and showed that slip-lines are orthogonal families of logarithmic spirals around a hole or the tip of a cylindrical notch. Hill (1950) provided the first rigorous description of plastically deformed solids from a mathematical point of view and provided the context of slip-line field theory in terms of an upper bound of plastic work. Johnson et al. (1983) summarized the slip-line field theory for plane strain conditions and emphasized its practical applications. Recent advances in numerical techniques have cultivated fusion of this theory with adjacent domains, for example a phase-field model (Freddi and Royer-Carfagni, 2016) correlating the generalized fracture theory (Freddi and Royer-Carfagni, 2010) with the slip-line field of plasticity based on variational principles.
This paper focuses on the uncertainty quantification of analytical and numerical solutions of the cavity expansion process within an entropic framework (Andresen, 2018). Uncertainty arises due to the path dependence of the time integration of dissipation and the resulting total amount of work that is required to expand the cavity. This inherent non-uniqueness of the plasticity problem (Bigoni and Hueckel, 1991a,b) has been dealt with in the past through upper and lower bound theorems. We use the analytical solutions in comparison with numerical solutions as an ideal illustrator for the validity of fundamental theories, and the potential for benchmarking numerical codes is discussed.
The upper and lower bound theorems are useful for the quasi-static scenarios where time does not play a role and the process of cavity expansion is independent of the rate of the expansion mechanism. In many operations of impact studies the rate effects are dynamic and influenced by material inertia controlled by the expansion velocity (Masri and Durban, 2006). We discuss here the case of slow deformation where kinetic energy is negligible and the deformation is in the so-called creeping flow regime. In this case, the classical thermomechanical approach is expanded into a thermodynamic approach where the evolution of the deformation is entirely controlled by the time dependence of the thermal energy fluxes. We show in this paper that the temperature equation is incorporating a number of thermal-mechanical feedback mechanism which are due to multi-physics phenomena such as phase transformations, thermo-elastic effects or chemical reactions. For the creeping flow regime the limit analysis design can be generalized into a limit theorem for entropy production (Regenauer-Lieb et al., 2010). This provides an expansion of the classical limit analysis design into more complicated modeling scenarios that allow assessment of multiphysics interactions and multiscale modeling of the cavity expansion problem and other creeping flow elasto-visco-plastic processes.
2. Thermodyamics Origins of Path Dependence
First, we go through a brief review of thermomechanics. State variables are used to describe the mathematical state of a dynamic system, which means a state variable remains the same when the system completes a complete cycle in the Entropy-Temperature space, such as the Carnot cycle. Considering a continuum element, there are a set of state variables that uniquely define the thermo-mechanical state of this element, for example the strain tensor ϵij (assuming small deformation), temperature T, internal variables αk.
The first law of thermodynamics states that the change in the internal energy of a closed system dU is equal to the amount of work done to the system δW plus the amount of heat supplied to the system δQ that is:
The internal energy U is a state function (i.e., dU is a proper differential) while δW and δQ are not, implying path dependence upon taking an integration over time. In the following we will denote complete differential with respect to time by over-dots, while we refer to over-tilde to denote incomplete differentials where the path dependence of dissipation is embedded.
The second law of thermodynamics states that the increment in heat supplied to the system δQ is no larger than the product of absolute temperature T and entropy increase of the system dS, that is the heat supply is bounded from above: δQ ≤ TdS. Both T and S are state functions. If equality holds the process is reversible, meaning the system, in this case a continuum element, is in equilibrium or a steady state.
The total entropy increment of the system can be decomposed into reversible and irreversible parts:
where the reversible component is usually referred to as the “entropy supply,” meaning the entropy transfer inside the system may lead to the transfer of entropy through reversible processes from one portion to another of the interior defined as . The irreversible component of the entropy increment is referred to as “entropy production” and is non-negative by definition: . Entropy production is due to irreversible processes via dissipation occurring within a continuum element.
The Helmholtz free energy Ψ depends on state variables only, and can be expressed by a simple function of internal energy, absolute temperature and entropy:
Then we have
Hence, substituting for in Equation (1) and using the entropy decomposition in Equation (2) thus expanding the basic work equation can be written as
where the first term on the right hand side of the equation denotes the rate change in Helmholtz free energy; the second term corresponds to the change in temperature during deformation processes, which vanishes under isothermal conditions; the third term defines the dissipated power, which is the source of uncertainty brought into the system by different loading paths/methods.
In other words, during a deformation process both the Helmholtz free energy and the thermal changes are fully integrable in time, however, the irreversible entropy production is not. To overcome the uncertainty of path dependence it is useful to consider an extremum value of the last term. We emphasize in the following that there is no preference, from a thermodynamic point of view, over the choice of a maximum or minimum value. The uncertainty cannot be removed by either choice without additional assumptions. Deformation problems are inherently time dependent. However, with the assumption of infinite time for the deformation process and no work free plastic deformation the problem of uncertainty of dissipation is bracketed from above.
Under infinite time condition the diffusion of heat away from the deformation zone and the heat production through mechanical work inside the deformation zone can be assumed to reach a steady state equilibrium. If a steady state exists it results in isothermal conditions for the zone of deformation. This allows dropping the second term in Equation (5). If we now choose the upper bound of the third term as the suitable extremum one obtains the well-known maximum irreversible entropy production or maximum dissipation assumption as the suitable extremum. Ziegler (1983) did just this and visualized both the first and last terms, i.e., the Helmholtz free energy and the irreversible entropy production as potential functions. He showed that the maximum irreversible entropy production leads to the orthogonality principle. The hypothesis of maximum irreversible entropy production functions applies to a wide range of applications where general plasticity theory is involved. The orthogonality assumption prescribes that the strain rate vector is always normal to the yield surface. Although Ziegler's maximum entropy principle may still hold for certain materials that demonstrate properties of weakly non-convex yield surface or non-associated plastic flow (Houlsby and Puzrin, 2007), it confronts difficulties when dealing with complex multi-physics coupled systems. To do so, we explore the possibilities of other entropic bounds in the light of Limit Analysis Design considering two types of system constraints. In what follows we first summarize the classical limit theorems, then apply them to the cavity expansion problems and finally suggest to extend the theorems for generalized THMC processes.
3. Limit Theorems: The Case of Cavity Expansion
3.1. Mathematical Description of Bounding Theorems
Limit analysis is widely used in many engineering design problems that are subject to static or dynamic mechanical loadings, due to its advantage of providing a quick estimate of critical values without full simulation of the process. Bounding theories for the mechanics of deformable bodies are based on the virtual work laws, which origin from the concept of least action required in a mechanical system (Hill, 1950; Johnson et al., 1983). In this subsection, σij and vi are used to describe the involved stress and velocity field inside rigid plastic bodies, yielding with prescribed surface tractions acting on part of the surface ST and prescribed velocities on part of the surface Sv.
The lower bound theorem or the static theorem states that a load factor for which a distribution of bending moments can be found which satisfy the equilibrium condition and the yield condition is less than or at most equal to the true value of the collapse load factor. Examples can be found in structural design for buildings or bridges where the designers look for the lowest bound of applied load to avoid any yield or collapse.
To derive the lower bound, we specify an equilibrium stress field σ*, which satisfies the traction boundary conditions on ST and nowhere violating the yield criterion. Virtual force is null on Sv and can only generate work on ST where surface tractions are applied. Then the principle of virtual work, also called the principle of virtual force, gives
where the superscript * denotes a force or stress field in equilibrium. k denotes the yield stress in shear, τ* the shear component of , the strain rate, [v] the velocity discontinuity on SD. On the right hand side of Equation (6), both terms are non-negative, via the second law of thermodynamics and the yield criterion τ* ≤ k, respectively. Hence we have the lower bound obtained from a statically admissible stress field:
The opposite engineering limit is encountered in situations where, contrary to the interest in the lower bound case, overall plastic yielding is desirable, for example in metal forming operations. This results in the upper bound approach which is extensively used in these applications as exact solutions for the applied force to induce unconstrained plastic flow are difficult to obtain. The upper bound theorem is also called a kinematic theorem as it requires a kinematically admissible velocity field that satisfies the boundary conditions. An additional constraint is that it satisfies plastic volume conservation and it states that the load factor obtained from the work equation written for any arbitrarily assumed mechanism is greater or equal to the true collapse load factor.
In the upper bound derivation, we specify a velocity field , which does not necessarily maintain stress equilibrium but satisfies the incompressibility requirements. The principle of virtual work now gives
where the superscript ** denotes a velocity or strain field satisfying volume conservation (i.e., an incompressible body). Let denote a stress field, not necessarily statically admissible but required to produce plastic flow. Based on the second law of thermodynamics,
Substituting Equation (9) and the yield criterion τ ≤ k into Equation (8), we have
Considering on Sv, the upper bound is obtained:
In a summary, the lower bound solution for a pure mechanical system, Equation (7), considers a statically admissible plastic stress field and disregards the displacement field. It can be obtained from imposing traction boundary conditions, while the upper bound solution according to Equation (11) is derived from velocity boundary conditions based on volume conservation. In the discussion section we propose to generalize the lower and upper bound principles for THMC processes in terms of their entropy production, and the system constraints become thermodynamic forces and thermodynamic fluxes, respectively.
3.2. Lower Bound Approach—Stress Equilibrium
For the lower bound solution, based on Equation (7), we consider a simple axisymmetric cavity expansion scenario with constant force applied on the interior (r = a) and traction-free boundary condition on the exterior (r = b), as illustrated in Figure 2. Plane strain conditions are assumed.
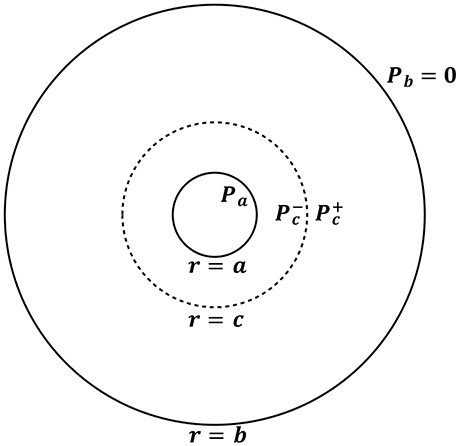
Figure 2. Sketch of a classical cavity expansion problem with constant stress Pa applied on the cavity. The exterior boundary (r = b) is assumed traction-free.
In the elastic zone (c < r < b),
The stress equilibrium equation gives
In the plastic zone (a < r < c), the plane-strain von Mises criterion gives
Substituting Equation (14) into Equation (13), we have
With the assumption of stress continuity on the interface of the outer elastic zone and the inner plastic zone, we derive the following relationships at r = c. Substituting Equation (12a) and Equation (12b) into criterion (14), we have
where Pc can be obtained via Equation (15):
With the assumption of stress continuity, i.e., , we have
If we assume an infinite outer boundary (i.e., the outer radius b is sufficiently large), c2/b2 vanishes. Hence,
3.3. Upper Bound Approach—Extremum/Work Principles
For the upper bound solution, we derive based on the slip-line field theory of plasticity (Hill, 1950; Nadai, 1950). The deformation of an ideal rigid-plastic body can be described by hyperbolic partial differential equations. The characteristics of the PDEs correspond to the slip-lines. For plane strain von Mises plasticity, the slip lines are orthogonal lines of sinistral (α-characteristics) and dextral (β-characteristics) maximum shear. Along the characteristic lines, stress variation is described by Hencky's equations and velocity variation by Geiringer's equations. For cavity enlargement or shrinkage, radial deformation is enabled by slip-lines in the form of logarithmic spirals (numerical visualization can be found in Hu et al., 2017).
For this axisymmetric problem we have continuous shear all over the plastic zone, and hence the total internal work rate is determined by integration of over the inner plastic domain. The upper bound solution corresponds to a constant velocity boundary condition (prescribed by Equation 11), i.e., v0 at the cavity (r = a) as shown in Figure 3. Hence the expansion rate at the outer boundary of the plastic domain (r = c) is , calculated from volume consistency.
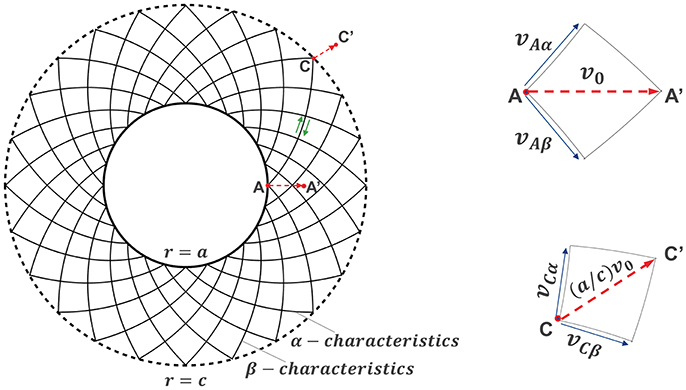
Figure 3. Zoom-in of the inner plastic zone (a < r < c) with constant velocity boundary conditions (i.e., the upper bound approach). The velocity distribution around a circular cavity is a radial expansion. This expansion is enabled by slip lines in the form of logarithmic spirals: orthogonal lines of α-characteristics and β-characteristics for plane strain von Mises plasticity. The radial velocity at point A (a random point on the interior r = a) is assumed v0, and the radial velocity at point C is (a/c)v0 via the hodograph solutions from Johnson et al. (1983).
The plastic strain rate along the α-line at point A is
where v0 denotes the radial velocity at r = a.
The plastic strain rate along the α-line at point C is
Then, the plastic strain rate along the α-line at a generic point within the plastic domain (a < r < c) can be written as
Via integration over the domain, the rate of internal work along the α-lines is derived:
The internal work done along the β-lines should be identical to the counterpart along the α-lines. Hence, the rate of total internal work is
For infinitesimal dt, Equation (24) reduces to
The total external work rate can be written as
The upper bound approach assumes
Recall that Pc = k (see Equation 16), given the outer radius of the entire zone b is sufficiently large. Equation (27) leads to
which coincides with the lower bound solution Equation (19).
4. Relaxing Isothermal Conditions
In non-isothermal conditions analytical solutions are difficult to derive as we not only need to consider the Continuity Equation and Momentum Conservation but also add a third equation of Energy Balance considering constraints on entropic evolution. This can lead to highly dynamic phenomena due to energy feedback. However, in terms of uncertainty quantification of the deformation process, the principles of limit analysis design can still be used in a rate formulation. The concept of upper and lower bounds of elasto-plastic work is then turned into an upper/lower bound of entropy production (Regenauer-Lieb et al., 2010) for the elasto-visco-plastic deformation. The assessment of uncertainty of the solution due to the time dependence of the problem can be obtained from numerical studies where thermodynamic flux boundary conditions provide a maximum of entropy production and thermodynamic force boundary conditions yield a minimum of entropy production (Regenauer-Lieb et al., 2014). The incorporation of the entropic evolution can be expressed through the time dependence in the entropic evolution equation. The simplest form of the relationship between the thermodynamic forces (e.g., temperature difference) and fluxes (e.g., heat flow) in 1-D is the following equation.
where T is the temperature, cT the thermal diffusivity, Cp the specific heat capacity, ρ the density and ( )m meaning a possible mixture of phases. χ denotes the proportion of the mechanical work dissipated into heat, the so-called Taylor-Quinney coefficient expressing the fraction of the mechanical work that is turned into heat. σij and denote the stress and the strain rate, respectively. The isothermal conditions used in the above discussed quasistatic thermomechanics assumptions for upper and lower bounds of plastic work are hence defined by:
Such condition is reached only after sufficient time has been given to the system to equilibrate. Equilibration in terms of shear heating and heat transfer is achieved when the heat production is exactly in equilibrium with the heat conduction. The approximated time scale to reach these conditions can be derived from the assumption that the heat source is the center of the shear zone and LT is the characteristic diffusion length of a heat pulse where according to the error function solution the heat production and diffusion terms are in equilibrium (see also in Regenauer-Lieb et al., 2013).
Due to the symmetry of this problem, we consider a scenario of an instantaneous heating in a semi-infinite half-space extending to infinity in the z-direction with a uniform initial temperature of T1 in the half-space. A temperature of T0 is suddenly applied and maintained on the horizontal surface. The far-field boundary condition is assumed remaining T → T1 at x → ∞. In order to describe the temporal and spatial propagation of this diffusive heat pulse, we define a dimensionless temperature θ as follows
where erfc(η) is the complementary error function defined as
and is used to represent the thermal diffusion distance considering the nature of error function distribution. To characterize heat localization in the shear zone (i.e., the vicinity of the horizontal boundary in the semi-infinite half-space case), we consider a thermal diffusion length scale of , where θ(z)≈0.84. Hence the corresponding characteristic time scale of thermal diffusion can be expressed as
There exists a second time scale that defines another extremum of the thermal-mechanical coupling. This is the time scale for the adiabatic limit ta. The adiabatic limit can be derived by setting the diffusion term in Equation (29) to zero, that is
As emphasized by Gruntfest (1963) the adiabatic process is in its very nature thermally unstable after an adiabatic runaway time scale ta of heating process triggered by shear heating which follows from Equation (34) to be:
where Tref is the background ambient reference temperature outside the adiabatic shear band.
The ratio of the characteristic diffusional cooling time scale tTd of Equation (33) and the explosive adiabatic time scale ta defines the Gruntfest number:
where k = cT(ρCp)m is the thermal conductivity of the material.
Between these time scales the deformation process can either be continuous creep or localized creep. Gruntfest (1963) showed that a critical Gruntfest number exists where the competition between the two processes (corresponding to the time scale of diffusion of heat away from the creeping zone and the time scale for thermal weakening of the creeping zone) leads to a creep localization phenomenon. The dual possible material response after reaching the bifurcation point results in the thermodynamic uncertainty of the deformation problem. Although our cavity expansion process is in the creeping flow regime and does not feature dynamic effects in the sensu stricto as in cavity expansion problem for impact studies (Masri and Durban, 2006), the Gruntfest number in its nature defines a non-dimensional time scale which introduces an additional time dependent dynamics of localization processes in the creeping flow regime.
We are now in a position to apply this important conclusion to the scenarios of radial cavity expansion. This insight can be used to illustrate the infinite time scale assumption of the classical thermal-mechanical approach of plasticity theory. Equation (29) is extended to be
where ∇2 denotes the Laplacian, which is expressed as with 2-D cylindrical coordinates. A Gruntfest number of zero equates to instantaneous time scale of the diffusive limit, i.e., infinite time scale for the adiabatic limit, or for a finite adiabatic time scale a zero time scale for diffusion. The classical thermo-mechanical solution describes this idealized limit with the continuous radial expansion of the cavity where the plastic zone grows continuously and axisymmetrically without any localized dissipation, as shown in Figure 4A calculated for zero Gruntfest number. The other solution is the cavity expansion where localized shear zones grow outwards in the plastic zone and the cavity expands along the major heat lines. This condition is reached at the critical Gruntfest number and is shown in Figure 4B. The numerical examples illustrated in Figure 4 are temperature profiles of a quarter of a hollow cylinder, which is subject to a uniformly distributed internal pressure and free of traction on the external boundary. Plane strain conditions are assumed. Small random thermal perturbation is implemented as the initial condition for the visualization of localized heat dissipation (i.e., the logarithmic spirals shown in Figure 4B with Gr = 5.0). The simulation results are obtained via fully coupled finite element implementation in a MOOSE (Gaston et al., 2009) based application, REDBACK, following our previous numerical studies in Hu et al. (2017).
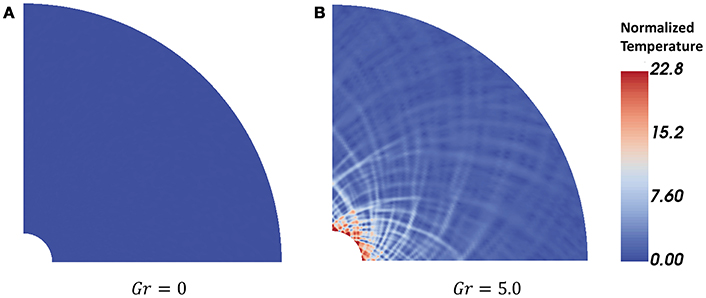
Figure 4. Temperature profiles obtained from implementing small random thermal perturbation as the initial condition: (A) Gr = 0, in which the plastic zone grows continuously and axisymmetrically without any localization of heat; (B) Gr = 5.0, where shear instabilities emerge and build up, forming major heat lines (following the traces of logarithmic spirals) which enable the expansion of the cavity.
The dynamics of the creeping flow process relies on an interaction of discrete material length scales (related to energy eigenstates of the materials) with the discrete length scales introduced by the geometry. In the simple cavity expansion problem it is a positive selection of shear bands on multiple reflections on the 2πr cylindrical symmetry of the inner and outer radius of the cavity and limit of the plastic zone, respectively. An in-depth study of the effect of geometry and the constructive interference of localization bands has been performed but is beyond the scope of this paper and will be presented elsewhere. This contribution is concerned with the more fundamental problem of implications of length scales stemming from THMC coupling alone. The problem of these characteristic material length scales defining the steady state width of the localization bands will be discussed next.
5. Discussion
This paper presents an approach that can be used to expand the classical thermo-mechanical quasistatic approach into a fully coupled multiscale and multiphysics framework using the example of axisymmetric cavity expansion. In the simplified case of von Mises rheology and ideal plasticity (no weakening or hardening) we have shown that limit analysis design delivers an upper bound of the plastic work that coincides with the value estimated from the lower bound method. The amount of work required to expand the circular cavity therefore has no uncertainty.
A different situation arises if strain-weakening or hardening laws are added. We calculated the strain weakening of the system as a function of the thermal evolution. This allowed us to replace the parametrization of the problem in terms of experimentally derived strain hardening into a physics derived thermal energy feedback problem. This is particularly useful for the conditions where laboratory experiments are difficult to perform or when the conditions beyond the range of laboratory constraints are under investigation.
If a cavity expansion problem for an engineering time scale of 20 years is supposed to be investigated then a physics-based formulation with uncertainty quantification as presented here is mandatory. This is because it is difficult to constrain uncertainty of hardening laws through controlled experiments on such long time frame. An example is the hole expansion due to creep of the pressure vessel of a nuclear reactor that may lead to a potential instability. Another extreme example is the cavity expansion problem of a magma chamber where creep on geological time scales of million years occurs, and temperatures are higher than thousand Celsius and pressures can be in the GPa range. The uncertainty quantification of these two example problems of cavity expansion is of pivotal interest to human safety and the proposed framework allows an assessment of a narrowed-down stability regime. We note that in these scenarios there exists uncertainty due the built-in time-evolution of the processes and hence the upper and lower bounds no longer coincide. Therefore, a comprehensive analysis based on THMC process understanding is required.
In the following subsections we propose to extend the classical limit analysis design technique to a more generalized entropy production limit analysis for THMC processes. In this sense evaluation of upper and lower bounds of the deformation work are interpreted as upper and lower bounds of the entropy production (see Table 1).
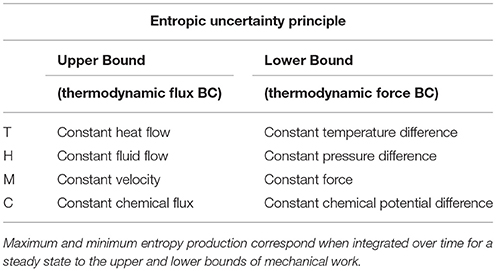
Table 1. Multi-physics boundary conditions to calculate upper and lower limits of entropy production from each length scale.
5.1. Multiphysics Feedbacks
In order to estimate entropic bounds of THMC processes it is first necessary to evaluate the dominant physics driving the localization phenomenon. In the example discussed above we have illustrated how the thermal reaction-diffusion equation leads to a localization phenomenon at critical Gruntfest number. We can now generalize this finding due to the similarity of the partial differential equation for reaction-diffusion of multiphysics feedback. If a chemical process leads to instability then the chemical reaction-diffusion process drives instability at critical Damköhler number. This in turn defines through Equation (33) the critical time and length scale for the localization phenomenon where the thermal diffusivity is replaced by the chemical diffusivity. The same applies for fluid pressure diffusion where a critical Lewis number defines instability and the steady state limit for formation of shear bands is defined again by Equation (33), however, now replacing thermal diffusivity with pressure diffusivity. This leads to a cascade of length scales where the smallest diffusional length scale corresponds to the chemical-reaction diffusion process followed by the fluid reaction-diffusion equation followed by the thermal reaction diffusion equation (Alevizos et al., in press; Regenauer-Lieb et al., in press).
5.2. Localization Length Scales
Multiscale and multiphysics problems do not lend themselves to an analytical assessment and the extension of the limit analysis design to an entropic uncertainty principle is particularly appealing. Numerical tools need to be used for solving the coupled deformation problem. Here we identify two cases: one in which the three localization length scales are far apart and localization phenomenon based on chemical length scales LC is substantially smaller than the hydrous length scale LH and the thermal length scale: LC ≪ LH ≪ LT. In this case it is safe to assume that there is no cross-scale coupling and the material parameters for the next scale up can be derived from a series of calculation using the upper and lower bounds of entropy production. The suggested framework is shown in Table 1. The material parameters for an immediate larger scale can then be evaluated from an explicit calculation of the uncertainties of the material parameters at the lower scale. This multiscale coupling leads to a steady deformation process similar to the classical theories of thermomechanics but controlled by elasto-visco-plastic creep (Alevizos et al., in press).
The other case of overlapping localization phenomena where LC ≤ LH ≤ LT requires explicit calculation of the full cross-scale thermo-hydro-chemo-mechanical problem where feedback mechanisms interact with each other. In this case the fully coupled matrix of all reaction-diffusion equations needs to be solved numerically with a multiscale code and the upper and lower bounds of the largest energetic driver is used for the evaluation of the large scale system. The full cascade of reaction-diffusion equations from Fick's to Darcy's to Fourier's is likely to be stable for the upper bound but highly unstable with complex dynamics for the lower bound conditions (Regenauer-Lieb et al., in press).
5.3. Entropic Bounds of THMC Processes
Plasticity theory describes the mechanical problem (M) and the traction boundary condition can be identified in the thermodynamic sense as a thermodynamic force boundary conditions. Generalized thermodynamic force boundary conditions for THC processes are: a difference in temperature, pressure and chemical potential for thermal, hydrological and chemical processes, respectively (Regenauer-Lieb et al., 2010). With this assumption the lower bound theorem translates into a principle of minimum entropy production. On the other extreme, the upper bound theorem corresponds to the principle of maximum entropy production, which can be obtained from imposing at the boundary a constant thermodynamic flux, e.g., a constant velocity for the mechanical problem. Corresponding fluxes for THC are heat flow, fluid flow velocity and chemical flow, respectively (see Table 1).
6. Conclusions
We have shown that the methods of evaluating uncertainties in classical limit analysis design can be extended to the complex multiphysics, multiscale problems encountered in nature and engineering applications. For the more complicated cases the upper bound of plastic work corresponds to the well known maximum entropy production principle (Ziegler, 1983) and the lower bound corresponds to the minimum of entropy production. These bounds address the path dependence problem of the integration over time and can be used to validate fully coupled numerical solution of multiphysics problems. We chose to illustrate the basic principles by the simple cylindrical cavity expansion case, which is an ubiquitous problem in a broad context of engineering and provides an ideal benchmark for testing numerical approaches developed for THMC coupling. Its application to black shale (Figure 1) illustrates the analytical solution of shear banding in the form of logarithmic spirals. The shear localization phenomenon can be understood as a thermo-mechanical feedback mechanism (Figure 4). We have illustrated a framework of thermodynamic uncertainty principles that is useful for THMC coupling simulations and shown its relationship to the classical limit analysis design. The proposed method allows estimation of risk of failure for conditions that are outside the realm of laboratory measurements thus expanding rock mechanics approaches into adjacent fields such as geological and geodynamic scenarios.
Future work will address the competition between the material length scales, identified in this work to be characteristic properties of the reaction-diffusion equation underpinning the instability, and the geometrical length scales of the coupled deformation problem. This interaction can lead to oscillatory behavior during the process of deformation through constructive and destructive interference between two adjacent length scales. Following on more complicated geometries will be investigated and the suggested framework be applied to real life engineering and geological problems.
Funding
MH did the analytical derivation and numerical investigation. KR-L supervised the work. The authors wrote the manuscript together.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Australian Research Council (ARC DP170104550, DP170104557) and the strategic SPF01 fund of UNSW, Sydney.
References
Alevizos, S., Poulet, T., Walsh, S., Durdez, T. M., Veveakis, M., and Regenauer-Lieb, K. (in press). The dynamics of multiscale, multiphysics faults: part II-episodic stick-slip can turn the jelly sandwich into a crème brûlée. Tectonophysics. doi: 10.1016/j.tecto.2017.06.010
Andresen, B. (2018). The need for entropy in finite-time thermodynamics and elsewhere. AIP Conf. Proc. 1033, 213–218. doi: 10.1063/1.2979032
Bigoni, D., and Hueckel, T. (1991a). Uniqueness and localization-I. Associative and non-associative elastoplasticity. Int. J. Solids Struct. 28, 197–213.
Bigoni, D., and Hueckel, T. (1991b). Uniqueness and localization-II. Coupled elastoplasticity. Int. J. Solids Struct. 28, 215–224.
Fjar, E., Holt, R., Raaen, A., Risnes, R., and Horsrud, P. (2008). Petroleum Related Rock Mechanics, 2nd Edn. Amsterdam: Elsevier Science.
François, B., Labiouse, V., Dizier, A., Marinelli, F., Charlier, R., and Collin, F. (2014). Hollow cylinder tests on boom clay: modelling of strain localization in the anisotropic excavation damaged zone. Rock Mech. Rock Eng. 47, 71–86. doi: 10.1007/s00603-012-0348-5
Freddi, F., and Royer-Carfagni, G. (2010). Regularized variational theories of fracture: a unified approach. J. Mech. Phys. Solids 58, 1154–1174. doi: 10.1016/j.jmps.2010.02.010
Freddi, F., and Royer-Carfagni, G. (2016). Phase-field slip-line theory of plasticity. J. Mech. Phys. Solids 94, 257–272. doi: 10.1016/j.jmps.2016.04.024
Gaston, D., Newman, C., Hansen, G., and Lebrun-Grandie, D. (2009). Moose: a parallel computational framework for coupled systems of nonlinear equations. Nucl. Eng. Design 239, 1768–1778. doi: 10.1016/j.nucengdes.2009.05.021
Gruntfest, I. J. (1963). Thermal feedback in liquid flow - plane shear at constant stress. Trans. Soc. Rheol. 7, 195–207. doi: 10.1122/1.548954
Haimson, B. (2007). Micromechanisms of borehole instability leading to breakouts in rocks. Int. J. Rock Mech. Mining Sci. 44, 157–173. doi: 10.1016/j.ijrmms.2006.06.002
Houlsby, G., and Puzrin, A. (2007). Principles of Hyperplasticity, an Approach to Plasticity Theory Based on Thermodynamic Principles, Vol. XXIV. Berlin: Springer.
Hu, M., Veveakis, M., Poulet, T., and Regenauer-Lieb, K. (2017). The role of temperature in shear instability and bifurcation of internally pressurized deep boreholes. Rock Mech. Rock Eng. 50, 3003–3017. doi: 10.1007/s00603-017-1291-2
Johnson, W., Sowerby, R., Venter, R., and Kobayashi, S. (1983). Plane-strain slip-line fields for metal-deformation processes. J. Appl. Mech. 50:702.
Masri, R., and Durban, D. (2006). Dynamic cylindrical cavity expansion in an incompressible elastoplastic medium. Acta Mech. 181, 105–123. doi: 10.1007/s00707-005-0245-z
Meier, T., Rybacki, E., Reinicke, A., and Dresen, G. (2013). Influence of borehole diameter on the formation of borehole breakouts in black shale. Int. J. Rock Mech. Mining Sci. 62(Suppl. C):74–85.
Papamichos, E., Vardoulakis, I., Tronvoll, J., and Skjaerstein, A. (2001). Volumetric sand production model and experiment. Int. J. Numer. Analyt. Methods Geomech. 25, 789–808. doi: 10.1002/nag.154
Regenauer-Lieb, K., Karrech, A., Chua, H., Horowitz, F., and Yuen, D. (2010). Time-dependent, irreversible entropy production and geodynamics. Philos. Trans. R. Soc. Lond. A 368, 285–300. doi: 10.1098/rsta.2009.0204
Regenauer-Lieb, K., Karrech, A., Chua, H. T., Poulet, T., Veveakis, M., Wellmann, F., et al. (2014). “Entropic bounds for multi-scale and multi-physics coupling in earth sciences,” in Beyond the Second Law. Understanding Complex Systems, eds R. Dewar, C. Lineweaver, R. Niven, and K. Regenauer-Lieb (Berlin; Heidelberg: Springer). doi: 10.1007/978-3-642-40154-1_17
Regenauer-Lieb, K., Poulet, T., Veveakis, M., and Alevizos, S. (in press). The dynamics of multiscale, multiphysics faults: part I - The long-term behaviour of the lithosphere. Tectonophysics. doi: 10.1016/j.tecto.2017.06.011
Regenauer-Lieb, K., Veveakis, M., Poulet, T., Wellmann, F., Karrech, A., Liu, J., et al. (2013). Multiscale coupling and multiphysics approaches in earth sciences: theory. J. Coupled Syst. Multisc. Dyn. 1, 2330–152X. doi: 10.1166/jcsmd.2013.1012
Keywords: cavity expansion, von Mises plasticity, logarithmic spiral, slip-line field, work principle, limit analysis, energy methods
Citation: Hu MM and Regenauer-Lieb K (2018) Entropic Limit Analysis Applied to Radial Cavity Expansion Problems. Front. Mater. 5:47. doi: 10.3389/fmats.2018.00047
Received: 22 March 2018; Accepted: 19 July 2018;
Published: 08 August 2018.
Edited by:
Davide Bigoni, University of Trento, ItalyReviewed by:
Giuseppe Zurlo, National University of Ireland Galway, IrelandMarco Gigliotti, École Nationale Supérieure de Mécanique et d'Aérotechnique, France
Gianni F. Royer Carfagni, Università degli Studi di Parma, Italy
Copyright © 2018 Hu and Regenauer-Lieb. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: ManMan Hu, bWFubWFuLmh1QHVuc3cuZWR1LmF1
 ManMan Hu
ManMan Hu Klaus Regenauer-Lieb
Klaus Regenauer-Lieb