- 1State Key Laboratory for Advanced Metals and Materials, University of Science and Technology Beijing, Beijing, China
- 2Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, China
- 3Songshan Lake Materials Laboratory, Dongguan, China
- 4High Magnetic Field Laboratory, Chinese Academy of Sciences, Hefei, Anhui, China
- 5Laboratory for Microstructures, Institute of Materials, Shanghai University, Shanghai, China
The body-centered cubic (BCC) Ti15Zr15Nb35Ta35 high-entropy alloy showed superconducting behavior at around 8 K. The electronic specific heat coefficient γ and the lattice specific heat coefficient β were determined to be γ = 9.3 ± 0.1 mJ/mol K2 and β = 0.28 ± 0.01 mJ/mol K4, respectively. It was found that the electronic specific heat Ces does follow the exponential behavior of the Bardeen-Cooper-Schrieffer (BCS) theory. Nevertheless, the specific heat jump (ΔC/γTc) at the superconducting transition temperature which was determined to be 1.71 deviates appreciably from that for a weak electron-phonon coupling BCS superconductor. Within the framework of the strong-coupled theory, our analysis suggests that theTi15Zr15Nb35Ta35 HEA is an intermediate electron-phonon coupled BCS-type superconductor.
Introduction
Within the past decade, high-entropy alloys (HEAs) have attracted extensive attention due to their unique compositions, interesting microstructures, and promising properties. Traditional alloys usually contain one element as the principle constituent with some other minor elements incorporated for property optimization (Lu et al., 2015). However, HEAs contain at least four principle elements in equal or near-equal atomic ratio (Li et al., 2017). It is interesting to note that, despite containing a large number of components, HEAs tend to form simple face-centered cubic (FCC), body-centered cubic (BCC), and hexagonal close-packed (HCP) structure instead of complex phases and intermetallic compounds (Urban and Feuerbacher, 2004; Conrad et al., 2009). Most current studies are focusing on the relationship between microstructure and mechanical properties (Yeh et al., 2004; Yeh, 2006; Zhou et al., 2007; Wen et al., 2009; Senkov et al., 2010, 2011; Chuang et al., 2011; Hsu et al., 2011), but limited work on the physical properties. Recently, it was revealed that the Ta34Nb33Hf8Zr14Ti11 HEA became a superconductor at 7.3 K in a weak electron-phonon coupled matter (Koželj et al., 2014), which attracted tremendous interests. Recently, it was reported that (TaNb)0.67(HfZrTi)0.33 HEA even showed a robust superconducting (SC) behavior under extreme pressure up to 160 GPa, a pressure like that within the outer core of the earth (Guo et al., 2017). Note that Ti, Zr, Nb, and Ta are known to be SC elements under ambient pressure, and proper mixing of these elements is favorable for a formation of a single solid solution phase (Todai et al., 2017). Therefore, careful studies on the SC behavior of the Ti-Zr-Nb-Ta HEA system is interesting, which may offer new clues for understanding SC mechanism of HEAs. Herein, we report synthesis and characterization of a novel four-component Ti15Zr15Nb35Ta35 HEA with a SC transition temperature Tc (Tc ≈ 8 K). Our analysis indicates that the Ti15Zr15Nb35Ta35 HEA is an intermediate electron-phonon coupled superconductor, which naturally explains its higher Tc in comparison with Ta34Nb33Hf8Zr14Ti11 HEA compound.
Materials and Methods
99.9% pure Ti, Zr, Nb, and Ta were used as starting materials for the preparation of alloy ingots with a nominal composition of Ti15Zr15Nb35Ta35 (at. %). The materials were put in a water-cooled copper crucible in a vacuum arc furnace. Then the materials were melted by an argon arc plasma flame at half atmospheric pressure under argon atmosphere. A dc power source with about 100 A was adjusted for 10 s and then increased to 300–400 A for about 1 min. The arc-flame between the tungsten electrode and the surface of the molten sample was maintained at about 20 mm during the arc melting process. The ingots were re-melted at least six times to ensure chemical homogeneity and subsequently drop-cast into a copper mold with a dimension of Φ10 × 60 mm. Phase constituents were characterized by X-ray diffraction (XRD) using Cu-Kα radiation. Specific heat, resistivity and magnetization measurements were carried out on a physical property measurement system (PPMS) from Quantum Design Company.
Results and Discussion
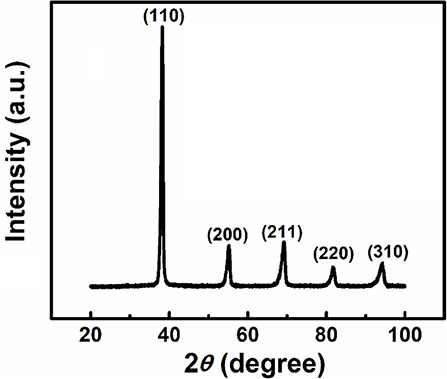
X-ray diffraction pattern of the as-cast Ti15Zr15Nb35Ta35 sample is shown in Figure 1 in which all diffraction peaks can be indexed to a BCC lattice, indicating formation of a single crystalline phase in the current alloy. The lattice constant of the current HEA using Vegard's rule of mixture(Vegard, 1921), amix = ∑iciai, which is valid for completely random mixing of the elements, was calculated to be a = 3.340 Å. Here ci is atomic fraction and ai is lattice parameter of the element i (Table 1) (Koželj et al., 2014). The calculated value is in good agreement with experimental value (i.e., a = 3.329 Å, suggesting that the constituent elements are likely randomly mixed in the current BCC lattice.
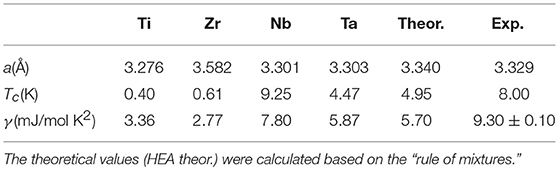
Table 1. Lattice constant a (Koželj et al., 2014), SC transition temperature Tc (Ashcroft and Mermin, 1976) and the specific heat coefficients γ (Tari, 2003) of pure constituent elements and the investigated Ti15Zr15Nb35Ta35 HEA.
Temperature dependence of electrical resistivity ρ (T) in zero field is shown in Figure 2, and the inset shows the variation of resistivity as a function of temperature under magnetic field ρ(T)H up to 10 T field. The resistivity value is 25 ± 1 μΩ cm at room temperature, and decreases with temperature as expected for metallic behavior(Awana et al., 2010). At 8 K, the Ti15Zr15Nb35Ta35 sample exhibits SC behavior, as the resistivity gradually approaches zero. Theρ (T)H measurements reveal that the SC transition temperature is shifted to lower temperatures as the applied magnetic field is increases. Figure 3 shows C (T) of the Ti15Zr15Nb35Ta35 HEA in the magnetic field of 0, 4, 8, and10 T. An anomaly at about 8 K associated with the SC transition is visible in the magnetic field of 0 and 4 T, but disappear in the magnetic field of 10 T. This observation is in good agreement with the results of electrical resistivity ρ (T) (shown in Figure 2).
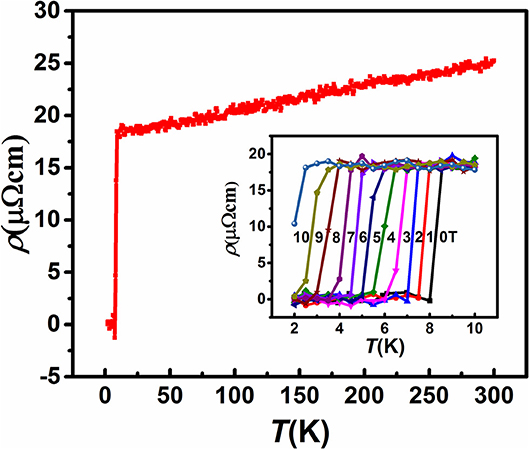
Figure 2. Temperature dependence of electrical resistivity ρ(T) in zero field of the Ti15Zr15Nb35Ta35 HEA. The inset shows the variation of resistivity as a function of temperature under magnetic field ρ (T)H up to10 T field.
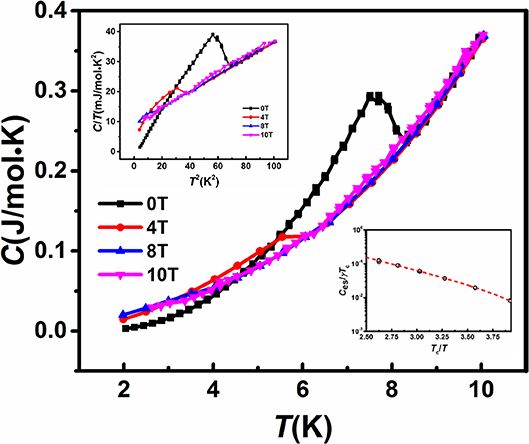
Figure 3. C(T)of Ti15Zr15Nb35Ta35for H = 0, 4, 8 and 10 T. The upper inset shows C/T vs T2 under magnetic field. And the lower right inset is Ces/γTc plotted on a logarithmic scale as a function of Tc/T.
Figure 4 shows temperature dependence of magnetic susceptibility χ (T) under zero-field-cooled (ZFC) and field-cooled (FC) conditions at 3 mT for the current Ti15Zr15Nb35Ta35 HEA. The susceptibility becomes negative (diamagnetic) below temperature 8.5 K, with a strong diamagnetic response due to the Meissner effect. Here, the measured χ0 was corrected for demagnetization fieldsχ = χ0/(1−Dχ0), where χ is the susceptibility corrected for demagnetization, and D is the demagnetization factor. Exact value of D was obtainable only for ellipsoids. The ratio of length to diameter for our cylinder-like sample is about 0.6, then the average value of D for uniformly magnetized cylinders is 0.43 according to the results computed by Brown (1960) and Crabtree (1977). Thus, it can also be clearly observed that the value of magnetic susceptibility (χ) is about −1, corrected for the demagnetization factor. This observation indicates that the SC volume fraction is almost 100%. The left inset of Figure 4 shows isothermal magnetization M(H) curves at 3–10 K in the field range up to 80 kA/m. A linear response due to Meissner effect is observed with a slope nearly −1, which confirms the bulk superconductivity. Then the magnitude of M decreases with increasing H, which is typical in the vortex state of a type-II superconductor (Awana et al., 2010). Based on the method reported in Ref. (Abdel-Hafiez et al., 2013), the lower critical field (Hc1) was obtained by measuring the virgin M(H) curve at various temperatures, where the regression coefficient function R(H) of a linear fit to the data between 0 and H departs from 1. Then the plot of Hc1 (T) is shown in the lower right inset of Figure 4. By linearly extrapolating Hc1(T) to zero temperature, we obtain Hc1 (0) = 55 mT. It should be noted that this is a very rough approximation in the absence of data at lower T.
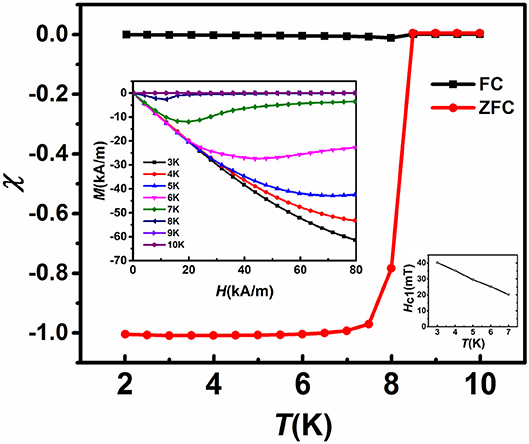
Figure 4. Temperature dependence of magnetic susceptibility χ(T) measured under zero-field-cooled (ZFC) and field-cooled (FC) conditions at 3 mT for Ti15Zr15Nb35Ta35 samples. The left inset shows isothermal magnetization M(H)curves for Ti15Zr15Nb35Ta35 HEA at 3-10 K in the field range up to 80 kA/m. The lower right inset is the temperature dependence of the lower critical fieldHc1(T).
The upper critical field Hc2 corresponding to the temperatures where the resistivity drops to 90% of the normal state resistivity ρ(T, H) (see inset of Figure 2) at the onset critical temperature determined from the intersection of the two extrapolated lines of ρ (T) in the applied magnetic fields (Jha et al., 2014). The upper critical field Hc2 determined from resistivity (black circles) and from specific heat measurements (red squares) are shown in Figure 5. For a single-band superconductor in the dirty limit (Werthamer and Helfand, 1966; Wang et al., 2015), the orbital limit is given by . Alternatively, the Pauli-limiting field for a weakly coupled BCS superconductor in the absence of spin-orbit scattering can be estimated as (Clogston, 1962) HP(0) = 1.86Tc. The Maki parameter α is defined as . Assuming TC = 8.5 K, and we have dHc2/dT|T = TC = −2 T/K from Figure 5. Then α is calculated to be 1.05. We used the full Werthamer-Helfand-Hohenberg (WHH) formula that incorporates the spin-paramagnetic effect via the Maki parameter α and the spin-orbit scattering constant λso to describe the experimental Hc2 data (Werthamer and Helfand, 1966):
where t = T/Tc and . As shown in Figure 5, the best fit can reproduce the experimental Hc2 very well. By fixing α = 1.05 to fit the Hc2 data, we have λso = 23.2, Hc2 (0) = 11.6 T. With these results for Hc1 (0) and Hc2 (0), we can calculate several SC parameters for our HEA. From , where Φ0 is the quantum flux (= h/2e = 2.07 × 10−15 Wb), we find a Ginzburg-Landau coherence length ξGL(0) = 53.3 Å = 5.33 × 10−9 m. Assuming κ = λGL/ξGL is temperature independent, then λGL(0) = κξGL(0). KnowingξGL(0), Hc1(0), and , and hence the Ginzburg-Landau parameter, κ = 17.3.
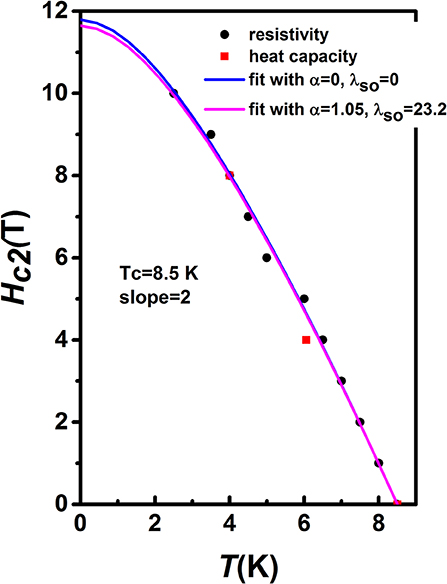
Figure 5. The upper critical field Hc2 from resistivity (black circles) and from specific heat measurements (red squares) as a function of temperature for the Ti15Zr15Nb35Ta35 HEA. The blue and pink lines are the WHH predictions with the parameter α = 0, λso = 0, and α = 1.05, λso = 23.2, respectively.
With respect to the superconductivity in Ti15Zr15Nb35Ta35 HEA, the most interesting part is the detailed analysis of the anomaly in the specific heat C(T). The low-temperature specific heat in the normal state is expressed as C(T) = γT+Clattic(T), where the electronic specific heat coefficient γ measures the degree of electronic contribution and represents the phonon contribution in which β is the lattice specific heat coefficient. Then the plot of C/T vs. T2 is shown in the upper inset of Figure 3. The analysis of the normal-state specific heat (in 8 or 10 T field) with the expression C/T = γ+βT2 yields the intercept γ = 9.3 ± 0.1 mJ/mol K2, the slope β = 0.28 ± 0.01 mJ/mol K4 and the Debye temperature 191 ± 3 K. Clearly, for the current HEA, the electronic specific heat coefficient γ increases by about 12% as compared with that of the reported Ta34Nb33Hf8Zr14Ti11 HEA.
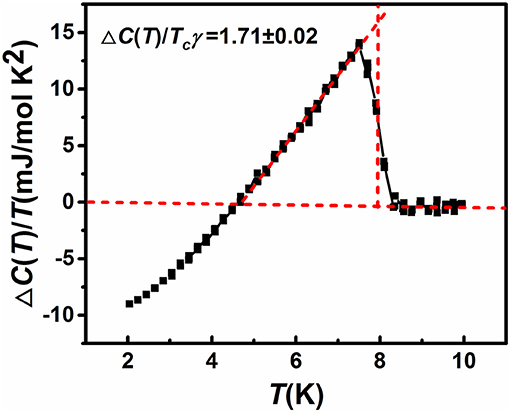
To elucidate the nature of the SC state of theTi15Zr15Nb35Ta35 HEA, e.g., Bardeen-Cooper-Schrieffer (BCS) type (Bardeen et al., 1957) or unconventional, it is of interest to calculate the discontinuous jump of specific heat at the SC transition temperature, i.e., ΔC(T) = C(T)−Clattice(T)−γT. The resultant ΔC(T)/T at H = 0 is shown in Figure 6. Utilizing the balance of entropy around the transition, ΔC/γTc (the specific-heat jump) is 1.71 ± 0.02 for the current HEA which deviates appreciably from that for a weak electron-phonon coupling BCS superconductor (ΔC/γTc = 1.43).
Based on the BCS theory (Tinkham, 2004), the energy required to break up a Cooper pair is about 2Δ0, and the number of Cooper pairs broken up is proportional to exp(−2Δ(0)/kBT), which leads an exponential temperature dependence of the specific heat at sufficiently low temperature. The electronic specific heat Ces(T) [Ces(T) = C(T, H)−Clattice(T)] in the BCS theory is expressed by Ces/γTc = Aexp(−BTc/T) (Tari, 2003), where A and B are two constants whose values relate to the temperature interval used. Evidently in the lower inset of Figure 3, Ces(T)of the Ti15Zr15Nb35Ta35 HEA reflects clearly an exponential behavior. The fit Ces(T) of the current HEA at 2.5 < TC/T < 6 yields Ces/γTc = 10.1 × exp(-1.66Tc/T). Evidently, it does have the characteristics of exponential behavior predicted by the BCS theory, but the factors are far from the weak electron-phonon coupling (Takeya et al., 2005). This phenomenon is different from the reported Ta34Nb33Hf8Zr14Ti11 HEA (Koželj et al., 2014).
It is found that the measured SC properties in Ti15Zr15Nb35Ta35 HEA agree extremely well with the following strong electron-phonon coupling corrections (valid for Tc/ωlog < < 1, where ωlog is a characteristic phonon temperature; McMillan, 1968; Ishikawa and Toth, 1971; Allen and Dynes, 1975; Carbotte, 1990):
where kBis the Boltzmann constant, λ the electronic-phonon coupling parameter, and μ* the Coulomb pseudopotential taken to be 0.13 here, which is an average value used commonly for intermetallic superconductors (Klimczuk et al., 2012; von Rohr et al., 2016). The values of ωlog,2Δ0 and λ were determined by Equations (2–4) based on the experimentally measuredΔC/γTc, as compiled in Table 2. It is apparent that the calculated results are reasonably satisfied with the condition Tc/ωlog < < 1. The value of 2Δ0/kBTc is 3.52 for the weak-coupling BCS conventional superconductors. In our HEA, 2Δ0/kBTcis calculate to be 3.72 ± 0.02 using the energy gap 2Δ0 of 2.57 ± 0.01 meV, larger than the reported Ta 34Nb33Hf8Zr14Ti11 HEA of 3.50 indicating the stronger electron-phonon coupling (Takeya et al., 2005). Therefore, these values suggest that the Ti15Zr15Nb35Ta35 HEA is an intermediate-coupled superconductor, when compared with the reported weak-coupled Ta 34Nb33Hf8Zr14Ti11 HEA.

Table 2. SC parameters of Ti15Zr15Nb35Ta35 HEA and the reported Ta34Nb33Hf8Zr14Ti11 HEA (Koželj et al., 2014).
The electronic-phonon coupling parameter λ in the reported weak-coupling Ta34Nb33Hf8Zr14Ti11 HEA is calculated to be 0.66 ± 0.01 using the equation (Takeya et al., 2005). Clearly this value of λ is lower than that of the current HEA (0.84 ± 0.02). The electron density of state at the Fermi level N(EF) is estimated to be 1.07 ± 0.01 and 1.06 ± 0.02 by for theTi15Zr15Nb35Ta35 HEA and the reported Ta34Nb33Hf8Zr14Ti11HEA, respectively. Therefore, the improvement of SC temperature Tc is related to the increase of the electron density of state at the Fermi levelN(EF). In addition, the electron-phonon coupling is enhanced, which also might contribute to the increase of Tc. It was also found in the current HEA that the SC properties, e.g., Tc and γ ,do not obey the Vegard's rule of mixture (Vegard, 1921), , where ci and pi are the atomic percentage and the SC property of each constituent element (Table 1), respectively. This observation suggests that electronic properties are not a “cocktail” of properties of the constituent elements. Theoretical description of the electronic properties of HEAs is thus a highly complex problem.
Conclusions
The Ti15Zr15Nb35Ta35 HEA with a single BCC lattice was synthesized and found to be a type-II superconductor. The analysis of all the specific heat data shows that this new Ti15Zr15Nb35Ta35HEA is a BCS-type phonon-mediated superconductor in the intermediate electron-phonon coupling regime, which is different from the previous report. Despite the complex electronic properties, our results also indicate that the characteristics of superconductivity of HEAs can be tailored by varying their chemical composition. Further experiments on its transport properties under high pressure would be very interesting to check the robustness of superconductivity.
Author Contributions
YY performed the experiments. YW, HL, ZW, XL, ZY, HW, XL, and ZL supervised the project. YY, HL, and ZW analyzed the data. YY, YW, and ZL wrote the paper. All authors commented on the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by National Natural Science Foundation of China (Nos. 11790293, 51871016, 51671018, 51671021, 51531001 11822411, 11674372, 11704385 and 11874359), 111 Project (B07003), International S&T Cooperation Program of China (2015DFG52600), Program for Changjiang Scholars and Innovative Research Team in University of China (IRT_14R05), and the Projects of SKLAMM-USTB (2016Z-04, 2016-09, 2016Z-16). YW acknowledges the financial support from the Top-Notch Young Talents Program and Fundamental Research Fund for the Central Universities. HL acknowledges the financial support from the Chinese Academy of Sciences (SPRP-B: XDB25000000 and the Youth Innovation Promotion Association).
References
Abdel-Hafiez, M., Ge, J., Vasiliev, A., Chareev, D., Van de Vondel, J., Moshchalkov, V., et al. (2013).Temperature dependence of lower critical field Hc1(T) shows nodeless superconductivity in FeSe. Phys. Rev. B 88:174512. doi: 10.1103/PhysRevB.88.174512
Allen, P. B., and Dynes, R. (1975). Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12:905. doi: 10.1103/PhysRevB.12.905
Ashcroft, N., and Mermin, N. (1976). Solid State Physics (Saunders, Philadelphia). Phil. Mag. 3:445.
Awana, V., Pal, A., Vajpayee, A., Meena, R., Kishan, H., Husain, M., et al. (2010). Superconductivity in SmFe1−xCoxAsO (x = 0.0-0.30). J. Appl. Phys. 107:09E146. doi: 10.1063/1.3366601
Bardeen, J., Cooper, L. N., and Schrieffer, J. R. (1957). Theory of superconductivity. Phys. Rev. 108:1175. doi: 10.1103/PhysRev.108.1175
Brown, W. F. Jr. (1960). Single-domain particles: new uses of old theorems. Am. J. Phys. 28, 542–551. doi: 10.1119/1.1935878
Carbotte, J. (1990). Properties of boson-exchange superconductors. Rev. Mod. Phys. 62:1027. doi: 10.1103/RevModPhys.62.1027
Chuang, M. H., Tsai, M. H., Wang, W. R., Lin, S. J., and Yeh, J. W. (2011). Microstructure and wear behavior of AlxCo1.5CrFeNi1.5Tiy high-entropy alloys. Acta Mater. 59, 6308–6317. doi: 10.1016/j.actamat.2011.06.041
Clogston, A. M. (1962). Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 9:266. doi: 10.1103/PhysRevLett.9.266
Conrad, M., Harbrecht, B., Weber, T., Jung, D. Y., and Steurer, W. (2009). Large, larger, largest–a family of cluster-based tantalum copper aluminides with giant unit cells. II. The cluster structure. Acta Crystallogr. Sect. B Struct. Sci. 65, 318–325. doi: 10.1107/S0108768109014013
Crabtree, G. (1977). Demagnetizing fields in the de Haas-van Alphen effect. Phys. Rev. B 16:1117. doi: 10.1103/PhysRevB.16.1117
Guo, J., Wang, H., von Rohr, F., Wang, Z., Cai, S., Zhou, Y., et al. (2017). Robust zero resistance in a superconducting high-entropy alloy at pressures up to 190 GPa. PNAS 114:13144. doi: 10.1073/pnas.1716981114
Hsu, C. Y., Juan, C. C., Wang, W. R., Sheu, T. S., Yeh, J. W., and Chen, S. K. (2011). On the superior hot hardness and softening resistance of AlCoCrxFeMo0.5Ni high-entropy alloys. Mater. Sci. Eng. A 528, 3581–3588. doi: 10.1016/j.msea.2011.01.072
Ishikawa, M., and Toth, L. E. (1971). Electronic specific heats and superconductivity in the group-V transition metals. Phys.Rev. B 3:1856. doi: 10.1103/PhysRevB.3.1856
Jha, R., Kishan, H., and Awana, V. (2014). Superconducting and magneto-transport properties of BiS2 based superconductor PrO1−xFxBiS2 (x = 0 to 0.9). J. Appl. Phys. 115:013902. doi: 10.1063/1.4859535
Klimczuk, T., Wang, C., Gofryk, K., Ronning, F., Winterlik, J., Fecher, G., et al. (2012). Superconductivity in the Heusler family of intermetallics. Phys. Rev. B 85:174505. doi: 10.1103/PhysRevB.85.174505
Koželj, P., Vrtnik, S., Jelen, A., Jazbec, S., Jaglicić, Z., Maiti, S., et al. (2014). Discovery of a superconducting high-entropy alloy. Phys. Rev. Lett. 113:107001. doi: 10.1103/PhysRevLett.113.107001
Li, D. Y., Li, C. X., Feng, T., Zhang, Y. D., Sha, G., Lewandowski, J. J., et al. (2017). High-entropy Al0.3CoCrFeNi alloy fibers with high tensile strength and ductility at ambient and cryogenic temperatures. Acta Mater. 123, 285–294. doi: 10.1016/j.actamat.2016.10.038
Lu, Z. P., Wang, H., Chen, M. W., Baker, I., Yeh, J. W., Liu, C. T., et al. (2015). An assessment on the future development of high-entropy alloys: summary from a recent workshop. Intermetallics 66, 67–76. doi: 10.1016/j.intermet.2015.06.021
McMillan, W. (1968). Transition temperature of strong-coupled superconductors. Phys. Rev. 167:331. doi: 10.1103/PhysRev.167.331
Senkov, O., Scott, J., Senkova, S., Miracle, D., and Woodward, C. (2011). Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J.Alloys Compd. 509, 6043–6048. doi: 10.1016/j.jallcom.2011.02.171
Senkov, O., Wilks, G., Miracle, D., Chuang, C., and Liaw, P. (2010). Refractory high-entropy alloys. Intermetallics 18, 1758–1765. doi: 10.1016/j.intermet.2010.05.014
Takeya, H., Hirata, K., Yamaura, K., Togano, K., El Massalami, M., Rapp, R., et al. (2005). Low-temperature specific-heat and neutron-diffraction studies on Li2Pd3B and Li2Pt3B superconductors. Phys. Rev. B 72:104506. doi: 10.1103/PhysRevB.72.104506
Todai, M., Nagase, T., Hori, T., Matsugaki, A., Sekita, A., and Nakano, T. (2017). Novel TiNbTaZrMo high-entropy alloys for metallic biomaterials. Scr. Mater. 129, 65–68. doi: 10.1016/j.scriptamat.2016.10.028
Urban, K., and Feuerbacher, M. (2004). Structurally complex alloy phases. J. Non-Cryst. Solids 334, 143–150. doi: 10.1016/j.jnoncrysol.2003.11.029
Vegard, L. (1921). Die konstitution der mischkristalle und die raumfüllung der atome. Zeitschrift Physik 5, 17–26.
von Rohr, F., Winiarski, M. J., Tao, J., Klimczuk, T., and Cava, R. J. (2016). Effect of electron count and chemical complexity in the Ta-Nb-Hf-Zr-Ti high-entropy alloy superconductor. PNAS 113, E7144–E7150. doi: 10.1073/pnas.1615926113
Wang, Z., Xie, T., Kampert, E., Förster, T., Lu, X., Zhang, R., et al. (2015). Electron doping dependence of the anisotropic superconductivity in BaFe2−xNixAs2. Phys. Rev. B 92:174509. doi: 10.1103/PhysRevB.92.174509
Wen, L., Kou, H., Li, J., Chang, H., Xue, X., and Zhou, L. (2009). Effect of aging temperature on microstructure and properties of AlCoCrCuFeNi high-entropy alloy. Intermetallics 17, 266–269. doi: 10.1016/j.intermet.2008.08.012
Werthamer, N. R., Helfand, E., and Hohenberg, P. C. (1966). Temperature and purity dependence of the superconducting critical field, Hc2. III. electron spin and spin-orbit effects. Phys. Rev. 147:295.
Yeh, J. W. (2006). Recent progress in high entropy alloys. Ann. Chim. Sci. Mat 31, 633–648. doi: 10.3166/acsm.31.633-648
Yeh, J. W., Chen, S. K., Lin, S. J., Gan, J. Y., Chin, T. S., Shun, T. T., et al. (2004). Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303. doi: 10.1002/adem.200300567
Keywords: high-entropy alloys, superconducting, BCS-type, specific heat jump, intermediate electron-phonon coupled
Citation: Yuan Y, Wu Y, Luo H, Wang Z, Liang X, Yang Z, Wang H, Liu X and Lu Z (2018) Superconducting Ti15Zr15Nb35Ta35 High-Entropy Alloy With Intermediate Electron-Phonon Coupling. Front. Mater. 5:72. doi: 10.3389/fmats.2018.00072
Received: 04 July 2018; Accepted: 09 November 2018;
Published: 29 November 2018.
Edited by:
John L. Provis, University of Sheffield, United KingdomReviewed by:
Jacqueline Krim, North Carolina State University, United StatesAlexander Petrovic, Nanyang Technological University, Singapore
Copyright © 2018 Yuan, Wu, Luo, Wang, Liang, Yang, Wang, Liu and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuan Wu, d3V5dWFuQHVzdGIuZWR1LmNu
Zhaoping Lu, bHV6cEB1c3RiLmVkdS5jbg==
 Yuan Yuan1
Yuan Yuan1 Yuan Wu
Yuan Wu