Magnetic Field Induced Surface Micro-Deformation of Magnetorheological Elastomers for Roughness Control

In this work, we propose mesoscopic model to investigate the surface micro structures of magnetorheological elastomers (MREs) under a magnetic field. By comparing the surface roughness changes of MREs, we found that the surface micro-deformation of MREs, not the field-induced hardness, mainly accounts for the controllable friction characteristics of MREs. The results also demonstrate that the field-induced friction of MREs depends on the particle contents as well as the initial surface roughness. The model predicts that the maximum relative roughness change of MREs occurs when the MRE has particle volume fraction of around 9%, which is validated by experimental results.

Introduction

Polymers are hyperplastic materials that can be subjected to a large recoverable deformation under a relatively small loading. In taking advantage of this natural property, researchers have developed adaptive materials called magnetorheological elastomers (MREs), by embedding magnetic particles (micron size) in the polymer matrix (Jolly et al., 1996; Ginder et al., 1999). The magnetizing particles in the matrix would interact with each other under an external magnetic field, and consequently induce deformation and modulus changes of MREs. With these unique controllable properties, MREs could be possible candidates for a variety of applications, such as in soft actuators (Böse et al., 2012), vibration absorber (Menzel, 2015; Chen et al., 2016), and magnetic sensor (Sutrisno et al., 2015) etc.

Recently, several experimental studies (Lee et al., 2013; Lian et al., 2015, 2016; Li et al., 2018) have shown that the tribological properties of MREs also change with external magnetic fields, which would possibly extend the MRE's application in interfacial friction control. However, the mechanism of field-induced friction behavior of MREs is still unclear. Lee et al. (2013) employed a homemade linear sliding tester to evaluate the friction characteristics of MREs, and found that the friction coefficient of MRE decreased with the external magnetic field. Later, the same group (Lian et al., 2015, 2016) applied a reciprocating friction tester to characterize four MRE samples, which were prepared by embedded particles in different matrix materials, and found the same phenomenon for all test conditions. The authors argued that the friction reduction of MREs under a magnetic field was due to the field-stiffening effect. According to the classic contact theory, the large stiffness of materials will result in less interfacial friction (Popov, 2010). However, in a previous study (Li et al., 2018), we observed that even though the friction coefficient of MREs increases with external magnetic fields in some cases, the MREs are getting stiffer. Accordingly, this phenomenon challenges existing theoretical interpretation.

In fact, the surface micro-scale morphology may mainly contribute to the tribological characteristics of the MREs in a magnetic field. However, few studies (Gong et al., 2012) have been carried out to investigate the surface micro-deformation of the MREs under magnetic fields.

Although theoretical modeling of the deformation behavior of MREs has been studied by many others, these models originated from either the continuum mechanics (Dorfmann and Ogden, 2004; Kankanala and Triantafyllidis, 2004), or the multiscale theories (Davis, 1999; Cremer et al., 2015) mostly focus on prediction of the magnetic induced properties of MRE in macro conditions. The models from the point of view of continuum mechanics (Allahyarov et al., 2014; Menzel, 2014) hardly take into account the surface morphology of MREs. And almost all of the representative volume unit models (Yin et al., 2002; Ivaneyko et al., 2014) based on multiscale theories ignore the surface micro profile of MREs. Therefore, all the reported theoretical work on modeling of MREs can only predict the average bulk deformation of MREs. In order to fully understand the field-induced friction behavior of MREs, it is essential to develop a new model to analyze the surface micro structures of MRE under external magnetic fields.

Meanwhile, experimental studies have been performed to measure and analyze the deformation of MREs in magnetic fields. A testing platform with a CCD camera was established by Zrínyi et al. (1996) to measure deformation of ferrogels under non-uniform magnetic fields. The effects of compress force and particle volume fraction on magnetic field induced deformation of MRE were investigated by Martin et al. (2006) and Danas et al. (2012) by using similar testing platforms. However, most experimental studies were only interested in measuring the average deformation of MRE samples. Gong et al. (2012) constructed a digital holographic interferometry to achieve so called full-field deformation of MREs. However, they did not investigate the transition of surface micro structures of MREs under magnetic fields.

To fully understand how the external magnetic field affects the surface roughness of MRE, and how the initial roughness and particle volume fractions impact on the variation of the roughness, a 2 dimension mesoscopic model is proposed in this paper. By employing the Monte-Carlo method (Tsang et al., 2004), our model could incorporate the initial surface irregularities of MRE. Based on this, the changes of MREs surface roughness in magnetic field are analyzed by utilizing magneto-mechanical coupling (FEM) algorithms. Besides, several MRE samples with different particle fractions and initial surface roughness are prepared and their roughness are measured by a white light interferometer to reveal the mechanism of magneto induced roughness changes.

Modeling

In the proposed model, we assume that the radius of magnetic particle sizes follow normal distribution, and the particles are tightly bonded to the matrix. In addition, the effect of polymer networks on particle interaction is negligible in the theoretical simulation (Davis, 1999; Yin et al., 2002; Ivaneyko et al., 2014). Since the magnetic induced deformation of MRE is usually tiny (Zrínyi et al., 1996; Martin et al., 2006; Danas et al., 2012), both magnetic particles and polymer matrixes are considered as standard incompressible liner elastic materials. The Young's modulus of particles is 200Mpa, and the Young's modulus of matrixes is 1Mpa.

Figure 1A shows the statistic sizes of 175 particles which are uniformly distributed in matrix. Meanwhile, the 2D Gaussian random contour surfaces are generated by employing the Monte-Carlo method (Tsang et al., 2004) representing the initial surface micro profile of the MRE model (Figure 1B). In the model, the surface profiles of MRE can be linear superposed by different sinusoidal curves. The coordinate of the scatter point in the profile curve can be obtained as:

$\begin{array}{rc}{y}_n=f(x_n)=\frac{1}{l}{\sum }_{j=-\frac{n}{2+1}}^{\frac{n}{2}}F({\omega }_j)e^{i{\omega }_j{x}_n}& (1)\end{array}$

FIGURE 1

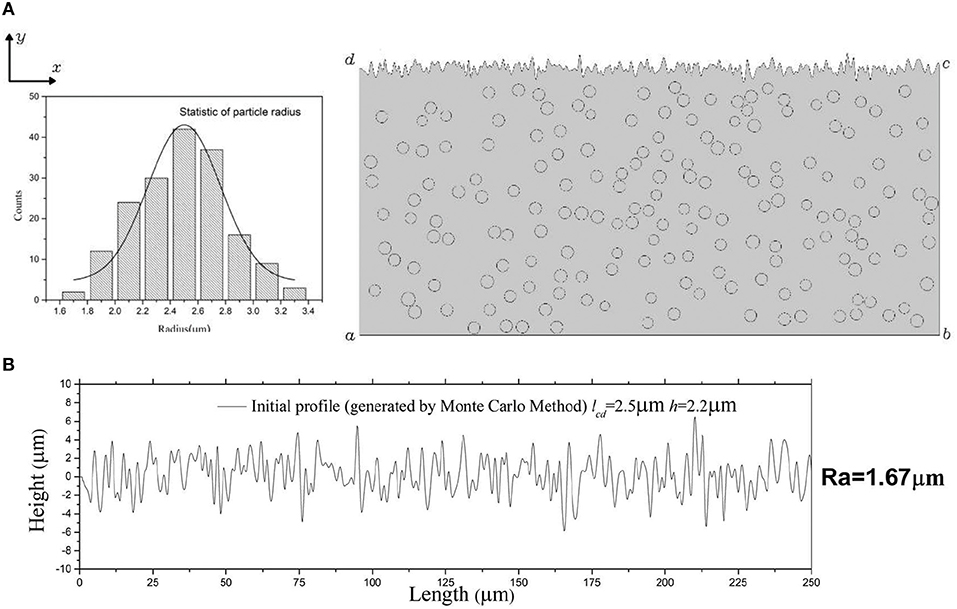
Figure 1. The two dimension mesoscopic model of MRE. (A) Left: statistic distribution of particle sizes, the total number of particles N = 175 and the average of the particle radius is 2.5 μm. Right: the particles are uniform distributed in a (250 × 130 μm) matrix area, and the particles volume fraction of MRE ϕ≈10.5%. (B) The generated initial surface micro profile of the MRE model. The surface roughness of the MRE (Ra) is 1.67 μm.

Where n is the scatter point number, (x_n,y_n) represents the coordinate of the n-th scatter point in the profile curve, F(ω_j) is the Fourier transform pair of f (x_n), and can be expressed as:

$F\left({\omega }_j\right)=\frac{2\pi }{\sqrt{2\Delta x}}\sqrt{S\left({\omega }_j\right)}\cdot \{\begin{array}{c}\left[N\left(0,1\right)+iN\left(0,1\right)\right]j=-\frac{n}{2+1},\cdots ,\text{}-1\\ N\left(0,1\right)j=0,\frac{n}{2}& (2)\end{array}$

Where N(0,1) represents a random number of normal distribution with a mean value of 0 and a variance of 1. Δx is the distance between the nearest two scatter points in x-th direction. S(ω_j) is the power spectral density of random surface profiles, and obeys gauss distribution function. And it can be expressed as follows:

$\begin{array}{rc}S(\omega )=\frac{h{l}_{cd}}{2\sqrt{\pi }}exp\left(\frac{-{\omega }^2{l}_{cd}^2}{4}\right)& (3)\end{array}$

Where h is the expectation of profiles' amplitudes, and l_cd is the expectation of distance between two peaks of profiles.

In this work, we use parameter R_a to describe the roughness of the MREs' surface micro profiles. It can be expressed as follows:

$\begin{array}{ll}{R}_a=\frac{1}{l}{\displaystyle {\int }_0^l}|y(x)-\frac{1}{l}{\displaystyle {\int }_0^l}y\left(x\right)dx|dx& (4)\end{array}$

Simulation Results and Discussions

A sequential FEM²⁵ is adopted in this paper to solve the magneto-mechanical coupling problem and obtain the micro deformation of MRE model in Figure 1 by using commercial software COMSOL Multiphysics. Besides, in the mesoscopic scale, the applied magnetic field can be assumed to follow a uniform distribution. Therefore, in the magneto module (MFNC module in COMSOL), the magnetic scalar potential is equal zero on the boundary ab. The magnetic field applied on the MREs is in y-direction, and the particles will be magnetized in the same direction, and their magnetization is set to 1,000 kA/m. in the simulation. The other boundaries are considered as magnetic insulation. Meanwhile, in the structural mechanical module (SOLID module in COMSOL), we use U = (u,v) to describe the displacement field of MRE. The boundary condition is chosen in such a way where u = 0 for boundary ad, and v = 0 for boundary ab, and other boundaries are free to move. Also, the magnetic force F_i on each particle surface ∂Ω_i can be calculated from the local field H with the aid of the Maxwell stress tensor σ^M as follow (Ly et al., 1999):

$\begin{array}{rc}{\text{F}}_i=\frac{1}{2\pi {\mu }_0}{\oint }_{\partial {\Omega }_i}{\sigma }^M·\text{n}\text{ds}=\frac{1}{2\pi }{\oint }_{\partial {\Omega }_i}{\mu }_i(\text{H}\text{H}-\frac{1}{2}\left|\right|\text{H}|{|}^2\text{I})·\text{n}\text{ds}& (5)\end{array}$

Where n is the unit normal vector on ∂Ω_i, μ_i, μ₀ is the permeability for the particles and matrix, respectively, I is the 2th rank unit tensor.

The simulation results of the MRE model under an applied magnetic field of 1,000 kA/m are shown in Figure 2. Figure 2A gives the results of magnetic flux density distribution in the simulation domain. Figure 2B shows the stress field of MRE induced by the magnetic field. These results illustrate that the magnetized particles in the matrix would interact with each other though magnetic force and create the magnetic induced stress in the MRE. As a result, the MRE will deform irregularly.

FIGURE 2

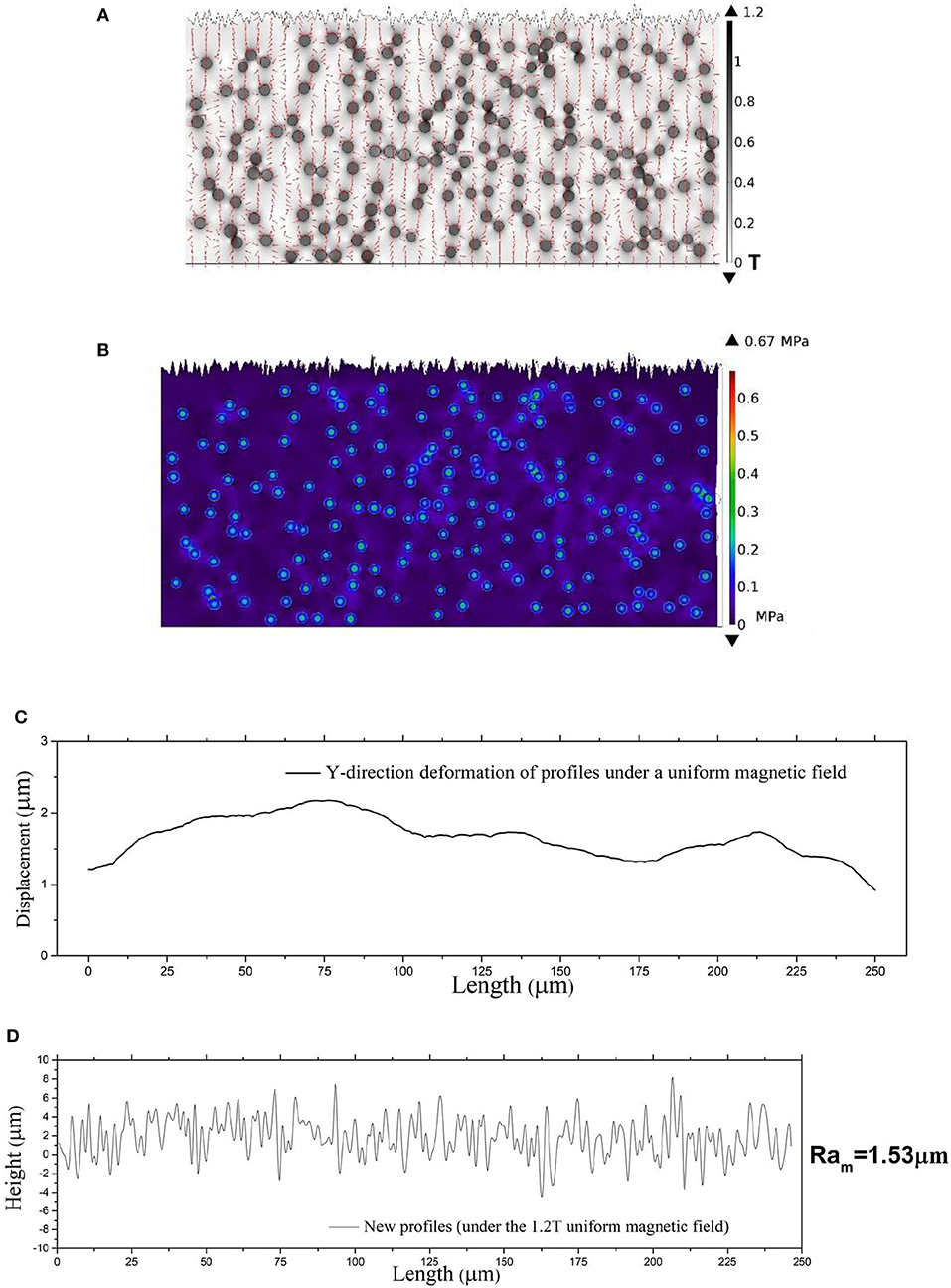
Figure 2. Simulation results with proposed model (A) Magnetic flux density distribution. (B) Stress field. (C) Magnetic induced displacements of the surface profile in Y-direction. (D) The new surface profile after the magnetization of 1,000 KA/m is applied on. And the roughness of the surface is 1.53 μm.

Figure 2C shows the positive field-induced displacements of MRE which are consistent with previous studies is shown. However, the irregularity of the surface deformation by the magnetic field is ignored by most theoretical predictions (Davis, 1999; Yin et al., 2002; Dorfmann and Ogden, 2004; Kankanala and Triantafyllidis, 2004; Chen et al., 2013; Allahyarov et al., 2014; Andriushchenko et al., 2014; Menzel, 2014; Cremer et al., 2015). The cause of the irregular deformation of MREs can be explained by the magnetic induced stress field shown in Figure 2B. It can be seen that the magnetic stress is not uniformly distributed in the matrix. The stress is larger where particles are assembled, while it is smaller where the particles are scattered. Figure 2D shows the new surface profile of MRE after the magnetic field is applied. It is obtained by superposing the initial profile of Figure 1B and the magnetic induced displacement of Figure 2C together. Figure 2D shows that the roughness of the MRE is 1.53 μm. Comparing with the initial roughness Ra = 1.67 μm, the roughness of the MRE is decreased. The simulation results are consistent with previous experimental observations (Lian et al., 2015, 2016; Li et al., 2018) where the magnetic fields reduce the friction coefficient of MREs. However, when we evaluate the relative roughness changes as a function of the initial surface roughness of MREs, the magnetic fields do not always induce negative changes in surface roughness. Figure 3A presents the simulation results of the relative roughness changes Ra_r with initial surface roughness of MREs. The relative roughness change is defined as: Ra_r = (Ra_m-Ra)/Ra, where Ra_m, is the roughness under a magnetic field, Ra is the initial surface roughness. We can see that when the initial profile roughness Ra < 1 μm, the relative roughness changes under a magnetic field are positive. This suggests that the smooth surface profiles of MREs will become rough under magnetic field; in other words, the friction coefficient of MREs will increase by an applied magnetic field. We suggested that this phenomenon is a result of that the roughness of the magnetic induced deformation itself will be the dominant role of Ra_r, When initial profile is smooth. And we can also explain it by an extreme assumption; we can imagine a MRE which has an absolute smooth surface that should become rough when superimposed on inhomogeneous deformation, which is the result of external magnetic loading.

FIGURE 3

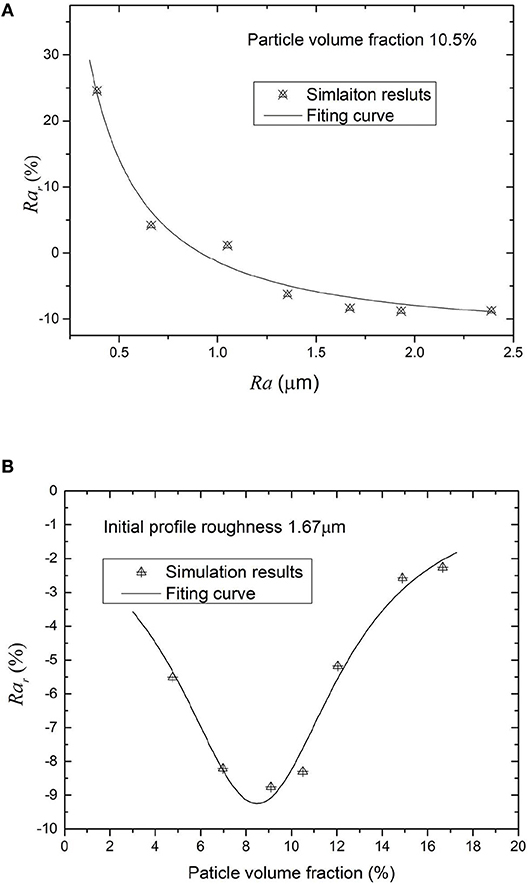
Figure 3. Magnetic induced relative roughness Ra_r. (A) Relationship with initial roughness. (B) Relationship with particle volume fraction.

Further, we investigate how the particle contents in MREs affect the relative roughness changes under the same applied magnetic field. We set the initial surface roughness of MREs to be 1.67 μm, and analyze the field-induced surface profiles for the MREs with different particle volume fractions. Figure 3B shows the simulation results of the relative roughness changes as a function of particle volume fractions of MREs.

It can be seen that there is an optimal particle volume fraction for the relative roughness changes, in which the Ra_r has the maximum absolute value. It is interesting to note that optimal particle volume fraction for the Ra_r is around 9%, but is not 27%, in which the magnetorheological effect is predicted the strongest (Davis, 1999). It is suggested that it is a result of the particle distribution which varies with the particle volume fraction. When the particle volume fraction of MREs is low (<9%), the interactions between particles would be increased with its volume fraction, then the irregularity of the magnetostriction is also increased with it. However, when the particle volume fraction is higher than 9%, the distance between particles would be decreased and particle distribution becomes more uniform. Then the irregularity of the magnetostriction is reduced although the particle interactions are increasing. This finding could give an explanation as to why the MRE with 10% particle fraction has the largest tunable friction coefficients in reference Li et al. (2018)

Experimental Validation

In this section, two kinds of isotropic MREs are manufactured by uniformly embedded magnetic particles into silicon rubber (HT-18; Shanghai Tongshuai Co., Ltd, China). As shown in Figure 4, One kind of MREs is the samples are prepared by using the glass mold, and the other is made by the iron mold. So, the latter has rougher surface than the former. A white light interferometer (ContourGT-K, Germany BRUKER company), of which the vertical resolution can reach 0.01 nm is used to obtain the three-dimensional morphology of all MRE samples.

FIGURE 4

Figure 4. MRE samples (A) the glass mold (B) the MRE generated in glass mold (C) iron mold (D) the MRE generated in iron mold.

Figure 5 gives the white light interferometer test results of a 10% particle volume fraction MRE that is generated by iron mold. Figure 5A gives the initial surface contour of the MRE, Figure 5B gives the surface contour of MRE under a uniform vertical magnetic field of 450 mT, and Figure 5C gives the 2 dimension picture of the MRE surface profiles with/without a uniform vertical magnetic field. It can be seen that the roughness of MRE sample decreases from 2.76 to 2.36 μm when a magnetic field is applied. However, for the MRE samples made by glass mold, the magnetic field increases the surface roughness (see Figure 6).

FIGURE 5

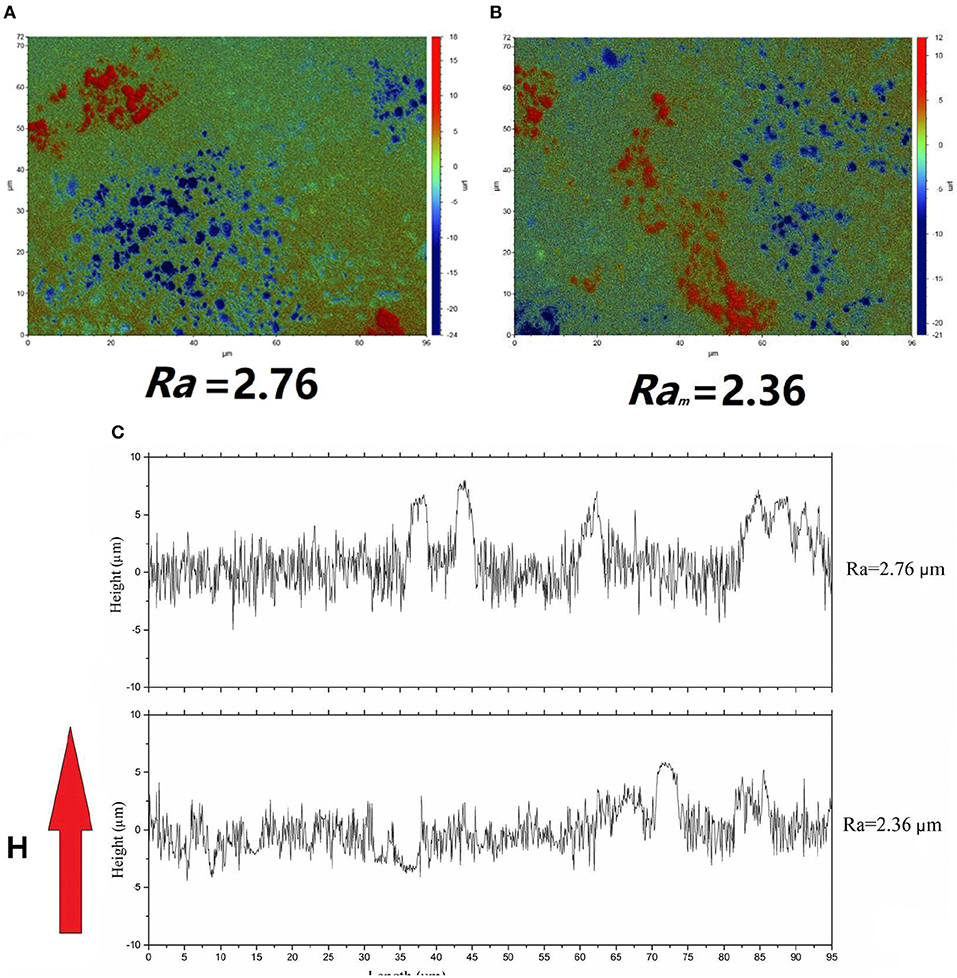
Figure 5. White light interferometer test results of a typical MRE (10% particle volume fraction, generated by iron mold) (A) the initial surface contour, the roughness is 2.76 μm (B) the surface contour under a magnetic field of 450 mT, the roughness is 2.36 μm (C) the 2-demension profiles of MRE.

FIGURE 6

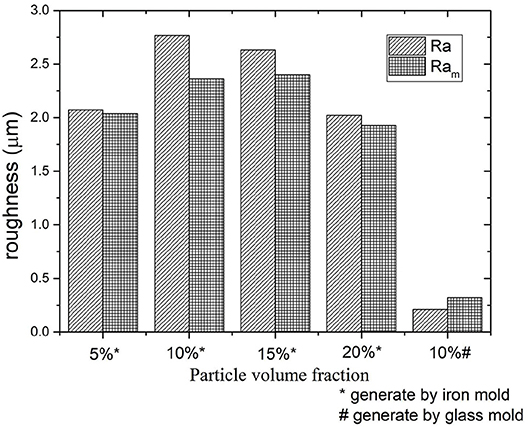
Figure 6. Comparisons of roughness of MREs for different particle volume fractions with/without magnetic field.

Figure 6 shows the results of surface roughness of MREs with different particle contents made by iron mold with/without magnetic field. The results of roughness of MRE samples with 10% particle volume fraction made by glass mold are also presented in the Figure 6. As can be seen, the initial roughness of MREs mainly depends on the roughness of corresponding molds. And MREs fabricated by the steel mold has the similar roughness. Besides, Figure 6 shows that the MRE with 10% particle volume fraction has the largest relative roughness change, which conforms to the theoretical prediction. This is different to MREs made by iron mold, as the surface roughness of MREs generated by glass mold increases with magnetic fields.

Conclusion

In summary, a mesoscopic model that considers deformation of surface micro-structures of MREs has been established to predict the surface roughness of MREs under magnetic fields. The model can explain how the field-induced friction of MRE changes as a function of particle contents, and how the initial surface roughness affects the changes. In addition, the proposed model has been verified experimentally. These findings may contribute to the area of interfacial friction control, in which controllable friction surfaces or techniques are expected to apply for the design of high efficient smart devices and mechanical systems.

Author Contributions

RL and XL contribute the experimental parts of this works. XW gives some advises of this manuiscript and farbricates the MRE. SC writes the paper and establishes the surface model of MRE.

Funding

Financial supports from the National Natural Science Foundation of China (Grant NO.11502038, NO.11572320, NO.11372366). And it also supports from China Postdoctoral Science Foundation (NO. 2017M610386).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Allahyarov, E., Menzel, A. M., Zhu, L., and Löwen, H. (2014). Magnetomechanical response of bilayered magnetic elastomers. Smart Mater. Struct. 23:115004. doi: 10.1088/0964-1726/23/11/115004

CrossRef Full Text | Google Scholar

Andriushchenko, P., Nefedev, k., and Stepanov, G. V. (2014). Calculations of magnetoactive elastomer reactions in a uniform external magnetic field. Eur. Phys. J. B 87:11. doi: 10.1140/epjb/e2013-31097-1

CrossRef Full Text | Google Scholar

Böse, H., Rabindranath, R., and Ehrlich, J. (2012). Soft magnetorheological elastomers as new actuators for valves. J. Intell. Mater. Syst. Struct. 23, 989–994. doi: 10.1177/1045389

CrossRef Full Text | Google Scholar

Chen, S., Wang, X., Zhang, Z., Mu, W., and Li, R. (2016). Optimal design of laminated-MRE bearings with multi-scale model. Smart Mater. Struct. 25:105037. doi: 10.1088/0964-1726

CrossRef Full Text | Google Scholar

Chen, W., Sun, L., Li, X., and Wang, D. (2013). Numerical investigation on the magnetostrictive effect of magneto-sensitive elastomers based on a magneto-structural coupling algorithm. Smart Mater. Struct. 22:105012. doi: 10.1088/0964-1726/22/10/105012

CrossRef Full Text | Google Scholar

Cremer, P., Löwen, H., and Menzel, A. M. (2015). Tailoring superelasticity of soft magnetic materials. Appl. Phys. Lett. 107:171903. doi: 10.1063/1.4934698

CrossRef Full Text | Google Scholar

Danas, K., Kankanala, S. V., and Triantafyllidis, N. (2012). Experiments and modeling of iron-particle-filled magnetorheological elastomers. J. Mech. Phys. Solids 60, 120–138. doi: 10.1016/j.jmps.2011.09.006

CrossRef Full Text | Google Scholar

Davis, L. C. (1999). Model of magnetorheological elastomers. J. Appl. Phys. 85, 3348–3351. doi: 10.1063/1.369682

CrossRef Full Text | Google Scholar

Dorfmann, A., and Ogden, R. W. (2004). Nonlinear magnetoelastic deformations of elastomers. Acta Mech. 167, 13–28. doi: 10.1007/s00707-003-0061-2

CrossRef Full Text | Google Scholar

Ginder, J. M., Nichols, M. E., Elie, L. D., and Tardiff, J. L. (1999). Magnetorheological elastomers: properties and applications. Smart Struct. Mater. 3675, 131–139. doi: 10.1117/12.352787

CrossRef Full Text | Google Scholar

Gong, X., Liao, G., and Xuan, S. (2012). Full-field deformation of magnetorheological elastomer under uniform magnetic field. Appl. Phys. Lett. 100:211909. doi: 10.1063/1.4722789

CrossRef Full Text | Google Scholar

Ivaneyko, D., Toshchevikov, V., Saphiannikova, M., and Heinrich, G. (2014). Mechanical properties of magneto-sensitive elastomers: unification of the continuum-mechanics and microscopic theoretical approaches. Soft Matter 10, 2213–2225. doi: 10.1039/C3SM52440J

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolly, M. R., David Carlson, J., and Munoz, B. C. (1996). A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 5, 607–612.

Google Scholar

Kankanala, S. V., and Triantafyllidis, N. (2004). On finitely strained magnetorheological elastomers. J. Mech. Phys. Solids 52, 2869–2908. doi: 10.1016/j.jmps.2004.04.007

CrossRef Full Text | Google Scholar

Lee, D. W., Lee, K., Lee, C. H., Kim, C. H., and Cho, W. O. (2013). A study on the tribological characteristics of a magneto-rheological elastomer. J. Tribol. 135, 014501. doi: 10.1115/1.4023080

CrossRef Full Text | Google Scholar

Li, R., Ren, D., Wang, X., Chen, X., Chen, S., and Wu, X. (2018). Tunable friction performance of magneto-rheological elastomer induced by external magnetic field. J. Intell. Mater. Syst. Struct. 29, 160–170 doi: 10.1177/1045389X17708043

CrossRef Full Text | Google Scholar

Lian, C., Lee, K. H., and Lee, C. H. (2015). Friction and wear characteristics of magneto-rheological elastomers based on silicone/polyurethane hybrid. J. Tribol. 137:031607. doi: 10.1115/1.4029942

CrossRef Full Text | Google Scholar

Lian, C., Lee, K. H., and Lee, C. H. (2016). Friction and wear characteristics of magnetorheological elastomer under vibration conditions. Tribol. Int. 98, 292–298. doi: 10.1116/j.triboint.2016.02.037

CrossRef Full Text | Google Scholar

Ly, H. V., Reitich, F., Jolly, M. R., Banks, H. T., and Ito, K. (1999). Simulations of particle dynamics in magnetorheological fluids. J. Comput. Phys. 155, 160–177. doi: 10.1006/jcph.1999.6335

CrossRef Full Text | Google Scholar

Martin, J. E., Anderson, R. A., Read, D., and Gulley, G. (2006). Magnetostriction of field-structured magnetoelastomers. Phys. Rev. E 74:051507. doi: 10.1103/PhysRevE.74.051507

PubMed Abstract | CrossRef Full Text | Google Scholar

Menzel, A. M. (2014). Bridging from particle to macroscopic scales in uniaxial magnetic gels. J. Chem. Phys. 141, 194907. doi: 10.1063/1.4901275

PubMed Abstract | CrossRef Full Text | Google Scholar

Menzel, A. M. (2015). Tuned, driven, and active soft matter. Phys. Rep. 554, 1–45. doi: 10.1016/j.physrep.2014.10.001

CrossRef Full Text | Google Scholar

Popov, V. L. (2010). Contact Mechanics and Friction. Berlin: Springer.

PubMed Abstract | Google Scholar

Sutrisno, J., Purwanto, A., and Mazlan, S. A. (2015). Recent progress on magnetorheological solids: materials, fabrication, testing, and applications. Adv. Eng. Mater. 17, 563–597. doi: 10.1002/adem.201400258

CrossRef Full Text | Google Scholar

Tsang, L., Chen, D., Xu, P., Li, Q., and Jandhyala, V. (2004). Wave scattering with the UV multilevel partitioning method: 1. Two-dimensional problem of perfect electric conductor surface scattering. Radio Sci. 39, 1–13. doi: 10.1029/2003RS003009

CrossRef Full Text | Google Scholar

Yin, H. M., Sun, L. Z., and Chen, J. S. (2002). Micromechanics-based hyperelastic constitutive modeling of magnetostrictive particle-filled elastomers. Mech. Mater. 34, 505–516. doi: 10.1016/S0167-6636(02)00178-3

CrossRef Full Text | Google Scholar

Zrínyi, M., Barsi, L., and Büki, A. (1996). Deformation of ferrogels induced by nonuniform magnetic fields. J. Chem. Phys. 104, 8750–8756. doi: 10.1063/1.471564

CrossRef Full Text | Google Scholar