Elastic Response of an Optimal Tensegrity-Type Metamaterial

We study the elastic response of a class of optimal planar metamaterials designed as periodic patterns of tensegrity cells. Specifically, we consider an infinite slab constituted by prismatic cells whose sections on the middle plane are regular hexagons, squares or equilateral triangles subjected to a uniform normal stress. An attracting property of the proposed metamaterial is a very small tangential stiffness compared with the normal one. This property suggests the design of innovative isolation devices with extreme properties.

1. Introduction

Metamaterials represent an innovative approach to the problem of obtaining unusual or extreme physical responses for advanced applications. Since their extreme macroscopic responses depend primarily on the internal low scale pattern, the understanding of how the microstructure topology influences the macroscopic properties is the key-point in the design of new advanced metamaterials.

The growing scientific and technological interest on these new designed materials is due to the possibility of getting electromagnetic and optical properties (Chen et al., 2010) or mechanical responses unreached by standard materials. Metamaterials can exhibit extreme static or dynamical behaviors, such as negative effective dynamic modulus (Fang et al., 2006), vanishing macroscopic shear modulus (Schittny et al., 2013) or selective buckling under external stresses (Paulose et al., 2015). Recently, the possibility of harnessing the postbuckling response of cellular materials for auxetic and dissipative properties has been analyzed by Bertoldi (2017). Based on these specific mechanical properties also the design of tensegrity-based metamaterials has been oriented to produce extreme or controllable behaviors. In particular, extreme behaviors in the propagation of mechanical waves have been considered by Amendola et al. (2018) and Fraternali et al. (2012, 2014), whereas elastic responses controllable by adjusting the level of self-equilibrated forces have been studied by Sabouni-Zawadzka and Gilewski (2019). Further, it has been recognized that the transmission and the control of forces in biological systems is diffusely achieved by means of systems based on tensegrity schemes (see e.g., Volokh et al., 2000; Ingber et al., 2014; Fraldi et al., 2019).

Metamaterials are usually classified into three-dimensional and surface (planar) materials and are frequently based on elementary geometric patterns (see e.g., Koohestani, 2017; Salahshoor et al., 2018; Zhang et al., 2018). Many studies approaching these periodic materials by means of lattice theory have been carried out. Within this research line, Hutchinson and Fleck (2006) studied the structural performance of periodic planar trusses. Buckling of a planar periodic frame was considered by Triantafyllidis and Schnaidt (1993). More recently, Thomsen et al. (2018) performed a topological optimization of 2D periodic materials undergoing buckling type instabilities. Moreover, the non-linear response of planar periodic materials has been analyzed by Vigliotti et al. (2014).

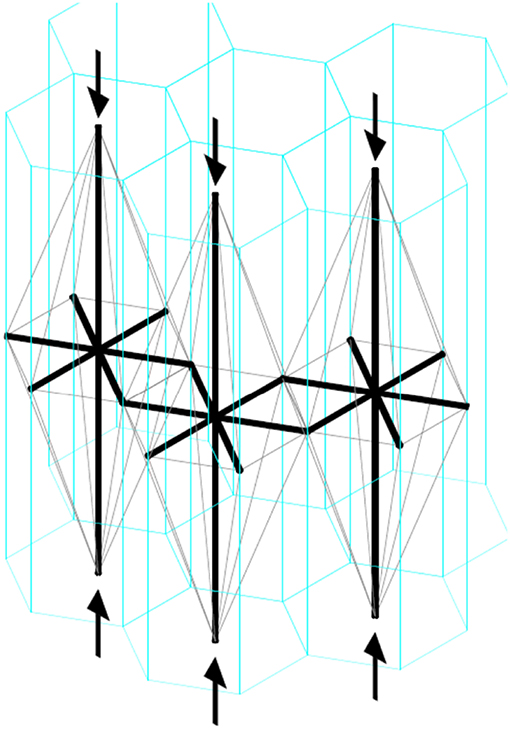
This paper is focused on the elastic response of a planar metamaterial made up of a pattern of equal tensegrity units, where each unit cell is a three dimensional T-bar (Skelton et al., 2017). In particular, we consider an infinite slab undergoing a uniform compressive macro stress. Based on a well-known result on planar tessellation, we consider systems with three different periodic patterns of identical prismatic cells filling the space, whose sections on the middle plane of the slab are equilateral triangles, squares, and regular hexagons (see Figures 1, 2). The mass optimization of this metamaterial was discussed in a previous paper (DeTommasi et al., 2017b). Here we determine the overall (macro) elastic properties of these optimal slabs as functions of both design and actual applied loads. Interestingly, the proposed metamaterial exhibits a low shear stiffness coupled with a high extensional stiffness. This property suggests the possibility of obtaining isolation devices with extreme properties.

FIGURE 1

Figure 1. The three tensegrity-type unit cells (equilateral triangles, squares, regular hexagons).

FIGURE 2

Figure 2. Scheme of the slab composed of hexagonal cells.

2. Morphological Optimization

As already stated, in our optimization problem we consider only slabs made up of periodic sequences of tensegrity cells having equilateral triangular, square, or regular hexagonal shapes, which are the unique shapes allowing us to tessellate the plane into identical regular polygons. On the external plane surfaces of the slab a normal compression macro stress Σ is applied, so that

$\begin{array}{ll}P=A_{cell}\Sigma .& (1)\end{array}$

is the load applied to the single tensegrity cell (see Figure 1). Here, the cross section area A_cell for a cross section having p sides (p = 3, 4, 6) is given by

$\begin{array}{ll}{A}_{cell}=\frac{p{H}^2}{8}sin\left(\frac{2\pi }{p}\right){tan}^2\alpha ,p=3,4,6,& (2)\end{array}$

where H is the height of a cell and α is the angle formed by the principal struts and the principal cables (see Figure 1). Once the cell shape is defined, α represents the optimization geometrical parameter of the described metamaterial. The following assumptions are introduced:

(i) A prestress must be assigned such that both in the loaded and unloaded states only traction forces are exerted on cables;

(ii) Both in the loaded and unloaded states, cables respect material failure condition and struts both material failure and local Euler buckling conditions;

(iii) Equilibrium is globally stable.

For a fixed Σ, we aim to minimize the metamaterial volume density

$\begin{array}{ll}\rho :=\frac{\mathrm{\text{tensegrity volume}}}{A_{cell}H},& (3)\end{array}$

where tensegrity volume is the global volume of all members of a tensegrity cell and A_cell is given by (2). We remark that, since we assume that all tensegrity units are made of the same material, the minimum value of ρ corresponds to the slab of minimal mass. Furthermore we observe that neighboring tensegrity units (see Figure 2) share the same transversal cables. Thus the areas of these cables considered for a singular unit are the half of the total ones. The above statements lead to the constrained minimum problem already discussed in DeTommasi et al. (2017b).

2.1. Elastic Equilibrium of Tensegrity Cells

Due to periodicity and symmetry properties of the metamaterial introduced above, any cell is two-degrees statically indeterminate. In the loaded state (P = ΣA_cell) two parameters β and τ are introduced to describe the internal forces

$\begin{array}{ll}\{\begin{array}{lll}\beta \hfill & =\hfill & \frac{N}{P}>1\hfill \\ \tau \hfill & =\hfill & \frac{T_t}{P}>0\hfill \end{array}.& (4)\end{array}$

Here N is the compression force in the struts orthogonal to the middle plane and T_t is the traction force in the cables laying in the middle plane. Then the internal axial forces in the loaded state can be written as

$\begin{array}{ll}\{\begin{array}{lll}N\hfill & =\hfill & \beta P\hfill \\ N_t\hfill & =\hfill & \frac{2}{p}(\beta -1)P\tan \alpha +2\tau P\sin \frac{\pi }{p}\hfill \\ T\hfill & =\hfill & \frac{(\beta -1)P}{p\sin \alpha }\hfill \\ T_t\hfill & =\hfill & \tau P\hfill \end{array},& (5)\end{array}$

where T denotes the traction force in the cables out of the middle plane and N_t the compression force in the transversal struts laying on the middle plane.

Similarly, in the unloaded state (P = 0) we can describe the distribution of the internal forces by the parameters $\bar{\beta }$ and $\bar{\tau }$, defined as β and τ and given by

$\begin{array}{ll}\{\begin{array}{lll}\beta \hfill & =\hfill & \overline{\beta }+N_{[1]}\hfill \\ \tau \hfill & =\hfill & \overline{\tau }+T_{t[1]}\hfill \end{array}.& (6)\end{array}$

Here N_[1] is the compression force induced in the principal struts by a unitary compression force (P = 1) and T_t[1] is the traction force induced in the tranversal cables by the same external force. In the unloaded state we have

$\begin{array}{ll}\{\begin{array}{lll}\overline{N}\hfill & =\hfill & \overline{\beta }P\hfill \\ {\overline{N}}_t\hfill & =\hfill & \frac{2}{p}\overline{\beta }P\tan \alpha +2\overline{\tau }P\sin \frac{\pi }{p}\hfill \\ \overline{T}\hfill & =\hfill & \frac{\overline{\beta }P}{p\cos \alpha }\hfill \\ {\overline{T}}_t\hfill & =\hfill & \overline{\tau }P\hfill \end{array}.& (7)\end{array}$

Though, as already discussed in DeTommasi et al. (2017b), a complete stability analysis should be carried out in the context of lattice theory (Triantafyllidis and Schnaidt, 1993), here, for sake of simplicity we assume that all cells undergo identical critical displacements. We deem that this assumption is satisfactory within the present analysis. Moreover, precritical displacements are assumed to be small with the deformed lengths of the members identified with the natural ones. Under these hypotheses the total potential energy (set equal to zero in the unloaded state) of the system can be written as

$\begin{array}{ll}V(u,P)={\displaystyle \sum _{j=1}^{2+3p}}\left[\frac{E{A}^{(j)}}{2}{\left(\frac{\Delta l^{(j)}}{l^{(j)}}\right)}^2{l}^{(j)}+N^{(j)}\Delta l^{(j)}\right]-2P{u}_1,& (8)\end{array}$

where

$\Delta l^{(j)}=\Vert \Delta x^{(j)}+T^{(j)}u\Vert -l^{(j)}.$

Here u is the vector of generalized incremental displacements (see Figure 3); 2u₁ is the contraction orthogonal to the middle plane; l^(j), Δl^(j), and A^(j) are the length, the elongation and the area of the (j)-th member, respectively; Δx^(j) is the length vector and T^(j)u is the relative incremental displacement vector between the end joints of the (j)-th member. Furthermore, the Young modulus E has a unique value for all the bars and cables, made up of the same material. In particular, we have

$\begin{array}{ll}{A}^{(j)}=\{\begin{array}{ll}A,\hfill & j=1,2\hfill \\ A_t,\hfill & j=3,4,\mathrm{...},p+2\hfill \\ A_c,\hfill & j=p+3,p+4,\mathrm{...},2p+2\hfill \\ A_{ct},\hfill & j=2p+3,2p+4,\mathrm{...},3p+2\hfill \end{array},& (9)\end{array}$

where A and A_t are the areas of the cross sections of the principal and transversal struts, respectively, and A_c and A_ct the cross section areas of the principal and traversal cables, respectively.

FIGURE 3

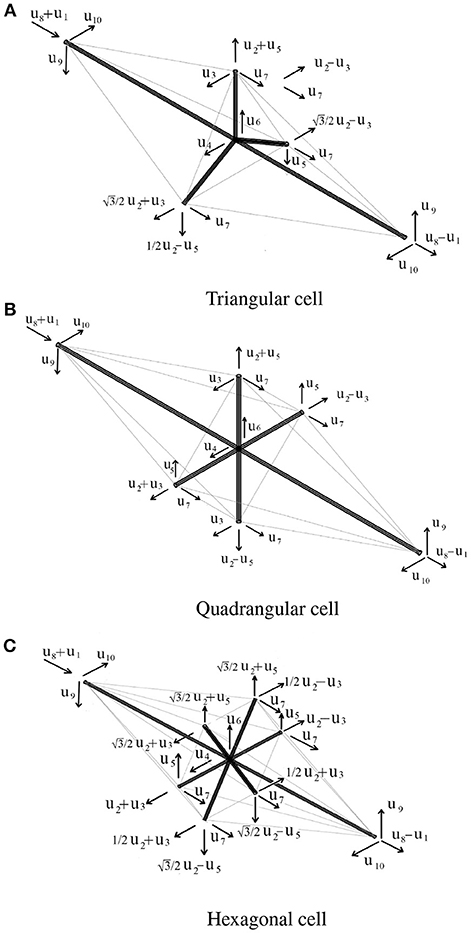
Figure 3. Generalized displacements considered in the stability analysis for the three tensegrity cells. (A) Triangular cell. (B) Quadrangular cell. (C) Hexagonal cell.

The lengths l^(j) of the members are given by

$\begin{array}{ll}{l}^{(j)}=\{\begin{array}{ll}\frac{H}{2},\hfill & j=1,2\hfill \\ \frac{H\tan \alpha }{2},\hfill & j=3,4,\mathrm{..},p+2\hfill \\ \frac{H}{2\cos \alpha },\hfill & j=p+3,p+4,\mathrm{...},2p+2\hfill \\ H\sin \frac{\pi }{p}\tan \alpha ,\hfill & j=2p+3,2p+4,\mathrm{...},3p+2\hfill \end{array}.& (10)\end{array}$

The axial forces N^(j) (numbered with the same index of the lengths and the areas of the corresponding members) are given by (5). The tangent stiffness matrix K is the 10 × 10 Hessian matrix of the total potential energy in the loaded configuration:

$\begin{array}{ll}K=\frac{{\partial }^{2}V}{\partial u\partial u}{|}_{u=0},& (11)\end{array}$

that, for stable or critical equilibrium states, must be semidefinite positive

$\begin{array}{ll}K\succcurlyeq 0.& (12)\end{array}$

Based on the symmetry properties of the tensegrity cell, in our numerical analysis we choose the generalized displacements shown in Figure 3. Thanks to this approach, the Hessian matrix K is a block diagonal matrix, with maximum dimension of the submatrices equal to 2 × 2. This choice significantly simplifies the numerical analysis of positiveness in the following described optimization procedure. In particular, the above positivity condition is imposed by requiring that its leading principal minors are all non-negative.

3. Macro Elastic Constants

In this section the elastic constants of the slabs are evaluated. The tangent Young modulus E_m in the direction orthogonal to the middle plane is determined as

$\begin{array}{ll}{E}_m=\frac{\stackrel{·}{\Sigma }}{\stackrel{·}{{ϵ}_1}}=H\frac{\stackrel{·}{\Sigma }}{2{\stackrel{·}{u}}_1}& (13)\end{array}$

where $\stackrel{·}{{ϵ}_1}=2{\stackrel{·}{u}}_1/H$ is the normal strain of the slab and $2{\stackrel{·}{u}}_1$ is the incremental contraction of the thickness H of the slab (see Figure 3). In order to determine E_m, we determine the incremental contraction induced by a unitary incremental value of the compressive macrostress $2{\stackrel{·}{u}}_1=2A_{cell}{\left\{K^{-1}{1}_{\mathrm{\text{E}}}\right\}}_1$, where the column vector 1_E has all components equal to zero, except the first one, set equal to 1. Then (13) becomes

$\begin{array}{ll}{E}_m=\frac{H}{2A_{cell}{\left\{K^{-1}{1}_E\right\}}_1}.& (14)\end{array}$

Analogously, the effective shear modulus of the slab is determined as

$\begin{array}{ll}{G}_m=\frac{Ṫ}{\stackrel{·}{\gamma }}=H\frac{Ṫ}{2{\stackrel{·}{u}}_9}& (15)\end{array}$

where $\stackrel{·}{\gamma }=2{\stackrel{·}{u}}_9/H$ is the incremental shear strain, $2{\stackrel{·}{u}}_9$ is the incremental tangential relative displacement between the two end faces of the slab (see Figure 3) and Ṫ is the incremental effective shear stress applied to the two end faces. As in the previous case, G_m is evaluated by determining the incremental displacement vector induced by a unitary incremental shear stress $A_{cell}{K}^{-1}{1}_{\mathrm{\text{G}}}$, where the column vector 1_G has all components are equal to zero, except the ninth one, set equal to 1. Then (15) becomes

$\begin{array}{ll}G=\frac{H}{2A_{cell}{\left\{K^{-1}{1}_G\right\}}_9}.& (16)\end{array}$

It must be noted that for the three cells here considered the two last diagonal blocks of K are equal scalars. In other words, the only non-zero elements of the two last rows and columns are always the diagonal elements K_9,9 and K_10,10, which are identical. Then (16) can be also written as

$\begin{array}{ll}G=H\frac{K_{9,9}}{2A_{cell}}=H\frac{K_{10,10}}{2A_{cell}}.& (17)\end{array}$

The two last expressions (17) show that the elastic modulus G is independent from the direction of incremental shear macro stress Ṫ, so that the slabs exhibits a transversely isotropic type behavior.

4. Numerical Results

To discuss previous results, consider a slab with thickness H = 100 mm and struts with thin annular sections, whose ratio between the average radius and the thickness is equal to 10. The Young modulus is fixed to E = 200 GPa and the yield stress to σ_y = 200 MPa. The minimum volume density (3) has been determined for values of the design monoaxial macrostress Σ_d in the range [10⁻⁵, 10⁻¹] MPa.

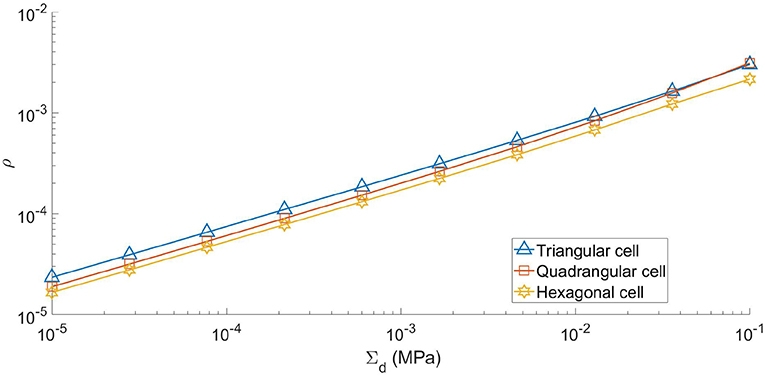
In Figure 4, the optimal density is shown vs. Σ_d for the three tensegrity shapes considered here. As the figure shows, the hexagonal shape is the most convenient. Interestingly we find an almost linear log-log dependence. This “scale invariant” behavior has been previously observed for similar tensegrities in DeTommasi et al. (2015) and had been used in DeTommasi et al. (2017a) to obtain optimal fractal like tensegrity structures.

FIGURE 4

Figure 4. Optimal volume density.

This is coherently reflected in the observation that the optimal value of the geometrical parameter α, which describes the cell geometry, varies only very slightly in the considered range of the design macro stress Σ_d. In particular, for all the three different shapes we have tanα∈[0.10, 0.11]. Interestingly also the optimal prestress parameters β and τ change only very slightly in the considered range of the design macro stress: β∈[1.18, 1.20], τ∈[0.04, 0.05]. We then deduce that our solution identifies an optimal shape which is almost independent from the design macro stress in the considered range. Of course, on the contrary the optimal cross section areas strongly depend on the design macro stress.

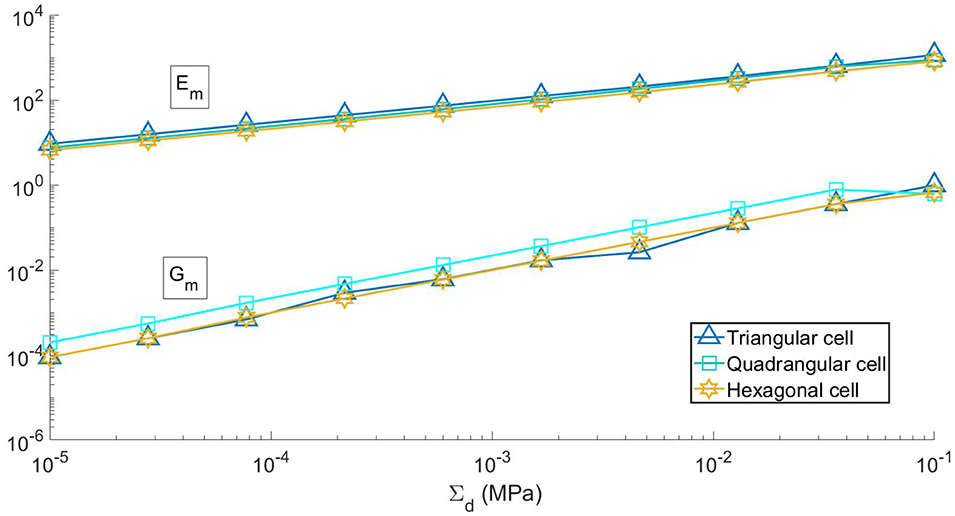
Figure 5 shows the dependence of the macro elastic moduli E_m and G_m of the optimal slabs from the design macro stress Σ_d. Also here we notice that the log-log graph is almost linear. Due to the small values of the shear modulus, we argue that the small deviations from the power law regime of graph can be ascribed to numerical reasons. A very important property of the considered metamaterial is that it is characterized by a difference of several orders of magnitude (from 2 to 5) between the Young's modulus E_m and the tangential elastic modulus G_m, especially for low values of the design macro stress. This feature can be explained by observing that, in the considered range of the design data, the cross sections of the struts are always determined by the local buckling constraints and are much greater than those of the cables, especially for low values of the design macrostress. Furthermore, as we already stated, the optimal value of the angle between the principal cables and the struts is always small (tanα ≃ 0.10).

FIGURE 5

Figure 5. E_m and G_m (MPa) vs. design macro stress.

In Figure 6, we represent the variation of the tangent Young modulus E_m with respect to both the actual applied macrostress Σ and the design macrostresses Σ_d. In particular, for each value of Σ_d it is shown that the tangent macro elastic modulus E_m is almost independent from Σ, which is varying from the unloaded state (Σ = 0) to the loaded state (Σ = Σ_d). Therefore we argue that the proposed metamaterial has a linear behavior with respect to the axial load Σ.

FIGURE 6

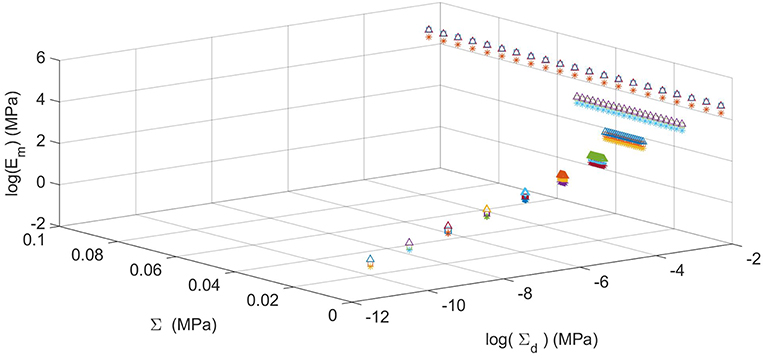
Figure 6. Young modulus vs. the actual macrostress Σ at different values of the design macrostress Σ_d. The symbols ▵, □, *, refer to triangular, quadrangular, and hexagonal cells, respectively.

Similarly, in Figure 7A, we represent the tangent shear modulus G_m (MPa) of the optimal slabs. As in the previous figure, for different fixed design macrostresses Σ_d we analyze its dependence on the actual applied macrostress Σ, with Σ ranging from the unloaded state (Σ = 0MPa) to the loaded state (Σ = Σ_d). We point out that, differently from the previous case, for each value of Σ_d the tangent shear modulus G_m varies with the applied macro stress, even if its decrease (softening) with respect increasing values of the actual macro stress is quite limited. This is shown in detail in Figure 7B for a single fixed value of the design macro stress (Σ_d = 0.1MPa). Observe that the tangent shear modulus G_m decreases linearly as the applied macrostress grows, showing the same slope for the three geometries. A similar softening behavior has been also observed in the non-linear elastic analysis for laminated rubber bearings (see D'Ambrosio et al., 1995). Several augmentations of the obtained interesting behavior of these tensegrity slabs should be obtained by extending the optimization to multiscale tensegrity structures (see e.g., DeTommasi et al., 2015, 2017a) and by considering multilayer slabs.

FIGURE 7

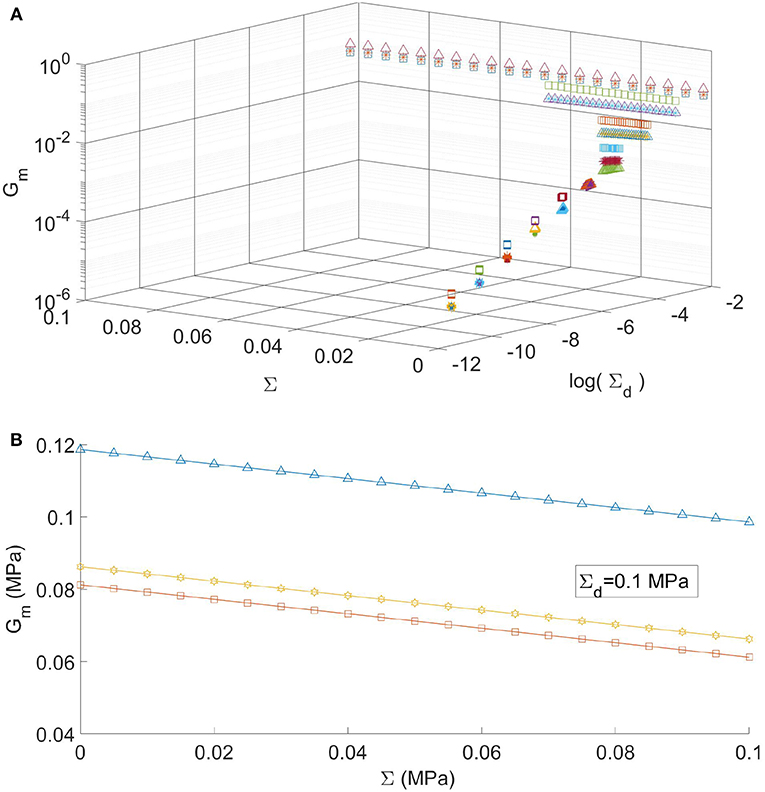
Figure 7. (A) Tangent shear modulus G_m vs. the actual macrostress Σ for different values of the design macrostress Σ_d. The symbols ▵, □, * refer to triangular, quadrangular and hexagonal cells, respectively. (B) Tangent shear modulus vs. the actual macrostress Σ at (Σ_d = 0.1MPa).

Conclusions

In this paper he have optimized a planar metamaterial made up of periodically patterned tensegrity-type unit cells. With reference to different values of the design macro stress we have compared the mechanical responses of three different geometries of unit cells. Further, for each value of the design macro stress the optimal densities are compared, showing that the minimal density metamaterial is made up by hexagonal cells (see Figure 2). As already found previously, the optimal density of these slabs exhibits a log-log dependence on the applied macrostress. Here this result has been extended to the elastic macroscopic response, showing again a power law dependence of the macroscopic elastic moduli on the design macro stress. Interestingly, for each adopted geometry we have found shapes of the optimal tensegrity cells almost independent by the design macro stress. These results suggest a scale-invariant behavior of the proposed metamaterial. Finally, we remark that the optimal proposed metamaterial is characterized by a shear elastic modulus which is up to five orders of magnitude smaller than the Young modulus. This indicates that the proposed scheme of metamaterial is suitable for the design of new isolation devices.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication. In particular, all authors equally contributed to the theoretical modelling, while FT also developed numerical analysis.

Funding

DD and GP have been supported by the Italian Ministry MIUR-PRIN project COAN 5.50.16.01 code 2015JW9NJT.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Amendola, A., Krushynska, A., Daraio, C., Pugno, N. M., and Fraternali, F. (2018). Tuning frequency band gaps of tensegrity mass-spring chains with local and global prestress. Int. J. Solids Struct. 155, 47–56. doi: 10.1016/j.ijsolstr.2018.07.002

CrossRef Full Text | Google Scholar

Bertoldi, K. (2017). Harnessing instabilities to design tunable architected cellular materials. Annu. Rev. Mater. Res. 47, 51–61. doi: 10.1146/annurev-matsci-070616-123908

CrossRef Full Text | Google Scholar

Chen, H., Chan, C. T., and Sheng, P. (2010). Transformation optics and metamaterials. Nat. Mater. 9, 387–396. doi: 10.1038/nmat2743

PubMed Abstract | CrossRef Full Text | Google Scholar

D'Ambrosio, P., DeTommasi, D., and Marzano, S. (1995). Nonlinear elastic deformations and stability of laminated rubber bearings. J. Eng. Mech. 121, 1041–1048. doi: 10.1061/(ASCE)0733-9399(1995)121:10(1041)

CrossRef Full Text | Google Scholar

DeTommasi, D., Maddalena, F., Puglisi, G., and Trentadue, F. (2017a). Fractality in selfsimilar minimal mass structures. J. Mech. Phys. Solids 107, 433–450. doi: 10.1016/j.jmps.2017.07.002

CrossRef Full Text | Google Scholar

DeTommasi, D., Marano, G., Puglisi, G., and Trentadue, F. (2015). Optimal complexity and fractal limits of self-similar tensegrities. Proc. R. Soc. A 471:20150250. doi: 10.1098/rspa.2015.0250

CrossRef Full Text | Google Scholar

DeTommasi, D., Marano, G., Puglisi, G., and Trentadue, F. (2017b). Morphological optimization of tensegrity-type metamaterials. Composites B Eng. 115, 182–187. doi: 10.1016/j.compositesb.2016.10.017

CrossRef Full Text

Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C., et al. (2006). Ultrasonic metamaterials with negative modulus. Nat. Mater. 5, 452–456. doi: 10.1038/nmat1644

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraldi, M., Palumbo, S., Carotenuto, A., Cutolo, A., Deseri, L., and Pugno, N. (2019). Buckling soft tensegrities: fickle elasticity and configurational switching in living cells. J. Mech. Phys. Solids 124, 299–324. doi: 10.1016/j.jmps.2018.10.017

CrossRef Full Text | Google Scholar

Fraternali, F., Carpentieri, G., Amendola, A., Skelton, R., and Nesterenko, V. (2014). Multiscale tunability of solitary wave dynamics in tensegrity metamaterials. Appl. Phys. Lett. 105:201903. doi: 10.1063/1.4902071

CrossRef Full Text | Google Scholar

Fraternali, F., Senatore, L., and Daraio, C. (2012). Solitary waves on tensegrity lattices. J. Mech. Phys. Solids 60, 1137–1144. doi: 10.1016/j.jmps.2012.02.007

CrossRef Full Text | Google Scholar

Hutchinson, R., and Fleck, N. (2006). The structural performance of the periodic truss. J. Mech. Phys. Solids 54, 756–782. doi: 10.1016/j.jmps.2005.10.008

CrossRef Full Text | Google Scholar

Ingber, D. E., Wang, N., and Stamenovic, D. (2014). Tensegrity, cellular biophysics, and the mechanics of living systems. Rep. Progr. Phys. 77:046603. doi: 10.1088/0034-4885/77/4/046603

PubMed Abstract | CrossRef Full Text | Google Scholar

Koohestani, K. (2017). On the analytical form-finding of tensegrities. Composite Struct. 166, 114–119. doi: 10.1016/j.compstruct.2017.01.059

CrossRef Full Text | Google Scholar

Paulose, J., Meeussen, A. S., and Vitelli, V. (2015). Selective buckling via states of self-stress in topological metamaterials. Proc. Natl. Acad. Sci. U.S.A. 112, 7639–7644. doi: 10.1073/pnas.1502939112

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabouni-Zawadzka, A., and Gilewski, W. (2019). Soft and stiff simplex tensegrity lattices as extreme smart metamaterials. Materials 12:187. doi: 10.3390/ma12010187

PubMed Abstract | CrossRef Full Text | Google Scholar

Salahshoor, H., Pal, R., and Rimoli, J. (2018). Material symmetry phase transitions in three-dimensional tensegrity metamaterials. J. Mech. Phys. Solids 119, 382–399. doi: 10.1016/j.jmps.2018.07.011

CrossRef Full Text | Google Scholar

Schittny, R., Buckmann, T., Kadic, M., and Wegener, M. (2013). Elastic measurements on macroscopic three-dimensional pentamode metamaterials. Appl. Phys. Lett. 30:11905. doi: 10.1063/1.4838663

CrossRef Full Text | Google Scholar

Skelton, R., Helton, J., Adhikari, R., Pinaud, J., and Chan, W. (2017). “An introduction to the mechanics of tensegrity structures”, in The Mechanical Systems Design Handbook: Modeling, Measurement, and Control, ed Y. Hurmuzlu (Boca Raton, FL: CRC Press), 872.

Google Scholar

Thomsen, C., Wang, F., and Sigmund, O. (2018). Buckling strength topology optimization of 2d periodic materials based on linearized bifurcation analysis. Comput. Methods Appl. Mech. Eng. 339, 115–136. doi: 10.1016/j.cma.2018.04.031

CrossRef Full Text | Google Scholar

Triantafyllidis, N., and Schnaidt, W. (1993). Comparison of microscopic and macroscopic instabilities in a class of two-dimensional periodic composites. J. Mech. Phys. Solids 41, 1533–1565. doi: 10.1016/0022-5096(93)90039-I

CrossRef Full Text | Google Scholar

Vigliotti, A., Deshpande, V., and Pasini, D. (2014). Non linear constitutive models for lattice materials. J. Mech. Phys. Solids 64, 44–60. doi: 10.1016/j.jmps.2013.10.015

CrossRef Full Text | Google Scholar

Volokh, K., Vilnay, O., and Belsky, M. (2000). Tensegrity architecture explains linear stiffening and predicts softening of living cells. J. Rep. Prog. Phys 33, 1543–1549. doi: 10.1016/S0021-9290(00)00157-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Li, S., Zhu, S., Zhang, B., and Xu, G. (2018). Automatically assembled large-scale tensegrities by truncated regular polyhedral and prismatic elementary cells. Composite Struct. 184, 30–40. doi: 10.1016/j.compstruct.2017.09.074

CrossRef Full Text | Google Scholar