The Influence of a Lattice-Like Pattern of Inclusions on the Attenuation Properties of Metaconcrete

1. Introduction

Metaconcrete is a new type of concrete where engineered inclusions, made of heavy spherical (e. g., steel) cores coated by a compliant (e. g., polymeric) layer, replace part of the traditional stone and gravel aggregates embedded into a standard Portland cement matrix. Because of the unconventional mechanical behavior exhibited under dynamic excitation, metaconcrete is regarded as a metamaterial. Specifically, it has been demonstrated theoretically in Mitchell et al. (2014) and numerically in Mitchell et al. (2015) that, when the frequency range of a dynamic load approaches one of the resonance frequencies of the metaconcrete inclusions, aggregates sequester part of the mechanical energy of the system to activate their resonant behavior, thus reducing the mechanical engagement of the concrete matrix. An explanation of the observed energy sequestration resides in the opposition of phase of the motion of the heavy core with respect to the motion of the matrix.

The dominant resonant oscillation frequency $f_I^T$ of the inclusions is estimated with a simple analytical expression derived from a mass-spring one-dimensional model. A targeted frequency can be tuned by a suitable choice of core and coating materials, core diameter, and coating thickness, cf. Mitchell et al. (2014). The elastic modulus of the coating is the design parameter most influent on the value of $f_I^T$, thus the coating material is the key design parameter, although the choice might be restricted by all important considerations concerning fabrication and durability issues.

Numerical modal analysis conducted on a metaconcrete unit cell revealed the presence of lower and higher eigenfrequencies associated to deformative modes, Mitchell et al. (2014). The brittle behavior of metaconcrete under dynamic load has been investigated numerically modeling fracture within an eigenerosion approach proposed in Pandolfi and Ortiz (2012), revealing a slower propagation of the fracture front and an overall behavior comparable to the one of the standard plain concrete, see Mitchell et al. (2016). The attenuation properties of metaconcrete in the supersonic range (frequencies f > 20 kHz) have been verified in an experimental program conducted on cylindrical samples with randomly disposed inclusions, fabricated according to the ASTM C192/C 12M-06 (Standard Practice for Making and Curing Concrete Test Specimens in the Laboratory), see Briccola et al. (2017).

The concept of metaconcrete is becoming familiar in the literature on metamaterials. An experimental investigation on an epoxy-matrix metaconcrete has been recently described in Kettenbeil and Ravichandran (2018), documenting a reduction of the dynamic strain in the matrix up to 70% with respect to the homogeneous material. The scarce relevance of the stiffness of the matrix where the resonant inclusion is embedded had been pointed out in El Sherbiny and Placidi (2018).

In the broader field of acoustic metamaterials, several recent works investigated the possibility to reduce the amplitude of mechanical waves by playing with the combination of materials and geometries. Khan et al. (2018) demonstrated that a one-dimensional array of resonating cells impacted by a pendulum demonstrated that the arrangement of different local resonators has negligible influence on wave attenuation, while a good design of the system can enhance the performance of elastic metamaterials. By varying the contact interaction between three-component resonant particles disposed in one-dimensional arrays, Bonanomi et al. (2015) proved theoretically and experimentally that is possible to tune the acoustic transmission.

Numerical studies conducted within a two-dimensional setting documented in An et al. (2018) indicated that the vibration attenuation properties of acoustic metamaterials consisting of discrete masses and springs is enhanced by increasing the number of the unit-cells. Numerical investigations discussed in Hu and Oskay (2018) considered transient shear wave propagation in two-dimensional domains characterized by periodic elastic and viscoelastic microstructures using spatial-temporal homogenization procedures. Multiscale nonlocal homogenization that accounts for dispersion and attenuation due to Bragg scattering was presented in Hu and Oskay (2019), and more complex techniques that account for the micro-inertia effects of the inclusions are reported in Sridhar et al. (2016). Multi-layered metamaterials have been also proposed theoretically and numerically (Wang et al., 2017). More in general, investigations on locally resonant acoustic metamaterials are becoming more and more appealing, in the view of producing materials with specific attenuation properties, see Krushynska et al. (2014), or of showing negative properties, see Li et al. (2018), within well defined frequency bands.

Theoretical and numerical studies in the field of civil engineering, where metaconcrete is likely employable, have been reported in Cheng et al. (2018): the dynamic performance of a multi-story frame building structure has been investigated by playing with material and geometrical parameters. Innovative tensegrity structures share the concept of combining materials and geometry to enhance the dynamic performance of the system, cf. Fabbrocino and Carpentieri (2017). Currently, a large part of the civil engineering research in metamaterials focuses in the definition of combinations of materials and geometry that can provide protection against seismic actions, see Krödel et al. (2015). As an additional example, the performance of a I-Girder metamaterial under dynamic excitation has been analyzed numerically in Zhong et al. (2018). Applications of metamaterials in soils have been also investigated in Maleki and Khodakarami (2017) and Dertimanis et al. (2016).

Yet, an accurate experimental investigation of metaconcrete to verify the presence of deformation eigen-modes in the sonic range (frequencies f < 20 kHz) is missing. Furthermore, all numerical tests described in previous works have been conducted using an ideal metaconcrete with a regular disposition of inclusions Mitchell et al. (2014, 2015) and no verification has been done to check whether numerical results are affected by the Bragg scattering. Finally, no investigations have been conducted considering multiple spatial directions of the transmitted signal.

With the objective to verify the observations of previous numerical studies, and to quantify the differences between the theoretical prediction and the actual performance of regularly manufactured specimens, a new experimental program has been planned. The main goals of the present study are to address specifically the presence of eigenfrequencies within the sonic range, to assess the relevance of the regular disposition of the inclusions on the attenuation performance along different directions, and to identify the anisotropy of the resonant behavior due to possible stratification of the components during the casting of the material. The results of this investigation are reported in the present work.

The paper is organized as follows. Section 2 describes the structure of the specimens, the experimental setup, and the experimental program. Section 3 illustrates the outcomes of the experiments. Section 4 collects considerations about the results and draws some conclusions and perspectives.

2. Materials and Methods

Nondestructive tests on metaconcrete specimens loaded with waves spanning the sonic range (400 Hz–12.2 kHz) have been set up at the Laboratory of Materials Testing (LPM) at the Politecnico di Milano, Italy. The test layout was inspired by the specifications in ASTM C215-14 (Standard test method for fundamental transverse, longitudinal, and torsional resonant frequency of concrete specimens).

In the view of the goals of the investigation, specimens were cast in a cubic shape allowing the application of an electro-mechanical mass vibration exciter (transmitting unit) along the three symmetry axes in turn. Two receiving units (piezoelectric transducers), measuring the output signals on the two faces normal to the excited axis, allowed the recording of the frequency-response function of the samples. Details of the specimen casting and of the experimental setup are provided in the following.

2.1. Metaconcrete Specimens

To facilitate the comparison of the attenuation properties of metaconcrete along three mutually orthogonal directions (the casting and other two perpendicular to it), a cubic shape was chosen instead of the prismatic shape recommended by ASTM C215-14. The choice allowed the arrangement of the inclusion in a regular lattice with the same geometrical structure along the three symmetry axes.

Cubic prototypes of metaconcrete (edge d = 15 cm) with regularly disposed inclusions have been cast according to UNI EN 206:2016 (Concrete-Specification, performance, production and conformity) and UNI EN 12390-1:2002 (Testing hardened concrete-Shape, dimensions, and other requirements for specimens and molds).

Specimens were cast using cubic disposable plastic molds using a mortar paste made of a mix of Portland cement, sand, and water. As done in previous experiments documented in Briccola et al. (2017), old-fashion mouse balls have been utilized as resonant inclusions. Commercially available mouse balls made of 10 mm radius steel spheres covered with a 1 mm thickness polydimetilsyloxhane (PDMS) coating matched the fundamental requirement of showing a primary resonance within the sonic range.

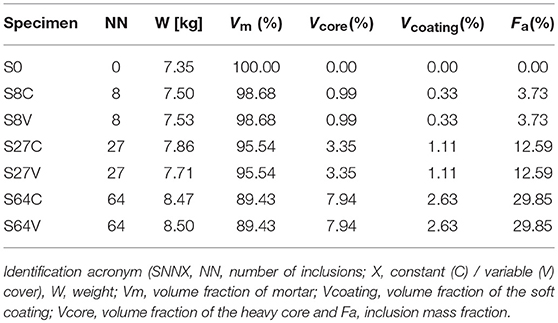
A neutral specimen with no inclusions was cast first to be taken as a reference for the estimate the attenuation properties of metaconcrete, see Figure 1A. Metaconcrete specimens were obtained from two batches of cubic specimens with different lattice length and cement cover. Each batch consisted of three specimens with a three-dimensional grid of 2×2×2, 3×3×3, and 4×4×4 inclusions respectively, see Figures 1B–D. The inclusion patterns are shown in Figure 2.

FIGURE 1

Figure 1. Specimens used in the experiments. (A) S0: specimen without inclusions. (B) S8C-S8V: specimens with 8 inclusions (constant and variable cement cover and interspacing, respectively). (C) S27C-S27V: specimens with 27 inclusions (constant and variable cement cover and interspacing respectively). (D) S64C-S64V: specimens with 64 inclusions (constant and variable cement cover and interspacing respectively).

FIGURE 2

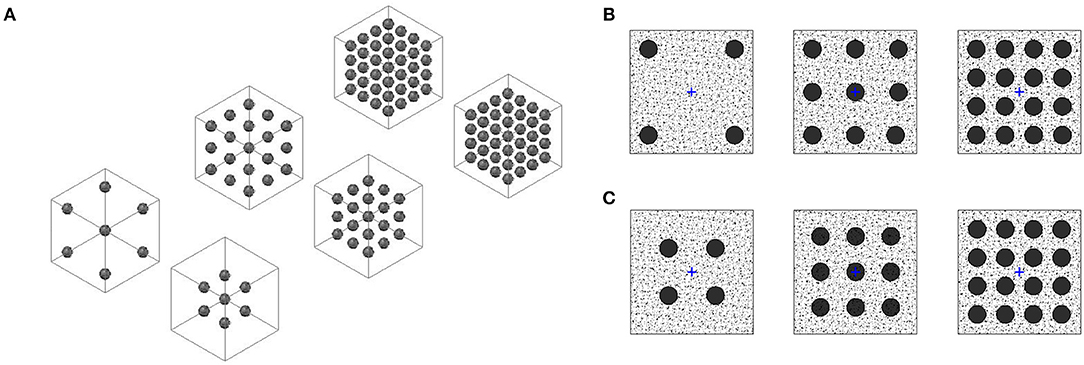
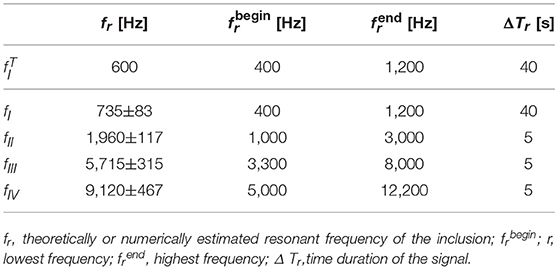
Figure 2. Lattice-like patterns of the two batches of specimens with 8/27/64 inclusions and constant or variable cement cover. (A) Axonometric view of the two batches. (B) Top view of the specimens of batch 1 (S8C/S27C/S64C) with constant cement cover. (C) Top view of the specimens of batch 2 (S8V/S27V/S64V) with variable cement cover.

The particular arrangement of inclusions in the mortar matrix imposed to adopt a specific casting procedure by layers, that required the use of plastic jigs with equi-spaced holes. Once the cement, sand, and water mix was prepared, the first concrete layer (with the thickness of the cover) was poured in the plastic molds. The subsequent layer containing the inclusions was arranged using the plastic jig. A new layer with the thickness of the interspacing was poured. The top surface of the interspacing layer was flattened as much as possible with the aid of a flat plastic jig with no holes. After the setting, each layer was compacted by means of a small tamping rod with rounded ends. To avoid the presence of cavities the external surface of the mold was tapped with a mallet. A lapse of a proper time after the casting of each layer was necessary to avoid the segregation of the inclusions.

Mechanical features of the specimens could be affected by the casting, therefore the casting direction was marked. Next, specimens were moved into the curing room and stored for 24 h. After one day, specimens were removed from molds, polished, and kept in a water storage tank for curing for 28 days. The weight of each specimen is shown in Table 1.

TABLE 1

Table 1. Characteristics of the specimens.

According to the theoretical derivation in Mitchell et al. (2014), by considering each inclusion as an ideal mass-spring system the first natural frequency $f_I^T$ of the inclusion can be estimated as

$\begin{array}{rc}{f}_I^T=\frac{1}{2\pi }\sqrt{\frac{3}{2}\frac{E_s}{R_c{t}_s{\rho }_c}}& (1)\end{array}$

where R_c = 10 mm is the core radius, ρ_c = 7, 850 kg/m³ is the core density, t_s = 1 mm is the coating thickness, and E_s = 750 kPa is the coating elastic modulus, leading to $f_I^T=600$ Hz.

The values of the first four eigenfrequencies and eigen-modes of a unit cell of metaconcrete, geometrically similar to the one used here, were numerically computed by a finite element modal analysis in Mitchell et al. (2014), considering 10 mm radius lead spheres coated with 1 mm or 3 mm thickness rubber or nylon layer. The expected eigenfrequencies of the actual mouse balls, where lead is replaced with steel and rubber or nylon are replaced with PDMS, have been estimated from the values reported in Mitchell et al. (2014) through linear regression, obtaining f_I = 735 ± 83 Hz, f_II = 1, 960 ± 117 Hz, f_III = 5, 715 ± 315 Hz and f_IV = 9, 120 ± 467 Hz.

2.2. Experimental Setup

The experimental setup is shown in Figure 3. The driving circuit included a variable frequency audio oscillator, an amplifier, and a driving unit. The electric signal was triggered by a stand-alone audio oscillator driven by an engineering workbench (LabVIEW) and transformed into a mechanical wave by the driving unit. The driving unit consisted into an electro-mechanical mass vibration exciter (a commercially available VibeTribe Troll 2.0 characterized by 0.38 kg mass, 54 mm diameter, and 54 mm length), featuring a high signal-to-noise ratio. In each test, the vibration speaker was applied to one of the specimen surfaces normal to the excitation direction.

FIGURE 3

Figure 3. Experimental setup, showing a metaconcrete specimen, the two transducers, and the vibration speaker pressurized with a weight to increase adherence.

Two accelerometers (contact piezoelectric shear type transducers-PCB 353B15 SN) were mounted at the center of two opposite faces of the cubic specimens, see Figure 2, and made adherent by a thin layer of wax. The two transducers were used as pickup units for the acceleration at the opposite faces of the specimens. A data acquisition system (4 Channel, 24-Bit Analog Input Modules - NI USB-9239) transformed the accelerations into electric signals. The time-domain electric waveforms labeled Channel 1 represented the signals received at the face opposite to the vibration speaker. The waveforms labeled Channel 2 represented the signals received at the face where the vibration speaker was applied to.

From the geometrical point of view, specimens were characterized by a regular arrangement of inclusions and were expected to show an orthotropic behavior along the symmetry axes. The regularity of the distribution of the in-plane inclusion obtained by means of equi-spaced hole jigs guaranteed that the in-plane behavior along the x and y directions was very similar. Contrariwise, the behavior in the casting direction (the one marked) was expected to differ from the in-plane behavior in the view of possible segregation of the components due to the layered casting procedure. Therefore, specimens were tested dynamically in two directions, x and z.

Linear swept-frequency sinusoidal excitations with constant amplitude A = 2 Vpp were applied to each specimen along both x and z axes. Specimens were regularly rotated as so as the direction of propagation of the signal was always vertical, from top side to bottom side. Measurements were taken for signals transmitted in two opposite directions of each axis by flipping the specimen upside-down, and repeated three times for each specimen.

The range of experimental frequencies spanned by the swept-sine excitation were defined by taking into account both the inclusion eigenfrequencies, estimated theoretically and numerically, and the operative bandwidth of the transducers (±% 10 0.7–18,000 Hz). The width of the interval centered at the eigenfrequency f_r was set equal to 0.8f_r, obtaining the interval $\Delta f_r=f_r^{\text{end}}-f_r^{\text{begin}}$ where

$\begin{array}{rc}{f}_r^{\text{begin}}=(1-0.4)f_r{f}_r^{\text{end}}=(1+0.4)f_r.& (2)\end{array}$

According to Gloth and Sinapius (2004), the attainment of a quasi-steady state response of the specimen within the frequency range Δf_r imposes an upperbound (in Hz/min) to the sweep rate

$\begin{array}{cc}{\dot{f}}_{\text{max}}=54\frac{f_r^2}{Q^2},Q=\frac{1}{2\zeta }& (3)\end{array}$

where f_r is the targeted eigenfrequency, Q the dynamic amplification at the resonant frequency, and ζ a characteristic damping value, that for standard concrete can be assumed ζ = 5.0%. The maximum sweep rate defines, in turn, a minimum experimental time for each frequency range Δf_r as

$\begin{array}{cc}\Delta T_{r \text{min}}=2\pi \frac{\Delta f_r}{{\dot{f}}_{\text{max}}}& (4)\end{array}$

The actual experimental time was incremented by 40% above the minimum, by setting ΔT_r = 1.4ΔT_{r min}. The operative parameters of the linear swept-frequency sinusoidal excitations used in the experiments are listed in Table 2.

TABLE 2

Table 2. Parameters adopted for each frequency range during a linear sweep.

At the beginning of each linear swept-sine excitation, a sine wave with frequency equal to the initial frequency of the sweep was applied for 2 s.

3. Results

Acquired data were stored in sequential files and post-processed with a data-signal processing software. The electric signals were transformed in acceleration time histories through the sensitivity s = 10/9.81 mV s²/m of the piezoelectric transducers. Figure 4 shows an example of the acceleration signal recorded by the transducer located at the face opposite to the vibration speaker. The accelerations signals were characterized by an average value not large enough to become dominant with respect to all the other frequencies considered.

FIGURE 4

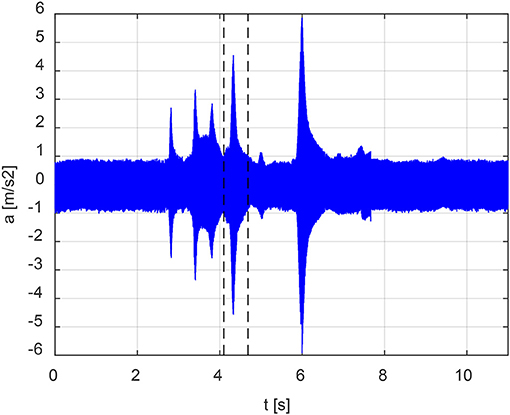
Figure 4. Example of time history recorded by the transducer located at the opposite face with respect to the vibration speaker for tests performed on the specimen without inclusions. A linear swept-sine excitation with a start frequency of 1,000 Hz and an end frequency of 3,000 Hz has been applied in 10s.

All acceleration records were analyzed by means of the Fast Fourier Transform (FFT) algorithm using a tracking low-pass filter in order to reduce noise at high frequencies. A feature of tracking filters, applied only to the frequency domain, is the preservation of the phase of the signal, thus the behavior of metaconcrete at resonance is expected to be captured.

The FFT has been evaluated on specific time domain windows covering the time intervals of interest. The time windows were set on the basis of the lowest and highest estimated eigenfrequencies that were expected to occur within the frequency band of the input signal reported in Table 2.

The operative procedure for the calculation of the time interval is explained with reference to the acceleration signal reported in Figure 4 referring to the zero inclusion specimen. After the initial 2 s sine-wave signal, a linear swept-sine excitation in the range 1,000–3,000 Hz has been applied in a 5 s time interval. The second eigenfrequency was estimated as f_II = 1, 960 Hz, thus the frequency bounds for the definition of the time interval were 1,843 and 2,077 Hz respectively, cf. Table 2. Therefore, the activation of the resonance of the inclusions was expected to occur within a time window comprised between 4.10 and 4.68 s, visualized with two broken vertical lines in Figure 4. Interestingly, although the specimen was normal concrete, the plot pointed out a resonance of the standard concrete.

Due to a linear swept-sine excitation, the FFT power-spectra are characterized by continuous plots between the frequency bounds of each eigenfrequency of the material. An example of FFT is visualized in Figure 5, with reference to Figure 4. The left graph represents the acceleration signal windowed in the bounded time interval (note that the time scale has been reset with respect to Figure 4). The right plot visualizes the corresponding amplitude of the FFT, which appears as a continuous line within the frequency limits 1,843 and 2,077 Hz.

FIGURE 5

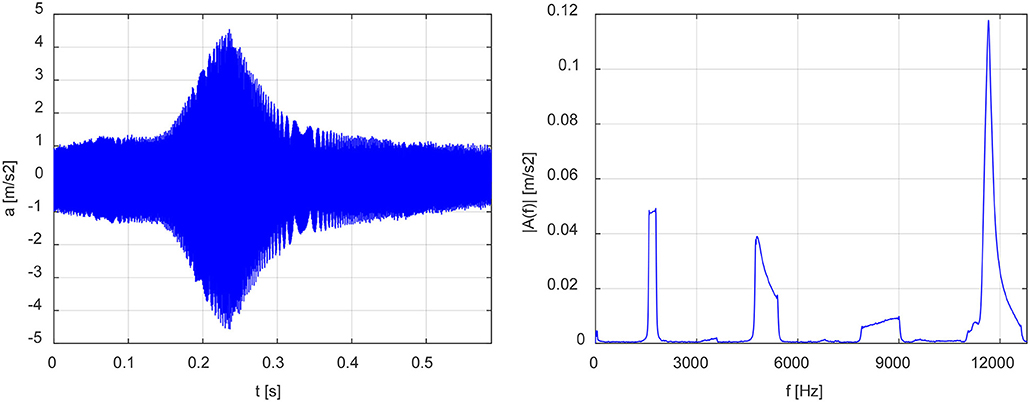
Figure 5. Example of the windowed time history and the corresponding FFT. A linear swept-sine excitation with a start frequency of 1,000 Hz and an end frequency of 3,000 Hz has been applied in 10 s. Frequency limits of about 1,800 and 2,000 Hz have been imposed for the FFT.

The value of the power-spectrum within the frequency bands of interest for the first four expected eigenfrequencies has been considered as indicative of the dynamic behavior of the material. Thus, the comparison between the behavior of plain concrete specimen and metaconcrete specimens has been conducted in terms of power-spectrum amplitude. The comparison includes all the tests conducted on all the metaconcrete samples, differing by number of inclusions and by cement cover.

For each specimen and each direction of excitation (x or z), the amplitude |A|_N of the power-spectrum corresponding to each frequency band was evaluated as the average of the power-spectra values falling within the band in the three corresponding time-history accelerations. The response of the seven specimens measured in linear swept-sine excitations along the x-axis, backward and forward, is reported in Table 3. The columns labeled η_N contain the efficiency ratio, defined as

$\begin{array}{rc}{\eta }_{\text{N}}=\frac{|A{|}_{\text{N}}-|A{|}_0}{|A{|}_0}& (5)\end{array}$

where |A|₀ is the amplitude referred to the zero inclusion specimen. Figure 6A visualizes the average amplitudes |A|_N for all the specimens considering the two direction of excitation. Figure 6B plots the corresponding efficiency η_N. Figures 6C,D report the same plots for the tests in direction z.

TABLE 3

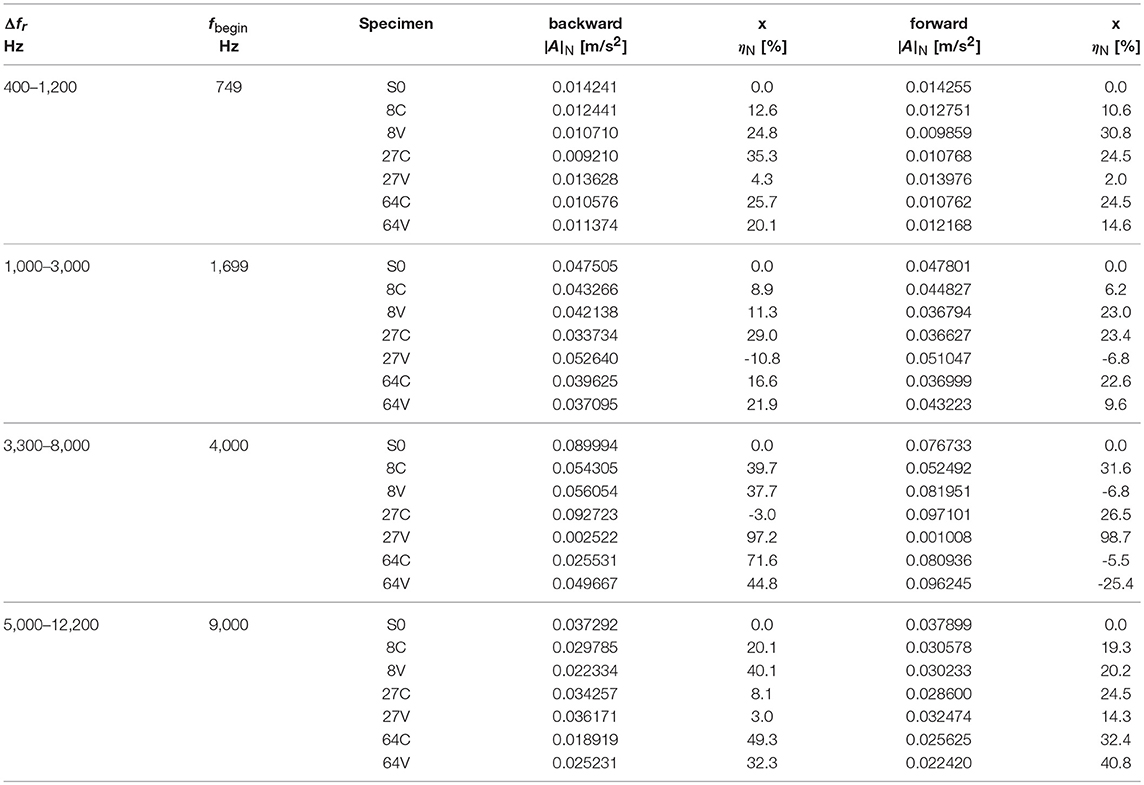
Table 3. Attenuation performance of specimens characterized by different both inclusion spacings and cement cover for linear swept-sine excitations along the x-axis, backward and forward.

FIGURE 6

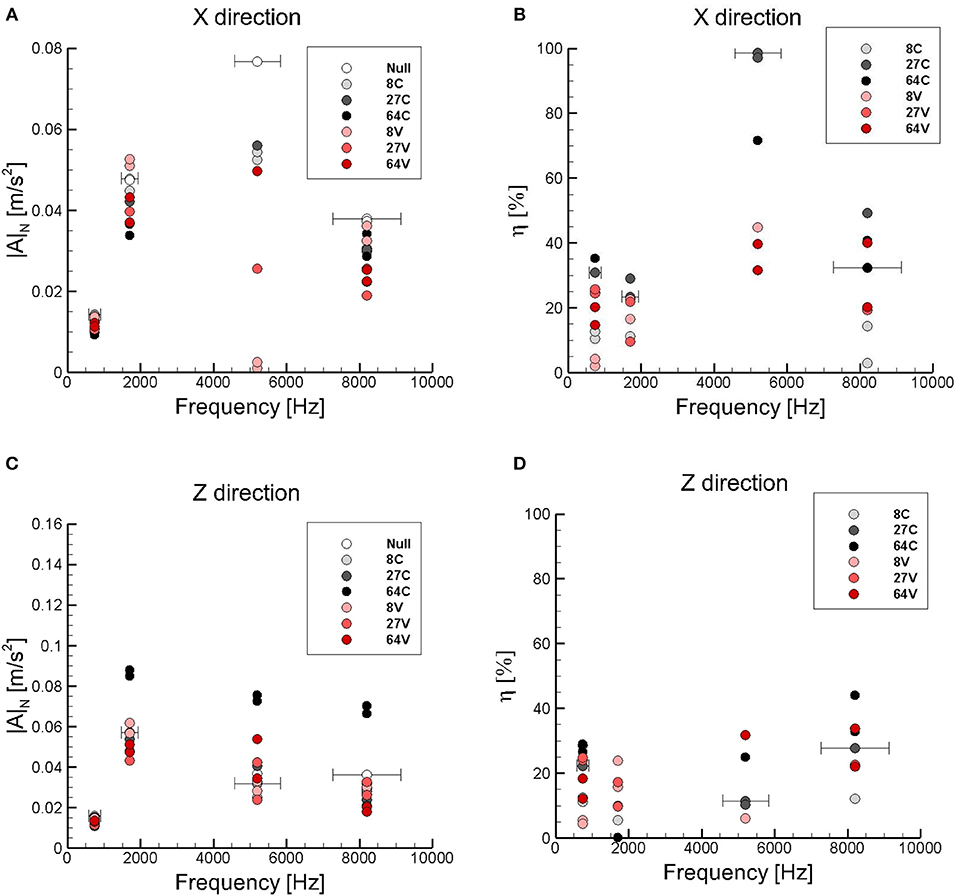
Figure 6. Values of the FFT acceleration amplitude |A|_N and efficiency η_N averaged in the eigenfrequency bands (visualized by the horizontal bars) for the seven specimens. Signal transmitted in x and z directions. (A) Average FFT acceleration amplitude for signal in x direction. (B) Efficiency for x direction. (C) Average FFT acceleration amplitude for signal in z direction. (D) Efficiency for z direction.

4. Discussion

The experimental program conducted on metaconcrete samples newly casted was planned with the aim of exploring the sonic range of frequency, and of revealing whether the regularity and the symmetry of the pattern of the inclusion may cause reductions or differences in the efficiency of waves attenuation, with respect to the behavior observed in the first experimental validation of metaconcrete, see Briccola et al. (2017).

Because of the different specimen geometry, the experimental setup differed from the one used in Briccola et al. (2017). First, a transient signal in the form of a linear swept-frequency sinusoidal excitation was chosen instead of a discretely dwelled-frequency sinusoidal waveform. This choice was done to exclude the possibility to miss the actual resonant behavior of the inclusions. Second, four windows of frequencies were defined centered at the numerically estimated resonance frequencies, to offer the opportunity to explore in larger detail the region where resonant is expected to occur. This choice was suggested by the observation that a linear sweep in the frequency range of interest may represent a good compromise between the amplitude of excitation needed and time necessary to perform all the tests on the seven specimens and to post-process the signals, cf. Gloth and Sinapius (2004).

The results, averaged over six (three forward and three backward), of the linear swept-sine excitation tests in direction x are collected in Table 2. The ratio η_N can be considered as a measure of the attenuation properties of the metaconcrete within each eigenfrequency band. The experimental values indicated that, with respect to the plain concrete, metaconcrete specimens reduce the average amplitude of the acceleration power-spectra up to 60%. The beneficial behavior was observed in particular for higher eigenfrequencies and more densely packed specimens, while at the lowest eigenfrequency the average reduction of the amplitude lowered to 20–30%.

In general, results indicated that the efficiency of metaconcrete increased with the density of the inclusions, while tests did not show a marked dependence on the cement cover. Table 2 shows that the first two experimental eigenfrequencies, estimated with a numerical analysis, were very close to the theoretical estimate $f_I^T$, Equation (1). In general, the third and fourth eigenvalues are not predictable from the composition and microstructure of metaconcrete and there is not any theoretical suggestion of their values. The two highest eigenvalues were related to a higher attenuation of the transmitted signal. Regrettably, the tackled frequencies were in the high side of the range of interest of this research, although still within the sound spectra.

The tests in x direction conducted on the specimen labeled 27 V gave contradictory results and were not considered in the subsequent analyses. The anomalous behavior was probably related to the imperfect casting of the specimen, which exhibited several holes and gaps on the surface. In fact, the abnormal average attenuation observed for this specimen (98%) was probably due to the presence of voids that activated a mechanism of wave attenuation different from the energy trapping typical of metaconcrete. The tests in y direction were perfectly corresponding to the test in the x direction. Also in this case, specimen 27 V did not behave in the expected manner.

The tests conducted in z direction did not provide uniform results. Also in this case, the anomalies could be attributed to the sub-segregation of the components due to the casting procedure. A refined casting technique can be implemented to avoid this problem before performing other tests.

A direct comparison with the results obtained in Briccola et al. (2017) was not possible, since in the present analysis attenuation ratios averaged over frequency intervals, instead of single values, have been considered. The type of attenuation parameter considered is necessarily less marked than the one introduced in the previous study (direct comparison of the output signal magnitude). In the present setup, where the vibration was originated by a speaker, there was no the possibility to measure an input signal that could be used to define the attenuation of the single specimen. Therefore, the choice was to compare the behavior of metaconcrete specimens and the behavior of the plain concrete specimen.

In this terms, the conclusion on the results of the experimental program can be drawn as follows. Tests confirmed that metaconcrete provides attenuation of the acceleration signal within a limited range of frequencies centered at one of the numerically predicted resonant frequencies. The attenuation in lattice-like patterned specimens was not affected by the direction of the signal along the horizontal symmetry axis, while the behavior in vertical direction was rather different, suggesting the possible segregation of the inclusions. No differences were observed in the inversion of the direction of the signal.

As far as the attenuation due to Bragg scattering was concerned, tests were not able to reveal an evidence of the phenomenon and the influence of it on the global attenuation properties. Probably the small size of the specimens, with respect to the size of the inclusions, was not sufficient to establish the quantitative contribution of the phenomenon.

Data Availability

The dataset generated for this study can be requested to the authors.

Author Contributions

DB planned the experimental program, conducted part of the tests, and contributed to the writing of the paper. MT conducted the remaining tests and elaborated the results into tables and figures. TN has designed and cast the specimens. AP has supervised the research and completed the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The kind assistance of Marco Cucchi and Massimo Iscandri in the setup of the tests is gratefully acknowledged.

References

An, X., Fan, H., and Zhang, C. (2018). Elastic wave and vibration bandgaps in two-dimensional acoustic metamaterials with resonators and disorders. Wave Motion 80, 69–81. doi: 10.1016/j.wavemoti.2018.04.002

CrossRef Full Text | Google Scholar

Bonanomi, L., Theocharis, G., and Daraio, C. (2015). Wave propagation in granular chains with local resonances. Phys. Rev. 91:033208. doi: 10.1103/PhysRevE.91.033208

PubMed Abstract | CrossRef Full Text | Google Scholar

Briccola, D., Ortiz, M., and Pandolfi, A. (2017). Experimental validation of metaconcrete blast mitigation properties. J. Appl. Mech 84:6. doi: 10.1115/1.4035259

CrossRef Full Text | Google Scholar

Cheng, Z., Lin, W., and Shi, Z. (2018). Wave dispersion analysis of multi-story frame building structures using the periodic structure theory. Soil Dyn. Earthq. Eng. 106, 215–230. doi: 10.1016/j.soildyn.2017.12.024

CrossRef Full Text | Google Scholar

Dertimanis, V., Antoniadis, I., and Chatzi, E. (2016). Feasibility analysis on the attenuation of strong ground motions using finite periodic lattices of mass-in-mass barriers. J. Eng. Mech. 142:04016060. doi: 10.1061/(ASCE)EM.1943-7889.0001120

CrossRef Full Text | Google Scholar

El Sherbiny, M. G., and Placidi, L. (2018). Discrete and continuous aspects of some metamaterial elastic structures with band gaps. Arch. Appl. Mech. 88, 1725–1742. doi: 10.1007/s00419-018-1399-1

CrossRef Full Text | Google Scholar

Fabbrocino, F., and Carpentieri, G. (2017). Three-dimensional modeling of the wave dynamics of tensegrity lattices. Composite Struct. 173, 9–16. doi: 10.1016/j.compstruct.2017.03.102

CrossRef Full Text | Google Scholar

Gloth, G., and Sinapius, M. (2004). Analysis of swept-sine runs during modal identification. Mech. Syst. Signal Proc. 18, 1421–1441. doi: 10.1016/S0888-3270(03)00087-6

CrossRef Full Text | Google Scholar

Hu, R., and Oskay, C. (2018). Spatial–temporal nonlocal homogenization model for transient anti-plane shear wave propagation in periodic viscoelastic composites. Comput. Methods Appl. Mech. Eng. 342, 1–31. doi: 10.1016/j.cma.2018.07.037

CrossRef Full Text | Google Scholar

Hu, R., and Oskay, C. (2019). Multiscale nonlocal effective medium model for in-plane elastic wave dispersion and attenuation in periodic composites. J. Mech. Phys. Solids 124, 220–243. doi: 10.1016/j.jmps.2018.10.014

CrossRef Full Text | Google Scholar

Kettenbeil, C., and Ravichandran, G. (2018). Experimental investigation of the dynamic behavior of metaconcrete. Int. J.Impact Eng. 111, 199–207. doi: 10.1016/j.ijimpeng.2017.09.017

CrossRef Full Text | Google Scholar

Khan, M., Li, B., and Tan, K. (2018). Impact load wave transmission in elastic metamaterials. Int. J. Impact Eng. 118, 50–59. doi: 10.1016/j.ijimpeng.2018.04.004

CrossRef Full Text | Google Scholar

Krödel, S., Thomé, N., and Daraio, C. (2015). Wide band-gap seismic metastructures. Extreme Mech. Lett. 4, 111–117. doi: 10.1016/j.eml.2015.05.004

CrossRef Full Text | Google Scholar

Krushynska, A. O., Kouznetsova, V. G., and Geers, M. G. D. (2014). Towards optimal design of locally resonant acoustic metamaterials. J. Mech. Phys. Solids 71, 179–196. doi: 10.1016/j.jmps.2014.07.004

CrossRef Full Text | Google Scholar

Li, Z., Hu, H., and Wang, X. (2018). A new two-dimensional elastic metamaterial system with multiple local resonances. Int. J. Mech. Sci. 149, 273–284. doi: 10.1016/j.ijmecsci.2018.09.053

CrossRef Full Text | Google Scholar

Maleki, M., and Khodakarami, M. (2017). Feasibility analysis of using metasoil scatterers on the attenuation of seismic amplification in a site with triangular hill due to sv-waves. Soil Dyn. Earthq. Eng. 100, 169–182. doi: 10.1016/j.soildyn.2017.05.036

CrossRef Full Text | Google Scholar

Mitchell, S. J., Pandolfi, A., and Ortiz, M. (2014). Metaconcrete: designed aggregates to enhance dynamic performance. J. Mech. Phys. Solids 65, 69–81. doi: 10.1016/j.jmps.2014.01.003

CrossRef Full Text | Google Scholar

Mitchell, S. J., Pandolfi, A., and Ortiz, M. (2015). Investigation of elastic wave transmission in a metaconcrete slab. Mech. Mater. 91, 295–303. doi: 10.1016/j.mechmat.2015.08.004

CrossRef Full Text | Google Scholar

Mitchell, S. J., Pandolfi, A., and Ortiz, M. (2016). Effect of brittle fracture in a metaconcrete slab under shock loading. J. Eng. Mech. 142. doi: 10.1061/(ASCE)EM.1943-7889.0001034

CrossRef Full Text | Google Scholar

Pandolfi, A., and Ortiz, M. (2012). An eigenerosion approach to brittle fracture. Int. J. Numeric. Methods Eng. 92, 694–714. doi: 10.1002/nme.4352

CrossRef Full Text | Google Scholar

Sridhar, A., Kouznetsova, V., and Geers, M. (2016). Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput. Mech. 57, 423–435. doi: 10.1007/s00466-015-1254-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Liu, Z., Gao, L., Xu, D., and Zhuang, Z. (2017). Analytical and numerical modeling on resonant response of particles in polymer matrix under blast wave. Comput. Mater. Sci. 140, 70–81. doi: 10.1016/j.commatsci.2017.08.034

CrossRef Full Text | Google Scholar

Zhong, R., Pai, P. F., Zong, Z., Deng, H., and Ruan, X. (2018). Metamaterial i-girder for vibration absorption of composite cable-stayed bridge. J. Eng. Mech. 144:04018045. doi: 10.1061/(ASCE)EM.1943-7889.0001467

CrossRef Full Text | Google Scholar