- 1Civil, Architectural and Environmental Engineering Department, Drexel University, Philadelphia, PA, United States
- 2Laboratory of Acoustics and Noise Control, Swiss Federal Laboratories for Materials Science and Technology (EMPA), Dübendorf, Switzerland
The study aims at investigating the effect of a generic state of prestress on the passbands and bandgaps of a phononic crystal plate. To this end, an Updated Lagrangian scheme is developed, consisting in a two-step procedure: first, a static geometrically nonlinear analysis of a representative unit cell undergoing the action of an applied external load is conducted and then the Floquet-Bloch decomposition is applied to the linearized equations of the acousto-elasticity for the unit cell in the deformed configuration. In addition, a formula for the calculation of the energy velocity is proposed. In the case of an epoxy plate with cylindrical steel inclusions, it is shown that, even in the presence of prestress inducing full reversible deformation state, the bandgap experiences a shift towards higher frequencies when the cell is subjected to a compressive prestress, whereas a frequency downshift is registered when the cell is subjected to traction. In particular, it is demonstrated that the frequency downshift of the bandgap for the phononic plate undergoing a tensile prestress is approximately 3.5% with respect to the case of the phononic plate under compression. The results presented herein provide insights in the behavior of phononic crystal plates with tunable dispersive properties, and suggest new leverages for wave manipulation valuable in many application fields such as wave filters, waveguiding and beam splitting, sensing devices, and vibration shielding.
1. Introduction
The propagation of elastic waves in periodic structures is governed by the elastomorphic and material parameters of its unit cell (Kushwaha and Halevi, 1994; Sainidou et al., 2005). Properly conceiving their design in terms of size, shape, and arrangement, as well as choosing their density and elastic properties demonstrated great potential for attaining exceptional dynamic behavior, such as frequency bandgaps (Kushwaha and Halevi, 1994; Mártinez-Sala et al., 1995; Liu et al., 2000; Miniaci et al., 2018a), negative refraction (Morvan et al., 2010; Zhu et al., 2014; Zhu and Semperlotti, 2016), topological protection (Mousavi et al., 2015; Süsstrunk and Huber, 2015; Pal et al., 2016; Miniaci et al., 2018b), etc. This opened up new perspectives in many fields, ranging from microelectromechanical systems to nondestructive evaluation (Pennec et al., 2010; Craster and Guenneau, 2012; Deymier, 2013), including but not limited to wave filters, waveguiding and beam splitting, sensing devices, wave splitters, vibration shielding, subwavelength imaging (Sukhovich et al., 2009; Li et al., 2015; Trainiti et al., 2015; Colombi et al., 2016; Miniaci et al., 2016, 2017; Su et al., 2016; Miniaci et al., 2019).
However, most of the configurations proposed so far are limited by the fact that their unconventional dynamic properties are accessible to specific frequencies only, once the unit cell design is conceived, being its geometrical and mechanical properties constant with respect to time. To overcome this limitation, periodic systems with adaptive elastic properties have received great attention in the recent years. Indeed, introducing an additional degree of freedom, enables the reversible tailoring of the dispersive diagram of the structure, considerably enhancing their functionality and technological applications. To achieve this goal, several approaches have been proposed and explored so far. They include active systems, such as piezoelectric materials (Casadei et al., 2010; Bergamini et al., 2014; Kherraz et al., 2016), temperature (Jim et al., 2009; Airoldi et al., 2011; Cheng et al., 2011; Wu et al., 2018) and magneto-based techniques (Robillard et al., 2009; Matar et al., 2012; Guo and Wei, 2016; Zhang et al., 2017), actuated polymers via electromagnetic waves (Walker et al., 2014, 2017) as well as the application of an external mechanical load. Among them, the latter has shown to be particularly promising to achieve tunable dispersive properties. Bigoni et al. (2008) formulated a theoretical model for an orthotropic, prestressed (compressible) elastic layer vibrating on an elastic half space assuming long-wave asymptotics for the solution. It was found that the influence of the prestress over bandgaps and passbands, so that it could be exploited as a tuning parameter to shift the dispersion curves of the system. A modeling tool for the prediction of controlled bandgap structures responding to flexural vibrations was provided by Gei et al. (2009), also relaxing the hypothesis of perfect periodicity, allowing thus to consider quasi-periodic structures (Gei, 2010). Wang and Bertoldi (2012) showed how mechanical deformations enabled the tuning of the phononic bandgaps in 3D periodic elastomeric structures. The ability of the elastomers to undergo small as well as large strain deformations guaranteed the reversibility and repeatability of the process. Both the linear and nonlinear regimes of elastic deformation were explored, including different geometrical topology for triggering mechanical instability. Galich et al. (2016) showed how local deformations experienced by a composite structure can bring to local stiffening influencing the instability-induced interfaces on elastic wave propagation in finitely deformed layered materials. Finally, Norris and Parnell (2012) tried to exploit the effects of the prestress to theoretically show the feasibility of a hyperelastic cloaking via transformation elasticity.
In this paper, the effects of an applied mechanical load on the dispersive diagram for phononic crystal plates is investigated in the case of elastic deformations, so to have a complete reversibility of the phenomena. The paper is organized as follows: section 2 provides the description of an Updated Lagrangian scheme, in which a representative unit cell of the phononic crystal plate is studied in its static and dynamic deformed configurations. In section 3, the procedure to extract the band diagrams and in particular the energy velocity using the equations described in section 2 is detailed. Finally, section 4 investigates the effect of a reversible compressive and tensile state of prestress on an epoxy plate with cylindrical inclusions.
2. Floquet-Bloch Analysis of a Prestressed Phononic Crystal
2.1. Static Analysis
In what follows, the equations of static and dynamic equilibrium are derived with reference to the generic infinite phononic crystal (PC) shown in Figure 1, where C0 indicates the static undeformed configuration, C the static configuration resulting from the application of an external load, and C′ the dynamic configuration undergoing a harmonic motion. The so called Updated Lagrangian (UL) scheme is employed to analyze the PC in the three different equilibrium configurations. The UL approach consists of two steps: in the first step, C0 is used as the reference configuration to calculate the displacement and stress fields relative to the configuration C, while in the second step, C is used as the new reference configuration to evaluate the dynamic equilibrium of the unit cell in the configuration C′.
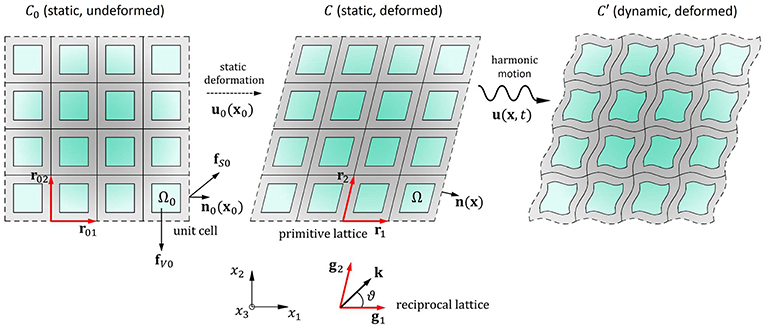
Figure 1. Schematic representation of the Updated Lagrangian (UL) scheme for the infinite phononic crystal (PC) plate.
Due to the periodicity of the system under consideration, in the undeformed configuration C0 any scalar, vector or tensor function ϕ satisfies the condition ϕ(x0 + r0m) = ϕ(x0), where m ∈ ℤ2 and r0 = [r01, r02] is the matrix of lattice vectors. This allows to restrict the computational domain to a unit cell of domain Ω0 and boundary ∂Ω0 (Collet et al., 2011; Mazzotti et al., 2017). Similarly, the unit cell in the configuration C satisfies the periodic condition ϕ(x + rm) = ϕ(x), with r = [r1, r2]. For this cell, the mapping between the coordinates of a material point in C0 and the coordinates of the same point in C is established by the deformation gradient F(x0) = ∇0x = I + ∇0u0, where ∇0 denotes the gradient operator defined with respect to C0, u0 is the pseudo-static displacement resulting from the application of external, Ω0-periodic, volume (fV) and surface (tS) loads. Following Zhang and Parnell (2017), the deformation gradient can be decomposed as F(x0) = FL(x0)FP(x0), where FL indicates the affine deformation gradient of the lattice points such that r = FLr0, while FP denotes a periodic non-affine deformation.
The specific material density of the unit cell in C0 is ρ0(x0), while, assuming a hyperelastic material behavior described by the Murnaghan's model (Murnaghan et al., 1937; Pau and Lanza di Scalea, 2015; Dubuc et al., 2017, 2018), the tensor of tangential elastic moduli with respect to C0 is expressed by , where the elastic energy density Ψ has the form
in which λ and μ denote the first and second Lamé parameters, respectively, (l, m, n) the third order Murnaghan parameters, C = FT F the right Cauchy-Green deformation tensor, the Green-Lagrange strain tensor and I1(E), I2(E), and I3(E) its first, second and third invariants, respectively.
Finding the coordinates of the deformed configuration C and the associated stress fields requires the solution of a variational functional of the form (Bonet and Wood, 2008)
subjected to the Dirichlet boundary conditions
in which δu0 is an arbitrary admissible kinematic variation of u0(x0), S = D0 : E the second Piola-Kirchhoff stress tensor and n(x0) the outward pointing normal at x0 ∈ ∂Ω0. The application of a standard Galerkin approach to Equation (2) results in the generalized system of equations
where K(Q0) is a static stiffness matrix, P0 represents the global vector of nodal forces, Q0 denotes a global vector of independent nodal displacements and Γ0 is a mapping operator resulting from Equation (3) and realizing the condition U0 = Γ0Q0, in which U0 indicates the full vector of nodal displacements. In this work, the solution of Equation (4) is carried out using the weak form module implemented in Comsol Multiphysics 5.3 (Comsol, 2017).
2.2. Geometry and Mechanical Properties Updating
Once the set of independent static displacements Q0 is obtained, the reference configuration is updated from C0 to C by calculating the corresponding nodal coordinates x = x0 + Γ0Q0(x0). The updated material properties in C are given by and , while the Cauchy stress tensor is obtained from the relation σ = (det F)−1 FSFT. The geometry of the unit cell in the configuration C is then re-meshed and used as the basis for the linear dynamic analysis presented in the next section.
2.3. Dynamic Analysis Using the Floquet-Bloch Decomposition
Assuming C as the new reference configuration, the position vector for the unit cell in the dynamic deformed configuration C′ is given by x′ = x + u(x, t), where u(x, t) = u(x)exp(−iωt) is a time-harmonic perturbation superimposed on C, being t the time and ω the angular frequency. In the rest of the paper, the time-dependence exp(−iωt) is dropped for conciseness. According to the small-on-large displacement hypotheses usually assumed in acousto-elasticity (Mazzotti et al., 2012; Pau and Lanza di Scalea, 2015; Shim et al., 2015), only small perturbations u(x, t) are considered. In this case, the approximations x′ ≈ x and C′ ≈ C hold and any displacement-dependent vector and tensor field can be obtained in a linearized incremental form. Following this procedure, the stress tensor is linearized in the direction of u(x, t) by applying a first order Taylor series expansion of σ(x) about x, resulting in (Mazzotti et al., 2012)
where denotes the linearized Green-Lagrange strain tensor.
From the application of the Floquet-Bloch theorem, any small harmonic perturbation u(x) can be expressed in the form (Collet et al., 2011)
in which is a Ω-periodic displacement amplitude and k ∈ Λ is the Bloch wavenumber vector, being Λ the reciprocal unit cell defined in C by the reciprocal lattice vector basis gj, j = 1, 2, satisfying the condition ri · gj = 2πδij, where δij is the Kronecker delta. These are related to the reciprocal lattice vector basis g0j in C0 by , j = 1, 2 (Zhang and Parnell, 2017). In the reciprocal lattice domain, the Bloch wavenumber vector is described in terms of its orientation angle ϑ as k(ϑ) = kΦ(ϑ), where ϑ is defined with respect to g1, k = ‖k(ϑ)‖2 and Φ(ϑ) = {cosϑ, sinϑ, 0}T. The relation between the orientation vector in C0 and C writes .
From Equation (6), and by defining the k-shifted gradient of a generic Ω-periodic vector field as
the solution of the elastodynamic problem for free vibrations of the unit cell in C subjected to an initial stress σ0 can be obtained from the variational statement
subjected to the Dirichlet boundary condition
in which (·)* stands for the conjugate of a complex vector or tensor field, follows from Equation (7) and n(x) represents the outpointing surface normal at x ∈ ∂Ω. After the application of a Galerkin discretization scheme, Equations (8) and (9) lead to the following generalized linear eigenvalue problem
which forms the basis of the band structure analysis for the prestressed PC. In Equation (10), Γ is a mapping operator implementing the Dirichlet boundary condition in Equation (9) such that is verified, where is the global vector of nodal displacement amplitudes and a subvector of collecting only its independent components. The mass operator M and the stiffness operators K1, K2, and K3 are given by
where Ω(e) denotes the domain of the e-th finite element of the mesh, ⋃e(·) stands for the standard direct stiffness assembling procedure, N(x) is a matrix of shape functions for the e-th element, Σ0(x) is a block-diagonal matrix of the form
while the different compatibility operators are expressed as
being zi a unit vector identifying the i-th coordinate in the Cartesian frame of reference. The operators Li and L0i are given in the Appendix. It should be noted that, since the mass and stiffness matrices in Equations (11)–(14) are evaluated with respect to the deformed configuration C, a new mesh for the deformed geometry of the unit cell needs to be generated after the static analysis described in section 2.1 has been completed and before the eigenvalue analysis is carried out.
3. Band Structure Analysis and Energy Velocity Extraction
The homogeneous problem in Equation (10) can be solved in the wavenumber k(ϑ, ω) and corresponding Floquet eigenvectors for any fixed direction ϑ and circular frequency ω ∈ ℝ, ω > 0, from which the band structures of the propagation and attenuation constants of a specific mode m are obtained by taking the real and imaginary components of the corresponding wavenumber km(ϑ, ω), respectively. For the particular case of a lossless structure (Im(D) = 0) immersed in vacuum, the modes supported by the crystal can be either propagative (Im(k) = 0) or evanescent (Re(k) = 0), the latter belonging to the so called deaf frequency range (bandgap).
In addition to the Bloch wavenumber k(ϑ, ω), from the computed set of solutions (km(ϑ, ω), Qm(ϑ, ω)) it is possible to extract the band structure of the energy velocity, which corresponds to the velocity of propagation of packets of waves having close central frequency (Brillouin, 1953; Mazzotti et al., 2012). The energy velocity of a specific Bloch mode can be found as the ratio between the time-averaged energy flux in the direction ϑ over one period T = 2π/ω and the time-averaged total mechanical energy over the same period, i.e.
where denotes the time-averaging operation, (ϑ, ω) denotes the total energy flux along the orientation ϑ of the Bloch wavenumber k, (ϑ, ω) indicates the total kinetic energy while (ϑ, ω) and σ0(ϑ, ω) represent the total stored elastic energy related to the harmonic motion and prestress, respectively. The time-averaged expressions for these quantities are given by
Equation (18) can be evaluated at any given solution km(ϑ, ω) by means of a Gauss quadrature scheme over the finite element mesh of the unit cell in the configuration C, in which the displacement, strain and stress fields can be post-processed from Qm(ϑ, ω) using nodal interpolations.
4. Numerical Applications: Epoxy Plate With Cylindrical Steel Inclusions
The numerical method presented in the previous section is here applied to study a PC plate made of steel cylinders embedded in an epoxy matrix. In the undeformed configuration, the plate is 2.5 mm thick, while the cylindrical inclusions have a radius of 3.0 mm and are arranged in a square lattice of 10.0 mm side length, as shown in Figure 2A. The material properties for the steel and the epoxy are reported in Table 1.
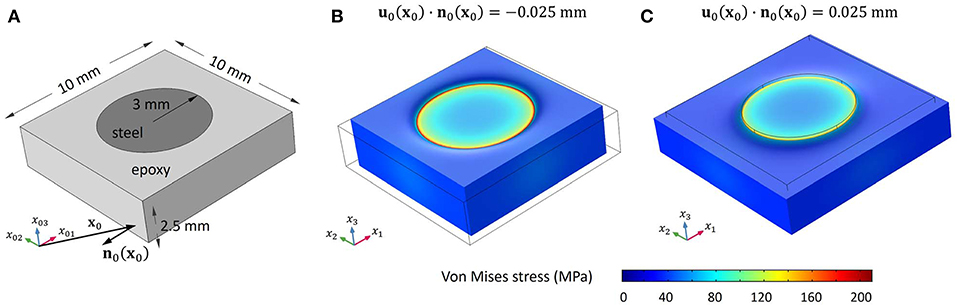
Figure 2. Unit cell of steel cylinders embedded in an epoxy matrix: undeformed geometry (A) and deformed geometry corresponding to isotropic traction (B) and compression (C). The deformation scale is amplified of 20 times.
To study how an initial state of stress affects the passbands and bandgaps of the PC plate, two different deformed configuration are considered. In the first configuration, the plate is subjected to a state of compressive stress representative of a normal displacement u0(x0) · n0(x0) = −0.025 mm applied at each point x0 belonging to a lateral face of the unit cell. In the second case, a generic tensile state is applied by assuming a normal displacement u0(x0) · n0(x0) = 0.025 mm for each point x0 belonging to a lateral face of the unit cell. Figures 2B,C report the von Mises stress consequent to the compression and tension prestress condition, respectively. It is worth noticing that the maximum magnitude of the applied prestretch has been limited to the typical strength at yield of both epoxy and steel in order to ensure the elastic behavior of the materials. This choice enables a full reversibility of the undeformed configuration, and thus of the dispersive behavior of the PC plate, once the load is removed, which is of more practical interest with respect to the case of a permanently induced deformation.
The band diagrams in terms of wavenumber k and energy velocity ce versus frequency are shown in Figure 3. In these diagrams, the blue and red dots denote the dispersion curves relative to the unit cell subjected to the compressive stress and tensile stress shown in Figures 2B,C, respectively. It should be noted that, since the deformation due to prestress applied to each face of the cell is isotropic in the xy-plane in both cases, the deformation gradient F and its affine component FL are diagonal and, as a consequence, the orientation of the reciprocal lattice vectors gj in the deformed configurations does not change with respect to that in the deformed configuration. This implies that the orientation angle θ of the Bloch wavevector also remains unchanged between the undeformed and deformed configurations. The results presented in Figure 3 have been obtained for an angle θ = 0 measured with respect to g01 and g1. In classical Bloch analysis, this angle corresponds to the Γ − X direction of the irreducible Brillouin zone.
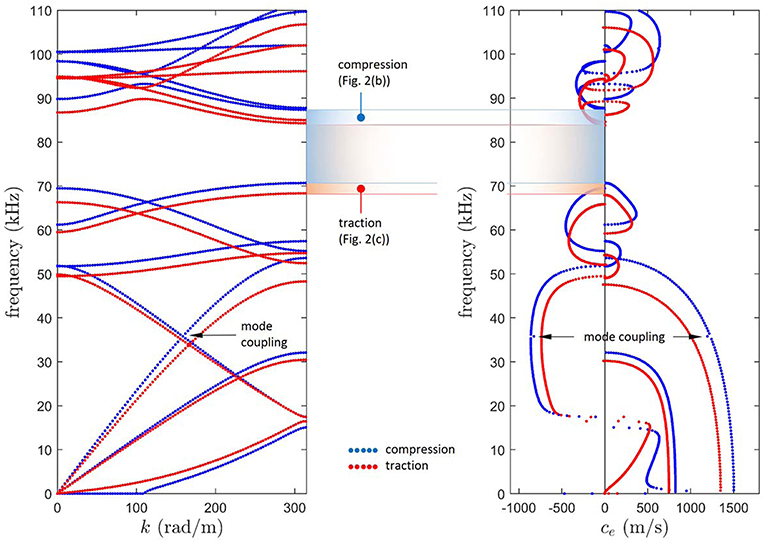
Figure 3. Band diagrams of the wavenumber k (Left) and energy velocity ce (Right) versus frequency for the PC plate under isotropic compression and isotropic traction reported in Figures 2B,C, respectively.
From the dispersion analysis of the undeformed unit cell, it can be found that, at frequencies below 110 kHz, only one bandgap is present along the direction ϑ = 0, which is located in the [68.3–88.6] kHz frequency range (see Figure A1 in Appendix B). This result, which has not been reported in the Figure 3 for the sake of clarity, can be readily obtained by carrying out the analysis of sections 2.3 and 3 on the undeformed geometry and by setting σ0 = 0 in Equation (15). However, when the cell is subjected to a compressive stress as shown in Figure 2B, the bandgap experiences a shift towards higher frequencies, being it located, in this case, in the [70.7 − 87.3] kHz frequency range. On the other hand, when the cell is subjected to traction, the lower bound of the bandgap is observed at 68.3 kHz while its upper bound at 84.3 kHz, which corresponds to a frequency downshift of approximately 3.5% of the bandgap with respect to the case of the PC plate under compression. These results suggest that, even in the elastic regime, a deformation due to prestress can lead to significant changes in the passband and bandgap behavior.
Furthermore, looking at the behavior of the energy velocity for the two deformed configurations, it is possible to infer that, similarly to the case of homogeneous plates (Pau and Lanza di Scalea, 2015), a generic state of compression leads to an increase of the energy velocity, whereas a state of traction leads, in general, to its decrease. This situation can be readily deduced from the inspection of the energy velocity band diagrams in Figure 3, from which it can be noted that the largest variations take place in proximity of the cutoff frequencies. Moreover, in the case of prestressed homogeneous plates (Dubuc et al., 2017), characteristic spikes in the energy velocity dispersion curves appear due to mode coupling. This behavior can also be observed for the third fundamental mode at around 36 kHz when the PC plate is subjected to a compression.
Finally, in the case of the PC plate under compression, it is possible to observe the presence of a cutoff wavenumber for the first fundamental mode at about 108 rad/m and null frequency. This value can be derived by solving the eigenvalue problem reported in Equation (10) in k(ϑ) by imposing ω = 0. In this case, the eigenvalue problem corresponds to that of the buckling load and, consequently, the lowest eigenvalue (the cutoff wavenumber) corresponds to a bifurcation point that indicates the onset of buckling for the infinite PC plate. It should be noted that the specific value of the cutoff wavenumber depends on the magnitude and distribution of the compressive stress in the PC.
5. Conclusions
An Updated Lagrangian computational scheme has been presented for the calculation of the band diagrams of phononic crystal plates subjected to a generic state of prestress. The scheme involves the solution of a geometrically nonlinear static problem for a representative unit cell and the application of the Floquet-Bloch theorem to the linearized equations of acousto-elasticity on the deformed configuration of the unit cell undergoing the static load. For the case of an epoxy plate with cylindrical steel inclusions, it has been demonstrated that the existence of a prestress state of compression or tension can lead to significant changes in the passbands and bandgaps of a phononic crystal plate, even in the case of prestress inducing full reversible deformation state, which is of more practical interest with respect to the case of a permanently induced deformation. It has been observed that when the cell is subjected to a compressive stress, the bandgap experiences a shift toward higher frequencies, whereas when the cell is subjected to traction, we observe a frequency downshift of approximately the 3.5% of the bandgap with respect to the case of the phononic plate under compression. Similarly to the case of homogeneous plates, a generic state of compression leads to an increase of the energy velocity, whereas a state of traction tends to lower its value. The largest variations have been observed in proximity of the cutoff frequencies. Characteristic spikes in the energy velocity dispersion curves appear due to mode coupling for the third fundamental mode at around 36 kHz when the phononic plate is subjected to a compression.
The results presented herein provide insights in the behavior of phononic crystal plates with tunable dispersive properties, and suggest new leverages for wave manipulation valuable in many application fields such as wave filters, waveguiding and beam splitting, sensing devices, and vibration shielding.
Author Contributions
MMa and MMi conceived the idea and wrote the first draft of the paper. MMa performed numerical calculations. All the authors discussed the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with MMa.
Acknowledgments
MMi has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement N. 754364.
References
Airoldi, L., and Ruzzene, M. (2011). Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos. New J. Phys. 13:113010. doi: 10.1088/1367-2630/13/11/113010
Bergamini, A., Delpero, T., De Simoni, L., Di Lillo, L., Ruzzene, M., and Ermanni, P. (2014). Phononic crystal with adaptive connectivity. Adv. Mater. 26, 1343–1347. doi: 10.1002/adma.201305280
Bigoni, D., Gei, M., and Movchan, A. (2008). Dynamics of a prestressed stiff layer on an elastic half space: filtering and band gap characteristics of periodic structural models derived from long-wave asymptotics. J. Mech. Phys. Solids 56, 2494–2520. doi: 10.1016/j.jmps.2008.02.007
Bonet, J., and Wood, R. D. (2008). Nonlinear Continuum Mechanics for Finite Element Analysis. New York, NY: Cambridge University Press.
Brillouin, L. (1953). Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 2nd Edn. New York, NY: Dover Publications (1953).
Casadei, F., Ruzzene, M., Dozio, L., and Cunefare, K. A. (2010). Broadband vibration control through periodic arrays of resonant shunts: experimental investigation on plates. Smart Mater. Struct. 19:015002. doi: 10.1088/0964-1726/19/1/015002
Cattani, C., and Rushchitsky, J. (2007). Wavelet and Wave Analysis as Applied to Materials with Micro or Nanostructure. Singapore: World Scientific.
Cheng, Y., Liu, X. J., and Wu, D. J. (2011). Temperature effects on the band gaps of lamb waves in a one-dimensional phononic-crystal plate (l). J. Acoust. Soc. Am. 129, 1157–1160. doi: 10.1121/1.3543970
Collet, M., Ouisse, M., Ruzzene, M., and Ichchou, M. (2011). Floquet-bloch decomposition for the computation of dispersion of two-dimensional periodic, damped mechanical systems. Int. J. Solids Struct. 48, 2837–2848. doi: 10.1016/j.ijsolstr.2011.06.002
Colombi, A., Colquitt, D., Roux, P., Guenneau, S., and Craster, R. V. (2016). A seismic metamaterial: the resonant metawedge. Sci. Rep. 6:27717. doi: 10.1038/srep27717
Comsol (2017). Comsol Multiphysics 5.3. Available online at: https://www.comsol.com/
Craster, R. V., and Guenneau, S. (2012). Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking. Springer Series in Materials Science. London: Springer (2012).
Deymier, P. A. (2013). Acoustic Metamaterials and Phononic Crystals, Springer Series in Solid-State Sciences. Berlin; Heidelberg: Springer (2013).
Dubuc, B., Ebrahimkhanlou, A., and Salamone, S. (2017). The effect of applied stress on the phase and group velocity of guided waves in anisotropic plates. J. Acoust. Soc. Am. 142, 3553–3563. doi: 10.1121/1.5016969
Dubuc, B., Ebrahimkhanlou, A., and Salamone, S. (2018). Higher order longitudinal guided wave modes in axially stressed seven-wire strands. Ultrasonics 84, 382–391. doi: 10.1016/j.ultras.2017.12.003
Galich, P., Slesarenko, V., and Rudykh, S. (2016). Elastic wave propagation in soft microstructured composites undergoing finite deformations. PAMM 16, 627–628. doi: 10.1002/pamm.201610302
Gei, M. (2010). Wave propagation in quasiperiodic structures: stop/pass band distribution and prestress effects. Int. J. Solids Struct. 47, 3067–3075. doi: 10.1016/j.ijsolstr.2010.07.008
Gei, M., Movchan, A., and Bigoni, D. (2009). Band-gap shift and defect-induced annihilation in prestressed elastic structures. J. Appl. Phys. 105:063507. doi: 10.1063/1.3093694
Guo, X., and Wei, P. (2016). Dispersion relations of elastic waves in one-dimensional piezoelectric/piezomagnetic phononic crystal with initial stresses. Ultrasonics 66, 72–85. doi: 10.1016/j.ultras.2015.11.008
Jim, K. L., Leung, C. W., Lau, S. T., Choy, S. H., and Chan, H. L. W. (2009). Thermal tuning of phononic bandstructure in ferroelectric ceramic/epoxy phononic crystal. Appl. Phys. Lett. 94:193501. doi: 10.1063/1.3136752
Kherraz, N., Haumesser, L., Levassort, F., Benard, P., and Morvan, B. (2016). Controlling bragg gaps induced by electric boundary conditions in phononic piezoelectric plates. Appl. Phys. Lett. 108:093503. doi: 10.1063/1.4943138
Kushwaha, M. S., and Halevi, P. (1994). Band gap engineering in periodic elastic composites. Appl. Phys. Lett. 64, 1085–1087. doi: 10.1063/1.110940
Li, J., Wu, F., Zhong, H., Yao, Y., and Zhang, X. (2015). Acoustic beam splitting in two-dimensional phononic crystals using self-collimation effect. J. Appl. Phys. 118:144903. doi: 10.1063/1.4932138
Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally resonant sonic materials. Science 289, 1734–1736. doi: 10.1126/science.289.5485.1734
Mártinez-Sala, R., Sancho, J., Sánchez, J. V., Gomez, V., Llinares, J., and Meseguer, F. (1995). Sound attenuation by sculpture. Nature 378:241. doi: 10.1038/378241a0
Matar, O. B., Robillard, J. F., Vasseur, J. O., Hladky-Hennion, A.-C., Deymier, P. A., Pernod, P., et al. (2012). Band gap tunability of magneto-elastic phononic crystal. J. Appl. Phys. 111:054901. doi: 10.1063/1.3687928
Mazzotti, M., Marzani, A., Bartoli, I., and Viola, E. (2012). Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the safe method. Int. J. Solids Struct. 49, 2359–2372. doi: 10.1016/j.ijsolstr.2012.04.041
Mazzotti, M., Miniaci, M., and Bartoli, I. (2017). Band structure analysis of leaky bloch waves in 2d phononic crystal plates. Ultrasonics 74, 140–143. doi: 10.1016/j.ultras.2016.10.006
Miniaci, M., Gliozzi, A. S., Morvan, B., Krushynska, A., Bosia, F., Scalerandi, M., et al. (2017). Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys. Rev. Lett. 118:214301. doi: 10.1103/PhysRevLett.118.214301
Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016). Large scale mechanical metamaterials as seismic shields. N. J. Phys. 18:083041. doi: 10.1088/1367-2630/18/8/083041
Miniaci, M., Mazzotti, M., Radzieski, M., Kherraz, N., Kudela, P., Ostachowicz, W., et al. (2018a). Experimental observation of a large low-frequency band gap in a polymer waveguide. Front. Mater. 5:8. doi: 10.3389/fmats.2018.00008
Miniaci, M., Pal, R. K., Manna, R., and Ruzzene, M. (2019). Valley based splitting of topologically protected helical waves in elastic plates. arXiv 1811.04814.
Miniaci, M., Pal, R. K., Morvan, B., and Ruzzene, M. (2018b). Experimental observation of topologically protected helical edge modes in patterned elastic plates. Phys. Rev. X 8:031074. doi: 10.1103/PhysRevX.8.031074
Morvan, B., Tinel, A., Hladky-Hennion, A.-C., Vasseur, J., and Dubus, B. (2010). Experimental demonstration of the negative refraction of a transverse elastic wave in a two-dimensional solid phononic crystal. Appl. Phys. Lett. 96:101905. doi: 10.1063/1.3302456
Mousavi, S. H., Khanikaev, A. B., and Wang, Z. (2015). Topologically protected elastic waves in phononic metamaterials. Nat. Comm. 6:8682. doi: 10.1038/ncomms9682
Murnaghan, F. D. (1937). Finite deformations of an elastic solid. Amer. J. Math. 59, 235–260. doi: 10.2307/2371405
Norris, A. N., and Parnell, W. J. (2012). Hyperelastic cloaking theory: transformation elasticity with pre-stressed solids. Proc. R. Soc. Lond. A 468, 2881–2903. doi: 10.1098/rspa.2012.0123
Pal, R. K., Schaeffer, M., and Ruzzene, M. (2016). Helical edge states and topological phase transitions in phononic systems using bi-layered lattices. J. Appl. Phys. 119:084305. doi: 10.1063/1.4942357
Pau, A., and Lanza di Scalea, F. (2015). Nonlinear guided wave propagation in prestressed plates. J. Acoust. Soc. Am. 137, 1529–1540. doi: 10.1121/1.4908237
Pennec, Y., Vasseur, J. O., Djafari-Rouhani, B., Dobrzyśki, L., and Deymier, P. A. (2010). Two-dimensional phononic crystals: examples and applications. Surf. Sci. Rep. 65, 229–291. doi: 10.1016/j.surfrep.2010.08.002
Robillard, J.-F., Matar, O. B., Vasseur, J. O., Deymier, P. A., Stippinger, M., Hladky-Hennion, A.-C., et al. (2009). Tunable magnetoelastic phononic crystals. Appl. Phys. Lett. 95:124104. doi: 10.1063/1.3236537
Sainidou, R., Stefanou, N., Psarobas, I., and Modinos, A. (2005). A layer-multiple-scattering method for phononic crystals and heterostructures of such. Comput. Phys. Commun. 166, 197–240. doi: 10.1016/j.cpc.2004.11.004
Shim, J., Wang, P., and Bertoldi, K. (2015). Harnessing instability-induced pattern transformation to design tunable phononic crystals. Int. J. Solids Struct. 58, 52–61. doi: 10.1016/j.ijsolstr.2014.12.018
Su, X., and Norris, A. N. (2016). Focusing, refraction, and asymmetric transmission of elastic waves in solid metamaterials with aligned parallel gaps. J. Acoust. Soc. Am. 139, 3386–3394. doi: 10.1121/1.4950770
Sukhovich, A., Merheb, B., Muralidharan, K., Vasseur, J. O., Pennec, Y., Deymier, P. A., et al. (2009). Experimental and theoretical evidence for subwavelength imaging in phononic crystals. Phys. Rev. Lett. 102:154301. doi: 10.1103/PhysRevLett.102.154301
Süsstrunk, R., and Huber, S. D. (2015). Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50. doi: 10.1126/science.aab0239
Trainiti, G., Rimoli, J. J., and Ruzzene, M. (2015). Wave propagation in periodically undulated beams and plates. Int. J. Solids Struct. 75–76, 260–276. doi: 10.1016/j.ijsolstr.2015.08.019
Walker, E., Reyes, D., Rojas, M. M., Krokhin, A., Wang, Z., and Neogi, A. (2014). Tunable ultrasonic phononic crystal controlled by infrared radiation. Appl. Phys. Lett. 105:143503. doi: 10.1063/1.4894489
Walker, E. L., Wang, Z., and Neogi, A. (2017). Radio-frequency actuated polymer-based phononic meta-materials for control of ultrasonic waves. NPG Asia Mater. 9:e350. doi: 10.1038/am.2016.209
Wang, L., and Bertoldi, K. (2012). Mechanically tunable phononic band gaps in three-dimensional periodic elastomeric structures. Int. J. Solids Struct. 49, 2881–2885. doi: 10.1016/j.ijsolstr.2012.05.008
Wu, Y., Yu, K., Yang, L., Zhao, R., Shi, X., and Tian, K. (2018). Effect of thermal stresses on frequency band structures of elastic metamaterial plates. J. Sound Vibrat. 413, 101–119. doi: 10.1016/j.jsv.2017.10.014
Zhang, P., and Parnell, W. J. (2017). Soft phononic crystals with deformation-independent band gaps. Proc. R. Soc. A Math. Phys. Eng. Sci. 473:20160865. doi: 10.1098/rspa.2016.0865
Zhang, S., Shi, Y., and Gao, Y. (2017). Tunability of band structures in a two-dimensional magnetostrictive phononic crystal plate with stress and magnetic loadings. Phys. Lett. A 381, 1055–1066. doi: 10.1016/j.physleta.2017.01.044
Zhu, H., and Semperlotti, F. (2016). Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Phys. Rev. Lett. 117:034302. doi: 10.1103/PhysRevLett.117.034302
Zhu, Q., Burtin, C., and Binetruy, C. (2014). Acoustoelastic effect in polyamide 6: linear and nonlinear behaviour. Polym. Testing 40, 178–186. doi: 10.1016/j.polymertesting.2014.09.007
Zhu, R., Liu, X. N., Hu, G. K., Sun, C. T., and Huang, G. L. (2014). Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 5, 241–241. doi: 10.1038/ncomms6510
Appendix A
The operators Li and L0i are expressed as
Appendix B
The band diagram in terms of wavenumber k and energy velocity ce for the undeformed unit cell of Figure 2 at ϑ = 0 is reported in Figure A1.
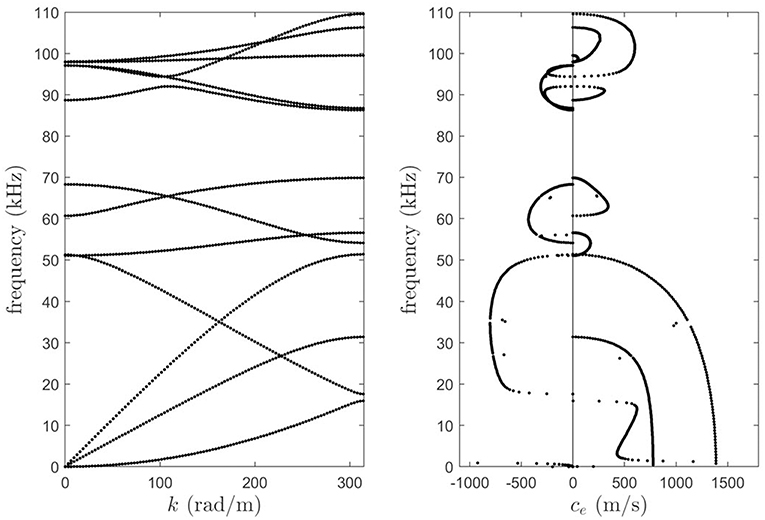
Figure A1. Band diagrams of the wavenumber k (Left) and energy velocity ce (Right) vs. frequency for the PC plate in the undeformed configuration reported in Figure 2A.
Keywords: phononic crystals, prestress, Floquet-Bloch, energy velocity, acousto-elasticity, Comsol
Citation: Mazzotti M, Bartoli I and Miniaci M (2019) Modeling Bloch Waves in Prestressed Phononic Crystal Plates. Front. Mater. 6:74. doi: 10.3389/fmats.2019.00074
Received: 13 January 2019; Accepted: 05 April 2019;
Published: 24 April 2019.
Edited by:
Nicola Maria Pugno, University of Trento, ItalyReviewed by:
Paolo S. Valvo, University of Pisa, ItalyEnrico Babilio, University of Naples Federico II, Italy
Copyright © 2019 Mazzotti, Bartoli and Miniaci. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marco Miniaci, bWFyY28ubWluaWFjaUBnbWFpbC5jb20=
 Matteo Mazzotti1
Matteo Mazzotti1 Marco Miniaci
Marco Miniaci