- 1Institute of Materials Research, Materials Mechanics, Helmholtz-Zentrum Geesthacht, Geesthacht, Germany
- 2Institute of Continuum and Materials Mechanics, Hamburg University of Technology (TUHH), Hamburg, Germany
- 3Institute of Materials Physics and Technology, Hamburg University of Technology (TUHH), Hamburg, Germany
- 4School of Mechanical Engineering and School of Computational Science and Engineering, Georgia Institute of Technology, Atlanta, GA, United States
- 5Institute of Product and Process Innovation, Leuphana University of Lüneburg, Lüneburg, Germany
Machine learning tools represent key enablers for empowering material scientists and engineers to accelerate the development of novel materials, processes and techniques. One of the aims of using such approaches in the field of materials science is to achieve high-throughput identification and quantification of essential features along the process-structure-property-performance chain. In this contribution, machine learning and statistical learning approaches are reviewed in terms of their successful application to specific problems in the field of continuum materials mechanics. They are categorized with respect to their type of task designated to be either descriptive, predictive or prescriptive; thus to ultimately achieve identification, prediction or even optimization of essential characteristics. The respective choice of the most appropriate machine learning approach highly depends on the specific use-case, type of material, kind of data involved, spatial and temporal scales, formats, and desired knowledge gain as well as affordable computational costs. Different examples are reviewed involving case-by-case dependent application of different types of artificial neural networks and other data-driven approaches such as support vector machines, decision trees and random forests as well as Bayesian learning, and model order reduction procedures such as principal component analysis, among others. These techniques are applied to accelerate the identification of material parameters or salient features for materials characterization, to support rapid design and optimization of novel materials or manufacturing methods, to improve and correct complex measurement devices, or to better understand and predict fatigue behavior, among other examples. Besides experimentally obtained datasets, numerous studies draw required information from simulation-based data mining. Altogether, it is shown that experiment- and simulation-based data mining in combination with machine leaning tools provide exceptional opportunities to enable highly reliant identification of fundamental interrelations within materials for characterization and optimization in a scale-bridging manner. Potentials of further utilizing applied machine learning in materials science and empowering significant acceleration of knowledge output are pointed out.
Introduction
A key motivation of applying machine learning methods in continuum materials mechanics is the prospect of enabling, accelerating or even simplifying the discovery and development of novel materials for future deployment. One of the main challenges is to gain information on how to tailor material characteristics in order to generate a successful combination of (all) anticipated properties and performance attributes. Therefore, identifying coupled physical phenomena at different spatiotemporal scales, accounting for statistical uncertainties and controlling the parameter space within the materials structures are core interests in designing (new) materials for specific applications. For scale-bridging, to couple the effects of process parameters to microstructural features and to resulting material properties and performance characteristics, it is also important to consider the statistical variance of the process at hand. Additionally, with respect to a more fundamental level, data mining enables scientists to investigate and understand complex nonlinear relationships. In these cases, data mining and machine learning approaches often appear as intermediate steps in approaching and penetrating a problem until a point where the nature of the relationship of interest can be captured by more general physics-based models replacing the trained algorithms. More specifically, machine learning approaches based on rigorous statistical approaches (e.g., Bayesian inference) offer unique opportunities to calibrate objectively (based on available data) unknown model forms and/or parameter values in physics-based models.
Methodology wise, there are soft boundaries between the disciplines of data mining and machine learning that are both also related to the discipline of applied statistics, as they compose toolsets in data science. These methods cannot be seen separately, as they are strongly interrelated (Witten et al., 2011). The process for data mining according to the cross-industry standard (Chapman et al., 1999) consists typically of (i) problem understanding; (ii) data understanding; (iii) data preparation; (iv) data modeling and (v) data evaluation via machine learning; as well as (vi) deploying the trained algorithm. Hence, the application of machine learning and data mining approaches usually involve an adequate pre-processing of the relevant data as well as training, testing and validating the applied algorithms. Subsequently, post-learning tasks such as feature optimization and decision-making are frequently performed for the prescriptive purpose of optimization.
For challenges within continuum materials mechanics, different databased approaches were proposed in literature. Due to the different spatial and temporal scales of various data that are often involved, we are addressing the issues along the process-structure-property-performance (p-s-p-p) chain. Therefore, we are dividing our review of different machine learning and data mining approaches into four main sections depending on the main field of application: process parameters, microstructure, mechanical properties and performance. Furthermore, each field is divided into three categories that refer to the type of machine learning or data mining task and pursued objective: descriptive (e.g., identifying unknown patterns), predictive (e.g., approximations based on available knowledge) and prescriptive (e.g., optimization based on machine learning controlled decision-making). This differentiation is according to Delen and Ram (2018) formulated for business analytics. Similarly, Tan et al. (2009) divided machine learning tasks into two major categories: predictive and descriptive. However, in the context of materials mechanics and process-structure-property-performance linkages, a prescriptive machine learning task section appears suitable to account for implemented optimizations. Consequently, we follow the subsequent classification of the different approaches investigated in this review:
A descriptive approach is of explanatory nature and means that patterns within data can be recognized based on correlations, trends or anomalies to answer questions on “why does microstructure Y with properties Z occur for process parameter X and how do they affect materials performances such as fatigue and failure?”
A predictive approach is used to foresee specific consequences induced by certain factors; thus, previously non-existing results are generated through applying correlation, regression, classification, or statistical inference techniques to process and analyze existing data for answering questions such as “what kind of microstructure Y will occur with particular properties Z if process parameter X is changed?”
A prescriptive approach in this context means to provide insight on “what should be done in terms of process parameters X to obtain microstructure Y with properties Z?” to not only identify and predict but also to implement optimized results with respect to improved actions, e.g., in terms of a process-microstructure-property relation.
A preliminary collection of descriptions about important machine learning methods is provided, as they are used either solely or diversely combined in the different studies discussed. In this regard, Witten et al. (2011) states: “Experience shows that no single machine learning scheme is appropriate to all data mining problems. The universal learner is an idealistic fantasy. As […] real datasets vary, and to obtain accurate models the bias of the learning algorithm must match the structure of the domain. Data mining is an experimental science.” The selection of studies presented in this article is based on the applicability of machine learning and data mining approaches to solve challenges in continuum materials mechanics and by no means exhaustive. An overview on linking process, structure, property and performance characteristics for additive manufacturing of metals via data analytics was provided by Smith et al. (2016). They focused on computational and experimental methods. Machine learning methods are not allocated into a unique class of methods but can be contained under subsections of the reduced-order modeling section of different data sources relevant for data analytics and data mining, as shown in Figure 1.
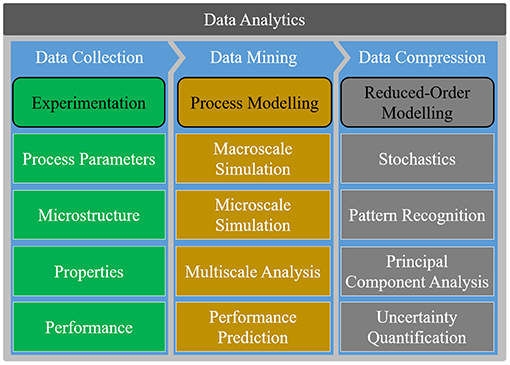
Figure 1. Overview of different data analytics methods applicable within the field of continuums materials mechanics, motivating to develop accurate and comprehensive databases and to make them accessible. Three data sources compose a common data structure: experiments, process models and reduced order models. Experiments lead to empirical determination of characteristics along the p-s-p-p chain. With process models, these characteristics can be described and predicted. Via reduced order models, data can be compressed and patterns recognized. Available data can be analyzed via data mining and machine learning to generate new knowledge. Own figure based on the idea of Smith et al. (2016).
Short Overview and Description of Machine Learning and Data Mining Methods
Machine learning as a scientific discipline is still emerging and thus undergoing continuous change. While many of the methods and algorithms employed have been known for decades, in recent years, new approaches have matured to a degree that it is valid to consider machine learning a new and still nascent field, despite its already comprehensive development over a considerable period of time. As such, what constitutes machine learning exactly (as opposed to, e.g., descriptive statistics) remains only fuzzily defined. With data-driven methodologies being incorporated into domains such as materials science, new variants and adapted machine learning methods have been devised or are in the process of being fitted to the challenges and data profiles unique to materials science. This methodological domain-specificity should not be construed to preclude the importance of “mainstay methods” of machine learning such as artificial neural networks, which are in theory all-purpose and adaptable to approximating (“learning”) any function inherent in data [Universal Approximation Theorem (Hornik, 1991)]. However, as approaches from data science augment and merge with traditional research procedures of materials science, the methods listed in this chapter cannot claim to be an exhaustive enumeration of machine learning methods viable for (continuum) materials mechanics, as constant changes within the next few years are expected.
Within this context, the most commonly encountered class of machine learning (to the extent that it is sometimes used interchangeably with the term machine learning itself) is the class of artificial neural networks (ANNs). Derived from a simple precursor formulation dating back as far as 1958, the perceptron (Rosenblatt, 1958), ANNs have gained in popularity as increasing computing power and availability of data alleviate the two bottlenecks which previously curtailed their use. The perceptron itself was conceived a simple one-layer neural network and used as a linear classifier.
In their simplest modern form, feedforward neural networks (FFNNs) (Haykin, 1998; Russell et al., 2016) are multilayer perceptrons, i.e., layers of vertices (neurons) in which each neuron computes an output based on inputs from the previous layer. The signal traverses through the network in a unidirectional manner, gradually transforming the input signal into an output signal as it percolates through the network, hence named “feedforward.” Such networks are usually trained using a back propagating gradient-descent error minimization approach. The error is determined by comparing the current network output to the correct output (which is available in a supervised learning scenario). Individual neuron behavior is then changed during the training/learning process by altering the connection weights associated with each edge within the network topology. Many different approaches exist to address the various difficulties that are typically intrinsic to neural networks, for instance, overfitting, local minima, determining the optimal number of layers and neurons per layers, choice of activation function, and human interpretability of the network, among others.
Once enough layers of neurons are stacked, which can be referred to as the depth of the underlying ANN, the network behavior enters the regime of deep learning (DL). With increased number of layers, new difficulties come into focus, such as vanishing gradient problem (Hochreiter, 1998) or computation time, among others, which are not absent with the simpler architectures but are exacerbated in the case of DL. DL architectures are, for the most part, agnostic concerning the type of ANN, i.e., any kind of ANN can form the basis for a DL architecture. Two subtypes of ANN architectures have gained in popularity particularly over the last two decades, to the degree that for complex problems, usually one of the two is encountered at least as a component of the overall ANN architecture, or as a pre-/post processing step of the learning pipeline. These are convolutional neural networks and long short-term memory networks.
Convolutional neural networks (CNNs) are mostly formulated as a variant of FFNNs and were pioneered in 1980 (Fukushima, 1980), and then reformulated in their contemporary form in 1999 (LeCun et al., 1999). They are suited particularly well for image recognition, i.e., recognizing patterns in visual data (Schmidhuber, 2015; Russell et al., 2016). Typically, a convolutional layer is shifted across the data akin to a filter/detector in computer vision algorithms, requiring only few parameters due to the convolving layer allowing for effective weight replication as the “filter” is replicated across the visual field. Pooling and normalization layers allow for stepwise data simplification and for variable feature sizes, respectively. While the suitability of CNNs for materials science may not be immediately apparent, there are examples of direct applications such as materials texture recognition (Cang and Ren, 2016; Lubbers et al., 2017; Cecen et al., 2018), as well as indirect application examples in which e.g., non-visual materials data may be interpreted (Schwarzer et al., 2019).
Long short-term memory (LSTM) (Hochreiter and Schmidhuber, 1997; Russell et al., 2016) can compose ANNs because they offer specialized memory neurons/units that chiefly deal with the vanishing gradient problem (or inversely the exploding gradient problem), which often lead to sub-optimal local minima, especially as the number of neuronal layers increases. As deep learning architectures are gaining increasingly in popularity, LSTMs or variants thereof have gained in popularity in lockstep with DL as a way of circumventing such local entrapments. In short, “saving” important data points over time from being drowned out and distributing their error correction signal over longer periods allows for better information storage concerning important events.
For dynamic problems in which a “data-point” is often exposed to a temporal evolution of the materials state and encompassing a series of actions, other approaches than for the static case are often preferred. While many of these have not migrated into materials science to a significant degree, yet, it can be expected that customized methods suited for dynamic problems will gain increasing importance, both as the complexity of the target functions to be learned rises, and with the incorporation of state dependencies (usually as a function of time). Two of the major approaches to such problems are reinforcement learning, which itself is comprised of different methods such as Q-learning (Watkins and Dayan, 1992) and recurrent neural networks (RNN) (Lipton, 2015; Russell et al., 2016), that allow for directed circles within the ANN topology, and thus for signals to oscillate and overlap with the computation of subsequent samples. As a result, data is selectively passed across sequence steps.
Worth mentioning are randomized neural networks, which add random excitatory/inhibitory spikes to individual neurons (Gallicchio et al., 2017) without stable internal states (Maass et al., 2002) and radial basis neural networks (Orr, 1996), which are typically shallow FFNNs using individual neuron-specific radial basis functions to sum over neuron inputs and thus allow for better individual neuron specialization.
One noteworthy alternative to neural networks are Support Vector Machines (SVMs), introduced by Cortes and Vapnik (1995). SVMs deviate from ANNs by not mapping to neither continuous (regression problem) nor discrete (decision problem) output, but rather by separating patterns through either hyperplanes in the linearly separable case or a Kernel function in the nonlinearly separable case. This Kernel-transformation (“trick”) maps support vectors into a transformed feature space in which separability is possible (using, e.g., a maximum margin). Whereas, ANNs usually employ several layers, often composed of simple neurons, SVMs can be interpreted as a specialized single neural node.
Q-learning is a noteworthy reinforcement learning algorithm concerned with learning policies, i.e., optimal choices for sequential decision problems (Watkins and Dayan, 1992; Mnih et al., 2013; van Hasselt et al., 2016), which is based on a reward signal. In this particular variant, the reward signal is based on a Q-function, which is a specific reward function that trades off maximum rewards using a discount factor. Reward-based learning methods such as Q-learning are of particular importance when the space of possible paths, i.e., the number of actions to be taken in sequence, is high but in relation to the training information available only sparsely populates that space.
Monte-Carlo methods (Andrieu et al., 2003) are usually a way of inferring numerical approximations via random (i.i.d.) sampling of a subset of the underlying data. In the context of machine learning, they typically refer to methods to decrease high-complexity environments and datasets and distill e.g., a workable, smaller set of actions to be used by a reinforcement learning algorithm such as Q-learning.
A random forest (Breiman, 2001) is an ensemble learning method that combines multiple (typically weak but computationally tractable) predictors, in this case decision trees, into a composite “super predictor” which (depending on the selection of the decision trees) is often not subject to the same constraints as the individual, weaker predictors.
Bayesian learning (Russell et al., 2016) in the context of machine learning is not a single class of methods but rather an approach into which other machine learning methods can be embedded. Utilizing Bayesian inferences, rooted in Bayes theorem, leads to an optimal update on prior distributions based on available observations. The approach is often used for the parameter estimation of a given learning algorithm or to compare the probabilistic fit between a model and the data to be modeled; either to infer the desired model complexity, or to decide between similarly complex models (Neal, 1996). Gaussian process regression models offer a nonparametric approach to building reduced-order models employing a special form of Bayesian learning that might be ideally suited to continuum materials mechanics problems because of their relatively small sizes of datasets and lack of prior knowledge of model forms.
Fuzzy c-means (FCM) clustering (Bezdek et al., 1984), which is related to k-means clustering, is usually used as a type of unsupervised learning, often in the context of feature extraction in data mining. The objective in such cases is to cluster data points alongside salient features which are not pre-defined (Mai et al., 2016). Fuzzy clustering denotes that feature-classification is not binary but rather given in terms of probability assignments to multiple features. The algorithm randomly distributes cluster centers among the data and iteratively changes the cluster positions until an objective cost function is minimized.
Principal component analysis (PCA) (Abdi and Williams, 2009) is typically used as a simplifying preprocessing step and not considered as a pure machine learning algorithm in itself. In cases where data points consist of more parameters (i.e., higher dimensionality) than the learning model can handle, a number of parameters may be merged until the data becomes tractable for the desired learning model (“dimensionality reduction”). PCA achieves this by projecting the data into a lower dimensional space to retain the maximum amount of variance. The projection leads to a reduced number of parameters, the “principal components,” which capture the maximum amount of information among their axes.
Multi-fidelity methods (Aydin et al., 2019) may grow to be especially relevant for materials research, which often involves computationally expensive simulations, in contrast to other domains where training data is either already present or inexpensive to generate. Multi-fidelity approaches use a large number of cheap low-fidelity computational models for generating the training data for the majority of the training process, only switching to higher-fidelity simulations once the learning contribution per computational cost spent surpasses that of the lower-fidelity model. The magnitude of saving depends on the type of simulation, especially on the feasibility of defining lower-fidelity versions of the computational model, and on the degree to which the used machine learning algorithm relies on gradient-descent-based methods.
In the context of materials science, all of the methods mentioned in this section (with the exception of PCA) are mostly used solitarily, i.e., as the only major component of the machine learning approach. However, as the subfield matures and gains further dissemination into materials science research, they are expected to be used in tandem more often in the future. They can be either combined into (parallel) ensemble methods for which each method contributes a prediction, or into a consecutive serial learning pipeline, in which e.g., clustering is used for feature determination in conjunction with a CNN for subsequent feature learning.
Lastly, it may be worth noting that simple (and borderline merely statistical) learning algorithms such as regression (Russell et al., 2016) and decision trees (Quinlan, 1986) should not be neglected, especially when only a low-sample regime is available offering only a limited amount of extractable information (as is often the case with time and resource expensive experimental setups). Typical machine learning methodologies may be inapplicable, in which case the aforementioned learning algorithms may constitute the most suitable tool to “train” a predictor.
Process Parameters
In this section, applications of machine learning approaches to identify, approximate and optimize process parameters for a variety of results are discussed. The choice of process parameters is responsible for many features that arise in the ensuing process-microstructure-property-performance chain. Examples include identifying correlations between process parameters and resulting microstructures (Popova et al., 2017), predicting process-time requirements and part-geometry results (Xiong et al., 2014) as well as correcting measurements, e.g., resulting residual stress fields (Chupakhin et al., 2017). One set of features arising from the process parameters relate to the material microstructure itself. On the one hand, direct models can be used to discover relevant relationships between causes (i.e., inputs) and effects (i.e., outputs) (Xiong et al., 2014; Popova et al., 2017). On the other hand, once such a forward model is validated, they can be suitably interrogated for inverse relationships needed in design, where the goal is to identify the specific process parameters (and histories) that lead to a desired optimization of the effects (Upadhyay et al., 2012).
Descriptive
Descriptive tasks such as pattern recognition and correlation have been performed by Popova et al. (2017) for the implementation of a data-driven workflow to identify relationships between process parameters and resulting microstructures in additive manufacturing. The proposed workflow included data pre-processing, microstructure quantification and dimensionality reduction to extract and validate process-structure linkages (in the form of reduced order models). The microstructures obtained via additive manufacturing techniques are complex and highly depend on specific process conditions. The generation of synthetic data of these microstructures was accomplished via applying the Monte-Carlo method. The dataset consisted of ~1,600 unique microstructures. The particular method applied in each step of the workflow depends on the amount and type of data available. For building a reduced-order model, three different approaches were used: first, a so-called chord length distribution was employed to quantify microstructural features such as grain sizes, shape distributions and anisotropies. Second, a dimensionality reduction and model reconstruction was achieved by PCA. Third, a multivariate polynomial regression was used for building a surrogate model to efficiently exploit the data. As a result, a framework was created to substitute constitutive models that are typically comprised of comprehensive multiscale and multiphysical field equations by approaches such as advanced statistics and machine learning that lead to highly efficient identification of process-structure-property linkages.
Predictive
For the prediction of bead layer geometries during the additive manufacturing process of robotic gas metal arc welding based on the chosen process parameters, Xiong et al. (2014) used two different prediction approaches: a feed forward artificial neural network, see Figure 2, and a second-order regression analysis. Important characteristics of the manufactured part, such as thickness of the weld bead layer, surface quality and dimensional accuracy affecting the geometry of the deposited layers were included in the training of the ANN. The predictive equation of the second-order regression analysis consisted of a quadratic polynomial considering four influential factors: wire feed rate, welding speed, arc voltage and the distance between nozzle and plate. When comparing the prediction results of both methods to experimental findings, the bead width was marginally underestimated and the bead height slightly overestimated. The deviations were assumed to be based on influential effects caused by heat accumulation that were not accounted for by both approaches. Overall, both prediction approaches lead to reasonable results; however, the error for the ANN was consistently lower than the one of the second order regression analysis. This is due to the superior capability of the ANN to approximate nonlinear processes. Thus, a neural network might be preferable to predict deposited layer width and height with reasonable accuracy for future research (Xiong et al., 2014).
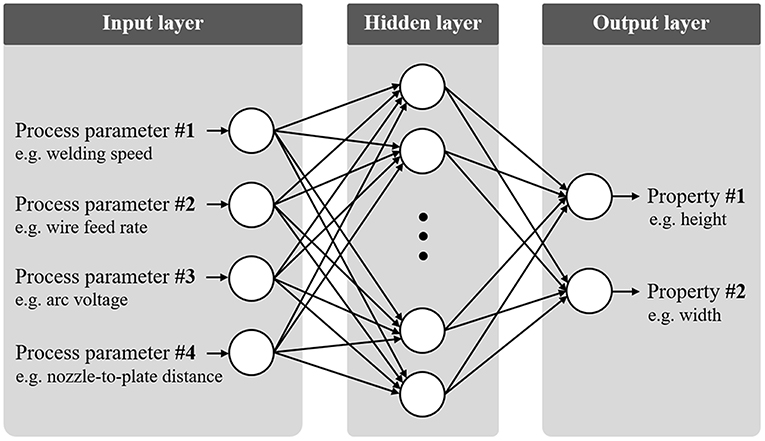
Figure 2. Illustration of a fully connected three-layered feedforward artificial neural network, with the ability to approximate non-linear processes, here, in particular, linking process parameters of the additive manufacturing process of robotic gas metal arc welding as inputs to their resulting outputs: height and width of deposited bead layer. Own figure based on the idea presented by Xiong et al. (2014).
Prediction of the required cutting force during the turning process of a titanium alloy was performed by Upadhyay et al. (2012) with a neural network. In comparison to the experiments that were conducted based on design of experiment (DOE) using the response surface method, the neural network predictions showed better performance on a small but statistically well-distributed dataset. Sahu et al. (2018) also used neural networks to predict the surface roughness in the turning process of a titanium alloy while considering the three controllable process parameters cutting speed, feed rate and cutting depth as input. Additionally, they were able to link them to the measureable outputs: cutting force, feed force and acceleration.
The prediction of higher-order microstructure statistics as a function of the process parameters from both multiscale experimental and simulation datasets was demonstrated in recent studies (Brough et al., 2017a; Khosravani et al., 2017; Yabansu et al., 2017; Popova et al., 2018). In these preliminary explorations, reduced-order models were built using a combination of dimensionality reduction (using PCA), feature engineering (using Pearson correlations), and regression. Clearly, there are many opportunities for the application of more advanced machine learning approaches to this class of problems.
Prescriptive
The identification of process parameters to be applied for obtaining anticipated results can be achieved by completing a prescriptive task. Such a prescriptive task for measurement correction on residual stress fields after laser shock peening (LSP), obtained through the hole drilling method, was performed by Chupakhin et al. (2017) via the use of an ANN. The process of LSP allows to locally introduce deep compressive residual stresses (Ding and Ye, 2006), which is of particular interest in applications prone to fatigue failure. Hole drilling is the commonly used technique to determine the depth dependent residual stress field, but the method is limited to residual stresses below 60% of the yield stress. Chupakhin et al. (2017) developed an ANN for correcting the measured residual stress profile. About 250 training patterns were computed from elastic-plastic FEM simulations of a pre-stressed plate with increasing hole depth by random combination of material properties and residual stress profiles covering the typical range of alloys and LSP profile shapes. The computed deformation field on the surface of the plate was analyzed using the Integral method (Schajer, 1988), which is also used in hole drilling experiments. This “measured” residual stress profile served as input while the residual stress profile applied to the plate served as desired output. The dataset revealed that the error is still below 10% up to a residual stress of 80% of the yield strength. For larger values, the error of the hole drilling method can rise up dramatically and requires a correction using the ANN. Based on the corrected residual stress profiles, the relationship between process parameters and residual stresses could be determined via DOE. This allowed for designing the LSP process to generate desired residual stresses in 2.0 mm-thick AA2024T3 sheet material (Chupakhin et al., 2019).
Microstructure
Numerous research results have been published on microstructural quantification (Altschuh et al., 2017; Voyles, 2017; Gobert et al., 2018), classification (DeCost and Holm, 2015; Chowdhury et al., 2016; DeCost et al., 2017), evolution (Gomberg et al., 2017) and reconstruction (Sundararaghavan and Zabaras, 2005; Bostanabad et al., 2016). Bridging length-scales around the microstructure can be pursued via either bottom-up approaches, e.g., through homogenization or via top-down approaches, e.g., through localization. Moreover, it can be achieved through descriptive, predictive and prescriptive approaches. Based on the descriptive identification of linkages between process parameters, generated microstructures and resulting mechanical properties (Deshpande et al., 2016; Cecen et al., 2018), as well as the related fatigue performances and failure mechanisms (Spear et al., 2018), it is possible to predict or even prescriptively tailor and optimize microstructural features.
Descriptive
The descriptive characterization of the microstructure of random heterogeneous materials remains an important challenge in materials mechanics. To this end, descriptors such as n-point spatial correlations (also called n-point statistics) are used. Sundararaghavan and Zabaras (2005) showed that SVMs in combination with PCA can help to classify microstructures and reconstruct three-dimensional representative volume elements (RVE) using such descriptors, as shown in Figure 3, with nearly real-time efficiency. This idea was significantly extended by Niezgoda et al. (2013) who suggested to represent the microstructure by stochastic processes that allow for a largely automated classification of microstructures. The framework also naturally leads to delineation of a comprehensive space of microstructures (Niezgoda et al., 2008), and the instantiations of microstructures from statistics (Fullwood et al., 2008; Turner and Kalidindi, 2016).
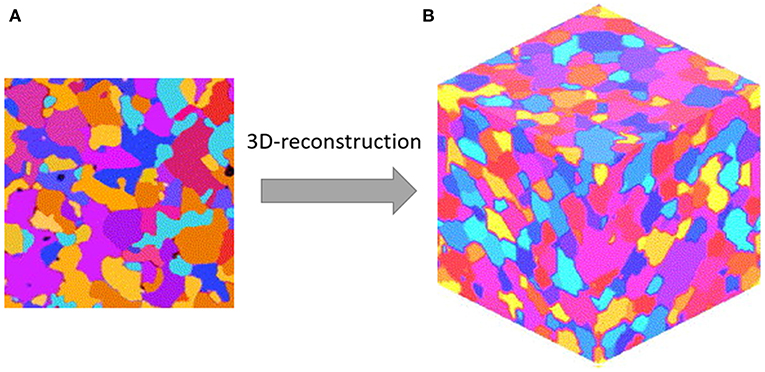
Figure 3. Comparison of experimental and reconstructed micrographs of rolled aluminum alloy AA3002. (A) Shows a two-dimensional polarized light micrograph of the alloy and (B) shows a representative three-dimensional reconstruction of the experimental micrograph in (A). Reprinted from Sundararaghavan and Zabaras (2005), Copyright (2005), with permission from Elsevier.
Fast and Kalidindi (2011) presented an efficient approach for localization, i.e., calculating the strain field in the relevant volume element for given loading conditions, based on the materials knowledge systems (MKS) (Kalidindi et al., 2010; Landi et al., 2010). Core of this approach is the description of the material response (e.g., microscale strain field) via a series of convolution integrals. Statistical continuum theory (Kröner, 1977) provides the basis for the approach, i.e., it inspires the model form for the reduced-order model. Central to the MKS is the calibration of the influence filters present in these linkages. This calibration is accomplished using results from numerical models, typically from finite element calculations of the responses of microscale volume elements (MVE) or RVE, respectively. Different model building approaches have been used in this body of work. Fast and Kalidindi (2011) used linear regression, removing redundancies by employing a reduced-row echelon form. This work demonstrates the suitability of the kernel-based series model form employed that systematically adds more terms as higher levels of microscale interactions are needed to be captured.
The MKS approach from Kalidindi et al. (2010) was also utilized in a study on elastic localization kernels for single phase polycrystalline microstructures (Yabansu et al., 2014) as well as for a wide range of cubic polycrystals (Yabansu and Kalidindi, 2015). The goal was also to efficiently achieve scale bridging in modeling and simulation of materials involving numerous scales. It is claimed that the most advanced material structures possess a highly hierarchical internal structure with different length scales. Therefore, the MKS framework is used to capture high dimensional local state spaces of advanced material systems for the prediction of elastic strain fields in a broad class of cubic polycrystalline microstructures (Figure 4). Significant reduction of required computational effort was achieved through spectral representations of the influence functions that are highly compact.
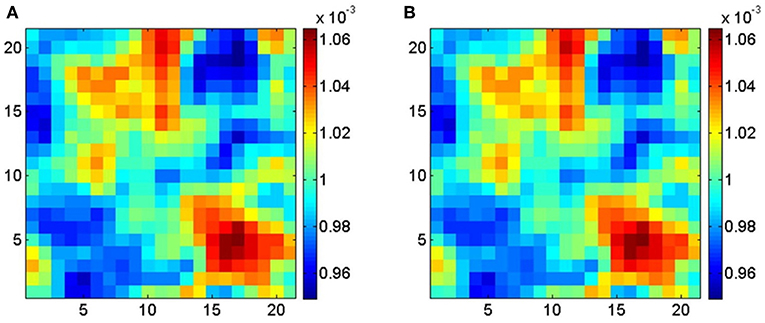
Figure 4. Comparison of strain field distributions within middle slices for a low elastic anisotropy cubic polycrystalline microstructure (21 × 21 × 21 pixels) obtained from predictions performed with (A) materials knowledge system (MKS) and (B) finite element method (FEM). Reprinted from Yabansu and Kalidindi (2015), Copyright (2015), with permission from Elsevier.
In the area of materials characterization and microscopy, Voyles (2017) focused on improving the quality of data obtained empirically from instruments (microscope, in this case), optimally deriving information from that, to ultimately develop generalizations and gain new knowledge. Besides that, microstructure quantification and feature identification in porous membranes was studied by Altschuh et al. (2017). Data generation was conducted via a newly developed microstructure generator, to generate a large ensemble of porous structures that contain a large variety of different features, such as pore shape, pore size, degree of porosity, and specific surface area. Experimental data was obtained via high-resolution X-ray tomography to measure the morphology of real porous membranes. To be able to compare the two different datasets, statistical representations for both simulated and real membrane microstructures were calculated and compared based on a PCA of two-point spatial correlations. This leads to an objective measure of the difference between any two selected microstructures; thus, to a quantification of the porous membrane structures. A PCA on these two-point statistics was used to obtain low dimensional representations of the microstructures and to classify them. For the basic microstructure, the most dominant features are porosity, pore size, stretching direction and stretching factor. These features were identified as a basis in the low dimensional space. A high variety of microstructure characteristics and its influence on the low dimensional space lead to the identification of linkages. As a result, the basis vector and the principal component value were successfully used to estimate the features of the real membranes.
Predictive
For the purpose of providing an efficient linkage for localization, Liu et al. (2015b) compared the performance of different approaches based on machine learning and data mining concepts. One particular goal was to overcome limits in terms of applicability of the previous linkage approach based on the extension of statistical continuum theory to higher elastic contrasts of the composition (Kalidindi et al., 2011). The linkage is established based on setting up a predictive model, consisting of the two aspects, feature extraction and regression. Three test cases were analyzed to evaluate the influence of different steps in generating the data-driven predictive model for localization. First, the influence of additional information about the neighboring voxels, called feature space, on predicting the response of the currently influenced voxel is studied. However, the computational performance is decreasing linearly due to the increased training time with growing number of included neighbors, meaning the feature dimensions, and the prediction might be even deteriorated. Secondly, the influence of differently defined features on the representation of considered voxels are systematically analyzed and subsequently ranked. Based on this ranking, a combination of different top-ranked features are juxtaposed, showing the improved performance in contrast to simply adding information of the neighboring grains. However, there exists a feature threshold where the error increases with increasing information. Thirdly, the performances of different regression models are compared, showing that a random forest regression model outperformed the considered support vector regression model and M5 model tree in terms of accuracy by only a moderately increased training time compared to the M5 model tree. This approach was extended by Liu et al. (2017) through considering context detection, i.e., “finding the right high-level, low dimensional, knowledge representation in order to create coherent learning environments” (Liu et al., 2017). In this regard, a two-step approach is used. First, identifying the context of the data and secondly constructing the predictive model for each context, also called multi-agent learning, lead to an increased efficiency and accuracy of the predictive model. Key difference to the previous work of the authors is the identification of microstructure similarities, called macro-features, and assembling them to a subset using k-means clustering algorithm. Subsequently, each subset is handled with the approach as presented in their previous work (Liu et al., 2015b) and discussed above, using the best 57 features, called micro-features. Three strategies of identifying the microstructure macro similarities are investigated and their performance compared. These strategies include context detection based on volume fractions alone, on “designed macroscale microstructure descriptors” (Liu et al., 2017) and on pair correlation functions. The results showed an improvement of 38% compared to the best results presented by Liu et al. (2015b). The accuracy of the different strategies for the macro feature extraction was nearly identical.
Automatic microstructure recognition was implemented by Chowdhury et al. (2016) in a case study on image-driven machine learning methods. The dendritic morphologies were of particular interest with the aim of performing classification with a minimum of required pre-expert-knowledge. Thus, the anticipated knowledge gain was claimed to be equivalent to human performance, but not beyond. The first classification task was to differentiate between dendritic and non-dendritic microstructures. The second classification task aimed to recognize longitudinal and transverse dendrite orientations via a successional binary classification task performed on cross-sectional views. Images with different magnitudes and from different material-compositions served as initial data input. Feature extraction and dimensionality reduction were used to represent micrographs as feature vectors. These feature vectors were then used for training, validating and testing various classification models. They consist of a set of detected features in an image; thus, images were represented by high-dimensional feature vectors (Figure 5). Feature selection is performed to increase computational efficiency by reducing the length of the feature vector and still retain all relevant image information (e.g., reducing sparsity of the vector). Various dimensionality reduction methods were tested, and in conclusion, convolutional neural networks were evaluated best for both classification tasks with an accuracy of 92–98% as generalization can be performed most sufficiently.

Figure 5. Schematic illustration of a micrograph classification approach on different material compositions including feature extraction, feature selection and classification methods used. The two classification tasks were to first differentiate between dendritic and non-dendritic microstructures and second to recognize longitudinal and transverse dendrite orientations. Reprinted from Chowdhury et al. (2016), Copyright (2016), with permission from Elsevier.
Microstructural images were used by Ling et al. (2017) to set-up a data-driven model for microstructure classification, using pre-trained convolutional neural networks within the framework of Keras (Chollet et al., 2015) and Tensorflow (Abadi et al., 2016). The specific model was trained, tested and validated with the aim to process different datasets through generalization, including the identification of the required number of features and an evaluation of the interpretability of results. First, the microstructural images were transformed by using CNNs, followed by texture featurization and classification through a random forest algorithm (Figure 6). The required computational effort is proportional to the number of features. Mean texture featurization showed good performance based on the comparatively low number of features that requires less memory space and enables efficient computation of the random forest classifier. Overall, an appropriate method for featurizing images obtained via Scanning Electron microscope (SEM) was developed and applied. Generalization was achieved sufficiently from the input based on different datasets as opposed to only one single dataset and allowed for various prediction targets.
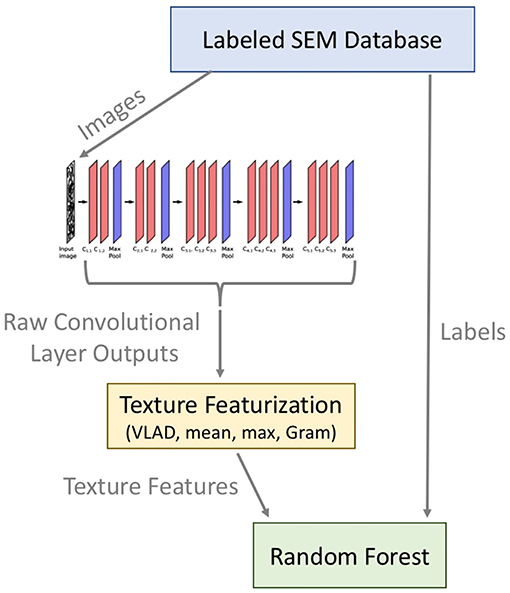
Figure 6. Schematic depiction of the workflow for microstructure feature evaluation. For the image transformation, five stacks of convolutional neural networks were used, each of them consisting of either two or three convolutional layers, succeeded by a max pooling layer. Indices of convolutional layers are referring to their stack position, e.g., first, seconds or third position within the e.g., first, second, third, fourth of fifth stack. The outputs were processed via featurization of the texture and the ultimate classification of these features was achived by using a random forest. Reprinted from Ling et al. (2017), Copyright (2017), with permission from Elsevier.
A descriptive and predictive approach is proposed by Hu et al. (2018) for the efficient simulation of grain and pore growth in aluminum alloys during solidification in a casting process. A cellular automaton (CA) is combined with backpropagation neural networks (BPNN), resulting in a so-called CA-BPNN method to simulate the growth of pores and grains. Computational effort is reduced since the continuous governing equations with high-dimensionality to account for porosity do not have to be solved. The neural network is used on data obtained from a process simulation of the solidification via CA to economically identify the relationship between porosity and solidification parameters1, such as solidus velocity, initial hydrogen content as well as spatial and temporal thermal gradients. These relationships are considered in the transition functions, which compose the rules for the cellular automaton model and affect the simulated pore growth in addition to the governing equations of the numerical simulation (Figure 7).
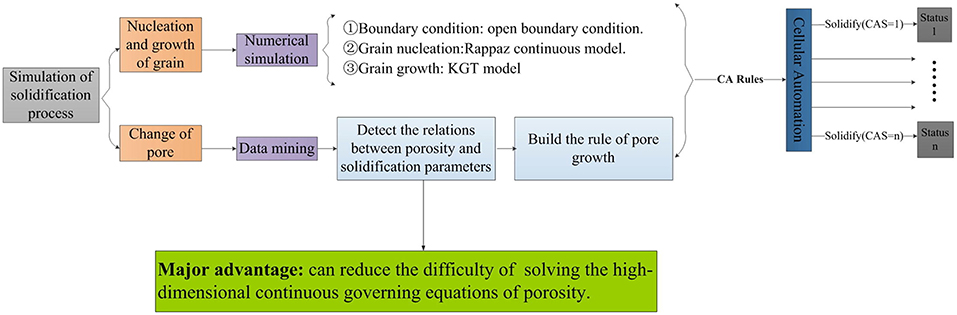
Figure 7. Schematic illustration of the cellular automaton backpropagation neural network (CA-BPNN) method for simulation of the solidification process of aluminum alloys during casting. The simulation is divided into two parts: grain growth and pore growth. For the simulation of grain growth, conventional numerical methods are used; whereas for the pore growth simulation, a BPNN was used to efficiently provide complementary rules for the CA. Reprinted from Hu et al. (2018), Copyright (2018), with permission from Elsevier.
For metallurgical texture analysis, in particular classification of zones of titanium alloy microstructures into either α and β or α+β phases, respectively, Mesquita Sá Junior et al. (2018) used a randomized neural network for identifying microstructural features. In particular, linear discriminant analysis (Fukunaga, 1990) and SVMs reached good and similar precisions for both types of microstructures. For example, this approach was applied for classifying titanium alloys processed via friction stir welding, as the existing phase type has a strong effect on the mechanical material properties.
An example of performing a predictive task based on the descriptive approach of defect pattern recognition was performed by Gobert et al. (2018). For in-situ detection of discontinuities, such as defects, during the process monitoring of additively manufactured metals via powder bed fusion, a supervised machine learning approach was implemented on high-resolution images recorded via computer tomography during the building of layers. For geometrically describing discontinuities, adjacent voxels that exhibit anomalies were clustered. The particular assignment of each anomaly voxel to their correlating discontinuity was achieved through k-means clustering, which is based on the minimum distance of a voxel to the center of its cluster. The aim was to detect discontinuities with diameters between 20 and 200 μm. Furthermore, visual features in the form of high-dimensional feature vectors were extracted and evaluated through binary classification via SVMs. Once the ensemble classifier was trained, the accuracies amounted to 80% and better for predictively detecting defects during the process, validated with three dimensional computer tomography images of the manufactured parts.
Prescriptive
A particular challenge is the identification and prediction of optimized microstructure configurations to prescribe the best material properties for specific applications. Liu et al. (2015a) presented an approach for microstructure optimization, enhanced by machine learning methods, as outlined in Figure 8. Although, a number of methods for determining the properties directly from a given representation are available, the traditional structure-property optimization, representing the inverse procedure, is complex. The optimization problem might be of high dimension, multiple objectives have to be fulfilled and the result is often non-unique; thus, deteriorate classical optimization methods. In Liu et al. (2015a), a machine learning-based structure-property optimization scheme, see Figure 8, is introduced and applied to the design of magneto elastic Fe-Ga alloy for five different design problems. At the core of the new scheme are random data construction as well as feature selection and classification algorithms to refine the search path and to reduce the search region, respectively. The latter two steps have the goal to reduce the search space and by this, to decrease the computational costs to find the optimal solution. The microstructure of the magneto elastic Fe-Ga alloy was represented by an orientation distribution function (ODF). In combination with a crystal plasticity model, all relevant properties considered in this work were obtained via homogenization. For the random microstructure data generation, four randomization methods were used to ensure the sufficient randomness and polarization: random intervals, random k intervals, random every k and best-first assignment. The search path refinement is based on supervised feature ranking methods [χ2 (Liu and Setiono, 1995), information gain (Quinlan, 1986), f-score (Steinwart and Christmann, 2008) and SVM-weight (Chang and Lin, 2008)] to identify the most promising path, i.e., crystal orientations or ODF dimension. For the search space reduction, a rule-based classification tree (decision tree) is used, e.g., to identify promising orientation regions. For the design problems published by Liu et al. (2015a), the original region could be reduced by 80–99%. A gradient-based line search is employed to perform the mathematical optimization. The authors compare the outcome and the performance of the machine learning-based scheme to three other approaches, namely an exhaustive search, a generalized pattern search and linear programming (LP) as well as a genetic algorithm (GA), respectively. Overall, the results by Liu et al. (2015a) illustrate that the machine learning-based scheme outperforms all other approaches, considering optimality, efficiency2 and completeness of the solution, in particular dealing with nonlinear problems.
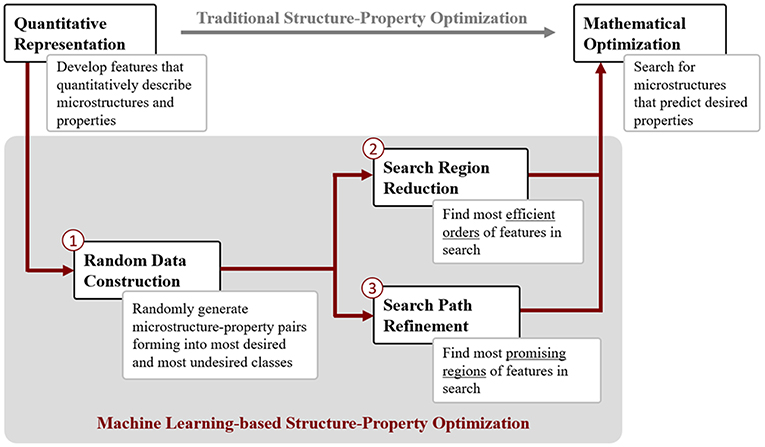
Figure 8. Illustration of two schemes for structure-property optimization as presented by Liu et al. (2015a). The top illustrates the traditional structure-property optimization, usually based on a search-based optimization method. On the bottom, the machine learning-based structure-property optimization approach is presented. It includes three additional steps. First, data is generated and subsequently used to refine and reduce the search space dimensions, leading to optimal results, better performance and providing a better solution completeness compared to methods following the traditional optimization route. Figure “Framework of material structure optimization” reprinted from Liu et al. (2015a), used under the Creative Commons Attribution 4.0 license. http://creativecommons.org/licenses/by/4.0, Copyright (2015), font type and colors altered from original.
Brough et al. (2017b) set-up a prescriptive framework for capturing and communicating critical information regarding the material structure evolution in spatiotemporal multiscale simulations to reduce the number of required experiments. They aimed for establishing the desired process-structure-property linkages by generalizing the MKS framework via introducing different basis functions and exploring their benefit. Using Cahn-Hilliard based phase field simulations to predict microstructure evolution and using Green's function based influence kernels as a method to identify the underlying embedded physics, lead to a calculation acceleration by the factor of three compared to an optimized numerical integration algorithm. It is important to distinguish the direction of relationships. Consequently, the kernels in the MKS localization approach are calibrated with results from numerical tools such as FEM. Once the linkages are calibrated and validated, the influence kernels can be used to predict the local responses of new microstructures at minimum computational costs. Thus, this approach is sufficient for exploring a very large number of potential microstructures. The extracted kernels were insensitive to details of the initial microstructure, enabling the application of the kernel to any initial microstructure within the material system selected for that kernel and allowing for expanding the domain size without significant alteration of the accuracy. The overall achievement of this study was the rapid exploration of the underlying physics via Green's function based influence kernels at exceptionally low computational costs, opening up superior opportunities for spatiotemporal multiscale bridging.
Mechanical Properties
Mechanical material properties are characteristics to be precisely predicted and controlled as they are strongly linked to and highly affected by process parameters and resulting microstructures. Mechanical behavior in simulations is often described by means of constitutive equations. Already before the most recent popularity rise of machine learning in the scientific community, several approaches had been suggested to replace constitutive equations by data-based methods such as artificial neural networks (Hashash et al., 2004; Oeser and Freitag, 2009). Such approaches are particularly promising for problems where it remains poorly understood how to describe the material behavior appropriately by means of constitutive equations, for example, remodeling of biological bones as discussed by Hambli et al. (2011). Other examples include the prediction of compressive strength and elastic modulus of sandcrete materials (Asteris et al., 2017) and approximation of yield strength while respecting diverse physical constraints for the design of a nickel-based superalloy (Conduit et al., 2017). In general, descriptive tasks, such as pattern recognition, predictive tasks, such as classification as well as prescriptive tasks, such as optimization, are implemented to fulfill the material property requirements of particular material applications.
Descriptive
Hambli et al. (2011) substituted constitutive equations by a data-driven ANN. A combined model composed of a finite element (FE) simulation and an ANN was developed for simulating the remodeling process of bones and linking the mesoscopic scale of the “trabecular network” level to the macroscopic scale of the complete bone level, as shown in Figure 9. While the FE simulation was implemented on the macroscopic scale, an ANN was used to provide predictions at the mesoscopic scale. The FE analysis was based on digital CT image voxels used to build mesoscale RVEs, whereas the ANN was provided with parameters of the bone materials as well as boundary conditions and applied stresses. The anticipated outputs were the updated bone properties.
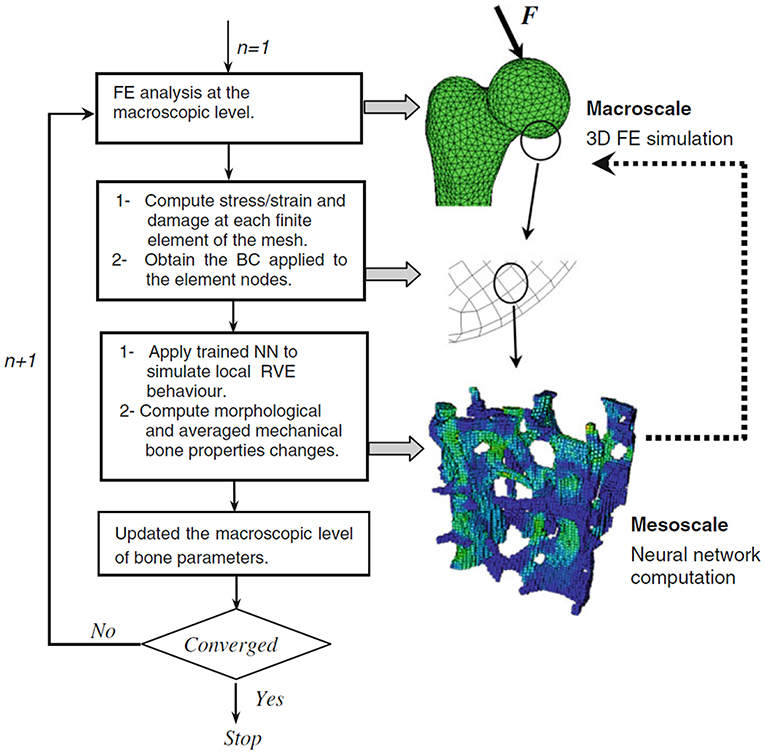
Figure 9. Multiscale finite element neural network (FENN) approach for bone analysis: two-level analysis for predicting the remodeling process. Macroscale level: whole bone computed using FE analysis. Mesoscale level: effective properties of trabecular bone structure computed using a trained neural network. Reprinted from Hambli et al. (2011), Copyright (2010), with permission from Springer Nature.
In the data-driven approach presented by Kirchdoerfer and Ortiz (2016), the need for empirical material modeling, which can require extensive efforts, is circumvented by performing more efficient calculations directly from a material dataset obtained through experiments. Through the combination of experimental data, relevant constraints and essential conservation laws, the data-driven calculations were restricted to remain within boundaries prescribed by principles of conservation and relevant limits related to the specific problem. In particular, through the data-driven model, the nearest possible state of a materials data-point of interest to the experimental dataset is assigned to a point in the computational material model that simultaneously fulfills the boundary conditions. This nearest possible state is determined via a distance-minimization function in the phase space between the experimental data points and the newly proposed data points from the data-driven computational model. The approach was applied to a mechanical problem of a non-linear three-dimensional truss system with linear elastic properties. The developed data-driven solvers showed good convergence, especially in comparison to a classical finite element model analysis. An extension of this approach was the investigation of its robustness with respect to noise induced by outliers within experimental datasets, which was achieved through a cluster analysis (Kirchdoerfer and Ortiz, 2017). Furthermore, the data-driven computing approach is extended in Kirchdoerfer and Ortiz (2018) to time-dependent problems such as predicting annealing processes.
Ibañez et al. (2018a) proposed a data-driven computational approach to compensate for the inability of existing constitutive models to be extended or generalized for describing new experimental results without significant adaptation efforts. To describe the elastic material behavior, there was no need for a constitutive model that could reflect linear and non-linear elastic behavior or yield conditions. Proposed were two different linearization strategies for utilizing an iteration solver to define points in the material model that fulfill both constitutive and equilibrium equations within large experimental datasets.
However, more recently, Ibáñez et al. (2018b) proposed an approach on combining governing equations with constitutive plasticity models and experimental data via machine learning. Based on the benefit of contained constitutive equations, the approach is claimed to be more accurate and efficient than approaches without a model. The use of sparse proper generalized decomposition (s-PGD) enabled to correct constitutive plasticity models in order to minimize the error between the results generated by the model and those obtained via experiments. Through this approach, it was possible to utilize substantial knowledge already contained in the model, as opposed to training an algorithm from scratch.
Liu et al. (2018) proposed a so-called deep material network that was implemented for modeling materials on multiple scales, based on homogenization of two-dimensional RVE's. With data obtained from linear elastic RVE calculations, the deep generic material network was trained via stochastic gradient descent with backpropagation and enhanced via model compression by removing redundancies3 in the network. As a result, learning and convergence was achieved in less time. A number of connected building blocks, as common for generic algorithms, are used in combination with solutions from homogenization of two dimensional elastic RVE's to preserve important information about the mechanical physics. The trained network was validated with numerical simulations for cases of linear elasticity, nonlinear plasticity and finite-strain hyperelasticity exposed to large deformations; thus, it provides a description of mechanical microstructure-property linkages, however, it can also be used for prediction purposes during material development.
To derive relationships between process parameters, microstructure and mechanical properties for additively manufactured materials, Yan et al. (2018) proposed a comprehensive, data-driven model, containing multiple scales to respect numerous underlying physical phenomena. To enable an efficient and accurate data-driven mechanical simulation for material design, a reduced order modeling technique was developed, the so-called self-consistent clustering analysis (SCA), which is based on the works of Liu et al. (2016a) and Liu et al. (2016b). The SCA was used on the mesoscale to connect the microstructural model to macroscopic properties. Processed data consisted of voxels from non-linear materials with complex microstructural morphologies. Instead of solving constitutive equations for each voxel, clusters of voxels are formed, e.g., via the k-means method, and constitutive equations were solved for each of those clusters. As a result, SCA served as reduced order method that leads to a valuable compromise between efficiency and accuracy of the results.
Huber (2018) addressed a number of fundamental questions regarding the topological description of materials characterized by a highly porous three-dimensional structure with bending as the major deformation mechanism. This is the dominant deformation mechanism in nanoporous gold, foams, porous membranes and some architecture materials. Highly efficient finite-element beam models were used for generating data on the mechanical behavior of structures with different topologies, ranging from highly coordinated bcc to Gibson–Ashby structures (Gibson and Ashby, 1997). Random cutting enabled a continuous modification of average coordination numbers ranging from the maximum connectivity to the percolation-cluster transition of the 3D network. Via data mining, the interdependencies of topological parameters as well as relationships between topological parameters with mechanical properties were discovered. It was found that the average coordination number serves as a common key for determining the cut fraction, the scaled genus density, and the macroscopic mechanical properties. The dependencies of macroscopic Young's modulus, yield strength, and Poisson's ratio on the cut fraction (or average coordination number) could be represented as master curves, covering a large range of structures from a coordination number of 8 (bcc reference) to 1.5, close to the percolation-cluster transition. As an interesting outcome, the data for macroscopic Young's modulus and yield strength are covered by a single master curve. This lead to the important conclusion that the relative loss of macroscopic strength due to pinching-off of ligaments corresponds to that of macroscopic Young's modulus. In principle, the derived master curves can be used to design the macroscopic stiffness, strength and Poisson's ratio of open pore materials by adjusting the connectivity of the material, leading to a prescriptive approach.
Predictive
Effective macroscopic mechanical properties of a material with a given microstructure can be predicted via computational homogenization and is another typically time-consuming task in materials mechanics, for which recently machine learning techniques such as ANNs have been proposed as a viable and computationally efficient alternative (Le et al., 2015). Predicting the mechanical properties of a material depending on its processing can be a challenge and hard to tackle even with computational methods because an accurate physical model that could reliably link processing parameters and materials properties is often lacking. In such cases, artificial neural networks are often used to predict mechanical properties based on mechanical models and experimental data (Chopra et al., 2016).
The prediction of rising or falling material hardness, based on residual stresses and contact pressure of spherical indentation tests was investigated by several groups via experimental and FEM simulations. Heerens et al. (2009) presented a model that allows to compute the change in hardness for arbitrary in-plane biaxial residual stress states including the special cases of uniaxial, equibiaxial, and pure shear residual stress. Relevant for this review is the way this model was found. Based on a 3D FEM model, hardness training patters were generated for randomly chosen elastic-plastic materials with nonlinear work hardening. For each pattern, a pair of data with and without residual stresses was computed. It turned out that an ANN could easily predict the increase or decrease of the hardness relative to the material without residual stress when the two in-plane residual stress components σ1, σ3, and the average contact pressure σr are given as inputs. When this happens, there is a high chance that the underlying relationship Π(σ1, σ3, σr) can be represented by a simple model. Motivated by this, the data was systematically analyzed with respect to the interdependencies using an ANN. To this end, physical knowledge was incorporated in the formulation of the ANN inputs and output. The authors studied the ANN prediction error by feeding the following information as inputs: indentation depth to spherical indenter radius h/R, normalized Mises stress σf/σr, and normalized hydrostatic pressure p/σr. As not explicitly illustrated in the original contribution by the authors, a sequential omission of single inputs reveals an error pattern in the predicted output specific for each input, see Figure 10. Therefore, as major outcome of the applied machine learning approach, it can be concluded that both the normalized von-Mises stress and hydrostatic pressure are equally important to solve the problem. The model published by Heerens et al. (2009) is based on this insight and would not exist without the intermediate step of using the ANN. While the ANN was descriptive and limited to the range of training data, the derived model is general and predictive.
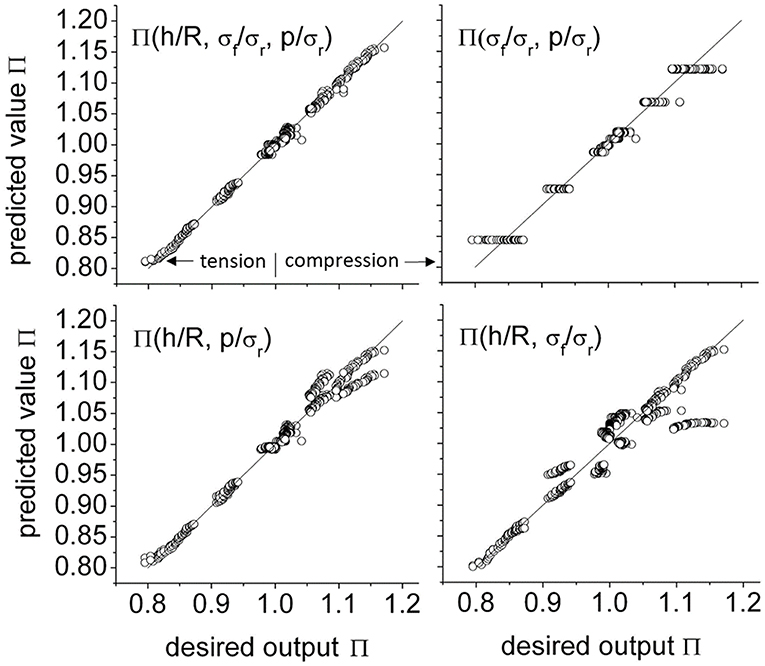
Figure 10. Analysis of the interdependency in the nonlinear relationship of hardness ratio by variation of the input information. Top row left: using all inputs; top row right: omitting indentation depth to spherical indenter radius h/R; bottom left: omitting mormalized Mises stress σf/σr; bottom right: omitting normalized hydrostatic pressure p/σr. Omitting an input is visible in a specific pattern of error in the predicted output.
Ghosh et al. (2014) used a multilayer neural network to predict the porosity, the yield strength, the ultimate tensile strength and the elongation of aluminum alloys during solidification, based on input parameters, such as solidus velocity, initial hydrogen content as well as spatial and temporal thermal gradients. The training error and number of cycles were reduced via numerical optimization of the ANN training structure by using the quasi-Newtonian Broyden-Fletcher-Goldfarb-Shanno algorithm (Nocedal and Wright, 2006). Good agreement between ANN predictions and empirically determined mechanical properties was obtained.
The effective stiffness of high contrast elastic composites is predicted by Yang et al. (2018), based on a deep learning approach. They used a multi-layered CNN with a rectified linear unit (ReLU) function for neuronal activation to model linkages between microstructure and mechanical properties at the macroscale. The architecture of a CNN, as shown in Figure 11, usually consists of a convolutional layer for objective extraction of important features from two or three-dimensional images, followed by a pooling layer for reducing feature map dimensions and a fully connected layer before concluding with the output layer that consists of one node, yielding the anticipated material property.
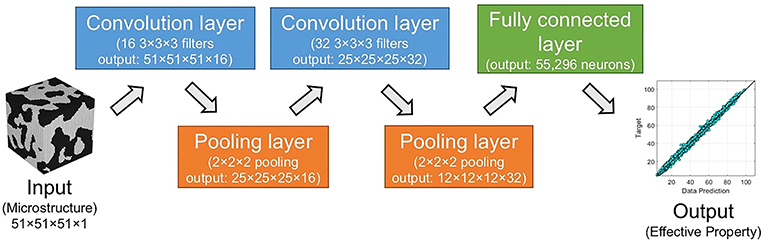
Figure 11. Schematic image of the three-dimensional convolutional neural network (CNN) architecture, containing a convolutional layer for feature extraction, a pooling layer for dimensionality reduction of feature maps, as well as a fully connected layer and a single-noded output layer, yielding the desired material property. Reprinted from Yang et al. (2018), Copyright (2018), with permission from Elsevier.
Enhancing the accuracy for predicting mechanical properties of heterogeneous materials based on image data by using a CNN in combination with a morphology-aware generative model was achieved by Cang et al. (2018). The generative machine learning model was used at low computational cost to generate artificial but authentic material samples that are required when only a limited set of original data typically from experiments, is available for training. Morphology constraints lead to a morphology distribution of the generated samples that is identical to the one of the original data. Through a comparison, it could be shown that this material property distribution matched the original material property distribution better than that one generated with a state-of-the-art Markov Random Field model (Li, 1995); hence an improvement of a predictive structure-property model was reached.
Prescriptive
The identification of material parameters for constitutive models is commonly the key for optimization of processes and for designing parts that undergo complex loading histories. Irrespective of whether a deterministic or stochastic optimization algorithm is used, they intend to lead to a set of parameters that correspond to the best fit. However, it is mostly not clear, if the result is unique. Huber and Tsakmakis (2001) developed a neural network tool that allowed identifying the material parameters of a finite deformation viscoplasticity model with static recovery. This complex inverse problem was solved in a very general way by enriching the information fed to the machine learning approach via a specifically designed loading history for cyclic loading with different loading rates and inserted relaxation phases. The identification process was split into a sequence of specialized ANNs, which used the results from the previous steps. All inputs and outputs are defined in dimensionless form. The outputs are normalized by measurable quantities that incorporate a priori knowledge, wherever possible, via a simple estimate of the desired output. This improves the accuracy of the ANN considerably, due to the reduction of the approximation task to the correction of the estimate. In this way, the Young's modulus was determined first, then the equilibrium behavior of the nonlinear isotropic and kinematic hardening rules, and finally the parameters responsible for viscosity and static recovery terms. Subsequently, the nonlinear elastic-plastic deformation behavior of thin Al films was identified by Huber et al. (2002) from nanoindentation experiments. In contrast to the common rule of maximum 10% indentation depth, the required additional information for a unique identification was provided by purposely deep penetration of twice the film thickness. This concept allowed to break the geometric similarity of the pyramidal indent and to enrich the input data of the ANN by sufficient independent information about the mechanical behavior of the film. To minimize the computational costs for pattern generation, a strategy was applied, where five patterns served for training and another five patterns for validation. With each training cycle, the previous validation patterns were added to the training dataset and five new validation patterns were generated. Based on this approach, 40 patterns turned out to be sufficient to achieve a comparable training and validation error. The enrichment of the input information by modifying the loading history was also key for a successful unique parameter identification based on spherical indentation tests (Huber and Tyulyukovskiy, 2004; Klötzer et al., 2006; Tyulyukovskiy and Huber, 2006). The developed identification approach was successfully applied to determine the material parameters of EUROFER 97 steel. The high quality of the identified material behavior and the prescriptive capability for generating very different loading histories was demonstrated by a comparison of the predicted stress-strain behavior with cyclic tension-compression tests from specimens made from the same material.
Conduit et al. (2017) utilized a neural network for the design of a nickel-based polycrystalline superalloy. Specifically defined physical criteria were fulfilled by the approach; therefore, modeling, discovering and optimizing novel alloys with respect to required design specifications was possible. Experimental validation of parameters, such as the yield stress, showed that the relevant properties for a particular application were improved in comparison to commercially available materials through the prescriptive discovery of a material composition that is most suited for the particular use-case. Examples of the successful application of this approach are the development of a new nickel-based superalloy for high temperature application (Conduit et al., 2014) as well as the predictive and prescriptive design of a molybdenum-based alloy that fulfills desired requirements such as yield stress and hardness properties for a die-forging application (Conduit et al., 2018).
Performance
When materials are exposed to loads that are significantly dependent on the temporal scale, the performance of the material, such as fatigue and failure, become highly relevant. Specific material behavior that eventually leads to fatigue are governed by phenomena such as crack initiation, growth, and coalescence under static and cyclic loading, among others. Using machine learning approaches for the identification of linkages to fracture initiation (Jha et al., 2018), crack growth (Younis et al., 2018) as well as fatigue life performance (Paulson et al., 2018) is substantial for choosing and designing the best characteristics along the process-structure-property-performance chain.
Descriptive
To uncover and quantify relevant microstructural factors influencing the fatigue behavior, Jha et al. (2018) used a data-analytics approach based on principal component analysis (PCA) (Jolliffe, 1986) and fuzzy c-means (FCM) clustering (Bezdek et al., 1984). Through crystal plasticity finite element (CPFEM) calculations of RVEs, statistically representative for Ti-6242S microstructures, 33 different metrics (slip and geometry) for 25 grains, as well as for their neighborhood (8) were determined. To predict early fatigue crack growth, the Fatemi–Socie fatigue indicator parameter (FIP) (Fatemi and Socie, 1988) was calculated from the CPFEM results as well. Jha et al. (2018) showed that the consideration of single metrics/factors alone is not sufficient to determine or to rate their influence on the fatigue behavior. Thus, linear PCA was used to reveal the influence of the different metrics onto the FIP. This is obtained by analyzing the FIP value in dependence of the principal components and identifying the critical regions of principal components showing a high FIP value. Afterwards, the contribution of each metric to the principal component (variable coefficients) leading to the critical regions is obtained. By this analysis, the authors could conclude that the “microstructural configuration with high FIP roughly corresponds to a combination of α particles oriented to produce high normal stress on the basal plane and a neighborhood that imposes high shear strain” (Jha et al., 2018). The authors showed that via the suggested data analysis, contributions of several parameters could be revealed which would be impossible by direct analysis as well as by experimental characterization alone. To “reveal unique microstructural configurations” (Jha et al., 2018) leading to high FIP values and the occurrence rate of configurations, a clustering analysis in principal component space was performed. For this purpose, kernel based PCA in combination with FCM data clustering is applied. The results of this analysis showed that only certain configurations have a high FIP, appearing at low occurrence rate, as expected from experimental observations.
Corrosion is another mechanism that is very complex and strongly influenced but not only controlled by alloy composition and microstructure, rather also by the environmental conditions under which the alloy shall bear mechanical loads. Metallic biomaterials made from Mg alloys have the potential to be biodegradable. For implants in form of screws and plates, the degradation rate needs to be designed such that the implant bears the load until the bone sufficiently healed and takes over the mechanical load. The challenge is the large number of parameters in conjunction with the long duration for a corrosion test. Based on a very limited number of 69 samples, Willumeit et al. (2013) applied an ANN to first analyze the most important parameters and then visualize and identify the dependencies on all parameters under investigation. As the most important outcome, it was found that in addition to the concentration of NaCl, the concentration of CO2 are the two most important factors that control the corrosion rate. While the first was well-known, the second was revealed by this study. This finding is particularly important because the CO2 concentration differs significantly between in vitro and in vivo experiments. The trained ANN allows to further design experiments in specific areas of interest as well as to quantitatively predict the corrosion rate for given environmental parameters.
Predictive
In general, health monitoring and lifetime prediction for engineering structures has traditionally been a largely data-driven area. Recent progress in Bayesian methods and machine learning, in particular artificial neural networks, has motivated a considerable number of publications introducing new data-driven approaches for lifetime prediction (Freitag et al., 2009; Silverio Freire Júnior et al., 2009; Figueira Pujol and Andrade Pinto, 2011; Sikorska et al., 2011; Mosallam et al., 2016).
Machine learning has proven beneficial for lifetime predictions in particular for systems where accurate physical models for mechanical analysis are absent so far. A typical example is lifetime prediction for interfaces (e.g., Jia and Davalos, 2006). To predict fatigue properties not only on the microscopic material level but rather on the system level including factors such as macroscopic geometry, Wang et al. (2016) proposed a framework based on artificial neural networks. For a review of machine learning approaches specifically for crack growth prediction, the reader is referred to Wang et al. (2017).
Vassilopoulos et al. (2007) used ANNs to predict the fatigue life of composite materials based on experimental data that measured only approximately half of the amount usually required for the analysis. Thus, stress-cycle (S-N) curves and constant life diagrams (CLDs), which are helpful for structural designing, could be generated more efficiently and with satisfying accuracy for 104-107 cycles. The loading condition investigated, modeled and validated were tension-tension, tension-compression and compression-compression, respectively. The R-ratio refers to the different loading amplitudes imposed onto the specimens (Schijve, 2001). The approach was validated for two different glass-fiber reinforced polymers (GFRP) with dissimilar laminate sequences, as shown in Figure 12.
Figure 12. Constant life diagrams (CLD) obtained via experiments and predicted via an artificial neural network (ANN) for coupons loaded in on-axis direction for 104-107 load cycles for two glass-fiber reinforced polymers (GFRP) with laminate structure (A) [0/(±45)2/0]T and (B) [90/0/(±45)/0]S. Reprinted from Vassilopoulos et al. (2007), Copyright (2007), with permission from Elsevier.
For predicting the fatigue crack growth in aluminum alloys, Zhi et al. (2016) utilized a recurrent neural network. The linkage between applied stress load and the resulting crack growth within the material was approximated via feedback loops at the output layer. As a result, the fine crack growth evolution could be accurately simulated, as validated by experiments.
Wang et al. (2017) compared three different machine learning approaches for predicting fatigue crack growth within aluminum alloys. Three-layered, fully connected feed forward neural network (one hidden layer) is advantageous over both radial basis function network (RBFN) and genetic algorithms optimized back-propagation network (GABP) so that the optimization and extrapolation results agreed best with the experimentally obtained data.
To predict the fatigue strength of numerous steels based on composition and process parameters, Agrawal et al. (2014) applied successful machine learning techniques, such as feature selection, regression and classification through the use of artificial neural networks, decision trees, and multivariate polynomial regression. For evaluating the capability of predicting the fatigue strength of steels, the most promising parameters were successfully ranked accordingly. Identifying the salient linkages between composition, processing and properties was realized through using the open access material database MatNavi from the Japan National Institute for Material Science (NIMS)4 (Ogata and Yamazaki, 2012). It was shown that the most appropriate predictive modeling technique can vary in dependence on the steel type. “Hierarchical predictive modeling” was used for sequential processing of the data at different scales starting with an initial classification to determine the steel type and followed by choosing and applying the most appropriate method for the particular steel grade to predict the fatigue strength (Agrawal et al., 2014).
Further development of successfully applied predictive modeling techniques to fatigue strengths of steels was used to build an open access online tool by Agrawal and Choudhary (2018). The so called Steel-Fatigue-Strength-Predictor (Agrawal and Choudhary, 2016) is based on data-driven ensemble data mining based on composition and process characteristics of steels to predict their fatigue strength5 Datasets on the fatigue behavior of steel were again taken from the MatNavi materials database and build into a forward process-structure-property-performance model. The framework provides a selection of 40 different modeling techniques that are selected based on the specific properties of the steel alloy(s) of interest. To identify composition and processing parameters that have a significant impact on the fatigue strength, feature selection techniques were applied to determine a small sub-set of the corresponding attributes. Thus, the model with the highest accuracy is tailored to the data of specific material in the steel fatigue strength predictor to provide insight to design preferences for optimal fatigue strength of parts of various types of steel.
To identify and predict the impact of the microstructure on the high-cycle fatigue performance, a data-driven mechanical model of a matrix using crystal plasticity was built by Smith et al. (2016) and Kafka et al. (2018) for the specific application of manufacturing drawn tubes of nickel titanium for arterial stents, as shown in Figure 13. The fatigue crack incubation life is simulated according to a particular microstructure exposed to high-cycle fatigue loads. Via a parametric study, the authors showed that the width of included voids in the material had an inverse proportional relationship to the fatigue life, whereas the diameter of the voids showed a direct proportional relation to the predicted fatigue performance, respectively.
Figure 13. Schematic overview of the implemented self-consistent clustering method based on an RVE of the material, sliced in the middle to show the matrix phase and hide inclusion and void phases (except in the first step). The workflow from left to right: training stage (blue) considers (1) gray inclusions and red voids, (2) matrix strain component (εxx) of the linear elastic analysis; (3) strain clusters obtained through k-means clustering; and the prediction stage yields (4) plastic shear strain field from crystal plasticity and (5) the anticipated Fatigue Indicator Parameter. Reprinted from Kafka et al. (2018), Copyright (2018), with permission from Springer Nature.
For predicting the dynamic fracture growth and coalescence in brittle materials and to foresee failure, Moore et al. (2018) used random forests and decision trees, whereas Schwarzer et al. (2019) utilized recurrent graph convolutional neural networks. The overall aim of both studies was to bypass computationally intensive simulations for predicting fracture evolution. By applying machine learning approaches whose training is based on high accuracy finite-discrete simulations, prediction of statistic fracture growth was achieved in a few seconds. Even though training with simulation results from a microscale model requires computational effort, the predictions of fracture growth statistics and time to failure of the material via the trained random forest or neural network was very efficient. Moore et al. (2018) disregarded ANNs despite an increase in accuracy of about 10% compared to random forests, because of the extensive amount of data required to prevent over-fitting and accompanied computational effort. Instead, they used random forests and decision trees to efficiently perform an uncertainty quantification. Schwarzer et al. (2019) circumvented the challenge of needing a large experimental dataset that is statistically meaningful via using a significant number of simulations; thus, the accuracy could be increased. For that, a deep neural network was used; specifically, a graph convolutional network for fracture feature recognition within the material. Subsequently, a recurrent neural network was utilized for modeling the corresponding feature evolution. Training was achieved with a set of time series of graphs that represent the results of a total number of 145 simulations. Based on their initial state, evolution of multiple material properties can be predicted simultaneously. The error for the averaged fracture size prediction in comparison to the corresponding simulation results was 2%, for the fracture size distribution, the error was 13%, and for the predicted time to failure, the absolute error was 15%. Due to the relatively modest size of the initial dataset used for training, further accuracy was achieved by training the network on incorrect predictions that were previously produced as output. As a result, the loss function could be further reduced; thus, the network learned from its mistakes and the error of the predictions could be gradually decreased.
Prescriptive
Performance properties of components that highly depend on an ideal design of the part can also be optimized via an improved non-dominated sorting generic algorithm (NSGA)-II (Deb et al., 2002), as shown by Wang et al. (2011) for the multi-objective optimization of wind turbine blades, specifically with respect to ideal so-called maximum power coefficient and minimum blade mass. Wang et al. (2011) modified the NSGA-II via incorporating the controlled elitism and dynamic crowding distance (DCD) methods. Ultimately, the design for a 5 megawatts wind turbine blade was optimized by increasing the performance and simultaneously decreasing its mass. Further examples of prescriptive approaches that strongly touch the field of control theory can be found (Padhye and Deb, 2011; Gao et al., 2016; Klancnik et al., 2016) but a discussion of these is out of the scope of the current paper.
Summary and Outlook
In conclusion, it was shown that numerous machine learning approaches are already applied successfully within the field of continuum materials mechanics, either solely or in various combinations for performing tasks that are descriptive, predictive or prescriptive in nature. As a result, acceleration of the discovery and development of novel materials can be enabled through highly reliant descriptions, predictions or prescriptions of anticipated characteristics along the process-structure-property-performance chain, often in a scale-bridging manner.
Machine learning and data mining approaches need to be established as standard tools for scientists and engineers that are experts in generating data through experiments and numerical analyses and sit at the key position to their data sources with the best and most comprehensive access to it (Agarwal and Dhar, 2014). This can be achieved when materials scientists and engineers collaborate closely with computer and data scientists, statisticians, physicists and other experts across various fields to further incorporate data science tools into established workflows for solving problems in materials mechanics and engineering. For example, combining data-driven machine learning and statistical approaches and traditional constitutive model-based simulation tools to perform data-driven simulations (Ibáñez et al., 2018b). In particular, databased and physics-based modeling can complement one another in the sense that a combination of purely data-driven approaches with well-tested physics-based models that are built on known constitutive equations, leads to creating highly reliant and efficient hybrid analytics and simulations.
Award-winning algorithms in other learning domains as diverse as handwritten digit recognition [e.g., using the standardized MNIST dataset as a benchmark (LeCun et al., 1999) and AlphaGo for the Go board game (Silver et al., 2017)] are often noteworthy not only for their performance, but moreover for their simplicity and lack of complex architectures. It is thus reasonable to predict that for materials science, learning algorithms will diverge in both directions, with more composite methods employing many of the algorithms expounded in this review, and with simple learning architectures that will have been proven adaptable and performant within the scope of most materials research. In this regard, so-called capsules, which are embedded in multiple layers within a neural network, exhibit potential for future use, as they achieve improved results on the MNIST handwritten digit database in terms of highly overlapping digit recognition with state-of-the-art performance in comparison to CNNs (Sabour et al., 2017). Thus, they will also be useful in areas of materials mechanics. Reinforcement learning is another example of a promising method for future application within continuum materials mechanics. A successful application on materials outside continuum material mechanics was provided by Popova et al. (2018) on applying deep reinforcement learning for the design of a chemical library, in particular, to the de novo design of drug molecules with specifically desired properties. Thus, in general, reinforcement learning is a suitable approach where materials are involved and decision-making is required.
As machine learning and data mining are fueled by data, the availability of useful and comprehensive datasets to machine learning experts within the field of continuum materials mechanics needs to be increased through establishing common data infrastructures and shared databases. One noteworthy difference between materials mechanics and other, more traditional machine learning domains is the comparative expense of obtaining training data, either by experimental gathering or via simulation. Such simulations can be prohibitively expensive, which may require new methods of synergizing materials simulations to machine learning, for example via multi-fidelity models for generating data for machine learning (Aydin et al., 2019), which have been shown to realize significant computational savings. Because data collection and assimilation may require significant costs, materials data management is important for data-driven approaches. How to store, archive, retrieve and share reliable data; including metadata, providing information on context and content of the data, is essential for increasing the usefulness of shared data, including information on when, where, how and under what conditions data was created and the type of data-processing already performed. Additionally, online tools that are designed for collaborations in research across various disciplines can help to integrate novel machine learning and data mining tools into existing workflows. Besides making decisions along the materials development progress based on empirical knowledge and instincts, experts would benefit extremely, in terms of cost and time reduction, by incorporating data-driven approaches such as machine learning into the development of materials and their processing. That way, knowledge that is gained from investigations that were either successful or failures can be recorded, stored, accessed and transferred to other challenges; therefore be extremely valuable as costs can be saved (Kalidindi and Graef, 2015).
Open source tools such as the highly abstracted neural network library Keras6, which works within the framework of other libraries such as Tensor flow7, empower scientists and engineers to efficiently use machine learning and data mining tools that are implemented with the programming language Python—the de facto standard programming language for machine learning. Due to the good readability of Python's syntax, the convenience and easy access for machine learning and data mining newcomers is increased (Chollet, 2018). Another example for a platform for shared computing and data resources is UNICORE8, which is a maturely developed software interface that provides access to a computing and data infrastructure including high-performance computing, clusters and file systems (Benedyczak et al., 2016).
Ultimately, proper usage of machine learning and data mining approaches has to be practiced and made easily accessible to materials researchers and engineers in order to enable employment across the range from theoretical foundations to practical applications. Furthermore, synergies between various disciplines such as data science and materials science still hold a substantial potential for applying machine learning tools most efficiently to face particular challenges within the field of materials mechanics.
Author Contributions
FB and BK conceptualized and created the basic structure of the article. FB wrote the main part and assembled all of the manuscript. All authors contributed substantially to the comprehensiveness of this review and wrote sections of the manuscript. All authors read, discussed, and revised the article and approved the submitted version.
Funding
FB and BK acknowledge support from the Helmholtz-Association via an ERC-Recognition-Award under contract number ERC-RA-0022. From CC and NH, support from Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer 192346071—SFB 986 is acknowledged. SK acknowledges support from NIST 70NANB18H039.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^Consequently, this work simultaneously qualifies for the Predictive Section of this article: prediction of process parameters.
2. ^LP was faster for linear problems. GA was reported to be faster for nonlinear problems as well but the authors Liu et al. (2015a) reported that the algorithm worked poorly for the considered problem.
3. ^Removing redundancies refers to the deletion of nodes those function is f = 1.
4. ^https://mits.nims.go.jp/index_en.html
5. ^http://info.eecs.northwestern.edu/SteelFatigueStrengthPredictor.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., et al. (2016). “TensorFlow: a system for large-scale machine learning,” in This paper is included in the Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI '16) (Savannah, GA).
Abdi, H., and Williams, L. J. (2009). “Principal component analysis,” in Encyclopedia of Biometrics, eds S. Z. Li and A. Jain (Boston, MA: Springer). doi: 10.1007/978-0-387-73003-5_479
Agarwal, R., and Dhar, V. (2014). Editorial —big data, data science, and analytics: the opportunity and challenge for IS research. Inform. Syst. Res. 25, 443–448. doi: 10.1287/isre.2014.0546
Agrawal, A., and Choudhary, A. (2016). “A fatigue strength predictor for steels using ensemble data mining: steel fatigue strength predictor,” in Proceedings of the 25th ACM International on Conference on Information and Knowledge Management (New York, NY: ACM), 2497–2500.
Agrawal, A., and Choudhary, A. (2018). An online tool for predicting fatigue strength of steel alloys based on ensemble data mining. Int. J. Fatigue 113, 389–400. doi: 10.1016/j.ijfatigue.2018.04.017
Agrawal, A., Deshpande, P. D., Cecen, A., Basavarsu, G. P., Choudhary, A. N., and Kalidindi, S. R. (2014). Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. 3:40. doi: 10.1186/2193-9772-3-8
Altschuh, P., Yabansu, Y. C., Hötzer, J., Selzer, M., Nestler, B., and Kalidindi, S. R. (2017). Data science approaches for microstructure quantification and feature identification in porous membranes. J. Membr. Sci. 540, 88–97. doi: 10.1016/j.memsci.2017.06.020
Andrieu, C., Freitas, N., de Doucet, A., and Jordan, M. I. (2003). An Introduction to MCMC for Machine Learning. Mach. Learn. 50, 5–43. doi: 10.1023/A:1020281327116
Asteris, P. G., Roussis, P. C., and Douvika, M. G. (2017). Feed-forward neural network prediction of themechanical properties of sandcretematerials. Sensors (Basel).17:E1344. doi: 10.3390/s17061344
Aydin, R. C., Braeu, F. A., and Cyron, C. J. (2019). General multi-fidelity framework for training artificial neural networks with computational models. Front. Mater 6:61. doi: 10.3389/fmats.2019.00061
Benedyczak, K., Schuller, B., Sayed, M. P.-E., Rybicki, J., and Grunzke, R. (2016). “UNICORE 7 — Middleware services for distributed and federated computing,” in 2016 International Conference on High Performance Computing Simulation (HPCS) (Innsbruck), 613–620.
Bezdek, J. C., Ehrlich, R., and Full, W. (1984). FCM: The fuzzy c-means clustering algorithm. Comp. Geosci. 10, 191–203. doi: 10.1016/0098-3004(84)90020-7
Bostanabad, R., Bui, A. T., Xie, W., Apley, D. W., and Chen, W. (2016). Stochastic microstructure characterization and reconstruction via supervised learning. Acta Mater. 103, 89–102. doi: 10.1016/j.actamat.2015.09.044
Brough, D. B., Kannan, A., Haaland, B., Bucknall, D. G., and Kalidindi, S. R. (2017a). Extraction of process-structure evolution linkages from X-ray scattering measurements using dimensionality reduction and time series analysis. Integr. Mater. Manuf. Innov. 6, 147–159. doi: 10.1007/s40192-017-0093-4
Brough, D. B., Wheeler, D., Warren, J. A., and Kalidindi, S. R. (2017b). Microstructure-based knowledge systems for capturing process-structure evolution linkages. Curr. Opin. Solid State Mater. Sci. 21, 129–140. doi: 10.1016/j.cossms.2016.05.002
Cang, R., Li, H., Yao, H., Jiao, Y., and Ren, Y. (2018). Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comp. Mater. Sci. 150, 212–221. doi: 10.1016/j.commatsci.2018.03.074
Cang, R., and Ren, M. Y. (2016). “Deep network-based feature extraction and reconstruction of complex material microstructures,” in ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, (Charlotte, NC) V02BT03A008.
Cecen, A., Dai, H., Yabansu, Y. C., Kalidindi, S. R., and Le, S. (2018). Material structure-property linkages using three-dimensional convolutional neural networks. Acta Mater. 146, 76–84. doi: 10.1016/j.actamat.2017.11.053
Chang, Y.-W., and Lin, C.-J. (2008). “Feature ranking using linear SVM,” in Causation and Prediction Challenge, eds I. Guyon, C. Aliferis, G. Cooper, A. Elisseeff, J.-P. Pellet, P. Spirtes, and A. Statnikov, Proceedings of Machine Learning Research (PMLR) (Taipei), 53–64.
Chapman, P., Clinton, J., Kerber, R., Khabaza, T., Reinartz, T., Shearer, C., et al. (1999). “The CRISP-DM user guide,” in 4th CRISP-DM SIG Workshop (Brussels).
Chollet, F. (2015). Keras: Deep Learning for Humans. Available online at: https://github.com/keras-team/keras (accessed January 21, 2019).
Chopra, P., Sharma, R. K., and Kumar, M. (2016). Prediction of compressive strength of concrete using artificial neural network and genetic programming. Adv. Mater. Sci. Eng. 2016, 1–10. doi: 10.1155/2016/7648467
Chowdhury, A., Kautz, E., Yener, B., and Lewis, D. (2016). Image driven machine learning methods for microstructure recognition. Comp. Mater. Sci. 123, 176–187. doi: 10.1016/j.commatsci.2016.05.034
Chupakhin, S., Kashaev, N., Klusemann, B., and Huber, N. (2017). Artificial neural network for correction of effects of plasticity in equibiaxial residual stress profiles measured by hole drilling. J. Strain Anal. Eng. Design 52, 137–151. doi: 10.1177/0309324717696400
Chupakhin, S., Klusemann, B., Huber, N., and Kashaev, N. (2019). Application of design of experiments for laser shock peening process optimization. Int. J. Adv. Manuf. Technol. 29:421. doi: 10.1007/s00170-018-3034-2
Conduit, B., Conduit, G., Stone, H., and Hardy, M. (2014). Development of a New Nickel Based Superalloy for a Combustor Liner and Other High Temperature Applications. Patent GB1408536.
Conduit, B. D., Jones, N. G., Stone, H. J., and Conduit, G. J. (2017). Design of a nickel-base superalloy using a neural network. Mater. Design 131, 358–365. doi: 10.1016/j.matdes.2017.06.007
Conduit, B. D., Jones, N. G., Stone, H. J., and Conduit, G. J. (2018). Probabilistic design of a molybdenum-base alloy using a neural network. Scripta Mater. 146, 82–86. doi: 10.1016/j.scriptamat.2017.11.008
Cortes, C., and Vapnik, V. (1995). Support-vector networks. Mach. Learn. 20, 273–297. doi: 10.1023/A:1022627411411
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Computat. 6, 182–197. doi: 10.1109/4235.996017
DeCost, B. L., Francis, T., and Holm, E. A. (2017). Exploring the microstructure manifold: Image texture representations applied to ultrahigh carbon steel microstructures. Acta Mater. 133, 30–40. doi: 10.1016/j.actamat.2017.05.014
DeCost, B. L., and Holm, E. A. (2015). A computer vision approach for automated analysis and classification of microstructural image data. Comp. Mater. Sci. 110, 126–133. doi: 10.1016/j.commatsci.2015.08.011
Delen, D., and Ram, S. (2018). Research challenges and opportunities in business analytics. J. Business Anal. 1, 2–12. doi: 10.1080/2573234X.2018.1507324
Deshpande, P. D., Gautham, B. P., Cecen, A., Kalidindi, S., Agrawal, A., and Choudhary, A. (2016). “Application of statistical and machine learning techniques for correlating properties to composition and manufacturing processes of steels,” in Proceedings of the 2nd World Congress on Integrated Computational Materials Engineering (ICME), eds. M. Li, C. Campbell, K. Thornton, E. Holm, and P. Gumbsch (Cham: Springer International Publishing), 155–160.
Ding, K., and Ye, L. (eds.). (2006). Laser Shock Peening: Performance and Process Simulations. Cambridge: Woodhead.
Fast, T., and Kalidindi, S. R. (2011). Formulation and calibration of higher-order elastic localization relationships using the MKS approach. Acta Mater. 59, 4595–4605. doi: 10.1016/j.actamat.2011.04.005
Fatemi, A., and Socie, D. F. (1988). A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fat. Frac. Eng. Mat. Struct. 11, 149–165. doi: 10.1111/j.1460-2695.1988.tb01169.x
Figueira Pujol, J. C., and Andrade Pinto, J. M. (2011). A neural network approach to fatigue life prediction. Int. J. Fatigue 33, 313–322. doi: 10.1016/j.ijfatigue.2010.09.003
Freitag, S., Beer, M., Graf, W., and Kaliske, M. (2009). Lifetime prediction using accelerated test data and neural networks. Comp. Struc. 87, 1187–1194. doi: 10.1016/j.compstruc.2008.12.007
Fukushima, K. (1980). Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybernetics 36, 193–202. doi: 10.1007/BF00344251
Fullwood, D. T., Niezgoda, S. R., and Kalidindi, S. R. (2008). Microstructure reconstructions from 2-point statistics using phase-recovery algorithms. Acta Mater. 56, 942–948. doi: 10.1016/j.actamat.2007.10.044
Gallicchio, C., Martin-Guerrero, J. D., Micheli, A., and Soria-Olivas, E. (2017). “Randomized machine learning approaches: Recent developments and challenges,” in Proceedings of the 25th European Symposium on Artificial Neural Networks (ESANN) (Bruges), 77–86.
Gao, Z., Shao, X., Jiang, P., Wang, C., Zhou, Q., Cao, L., et al. (2016). Multi-objective optimization of weld geometry in hybrid fiber laser-arc butt welding using Kriging model and NSGA-II. Appl. Phys. A 122:94. doi: 10.1007/s00339-016-0144-2
Ghosh, I., Das, S. K., and Chakraborty, N. (2014). An artificial neural network model to characterize porosity defects during solidification of A356 aluminum alloy. Neural Comput. Appl. 25, 653–662. doi: 10.1007/s00521-013-1532-6
Gibson, L. J., and Ashby, M. F. (1997). Cellular Solids: Structure and Properties. Cambridge: Cambridge University Press.
Gobert, C., Reutzel, E. W., Petrich, J., Nassar, A. R., and Phoha, S. (2018). Application of supervised machine learning for defect detection during metallic powder bed fusion additive manufacturing using high resolution imaging. Additive Manufac. 21, 517–528. doi: 10.1016/j.addma.2018.04.005
Gomberg, J. A., Medford, A. J., and Kalidindi, S. R. (2017). Extracting knowledge from molecular mechanics simulations of grain boundaries using machine learning. Acta Mater. 133, 100–108. doi: 10.1016/j.actamat.2017.05.009
Hambli, R., Katerchi, H., and Benhamou, C.-L. (2011). Multiscale methodology for bone remodelling simulation using coupled finite element and neural network computation. Biomech. Model. Mechanobiol. 10, 133–145. doi: 10.1007/s10237-010-0222-x
Hashash, Y. M. A., Jung, S., and Ghaboussi, J. (2004). Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Meth. Eng. 59, 989–1005. doi: 10.1002/nme.905
Haykin, S. S. (1998). Neural Networks: A Comprehensive Foundation. Upper Saddle River, NJ: Prentice Hall.
Heerens, J., Mubarok, F., and Huber, N. (2009). Influence of specimen preparation, microstructure anisotropy, and residual stresses on stress–strain curves of rolled Al2024 T351 as derived from spherical indentation tests. J. Mater. Res. 24, 907–917. doi: 10.1557/jmr.2009.0116
Hochreiter, S. (1998). The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Unc. Fuzz. Knowl. Based Syst. 06, 107–116. doi: 10.1142/S0218488598000094
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi: 10.1162/neco.1997.9.8.1735
Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Netw. 4, 251–257. doi: 10.1016/0893-6080(91)90009-T
Hu, Y., Xie, J., Liu, Z., Ding, Q., Zhu, W., Zhang, J., et al. (2018). CA method with machine learning for simulating the grain and pore growth of aluminum alloys. Comp. Mater. Sci. 142, 244–254. doi: 10.1016/j.commatsci.2017.09.059
Huber, N. (2018). Connections between topology and macroscopic mechanical properties of three-dimensional open-pore materials. Front. Mater. 5:69. doi: 10.3389/fmats.2018.00069
Huber, N., Nix, W. D., and Gao, H. (2002). Identification of elastic-plastic material parameters from pyramidal indentation of thin films. Proc. R. Soc. A Math. Phys. Eng. Sci. 458, 1593–1620. doi: 10.1098/rspa.2001.0927
Huber, N., and Tsakmakis, C. (2001). A neural network tool for identifying the material parameters of a finite deformation viscoplasticity model with static recovery. Comp. Methods Appl. Mech. Eng. 191, 353–384. doi: 10.1016/S0045-7825(01)00278-X
Huber, N., and Tyulyukovskiy, E. (2004). A new loading history for identification of viscoplastic properties by spherical indentation. J. Mater. Res. 19, 101–113. doi: 10.1557/JMR.2004.0012
Ibañez, R., Abisset-Chavanne, E., Aguado, J. V., Gonzalez, D., Cueto, E., and Chinesta, F. (2018a). A manifold learning approach to data-driven computational elasticity and inelasticity. Arch. Comp. Methods Eng. 25, 47–57. doi: 10.1007/s11831-016-9197-9
Ibáñez, R., Abisset-Chavanne, E., González, D., Duval, J.-L., Cueto, E., and Chinesta, F. (2018b). Hybrid constitutive modeling: data-driven learning of corrections to plasticity models. Int. J. Mater. Form. 326, 565. doi: 10.1007/s12289-018-1448-x
Jha, S. K., Brockman, R. A., Hoffman, R. M., Sinha, V., Pilchak, A. L., Porter, W. J., et al. (2018). A data analytics approach to discovering unique microstructural configurations susceptible to fatigue. JOM 70, 1147–1153. doi: 10.1007/s11837-018-2881-5
Jia, J., and Davalos, J. F. (2006). An artificial neural network for the fatigue study of bonded FRP–wood interfaces. Composite Struc. 74, 106–114. doi: 10.1016/j.compstruct.2005.03.012
Kafka, O. L., Yu, C., Shakoor, M., Liu, Z., Wagner, G. J., and Liu, W. K. (2018). Data-driven mechanistic modeling of influence of microstructure on high-cycle fatigue life of nickel titanium. JOM 70, 1154–1158. doi: 10.1007/s11837-018-2868-2
Kalidindi, S., Niezgoda, S., Landi, G., Vachhani, S., and Fast, T. (2010). A Novel Framework for Building Materials Knowledge Systems. Comp. Mater. Continua 17, 103–125. doi: 10.3970/cmc.2010.017.103
Kalidindi, S. R., Graef, M., and de (2015). Materials data science: current status and future outlook. Annu. Rev. Mater. Res. 45, 171–193. doi: 10.1146/annurev-matsci-070214-020844
Kalidindi, S. R., Niezgoda, S. R., and Salem, A. A. (2011). Microstructure informatics using higher-order statistics and efficient data-mining protocols. JOM 63, 34–41. doi: 10.1007/s11837-011-0057-7
Khosravani, A., Cecen, A., and Kalidindi, S. R. (2017). Development of high throughput assays for establishing process-structure-property linkages in multiphase polycrystalline metals: application to dual-phase steels. Acta Mater. 123, 55–69. doi: 10.1016/j.actamat.2016.10.033
Kirchdoerfer, T., and Ortiz, M. (2016). Data-driven computational mechanics. Comp. Methods Appl. Mech. Eng. 304, 81–101. doi: 10.1016/j.cma.2016.02.001
Kirchdoerfer, T., and Ortiz, M. (2017). Data driven computing with noisy material data sets. Comp. Methods Appl. Mech. Eng. 326, 622–641. doi: 10.1016/j.cma.2017.07.039
Kirchdoerfer, T., and Ortiz, M. (2018). Data-driven computing in dynamics. Int. J. Numer. Meth. Eng. 113, 1697–1710. doi: 10.1002/nme.5716
Klancnik, S., Hrelja, M., Balic, J., and Brezocnik, M. (2016). Multi-objective optimization of the turning process using gravitational search algorithm (GSA) and NSGA-II approach. Adv. Produc. Eng. Manage. 11, 366–376. doi: 10.14743/apem2016.4.234
Klötzer, D., Ullner, C., Tyulyukovskiy, E., and Huber, N. (2006). Identification of viscoplastic material parameters from spherical indentation data: part II. Experimental validation of the method. J. Mater. Res. 21, 677–684. doi: 10.1557/jmr.2006.0077
Kröner, E. (1977). Bounds for effective elastic moduli of disordered materials. J. Mech. Phys. Solids 25, 137–155. doi: 10.1016/0022-5096(77)90009-6
Landi, G., Niezgoda, S. R., and Kalidindi, S. R. (2010). Multi-scale modeling of elastic response of three-dimensional voxel-based microstructure datasets using novel DFT-based knowledge systems. Acta Mater. 58, 2716–2725. doi: 10.1016/j.actamat.2010.01.007
Le, B. A., Yvonnet, J., and He, Q.-C. (2015). Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Meth. Engng 104, 1061–1084. doi: 10.1002/nme.4953
LeCun, Y., Haffner, P., Bottou, L., and Bengio, Y. (1999). “Object Recognition with Gradient-Based Learning,” in Shape, Contour and Grouping in Computer Vision (Berlin, Heidelberg: Springer Berlin Heidelberg), 319–345.
Ling, J., Hutchinson, M., Antono, E., DeCost, B., Holm, E. A., and Meredig, B. (2017). Building data-driven models with microstructural images: generalization and interpretability. Mater. Disc. 10, 19–28. doi: 10.1016/j.md.2018.03.002
Lipton, Z. C. (2015). A Critical Review of Recurrent Neural Networks for Sequence Learning. CoRR. (2015) arXiv:1506.00019.
Liu, H., and Setiono, R. (1995). “Chi2: Feature selection and discretization of numeric attributes,” in Tools with artificial intelligence, 1995. proceedings., seventh international conference on (Herndon, VA), 388–391.
Liu, R., Kumar, A., Chen, Z., Agrawal, A., Sundararaghavan, V., and Choudhary, A. (2015a). A predictive machine learning approach for microstructure optimization and materials design. Sci. Rep. 5:11551. doi: 10.1038/srep11551
Liu, R., Yabansu, Y. C., Agrawal, A., Kalidindi, S. R., and Choudhary, A. N. (2015b). Machine learning approaches for elastic localization linkages in high-contrast composite materials. Integr. Mater. Manufac. Innovation 4:13. doi: 10.1186/s40192-015-0042-z
Liu, R., Yabansu, Y. C., Yang, Z., Choudhary, A. N., Kalidindi, S. R., and Agrawal, A. (2017). Context aware machine learning approaches for modeling elastic localization in three-dimensional composite microstructures. Integr. Mater. Manuf. Innov. 6, 160–171. doi: 10.1007/s40192-017-0094-3
Liu, Z., Bessa, M. A., and Liu, W. K. (2016a). Self-consistent clustering analysis: an efficient multi-scale scheme for inelastic heterogeneous materials. Comp. Methods Appl. Mech. Eng. 306, 319–341. doi: 10.1016/j.cma.2016.04.004
Liu, Z., Moore, J. A., and Liu, W. K. (2016b). An extended micromechanics method for probing interphase properties in polymer nanocomposites. J. Mech. Phys. Solids 95, 663–680. doi: 10.1016/j.jmps.2016.05.002
Liu, Z., Wu, C. T., and Koishi, M. (2018). A deep material network for multiscale topology learning and accelerated nonlinear modeling of heterogeneous materials. Comp. Methods Appl. Mech. Eng 345, 1138–1168. doi: 10.1016/j.cma.2018.09.020
Lubbers, N., Lookman, T., and Barros, K. (2017). Inferring low-dimensional microstructure representations using convolutional neural networks. Phys. Rev. E 96:52111. doi: 10.1103/PhysRevE.96.052111
Maass, W., Natschläger, T., and Markram, H. (2002). Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comp. 14, 2531–2560. doi: 10.1162/089976602760407955
Mai, H., Song, G., and Liao, X. (2016). Time-delayed dynamic neural network-based model for hysteresis behavior of shape-memory alloys. Neural Comput. Appl. 27, 1519–1531. doi: 10.1007/s00521-015-1950-8
Mesquita Sá Junior, J. J., de Backes, A. R., and Bruno, O. M. (2018). “Randomized neural network based signature for classification of titanium alloy microstructures,” in Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, eds. M. Mendoza, and S. Velastín (Cham: Springer International Publishing), 669–676.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., et al. (2013). Playing atari with deep reinforcement learning. CoRR arXiv:1312.5602.
Moore, B. A., Rougier, E., O'Malley, D., Srinivasan, G., Hunter, A., and Viswanathan, H. (2018). Predictive modeling of dynamic fracture growth in brittle materials with machine learning. Comput. Mater. Sci. 148, 46–53. doi: 10.1016/j.commatsci.2018.01.056
Mosallam, A., Medjaher, K., and Zerhouni, N. (2016). Data-driven prognostic method based on Bayesian approaches for direct remaining useful life prediction. J. Intell. Manuf. 27, 1037–1048. doi: 10.1007/s10845-014-0933-4
Niezgoda, S. R., Fullwood, D. T., and Kalidindi, S. R. (2008). Delineation of the space of 2-point correlations in a composite material system. Acta Mater. 56, 5285–5292. doi: 10.1016/j.actamat.2008.07.005
Niezgoda, S. R., Kanjarla, A. K., and Kalidindi, S. R. (2013). Novel microstructure quantification framework for databasing, visualization, and analysis of microstructure data. Integr. Mater. 2:15. doi: 10.1186/2193-9772-2-3
Nocedal, J., and Wright, S. J. (2006). Numerical Optimization. New York, NY: Springer Science+Business Media LLC.
Oeser, M., and Freitag, S. (2009). Modeling of materials with fading memory using neural networks. Int. J. Numer. Meth. Engng 78, 843–862. doi: 10.1002/nme.2518
Ogata, T., and Yamazaki, M. (2012). “New stage of MatNavi, materials database at NIMS,”. in Harnessing The Materials Genome: Accelerated Materials Development via Computational and Experimental Tools, 2012. Available online at: http://dc.engconfintl.org/materials_genome/9/ (accessed January 21, 2019).
Orr, M. J. L. (1996). Introduction to Radial Basis Function Networks. Technical Report, Center for Cognitive Science, University of Edinburgh, Edinburgh, UK.
Padhye, N., and Deb, K. (2011). “Multi-objective optimisation and multi-criteria decision making for FDM using evolutionary approaches,” in Multi-objective Evolutionary Optimisation for Product Design and Manufacturing, eds. L. Wang, A. H. C. Ng, and K. Deb (London: Springer London), 219–247.
Paulson, N. H., Priddy, M. W., McDowell, D. L., and Kalidindi, S. R. (2018). Data-driven reduced-order models for rank-ordering the high cycle fatigue performance of polycrystalline microstructures. Mater. Design 154, 170–183. doi: 10.1016/j.matdes.2018.05.009
Popova, E., Rodgers, T. M., Gong, X., Cecen, A., Madison, J. D., and Kalidindi, S. R. (2017). Process-structure linkages using a data science approach: application to simulated additive manufacturing data. Integr. Mater. Manuf. Innov. 6, 54–68. doi: 10.1007/s40192-017-0088-1
Popova, M., Isayev, O., and Tropsha, A. (2018). Deep reinforcement learning for de novo drug design. Sci. Adv. 4:eaap7885. doi: 10.1126/sciadv.aap7885
Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408. doi: 10.1037/h0042519
Russell, S. J., and Peter, N. (2016). Artificial Intelligence: A Modern Approach. Malaysia: Pearson Education Limited.
Sabour, S., Frosst, N., and Hinton, G. E. (2017). “Dynamic routing between capsules,” in Advances in Neural Information Processing Systems 30, eds. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, et al. (Long Beach, CA: Curran Associates, Inc), 3856–3866.
Sahu, N. K., Andhare, A. B., Andhale, S., and Abraham, R. R. (2018). Prediction of surface roughness in turning of Ti-6Al-4V using cutting parameters, forces and tool vibration. IOP Conf. Ser. Mater. Sci. Eng. 346:12037. doi: 10.1088/1757-899X/346/1/012037
Schajer, G. S. (1988). Measurement of non-uniform residual stresses using the hole-drilling method. Part II—practical application of the integral method. J. Eng. Mater. Technol. 110:344. doi: 10.1115/1.3226060
Schmidhuber, J. (2015). Deep learning in neural networks: an overview. Neural Netw. 61, 85–117. doi: 10.1016/j.neunet.2014.09.003
Schwarzer, M., Rogan, B., Ruan, Y., Song, Z., Lee, D., Percus, A. G., et al. (2019). Learning to fail: predicting fracture evolution in brittle materials using recurrent graph convolutional neural networks. Comput Mater Sci. 162, 322–332. doi: 10.1016/j.commatsci.2019.02.046
Sikorska, J. Z., Hodkiewicz, M., and Ma, L. (2011). Prognostic modelling options for remaining useful life estimation by industry. Mech. Syst. Signal Proc. 25, 1803–1836. doi: 10.1016/j.ymssp.2010.11.018
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., et al. (2017). Mastering the game of Go without human knowledge. Nature 550:354 EP. doi: 10.1038/nature24270
Silverio Freire Júnior, R. C., Dória Neto, A. D., Aquino, E. M. F., and de (2009). Comparative study between ANN models and conventional equations in the analysis of fatigue failure of GFRP. Int. J. Fatigue 31, 831–839. doi: 10.1016/j.ijfatigue.2008.11.005
Smith, J., Xiong, W., Yan, W., Lin, S., Cheng, P., Kafka, O. L., et al. (2016). Linking process, structure, property, and performance for metal-based additive manufacturing: computational approaches with experimental support. Comput. Mech. 57, 583–610. doi: 10.1007/s00466-015-1240-4
Spear, A. D., Kalidindi, S. R., Meredig, B., Kontsos, A., and Le Graverend, J.-B. (2018). Data-driven materials investigations: the next frontier in understanding and predicting fatigue behavior. JOM 70, 1143–1146. doi: 10.1007/s11837-018-2894-0
Sundararaghavan, V., and Zabaras, N. (2005). Classification and reconstruction of three-dimensional microstructures using support vector machines. Comput. Mater. Sci. 32, 223–239. doi: 10.1016/j.commatsci.2004.07.004
Tan, P.-N., Steinbach, M., and Kumar, V. (2009). Introduction to Data Mining. Boston: Pearson Addison-Wesley.
Turner, D. M., and Kalidindi, S. R. (2016). Statistical construction of 3-D microstructures from 2-D exemplars collected on oblique sections. Acta Mater. 102, 136–148. doi: 10.1016/j.actamat.2015.09.011
Tyulyukovskiy, E., and Huber, N. (2006). Identification of viscoplastic material parameters from spherical indentation data: Part I. Neural networks. J. Mater. Res. 21, 664–676. doi: 10.1557/JMR.2006.0076
Upadhyay, V., Jain, P. K., and Mehta, N. K. (2012). “Artificial neural network modeling of cutting force in turning of Ti-6Al-4V alloy and its comparison with response surface methodology,” in Proceedings of the International Conference on Soft Computing for Problem Solving (SocProS 2011) December 20-22, 2011, eds. K. Deep, A. Nagar, M. Pant, and J. C. Bansal (New Delhi: Springer India), 761–768.
van Hasselt, H., Guez, A., and Silver, D. (2016). “Deep reinforcement learning with double Q-learning,” (Phoenix, AZ) in AAAI.
Vassilopoulos, A. P., Georgopoulos, E. F., and Dionysopoulos, V. (2007). Artificial neural networks in spectrum fatigue life prediction of composite materials. Int. J. Fatigue 29, 20–29. doi: 10.1016/j.ijfatigue.2006.03.004
Voyles, P. M. (2017). Informatics and data science in materials microscopy. Curr. Opin. Solid State Mater. Sci. 21, 141–158. doi: 10.1016/j.cossms.2016.10.001
Wang, B., Zhao, W., Du, Y., Zhang, G., and Yang, Y. (2016). Prediction of fatigue stress concentration factor using extreme learning machine. Comput. Mater. Sci. 125, 136–145. doi: 10.1016/j.commatsci.2016.08.035
Wang, H., Zhang, W., Sun, F., and Zhang, W. (2017). A comparison study of machine learning based algorithms for fatigue crack growth calculation. Materials 10:E543. doi: 10.3390/ma10050543
Wang, L., Wang, T.-,g., and Luo, Y. (2011). Improved non-dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades. Appl. Math. Mech. 32, 739–748. doi: 10.1007/s10483-011-1453-x
Watkins, C. J. C. H., and Dayan, P. (1992). Q-learning. Mach. Learn. 8, 279–292. doi: 10.1007/BF00992698
Willumeit, R., Feyerabend, F., and Huber, N. (2013). Magnesium degradation as determined by artificial neural networks. Acta Biomater. 9, 8722–8729. doi: 10.1016/j.actbio.2013.02.042
Witten, I. H., Frank, E., and Hall, M. A. (2011). Data mining: Practical Machine Learning Tools and Techniques. Amsterdam: Elsevier/Morgan Kaufmann.
Xiong, J., Zhang, G., Hu, J., and Wu, L. (2014). Bead geometry prediction for robotic GMAW-based rapid manufacturing through a neural network and a second-order regression analysis. J. Intell. Manuf. 25, 157–163. doi: 10.1007/s10845-012-0682-1
Yabansu, Y. C., and Kalidindi, S. R. (2015). Representation and calibration of elastic localization kernels for a broad class of cubic polycrystals. Acta Mater. 94, 26–35. doi: 10.1016/j.actamat.2015.04.049
Yabansu, Y. C., Patel, D. K., and Kalidindi, S. R. (2014). Calibrated localization relationships for elastic response of polycrystalline aggregates. Acta Mater. 81, 151–160. doi: 10.1016/j.actamat.2014.08.022
Yabansu, Y. C., Steinmetz, P., Hötzer, J., Kalidindi, S. R., and Nestler, B. (2017). Extraction of reduced-order process-structure linkages from phase-field simulations. Acta Mater. 124, 182–194. doi: 10.1016/j.actamat.2016.10.071
Yan, W., Lin, S., Kafka, O. L., Lian, Y., Yu, C., Liu, Z., et al. (2018). Data-driven multi-scale multi-physics models to derive process–structure–property relationships for additive manufacturing. Comput. Mech. 61, 521–541. doi: 10.1007/s00466-018-1539-z
Yang, Z., Yabansu, Y. C., Al-Bahrani, R., Liao, W.-,k., Choudhary, A. N., Kalidindi, S. R., et al. (2018). Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci. 151, 278–287. doi: 10.1016/j.commatsci.2018.05.014
Younis, H. B., Kamal, K., Sheikh, M. F., Hamza, A., and Zafar, T. (2018). “Prediction of fatigue crack growth rate in aircraft aluminum alloys using radial basis function neural network,” in 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI) (Xiamen), 825–830.
Keywords: machine learning, materials mechanics, data mining, process-structure-property-performance relationship, knowledge discovery
Citation: Bock FE, Aydin RC, Cyron CJ, Huber N, Kalidindi SR and Klusemann B (2019) A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 6:110. doi: 10.3389/fmats.2019.00110
Received: 04 February 2019; Accepted: 26 April 2019;
Published: 15 May 2019.
Edited by:
Roberto Brighenti, University of Parma, ItalyReviewed by:
Andreas Menzel, Technical University Dortmund, GermanyDaojian Cheng, Beijing University of Chemical Technology, China
Copyright © 2019 Bock, Aydin, Cyron, Huber, Kalidindi and Klusemann. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frederic E. Bock, ZnJlZGVyaWMuYm9ja0BoemcuZGU=
 Frederic E. Bock
Frederic E. Bock Roland C. Aydin
Roland C. Aydin Christian J. Cyron
Christian J. Cyron Norbert Huber
Norbert Huber Surya R. Kalidindi
Surya R. Kalidindi Benjamin Klusemann
Benjamin Klusemann