Coupled Cluster Theory in Materials Science

The workhorse method of computational materials science is undeniably the density functional theory (DFT) in the Kohn-Sham framework of approximate exchange and correlation energy functionals. However, the need for highly accurate electronic structure theory calculations in materials science motivates the further development and exploration of alternative as well as complementary techniques. Among these alternative approaches, quantum chemical wavefunction based theories and in particular coupled cluster theory hold promise in filling the gap in the toolbox of computational materials scientists. Coupled cluster (CC) theory provides a compelling framework of approximate infinite-order perturbation theory, in the form of an exponential of cluster operators describing the true quantum many-body effects of the electronic wave function at a computational cost that, despite being significantly more expensive than DFT, scales polynomially with system size. The hierarchy of size-extensive approximate methods established in the framework of CC theory, achieves systematic improvability for many materials properties. This is in contrast to currently available density functionals that often suffer from uncontrolled approximations that limit the accuracy in the prediction of materials properties. In this tutorial-style review we will introduce basic concepts of coupled cluster theory and recent developments that increase its computational efficiency for calculations of molecules, solids and materials in general. We will touch upon the connection between coupled cluster theory and the random-phase approximation that is widely used in the field of solid-state physics. We will discuss various approaches to improve the computational performance without compromising on accuracy. These approaches include large-scale parallel design as well as techniques that reduce the pre-factor of the computational complexity. A central part of this article discusses the convergence of calculated properties to the thermodynamic limit, which is of significant importance for reliable predictions of materials properties and constitutes an additional challenge compared to calculations of large molecules. We mention technical aspects of computer code implementations of periodic coupled cluster theories in different numerical frameworks of the one-electron orbital basis; the projector-augmented-wave formalism using a plane wave basis set and the numeric atom-centered-orbital (NAO) with resolution-of-identity. We will discuss results and the possible scope of these implementations and how they can help advance the current state of the art in electronic structure theory calculations of materials.

1. Introduction

The solution of the many-electron Schrödinger equation is at the heart of ab-initio computational materials science. Density functional theory (DFT) in the Kohn-Sham framework of approximate exchange and correlation energy functionals is irrefutably the method of choice for the study of computational materials science problems, due to its good trade-off between accuracy and computational cost. However, despite the great successes of DFT in the last decades, it remains difficult to systematically improve upon the accuracy of currently available approximate density functionals, which sometimes fail even qualitatively in cases where strong electronic correlation effects, non-local van der Waals interactions or density-driven errors, arising from the non-vanishing self-interaction, occur (Cohen et al., 2012). As a consequence, the community of ab-initio computational materials scientists explores the accuracy and computational efficiency of alternative methods to solve the many-electron problem, such as Green's function-based methods or many-electron wavefunction theories. Quantum chemical wavefunction theories have the potential to treat electronic exchange and correlation effects in a systematically improvable manner. Their computational cost is in general significantly larger than that required for DFT calculations, which limits their application to relatively small system sizes only. In this work we discuss recent efforts and improvements that expand the scope of quantum chemical wavefunction theories and in particular that of coupled cluster methods. Furthermore, we outline implementation details and the relationship between the coupled cluster ansatz and the random phase approximation briefly. The latter method is becoming an increasingly efficient technique to treat electronic exchange and correlation effects in solids and molecules.

Quantum chemical wavefunction theories include a wide range of methods that are capable of treating weak as well as strong electronic correlation effects. In contrast to multi-reference methods, single reference coupled cluster theory is in general not suited to treat strong correlation problems. However, coupled cluster theories have successfully been applied to calculate a wide range of materials properties including (i) cohesive energies of (molecular) solids (Rościszewski et al., 1999; Nolan et al., 2009; Schwerdtfeger et al., 2010; Grüneis et al., 2011; Stoll and Doll, 2012; Booth et al., 2013; Yang et al., 2014; Gruber et al., 2018), (ii) pressure-temperature phase diagrams (Gruber and Grüneis, 2018) (iii) exfoliation energies of layered materials (Hummel et al., 2016; Sansone et al., 2016; Usvyat et al., 2018) (iv) defect formation energies (Grüneis, 2015b), and (v) adsorption and reaction energies of atoms and molecules on surfaces (Voloshina et al., 2011; Usvyat et al., 2012; Boese and Sauer, 2016; Kubas et al., 2016; Tsatsoulis et al., 2017, 2018). Furthermore, the equation of motion coupled cluster theories has been implemented to calculate the excited state and single-electron related properties including electron-addition and removal energies in solids (McClain et al., 2017). As a model Hamiltonian for real metallic systems, the uniform electron gas has also been studied extensively using CC and related approaches (Freeman, 1977; Bishop and Lührmann, 1978; Shepherd and Grüneis, 2013; McClain et al., 2016). This list of applications is by no means complete but illustrates the potential of coupled cluster methods for computational materials science simulations. The achieved accuracy depends on the employed level of truncation in the coupled cluster wavefunction ansatz. Comparison to experimental findings and high-level quantum Monte Carlo (QMC) results for solids reveals that coupled cluster singles and doubles theory, including perturbative triples [CCSD(T)], achieves a similar level of accuracy in solids as for molecular quantum chemistry applications, indicating that it is possible to obtain results with chemical accuracy (1 kcal/mol) or even better for most energetic properties, such as cohesive energies. This level of accuracy is similar to the accuracy that can be achieved using QMC calculations although a systematic assessment for solids as it was carried out for molecules is still missing Nemec et al. (2010). However, in contrast to QMC, perturbative Møller-Plesset and coupled cluster theories, such as the perturbative triples approach are not suitable for the treatment of metallic systems, and more work is needed to understand and possibly correct for these deficiencies (Shepherd and Grüneis, 2013). We stress that non-perturbative coupled cluster methods, such as coupled cluster singles and doubles (CCSD) will yield convergent correlation energies even for metallic systems. The applications referred to above have been obtained using a variety of different computer code implementations of CC theories that can roughly be divided in three different categories: (i) local schemes that are based on a localized occupied orbital manifold and take advantage of the short-rangedness of electronic correlation explicitly (Pisani et al., 2012), (ii) the incremental method that is extremely efficient for weakly interacting fragments, such as molecular crystals (Rościszewski et al., 1999; Schwerdtfeger et al., 2010; Stoll and Doll, 2012) and (iii) canonical schemes that explicitly account for the translational symmetry of periodic systems by employing delocalized Bloch orbitals (McClain et al., 2017; Gruber et al., 2018). Recently another approach to coupled cluster theory using stochastic techniques has been developed and successfully applied to a range of systems including the uniform electron gas (Thom, 2010; Neufeld and Thom, 2017; Spencer et al., 2019). In this article we will mostly focus on canonical schemes that employ delocalized Bloch orbitals and we will discuss their advantages and disadvantages in comparison to other methods.

The general purpose of computationally expensive yet highly accurate electronic structure theories in materials simulations is 2-fold: (i) production of benchmark results and (ii) prediction of materials properties without depending on uncontrolled approximations. Benchmark results are very valuable because they can be used to further test and improve upon the accuracy of computationally more efficient yet less accurate methods or adjust parameters used in simplified models of real systems. Although experiments can also provide benchmark results, experimental findings need to be corrected for the effect of lattice vibrations, finite temperature and possibly relativistic contributions in order to be directly comparable to non-relativistic zero temperature electronic structure theory calculations in the Born-Oppenheimer approximation. As such it is often more efficient to employ theoretical benchmark results obtained using high-level theories. Ideally it should be possible to perform benchmark calculations in a black-box manner. A black-box method allows for high-throughput calculations and enables non-expert users to obtain reliable simulation results for real materials. Compared to density functional theory, many-electron wavefunction theory calculations are more difficult to apply in practice because calculated properties, such as the ground state energy converge much slower with respect to the employed computational parameters, such as k-point mesh density and basis set size, often requiring extrapolation techniques that need to be checked carefully. Recent progress makes it possible to accelerate the convergence with respect to such computational parameters significantly and control approximations in an automated way such that coupled cluster methods become more “user-friendly.” In this article we will review some of the most important and recent improvements that aim at expanding the scope of coupled cluster theories to the field of computational materials science. Many methodological developments are inspired by related techniques in the field of molecular quantum chemistry and quantum Monte Carlo.

Due to the potential use of coupled cluster theory as an accurate benchmark tool in materials simulations, it is also necessary to understand and revisit the influence of widely used approximations in modern electronic structure theory codes. Obviously, the precision of the underlying numerical approach to solve the Schrödinger equation must not be lower than the accuracy of the employed many-electron theory. Pseudopotentials, basis sets and even frozen core approximations that have become standard practice in DFT calculations of solids can not necessarily be transferred directly to wavefunction theory calculations. To this end it is important to assess the influence of such approximations by comparing wavefunction theory calculations on different footings. In this article we will report on two different implementations of CC theory employing the numeric atom-centered orbital (NAO) and the projector augment wave (PAW) framework.

The coupled cluster method accounts for many-electron correlation effects explicitly using an exponential ansatz for the wavefunction. The wavefunction amplitudes are obtained by solving a set of non-linear equations that can be derived using different methods including second quantization in combination with Wick's theorem, Slater rules or diagrammatic techniques. The latter are also popular in the field of Green's function-based methods, where Feynman diagrams serve as a representation of quantum field theoretical expressions of many-particle interactions. Diagrammatic methods allow for characterizing the CC method as an approximate perturbation theory that performs a summation of a certain type of diagrams to infinite order. In a diagrammatic language the close relationship between coupled cluster theory and other approaches such as the random-phase approximation (RPA) becomes more obvious for both ground and excited state properties as discussed in detail in Scuseria et al. (2008); Berkelbach (2018). This relationship also implies that the RPA and CC theory share computational characteristics, such as a slow convergence with respect to the employed independent particle basis sets and k-point mesh. Therefore, methodological improvements, such as basis set extrapolation methods and finite size corrections can often be readily transferred between these approaches.

2. Theory and Concepts

2.1. Coupled Cluster Theory

Coupled cluster theory was initially proposed by Fritz Coester and Hermann Kümmel in the field of nuclear physics (Coester, 1958; Coester and Kümmel, 1960). In the 1960s Jiri Cizek and Josef Paldus introduced the method for electron correlation (Cizek, 1966; Cizek and Paldus, 1971) and since then it has become a widely used electronic structure theory method for quantum chemical calculations on systems that do not exhibit strong static correlation (Bartlett and Musiał, 2007). For a more detailed introduction to coupled cluster theory we refer the reader to Helgaker et al. (2000); Bartlett and Musiał (2007); Crawford and Schaefer (2007); Shavitt and Bartlett (2009). Coupled cluster theory uses an exponential ansatz of cluster operators for the many-electron wavefunction

$\begin{array}{ll}|{\Psi }^{\text{CC}}\rangle =e^{\widehat{T}}|{\Phi }^{\text{HF}}\rangle ,& (1)\end{array}$

where Φ^HF is a single Slater determinant constructed from the Hartree-Fock (HF) one-electron orbitals that best approximates the ground state energy of a many-electron system. In passing we stress, however, that CC theory can in principle employ any single reference determinant, though this can affect the accuracy. The cluster operator in the exponent is defined by $\widehat{T}=\sum _{m=1}^n{\widehat{T}}_m$, where n corresponds to the order of the coupled cluster approximation. ${\widehat{T}}_m$ is an m-fold excitation operator that generates m-fold excited Slater determinants $|{\Phi }_{i_1..i_m}^{a_1..a_m}\rangle$ multiplied by corresponding amplitudes ($t_{i_1..i_m}^{a_1..a_m}$) when applied to the HF ground state (|Φ^HF〉):

$\begin{array}{ll}{\widehat{T}}_m|{\Phi }^{\text{HF}}\rangle ={\displaystyle \sum _{\begin{array}{c}{i}_1,..,i_m\in \text{occ}.\\ a_1,..,a_m\in \text{unocc}.\end{array}}{t}_{i_1..i_m}^{a_1..a_m}}|{\Phi }_{i_1..i_m}^{a_1..a_m}\rangle .& (2)\end{array}$

We will return to the discussion on the procedure for determining the amplitudes later. The mean-field wavefunction obtained from HF theory serves as a single reference determinant for the CC wavefunction and electronic correlation effects are accounted for explicitly using excitation operators and corresponding amplitudes. The indices i and a refer to occupied and unoccupied orbitals, respectively. We stress that depending on the choice of orbitals and their symmetry, the wavefunction amplitudes will reflect a different degree of sparsity. In the case of Bloch orbitals, as commonly used in periodic systems, the amplitudes vanish unless the sum of the momenta of the occupied orbitals is equal to the sum of the momenta of the unoccupied orbitals modulo a reciprocal lattice vector. We note that this property holds only for momentum-conserving Hamiltonians.

In coupled cluster singles and doubles theory the cluster operator is approximated using $\widehat{T}\approx {\widehat{T}}_1+{\widehat{T}}_2$. Due to the exponential ansatz of the CCSD wavefunction, the coefficients of all i-fold excited Slater determinants with i ≥ 2 are approximated using anti-symmetrized products of single and double excitation amplitudes. For two-electron systems, 2-fold excited Slater determinants can be generated at most and therefore CCSD theory becomes exact. Higher orders of coupled cluster theory become exact for systems with the corresponding number of electrons. The cluster amplitudes $t_i^a$ and $t_{ij}^{ab}$ are obtained by inserting the wavefunction ansatz in the Schrödinger equation, projecting on the left by $\langle {\Phi }_i^a|e^{-\widehat{T}}$ and $\langle {\Phi }_{ij}^{ab}|e^{-\widehat{T}}$, and solving the amplitude equations $\langle {\Phi }_i^a|e^{-\widehat{T}}H{e}^{\widehat{T}}|{\Phi }^{\text{HF}}\rangle =0$ and $\langle {\Phi }_{ij}^{ab}|e^{-\widehat{T}}H{e}^{\widehat{T}}|{\Phi }^{\text{HF}}\rangle =0$, respectively. For practical computer implementations the latter equations are not useful but need to be recast in expressions that depend explicitly on Hamiltonian matrix elements and amplitudes, which can be achieved using further algebraic transformations including the Baker-Campbell-Hausdorff formula and Wick's theorem, Slater rules or diagrammatic techniques (Helgaker et al., 2000; Bartlett and Musiał, 2007; Crawford and Schaefer, 2007;Shavitt and Bartlett, 2009).

For most applications a good trade-off between computational cost and high accuracy is achieved by truncating the cluster operator at doubles (CCSD) and accounting for the effect of triples in a perturbative manner. This approach is referred to as CCSD(T) theory (Raghavachari et al., 1989) and achieves chemical accuracy for the prediction of reaction energies and barrier heights for a wide range of chemical reactions (Helgaker et al., 2000; Bartlett and Musiał, 2007). We note that CCSD and CCSD(T) theory include all diagrams for the correlation energy that occurs in third- and fourth-order perturbation theory, respectively. However, as a consequence of the single-reference approximation in CC theory, the treatment of strong correlation problems is extremely limited. Examples for strong correlation problems include molecular dissociation problems where the HF approximation to the wavefunction fails dramatically due to the multideterminant nature of the true wavefunction. Conventional single-reference CC theory are accurate only for wavefunctions that are dominated by single-reference determinants. We note in passing that multireference coupled cluster theories aim at the treatment of strong correlation problems (Köhn et al., 2013; Evangelista, 2018).

To establish a connection between coupled cluster methods and the random-phase approximation, we now turn to coupled cluster doubles (CCD) theory. CCD theory approximates the cluster operator using $\widehat{T}\approx {\widehat{T}}_2$. The cluster amplitudes $t_{ij}^{ab}$ are obtained by solving the quadratic amplitude equations $\langle {\Phi }_{ij}^{ab}|e^{-{\widehat{T}}_2}H{e}^{{\widehat{T}}_2}|{\Phi }^{\text{HF}}\rangle =0$ that in a canonical spin-orbital basis read

$\begin{array}{l}{t}_{ij}^{ab}=\frac{1}{{ϵ}_i+{ϵ}_j-{ϵ}_a-{ϵ}_b}(\langle ij||ab\rangle +\langle cj||kb\rangle t_{ik}^{ac}+\langle ci||ka\rangle t_{jk}^{bc}+\langle cd||kl\rangle t_{lj}^{db}{t}_{ik}^{ac}\\ +\frac{1}{2}\langle cd||ab\rangle t_{ij}^{cd}+\frac{1}{2}\langle ij||kl\rangle t_{kl}^{ab}+\frac{1}{4}\langle cd||kl\rangle t_{ij}^{cd}{t}_{kl}^{ab}\\ -\langle cj||ka\rangle t_{ik}^{bc}-\langle ci||kb\rangle t_{jk}^{ac}-\langle cd||kl\rangle t_{lj}^{da}{t}_{ik}^{bc}\\ +\frac{1}{2}\langle cd||kl\rangle \left[t_{lj}^{ab}{t}_{ik}^{cd}-t_{li}^{ab}{t}_{jk}^{cd}+t_{ij}^{db}{t}_{kl}^{ac}-t_{ij}^{da}{t}_{kl}^{bc}\right])& (3)\end{array}$

In the above equation we use Einstein summation convention. The indices i, j, k, and l label occupy orbital indices, whereas a, b, c, and d label virtual orbital indices. ϵ corresponds to the HF one-electron energies and the anti-symmetrized electron repulsion integrals (ERIs) are defined as $\langle ij\left|\right|ab\rangle =\langle ij\left|r_{12}^{-1}\right|ab\rangle -\langle ij\left|r_{12}^{-1}\right|ba\rangle$, where the ERIs are defined by

$\begin{array}{ll}\langle ij|r_{12}^{-1}|ab\rangle ={\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }d}}{x}_{1}d{x}_2\frac{{\chi }_i^{*}(x_1){\chi }_j^{*}(x_2){\chi }_a(x_1){\chi }_b(x_2)}{|r_1-r_2|}.& (4)\end{array}$

In the above expression the spin-orbitals χ depend on the space-spin coordinate x = (r, σ) and the spatial coordinates are integrated over all space. In section 3 we will return to the discussion of the evaluation of these integrals using different frameworks of the independent particle basis sets. Equation (3) is solved for the amplitudes in an iterative manner by updating the amplitudes in every iteration using the right-hand side of Equation (3). To accelerate convergence standard techniques such as direct inversion of the iterative subspace (DIIS) can be employed (Pulay, 1980). Once the amplitudes are obtained, the CCD correlation energy can be calculated by

$\begin{array}{ll}{E}_c^{\text{CCD}}=\frac{1}{4}\langle ij\Vert ab\rangle t_{ij}^{ab}& (5)\end{array}$

As a consequence of the large number of virtual orbitals, N_v, compared to the number of occupied orbitals, N_o, needed to obtain converged correlation energies even when extrapolation techniques are employed, the computation and storage of ERIs as well as their contraction with amplitudes constitute the main source of computational cost and memory in canonical CC calculations. In terms of computational cost and memory the so-called particle-particle ladder term $\langle cd\left|\right|ab\rangle t_{ij}^{cd}$ exhibits the most unfavorable scaling with respect to the number of virtual orbitals ${O}(N_v^4{N}_o^2)$. In passing we note that a number of techniques have been suggested to reduce the computational cost of the $\langle cd\left|\right|ab\rangle t_{ij}^{cd}$ term in CC calculations (Hummel et al., 2017; Dutta et al., 2018) and that local schemes can treat this term very efficiently through construction, since it couples a single electron-pair to itself only. The distribution of memory and computational load in parallel computer implementations as well as the possible on-the-fly calculation of the required ERIs make it possible to study systems containing several hundreds of virtual orbitals routinely. Furthermore, modern tensor framework libraries greatly simplify the development of compact and also fully parallel coupled cluster theory computer codes (Solomonik et al., 2014).

Equation (3) arranges the terms of the amplitude equations in the same manner as Shepherd et al. (2014), who investigated different approximations to coupled cluster doubles theory for the uniform electron gas. The various terms are labeled in agreement with the corresponding diagrams such that the top line of Equation (3) represents the driver and the ring terms, the second line ladder terms, the third line crossed-ring terms, and the bottom-line mosaics (Scuseria et al., 2013). The quadratic amplitude equations of coupled cluster doubles theory couple all electron pairs of a many-electron system using perturbation theory diagrams of a certain type to infinite order. This is illustrated by the iterative solution for the amplitudes in Equation (3): in the first iteration it follows that $t_{ij}^{ab}=\frac{\langle ij\left|\right|ab\rangle }{{ϵ}_i+{ϵ}_j-{ϵ}_a-{ϵ}_b}$. In subsequent iterations the approximate first-order amplitudes are coupled via the corresponding ladder, ring, crossed-ring, and mosaic terms to each other. In this manner a summation of all possible couplings between different diagrams to the infinite order is performed. The included diagrams balance and account for important physical effects of many-electron systems. All terms are accompanied by so-called exchange terms that are needed to correct for exclusion principle violating (EPV) contributions and account for the fermionic character of the many-electron wavefunction. EPV contributions cause self-interaction errors that are not necessarily restricted to approximate DFT methods. Furthermore, the magnitude of ring and ladder contributions to the electronic correlation energy is system dependent. For homogeneous systems the dimensionality and electronic density plays a crucial role. In the high-density limit the ring approximation becomes exact for three-dimensional systems, whereas ladder terms become more important for lower-densities and lower dimensions (Freeman, 1977, 1978, 1983; Bishop and Lührmann, 1978). The inclusion of ring diagrams is important to describe collective polarization effects and obtain effectively screened inter-electronic interactions that yield convergent correlation energies in metals.

Coupled cluster theory is based on a systematically improvable many-electron wavefunction ansatz and derived without using uncontrolled approximations. However, various approximations to the amplitude equations have been investigated and have proven to sometimes be more accurate and even more stable than their parent method. The distinguishable cluster approximation (DCSD) (Kats and Manby, 2013; Kats et al., 2015) demonstrates that disregarding certain diagrams in the amplitude equations and reweighting others such that the resultant method remains exact for two-electron systems yields results that clearly outperform CCSD in terms of accuracy. Furthermore, it is possible to show that by a change of representation DCSD exhibits a computational complexity that scales with respect to system size only as ${O}(N^5)$ instead of ${O}(N^6)$ as in the case of CCSD (Mardirossian et al., 2018). This illustrates that the key to efficient and accurate many-electron perturbation theories lies in carefully chosen and well-balanced truncations of the many body perturbation series. In this regard the random-phase approximation is a showcase for an efficient and reasonably accurate perturbation theory.

2.2. The Random-Phase Approximation and Its Connection to CC Theory

The random phase approximation (RPA) to the correlation energy dates back to the 1950s. It was first introduced by Macke to predict convergent correlation energies (Macke, 1950) in the uniform electron gas and was also developed by Pines and Bohm (1952) for the collective description electron interactions. In the field of ab-initio computational materials science the exact-exchange plus correlation in the random-phase approximation has attracted renewed and widespread interest in the last two decades (Paier et al., 2012). This is due to the fact that computationally increasingly efficient implementations have become available making this method capable of describing all interatomic bonding situations reasonably well: ionic, covalent, metallic, and even van der Waals bonding. The computational complexity can even be lowered to ${O}(N^3)$ in real space formulations (Kaltak et al., 2014). Thus, the complexity of an RPA calculation does not exceed that of a canonical hybrid density functional theory calculation, the pre-factor is however considerably larger. The RPA correlation energy can be derived from many-electron Green's function theory, or using the adiabatic-connection fluctuation-dissipation theorem (ACFDT), or from coupled cluster theory.

As shown in Scuseria et al. (2008), it is possible to transform the RPA equations, that are usually expressed in a general eigenvalue problem, to a quadratic Riccati equation that reads

$\begin{array}{l}{t}_{ij}^{ab}=\frac{1}{{ϵ}_i+{ϵ}_j-{ϵ}_a-{ϵ}_b}\\ \left(\langle ij|ab\rangle +\langle cj|kb\rangle t_{ik}^{ac}+\langle ci|ka\rangle t_{jk}^{bc}+\langle cd|kl\rangle t_{lj}^{db}{t}_{ik}^{ac}\right).& (6)\end{array}$

We stress that in the above equation ϵ corresponds to the DFT one-electron energies. Once the amplitudes are obtained, the RPA correlation energy can be calculated by

$\begin{array}{ll}{E}_c^{\text{RPA}}=\frac{1}{2}\langle ij|ab\rangle t_{ij}^{ab}& (7)\end{array}$

Although the above formulation does not allow for an efficient computer implementation of the RPA, it illustrates that the RPA and CCSD are closely related. In the rings-only approximation, the second, third and fourth lines of Equation (3) are disregarded. Furthermore, the random-phase approximation includes the direct rings only. This implies that instead of using the (double bar) anti-symmetrized integrals, only 〈ij|ab〉 integrals are employed in the RPA amplitude and energy equations, making it necessary to employ a different pre-factor in the correlation energy expression to stay consistent with the many-body perturbation theory. Consequently, RPA cannot be viewed as a wavefunction theory, though it can be obtained from the CC amplitude equations as explained above. The close relationship between these approaches has motivated a number of post-RPA corrections, of which we will discuss only a small selection.

In the RPA, the magnitude of total correlation energies is significantly overestimated and binding energies are systematically underestimated compared to experiment even for weakly interacting systems. The origin of these shortcomings can in some cases be understood by comparing the RPA amplitude and energy expressions in Equations (6, 7) to the coupled cluster doubles amplitude and energy expressions in Equations (3, 5), respectively.

The lack of exchange-like terms in the RPA leads to the inclusion of EPV contributions (such as $\langle ii|ab\rangle t_{ii}^{ab}$) causing self-correlation errors; for example, RPA yields non-zero electron correlation energies for one-electron systems. This has motivated the introduction of various post-RPA corrections, such as second-order screened exchange (SOSEX), AC-SOSEX, or approximate exchange kernel methods (AXK). The inclusion of SOSEX to the random-phase approximation dates back to Monkhorst and Freeman in the 70s (Monkhorst and Oddershede, 1973; Freeman, 1977). Freeman showed in Freeman (1977) that absolute correlation energies of the uniform electron gas become significantly improved when compared to more accurate methods if SOSEX correlation energy contributions are included. Furthermore, the underestimation of cohesive energies calculated in the RPA originates from the fact that EPV contributions are larger for spin-polarized atoms than for non-spin-polarized solids. Therefore, the RPA + SOSEX approximation yields more accurate cohesive energies compared to experiment than the RPA. We note that similar findings have been obtained using related corrections to the RPA, such as AXK (Chen et al., 2018).

Another important difference between RPA and coupled cluster theory is the choice of the reference determinant and orbital energies. In the framework of ACFDT-RPA, the KS-DFT reference determinant is well-justified. However, from the perspective of the CC theory the KS-DFT orbitals violate the Brillouin's theorem and the correlation energy expression would therefore have to include terms that depend on the off-diagonal Fock matrix elements. These considerations have motivated the renormalized singles excitations (rSE) and related methods (Paier et al., 2012; Ren et al., 2013; Klimeš et al., 2015). The inclusion of these contributions improves upon the description of weakly-bound molecules and solids compared to the RPA.

2.3. Size Extensivity and the Thermodynamic Limit

In this section we discuss size extensivity and methods that accelerate the convergence to the thermodynamic limit (TDL). Both concepts are highly relevant for the application of quantum chemical methods to solids. In contrast to molecular systems, properties of solids or surfaces need to be calculated in the TDL in order to allow for a direct comparison to experiment and truly model an infinite periodic system. The TDL can be approached in different ways using; for example, (i) sampling of the Brillouin zone with increasingly dense k-point meshes and in periodic boundary conditions, (ii) studying increasingly large supercells in periodic boundary conditions, or employing (iii) increasingly large clusters with open boundary conditions and/or embedding methods. Once the TDL is approached with respect to the number of k-points or the number of atoms in the cluster, intensive properties, such as the correlation energy per atom are converged to a constant value.

An important advantage of truncated coupled cluster theories compared to truncated configuration interaction methods is their size extensivity. Size extensivity is a concept of particular importance in quantum chemistry, which judges if the calculated quantities have the correct asymptotic size dependence or not. For extensive quantities, like the (correlation) energy, a given size extensive method should yield the asymptotic N¹ dependence with N being the number of unit cells or wave vector sampling points in the Brillouin zone (Hirata, 2011). Obviously, the methods with incorrect asymptotic N^α dependence of α < 1, like the truncated configuration interaction methods, lead to the total energy per unit cell equal to that of the HF mean-field approximation, which is clearly useless for condensed-matter systems. The size extensivity of coupled cluster theories can also be understood via either the diagrammatic criteria (Bartlett, 1981) or the super-molecule criterion (Szabo and Ostlund, 1996). Moreover, it was argued that approximate post-HF correlation methods cannot capture the variational and size-extensive properties simultaneously (Hirata and Grabowski, 2014).

The TDL is approached as the number of particles becomes infinite in the simulation (super-)cell while the density is kept constant. Once the TDL is approached, correlation energies per atom need to be converged to a constant for periodic systems, corresponding to α = 1. Finite size errors are defined as the difference between the TDL and the finite simulation cell results. However, converging calculated properties with respect to the system size can be very slow, requiring substantial computational resources due to the steep scaling of the computational complexity of coupled cluster methods with respect to system size. We stress that many properties, such as the binding energy of molecules on surfaces converge even slower than their counterparts calculated on the level of mean-field theories, such as DFT. Correlated wavefunction based methods capture long-range electronic correlation effects; for example, dispersion interactions, explicitly. Although the respective contribution to the electronic correlation energy can be small, the accumulation of such interactions can become a non-negligible contribution to the property of interest. Various different strategies have been developed to correct for finite size errors that are defined as the difference between the TDL and the finite simulation cell results. These strategies often involve extrapolation methods or range-separation techniques. Local theories that employ correlation energy expressions depending on localized electron pairs, can approximate correlation energy contributions of long-distant pairs using computationally more efficient yet less accurate theories. Alternatively, local theories can account for electron pairs that are disregarded based on a distance criterion by using an R⁻⁶-type extrapolation (Usvyat et al., 2012). Canonical implementations of periodic post-HF methods employ scaling laws for extrapolations to the TDL that are based on an analog rationale (Del Ben et al., 2013; Booth et al., 2013; McClain et al., 2017). Auxiliary field quantum Monte Carlo theory employs finite size corrections that are based on parametrized density functionals obtained from finite uniform electron gas simulation cells (Kwee et al., 2008).

We stress that the problem of slow thermodynamic limit convergence and concomitantly large finite size errors is a common feature of Quantum Monte Carlo (QMC) and many-electron quantum chemical methods due to their explicit treatment of electronic correlation effects. Recently structure factor interpolation and twist averaging (TA) techniques have been introduced in Gruber et al. (2018) to correct efficiently for finite size errors in CC calculations of solids. These techniques are inspired by related methods used in QMC calculations (Chiesa et al., 2006; Holzmann et al., 2016). These finite size (FS) corrections allows for thermodynamic limit results of solids and surfaces to be achieved using quantum chemical wavefunction theories in a very efficient manner (Liao and Grüneis, 2016; Gruber et al., 2018), reducing the computational cost significantly. As shown in Figure 1, it is possible to achieve a much more rapid TDL convergence for simple solids, such as carbon graphite and diamond by virtue of these corrections. Furthermore, the fact that the converged energies per atom remain constant as the k-mesh density is increased, reflects that CC theories are size extensive.

FIGURE 1

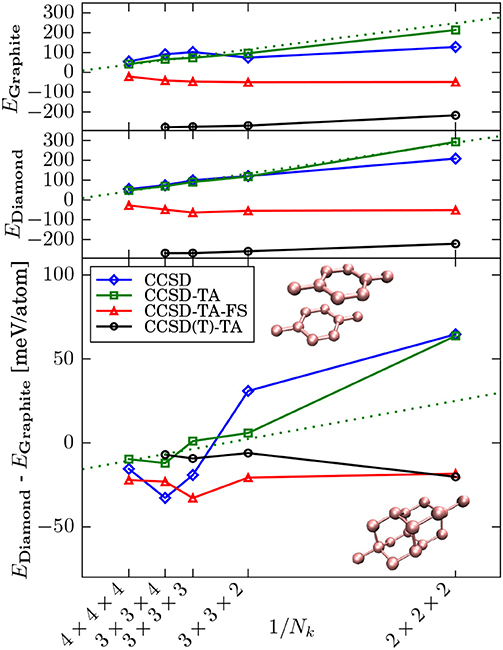
Figure 1. This figure has been taken from Gruber et al. (2018). Convergence of the correlation energy (difference) to the thermodynamic limit with respect to the number of k-points (N_k) for carbon graphite (top panel), carbon diamond (middle panel), and the difference between carbon diamond and graphite (bottom panel). The dotted line represents the linear fit of the uncorrected values. (T) corrections (black) are on top of CCSD-TA-FS energy obtained using a 4×4×4 k-point mesh (red). Zero-point energies are included, and they stabilize graphite compared to diamond by 9 meV/atom.

3. Implementation and Application

3.1. Projector-Augmented Wave Method

In this section, we briefly review the calculation of two-electron repulsion integrals in the framework of the projector augmented wave (PAW) method using a plane wave basis set. These integrals are the most important quantities in addition to the cluster amplitudes for coupled cluster theory calculations. In the PAW method, the all-electron orbitals (|ψ_n〉) are obtained from the pseudo orbitals ($|{\tilde{\psi }}_n\rangle$) using a linear transformation (Blöchl, 1994),

$\begin{array}{ll}|{\psi }_n\rangle =|{\tilde{\psi }}_n\rangle +{\displaystyle \sum _i(|{\phi }_i\rangle }-|{\tilde{\phi }}_i\rangle )\langle {\tilde{p}}_i|{\tilde{\psi }}_n\rangle .& (8)\end{array}$

The index n, labeling the orbitals ψ, is understood to be shorthand for the band index and the Bloch wave vector k_n, while the index i is a shorthand for the atomic site R_i, the angular momentum quantum numbers l_i and m_i, and an additional index ϵ_i denoting the linearization energy. The wave vector is conventionally chosen to lie within the first Brillouin zone. The pseudo orbitals are the variational quantities of the PAW method and are expanded in reciprocal space using plane waves, $\langle r|{\tilde{\psi }}_n\rangle =\frac{1}{\sqrt{\Omega }}{\displaystyle {\sum }_G{C}_G^n{e}^{i(k_n+G)r}}$. In this framework, it is possible to evaluate two-electron repulsion integrals approximately using the following expression:

$\begin{array}{ll}\begin{array}{l}\langle ij|r_{12}^{-1}|ab\rangle ={\displaystyle \sum _G{\rho }_i^a}(G)\tilde{v}(G){\rho }^{\ast }{}_b^j(G),\hfill \end{array}& (9)\end{array}$

where ṽ is the diagonal Coulomb kernel in reciprocal space $\frac{4\pi }{G^2}$. We note the reciprocal Coulomb kernel exhibits a singularity a G = 0. We employ a correction for the Coulomb kernel at the singularity that is obtained using a scheme introduced by Gygi and Baldereschi (1986). In the present PAW implementation, the Fourier transformed codensities ${\rho }_i^a(G)$ are approximated using Equation (2.87) of Harl (2008) as originally implemented by Kresse et al. for the calculation of correlation energies within the random phase approximation (Harl and Kresse, 2008). The codensities and the diagonal Coulomb kernel make it possible to calculate the ERIs in a computationally efficient on-the-fly manner. We note that the memory footprint of the transformed codensities scales cubic with respect to the system size. Furthermore, it is also possible to further reduce the dimension of the auxiliary plane-wave index G significantly for system where the large number of degrees of freedom provided by the plane-waves are not needed to describe the employed codensities. A significant down-folding of the plane wave basis set size is possible without compromising accuracy for calculations of surfaces as well as atoms or molecules in a box. A convenient and computational efficient method to achieve this downfolding is based on singular value decomposition and outlined in Hummel et al. (2017). We note that our more recent implementation of CC theory that calculates the ERIs according to Equation (2) (cc4s) employs the cyclops tensor framework (CTF, Solomonik et al., 2014) and will be released in the near future.

3.2. Numeric Atom-Centered Orbital Framework

The implementation of quantum-chemistry methods in the numeric atom-centered orbital (NAO) framework utilizes the resolution-of-identity (RI) technique (also known as “density fitting”) to calculate the two-electron repulsion integrals which scale as N⁴ in memory with respect to system size N. The key idea is to decompose the four-rank repulsion integrals in terms of three-rank tensors with an N³ scaling of memory and is therefore better suited to be pre-stored:

$\begin{array}{ll}\langle rs|r_{12}^{-1}|pq\rangle \approx {\displaystyle \sum _{\mu }{m}_{pr}^{\mu }}{m}_{qs}^{\mu },& (10)\end{array}$

where the index μ runs over an auxiliary basis {P_μ(r)}, and $m_{pr}^{\mu }$ is a decomposed three-rank tensor in the molecular orbital basis. In RI-V approximation, $m_{pr}^{\mu }$ is determined by directly minimizing the errors in the repulsion integral of atomic orbitals using Equations (47, 55) of Ren et al. (2012). A hybird-RI algorithm has been designed to balance the computing cost and communication in the CCSD(T) implementation for molecules in the Fritz Haber Institute ab initio molecular simulation (FHI-aims) package. Together with a domain-based distributed-memory strategy, it allows for an effective utilization of the quickly increasing memory bandwidth of today's supercomputers to avoid the on-the-fly disk storage and minimize interconnect communication, particularly for the tensor contraction in the evaluation of the particle-particle terms. As a result, an excellent strong scaling can be achieved up to over 10,000 cores (Shen et al., 2018). The parallel efficiency is competitive with the CC implementations in state-of-the-art high-performance computing computational chemistry packages.

Furthermore, a local variant of RI-V, namely RI-LVL, has been developed in the numeric atom-centered orbital framework. Unlike the standard RI-V approximation in Equation (10), RI-LVL expands the products of basis functions only in the subset of those auxiliary basis functions $\left\{{P}(IJ)\right\}$ which are located at the same atoms of I and J as the basis functions of χ_i and χ_j:

$\begin{array}{ll}\langle rs|r_{12}^{-1}|pq\rangle \approx {\displaystyle \sum _{\begin{array}{c}\mu \lambda \in {P}(RP)\\ \nu \sigma \in {P}(SQ)\end{array}}(rp|\lambda )L_{\lambda \mu }^{RP}(\mu |\nu )L_{\nu \sigma }^{SQ}(\sigma |sq)},& (11)\end{array}$

where the three-center (rp|λ) and two-center (μ|ν) integrals are defined as

$\begin{array}{ll}(rp|\lambda )={\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }d}}{x}_{1}d{x}_2\frac{{\chi }_r^{*}(x_1){\chi }_p(x_1){\chi }_{\lambda }(x_2)}{|r_1-r_2|},& (12)\end{array}$

and

$\begin{array}{ll}(\mu |\nu )={\displaystyle {\int }_{\Omega }{\displaystyle {\int }_{\Omega }d}}{x}_{1}d{x}_2\frac{{\chi }_{\mu }^{*}(x_1){\chi }_{\nu }(x_2)}{|r_1-r_2|},& (13)\end{array}$

respectively. L^RP = (μ|ν)⁻¹ with μ, $\nu \in {P}(RP)$. This choice further reduces the memory scaling to N² without compromising the accuracy (Ihrig et al., 2015). For molecules, it is a useful alternative to the standard RI-V, which, however, is the only option for solids, since the memory consumption of RI-V quickly becomes unaffordable with the increase of k-grid numbers in periodic boundary conditions (Levchenko et al., 2015). For MP2 and RPA, we demonstrated that the NAO-based periodic implementation can provide a smooth and consistent convergence toward the complete k-grid limit (Zhang et al., 2018). The periodic CCSD in FHI-aims has been implemented, but not yet fully optimized.

4. Results

4.1. PAW-Based Coupled Cluster Applications

We now turn to a brief overview of ab-initio computational materials science studies that have been performed using periodic coupled cluster theory. This overview is by no means complete but reflects the general purpose and scope of the CC implementation based on the PAW formalism and its relation to other approaches, such as the method of increments. A selection of the investigated systems is depicted in Figure 2. PAW-based periodic CC calculations have initially been limited to insulating solids with two-atomic unit cells, such as the LiH crystal or the uniform electron gas simulation cell (Grüneis et al., 2011; Booth et al., 2013; Shepherd and Grüneis, 2013). However, recent methodological improvements make the study of surfaces and supercells containing approximately thirty atoms possible. In particular the development of finite size corrections (Gruber et al., 2018), improved compact approximations to the virtual orbital manifold (Grüneis et al., 2011; Booth et al., 2016) and auxiliary basis sets (Hummel et al., 2017) have substantially expanded the scope of periodic CC calculations. The advancement of explicitly correlated techniques in combination with a plane wave basis set holds the promise to reduce the computational cost further in the near future (Grüneis et al., 2013, 2017).

FIGURE 2

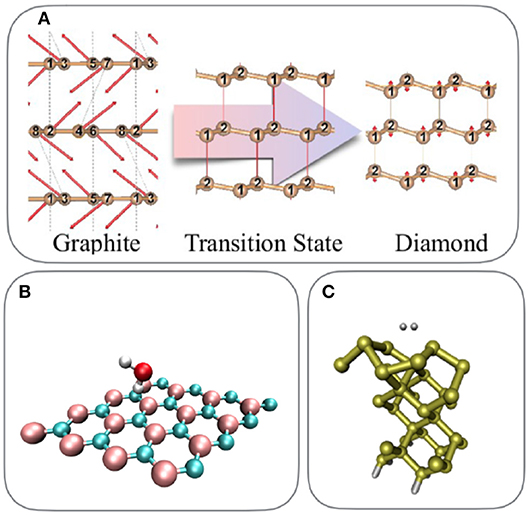
Figure 2. Overview of recent PAW-based periodic coupled cluster theory calculations: (A) pressure-driven phase transition from carbon graphite to diamond (Gruber and Grüneis, 2018), (B) water adsorption on an h−BN sheet (Gruber et al., 2018), and (C) dissociative hydrogen molecule adsorption on the Si(100) surface (Tsatsoulis et al., 2018).

We first review studies that aim at assessing the precision of periodic CC calculations. An important task of method development includes demonstrating convergence of calculated properties, such as the ground state energy with respect to the employed computational parameters; for example, basis set and k-mesh, and achieve agreement with results obtained using entirely different computational approaches. In this regard the calculation of the cohesive energy of the LiH solid on the level of HF, MP2, and CC theory has become common practice for benchmarking various implementations. The first quantum chemical calculations of the LiH crystal were performed by Egil Hylleraas in 1930 (Hylleraas, 1930). In 2009, Nolan et al. have presented MP2 and coupled cluster ground state energy calculations of the LiH crystal converged with respect to basis set and system size through a combination of periodic and finite-cluster electronic structure calculations (Nolan et al., 2009). These findings have served as a reliable reference for other approaches including (local) periodic and incremental methods used to calculate MP2 or CC cohesive energies (Marsman et al., 2009; Grüneis et al., 2011; Stoll and Doll, 2012; Del Ben et al., 2013; Usvyat, 2013). Table 1 summarizes the obtained cohesive energies, indicating the achieved level of precision of the various calculations is better than chemical accuracy. Furthermore, the CCSD(T) estimates agree with the experimental value (4.98 eV/LiH) to within a few ten meV. In a similar context, the adsorption energy of a single water molecule on the LiH surface has been studied and results have been compared among different theories and implementations to test their precision and accuracy (Tsatsoulis et al., 2017). The corresponding adsorption energies are summarized in Table 2 and demonstrate an agreement of a few meV between different implementations. Such benchmark calculations are useful despite their lack of reference to experiment. However, to further assess the scope of an implementation it is necessary to investigate different bonding situations. Weakly bound molecular and rare-gas crystals have been studied intensively using the incremental method with high accuracy (Rościszewski et al., 1999; Schwerdtfeger et al., 2010). These systems are composed of many weakly interacting fragments, making them ideally suited for an expansion of the correlation energy into few-body incremental contributions. In contrast to the incremental method, a particular challenge for fully periodic and canonical approaches originates from the long-rangedness of correlation energy contributions to the binding energy, requiring dense k-mesh calculations or reliable finite size corrections (Gruber et al., 2018). However, by using recently proposed finite size corrections, it is possible to achieve well-converged CC cohesive energies of the neon solid in good agreement with results obtained using the method of increments despite employing relatively coarse k-meshes (Schwerdtfeger et al., 2010; Gruber et al., 2018). The results obtained for the cohesive energy of the neon solid are summarized in Table 3. The periodic CCSD(T) estimate for the cohesive energy agrees to within 3 meV/atom with experimental value of 27 meV/atom, which has been corrected for zero-point fluctuations (Rościszewski et al., 1999).

TABLE 1

Table 1. Calculated energy contributions to the cohesive energy of the LiH crystal as obtained using different theories and techniques.

TABLE 2

Table 2. Calculated energy contributions to the adsorption energy of water on a (001) LiH surface model as obtained using different theories and techniques.

TABLE 3

Table 3. Calculated cohesive energy of the neon crystal as obtained using different theories and techniques.

To benchmark the accuracy of periodic ab-initio methods in a systematic manner it is common practice to calculate cohesive energies, lattice constants and bulk moduli for a range of solids exhibiting different chemical bonding including van-der Waals, ionic, covalent and metallic systems. In molecular quantum chemistry similar calculations are routinely performed for a range of test sets that reflect a range of different chemical bonding situations as discussed in the following section. In solids, the systematic comparison to experimental findings, which have been corrected for beyond Born-Oppenheimer approximation effects, allows to identify and understand systematic errors for different levels of theory; for example, MP2 theory overestimates correlation energies for systems with small band gaps, which results in an overestimation of corresponding cohesive energies (Grüneis et al., 2010). However, the computational cost of coupled cluster calculations using the PAW-based periodic implementation limits the number of benchmark systems so far. The range of simple solids for which cohesive energies have been calculated in the complete basis set limit on the level of CC theory include LiH (rock-salt), Ne (fcc), C (diamond), BN (zinc-blende), and AlP (zinc-blende) (Booth et al., 2013; Gruber et al., 2018). Furthermore, phase transitions and energy differences of different LiH, C, and BN allotropes have also been investigated (Grüneis, 2015a; Gruber and Grüneis, 2018; Gruber et al., 2018). The study of pressure-temperature phase diagrams allows to investigate the relative level of accuracy of electronic structure theories for different chemical bonds that are present in the investigated phases. As such the predicted equilibrium phase boundaries often change significantly with respect to the employed electronic structure theory. In Gruber and Grüneis (2018) we have employed periodic CCSD(T) theory to calculate relative enthalpies and pressure-temperature phase diagrams for C and BN allotropes. In contrast to currently available DFT methods, quantum chemical wavefunction theories allow for achieving reliable and systematically improvable benchmark results for the relative stability of C and BN allotropes.

Another promising area of application for quantum chemical wavefunction theories is the study of surface science problems including molecular adsorption and reactions on surfaces. CC theories are widely used for predicting benchmark results for molecular gas-phase reaction energies as well as activation barrier heights. A similar level of accuracy for molecular surface reactions can currently only be achieved by QMC calculations and it would be advantageous to fully transfer quantum chemical wavefunction based methods to this area. Currently available QC approaches are based mostly on embedding, fragment models, the incremental technique or finite-cluster calculations (Voloshina et al., 2011; Libisch et al., 2012; Usvyat et al., 2012; Boese and Sauer, 2016; Kubas et al., 2016). Recently we have performed fully periodic calculations of adsorption energies for water on h−BN and graphene sheets, confirming the expected level of accuracy (Gruber et al., 2018; Brandenburg et al., 2019). Table 4 summarizes the results of the water adsorption energies and compares them to DMC findings that agree well. Furthermore, the dissociative H₂ adsorption on the Si(001) surface has also been investigated in Tsatsoulis et al. (2018). The obtained results indicate that CC theory can predict accurate adsorption energies and study chemical reactions on surfaces in a reliable manner. However, we stress that, despite the accurate findings discussed above, the level of accuracy always depends on the electronic structure of the system and the level of many-electron wavefunction approximation. Therefore, high accuracy can only be achieved using CCSD(T) theory for systems that do not exhibit strong correlation effects.

TABLE 4

Table 4. Calculated adsorption energy of water on h−BN and graphene sheets.

4.2. NAO-Based Coupled Cluster Applications

As an alternative basis set choice instead of GTOs and plane waves, NAOs, in particular those with valence correlation consistency namely NAO-VCC-nZ, hold the promise to provide improved description of advanced correlation methods with the increase of the basis set size. NAO-VCC-nZ allows for extrapolating the results of advanced quantum-chemistry methods to the complete-basis-set (CBS) limit. NAO-VCC-nZ was generated by minimizing frozen-core RPA total energies of individual atoms from H to Ar. The consistent convergence of RPA and MP2 binding energies of small molecules is demonstrated by using NAO-VCC-nZ basis sets in the original paper (Zhang et al., 2013). The applicability of NAO-VCC-nZ for solids has been benchmarked comprehensively for MP2 and RPA calculations of cohesive energy, lattice constants, and bulk modulus for representatives of first- and second-row elements and their binaries with cubic crystal structures and various bonding characters (Zhang et al., 2018). The generalization of the periodic RPA and MP2 implementation to CCSD(T) for solids is straightforward, but strong effort should be paid in order to achieve an efficient and practical implementation of the NAO-based periodic CCSD(T) method, which is still under development.

As the first step, the CCSD(T) has been implemented in FHI-aims for molecules, which has been used together with NAO-VCC-nZ basis sets to deliver accurate CCSD(T) results in the CBS limit for manifold properties of great chemical or physical interest. For 22 bio-orient weak interactions in the S22 test sets and 10 relative energies of cysteine conformers in the CYCONF test set, the CCSD(T)/CBS results by using NAO-VCC-nZ repeat the up-to-date reference data based on GTO basis sets with the deviation of <0.1 kcal/mol on average. For the first time, the high-level theoretical reference data at the CCSD(T)/CBS level has been generated for the 34 isomerization energies in the ISO34 test set in the NAO framework. For the sake of benchmarking newly developed electronic-structure methods, the use of the CCSD(T)/CBS reference data allows for the comparison based on exactly the same molecular geometry and immune to the experimental uncertainty (Shen et al., 2018).

4.3. Outlook

During the last years the scope of quantum chemical wavefunction theories and in particular coupled cluster methods have been expanded significantly in the field of complex systems and solids. Fully periodic and canonical approaches have become increasingly efficient due to methodological improvements that reduce the pre-factor of the computational cost. In this tutorial-style review we have given a brief overview of different frameworks for the implementation of periodic CC theories and their applications. Future work will focus on more systematic benchmark studies employing all recent methodological advancements including finite size corrections and explicit correlation techniques for solids. Furthermore, it is expected that local approaches, such as the use of truncated pair natural orbitals (Neese et al., 2009; Kubas et al., 2016; Ma et al., 2017) can also be transferred to solid state systems. The remaining technical and theoretical challenges are, however, significant and include the implementation of sparse tensor frameworks and the development of localization schemes that work reliable for metals as well as for insulators and semiconductors. Furthermore, the calculation of additional properties, such as gradients will eventually also be necessary in order to allow for structural relaxation. However, the high level of accuracy makes quantum chemical wavefunction theories and in particular CC theory a promising tool for future ab-initio computational materials science studies that can complement currently available DFT approaches and provide benchmark results. As discussed in this article, possible areas of application include the study of pressure-driven phase transitions, surface chemistry problems as well as optical properties of solids.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer DU declared a past co-authorship with one of the authors AG to the handling editor.

Acknowledgments

AG gratefully acknowledges support and funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No 715594). Work at Shanghai was supported by the 14th Recruitment Program of Young Professionals for IZ.

References

Al-Hamdani, Y. S., Rossi, M., Alfè, D., Tsatsoulis, T., Ramberger, B., Brandenburg, J. G., et al. (2017). Properties of the water to boron nitride interaction: from zero to two dimensions with benchmark accuracy. J. Chem. Phys. 147:044710. doi: 10.1063/1.4985878

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartlett, R. (1981). Many-body perturbation-theory and coupled cluster theory for electron correlation in molcules. Ann. Rev. Phys. Chem. 32, 359–401.

Google Scholar

Bartlett, R. J., and Musiał, M. (2007). Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 79, 291–352. doi: 10.1103/RevModPhys.79.291

CrossRef Full Text | Google Scholar

Berkelbach, T. C. (2018). Communication: random-phase approximation excitation energies from approximate equation-of-motion coupled-cluster doubles. J. Chem. Phys. 149:041103. doi: 10.1063/1.5032314

PubMed Abstract | CrossRef Full Text | Google Scholar

Bishop, R. F., and Lührmann, K. H. (1978). Electron correlations: I. Ground-state results in the high-density regime. Phys. Rev. B 17, 3757–3780. doi: 10.1103/PhysRevB.17.3757

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979.

PubMed Abstract | Google Scholar

Boese, A. D., and Sauer, J. (2016). Accurate adsorption energies for small molecules on oxide surfaces: Ch4/mgo(001) and c2h6/mgo(001). J. Comput. Chem. 37, 2374–2385. doi: 10.1002/jcc.24462

CrossRef Full Text | Google Scholar

Booth, G. H., Grüneis, A., Kresse, G., and Alavi, A. (2013). Towards an exact description of electronic wavefunctions in real solids. Nature 493, 365–70. doi: 10.1038/nature11770

PubMed Abstract | CrossRef Full Text | Google Scholar

Booth, G. H., Tsatsoulis, T., Chan, G. K., and Grüneis, A. (2016). From plane waves to local Gaussians for the simulation of correlated periodic systems. J. Chem. Phys. 145:084111. doi: 10.1063/1.4961301

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandenburg, J. G., Zen, A., Fitzner, M., Ramberger, B., Kresse, G., Tsatsoulis, T., et al. (2019). Physisorption of water on graphene: subchemical accuracy from many-body electronic structure methods. J. Phys. Chem. Lett. 10, 358–368. doi: 10.1021/acs.jpclett.8b03679

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G. P., Agee, M. M., and Furche, F. (2018). Performance and scope of perturbative corrections to random-phase approximation energies. J. Chem. Theory Comput. 14, 5701–5714. doi: 10.1021/acs.jctc.8b00777

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiesa, S., Ceperley, D. M., Martin, R. M., and Holzmann, M. (2006). Finite-size error in many-body simulations with long-range interactions. Phys. Rev. Lett. 97, 6–9. doi: 10.1103/PhysRevLett.97.076404

PubMed Abstract | CrossRef Full Text | Google Scholar

Civalleri, B., Orlando, R., Zicovich-Wilson, C. M., Roetti, C., Saunders, V. R., Pisani, C., et al. (2010). Comment on “accurate hartree-fock energy of extended systems using large gaussian basis sets”. Phys. Rev. B 81:106101. doi: 10.1103/PhysRevB.81.106101

CrossRef Full Text | Google Scholar

Cizek, J. (1966). On the correlation problem in atomic and molecular systems. calculation of wavefunction components in ursell type expansion using quantum field theoretical methods. J. Chem. Phys. 45, 4256–4266.

Google Scholar

Cizek, J., and Paldus, J. (1971). Correlation problems in atomic and molecular systems III. rederivation of the coupled-pair many-electron theory using the traditional quantum chemical methodst. Int. J. Quant. Chem. 5, 359–379.

Google Scholar

Coester, F. (1958). Bound states of a many-particle system. Nucl. Phys. 1, 421–424.

Google Scholar

Coester, F., and Kümmel, H. (1960). Short-range correlations in nuclear wave functions. Nucl. Phys. 17, 477–485.

Google Scholar

Cohen, A. J., Mori-Sánchez, P., and Yang, W. (2012). Challenges for density functional theory. Chem. Rev. 112, 289–320. doi: 10.1021/cr200107z

PubMed Abstract | CrossRef Full Text | Google Scholar

Crawford, T. D., and Schaefer, H. F. (2007). An Introduction to Coupled Cluster Theory for Computational Chemists. New York, NY: Wiley-Blackwell, 33–136.

Google Scholar

Del Ben, M. D., Hutter, J., and Vandevondele, J. (2013). Electron correlation in the condensed phase from a resolution of identity approach based on the Gaussian and Plane Waves scheme Electron correlation in the condensed phase from a resolution of identity approach based on the Gaussian and Plane Waves scheme. J. Chem. Theory Comput. 9, 2654–2671. doi: 10.1021/ct4002202

PubMed Abstract | CrossRef Full Text | Google Scholar

Dutta, A. K., Neese, F., and Izsak, R. (2018). Accelerating the coupled-cluster singles and doubles method using the chain-of-sphere approximation. Mol. Phys. 116, 1428–1434. doi: 10.1080/00268976.2017.1416201

CrossRef Full Text | Google Scholar

Evangelista, F. A. (2018). Perspective: multireference coupled cluster theories of dynamical electron correlation. J. Chem. Phys. 149:030901. doi: 10.1063/1.5039496

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeman, D. (1978). Application of the coupled-cluster expansion to the correlation energy of electrons in two-dimensional and quasi-two-dimensional systems. Solid State Commun. 26, 289–293.

Google Scholar

Freeman, D. L. (1977). Coupled-cluster expansion applied to the electron gas: inclusion of ring and exchange effects. Phys. Rev. B 15, 5512–5521.

Google Scholar

Freeman, D. L. (1983). Coupled-cluster summation of the particle-particle ladder diagrams for the two-dimensional electron gas. J. Phys. C Solid State Phys. 16:711.

Google Scholar

Gruber, T., and Grüneis, A. (2018). Ab initio calculations of carbon and boron nitride allotropes and their structural phase transitions using periodic coupled cluster theory. Phys. Rev. B 98:134108. doi: 10.1103/PhysRevB.98.134108

CrossRef Full Text | Google Scholar

Gruber, T., Liao, K., Tsatsoulis, T., Hummel, F., and Grüneis, A. (2018). Applying the coupled-cluster ansatz to solids and surfaces in the thermodynamic limit. Phys. Rev. X 8:021043. doi: 10.1103/PhysRevX.8.021043

CrossRef Full Text | Google Scholar

Grüneis, A. (2015a). A coupled cluster and Møller-plesset perturbation theory study of the pressure induced phase transition in the lih crystal. J. Chem. Phys. 143:102817. doi: 10.1063/1.4928645

PubMed Abstract | CrossRef Full Text | Google Scholar

Grüneis, A. (2015b). Efficient explicitly correlated many-electron perturbation theory for solids: application to the schottky defect in MGO. Phys. Rev. Lett. 115:066402. doi: 10.1103/PhysRevLett.115.066402

PubMed Abstract | CrossRef Full Text | Google Scholar

Grüneis, A., Booth, G. H., Marsman, M., Spencer, J., Alavi, A., and Kresse, G. (2011). Natural orbitals for wave function based correlated calculations using a plane wave basis set. J. Chem. Theory Comput. 7, 2780–2785. doi: 10.1021/ct200263g

PubMed Abstract | CrossRef Full Text | Google Scholar

Grüneis, A., Hirata, S., Ohnishi, Y.-Y., and Ten-no, S. (2017). Perspective: explicitly correlated electronic structure theory for complex systems. J. Chem. Phys. 146:080901. doi: 10.1063/1.4976974

PubMed Abstract | CrossRef Full Text | Google Scholar

Grüneis, A., Marsman, M., and Kresse, G. (2010). Second-order Møller-Plesset perturbation theory applied to extended systems. II. Structural and energetic properties. J. Chem. Phys. 133:74107. doi: 10.1063/1.3466765

PubMed Abstract | CrossRef Full Text | Google Scholar

Grüneis, A., Shepherd, J. J., Alavi, A., Tew, D. P., and Booth, G. H. (2013). Explicitly correlated plane waves: accelerating convergence in periodic wavefunction expansions. J. Chem. Phys. 139:084112. doi: 10.1063/1.4818753

PubMed Abstract | CrossRef Full Text | Google Scholar

Gygi, F., and Baldereschi, A. (1986). Self-consistent hartree-fock and screened-exchange calculations in solids: application to silicon. Phys. Rev. B 34, 4405–4408. doi: 10.1103/PhysRevB.34.4405

PubMed Abstract | CrossRef Full Text | Google Scholar

Harl, J. (2008). The Linear Response Function in Density Functional Theory : Optical Spectra and Improved Desciption of the Electron Correlation. [PhD thesis], Universität Wien, Austria.

Harl, J., and Kresse, G. (2008). Cohesive energy curves for noble gas solids calculated by adiabatic connection fluctuation-dissipation theory. Phys. Rev. B Condens. Matter Mater. Phys. 77:45136. doi: 10.1103/PhysRevB.77.045136

CrossRef Full Text | Google Scholar

Helgaker, T., Jørgensen, P., and Olsen, J. (2000). Molecular Electronic-Structure Theory. Chichester: Wiley.

PubMed Abstract | Google Scholar

Hirata, S. (2011). Thermodynamic limit and size-consistent design. Theor. Chem. Acc. 129, 727–746. doi: 10.1007/s00214-011-0954-4

CrossRef Full Text | Google Scholar

Hirata, S., and Grabowski, I. (2014). On the mutual exclusion of variationality and size consistency. Theor. Chem. Acc. 133, 1–9. doi: 10.1007/s00214-013-1440-y

CrossRef Full Text | Google Scholar

Holzmann, M., Clay, R. C., Morales, M. A., Tubman, N. M., Ceperley, D. M., and Pierleoni, C. (2016). Theory of finite size effects for electronic quantum monte carlo calculations of liquids and solids. Phys. Rev. B 94:035126. doi: 10.1103/PhysRevB.94.035126

CrossRef Full Text | Google Scholar

Hummel, F., Gruber, T., and Grüneis, A. (2016). A many-electron perturbation theory study of the hexagonal boron nitride bilayer system. Eur. Phys. J. B 89:235. doi: 10.1140/epjb/e2016-70177-4

CrossRef Full Text | Google Scholar

Hummel, F., Tsatsoulis, T., and Grüneis, A. (2017). Low rank factorization of the coulomb integrals for periodic coupled cluster theory. J. Chem. Phys. 146:124105. doi: 10.1063/1.4977994

PubMed Abstract | CrossRef Full Text | Google Scholar

Hylleraas, E. A. (1930). Wellenmechanische berechnung der gitterenergie und der gitterkonstante des lithiumhydrids. Z. Phys. 63, 771–794.

Google Scholar

Ihrig, A. C., Wieferink, J., Zhang, I. Y., Ropo, M., Ren, X., Rinke, P., et al. (2015). Accurate localized resolution of identity approach for linear-scaling hybrid density functionals and for many-body perturbation theory. N. J. Phys. 17:093020. doi: 10.1088/1367-2630/17/9/093020

CrossRef Full Text | Google Scholar

Kaltak, M., Klimeš, J., and Kresse, G. (2014). Low scaling algorithms for the random phase approximation: imaginary time and Laplace transformations. J. Chem. Theory Comput. 10, 2498–2507. doi: 10.1021/ct5001268

PubMed Abstract | CrossRef Full Text | Google Scholar

Kats, D., Kreplin, D., Werner, H.-J., and Manby, F. R. (2015). Accurate thermochemistry from explicitly correlated distinguishable cluster approximation. J. Chem. Phys. 142:064111. doi: 10.1063/1.4907591

PubMed Abstract | CrossRef Full Text | Google Scholar

Kats, D., and Manby, F. R. (2013). Communication: the distinguishable cluster approximation. J. Chem. Phys. 139:021102. doi: 10.1063/1.4813481

PubMed Abstract | CrossRef Full Text | Google Scholar

Klimeš, J., Kaltak, M., Maggio, E., and Kresse, G. (2015). Singles correlation energy contributions in solids. J. Chem. Phys. 143:102816. doi: 10.1063/1.4929346

PubMed Abstract | CrossRef Full Text | Google Scholar

Köhn, A., Hanauer, M., Mück, L. A., Jagau, T.-C., and Gauss, J. (2013). State-specific multireference coupled-cluster theory. Wiley Interdiscipl. Rev. Comput. Mol. Sci. 3, 176–197. doi: 10.1002/wcms.1120

CrossRef Full Text | Google Scholar

Kubas, A., Berger, D., Oberhofer, H., Maganas, D., Reuter, K., and Neese, F. (2016). Surface adsorption energetics studied with “gold standard” wave-function-based ab initio methods: small-molecule binding to TiO₂(110). J. Phys. Chem. Lett. 7, 4207–4212. doi: 10.1021/acs.jpclett.6b01845

PubMed Abstract | CrossRef Full Text | Google Scholar

Kwee, H., Zhang, S., and Krakauer, H. (2008). Finite-size correction in many-body electronic structure calculations. Phys. Rev. Lett. 100:126404. doi: 10.1103/PhysRevLett.100.126404

PubMed Abstract | CrossRef Full Text | Google Scholar

Levchenko, S. V., Ren, X., Wieferink, J., Johanni, R., Rinke, P., Blum, V., et al. (2015). Hybrid functionals for large periodic systems in an all-electron, numeric atom-centered basis framework. Comput. Phys. Commun. 192, 60–69. doi: 10.1016/j.cpc.2015.02.021

CrossRef Full Text | Google Scholar

Liao, K., and Grüneis, A. (2016). Communication: finite size correction in periodic coupled cluster theory calculations of solids. J. Chem. Phys. 145, 0–4. doi: 10.1063/1.4964307

PubMed Abstract | CrossRef Full Text | Google Scholar

Libisch, F., Huang, C., Liao, P., Pavone, M., and Carter, E. A. (2012). Origin of the energy barrier to chemical reactions of o₂ on al(111): evidence for charge transfer, not spin selection. Phys. Rev. Lett. 109:198303. doi: 10.1103/PhysRevLett.109.198303

CrossRef Full Text | Google Scholar

Ma, Q., Schwilk, M., Köppl, C., and Werner, H.-J. (2017). Scalable electron correlation methods. 4. Parallel explicitly correlated local coupled cluster with pair natural orbitals (pno-lccsd-f12). J. Chem. Theory Comput. 13, 4871–4896. doi: 10.1021/acs.jctc.7b00799

PubMed Abstract | CrossRef Full Text | Google Scholar

Macke, W. (1950). über die Wechselwirkungen im Fermi-Gas, Polarisationserscheinungen, Correlationsenergie, Elektronenkondensation. Z. Naturforsch. 5A, 192–208.

Google Scholar

Mardirossian, N., McClain, J. D., and Chan, G. K. (2018). Lowering of the complexity of quantum chemistry methods by choice of representation. J. Chem. Phys. 148:044106. doi: 10.1063/1.5007779

PubMed Abstract | CrossRef Full Text | Google Scholar

Marsman, M., Grüneis, A., Paier, J., and Kresse, G. (2009). Second-order Møller–Plesset perturbation theory applied to extended systems. I. Within the projector-augmented-wave formalism using a plane wave basis set. J. Chem. Phys. 130:184103. doi: 10.1063/1.3126249

PubMed Abstract | CrossRef Full Text | Google Scholar

McClain, J., Lischner, J., Watson, T., Matthews, D. A., Ronca, E., Louie, S. G., et al. (2016). Spectral functions of the uniform electron gas via coupled-cluster theory and comparison to the gw and related approximations. Phys. Rev. B 93:235139. doi: 10.1103/PhysRevB.93.235139

CrossRef Full Text | Google Scholar

McClain, J., Sun, Q., Chan, G. K., and Berkelbach, T. C. (2017). Gaussian-based coupled-cluster theory for the ground state and band structure of solids. J. Chem. Theory Comput. 13, 1209–1218. doi: 10.1021/acs.jctc.7b00049

PubMed Abstract | CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Oddershede, J. (1973). Random-phase-approximation correlation energy in metallic hydrogen using hartree-fock bloch functions. Phys. Rev. Lett. 30, 797–800.

Google Scholar

Neese, F., Wennmohs, F., and Hansen, A. (2009). Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method. J. Chem. Phys. 130:114108. doi: 10.1063/1.3086717

PubMed Abstract | CrossRef Full Text | Google Scholar

Nemec, N., Towler, M. D., and Needs, R. J. (2010). Benchmark all-electron ab initio quantum monte carlo calculations for small molecules. J. Chem. Phys. 132:034111. doi: 10.1063/1.3288054

PubMed Abstract | CrossRef Full Text | Google Scholar

Neufeld, V. A., and Thom, A. J. W. (2017). A study of the dense uniform electron gas with high orders of coupled cluster. J. Chem. Phys. 147:194105. doi: 10.1063/1.5003794

PubMed Abstract | CrossRef Full Text | Google Scholar

Nolan, S. J., Gillan, M. J., Alfè, D., Allan, N. L., and Manby, F. R. (2009). Calculation of properties of crystalline lithium hydride using correlated wave function theory. Phys. Rev. B Condens. Matter Mater. Phys. 80:165109. doi: 10.1103/PhysRevB.80.165109

CrossRef Full Text | Google Scholar

Paier, J., Ren, X., Rinke, P., Scuseria, G. E., Grüneis, A., Kresse, G., et al. (2012). Assessment of correlation energies based on the random-phase approximation. N. J. Phys. 14:043002. doi: 10.1088/1367-2630/14/4/043002

CrossRef Full Text | Google Scholar

Pines, D., and Bohm, D. (1952). A collective description of electron interactions: II. Collective vs individual particle aspects of the interactions. Phys. Rev. 85, 338–353.

Google Scholar

Pisani, C., Schütz, M., Casassa, S., Usvyat, D., Maschio, L., Lorenz, M., et al. (2012). Cryscor: a program for the post-hartree-fock treatment of periodic systems. Phys. Chem. Chem. Phys. 14:7615. doi: 10.1039/c2cp23927b

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulay, P. (1980). Convergence acceleration of iterative sequences. The case of scf iteration. Chem. Phys. Lett. 73, 393–398.

Google Scholar

Raghavachari, K., Trucks, G. W., Pople, J. A., and Head-Gordon, M. (1989). A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483.

Google Scholar

Ren, X., Rinke, P., Blum, V., Wieferink, J., Tkatchenko, A., Sanfilippo, A., et al. (2012). Resolution-of-identity approach to hartree-fock, hybrid density functionals, rpa, mp2 and gw with numeric atom-centered orbital basis functions. N. J. Phys. 14, 053020–053060. doi: 10.1088/1367-2630/14/5/053020

CrossRef Full Text | Google Scholar

Ren, X., Rinke, P., Scuseria, G. E., and Scheffler, M. (2013). Renormalized second-order perturbation theory for the electron correlation energy: concept, implementation, and benchmarks. Phys. Rev. B 88:035120. doi: 10.1103/PhysRevB.88.035120

CrossRef Full Text | Google Scholar

Rościszewski, K., Paulus, B., Fulde, P., and Stoll, H. (1999). Ab initio calculation of ground-state properties of rare-gas crystals. Phys. Rev. B 60, 7905–7910.

Google Scholar

Sansone, G., Maschio, L., Usvyat, D., Schütz, M., and Karttunen, A. (2016). Toward an accurate estimate of the exfoliation energy of black phosphorus: a periodic quantum chemical approach. J. Phys. Chem. Lett. 7, 131–136. doi: 10.1021/acs.jpclett.5b02174

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwerdtfeger, P., Assadollahzadeh, B., and Hermann, A. (2010). Convergence of the Møller-Plesset perturbation series for the fcc lattices of neon and argon. Phys. Rev. B Condens. Matter Mater. Phys. 82:205111. doi: 10.1103/PhysRevB.82.205111

CrossRef Full Text | Google Scholar

Scuseria, G. E., Henderson, T. M., and Bulik, I. W. (2013). Particle-particle and quasiparticle random phase approximations: connections to coupled cluster theory. J. Chem. Phys. 139:104113. doi: 10.1063/1.4820557

PubMed Abstract | CrossRef Full Text | Google Scholar

Scuseria, G. E., Henderson, T. M., and Sorensen, D. C. (2008). The ground state correlation energy of the random phase approximation from a ring coupled cluster doubles approach. J. Chem. Phys. 129:231101. doi: 10.1063/1.3043729

PubMed Abstract | CrossRef Full Text | Google Scholar

Shavitt, I., and Bartlett, R. J. (2009). Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory. Cambridge: Cambridge University Press.

Google Scholar

Shen, T., Zhang, I. Y., and Scheffler, M. (2018). Massive-parallel implementation of the resolution-of-identity coupled-cluster approaches in the numeric atom-centered orbital framework for molecular systems. arXiv:1810.08142.

Google Scholar

Shepherd, J. J., and Grüneis, A. (2013). Many-body quantum chemistry for the electron gas: convergent perturbative theories. Phys. Rev. Lett. 110:226401. doi: 10.1103/PhysRevLett.110.226401

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepherd, J. J., Henderson, T. M., and Scuseria, G. E. (2014). Coupled cluster channels in the homogeneous electron gas. J. Chem. Phys. 140:124102. doi: 10.1063/1.4867783

PubMed Abstract | CrossRef Full Text | Google Scholar

Solomonik, E., Matthews, D., Hammond, J. R., Stanton, J. F., and Demmel, J. (2014). A massively parallel tensor contraction framework for coupled-cluster computations. J. Parallel Distrib. Comput. 74, 3176–3190. doi: 10.1016/j.jpdc.2014.06.002

CrossRef Full Text | Google Scholar

Spencer, J. S., Blunt, N. S., Choi, S., Etrych, J., Filip, M.-A., Foulkes, W. M. C., et al. (2019). The HANDE-QMC project: open-source stochastic quantum chemistry from the ground state up. J. Chem. Theory Comput. 15, 1728–1742. doi: 10.1021/acs.jctc.8b01217

PubMed Abstract | CrossRef Full Text | Google Scholar

Stoll, H., and Doll, K. (2012). Approaching the bulk limit with finite cluster calculations using local increments: the case of LiH. J. Chem. Phys. 136:074106. doi: 10.1063/1.3687003

PubMed Abstract | CrossRef Full Text | Google Scholar

Szabo, A., and Ostlund, N. S. (1996). Modern Quantum Chemistry. New York, NY: McGraw-Hill.

Google Scholar

Thom, A. J. (2010). Stochastic coupled cluster theory. Phys. Rev. Lett. 105:263004. doi: 10.1103/PhysRevLett.105.263004

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsatsoulis, T., Hummel, F., Usvyat, D., Schütz, M., Booth, G. H., Binnie, S. S., et al. (2017). A comparison between quantum chemistry and quantum Monte Carlo techniques for the adsorption of water on the (001) LiH surface. J. Chem. Phys. 146:204108. doi: 10.1063/1.4984048

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsatsoulis, T., Sakong, S., Groß, A., and Grüneis, A. (2018). Reaction energetics of hydrogen on Si(100) surface: a periodic many-electron theory study. J. Chem. Phys. 149:244105. doi: 10.1063/1.5055706

PubMed Abstract | CrossRef Full Text | Google Scholar

Usvyat, D. (2013). Linear-scaling explicitly correlated treatment of solids: periodic local MP2-F12 method. J. Chem. Phys. 139:194101. doi: 10.1063/1.4829898

PubMed Abstract | CrossRef Full Text | Google Scholar

Usvyat, D., Civalleri, B., Maschio, L., Dovesi, R., Pisani, C., and Schütz, M. (2011). Approaching the theoretical limit in periodic local MP2 calculations with atomic-orbital basis sets: the case of LiH. J. Chem. Phys. 134:214105. doi: 10.1063/1.3595514

PubMed Abstract | CrossRef Full Text | Google Scholar

Usvyat, D., Maschio, L., and Schütz, M. (2018). Periodic and fragment models based on the local correlation approach. Wiley Interdiscipl. Rev. Comput. Mol. Sci. 8:e1357. doi: 10.1002/wcms.1357

CrossRef Full Text | Google Scholar

Usvyat, D., Sadeghian, K., Maschio, L., and Schütz, M. (2012). Geometrical frustration of an argon monolayer adsorbed on the MGO (100) surface: an accurate periodic ab initio study. Phys. Rev. B 86:045412. doi: 10.1103/PhysRevB.86.045412

CrossRef Full Text | Google Scholar

Voloshina, E., Usvyat, D., Schütz, M., Dedkov, Y., and Paulus, B. (2011). On the physisorption of water on graphene: a CCSD(t) study. Phys. Chem. Chem. Phys. 13, 12041–12047. doi: 10.1039/c1cp20609e

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Hu, W., Usvyat, D., Matthews, D., Schütz, M., and Chan, G. K. (2014). Ab initio determination of the crystalline benzene lattice energy to sub-kilojoule/mole accuracy. Science 345, 640–643. doi: 10.1126/science.1254419

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, I. Y., Logsdail, A. J., Ren, X., Levchenko, S. V., Ghiringhelli, L., and Scheffler, M. (2018). Main-group test set for materials science and engineering with user-friendly graphic tools for error analysis: systematic benchmark of the numerical and intrinsic errors in state-of-the-art electronic-structure approximations. N. J. Phys. 21:013025. doi: 10.1088/1367-2630/aaf751

CrossRef Full Text

Zhang, I. Y., Ren, X., Rinke, P., Blum, V., and Scheffler, M. (2013). Numeric atom-centered-orbital basis sets with valence-correlation consistency from H to Ar. N. J. Phys. 15:123033. doi: 10.1088/1367-2630/15/12/123033

CrossRef Full Text | Google Scholar