Material Characterization of MR Fluid on Performance of MRF Based Brake

Introduction

In last two decades, researches on the development and application of brake featuring magneto-rheological fluid (MRF) have interested many researchers. There have been numerous researches on improving performance of MRF based brake (MRB) with different configurations ad applications such as: disc-type MRB (An and Kwon, 2003; Liu et al., 2006; Park et al., 2006), drum-type MRBs (Huang et al., 2002; Smith et al., 2007), hybrid-type MRB with T-shaped rotor (Avraam et al., 2008; Nguyen and Choi, 2012; Mousavi and Sayyaadi, 2018). Avraam et al performed some analyses and comparisons of different types of MRB such as disc-type, drum type, and T-shape type in development of a rotational MRB for rehabilitation devices (Avraam et al., 2010). Inmaduddin et al. reviewed advances in MRBs, in terms of various innovations of structural and magnetic circuit designs, including disc-type, drum-type, and hybrid type as well as modeling techniques that have been involved with each innovation (Imaduddin et al., 2013). In order to have a more detailed comparison of different types of MRB, Nguyen and Choi (2011) investigated the optimal design of different types of MRB considering their maximum braking torque and specific volume. Later, Nguyen et al. (2014a) evaluated the effect of different shapes of envelope such as the rectangular, the polygonal and the spline to the performance and the mass of MRBs. Recently, Nguyen et al. (2014b, 2015) proposed a new configuration of MRB in which a magnetic coil is wound on each side of the housing of the MRB (in this research, it is named as side-coil MRB). The results showed that, with this configuration, some disadvantages of the traditional MRBs such as the “bottle-neck” problem of magnetic flux, the non-magnetic bobbin requirement, difficulties in manufacturing and maintenance can be eliminated or minimized. In addition, the optimal solutions showed that the mass of the side-coil MRB was significantly improved in producing the same braking torque as the conventional ones.

In the design of MRB, different types of MRF have been used. However, how the characterization of MRF's effects on the performance of MRB was not considered in detail. In order to fill this gap, this research investigates the effects of MRF characterizations on the performance of MRB through simulation results, from which guidelines on the selection of MRF types for MRBs are summarized. The remainder of the paper is arranged as follows. In section Conventional and Side-Coil MRBs, several configurations of MRB considered in this study are introduced. After that, in section Optimization of MRBs Based on Finite Element Analysis, the optimization solution of the MRB design is proposed based on the Bingham plastic model of the MRFs and finite element analysis of MRB magnetic circuit. In section Results and Discussions, optimal solutions of the MRBs with different MRFs are obtained, from which, performance characteristics of the MRBs such as braking torque, off-state torque, and power consumption are evaluated. Finally, some observations and guidance on selection of MRFs in MRB design are summarized.

Conventional and Side-Coil MRBs

As mentioned above, several types of MRB have been developed so far. In this study, two of the most typical types of MRB, the conventional disc-type MRB and the side-coil MRB, are considered. Figure 1A shows a typical conventional MRB and Figure 1B presents the side-coil one.

FIGURE 1

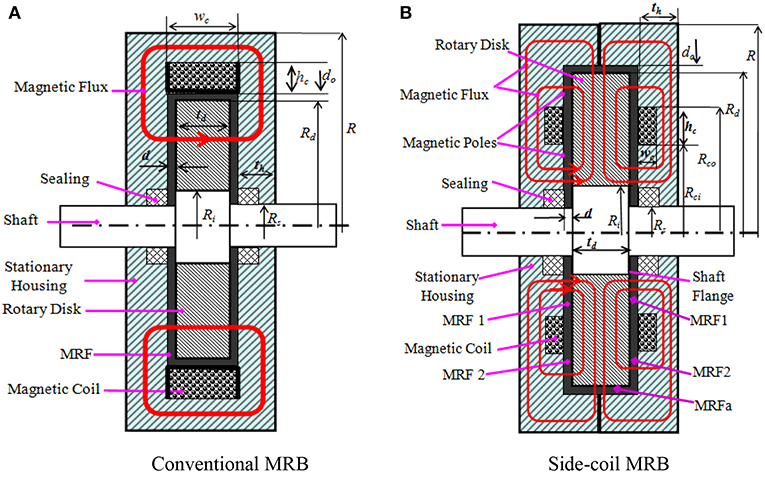
Figure 1. Configurations of the conventional and the side-coil MRBs. (A) Conventional MRB. (B) Side-coil MRB.

The first configuration represents conventional MRBs which use outside cylindrical coils such as disc-type, drum-type, while the second configuration represent for the MRBs which use side coils including T-shape MRBs. As shown in the figure, a disc (rotor) made of magnetic steel is fastened to the flange of the MRB shaft made of non-magnetic steel. The disc is embedded inside a stationary envelope (housing) made of magnetic steel. In Figure 1A, a wire-coil is wound on a non-magnetic bobbin which is fixed to the brake envelop while in Figure 1B, the coil is placed on each side housing of the brake. By using the side-coil configuration, it is observed that the coils can be placed directly on the housing. In addition, multiple coils can be implemented, especially for high braking torque MRBs.

It is obviously observed that the braking torque of the proposed MR brake comes from two sources: the friction of MRF acting on the two end-faces and on the outer annular face of the disc. Firstly, the friction between MRF and the end-faces of the disc is analyzed. The induced torque from MRF in radial duct acting on one end-face of a disc can be expressed as follows (Nguyen and Choi, 2012):

$\begin{array}{ll}{T}_e={\displaystyle \underset{A}{\int }}{\tau }_{e}rdA=2\pi {\displaystyle {\int }_{R_1}^{R_2}}{\tau }_e{r}^{2}dr& (1)\end{array}$

where A is the area of the end-face of the disc, r is the radius of an infinitesimal area of the disc, R₁ and R₂ are the inner and outer radius of the duct. τ_e is the shear stress of the MRF at the interface, which can be predicted from the Bingham-plastic model of the MRF as follows:

$\begin{array}{ll}{\tau }_e={\tau }_{ye}+{\mu }_e{\dot{\gamma }}_e& (2)\end{array}$

where, τ_ye and μ_e are, respectively, the yield stress and post yield viscosity of the MRF. ${\dot{\gamma }}_e$ is the shear rate of MR fluid at the interface. Because the gap size of the duct is very small, the shear rate of MRF in the gap is assumed to be linearly distributed which can be approximately determined as follows:

$\begin{array}{ll}{\dot{\gamma }}_e=\frac{r\Omega }{d}& (3)\end{array}$

where d is the gap size and Ω is the angular velocity of the drum.

Plug Equations (2, 3) into Equation (1) the following equation can be obtained.

$\begin{array}{ll}{T}_e=2\pi {\displaystyle {\int }_{R_1}^{R_2}}{r}^2{\mu }_e\left(\frac{r\Omega }{d}\right)dr+2\pi {\displaystyle {\int }_{R_1}^{R_2}}{r}^2{\tau }_{ye}dr& (4)\end{array}$

Generally, the magnetic density in the MRF gap is a function of radius r, thus the values of τ_ye and μ_e of the MRF in the gap are also functions of r. Equation (4) then have to be calculated by numerically integrating. In order to facilitate the calculation, it is assumed that the magnetic density in the MRF gap is constant and an average value of the magnetic density obtained from numerical integration is used. In this case, Equation (4) can be analytically integrated to yield

$\begin{array}{ll}{T}_e=\frac{\pi {\mu }_e{R}_2^4}{2d}\left[1-{\left(\frac{R_1}{R_2}\right)}^4\right]\Omega +\frac{2\pi {\tau }_{ye}}{3}(R_2^3-R_1^3)& (5)\end{array}$

The torque due to MRF in annular gap acting on the outer circular face of the disc can be determined by

$\begin{array}{ll}{T}_a={\displaystyle \underset{A_a}{\int }{R}_a}{\tau }_{a}dA={\displaystyle \underset{0}{\overset{L_a}{\int }}{R}_a{\tau }_{a}2\pi R_{a}dl}=2\pi R_a^2{\displaystyle \underset{0}{\overset{L_a}{\int }}({\tau }_{ya}+{\mu }_a\dot{\gamma })dl}& (6)\end{array}$

where A_a is the area of the outer annular face of the disc, L_a and R_a are radius and length of annular duct, τ_a is the shear stress at the annular face of the disc, τ_ya and μ_a are the yield stress and post yield viscosity of the MRF in the annular duct. Similarly to MRF in the end-face gap, by using average magnetic density obtained from numerical integration and assuming a linear distribution of shear rate in the MRF gap, the following can be obtained

$\begin{array}{ll}{T}_a=2\pi R_a^2{L}_a({\tau }_{ya}+{\mu }_a\frac{R_a\Omega }{d})& (7)\end{array}$

From Equations (5) to (7), by neglecting friction torque from sealing and bearing, the induced braking torque of the conventional disc-type MRB and the side-coil ones can be correspondingly obtained

$\begin{array}{ll}\begin{array}{l}{T}_c=2T_e+T_a=\frac{\pi {\mu }_e{R}_d^4}{d}[1-{(\frac{R_i}{R_d})}^4]\Omega +\frac{4\pi {\tau }_{ye}}{3}(R_d^3-R_i^3)\hfill \\ +2\pi R_d^2{t}_d({\tau }_{y0}+{\mu }_0\frac{\Omega R_d}{d_o})\hfill \end{array}& (8)\end{array}$

$\begin{array}{ll}\begin{array}{l}{T}_s=2(T_{e1}+T_{e2})+T_a=\frac{\pi {\mu }_1{R}_{ci}^4}{d}[1-{(\frac{R_i}{R_{ci}})}^4]\Omega +\frac{4\pi {\tau }_{y1}}{3}(R_{ci}^3-R_i^3)\hfill \\ +\frac{\pi {\mu }_2{R}_d^4}{d}[1-{(\frac{R_{co}}{R_d})}^4]\Omega +\frac{4\pi {\tau }_{y2}}{3}(R_d^3-R_{co}^3)+2\pi R_d^2{t}_d({\tau }_{ya}+{\mu }_a\frac{\Omega R_d}{d_o})\hfill \end{array}& (9)\end{array}$

and the off-state force (the torque of the MRB when no magnetic field is applied to MRF) of both considered MRBs can be expressed as Nguyen et al. (2015).

$\begin{array}{ll}\begin{array}{l}{T}_0=\frac{\pi {\mu }_0{R}_d^4}{d}[1-{(\frac{R_s}{R_d})}^4]\Omega +\frac{4\pi {\tau }_{y0}}{3}(R_d^3-R_s^3)\hfill \\ +2\pi R_d^2{t}_d({\tau }_{y0}+{\mu }_0\frac{\Omega R_d}{d_o})+2T_{sf}\hfill \end{array}& (10)\end{array}$

where T_c is the braking torque of the conventional MRB, T_s is the braking torque of the side coil MRB, T₀ is the off-state torque of MRBs, T_e1 and T_e2 are the friction torque of MRF in region 1 (MRF1) and MRF in region 2 (MRF2) acting on the disc in case of the side coil MRB, R_d is the outer radius of the disc, R_i is the inner radius of the active MRF volume in the end-face duct, R_s is the shaft diameter, d is the gap size of the end-face MRF ducts between the disc and the housing, d_o is the gap size of the annular MRF duct at the outer cylindrical face of the disc, t_d is the thickness of the disc, R_ci and R_co are the inner and outer radii of the coil in the case of the side-coil MRB, Ω is the angular velocity of the rotor, μ_e and τ_ye are, respectively, the average post yield viscosity and yield stress of MRF in the end-face duct of the conventional MRB, μ_j is the average post yield viscosity of the j^th active MRF volume (denoted by MRFj) in the end-face duct of the side-coil MRBs while τ_yj is the corresponding yield stress, μ_a and τ_ya are, respectively, the average post yield viscosity and yield stress of MRF in the annular duct of the side-coil MRBs, τ_y0 and μ₀ are the zero-field yield stress and viscosity of the MRF. The rheological properties of MRF such as the induced yield stress τ_ye, τ_yj, τ_ya, and the corresponding average post yield viscosity μ_e, μ_j, μ_a depend on the exerted magnetic flux density across the active MRF volumes and can be approximated by Zubieta et al. (2009).

$\begin{array}{ll}Y=Y_{\infty }+(Y_0-Y_{\infty })(2e^{-B{\alpha }_{SY}}-e^{-2B{\alpha }_{SY}})& (11)\end{array}$

where Y represents for a rheological parameters of MRF such as the yield stress and the post yield viscosity, Y₀ and Y_∞, respectively, represents for the value of Y in the absence of magnetic field and in saturated state of MRF, α_SY is the saturation moment index of the Y parameter, B is the applied magnetic density.

Optimization of MRBs Based on Finite Element Analysis

In this part, the optimal design problem of the conventional and the side-coil MRBs is constructed. In the design of MRBs, a required braking torque is usually given depending on the application. Therefore, the purpose of the MRB design is to determine geometric dimensions of the brake so that the brake can create a required braking torque while the mass of the brake is as small as possible. In addition, the power consumption of the coils and the off-state torque are also important issues should be accounted for. The power consumption should be as small as possible to save energy and to accommodate with available power for each application. The off-state torque should be small to reduce the energy lost and also to reduce the heating problem. In this study, an objective function, which is a linear combination of the above issues, is proposed, which is mathematically expressed as the following:

$\begin{array}{ll}Obj={\alpha }_m\frac{m_b}{m_{ref}}+{\alpha }_p\frac{P}{P_{ref}}+{\alpha }_{To}\frac{T_0}{T_{0ref}}& (12)\end{array}$

In the above, m_b, P, and T₀ are, respectively, the mass, the power consumption and the off-state torque of the brake, m_ref, P_ref, and T_0ref are, respectively, the reference mass, the power consumption and the off-state torque, and α_m, α_P, and α_To are the corresponding weighting coefficients determined based on the importance of the objectives. In this research, the reference values are obtained from the optimization problem in which the objective function is the mass of the MRB, Nguyen et al. (2014a, 2015). Generally, the MRB mass can be approximately calculated by Nguyen et al. (2015).

$\begin{array}{ll}{m}_b=V_d{\rho }_d+V_h{\rho }_h+V_s{\rho }_s+V_{MR}{\rho }_{MR}+V_{bob}{\rho }_{bob}+V_c{\rho }_c& (13)\end{array}$

where V_d, V_h, V_s, V_MR, V_bob, and V_c are, respectively, the geometric volume of the disc, the housing, the shaft, the MRF, the bobbin and the coil of the brake, ρ_d, ρ_h, ρ_s, ρ_MR, ρ_bob, and ρ_c are correspondingly density of the discs, the housing, the shaft, the MRF, the bobbin in case of conventional MRB (in case of the side-coil MRBs, this term is eliminated) and the coil material.

Power consumption of the MRBs can be calculated by

$\begin{array}{ll}P=I^2{R}_w& (14)\end{array}$

where I is the electric current applied to the coils and R_w is the resistance of the coil wires, which can be approximately calculated as follows:

$\begin{array}{ll}{R}_w=L_w{r}_w=2\pi R_c{N}_c\frac{r}{A_w}=2\pi R_c\epsilon \frac{A_c}{A_w}\frac{r}{A_w}=\frac{2R_c\epsilon w_c{h}_{c}r}{\pi d_w^2}& (15)\end{array}$

$\begin{array}{ll}{R}_w=2L_w{r}_w=4\pi R_c{N}_c\frac{r}{A_w}=4\pi R_c\epsilon \frac{A_c}{A_w}\frac{r}{A_w}=\frac{4R_c\epsilon w_c{h}_{c}r}{\pi d_w^2}& (16)\end{array}$

In the above, L_w is the length of the coil wire, r_w is the resistance per unit length of the coil wire, N_c is the number of coil turns, R_c is the average radius of the coil cross-sectional area, A_w is the cross sectional area of the wire, A_c is the cross sectional area of the coil, ε is the filling ratio of the coil which is assumed to be 0.8 in this study, r is the resistivity of the coil wire, r = 0.017 26 (Ωm) for copper wire.

In order to determine the braking torque of the MRBs, firstly, finite element analysis (FEA) is used to evaluate the magnetic density across the ducts of MRF based on quasi-static analysis. This is reasonable because the purpose of this research is to investigate the effect of MRF on performance characteristics of MRB and this can be archived by quasi-static simulation. In detail, the finite element models generated by 2D-axisymmetric couple element (PLANE 13) of commercial ANSYS software, as shown in Figure 2, are applied to solve the magnetic circuits of the MRB. It is noted in Figure 2 that the mesh size is specified by the number of elements per line rather than element size and the number of elements on the lines across the MR duct is specified as a parameter called the basic meshing number. The number of elements of other lines is chosen as a product of the basic meshing number and an appropriate scalar. It is well-known that the smaller the mesh size, the better the result is obtained. However, the small mesh size results in a high computational cost. When mesh size is reduced to a certain value, the convergence of solution is expected. In this study, the basic meshing number of 8 elements is sufficient to ensure the convergence of the FE solution.

FIGURE 2

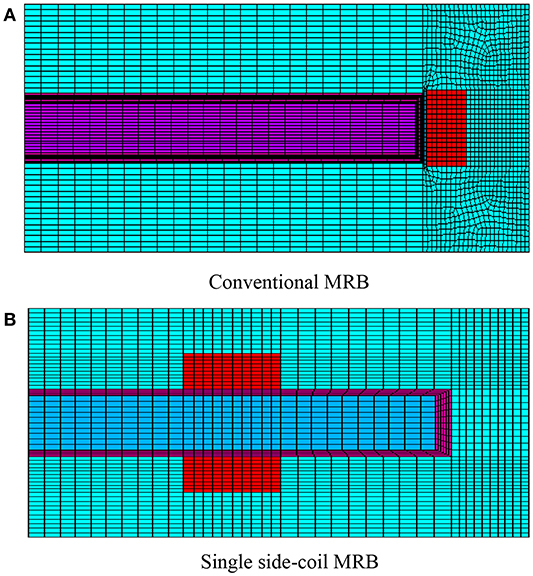
Figure 2. Finite element models to analyze the magnetic circuit of the MRBs. (A) Conventional MRB. (B) Single side-coil MRB.

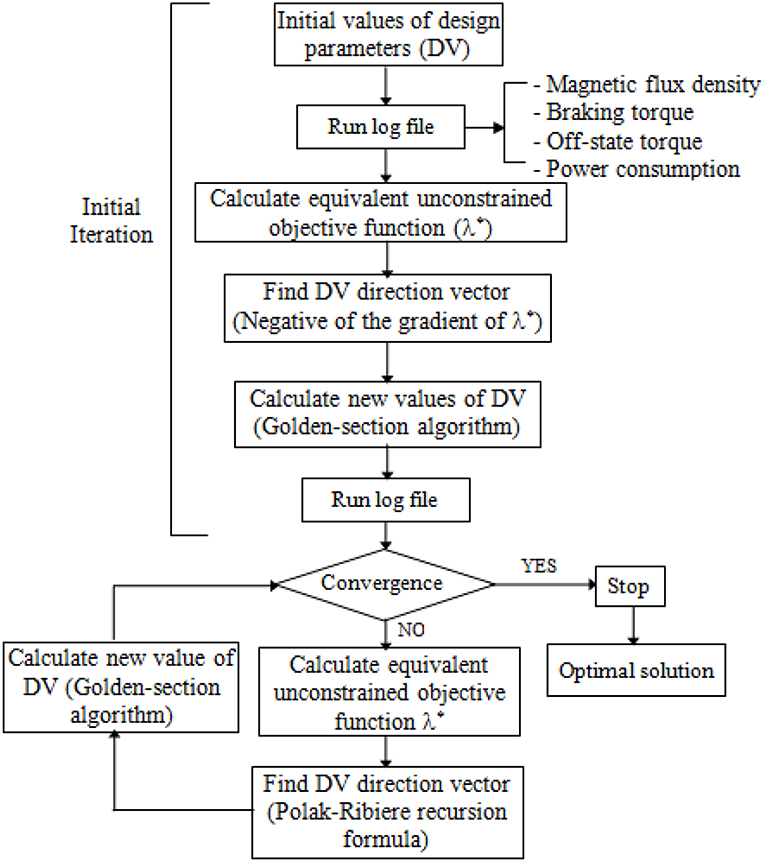
From the FE solution of the magnetic circuit, the induced MRF rheological properties in the ducts such as the yield stress (τ_ye, τ_yj, τ_ya,) and the post yield viscosity (μ_e, μ_ej, μ_a) are calculated by Equation (11) via the average induced magnetic density and its initial rheological parameters. From the obtained values of all abovementioned parameters, the on-state of each MRB can be then estimated by Equations (8, 9). From geometric dimensions, the off-state torque can be calculated by Equation (10) while the mass and the power consumption of the MRBs can be determined from Equations (13, 14), respectively. It is noted that these performance parameters are updated in each optimization loop. In this research, the optimization procedure is conducted by using the first order optimization method with the gradient decent algorithm. The procedures to achieve optimal design parameters of the MRBs using the first order method of ANSYS optimization tool is shown in Figure 3. Starting with initial value of design variables, by executing the ANSYS log-file, performance characteristics of the MRBs at the first iteration are calculated. The ANSYS optimization tool then transforms the constrained optimization problem to an unconstrained one via penalty functions. For the initial iteration, the search direction of DVs is assumed to be the negative of the gradient of the unconstrained objective function. In the subsequent iterations, the direction vectors are calculated according to Polak-Ribiere recursion formula. A detailed description of this algorithm integrated with ANSYS software is shown in previous research (Nguyen et al., 2007).

FIGURE 3

Figure 3. Flow chart for optimal design using FEM.

Results and Discussions

In this section, the optimal results of the MRBs are obtained with different types of MRF and discussions on the effects of MRF types on performance parameters of the MRBs are presented. Table 1 shows the materials selections for components of MRBs. As shown in the table, the commercial silicon steel is used for magnetic components of the MRB such as the housing and the disc, the bobbin is made of non-magnetic steel, the coil is made from copper wire sized as 24-gage (diameter = 0.511 mm) whose maximum working current is around 3 A and during the optimization process an applied current of 2.5 A is used. Three types of commercial MR fluid made by Lord Corporation: MRF-122-2ED (low yield stress), MRF-132-DG (medium yield stress) and MRF-140 CG (high yield stress) are considered. Parameters of the field dependent Bingham rheological model of the MRF are determined from experimental results using curve fitting method as shown in Figure 5. In this research work, a least square curve fitting method is used, and the results are presented in Table 2 (Nguyen and Choi, 2010).

TABLE 1

Table 1. Magnetic property of the brake components.

FIGURE 4

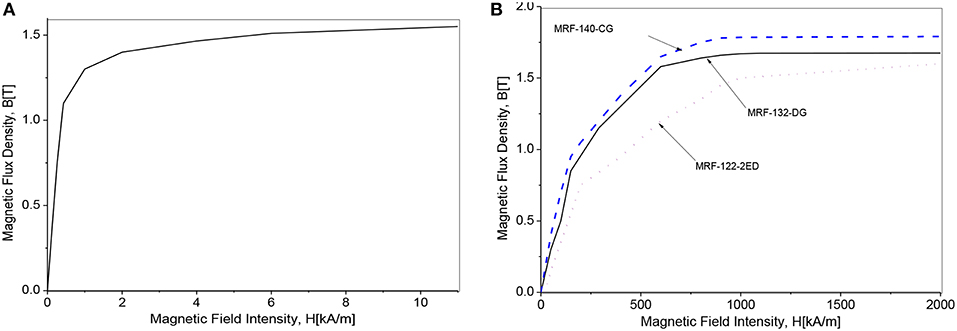
Figure 4. Magnetic properties of silicon steel and MR fluids. (A) B-H curve of silicon steel. (B) B-H curve of MR Fluid.

FIGURE 5

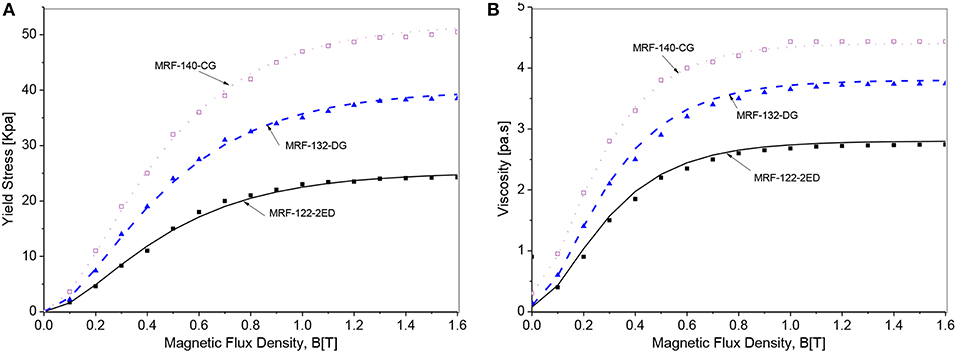
Figure 5. Rheological properties of MR fluids. (A) Field dependent yield stress. (B) Field dependent post-yield viscosity.

TABLE 2

Table 2. Rheological properties of MR fluids.

In the optimization, the design variables are significant geometric dimensions of the MRBs such as the coil height h_c, the coil width w_c, the inner radius of the disc R_i, the outer radius of the disc R_d, the disc thickness t_d, outer radius of the brake R, the housing thickness t_h, the inner radius of the coils in case of the side-coil MRBs R_c, and the gap size of the MRF ducts are also considered as design variables. It is noted that the shaft radius is set by R_s = 8 mm in the optimization.

Figures 6–11 show optimal solutions of the MRB when the mass is considered as the objective function at different values of the constrained braking torque, ranging from 5 to 100 Nm. It is noted that this case is equivalent to the case when the weighting coefficients in the objective function in Equation (12) are chosen at α_m = 1.0, α_P = α_To = 0. The smaller value of the MRF gap size in the higher braking torque can be archived and the smaller mass of the MRB is. Therefore, during the optimization process, the MRF gap size is not considered as a design variable and fixed at a certain value. In these figures, three typical values of the gap size, which are 0.6, 0.8, and 1.0 mm, are considered. In Figures 6, 7, the gap size is set by 0.6 mm. It is observed from the figure that when we consider only the mass of the MRBs in the optimization, MRBs employing the highest yield stress MRF have the smallest mass and power consumption at all values of the constrained braking torque. However, the off-state torque of the MRB with highest yield stress is significantly greater than the others. Therefore, if the brake normally works in off-state condition, this issue should be taken into account. It also observed from the figures that among the three MRFs, the medium yield stress MRF (MRF 132-DG) is the most compromised of the three mentioned performance parameters, the mass, the power consumption and the off-state force. The off-state torque in the case of MRB with MRF 132-DG is even smaller than the MRB with low yield stress MRF (MRF-122-2ED). The reason is that the MRB employing MRF-122-2ED has a larger disc radius to produce enough braking torque, which also results in corresponding higher off-state torque. By comparison at different values of the MRF gap size, it is observed that the smaller the gap size, the smaller the mass of the MRBs that can be archived, and the lower the power consumed by the coils. However, the off-state torque of the MRBs increases as the MRF gap size decreases and this should be taken into account especially when the MRBs work continuously such as in automotive application.

FIGURE 6

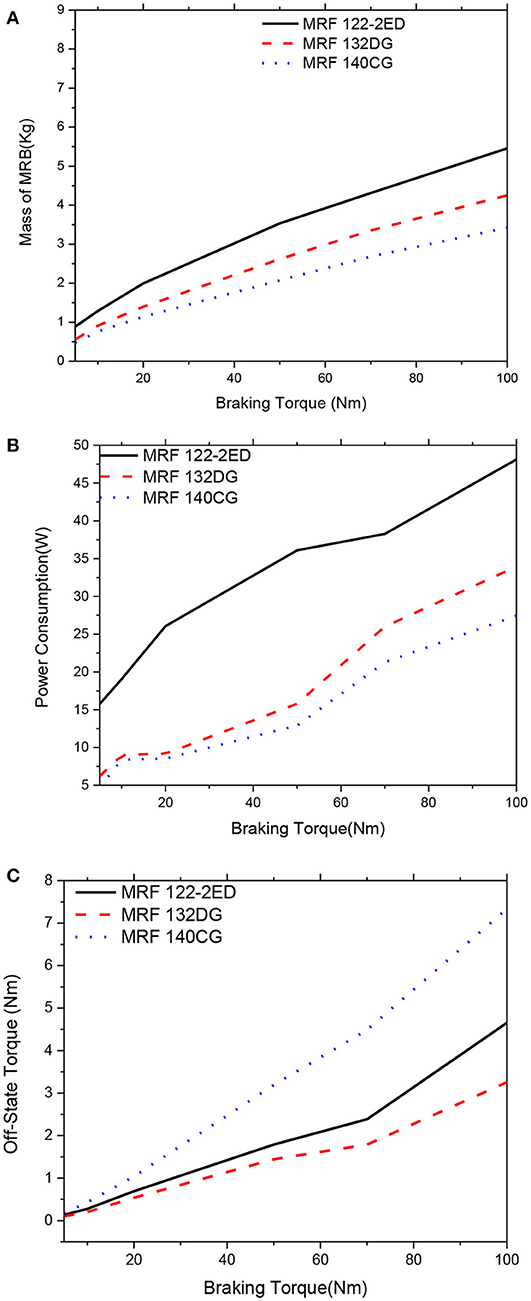
Figure 6. Mass optimization results of the MRBs as a function of braking torque of conventional MRB, d = 0.6 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 7

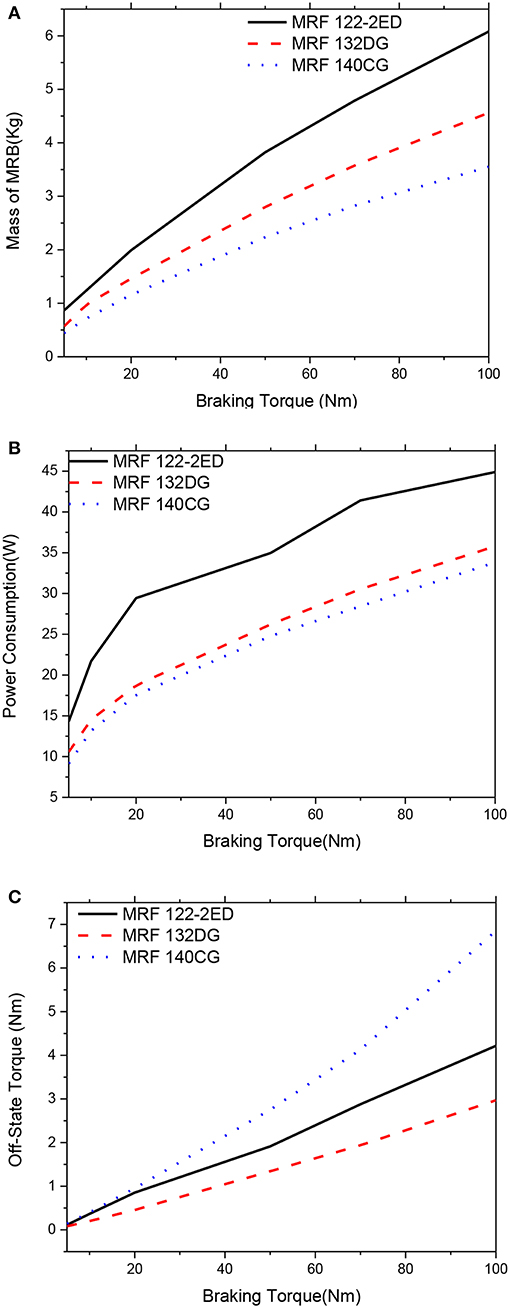
Figure 7. Mass optimization results of the MRBs as a function of braking torque of side-coil MRB, d = 0.6 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 8

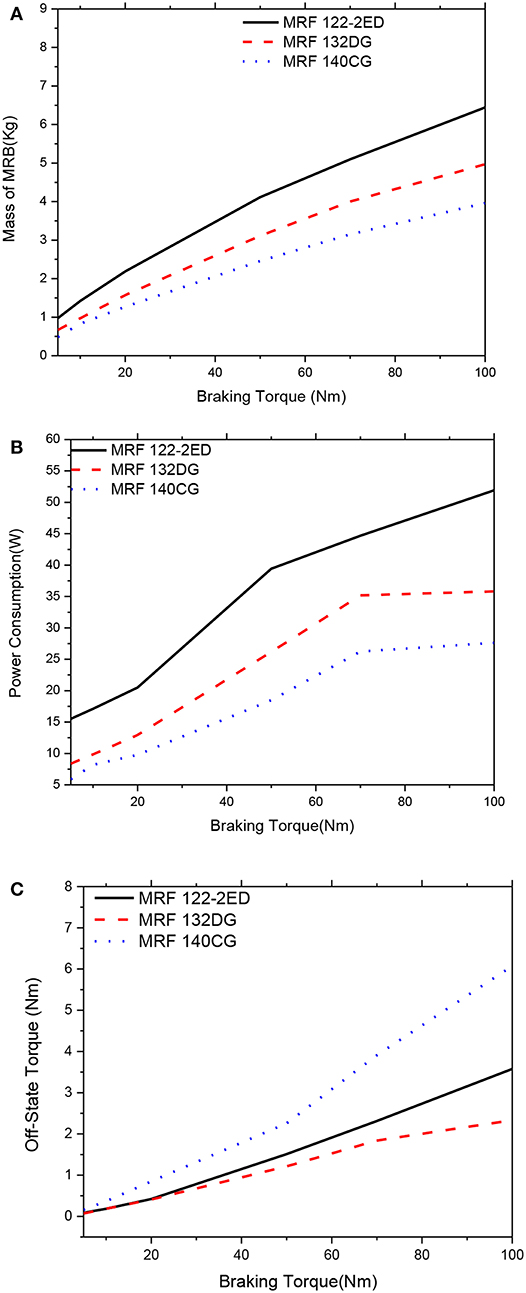
Figure 8. Mass optimization results of the MRBs as a function of braking torque of conventional MRB, d = 0.8 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 9

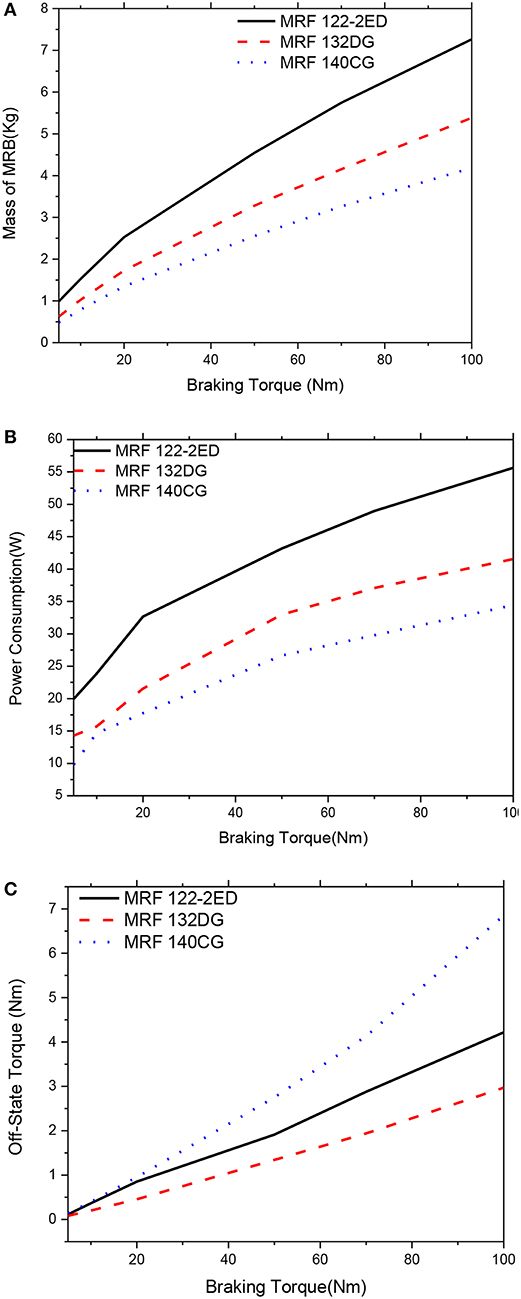
Figure 9. Mass optimization results of the MRBs as a function of braking torque of side-coil MRB, d = 0.8 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 10

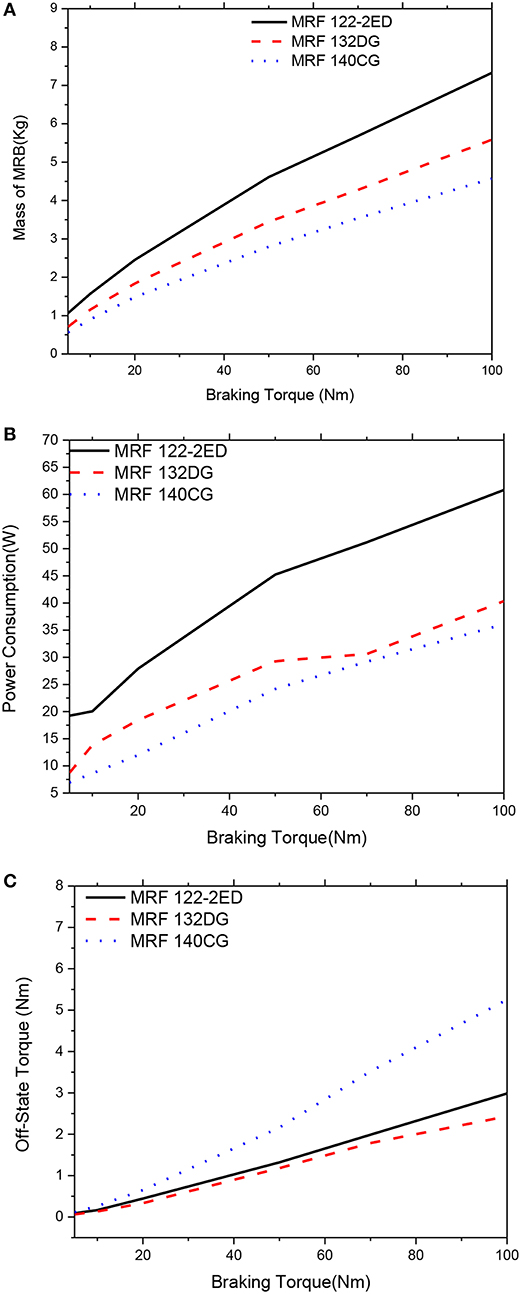
Figure 10. Mass optimization results of the MRBs as a function of braking torque of conventional MRB, d = 1.0 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 11

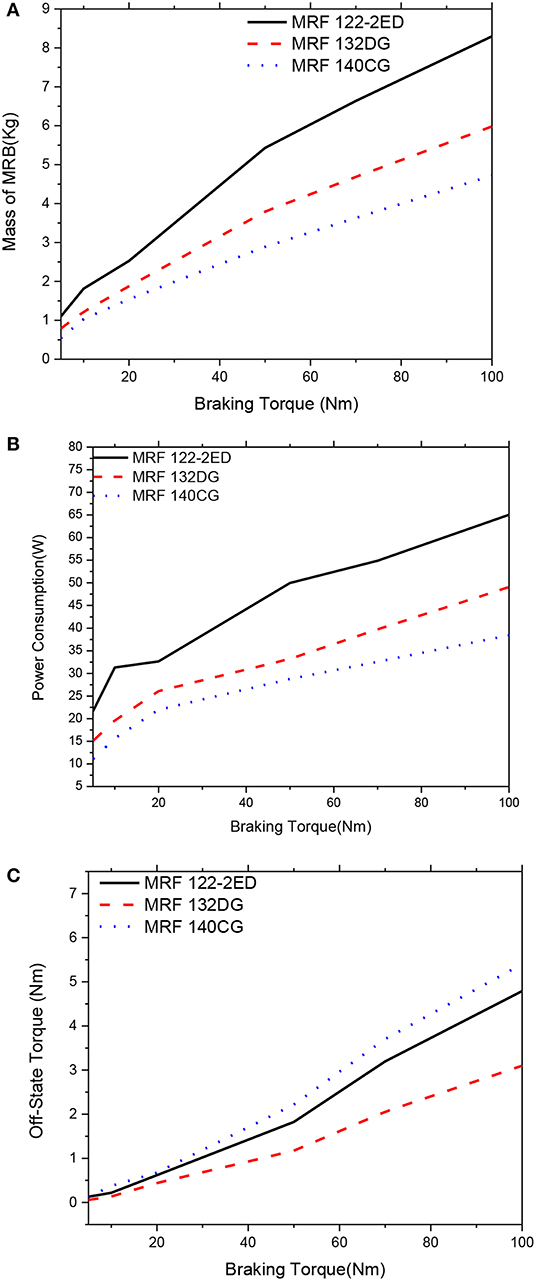
Figure 11. Mass optimization results of the MRBs as a function of braking torque of side-coil MRB, d = 1.0 mm. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

Figures 12, 13 show optimal solutions of the MRBs, when the weighting coefficients of the objective function in Equation (12) are chosen at α_m = α_P = α_To = 1/3, at different values of the constrained braking torque ranging from 5 to 100 Nm. This means that the importance of the three performance parameters (the mass, the power consumption and the off-state torque) are assumed equal. It is noted that in this case the gap size of MRF is also considered as a design variable, ranging from 0.6 to 1.0 mm. The results show that by considering all three issues (multi-objective optimization) in the optimization, a compromised optimal result can be archived. By comparing Figures 12, 13 with the previous figures (Figures 6–11), it is observed that in case of multi-objective optimization, the mass of the MRBs is a bit greater than that in case of mass optimization; however the power consumption and off-state torque are significantly smaller. Again, the same comments can be obtained by considering different types of MRF from Figures 12, 13, which mean that the medium yield stress MRF (MRF 132-DG) is the most compromised among the three considered MRFs. The gap size of MRBs at the optimum is equal to its lower limit, which is 0.6 mm.

FIGURE 12

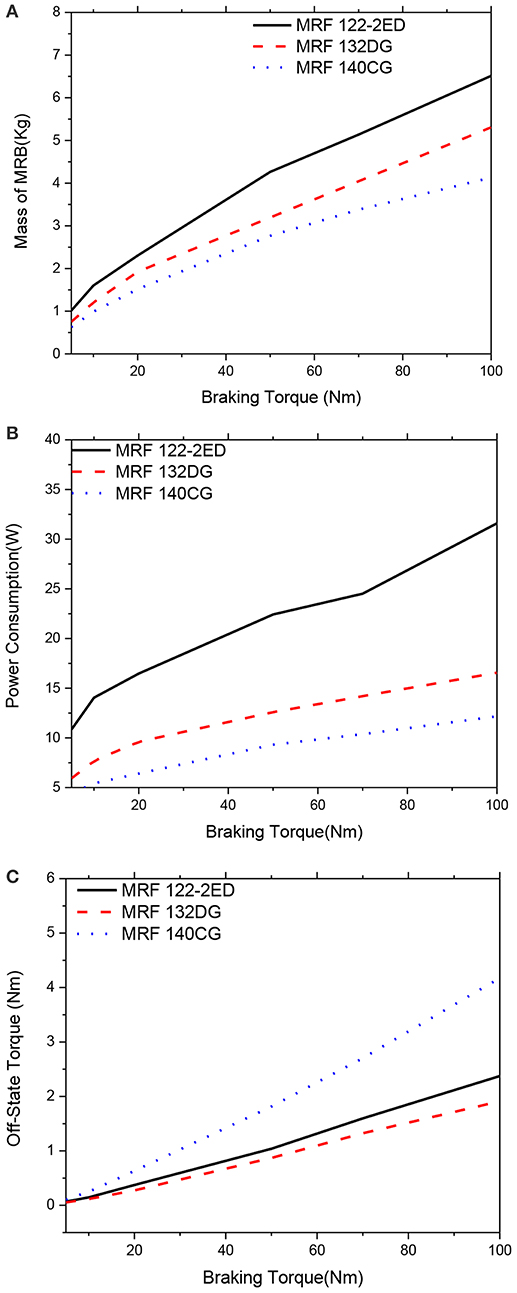
Figure 12. Multi-objective optimization results of the MRBs as a function of braking torque of conventional MRB, α_m = α_P = α_To = 1/3. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque. (C) Off-state torque as a function of braking torque.

FIGURE 13

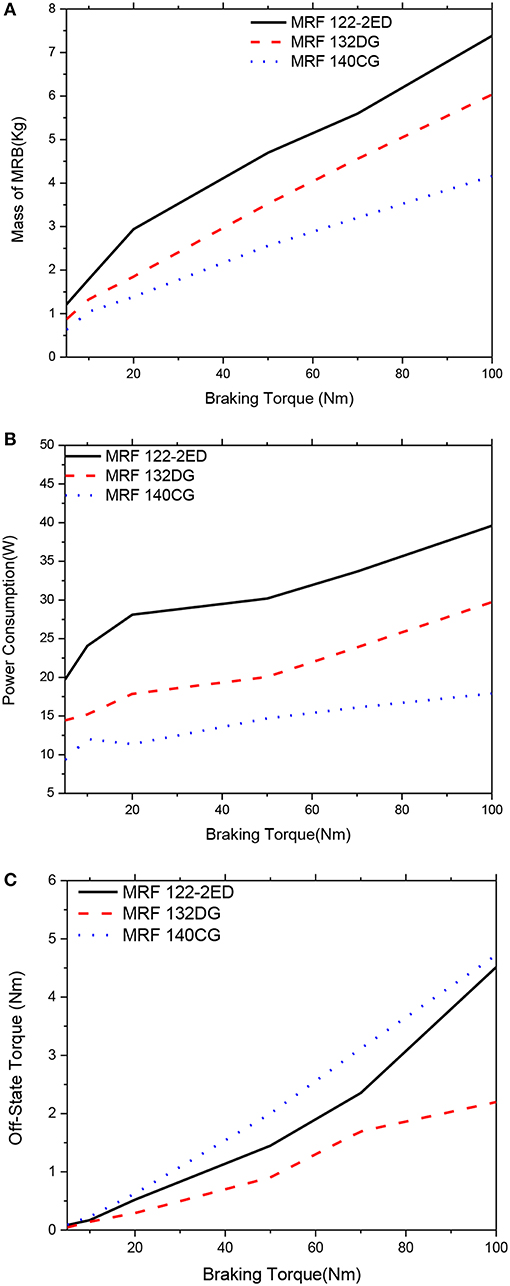
Figure 13. Multi-objective optimization results of the MRBs as a function of braking torque of side-coil MRB, α_m = α_P = α_To = 1/3. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

Figures 14, 15 show optimal solutions of the MRBs, when the weighting coefficients of the objective function in Equation (12) are chosen at α_m = α_P = 0.5 and α_To = 0, which means that the importance of the mass and the power consumption are assumed equal while the off-state torque is not considered. The results show that the mass of the MRBs is a bit smaller than that in Figures 12, 13 and the power consumption of the MRBs is significantly reduced, especially for the MRBs employing MRF 132-DG, while the off-state of the MRBs are slightly increased. From Figures 14, 15, again it is observed that the medium yield stress MRF (MRF 132-DG) is the most compromised among the three considered MRFs. The gap size of MRBs at the optimum is equal to its lower limit in this case, as well.

FIGURE 14

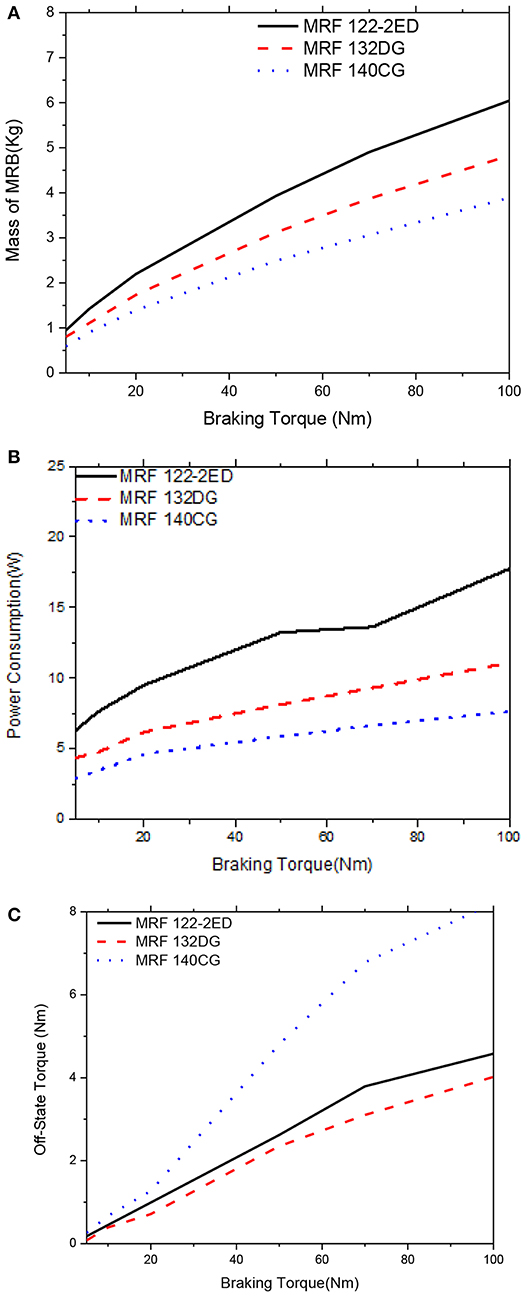
Figure 14. Multi-objective optimization results of the MRBs as a function of braking torque of conventional MRB, α_m = α_P = 0.5, α_To = 0. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 15

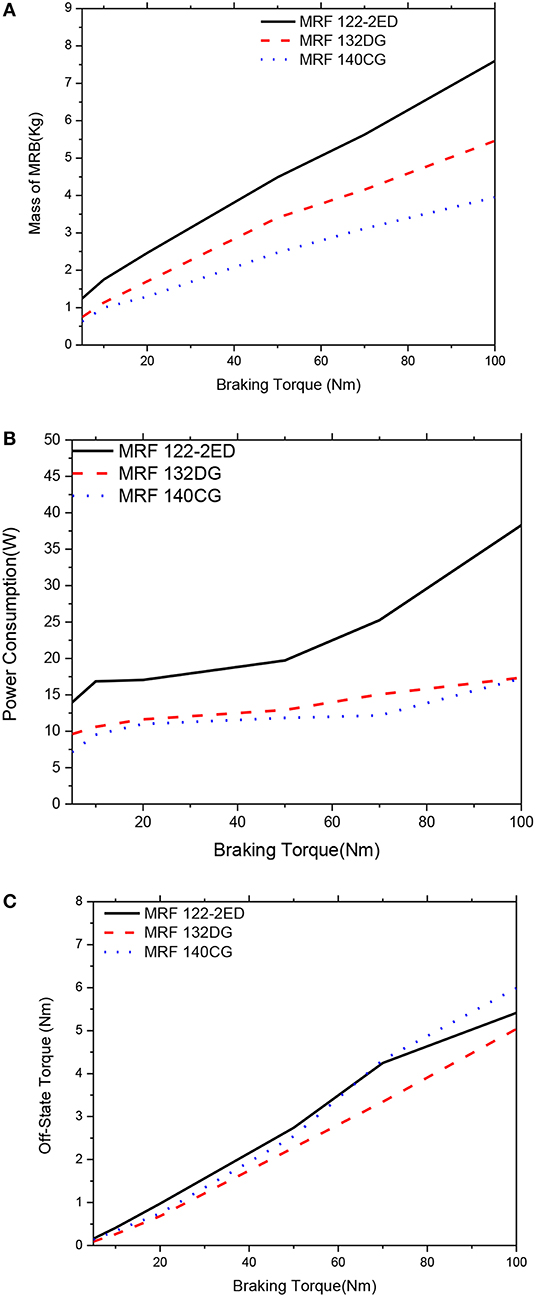
Figure 15. Multi-objective optimization results of the MRBs as a function of braking torque of side-coil MRB, α_m = α_P = 0.5, α_To = 0. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

Figures 16, 17 show optimal solutions of the MRBs, when the weighting coefficients of the objective function in Equation (12) are chosen at α_m = 0.5, α_P = 0.0 and α_To = 0.5, which means that the importance of the mass and the off-state torque are assumed equal while the power consumption is not considered. The results show that the mass of the MRBs is almost the same as that in Figures 14, 15. This is because the weighting coefficient is the same in both cases. However, the power consumption is much higher than that of the previous case, although the off-state torque is smaller. Similar to Figures 14, 15, the medium yield stress MRF (MRF 132-DG) is the most compromised among the three considered MRFs. Again, the gap size of MRBs at the optimum is equal to its lower limit.

FIGURE 16

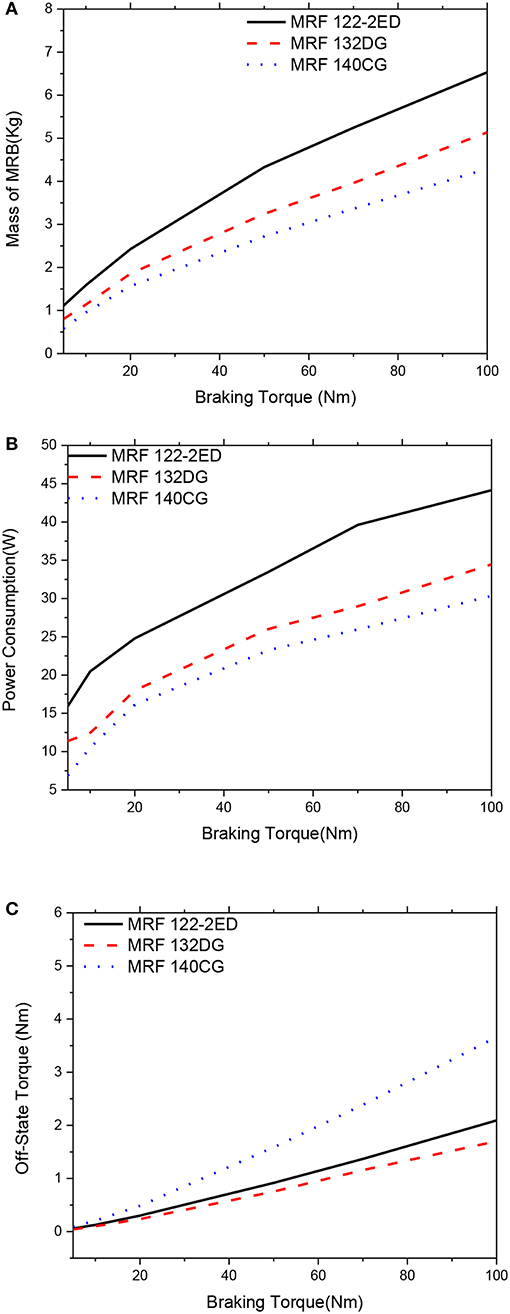
Figure 16. Multi-objective optimization results of the MRBs as a function of braking torque of conventional MRB, α_m = 0.5; α_P = 0.0; α_To = 0.5. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 17

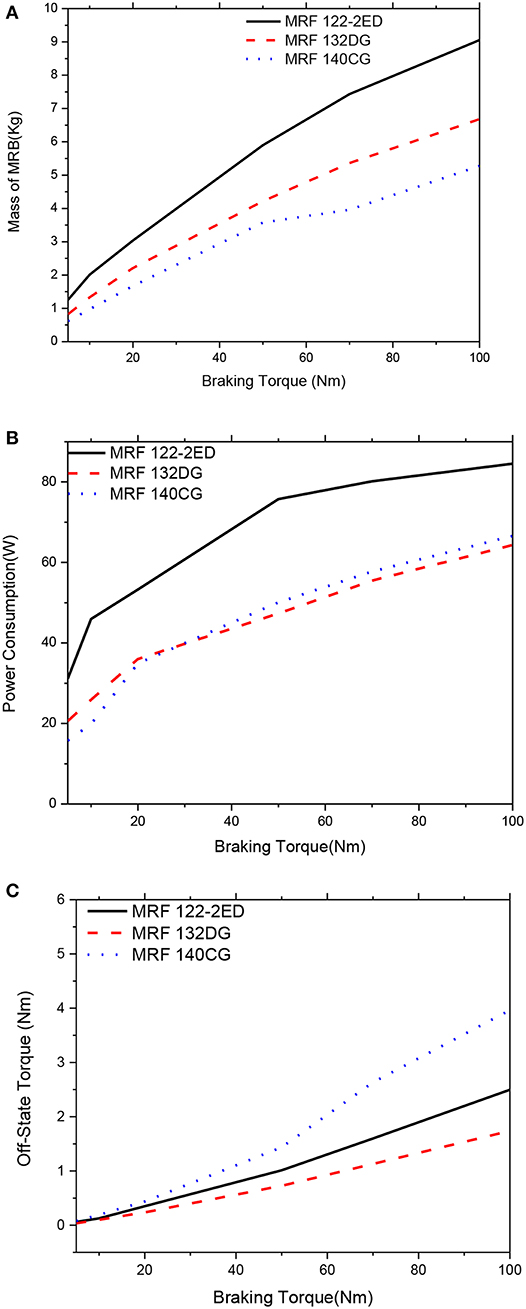
Figure 17. Multi-objective optimization results of the MRBs as a function of braking torque of side-coil MRB, α_m = 0.5; α_P = 0.0; α_To = 0.5. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

Figures 18, 19 show optimal solutions of the MRBs, when the weighting coefficients of the objective function in Equation (12) are chosen at α_m = 0.75, α_P = 0.0 (power consumption is not considered) and α_To = 0.25. By comparing with Figures 16, 17 it is observed that the mass of the MRBs is a bit smaller in this case while the off-state torque is a bit higher. However, the power consumption is much smaller than the previous case. Therefore, if the optimization considers only mass and off-state torque, it is recommended that the weighting coefficients should be set by α_m = 0.75, α_P = 0.0, and α_To = 0.25 rather than α_m = 0.5, α_P = 0.0, and α_To = 0.5. The gap size of MRBs at the optimum is also equal to its lower limit.

FIGURE 18

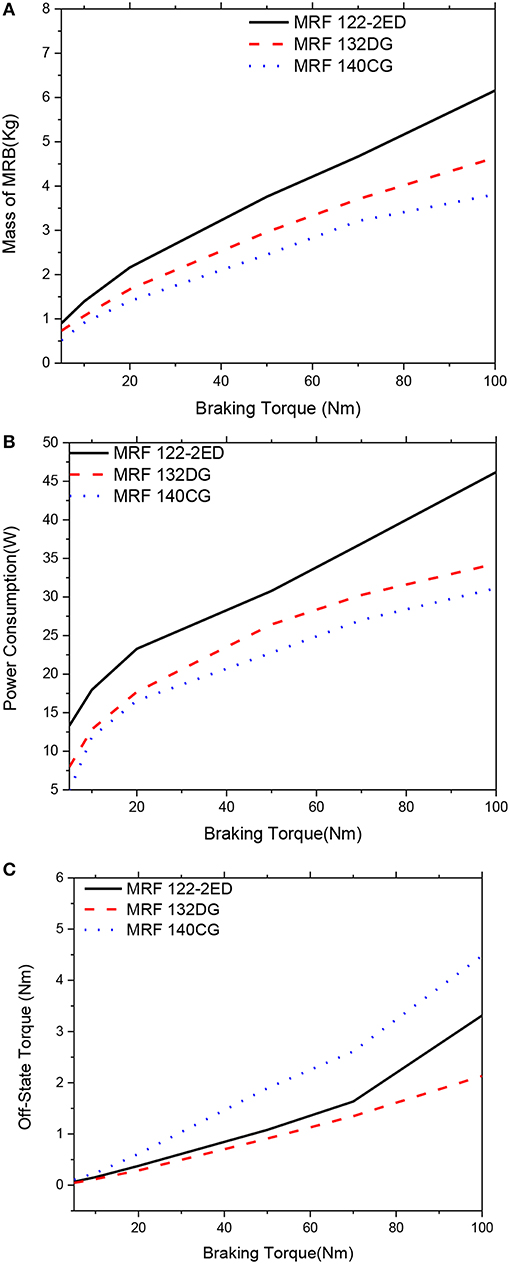
Figure 18. Multi-objective optimization results of the MRBs as a function of braking torque of conventional MRB, α_m = 0.75; α_P = 0.0; α_To = 0.25. (A) Mass as a function of braking torque, (B) Power consumption as a function of braking torque, (C) Off-state torque as a function of braking torque.

FIGURE 19

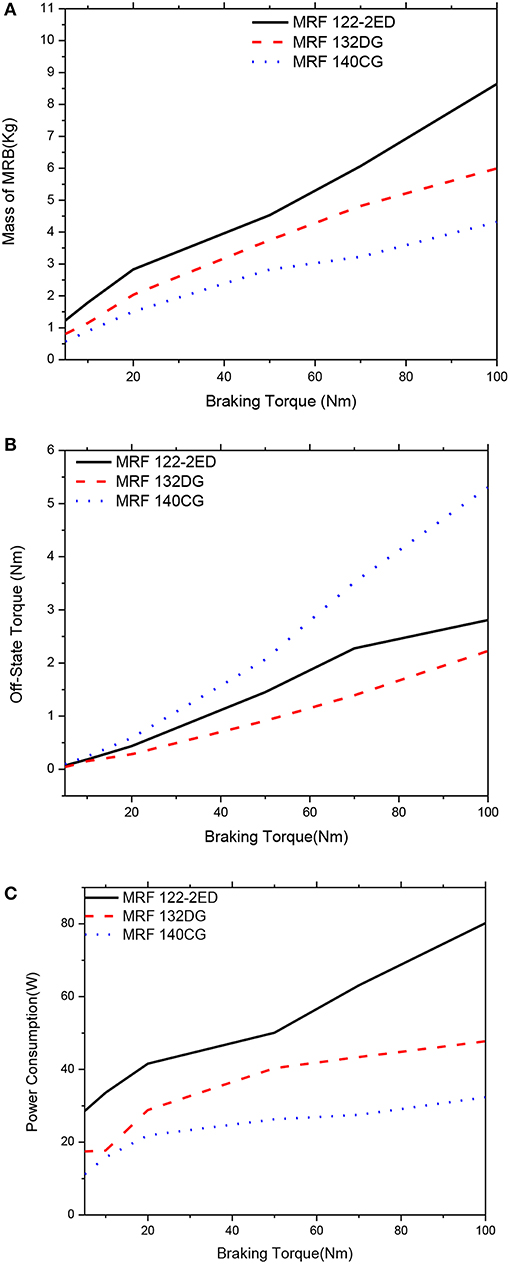
Figure 19. Multi-objective optimization results of the MRBs as a function of braking torque of side-coil MRB, α_m = 0.75; α_P = 0.0; α_To = 0.25. (A) Mass as a function of braking torque, (B) Off-state torque as a function of braking torque, (C) Power consumption as a function of braking torque.

From all of the above, it can be summarized as the following:

- An objective function which is a linear combination of the mass, the power consumption and the off-state torque can be used for multi-objective optimization of MRBs. By assigning different values of weighting coefficients in the objective function, different optimal solutions can be archived. To get the most compromised of the three objective performances, a real multiobjective algorithm to get Pareto front solution should be implemented.

- In the optimization, it is not necessary to consider the gap size of the MRF as a design variable. In most cases, the gap size of MRF should be selected to be as small as possible considering manufacturing convenience.

- At the optimum, the MRBs employing the highest yield stress MRF (MRF-140CG) always have the smallest mass and power consumption, however, the off-state torque is significantly larger than the others. Therefore, in case the off-state torque is not important for the brake, highest yield stress MRF (MRF-140CG) is recommended for MRB application.

- At the optimum, the MRBs employing the lowest yield stress MRF (MRF-122-2ED) have the largest mass and power consumption, while the off-state torque is larger than that in case of medium yield stress MRF (MRF132-DG). Therefore, lowest yield stress MRF (MRF-122-2ED) is not recommended for MRB application

- At the optimum, the MRBs employing the medium yield stress MRF (MRF-132DG) have the compromised performance when the off-state torque is considered in the objective function. Therefore, in most cases, the medium yield stress MRF (MRF-132DG) is the recommended MRB application.

Conclusions

In this research work, a multi-objective function considering mass, power consumption and off-state torque was proposed for the optimal design of MRBs. Based on the proposed optimization, material characterization of MRFs on the performance of the MRBs were investigated. Three different types of popular commercial MRFs: MRF-122-2ED (low yield stress), MRF-132-DG (medium yield stress) and MRF-140CG (high yield stress) and two typical disc type MRBs: the conventional and the side-coil MRB were considered. The simulation results show that, at the optimum, the MRBs employing MRF-140CG always have the smallest mass and power consumption, however, the off-state torque is significantly larger than the others. Therefore, in case the off-state torque is not important for the brake, MRF-140CG is recommended for MRB application. It is also found that performance of the MRBs employing MRF-122-2ED was always worse than the MRF132-DG. Therefore, the lowest yield stress MRF (MRF-122-2ED) is not recommended for MRB application. Among the three considered MRFs, MRF-132DG had the best compromised performance. Especially, in the case of α_m = 0.5; α_P = 0.0; α_To = 0.5. Therefore, in the design of MRBs that need to compromise different conflict benefit performance characteristics, MRF-132DG is the recommended MRB application. Finally, it is found that, in the optimization, it is not necessary to consider the gap size of the MRF as a design variable. In most cases, the gap size of MRF should be selected as small as possible considering manufacturing convenience.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 107.01-2016.32.

References

An, J., and Kwon, D.-S. (2003). Modeling of a magnetorheological actuator including magnetic hysteresis. J. Intellig. Mater. Syst. Struct. 14, 541–550. doi: 10.1177/104538903036506

CrossRef Full Text | Google Scholar

Avraam, M., Horodinca, M., Letier, P., and Preumont, A. (2008). “Portable smart wrist rehabilitation device driven by rotational MR-fluid Brake actuator for telemedecine applications,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, (Nice).

Google Scholar

Avraam, M., Horodinca, M., Romanescu, I., and Preumont, A. (2010). Computer controlled rotational MR-brake for wrist rehabilitation device. J. Intellig. Mater. Syst. Struct. 21, 1–15. doi: 10.1177/1045389X10362274

CrossRef Full Text | Google Scholar

Huang, J., Zhang, J. Q., Yang, Y., and Wei, Y. Q. (2002). Analysis and design of a cylindrical magneto-rheological fluid brake. J. Mater. Proc. Technol. 129, 559–562. doi: 10.1016/S0924-0136(02)00634-9

CrossRef Full Text | Google Scholar

Imaduddin, F., Mazlan, S. A., and Zamzuri, H. (2013). A design and modeling review of rotary magnetorheological damper. Mater. Design. 51, 575–591 doi: 10.1016/j.matdes.2013.04.042

CrossRef Full Text | Google Scholar

Liu, B., Li, W. H., Kosasih, P. B., and Zhang, X. Z. (2006). Development of an MR-brake-based haptic device. Smart Mater. Struct. 15, 1960–1966. doi: 10.1088/0964-1726/15/6/052

CrossRef Full Text | Google Scholar

Mousavi, S. H., and Sayyaadi, H. (2018). Optimization and testing of a new prototype hybrid MR brake with arc form surface as a prosthetic knee. IEEE ASME Trans. Mechatron. 23, 1204–1214. doi: 10.1109/TMECH.2018.2820065

CrossRef Full Text | Google Scholar

Nguyen, Q. H., and Choi, S. B. (2010). Optimal design of an automotive magnetorheological brake considering geometric dimensions and zero-field friction heat. Smart Mater. Struct. 19:115024. doi: 10.1088/0964-1726/19/11/115024

CrossRef Full Text | Google Scholar

Nguyen, Q. H., and Choi, S. B. (2011). Selection of magnetorheological brake types via optimal design considering maximum torque and constrained volume. Smart Mater. Struct. 21:15012. doi: 10.1088/0964-1726/21/1/015012

CrossRef Full Text | Google Scholar

Nguyen, Q. H., and Choi, S. B. (2012). Optimal design of a novel hybrid MR brake for motorcycles considering axial and radial magnetic flux. Smart Mater. Struct. 21:55003. doi: 10.1088/0964-1726/21/5/055003

CrossRef Full Text | Google Scholar

Nguyen, Q. H., Han, Y. M., Choi, S. B., and Wereley N. M. (2007). Geometry optimization of MR valves constrained in a specific volume using the finite element method. Smart Mater. Struct. 16, 2242–2252. doi: 10.1088/0964-1726/16/6/027

CrossRef Full Text | Google Scholar

Nguyen, Q. H., Lang, V. T., Nguyen, N. D., and Choi, S. B. (2014a). Geometric optimal design of a magneto-rheological brake considering different shapes for the brake envelope. Smart Mater. Struct. 23:15020. doi: 10.1088/0964-1726/23/1/015020

CrossRef Full Text | Google Scholar

Nguyen, Q. H., Nguyen, N. D., and Choi, S. B. (2014b). “Design and evaluation of a novel configuration of MR brake with coils placed on the side housings,” in Proceedings of the SPIE. doi: 10.1117/12.2044561

CrossRef Full Text | Google Scholar

Nguyen, Q. H., Nguyen, N. D., and Choi, S. –B. (2015). Design and evaluation of a novel MR brake with coils placed on side housings. Smart Mater. Struct. 24:90590I. doi: 10.1088/0964-1726/24/4/047001

CrossRef Full Text | Google Scholar

Park, E. J., Stoikov, D., Falcao da Luz, L., and Suleman A. (2006). A performance evaluation of an automotive magnetorheological brake design with a sliding mode controller. Mechatronics 16, 405–416. doi: 10.1016/j.mechatronics.2006.03.004

CrossRef Full Text | Google Scholar

Smith, A. L., Ulicny, J. C., and Kennedy, L. C. (2007). Magnetorheological fluid fan drive for trucks. J. Intellig. Mater. Syst. Struct. 18, 1131–1136. doi: 10.1177/1045389X07083136

CrossRef Full Text | Google Scholar

Zubieta, M., Eceolaza, S., Elejabarrieta, M. J., and Bou-Ali, M. M. (2009). Magnetorheological fluids: characterization and modeling of magnetization. Smart Mater. Struct. 18:95019. doi: 10.1088/0964-1726/18/9/095019

CrossRef Full Text | Google Scholar