- Department of Physics, Creighton University, Omaha, NE, United States
Glass fragility is a byproduct of early attempts to apply law of corresponding states scaling to the temperature dependent thickening of glass forming liquids. Efforts to plot the logarithm of the viscosity vs. inverse temperature scaled to the glass transition point (Tg) fail to collapse data to a common, universal curve but instead display an informative pattern: at one extreme, many “strong” oxide glasses exhibit a single Arrhenius dependence, and at the other extreme, many “fragile” molecular liquids display a highly non-Arrhenius pattern in which the viscosity increases far more rapidly just in advance of Tg. In this regard, network-forming glasses composed of 3D networks of covalently bonded atoms are of interest as they undergo systematic changes in both Tg and fragility depending on the topology of the network and display variations of the fragility index spanning from strong (m ≈ 17) to fragile (m ≈ 90) depending on the level of network connectivity. Here we review the merits of a special, coarse-grained definition for the topological connectivity of network-forming glasses that differs from conventional constraint-counting approaches but which allows the fragility of over 150 different network-forming glasses (both oxides and chalcogenides) to be collapsed onto a single function of the average network connectivity. We also speculate on what role this coarse-grained connectivity might play in determining the glass transition temperature.
Introduction
Through the ages, glass manufacturing has profited from an appreciation for the delicate balance between glass composition and properties. Ease of glass formation from the melt is closely tied to the working “length” of the glass composition; essentially a measure of how gradually the viscosity of the melt changes with changes in temperature just above the glass transition point. A “long” glass suffers only minor changes in viscosity and so can be manipulated for a longer period of time before needing to be reheated. Early glass research naturally focused on how glass chemistry might function to control the viscosity of the melt across a wide variety of glass compositions. Although similar efforts predated it (Oldekop, 1957; Laughlin and Uhlmann, 1972; Nemilov, 2007), it was a seminal paper by Austen Angell (1984) that really emphasized the deep pattern to how chemical structure of both traditional oxide glasses and simple glass-forming liquids might dictate viscous dynamics in the melt. His now famous plot (Angell, 1984, 1991), reproduced here as Figure 1, is in many ways reminiscent of an attempt to apply the “law of corresponding states” (Stanley, 1971) to the viscosity of glass-forming melts by scaling the data to the glass transition temperature, Tg, defined as that temperature where the viscosity reaches 1012 Pas. However, unlike the law of corresponding states that governs the liquid-vapor transition near the critical point (Stanley, 1971), the viscosity of these glass-forming materials fail to collapse to a single universal scaling curve in this scaled representation. Instead, one finds a pattern that is largely bimodal and for which Angell categorized (Angell, 1991) as either “strong” or “fragile” on the basis of whether the viscosity is highly Arrhenius or highly non-Arrhenius, respectively. Oxide glasses, like SiO2, are highly Arrhenius over their entire temperature range. These strong glass-formers are composed of a network of relatively strong covalent bonds and typically require refractory-level temperatures to produce a melt. At the opposite extreme are several fragile glass-forming liquids that are held together by weaker, non-directional, van der Waals forces which often exhibit a Tg well below ambient room temperature. Alongside this pattern of non-Arrhenius viscosity, Angell (1991) drew attention to an important correlation of the fragility with the magnitude of the change in specific heat that occurs upon crossing the glass transition point (see inset to Figure 1). In thermodynamics this specific heat is the (logarithmic) slope of the entropy with temperature and many have speculated (Adam and Gibbs, 1965; Debenedetti and Stillinger, 2001; Sidebottom, 2015) that the increase in viscosity with cooling is closely associated with how rapidly the entropy of the liquid decreases.
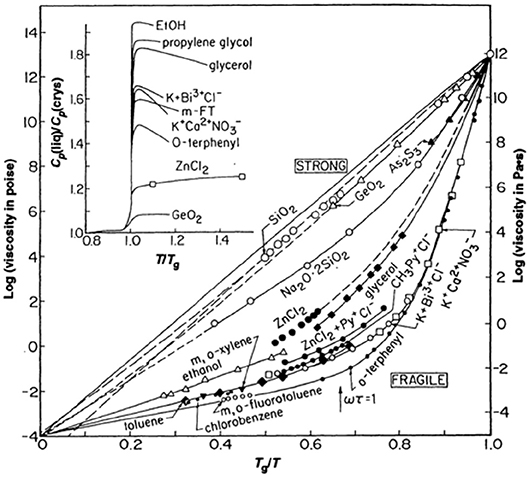
Figure 1. Fragility plot as originally published (Angell, 1984). The viscosity of a variety of glass-forming melts is plotted against inverse temperature scaled to the glass transition temperature where the viscosity equals 1012 Pa s. Inset illustrates the jump in specific heat of selected melts which is partly correlated to the degree of fragility from (Angell, 1991) with permission.
As can be seen from closer inspection of Figure 1, the pattern is not exactly bimodal but rather includes a number of intermediates such as ZnCl2 and sodium disilicate whose fragilities lie in between the extremes. The fragility index defined by the “steepness” of the limiting slope of the data in Figure 1 as:
has often been employed to characterize the specific level of fragility for any given glass-forming material and data in Figure 1, for example, range in fragility index from roughly m = 18 to m ≈ 85. With the exception of B2O3 whose fragility is intermediate (m ≈ 32), all of the other traditional network forming oxides (e.g., SiO2, GeO2, P2O5, As2O3) predicted by Zachariasen (1932) to form amorphous states have very low fragilities ranging from m = 17 to 20 which boarder on the strong limit in Angell's classification. Unlike the van der Waals liquids, these oxide glasses are constructed of highly directional covalent bonds with strict chemical rules regarding the number of bonds per atom (Zachariasen, 1932). As such, they are often modeled as a network of “balls” (the atoms) connected by “sticks” (the discrete bonds) for which simple topological analyses are applied (Phillips, 1979; He and Thorpe, 1985). For example, in SiO2 the rule is that every Si atom is connected by sticks to four oxygen atoms and every oxygen atom is connected by sticks to 2 Si atoms.
An important measure of this network topology would be the average number of bonds per atom, 〈r〉. In the case of SiO2 where one-third of the atoms are Si (with r = 4 bonds each) and two-thirds are O (with r = 2 bonds each), the bond density would be . In many topological theories (Phillips, 1979; He and Thorpe, 1985), 〈r〉 is a mean field parameter that represents a measure of how rigid the network is against applied stresses. Simple constraint-counting arguments indicate that networks with 〈r〉 = 2.4 have a number of atomic constraints equal to the degrees of freedom and that this specific bond density marks a separation between networks (with 〈r〉 < 2.4) that are “floppy” and networks (with 〈r〉 > 2.4) that are “rigid.”
While this atomic-weighted bond density appears frequently in many topological studies of glass forming materials, including many concerning the mechanical properties of network-forming chalcogenide glasses (Halfpap and Lindsay, 1986; Tatsumisago et al., 1990), we propose that the viscosity of network-forming oxide glasses is better described using an alternative metric of network connectivity. Unlike the chalcogenides which generally permit homo-polar bonding, oxide networks have strict chemical rules against such bonding. These additional rules result in a well-defined short-range order (SRO) in oxide glasses for which the structure is better viewed as one of polyhedra “hinged” to neighboring polyhedra through bridging oxygen vertices. For example, in SiO2 the structure is most commonly viewed as one of SiO4 tetrahedra that are connected by bridging oxygen (BO) bonds to form a continuous random network. Under low frequency stress relevant to viscous flow, deformation of the bulk network is chiefly achieved by bending and bond-breaking near these vertices as opposed to any substantial internal deformation of the SiO4 tetrahedron. Thus, in regards to viscous flow the network is better characterized by a coarse-grained connectivity, such as the average BOs per polyhedron, 〈n〉, that better incorporates these (and other) rigid structural units (RSUs) as autonomous elements within the network.
In a series of previous publications (Sidebottom and Schnell, 2013; Sidebottom et al., 2014; Sidebottom, 2015, 2019) we have investigated the potential ties between fragility of an oxide glass and its network connectivity. Our investigations have included alkali-modified phosphates, borates, germanates and, most recently, silicates and each study not only built upon but also refined and sometimes corrected the one previous. With the benefit of hindsight, we are now in a position to paint more broadly with a single, seamless brushstroke the picture of how the fragility of all network-forming glasses might be described solely by an appropriately coarse-grained network connectivity. In this paper we review these studies using a single consistent nomenclature for discussing how coarse-graining is to be performed. In addition, we close by offering some speculation as to the influence coarse-grained connectivity may have on the glass transition temperature itself.
Discussion
Alkali Phosphate Melts
Our story begins with efforts to measure the fragility of phosphorous pentoxide, P2O5, using dynamic light scattering techniques (Sidebottom and Changstrom, 2008). Although P2O5 is among the list of oxides likely to form a glass (Zachariasen, 1932), its extreme hygroscopic nature has rendered it largely useless for any practical application (Zarzycki, 1991). The structure of P2O5 consists of PO4 tetrahedra that are interlinked by only n = 3 bridging oxygen bonds to neighboring tetrahedra; one oxygen on the tetrahedron is double bonded and so is non-bridging (Brow, 2000). Like SiO2, the addition of alkali oxides results in the formation of non-bridging oxygens (Zarzycki, 1991) that depolymerize the network until the metaphosphate (50 mol% alkali oxide) composition is reached where all tetrahedra have n = 2 bridging oxygen. Here, the oxide structure of the metaphosphate can be characterized as one of polymeric [PO3]n chains. The average BO connectivity per PO4 unit can thus be determined (Brow, 2000) from the mole fraction of alkali oxide, x, as:
where the fractions of PO4 with n = 2 BOs increases as f2 = x/(1 − x) while those with n = 3 BOs decrease as f3 = (1 − 2x)/(1 − x).
In the dynamic light scattering study (Sidebottom and Changstrom, 2008) of P2O5, great care was exercised in eliminating the presence of unwanted water. Samples of P2O5 were sublimed under vacuum into an ampoule that could be flame sealed while still under vacuum and then used in situ to carry out photon correlation spectroscopy (PCS) of the viscous relaxation present in the melt above Tg. In this instance, PCS records the dynamic structure factor of the molten liquid to produce a view of the intrinsic structural relaxation occurring near the glass transition point. It provides a measure of the structural relaxation time which itself is proportional to the viscosity and which reaches values of roughly 100 s at Tg. The proportionality factor is the shear modulus which varies only slightly over the range of temperatures probed by PCS. This correspondence can be exploited to generate a plot of relaxation times as a function of inverse scaled temperature like that shown in Figure 2 that mirrors the Angell plot (Figure 1) and which provides an equivalent measure of the fragility index based on the corresponding steepness of the relaxation time.
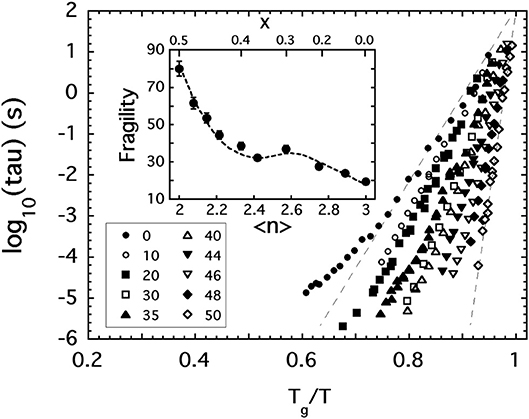
Figure 2. The structural relaxation time (tau) of various [Na2O]x[P2O5]1−x glass melts plotted against inverse temperature scaled to the glass transition temperature where tau = 100 s. Key shows values of x expressed as a mole % of Na2O. Inset shows how the fragility index of these melts depends on 〈n〉, the average BO per phosphate unit.
In addition to P2O5, Figure 2 includes the results of PCS measurements (Fabian and Sidebottom, 2009) conducted on a selection of sodium-modified phosphate melts, [Na2O]x[P2O5]1−x, spanning from x = 0 to the metaphosphate composition (x = 0.5). The variation of the fragility index, shown in the inset to Figure 2, increases with increasing depolymerization of the oxide network in a reasonably monotonic fashion and encompasses the two extremes of fragility (m = 20 to m ≈ 85) seen in Figure 1. Moreover, the variation with 〈n〉 shown in the inset again highlights the potential significance of the 〈n〉 = 2.4 rigidity threshold: this value is near the center of a fragility plateau (where m ≈ 35 ± 5) spanning from 〈n〉 ≈ 2.2 (below which the network is “floppy” and the fragility increases rapidly) and 〈n〉 ≈ 2.7 (beyond which glass melts are highly overconstrained and become less fragile).
The variation of the glass transition temperature over this same range of sodium phosphate glasses is presented in Figure 3 and shows a rapid decrease with the initial addition of alkali oxide followed at higher concentrations by a more gradual increase on approach to the metaphosphate. Moreover, the glass transition temperature of the metaphosphate depends on the specific alkali species and some (Eisenberg et al., 1966) have suggested it may be correlated to the ionic strength (charge per radius) of the alkali ion as shown in the inset to Figure 3. A satisfying interpretation for the anomalous minimum in Tg has been offered by Hoppe (Brow, 2000; Hoppe et al., 2000) on the basis of how the coordination requirements of the alkali ion are satisfied in different ways at low and high concentrations. Below about 20 mol%, alkali ions are able to satisfy their oxygen coordination in isolated regions within the 3d network but above 20 mol% they must share non-bridging oxygen between multiple phosphate tetrahedra to satisfy the coordination. The result is analogous to a frozen “lake” in which a great many “holes” are punched. At low concentrations the ions sit in isolated holes and their ionic bonds to the non-bridging oxygen of the oxide network surrounding the hole are ineffective in strengthening the overall structure. But, at higher concentrations the holes begin to percolate such that the structure develops into a great many separated rigid regions for which the ionic bonding by the alkali ion is now helpful in strengthening the overall network.
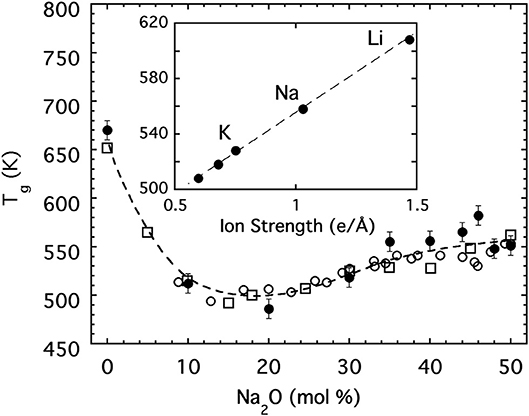
Figure 3. The glass transition temperature for [Na2O]x[P2O5]1−x glasses. Closed circles are values obtained from dynamic light scattering. Open symbols are literature values [(Eisenberg et al., 1966) (circles); (Hudgens et al., 1998) (squares)]. Dashed line is a guide for the eyes. The inset shows the glass transition temperature for metaphosphate glasses (x = 0.5) as a function of the ion strength.
At this junction it is worth stressing again that fragility and glass transition temperature are generally disconnected quantities. This is clearly the case for the alkali phosphates where the compositions (0.4 < x < 0.5) for which the greatest changes in fragility occur are those at which almost no change in glass transition temperature is occurring and, reversely, those compositions (0 < x < 0.2) were Tg is changing most dramatically are those for which the fragility is changing the least. This disconnect is not unexpected but is consistent with the law of corresponding states perspective raised earlier: there is no a priori reason for the scaled slope of the viscosity [Equation (1)] to be directly related to the temperature used in the scaling.
Chalcogenides
Chalcogenide glasses based, for example, on the crosslinking of Se or S chains (r = 2) by either Ge (r = 4) or As (r = 3) share a change in topology from 2d chains to 3d networks similar with that in the alkali phosphate discussed above (He and Thorpe, 1985; Tatsumisago et al., 1990; Böhmer and Angell, 1992). There too, the glass transition temperature decreases with decreasing connectivity (〈r〉) but, owing to the absence of any modifier ions or non-bridging oxygens, the decrease is largely monotonic unlike that of the phosphates. Remarkably, the fragility of these two systems is also very similar. This similarity is shown in Figure 4 where data for the sodium phosphate study plotted as a function of 〈n〉 are included with the fragility of a series of Se1−2xAsxGex melts (Tatsumisago et al., 1990; Böhmer and Angell, 1992) plotted as a function of 〈r 〉.
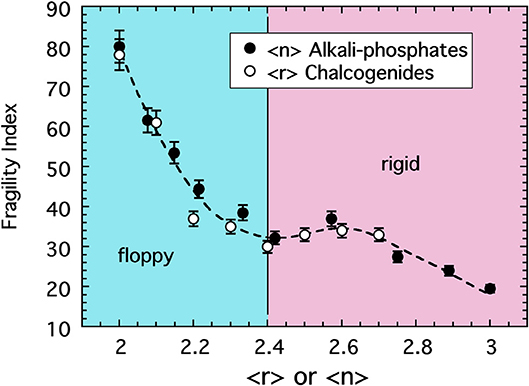
Figure 4. The fragility index of alkali phosphate melts (closed circles) plotted as a function of the average number of bridging oxygen per PO4 tetrahedra alongside the fragility index of chalcogenide melts (Tatsumisago et al., 1990) plotted as a function of the average bond per atom. The value of 〈r〉 = 2.4 marks the rigidity transition separating under-constrained floppy networks from over-constrained rigid ones.
The coincidence of these two data sets draws us again back to the notion of a law of corresponding states where hidden universalities often emerge when data are appropriately scaled. In determining the fragility, data were scaled by a glass transition temperature that is largely disconnected with the fragility itself. Akin to way the critical point temperature in a liquid-vapor phase transition is set largely by the interaction energy and so differs among different non-ideal gases, the glass transition temperature is an energy scale that differs among different glass compositions. But we see in Figure 4 the possibility that some additional scaling of the mean field connectivity of the network might expose a common pattern in the fragility of network-forming glasses. Only when the connectivity of the oxide network is defined through a coarse-graining over the RSUs of which it is constructed [i.e., 〈n〉] does this hidden universality seem appear. Fragility is a measure of viscous flow of the melt and this flow takes place through collective deformations under shear stress (in a zero-frequency limit). In the oxides, the persistence of SRO forces deformations and bond breaking to take place at the weakest linkages and this effectively renormalizes the network to one of rigid polyhedra hinged at vertices for which 〈n〉 becomes the more relevant mean field measure of connectivity.
Other Oxides
The fundamental problem with our idea that 〈n〉 is the relevant metric of connectivity for oxide networks is that it fails to produce a universal pattern for all the other major oxide glasses! This is evident in Figure 5 where the fragility of various commercially-relevant glass forming oxides including borates (Nemilov, 1966; Chryssikos et al., 1994), germanates (Nemilov, 1970; Shelby, 1974), and silicates (Poole, 1949) are plotted together as a function of 〈n〉 the average bridging oxygen connectivity per network-forming cation (i.e., Si, B, Ge, P, and As). In the case of alkali silicates, the fragility behaves like that of the phosphate melts in that it increases with the depolymerization of the network as alkali oxide is introduced. The data shown extend from SiO2 to the sodium disilicate composition, Na2O:2SiO2, where ~80% of the SiO4 tetrahedra possess n = 3 bridging bonds while 10% each have n = 4 or n = 2, respectively (Maekawa et al., 1991).
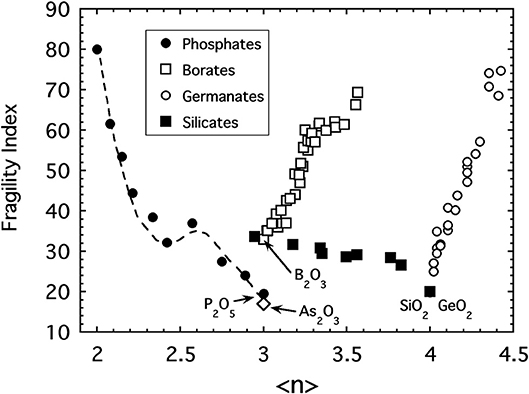
Figure 5. A compilation of fragility indices of various alkali oxide glasses including sodium phosphates (Fabian and Sidebottom, 2009), lithium and sodium borates (Nemilov, 1966; Chryssikos et al., 1994) sodium, potassium and rubidium germanates (Nemilov, 1970; Shelby, 1974), sodium and potassium silicates (Poole, 1949) and arsenic trioxide (Yannopoulos et al., 1999; Sidebottom et al., 2007) as a function of the average bridging oxygen per network-forming cation.
Sharply at odds with the silicate and phosphate glasses, the fragility of both the alkali borate and alkali germanate glasses display an unanticipated increase with increasing network connectivity. They appear to become “floppier” despite the addition of more constraints. In both of these systems, the initial addition of alkali oxide does not produce non-bridging oxygens leading to depolymerization but rather produce increased network polymerization via the formation of polyhedra with higher coordination numbers. In the borate system (Griscom, 1978), trigonal BO3 units in B2O3 are transformed to 4-coordinated, BO4 tetrahedra when alkali oxide is added (up to about 30 mol%). Similarly, in the germanate system (Henderson and Fleet, 1991) 4-coordinated GeO4 units are converted to 5-coordinated units as alkali oxide is added (up to about 20 mol%). Only at higher alkali concentrations do substantial numbers of non-bridging oxygens form in either system. The initial increase of network connectivity followed by a decrease causes a number of glass properties to display “anomalous” behavior (Henderson, 2007) with either a maximum or minimum occurring near 30 and 20 mol%, respectively. A prime example is the glass transition temperature (discussed later) which exhibits a maximum.
In the following section, we examine each of these other oxide glass systems to demonstrate how additional RSUs that appear in these materials beyond that of the short-range order alone can influence the mean field connectivity. Coarse-graining must be extended for these materials to include intermediate range order (IRO) structures when present and we emphasize how a consistent coarse-graining procedure places the fragility of these and other network-forming glasses onto a common master curve as a function of a generalized network connectivity.
Alkali Borates
In comparison with all the other primary oxide glasses whose fragility indices range between m ≈ 17 and 20, boron trioxide (B2O3) has an anomalously high value (m ≈ 32). Oddly, the fragility of B2O3 is far greater than that of arsenic trioxide, an otherwise chemically identical material that likewise favors trigonal (AsO3) units in its network structure (Galeener et al., 1979) and this suggests that something in B2O3 is structurally amiss. Owing in part to the superb NMR properties of the 11B nucleus, the literature (Krogh-Moe, 1962; Griscom, 1978; Youngman and Zwanziger, 1996) has developed an unparalleled understanding of the structure of boron trioxide and its alkali-modified variations that is summarized in Figure 6 for potassium borate glasses (Youngman and Zwanziger, 1996). It is now well established that roughly two-thirds of the trigonal BO3 units in B2O3 join together into larger-scaled RSUs known as “boroxol rings.” These small, 3-membered ring structures exhibit a very sharp Raman band associated with the breathing mode of the ring (Galeener et al., 1978; Walrafen et al., 1980) and this identifies the ring itself as a separate, autonomous rigid structure within the network likely to resist internal deformations under viscous flow. In addition to rings, both diborate and tetraborate structures are also observed (Krogh-Moe, 1962) and the distributions of these RSUs exhibit a complex variation with alkali concentration (see Figure 6).
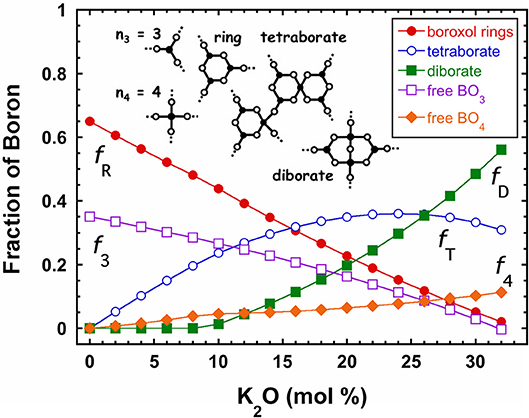
Figure 6. The fraction of boron atoms in various structural units in potassium borate glasses. Values are derived from an NMR investigation (Youngman and Zwanziger, 1996) and include five basic configurations illustrated as cartoons in the figure. These include free boron units of either 3 or 4 coordination as well as boroxol rings, diborate, and tetraborate structures discussed in the text.
In order to coarse-grain the connectivity, an accounting scheme is needed that can be faithfully applied whereby the connections in the network are properly enumerated on the same per network forming cation basis but with an accommodation made for the presence of these larger, IRO structures. The central ingredient is recognizing how the topological connectivity of a trigonal unit that participates in a ring (or other unit) is generally reduced when compared with a unit that is “free” of such IRO structures. In the case of the boroxol ring for example, the n = 3 connectivity of a trigonal unit is reduced to n = 2 since each such trigonal unit functions only to connect the external network to the ring itself. In other words, each trigonal unit employs two BO bonds to connect itself to the ring of which one is topologically redundant. Using this accounting scheme for B2O3 in which only fR = 65% of the trigonal units are in rings while the remaining fF = 35% are free, we obtain an adjusted connectivity 〈nIRO〉 = 0.65 × 2+0.35 × 3 = 2.35, that is reduced in comparison to the BO-only connectivity (〈n〉) and which relocates the fragility index of B2O3 onto the fragility pattern highlighted in Figure 4.
In the alkali-modified borates, addition of alkali oxide drives the production of 4-coordinated boron tetrahedra which, as seen in Figure 6, almost exclusively participate in either diborate or tetraborate structures illustrated in that figure. Using the same accounting scheme, we conclude that each of the borate units in a diborate structure (two BO3 units and two BO4 units) have a reduced connectivity of n = 2, while in a tetraborate structure, six of the eight borate units located on the periphery of the structure have connectivity of n = 2, while the other two units that are internal provide no connectivity with the external network (n = 0). Thus, the average connectivity of boron in a tetraborate structure is and we arrive at a formula for the coarse-grained connectivity in alkali borates:
where f4 is the fraction of free 4-coordinated boron, f3 the fraction of free 3-coordinated boron, fR the fraction of boron in boroxol rings, fD the fraction of boron in diborate units, and fT the fraction of boron in tetraborate units. Since these fractions are taken directly from the NMR results (Youngman and Zwanziger, 1996) of Figure 6, the coarse-graining formula in Equation (3) contains no adjustable parameters and is seen in Figure 7 to reposition the fragility indices of all the alkali borates coincident with fragility pattern of both the chalcogenide and alkali phosphate glass melts discussed earlier. As seen in the inset, this happens because the coarse-grained connectivity of the network actually decreases from a value near 2.35 for B2O3 to values near 2.05 for glasses with 33 mol% despite the increasing density of bridging oxygen. This decrease is a consequence of formation of diborate and tetraborate structures that promote a lowering of the effective network connectivity.
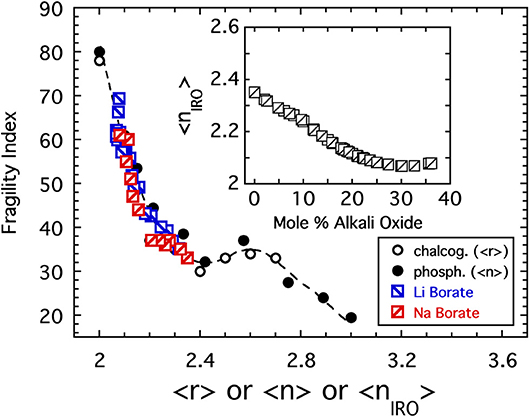
Figure 7. The fragility index of lithium and sodium borate glasses (Nemilov, 1966; Chryssikos et al., 1994) is plotted as a function of the connectivity coarse-grained to include IRO structures. Also shown are the data from Figure 4 for both the chalcogenides (plotted as a function of the average bond per atom) and the alkali phosphates (plotted as a function of the average BO per phosphate). The inset shows how the coarse-grained connectivity of the borates decreases with increasing alkali oxide addition.
Alkali Germanates
Given the success in relocating the fragility index of alkali borates, we might anticipate that RSUs are also present in alkali germanates and similarly decrease the coarse-grained network connectivity despite the increasing formation of BO bonds. Here, evidence for such structures is gleaned from Raman spectroscopy (Henderson and Fleet, 1991) in which one of two vibrational modes in the range between 350 and 650 cm−1 has been interpreted as being caused by 3-membered rings. The Raman spectra obtained by Henderson for sodium germanate glasses with compositions <20 mol% Na2O are shown in the inset to Figure 8 where one observes a progressive growth in the 520 cm−1 ring mode at the expense of the non-ring mode at lower energy. Unlike NMR, the extraction of quantitative populations of RSUs from Raman bandshapes is less accurate. Nevertheless, using data provided by Henderson, we have performed an analysis of the integrated area beneath these two modes to generate an estimate of the fraction, fR, of rings. The result is plotted in Figure 8 and indicates a rapid increase in rings from a starting value near 40 (±10)%; a value which is also supported by estimates taken from a molecular dynamics simulation (Giacomazzi et al., 2005) of GeO2.
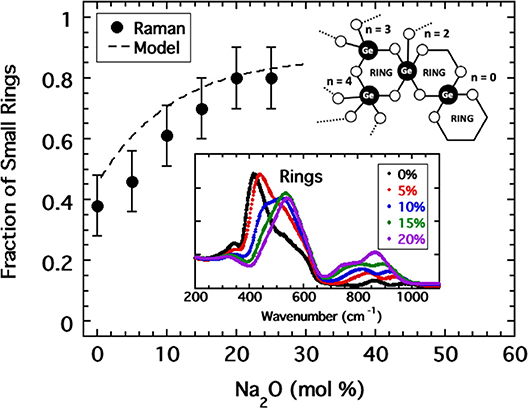
Figure 8. A curve fitting analysis of the low energy Raman band (shown as inset) of sodium germanate glasses (Henderson and Fleet, 1991) provided an estimate of the fraction of this band which is associated with 3-membered rings plotted as solid circles. The dashed line is the corresponding fraction of rings modeled as a continuous function of sodium oxide content by Equation (5) for which parameters were adjusted to best produce a collapse of fragility indices in Figure 9. Inset includes a cartoon illustration of various possible RSUs that occur as a consequence of 3-membered rings.
Given that a large fraction of rings might be present in these alkali-germanate glasses, coarse-graining efforts need to account for all the potential configurations that might appear in any substantial amounts. In addition to dividing the Ge units up by their coordination states where the fraction of four-coordinated units, f4 = (1−3x)/(1−x), and the fraction of five-coordinated units, f5 = 2x/(1−x), are established by requirements for charge neutrality, we also must divide these units with regards to the probability that a given unit will be participating in one or more ring structures. An added complication not seen in the case of boroxol rings is the possibility for a GeO4 (or GeO5) unit to participate in two rings simultaneously forming a “double ring” structure. Including this new possibility, one finds six possible configurations whose corresponding connectivities are summarized in Table 1.

Table 1. Coarse-grained connectivity of six possible RSUs found in alkali germanate glasses as discussed in the text.
If fR is again defined as the fraction of Ge participating in 3-membered rings, then, regardless of coordination state, a fraction (1 − fR) of the Ge will be “free” in the sense that they do not participate in any ring structure. Such a free Ge will have a connectivity of n = 4 if 4-coordinated and n = 5 if 5-coordinated, respectively. Likewise, a fraction fR(1 − fR) of the Ge will participate in a single ring but not in two rings simultaneously. In accord with the rules established for boroxol rings, each such Ge will suffer a reduction in connectivity owing to a single redundant BO bond. Finally, some Ge will be found that participte in two rings simultaneously with the joint probability . When a GeO5 unit participates in two rings simultaneously it functions topologically as n = 2 since three of the four BOs being contributed to the rings are redundant. However, when a GeO4 unit participates in two rings simultaneously it functions analogously to the BO4 unit in the interior of a tetraborate structure and so provides no topological connection to the external network whatsoever.
The coarse-grained connectivity is then given by the weighted average:
To model the rapid increase in the fraction of Ge in rings at arbitrary alkali concentrations, an inverted exponential decay function of the form:
was chosen (Sidebottom et al., 2014) in which fSAT, fo, and xo are parameters adjusted to maximize the coincidence of the fragility index with the pattern established in Figure 4. Values of fo = 0.45, fSAT = 0.87, and xo = 10.5% were found to provide good coincidence as shown in Figure 9. These parameters predict a fraction of rings plotted as a dashed line in Figure 8 that falls within the error of that estimated from analysis of the Raman modes.
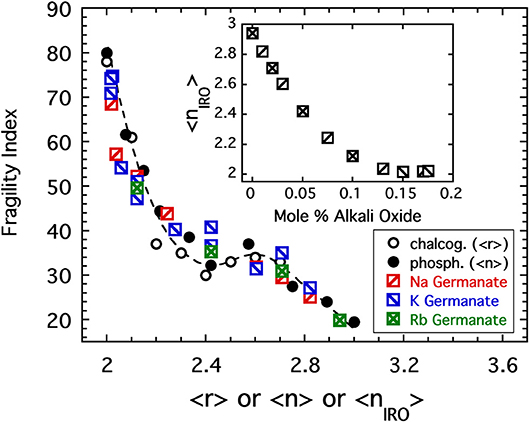
Figure 9. The fragility index of sodium, potassium, and rubidium germanate glasses (Nemilov, 1970; Shelby, 1974), is plotted as a function of the connectivity coarse-grained to include IRO structures as described in the text. Also shown are the data from Figure 4 for both the chalcogenides (plotted as a function of the average bond per atom) and the alkali phosphates (plotted as a function of the average BO per phosphate). The inset shows how the coarse-grained connectivity decreases rapidly with increasing alkali oxide addition.
Alkali Silicates
Like the alkali phosphates, addition of alkali oxide to the SiO2 network results in network depolymerization through the production of NBOs and NMR studies (Stebbins, 1987; Maekawa et al., 1991) have developed a reasonably clear understanding of the fractions of SiO4 tetrahedra (f4, f3, f2, f1, and f0) with n = 4, 3, 2, 1, or zero BO bonds, respectively. Less prominent in the literature is a discussion of possible IRO structures that might serve to reduce the effective connectivity of the network. Only rather recently has there emerged a handful of publications (Kalampounias et al., 2006a,b; Malfait et al., 2007) which suggest such structures exist and that provide quantitative indications for their numbers. Among these is a recent NMR study (Malfait et al., 2007) where the authors observed an additional resonance attributed to 3-membered rings in highly modified potassium, rubidium and cesium silicate glasses but which was absent in both lithium, and sodium silicates. The intensity of this additional mode was reported to increase exponentially with increasing potassium oxide and was used to estimate (Malfait et al., 2007) that as many as fR ≈ 20% of SiO4 tetrahedra participate in 3-membered rings for x = 40 mol% K2O.
Small 3-membered rings are virtually absent in SiO2 (Galeener, 1982), but a recent Raman study (Kalampounias et al., 2006a,b) of molten silica near Tg revealed the existence of other rigid structural units. In what had previously been assessed as a single broad symmetric stretching band the authors resolved three separately distinct modes. Drawing heavily upon a similar band structure found in ZnCl2, the authors have assigned these separated modes to represent fractions of SiO4 tetrahedra that are either “free” (fF), edge-sharing (fES), or participants in a so-called “super-tetrahedron” cluster (fST) consisting of four SiO4 tetrahedra combined into a larger replica tetrahedron.
Limiting the analysis only to compositions below 40 mol% alkali oxide for which f1 = f0 = 0, we arrive at 13 possible configurations that a SiO4 tetrahedron could adopt that are summarized in Table 2. The connectivity assignments in the table for free units and rings follow directly from the previous discussion on coarse-graining of the alkali germanates but must be augmented slightly to allow for SiO4 units in rings with NBOs. The presence of NBOs in the alkali silicates raises the topological complication of so-called “dangling bonds” (Thorpe, 1983; Boolchand and Thorpe, 1994) which arise when, for example, a SiO4 tetrahedra with two NBOs participates in a 3-membered ring. Our approach to these situations is to assign zero connectivity to the unit as others have advocated (Thorpe, 1983). This reflects the impression that the unit no longer provides connectivity to the external network but rather has been fully consumed into the RSU itself much in the way a GeO4 unit in a double ring is internalized and so assigned n = 0 (see Table 1). As for the super-tetrahedron, each SiO4 tetrahedron must complete 3 BO connections to this RSU of which two are redundant. An SiO4 unit with just 3 BO will be entirely consumed by the super-tetrahedron and have no remaining connection to the external network (so n = 0) while an SiO4 unit with only 2 BO would be incapable of existing in a super-tetrahedron at all. Although a pair of edge sharing SiO4 tetrahedra do not technically generate a RSU (in the sense that a RSU is by definition an autonomous object able to resist internal deformation under the low frequency stress associated with viscous flow), each SiO4 unit suffers a reduction in connectivity owing to the presence of a redundant BO bond. In the rarer instances for which a SiO4 tetrahedra participates in two edge sharing connections simultaneously, the unit functions, in a topological sense, as the linkage of a 2d chain (n = 2).
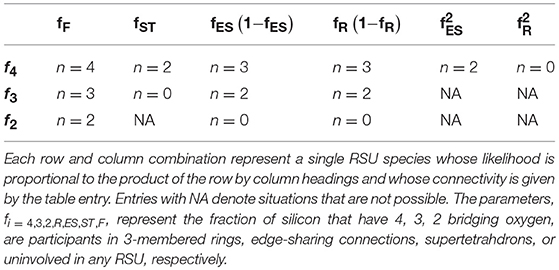
Table 2. Coarse-grained connectivity of 13 allowed configurations found in alkali silicate glass networks with <40 mol% alkali oxide as discussed in the text.
Coarse-graining the connectivity of these alkali silicate melts is thus an ambitious effort involving a properly-normalized weighted average of the form:
where
Not only is the greater diversity of potential structural motifs a challenge, so too is the limited availability of quantitative values of the compositional dependence of the fractions (fF, fST, fES, and fR) of these motifs needed to complete the calculations. In principle, these fractions together with the fractions of BO per Si (f4, f3, and f2) would present an ill-advised curve fitting exercise with seven adjustable parameters. In an effort to avoid a result that to the reader might appear to be merely contrived from some arbitrary, free adjustment of these parameters, the parameters have been fixed to values dictated by the literature sources cited earlier. The values of f4, f3, and f2, for example, are set by values taken directly from data tables in the NMR study (Maekawa et al., 1991). For the SiO2 glass, the minute fraction of rings (fR = 0) is ignored while the values of fF = 20%, fST = 30%, and fES = 50% are assigned the corresponding fractions of areas under the three curve fit bands based on analysis of a figure published in the Raman study (Kalampounias et al., 2006a). For alkali modified silicates with 20–40 mol% alkali, fES = 0 based on the absence of this band reported in the second Raman study (Kalampounias et al., 2006b). Here the values of fR for the potassium silicates are taken from an extrapolation published as a figure in (Malfait et al., 2007) while for the sodium silicates this fraction is set to fR = 0 and the values for fF and fST were set to make up the balance with the ratio 5.5 fixed to the value quoted in the Raman study of 20 mol% potassium silicate (Kalampounias et al., 2006b). Further details of this analysis, including alternative model distributions that avoid any substantial edge-sharing species in SiO2, may be found elsewhere (Sidebottom, 2019). Results of coarse graining for the fragility of the alkali silicates is shown in Figure 10, and given that no adjustment of parameters has been attempted, the collapse to the earlier master curve is deemed to be reasonably successful.
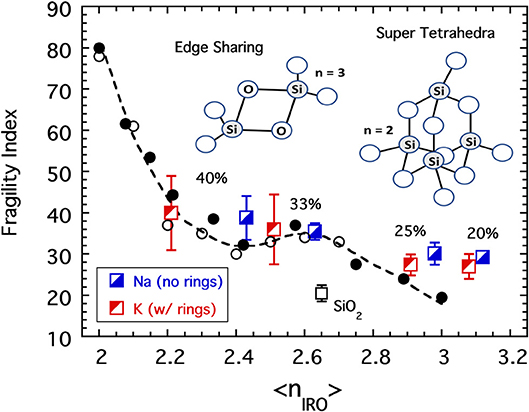
Figure 10. The fragility indices of SiO2 and selected sodium and potassium silicate glasses (Poole, 1949; Nascimento and Aparicio, 2007; Nemilov, 2007) plotted as a function of the connectivity coarse-grained to include IRO structures as described in the text. Also shown are the data from Figure 4 for both the chalcogenides (plotted as a function of the average bond per atom) and the alkali phosphates (plotted as a function of the average BO per phosphate). Cartoons illustrate two of the structures, edge-sharing tetrahedra and a super-tetrahedron unit, reported (Kalampounias et al., 2006a) to be present in silicate melts.
Network-Forming Intermediates
Throughout our analysis of network connectivity in alkali-modified oxide glasses, we have not attached any connectivity to the alkali ion itself. This decision stems from evidence that alkali ions are only weakly tethered to their charge-compensating site on the network (either a NBO or a higher coordinated unit, e.g., GeO5 or BO4) and remain considerably mobile in the glassy state well below Tg. Many impedance spectroscopy studies (Dyre et al., 2009) of ion-containing glasses observe relaxation processes associated with the hopping diffusion of the ion between charge compensating sites through the voids in the (frozen) oxide network. Unlike Si4+, Ge4+, and B3+ which are identified (Zachariasen, 1932) as network-forming cations, alkali ions are described as network-modifying cations (Zarzycki, 1991) as they often depolymerize the network via the formation of NBOs without actually participating in the oxide network itself. In between these extremes are several divalent and trivalent ions (e.g., Zn2+, Ca2+, Al3+) that are referred to as intermediates as they are capable of functioning either as a network-former or modifier.
In the sodium metaphosphate glass, NaPO3, the oxide structure consists of chains of PO4 tetrahedra with n = 2 BO connections each (Brow, 2000). The sodium ion is charge-compensated by the remaining two NBOs of which each shares half the negative charge and provides a weak crosslinking to the network (as was discussed earlier in regards to the glass transition temperature in Figure 3). In both Zn metaphosphate and Al metaphosphate glasses the structure continues to develop from chains of PO4 tetrahedra each making two BO connections with neighboring PO4 tetrahedra (Brow, 1993, 2000; Brow et al., 1993). However, these glass melts are stronger than that of NaPO3 (i.e., much lower fragility) and this is suggestive that both Zn2+ and Al3+ are functioning as network-forming ions that forge increasing connectivity most likely as a consequence of their greater ionic strength (Rodrigues and Wondraczek, 2014; Xia et al., 2019). Indeed, dynamic light scattering measurements (Tran and Sidebottom, 2013; Sidebottom and Vu, 2016) of the fragility in binary mixtures of both [Zn(PO3)2]y[NaPO3]1−y and [Al(PO3)3]y[NaPO3]1−y confirm a monotonic decrease in fragility with the substitution for Na by either Zn or Al.
If we treat Zn2+ and Al3+ as network-forming cations, we must presume that these cations form BO connections with PO4 tetrahedra that increase the connectivity of the network. In the instance of Zn(PO3)2 there are, in one chemical formula, two PO4 polyhedra associated with each Zn2+ cation allowing Zn2+ to complete its desired coordination of n = 4. Meanwhile each of the PO4 tetrahedra already maintain two BO connections to neighboring PO4 tetrahedra (to create a chain structure of polymeric [PO3]n) while the remaining two oxygen are free to coordinate to the Zn2+ cation. We assume that the Zn2+ cation can be coordinated either in a corner sharing fashion or an edge sharing fashion to the surrounding PO4 tetrahedra with equal likelihood and so arrive at three ways in which the Zn2+ cation in one chemical formula could be connected with the network. These are illustrated in the inset to Figure 11. Firstly, the Zn2+ cation could bond with four separate PO4 tetrahedra via corner sharing connections only. In this case both the ZnO4 tetrahedron and the two PO4 tetrahedra (per chemical formula) would be assigned a connectivity of n = 4. On a per chemical formula basis the average connectivity per network-forming cation of such a configuration would then be:
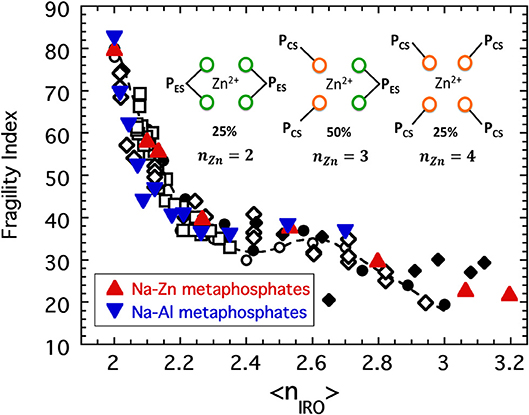
Figure 11. The fragility indices of [Al(PO3)3]y[NaPO3]1−y and [Zn(PO3)2]y[NaPO3]1−y plotted as a function of the connectivity coarse-grained to include both edge-sharing and corner-sharing configurations as described in the text. Also shown are the collective data from previous figures: sodium phosphates (solid circles), chalcogenides (open circles), alkali borates (open squares), alkali germanates (open diamonds), and alkali silicates (solid diamonds). The inset shows the three possible configurations of a Zn cation in Zn(PO3)2 glass.
Secondly, it could bond with just two separate PO4 tetrahedra via edge sharing connections only. In this case the ZnO4 tetrahedron would have a connectivity of n = 2 (one redundant BO bond to each PO4), while each PO4 tetrahedra would have n = 3 (one redundant BO bond to the Zn). In this instance the average connectivity would be:
Lastly, the Zn2+ could form a corner sharing connection to two PO4 tetrahedra and an edge sharing connection to another. In this last case, the ZnO4 tetrahedron would have a connectivity of n = 3 (one redundant bond to one PO4 unit) while one PO4 unit would have connectivity of n = 3 and the other n = 4. In this last scenario there are two permutations each with the same average connectivity:
If we now add to this the reasonable assumption of a purely random distribution in which the probability for corner sharing equals that for edge sharing (i.e., fCS = fES = 50%), then fCSfCS = fESfES = fCSfES = 1/4 and the coarse-grained connectivity of zinc metaphosphate glass would be:
and (assuming ideal mixing) the connectivity of mixtures of the form [Zn(PO3)2]y[NaPO3]1−y would have a connectivity given by:
A similar analysis (Sidebottom and Vu, 2016) for the four possible configurations of a 6-fold coordinated Al3+ cation predicts the connectivity of aluminum metaphosphate to be:
with mixtures of the form [Al(PO3)3]y[NaPO3]1−y having connectivity:
Using Equations (9) and (11), the fragility of both Zn-Na and Al-Na metaphosphate melts is plotted together with the master curve in Figure 11 and again show good coincidence.
Glass Transition Temperature
In this final section we turn attention to the nature of the glass transition temperature in network-forming oxides. The glass transition temperature should be viewed as a relevant energy scale associated with the average thermal energy needed to generate sufficient bond breaking so as to facilitate a viscous flow of 1012 Pas (as the Tg is commonly defined) and this identification is further supported by the well-known empirical “2/3 rule” (Wang et al., 2006) that for a large number of glassforming materials Tg is typically about 2/3 of the melting temperature. In light of our earlier theme regarding a law of corresponding states, this Tg need not have any formal relation to the fragility of the melt. One would not anticipate Tg to mimic the compositional variations in fragility and, indeed, we already have acknowledged this to be the case for alkali phosphate melts whose glass transition temperature is influence by both depolymerization of the oxide network and by the restorative effects of crosslinking by alkali ions. Nevertheless, there are a handful of examples that suggest the glass transition temperature may still be influenced by the network connectivity and we explore these here. Admittedly, the evidence presented here is largely anecdotal and so the discussion should be regarded as only a starting point for further investigations.
Firstly, consider the glass transition temperature of both the alkali borates and germanates which are plotted in Figure 12 as a function of the alkali oxide content just up to the levels where substantial numbers of NBOs would begin to develop. The general increase in the glass transition would suggest that this energy scale is mainly influenced by the degree of network polymerization (characterized either by 〈r〉 or 〈n〉) which initially increases as a result of increasing coordination. This suspicion is also supported at higher alkali concentrations (beyond that plotted in Figure 12) where the Tg of both systems begins to decrease due to the formation of NBOs that then depolymerize the network. In both cases, the initial absence of NBOs in the network preclude the possibility for the alkali ions to function as crosslinks between separate “patches” of disconnected oxide network and so the restorative effect seen in the alkali phosphate is not present at these lower concentrations and would not be anticipated until large numbers of NBOs have formed. This tie between network constraints and Tg has long been suggested as the cause for the borate and germanate “anomalies” (Henderson, 2007).
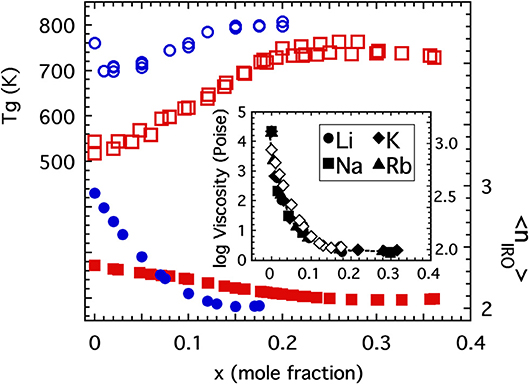
Figure 12. The glass transition temperature of alkali germanates (Shelby, 1974; open circles) and alkali borates (Gupta and Mauro, 2009; open squares) as a function of the mole fraction of alkali oxide with scale on the left side. Also plotted are the coarse-grained connectivity (discussed in the text) for alkali germanates (solid circles) and alkali borates (solid squares) with scale on the right side. Inset shows the close correspondence between the rapid decrease in 1,300°C viscosity of alkali germanate melts (Riebling, 1963; solid symbols) and the rapid decrease in coarse-grained connectivity (open diamonds).
Secondly, we highlight results of a study of borophophate glasses (Christensen et al., 2012) with a fixed alkali content. Extensive NMR investigations of this specific glass system provide a clear picture of the fractions of species with a given number of BO connections. The compositional variation of these fractions is presented as an inset to Figure 13 and shows a rather complex variation with exchange of P by B across the series. Using these fractions, one can compute the average connectivity per network forming cation and this has been plotted in Figure 13 along with the measured glass transition temperatures. The scale for Tg has been adjusted to best overlay the data points with those of 〈n〉 in the intermediate range of compositions and the match is quite reasonable over a range from 0.2 < x < 0.9. While this matching procedure is somewhat contrived, the agreement is rather remarkable especially as it captures the peculiar “peak and dip” that occurs for both 〈n〉 and Tg in the range 0.4 < x < 0.8. The ability for both quantities to capture this non-monotonic clearly indicates that Tg is dominated by 〈n〉 in this borophosphate series.
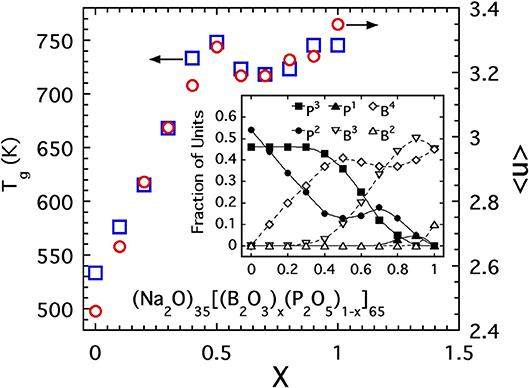
Figure 13. The glass transition temperature (open squares, scale on left side) and average bridging oxygen per network forming cation (open circles, scale on right side) of sodium borophosphate glasses (Christensen et al., 2012). Inset shows the fraction of boron and phosphate units with a given bridging oxygen coordination number used in computing 〈n〉.
Lastly, we reflect on the possibility for the coarse-grained connectivity, 〈nIRO〉, to influence the glass transition temperature. Returning to the glass transition temperatures of the alkali borates and alkali germanates in Figure 12, one sees that although the Tg of both generally increases with the polymerization of these oxide networks, the Tg of the alkali germanates actually decreases by some 80 degrees K with the initial addition of just 1 or 2 mol% alkali oxide (Shelby, 1974). This drop has long been associated with a rapid drop in the high temperature viscosity of these same melts (Riebling, 1963; Henderson, 2007) shown in the inset to Figure 12. Although some (Shelby, 1974) have speculated the drop could be the result of sample contamination by small amounts of water or due to formation of non-bridging oxygens with initial alkali addition, we suggest here an alternative explanation. As seen in the inset to Figure 12 the drop off of the high temperature viscosity is very closely mimicked by the rapid decrease in coarse-grained connectivity 〈nIRO〉 and so the drop in Tg might be a reflection of the rapid change in IRO structure taking place in these low alkali germanate glasses. By comparison, the decrease of 〈nIRO〉 in the alkali borates is far less rapid and this could explain why the Tg of these melts exhibits no initial drop off. Thus, we propose that while 〈n〉 is likely the most dominant structural influence for setting the glass transition temperature, the presence of larger-sized RSUs that comprise the IRO may also produce a significant influence in the right circumstances.
These examples support the general notion that the glass transition temperature increases with increasing network connectivity. This makes intuitive sense. Our view of kBTg is that of a level of thermal energy needed to break (and reform) sufficient numbers of bridging bonds to achieve a bulk viscosity of 1012 Pas. Increasing the density of these bridging bonds implies that a higher level of energy would be needed in order to re-establish the same transition-level viscosity. What might be more speculative is the notion that the generation of IRO structures could lower the glass transition temperature by virtue of lowering the density of those bridging bonds that matter to viscous flow. Despite an increasing number of BO per cation, the formation of IRO is accompanied by larger-scale rigid elements that flex primarily through bridging oxygen at their vertices and it is only these weaker linkages that need be broken to facilitate viscous flow. As we have witnessed in the alkali germanate glasses, the density of these weaker linkages can decrease very rapidly causing a similar drop in viscosity (see Figure 12) along with a drop in Tg.
Conclusions
The equilibrium viscosity of some glass forming materials can change by over 10 orders of magnitude for as little as a 10% increase in thermal energy and this sensitivity to temperature changes near the glass transition point is characterized by the fragility. The fragility varies quite appreciably among glasses across a spectrum of chemical compositions including traditional network-forming oxides and simple molecular liquids but appears to be most closely correlated to the nature of the structural bonding present in the glass. In the instance of network-forming materials, this then allows one to consider the role of network topology in determining the fragility. Here, we have demonstrated how the fragility of a great many network-forming oxide glasses is seen to follow a very common dependence on the topological connectivity of the network provided this connectivity is adjusted to reflect the presence of larger-scaled rigid structural units that form in some systems. Throughout, we have emphasized how the needed coarse-graining of these structural units is achieved in like fashion for several alkali oxide glasses using a single method.
The collapse of the fragility for a great many oxide glasses considered here suggests that fragility is determined only by a single, mean field parameter—either ϕ = 〈r〉, 〈n〉 or 〈nIRO〉– whichever captures the connectivity of weakest linkages present in the network structure. This result is in accord with our viewpoint that the sort of network deformations required for bulk viscous flow need not involve all the covalent bonds present but can be achieved while certain rigid structural units remain largely undeformed. An understanding for why this universality exists is not fully certain, but we have speculated that it is deeply rooted in the nature of the configurational entropy, SC, of cross-linked networks (Sidebottom, 2015). Simple thermodynamic arguments coupled with the Adam-Gibbs entropy picture (Adam and Gibbs, 1965) predict that fragility is proportional to the square of , the slope of the configurational entropy with respect to network connectivity. That is, fragility is a reflection of the sensitivity of the network's configurational entropy to small changes in network connectivity of weakest links. The very fragile glasses at ϕ < 2.2 are under-constrained networks resembling cross-linked polymer chains whose number of accessible conformations—the logarithm of which is the configurational entropy—can be greatly increased by even a small reduction in constraints. By contrast, strong glasses with ϕ > 2.8 are highly over-constrained and find little or no entropic benefit from the removal of a few constraints many of which are topologically redundant at these high levels of connectivity. In future work we hope to explore this entropic connection in more detail by employing computer modeling in an effort to reproduce the specific shape of the master curve.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author is grateful to Dr. G. S. Henderson for his willingness to share data files of Raman spectra in a series of sodium germanate glasses and provide advice on the analysis.
References
Adam, G., and Gibbs, J. H. (1965). On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 43, 139–146. doi: 10.1063/1.1696442
Angell, C. A. (1984). Strong and Fragile Liquids Relaxations in Complex Systems. National Technical Information Service, US Department of Commerce, 3–11.
Angell, C. A. (1991). Relaxation in liquids, polymers and plastic crystals - strong/fragile patterns and problems. J. Non-Cryst. Sol. 131–133, 13–31. doi: 10.1016/0022-3093(91)90266-9
Böhmer, R., and Angell, C. A. (1992). Correlations of the nonexponentiality and state dependence of mechanical relaxations with bond connectivity in Ge-As-Se supercooled liquids. Phys. Rev. B 45:10091. doi: 10.1103/PhysRevB.45.10091
Boolchand, P., and Thorpe, M. F. (1994). Glass-forming tendency, percolation of rigidity, and onefold-coordinated atoms in covalent networks. Phys. Rev. B 50, 10366–10368. doi: 10.1103/PhysRevB.50.10366
Brow, R. K. (1993). Nature of alumina in phosphate glass I: properties of sodium aluminophosphate glass. J. Am. Ceram. Soc. 76, 913–918. doi: 10.1111/j.1151-2916.1993.tb05315.x
Brow, R. K. (2000). Review: the structure of simple phosphate glasses. J. Non-Cryst. Sol. 263–264, 1–28. doi: 10.1016/S0022-3093(99)00620-1
Brow, R. K., Kirkpatrick, R. J., and Turner, G. L. (1993). Nature of alumina in phosphate glass II: structure of sodium aluminophosphate glass. J. Am. Ceram. Soc. 76, 919–928. doi: 10.1111/j.1151-2916.1993.tb05316.x
Christensen, R., Byer, J., Olson, G., and Martin, S. W. (2012). The glass transition temperature of mixed glass former 0.35 Na2O+ 0.65 [xB2O3+(1– x) P2O5] glasses. J. Non-Cryst. Sol. 358, 826–831. doi: 10.1016/j.jnoncrysol.2011.12.068
Chryssikos, G. D., Duffy, J. A., Hutchinson, J. M., Ingram, M. D., Kamitsos, E. I., and Pappin, A. J. (1994). Lithium borate glasses: a quantitative study of strength and fragility. J. Non-Cryst. Sol. 172, 378–383. doi: 10.1016/0022-3093(94)90460-X
Debenedetti, P. G., and Stillinger, F. H. (2001). Supercooled liquids and the glass transition. Nature 410, 259–267. doi: 10.1038/35065704
Dyre, J. C., Maass, P., Roling, B., and Sidebottom, D. L. (2009). Fundamental questions relating to ion conduction in disordered solids. Rep. Prog. Phys. 72:046501. doi: 10.1088/0034-4885/72/4/046501
Eisenberg, A., Farb, H., and Cool, L. G. (1966). Glass transitions in ionic polymers. J. Polymer Sci. A-2 4, 855–868. doi: 10.1002/pol.1966.160040603
Fabian, R. Jr., and Sidebottom, D. L. (2009). Dynamic light scattering in network-forming sodium ultraphosphate liquids near the glass transition. Phys. Rev. B 80:064201. doi: 10.1103/PhysRevB.80.064201
Galeener, F. L. (1982). Planar rings in vitreous silica. J. Non-Cryst. Sol. 49, 53–62. doi: 10.1016/0022-3093(82)90108-9
Galeener, F. L., Lucovsky, G., and Geils, R. H. (1979). Raman and infrared spectra of vitreous As2O3. Phys. Rev. B 19, 4251–4258. doi: 10.1103/PhysRevB.19.4251
Galeener, F. L., Mikkelsen, J. C. Jr., Geils, R., and Mosby, W. J. (1978). The relative Raman cross sections of vitreous SiO2, GeO2, B2O3, and P2O5. Appl. Phys. Lett. 32, 34–36. doi: 10.1063/1.89823
Giacomazzi, L., Umari, P., and Pasquarello, A. (2005). Medium-range structural properties of vitreous germania obtained through first-principles analysis of vibrational spectra. Phys. Rev. Lett. 98:075505. doi: 10.1103/PhysRevLett.95.075505
Griscom, D. L. (1978). “Borate glass structure,” in Borate Glasses: Structure, Properties and Applications, Vol. 12. eds L. D. Pye, V. D. Frechette, and N. J. Kreidel (New York, NY: Materials Science Research), 11–138. doi: 10.1007/978-1-4684-3357-9_2
Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. I. A topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130:094503. doi: 10.1063/1.3077168
Halfpap, B. L., and Lindsay, S. M. (1986). Rigidity percolation in the germanium-arsenic-selenium alloy system. Phys. Rev. Lett. 57:847. doi: 10.1103/PhysRevLett.57.847
He, H., and Thorpe, M. F. (1985). Elastic properties of glasses. Phys. Rev. Lett. 54:2107. doi: 10.1103/PhysRevLett.54.2107
Henderson, G. S. (2007). The germanate anomaly: what do we know? J. Non-Cryst. Sol. 353, 1695–1704. doi: 10.1016/j.jnoncrysol.2007.02.037
Henderson, G. S., and Fleet, M. E. (1991). The structure of glasses along the Na2O - GeO2 join. J. Non-Cryst. Sol. 134, 259–269. doi: 10.1016/0022-3093(91)90384-I
Hoppe, U., Walter, G., Kranold, R., and Stachel, D. (2000). Structural specifics of phosphate glasses probed by diffraction methods: a review. J. Non-Cryst. Sol. I, 29–47. doi: 10.1016/S0022-3093(99)00621-3
Hudgens, J. J., Brow, R. K., Tallant, D. R., and Martin, S. W. (1998). Raman spectroscopy study of the structure of lithium and sodium ultraphosphate glasses. J. Non-Cryst. Sol. 223, 21–31. doi: 10.1016/S0022-3093(97)00347-5
Kalampounias, A. G., Yannopoulos, S. N., and Papatheodorou, G. N. (2006a). Temperature-induced structural changes in glassy, supercooled, and molten silica from 77 to 2150 K. J. Chem. Phys. 124:014504. doi: 10.1063/1.2136878
Kalampounias, A. G., Yannopoulos, S. N., and Papatheodorou, G. N. (2006b). A high-temperature Raman spectroscopic investigation of the potassium tetrasilicate in glassy, supercooled, and liquid states. J. Chem. Phys. 125:164502. doi: 10.1063/1.2360275
Krogh-Moe, J. (1962). New evidence on the boron coordination in alkali borate glasses. Phys. Chem. Glasses 3, 1–6.
Laughlin, W. T., and Uhlmann, D. R. (1972). Viscous flow in simple organic liquids. J. Phys. Chem. 76, 2317–2325. doi: 10.1021/j100660a023
Maekawa, H., Maekawa, T., Kawamura, K., and Yokokawa, T. (1991). The structural groups of alkali silicate glasses determined from 29Si MAS-NMR. J. Non-Cryst. Sol. 127, 53–64. doi: 10.1016/0022-3093(91)90400-Z
Malfait, W. J., Halter, W. E., Morizet, Y., Meier, B. H., and Verel, R. (2007). Structural control on bulk melt properties: Single and double quantum 29Si NMR spectroscopy on alkali-silicate glasses. Geochim. Cosmochim. Acta 71, 6002–6018. doi: 10.1016/j.gca.2007.09.011
Nascimento, M. L. F., and Aparicio, C. (2007). Viscosity of strong and fragile glass-forming liquids investigated by means of principal component analysis. J. Phys. Chem. Sol. 68, 104–110. doi: 10.1016/j.jpcs.2006.09.013
Nemilov, S. V. (1966). A structural investigation of glasses in the B2O3-Na2O system by the viscosimetric Method. Izv. Akad. Nauk SSSR, Neorg. Mater. 2, 349–359.
Nemilov, S. V. (1970). Viscosity and structure of binary germanate glasses in the softening range. J. Appl. Chem. USSR 43, 2644–2651.
Nemilov, S. V. (2007). Structural aspect of possible interrelation between fragility (length) of glass forming melts and Poisson's ratio of glasses. J. Non-Cryst. Sol. 353, 4613–4632. doi: 10.1016/j.jnoncrysol.2007.08.045
Phillips, J. C. (1979). Topology of covalent non-crystalline solids I: short-range order in chalcogenide alloys. J. Non-Cryst. Sol. 34, 153–181. doi: 10.1016/0022-3093(79)90033-4
Poole, J. P. (1949). Low-temperature viscosity of alkali silicate glasses. J. Am. Ceram. Soc. 32, 230–233. doi: 10.1111/j.1151-2916.1949.tb18952.x
Riebling, E. F. (1963). Structure of molten oxides. I. Viscosity of GeO2 and binary germanates containing Li2O, Na2O, K2O, and Rb2O. J. Chem. Phys. 39, 1889–1895. doi: 10.1063/1.1734549
Rodrigues, B. P., and Wondraczek, L. (2014). Cationic constraint effects in metaphosphate glasses. J. Chem. Phys. 140:214501. doi: 10.1063/1.4879559
Shelby, J. E. (1974). Viscosity and thermal expansion of alkali germanate glasses. J. Am. Ceram. Soc. 57, 436–439. doi: 10.1111/j.1151-2916.1974.tb11376.x
Sidebottom, D. L. (2015). Fragility of network-forming glasses: a universal dependence on the topological connectivity. Phys. Rev. E 92:062804. doi: 10.1103/PhysRevE.92.062804
Sidebottom, D. L. (2019). The fragility of alkali silicate glass melts: part of a universal topological pattern. J. Non-Cryst. Sol. 516, 53–66. doi: 10.1016/j.jnoncrysol.2019.04.033
Sidebottom, D. L., and Changstrom, J. R. (2008). Viscoelastic relaxation in molten phosphorus pentoxide using photon correlation spectroscopy. Phys. Rev. B 77:020201. doi: 10.1103/PhysRevB.77.020201
Sidebottom, D. L., Rodenburg, B. V., and Changstrom, J. R. (2007). Connecting structure and dynamics in glass forming materials by photon correlation spectroscopy. Phys. Rev. B 75:132201. doi: 10.1103/PhysRevB.75.132201
Sidebottom, D. L., and Schnell, S. E. (2013). The role of intermediate range order in predicting fragility of network-forming liquids near the rigidity transition. Phys. Rev. B 87:054202. doi: 10.1103/PhysRevB.87.054202
Sidebottom, D. L., Tran, T. D., and Schnell, S. E. (2014). Building up a weaker network: the effect of intermediate range glass structure on liquid fragility. J. Non-Cryst. Sol. 402, 16–20. doi: 10.1016/j.jnoncrysol.2014.05.010
Sidebottom, D. L., and Vu, D. (2016). Assessing the network connectivity of modifier ions in metaphosphate glass melts: a dynamic light scattering study of Na-Zn mixtures. J. Chem. Phys. 145:164503. doi: 10.1063/1.4965815
Stanley, H. E. (1971). Introduction to Phase Transitions and Critical Phenomena. New York, NY: Oxford University Press.
Stebbins, J. F. (1987). Identification of multiple structural species in silicate glasses by 29Si NMR. Nature 330, 465–467. doi: 10.1038/330465a0
Tatsumisago, M., Halfpap, B. L., Green, J. L., Lindsay, S. M., and Angell, C. A. (1990). Fragility of Ge-As-Se glass-forming liquids in relation to rigidity percolation, and the Kauzmann paradox. Phys. Rev. Lett. 64:1549. doi: 10.1103/PhysRevLett.64.1549
Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non-Cryst. Sol. 57, 355–370. doi: 10.1016/0022-3093(83)90424-6
Tran, T. D., and Sidebottom, D. L. (2013). Glass-Forming dynamics of aluminophosphate melts studied by photon correlation spectroscopy. J. Am. Ceram. Soc. 96, 2147–2154. doi: 10.1111/jace.12444
Walrafen, G. E., Samanta, S. R., and Krishnan, P. N. (1980). Raman investigation of vitreous and molten boric oxide. J. Chem. Phys. 72, 113–120. doi: 10.1063/1.438894
Wang, L. M., Angell, C. A., and Richert, R. (2006). Fragility and thermodynamics in nonpolymeric glass-forming liquids. J. Chem. Phys. 125:074505. doi: 10.1063/1.2244551
Xia, Y., Zhu, W., Lockhart, M., Aitken, B., and Sen, S. (2019). Fragility and rheological behavior of metaphosphate liquids: Insights into their chain vs. network characters. J. Non-Cryst. Sol. 514, 77–82. doi: 10.1016/j.jnoncrysol.2019.03.036
Yannopoulos, S. N., Papatheodorou, G. N., and Fytas, G. (1999). Light-scattering study of slow and fast dynamics in a strong inorganic glass former. Phys. Rev. B 60, 15131–15142. doi: 10.1103/PhysRevB.60.15131
Youngman, R. E., and Zwanziger, J. W. (1996). Network modification in potassium borate glasses: structural studies with NMR and Raman spectroscopies. J. Phys. Chem. 100, 16720–16728. doi: 10.1021/jp961439
Zachariasen, W. H. (1932). The atomic arrangement in glass. J. Am. Chem. Soc. 54 3841–3851. doi: 10.1021/ja01349a006
Keywords: fragility, viscosity, networks, oxide glass, universality
Citation: Sidebottom DL (2019) Connecting Glass-Forming Fragility to Network Topology. Front. Mater. 6:144. doi: 10.3389/fmats.2019.00144
Received: 17 April 2019; Accepted: 07 June 2019;
Published: 25 June 2019.
Edited by:
Matthieu Micoulaut, Sorbonne Universités, FranceReviewed by:
Sabyasachi Sen, University of California, Davis, United StatesYann Gueguen, University of Rennes 1, France
Copyright © 2019 Sidebottom. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David L. Sidebottom, c2lkZWJvdHRvbUBjcmVpZ2h0b24uZWR1
 David L. Sidebottom
David L. Sidebottom