- 1Physics of AmoRphous and Inorganic Solids Laboratory (PARISlab), Department of Civil and Environmental Engineering, University of California, Los Angeles, Los Angeles, CA, United States
- 2Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, United States
- 3BGRIMM Technology Group, Beijing, China
- 4Department of Electrical Engineering and Computer Science, University of Cincinnati, Cincinnati, OH, United States
Topological constraint theory (TCT) classifies disordered networks as flexible, stressed-rigid, or isostatic based on the balance between the number of topological constraints and degrees of freedom. In contrast with the predictions from a mean-field enumeration of the constraints, the isostatic state—wherein the network is rigid but free of stress—has been suggested to be achieved within a range of compositions, the intermediate phase, rather than at a fixed threshold. However, our understanding of the nature and potential structural signatures of the intermediate phase remains elusive. Here, based on molecular dynamics simulations of calcium–silicate–hydrate systems with varying compositions, we seek for some mechanical and structural signatures of the intermediate phase. We show that this system exhibits a composition-driven rigidity transition. We find that the fracture toughness, fracture energy, mechanical reversibility, and creep compliance exhibit an anomalous behavior within a compositional window at the vicinity of the isostatic threshold. These features are argued to constitute a mechanical signature of an intermediate phase. Notably, we identify a clear structural signature of the intermediate phase in the medium-range order of this system, which is indicative of an optimal space-filling tendency. Based on these simulations, we demonstrate that the intermediate phase observed in this system arises from a bifurcation between the rigidity and stress transitions. These features might be revealed to be generic to isostatic disordered networks.
Introduction
Topological constraint theory (TCT), or rigidity theory, offers a convenient framework to describe the network topology of disordered networks (Phillips, 1979, 1981). In this framework, atomic networks are considered as mechanical trusses, wherein some nodes (the atoms) are connected to each other via some constraints (the chemical bonds) (Mauro, 2011; Bauchy, 2019). By simplifying complex disordered networks into simpler mechanical trusses, TCT captures the important network topology while filtering the second-order structural details of the atomic network—which facilitates the development of predictive composition–property models (Micoulaut and Yue, 2017; Bauchy, 2019).
In atomic networks, relevant topological constraints comprise the 2-body radial bond-stretching (BS) and 3-body angular bond-bending (BB) constraints, which keep the bond distances and bond angles fixed around their average values, respectively. In analogy with the stability of mechanical trusses (Maxwell, 1864), TCT then classifies atomic networks as (i) flexible, when the number of constraints is lower than the number of atomic degrees of freedom, (ii) stressed–rigid, when the number of constraints is larger than the number of atomic degrees of freedom, and (iii) isostatic, when the numbers of constraints and atomic degrees of freedom match each other. Due to the lack of constraints, undercoordinated flexible networks tend to exhibit some internal floppy modes of deformation (Thorpe, 1983; Boolchand et al., 1995). In contrast, overcoordinated stressed–rigid networks are fully locked but exhibit some internal stress since some constraints become mutually redundant and cannot all be satisfied at the same time (Wang et al., 2005; Li et al., 2019). In turn, isostatic networks are rigid but free of any internal stress.
A mean-field enumeration of the topological constraints predicts that the isostatic state should be achieved at a single threshold composition that is characterized by nc = 3, wherein nc is the number of BS and BB constraints per atom and 3 is the number of degrees of freedom per atom (Phillips, 1979). In a fully connected network wherein all BS and BB are active, this state is achieved when the network exhibits an average coordination number of 2.4 (Mauro, 2011). However, temperature-modulated differential scanning calorimetry tests have suggested that the isostatic character can be achieved within a range of compositions rather than at a fixed threshold—wherein glasses exhibit a nearly zero non-reversible enthalpy at the glass transition (Boolchand et al., 2001; Bhosle et al., 2012a,b). This suggests that the flexible-to-rigid and stressed-to-unstressed transitions may not occur at the same composition threshold, which has been suggested to arise from a self-organization of the network—which adapts its structure to become rigid while avoiding the formation of stress (Thorpe et al., 2000; Chubynsky et al., 2006; Micoulaut and Phillips, 2007). These two transitions define the intermediate phase (IP), which separates the flexible and stressed–rigid phases (i.e., the three topological phases of a disordered network).
Interestingly, isostatic chalcogenide glasses belonging to the intermediate phase exhibit some unique properties, namely a reversible glass transition (Boolchand et al., 2001; Chakravarty et al., 2005), weak relaxation and aging (Chakravarty et al., 2005; Chen et al., 2010), low propensity for creep (Bauchy et al., 2017), anomalous mechanical properties (Varshneya and Mauro, 2007; Bauchy et al., 2016a), superstrong behavior (Boolchand et al., 2018), optimal space-filling tendency (Phillips, 2006; Rompicharla et al., 2008), and stress-free character (Wang et al., 2005).
Although the intermediate phase has been observed in several families of chalcogenides (Mantisi et al., 2015; Boolchand and Goodman, 2017) and modified oxides (Vaills et al., 2005; Micoulaut, 2008; Vignarooban et al., 2014; Mohanty et al., 2019), several questions remain unanswered. What role, if any, does the material's synthesis play in the observation of the intermediate phase (Lucas et al., 2009; Boolchand et al., 2011; Zeidler et al., 2017)? Are intermediate phases a generic feature of disordered networks? Does the intermediate phase manifest itself in other properties than the non-reversible enthalpy at the glass transition? In which aspect(s), if any, of the local or intermediate atomic structure is the intermediate phase encoded? In particular, no clear short-range order structural signature of the intermediate phase is presently available. These gaps in knowledge partially arise from the fact that most of the theoretical works investigating the nature of the intermediate phase have thus far focused on model glasses (e.g., triangular lattices), which may not capture the complex structure of real glasses (Thorpe et al., 2000; Chubynsky et al., 2006; Yan and Wyart, 2014;Yan, 2018).
Here, based on molecular dynamics simulations of calcium–silicate–hydrate systems [i.e., CaO–SiO2-H2O or C–S–H, the binding phase of concrete (Taylor, 1997)] with varying compositions, we seek some mechanical and structural signatures of the intermediate phase. We show that C–S–H exhibits a composition-driven rigidity transition governed by its Ca/Si molar ratio. We find that a large body of mechanical properties exhibit an anomalous behavior within a range of composition at the vicinity of the isostatic threshold—which are argued to constitute some signatures of an intermediate phase. Based on this system, we identify a structural signature of the intermediate phase in the medium-range order of C–S–H. We demonstrate that the intermediate phase observed in C–S–H arises from a bifurcation between the rigidity and stress transitions.
Methods
Preparation of the Calcium–Silicate–Hydrate Samples
In the following of this manuscript, we consider a series of C–S–H samples to identify some mechanical, structural, and dynamical signature of the intermediate phase. To this end, we adopt the model introduced by Pellenq et al. to describe the structure and topology of C–S–H with varying Ca/Si molar ratios (Pellenq et al., 2009; Abdolhosseini Qomi et al., 2014b). Although fine structural details of this model have been discussed (Richardson, 2013, 2014; Scrivener et al., 2015), this model remains the only model that is capable of describing the structure of C–S–H systems across a wide range of Ca/Si molar ratios. In addition, we do not expect the overall atomic topology of C–S–H to strongly depend on the fine structural details of the chosen model.
In detail, the C–S–H atomic models developed by Pellenq et al. are obtained by introducing some defects in an 11 Å tobermorite configuration (Hamid, 1981) following a combinatorial approach (Abdolhosseini Qomi et al., 2014b). This initial tobermorite crystal consists of pseudo-octahedral calcium oxide sheets that are surrounded on each side by silicate chains. These negatively charged calcium–silicate layers are separated from each other by both dissociated and undissociated interlayer water molecules and charge-balancing calcium cations. Starting from this structure, the Ca/Si molar ratio is gradually increased from 1.0 to 1.9 by randomly removing some SiO2 groups (Qomi et al., 2019). The introduced defects offer some possible sites for the adsorption of extra water molecules, which is performed via the Grand Canonical Monte Carlo method—ensuring equilibrium with bulk water at constant volume and room temperature. Eventually, the ReaxFF potential—a reactive potential—was used to account for the chemical reaction of the interlayer water with the defective calcium–silicate sheets (Manzano et al., 2012a,b). The use of a reactive potential allows us to model the dissociation of water molecules into hydroxyl groups. This model has been shown to predict realistic compositions, structure, mechanical, dynamical, and thermal properties for C–S–H (Abdolhosseini Qomi et al., 2014a,b, 2015; Bauchy et al., 2015a, 2016a). The details of the methodology used for the preparation of the models, as well as multiple validations with respect to experimental data can be found in Abdolhosseini Qomi et al. (2014b) and in previous works (Abdolhosseini Qomi et al., 2013, 2014a, 2015; Bauchy et al., 2014a,b,c, 2015a,b, 2016b; Qomi et al., 2015; Bauchy, 2017; Liu et al., 2018). Figure 1 shows some snapshots of the C–S–H model herein for select Ca/Si molar ratios.
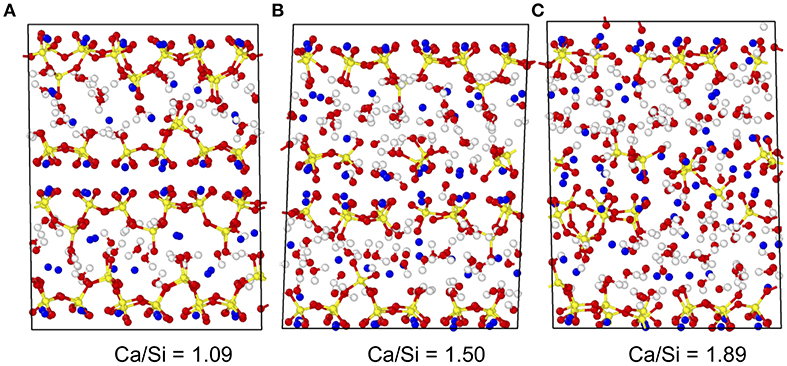
Figure 1. Snapshots of the atomic structure of select calcium–silicate–hydrate systems with (A) Ca/Si = 1.09, (B) Ca/Si = 1.50, and (C) Ca/Si = 1.89. Ca, Si, H, and O atoms are indicated in blue, yellow, white, and red, respectively.
Simulation Details
The structural, mechanical, and dynamical properties of the C–S–H samples considered herein are studied by MD simulations using the LAMMPS package (Plimpton, 1995). To account for the potential dissociation of water molecules into hydroxyl groups, we adopt the ReaxFF potential parameterized by Manzano et al. with a timestep of 0.25 fs (Manzano et al., 2012b). Unless specified otherwise, all the simulated samples comprise around 500 atoms. All the samples are relaxed under 300 K and zero pressure in the NPT ensemble prior to any further characterization. More simulation details can be found in Abdolhosseini Qomi et al. (2014b) and the supplementary material thereof.
Enumeration of the Topological Constraints
Assessing the state of rigidity of the disordered materials requires an accurate knowledge of their atomic structure—which is readily accessible from MD simulations. Here, we use the outcome of the MD simulations to enumerate the number of constraints per atom (nc) in C–S–H as a function of the Ca/Si molar ratio by following a well-established methodology (Bauchy and Micoulaut, 2011, 2013a,b,c; Bauchy et al., 2011, 2013, 2014d; Bauchy, 2013; Micoulaut and Bauchy, 2013; Micoulaut et al., 2013, 2015; Bauchy and Micoulaut, 2015). This method is based on the idea that topological constraints remove some internal degrees of freedom by preventing some relative motion between atoms. In turn, a large relative motion is indicative of the absence of any underlying constraints. In detail, the number of radial BS constraints acting on a central atom can be assessed by calculating the radial excursion of each neighbor. As detailed in Bauchy et al. (2014a), we observe a clear gap between intact (low radial excursion) and broken constraints (high radial excursions). The limit between intact and broken interatomic BS constraints was found to be at around 7% of relative motion (Bauchy and Micoulaut, 2011; Bauchy et al., 2014a), which is fairly close to the Lindemann criterion (Lindemann, 1910). Similarly, the number of BB constraints created by a central atom can be assessed by computing the excursion of all the angles formed by the central atom 0 and its neighbors 1, 2, 3, etc. (the neighbors are here ranked based on their respective distance from the central atom). Again, as detailed in Bauchy et al. (2014a), we observe a clear gap between intact (low angular excursion) and broken constraints (high angular excursions). Based on previous work, the limit between intact (low angular excursion) and broken (high angular excursion) BB constraints was found to be around 13–15° (Bauchy and Micoulaut, 2011; Bauchy et al., 2014a). Note that, since the excursions associated with intact and broken BS or BB constraints are significantly different from each other, the number of BS and BB constraints computed through this method does not depend on the specific choice of the threshold used to discriminate intact from broken constraints.
Mechanical Properties of Calcium–Silicate–Hydrate
In the following, we use previously reported values of fracture toughness, fracture energy, unrecovered volume, and creep compliance for the C–S–H samples considered herein and argue that such properties offer some signatures of the existence of an intermediate phase in C–S–H.
The fracture toughness and fracture energy of the C–S–H samples considered herein were reported in Bauchy et al. (2016a). To characterize the resistance to fracture of C–S–H, we first prepare some larger C–S–H systems made of around 4,500 atoms by replicating the initial systems into a 3×1×3 supercell. We then create a notch in these configurations by inserting a sharp initial crack into the structure while ensuring that the system remains neutral. The notched systems are then further relaxed in the NPT ensemble. The notched configurations are then elongated stepwise along the weakest direction z (i.e., the direction that is orthogonal to the silicate layers) by small 1% increments of the tensile strain. At each step, after an initial equilibration of 50 ps, the stress along the z-axis is averaged for an additional 50 ps—which yields a strain rate of 0.1 ns−1. As detailed in Bauchy et al. (2016a), such a strain rate was found to be low enough to offer an accurate description of the fracture response of the C–S–H samples considered herein. The fracture energy is then computed from the integral of the obtained stress–strain curve (Brochard et al., 2013). The fracture toughness is subsequently calculated based on the Irvin formula (Brochard et al., 2013). More details about the computation of the fracture energy and fracture toughness can be found in Bauchy et al. (2015a).
To assess the mechanical reversibility of the C–S–H samples, we subject them to a loading-unloading cycle and determine the extent of unrecovered volume (Bauchy et al., 2017). To this end, starting from C–S–H configuration relaxed under zero pressure, each system is hydrostatically compressed under 10 GPa. The system is then relaxed under this load for 10 ns in the NPT ensemble—which is found to be long enough to ensure a convergence of energy and volume. The system is then subsequently relaxed back to zero pressure for 10 ns in the NPT ensemble. We then define the fraction of unrecovered volume (Vunrecovered) by comparing the initial volume (Vi) of the system to that achieved after the loading-unloading cycle (Vf):
Note that a perfectly elastic/reversible system would not exhibit any unrecovered volume.
Finally, the creep compliance of the C–S–H samples considered herein was reported in Refs. (Pignatelli et al., 2016; Bauchy et al., 2017). Since a direct simulation of the creep dynamics of C–S–H is, at this point, unachievable by conventional MD simulations, we adopt the accelerated relaxation technique (ART), which was recently developed to investigate the relaxation of silicate glasses (Yu et al., 2015, 2017b). This method consists in subjecting the system to small, cyclic perturbations of isostatic stress ±Δσ. At each stress cycle, a minimization of the energy is performed, wherein the system has the ability to deform (in terms of both shape and volume) in order to reach the target stress. Note that the resulting relaxation does not depend on the choice of Δσ—provided that this stress remains sub-yield (see Bauchy et al., 2017). This method mimics the artificial aging observed in granular materials subjected to vibrations (Boutreux and de Geennes, 1997; Richard et al., 2005)—wherein small vibrations tend to induce the compaction of granular materials, that is, to make the system artificially age. In contrast, large vibrations would tend to randomize the arrangements of the grains, which decreases the overall compactness and, therefore, makes the system rejuvenate (Bauchy et al., 2016b). Here, we mimic the stress condition experienced in deviatoric creep by imposing a constant shear stress τ0, such that Δσ < τ0. As shown in Bauchy et al. (2017), we find that the stress perturbations induce a gradual shear deformation of the C–S–H samples. In detail, the configurations exhibit a shear strain γ that increases linearly with the applied shear stress τ0 and logarithmically with the number of stress cycles N—in agreement with experimental observations (Vandamme and Ulm, 2009). This allows us to define the creep modulus C as:
where N0 is a fitting parameter. We then define the creep compliance J as the inverse of the creep modulus C.
Structural Analysis
To seek a structural signature for the intermediate phase, we compute all the partial pair distribution functions. The partial structure factors are then computed from the Fourier transform of the partial pair distribution functions (Bauchy, 2012; Abdolhosseini Qomi et al., 2013). Special focus is placed on the first sharp diffraction peak (FSDP) of the partial structure factor, which captures the existence of medium-range order structural correlations within the structure (Wilson and Madden, 1994; Elliott, 1995). To this end, the position of the FSDP (QFSDP) is determined by fitting the FSDP with a Lorentzian function (Bauchy, 2012). This allows us to define a typical medium-range repetition distance (d) for each pair of atoms as (Du and Corrales, 2005):
Computation of the Internal Stress
To determine the degree of stress acting in the atomic network of the C–S–H, we adopt the concept of “stress per atom.” Although stress is ill-defined at the atomic level, we rely here on the formalism proposed by Thompson et al. (2009), which expresses the contribution of each atom to the virial of the system. The local “hydrostatic pressure” applied to each atom is then defined as the ratio of the trace of the calculated local stress tensor divided by the volume of the atom, which is here taken as the Voronoi volume. Note that, although the network as a whole is at zero pressure, some bonds are under compression while others are under tension—so that they mutually compensate each other. This approach was recently used to quantify the internal stress exhibited by stressed–rigid atomic networks (Li et al., 2019), mixed alkali glasses (Yu et al., 2015, 2017a,b, 2018), and colloidal systems (Liu et al., 2019). It should be noted that, in the thermodynamic sense, stress is only properly defined for a large ensemble of atoms, so that the physical meaning of the “stress per atom” is unclear. Nevertheless, this quantity can conveniently capture the existence of local instabilities within the gel due to competitive interatomic forces (Ioannidou et al., 2017).
Based on this framework, we compute the local stress experienced by each Si atom, since the silicate chains constitute the rigidity backbone of C–S–H. To isolate the contribution of the network connectivity to the stress of each Si atom, the “stress per atom” calculation is repeated in Qn clusters (n = 0-to-4) that are fully isolated, that is, with no effect of the network connectivity (here, a Qn unit denotes a SiO4 tetrahedron that is connected to n other SiO4 tetrahedra, i.e., with 4 – n terminating O atoms). The isolated clusters are prepared by placing the atoms as perfect SiO4 tetrahedra, charge-balancing the terminating O atoms by Na cations, and performing an energy minimization prior to the stress calculation. Finally, the internal stress of each Si atom in the system is calculated from the difference between its states of stress in the network and isolated cluster (ensuring a consistent Qn state in network and isolated cluster). More details about the stress calculation can be found in Li et al. (2019).
Computation of the Internal Mobility
Finally, we estimate the internal rigidity (or mobility) of the system. To this end, we first cool the C–S–H sample to 0 K in the NPT ensemble with a cooling rate of 1 K/s to access their inherent configuration. We then apply an instantaneous energy bump of 0.1 eV/atom. Due to the equipartition of the energy, half of the energy is used to increase the temperature while the other half is used to increase the potential energy of the system through some atomic displacements. Note that the energy is here chosen to be high enough to allow some atomic motion over low energy barriers, but low enough to avoid any melting of the system (Bauchy et al., 2014c). Following the energy bump, the system is then allowed to relax in the microcanonical NVE ensemble for 100 ps. During this stage, we track the mean square displacement (MSD) of each atom. Although the MSD of H atoms exhibit a diffusive regime and continuously increase over time (Abdolhosseini Qomi et al., 2014a), we note that the MSD of Si and Ca atoms exhibit a plateau. This indicates that the energy bump makes it possible for the Si and Ca atoms to overcome some small energy barriers and to experience some local reorganizations. We then use the final average MSD of Si and Ca atoms as a measure of the internal mobility of the system, whereas a low MSD is indicative of a rigid system, that is, characterized by large energy barriers.
Results and Discussion
Rigidity Transition
We first assess the rigidity state of the C–S–H samples considered herein as a function of composition. Figure 2 shows the number of constraints per atom (nc) computed from the MD simulations (see section Enumeration of the Topological Constraints) as a function of the Ca/Si molar ratio. Overall, we find that the number of constraints per atom decreases with increasing Ca/Si molar ratio (Bauchy et al., 2016a), which is in agreement with the fact that the degree of connectivity of the silicate chains (i.e., as captured by the mean chain length) decreases with increasing Ca/Si molar ratio (Abdolhosseini Qomi et al., 2014b). This also echoes the fact that both the stiffness and hardness of C–S–H decrease with increasing Ca/Si molar ratio (Abdolhosseini Qomi et al., 2014b), since these mechanical properties have been shown to scale with the number of topological constraints (Smedskjaer et al., 2010; Bauchy et al., 2015b; Yang et al., 2019).
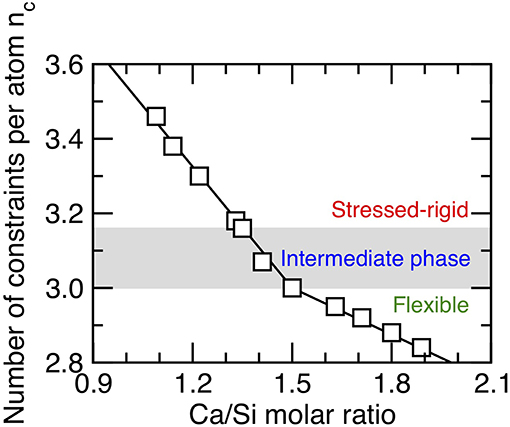
Figure 2. Number of constraints per atom (nc) in calcium–silicate–hydrate networks as a function of the Ca/Si molar ratio. The gray area indicates the location of the intermediate phase wherein structural and mechanical properties show some anomalous behaviors (see following figures).
More specifically, we observe the existence of a rigidity transition in C–S–H that is driven by composition (Bauchy et al., 2016a). Namely, C–S–H is found to be stressed–rigid (nc > 3) at low Ca/Si, flexible (nc < 3) at high Ca/Si, and isostatic (nc ≈ 3) at Ca/Si ≈ 1.5 (see Figure 2). Interestingly, this rigidity transition manifests itself in the structure of C–S–H, as the system is found to be largely crystalline and anisotropic for Ca/Si < 1.5, whereas it is fairly amorphous and isotropic for Ca/Si > 1.5 (see Figure 1) (Abdolhosseini Qomi et al., 2014b).
Mechanical Signatures of the Intermediate Phase
Fracture Toughness
Having established the existence of a composition-driven rigidity transition in C–S–H, we now seek some mechanical signatures associated with this transition. As previously mentioned, we first note that both the stiffness and hardness of C–S–H do not exhibit any anomalous behavior at the vicinity of the rigidity transition—in agreement with the fact that these mechanical properties simply scale with the number of topological constraints (Smedskjaer et al., 2010; Bauchy et al., 2015b; Yang et al., 2019). In contrast, the response to fracture of C–S–H presents a clear signature of the rigidity transition. Figures 3A,B shows the computed values of the mode I fracture toughness and fracture energy (see section Mechanical Properties of Calcium–Silicate–Hydrate) as a function of the number of constraints per atom. We observe that both the fracture toughness and fracture energy exhibit a maximum at the vicinity of the isostatic threshold (nc ≈ 3) (Bauchy et al., 2016a).
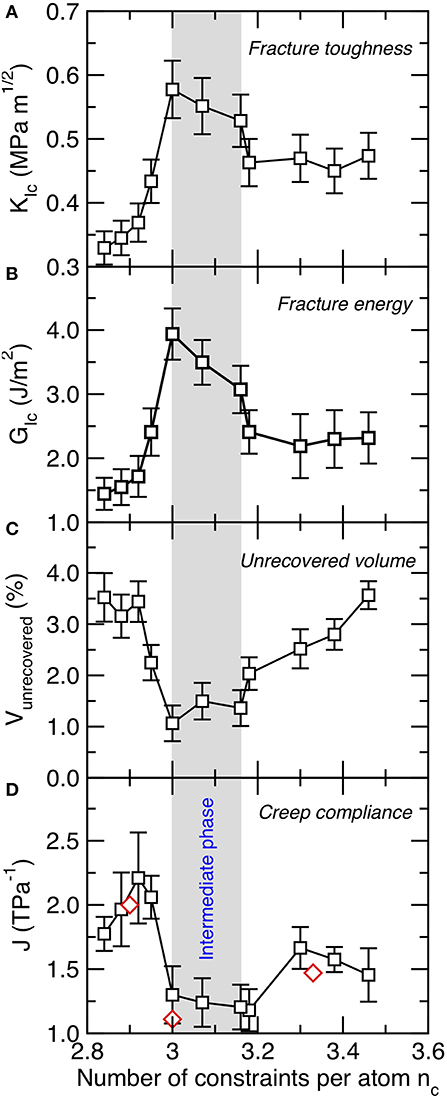
Figure 3. (A) Mode I fracture toughness (KIc), (B) fracture energy, (C) unrecovered volume after a loading-unloading cycle, and (D) creep compliance as a function of the number of constraints per atom (nc). The creep compliance values are compared with experimental measurements (red diamonds) obtained by micro-indentation (Nguyen et al., 2014) and nano-indentation (Vandamme and Ulm, 2009). The gray area indicates the location of the intermediate phase wherein structural and mechanical properties show some anomalous behaviors.
Interestingly, a local maximum of fracture toughness also observed at the vicinity of the isostatic threshold was also reported in sodium silicate and chalcogenide glasses (Guin et al., 2002; Varshneya and Mauro, 2007; Bauchy et al., 2016a; Bauchy, 2019). The harmony among these observations over various families of systems (i.e., oxides and chalcogenides) suggests that this feature might be generic to isostatic disordered materials (Bauchy et al., 2016a). This anomalous behavior has been explained by the fact that flexible networks (nc < 3) have the ability to locally deform due to the existence of some internal degrees of freedom but tend to easily break, and they exhibit a low cohesion due to their low connectivity. In contrast, highly connected stressed–rigid networks (nc > 3) feature higher cohesion but tend to break in a fully brittle fashion due to the existence of some internal stress that prevents any local ductile event (Wang et al., 2016). In turn, isostatic networks (nc ≈ 3) feature an optimal balance between cohesion and ability to show ductile deformation since they are rigid but free of internal stress (Bauchy et al., 2016a).
More interestingly, we observe that, rather than presenting a single maximum at the isostatic threshold (nc = 3), both the fracture toughness and fracture energy appear to exhibit a broad maximum within a window of composition ranging from Ca/Si = 1.3-to-1.5 or nc = 3.0-to-3.16. We note that, in turn, both of these properties exhibit a sudden drop at nc < 3.0 and nc > 3.16. These observations suggest that C–S–H may feature an isostatic atomic network (i.e., rigid but free of internal stress) within this range of composition rather than only at a single isostatic threshold (nc = 3). This suggests the existence of an intermediate phase (which separates the flexible and stressed–rigid phases) in C–S–H. As shown below, the fracture toughness and fracture energy are only some of the many features that present an unusual behavior within the compositional window.
Reversibility Under Load
We now assess the degree of mechanical reversibility of the atomic structure. To this end, we subject the C–S–H structure to a loading-unloading cycle and compute the fracture of unrecovered volume (see section Mechanical Properties of Calcium–Silicate–Hydrate). Note that a perfectly reversible, elastic structure would exhibit a zero unrecovered volume. Figure 3C shows the fracture of unrecovered volume as a function of the number of constraints per atom. In general, we observe that C–S–H is not mechanically reversible, that is, its volume tends to decrease following a loading-unloading cycle (i.e., C–S–H remains permanently densified even after being relaxed to zero pressure).
Interestingly, we observe that the fracture of unrecovered volume exhibits a minimum at the vicinity of the isostatic threshold (see Figure 3C), which indicates that such structures exhibit a nearly fully mechanically reversible structure. This echoes with previous results observed for Ge–Se glasses, wherein isostatic glasses were also found to exhibit minimum unrecovered volume (or maximum recovered volume) (Mauro and Varshneya, 2007). The fact that this feature has been observed both in oxide and chalcogenide systems suggests that it might be generic to isostatic disordered networks. This behavior has been explained from the fact that flexible networks (nc < 3) exhibit some internal floppy modes of deformation, which facilitate some irreversible reorganizations of the atoms upon loading, which, in turn, induce a permanent densification of the network upon loading. In contrast, stressed–rigid networks (nc > 3) tend to remain locked in their densified state, as the presence of internal stress prevents the full relaxation of the network during unloading. In turn, isostatic networks (nc ≈ 3), which are both free of internal stress and modes of deformation, tend to feature maximum volume recovery (Mauro and Varshneya, 2007; Bauchy et al., 2017; Bauchy, 2019).
Again, we note that this anomalous behavior (i.e., minimum in unrecovered volume) is observed within a range of composition rather than at a fixed threshold (see Figure 3C). Interestingly, this composition matches with that wherein the fracture toughness and fracture energy are found to be maximum (see Figures 3A,B), which suggests that the fracture of unrecovered volume may constitute another signature of the existence of an intermediate phase in C–S–H. Interestingly, the mechanical reversibility of isostatic networks evidenced herein echoes the thermodynamic reversibility of isostatic glasses during the glass transition (Bauchy and Micoulaut, 2015; Mantisi et al., 2015).
Creep
We now focus on the response of the C–S–H samples under sustained loading (i.e., creep). Figure 3D shows the computed creep compliance of C–S–H (see section Mechanical Properties of Calcium–Silicate–Hydrate) as a function of the number of constraints per atom. Note that low values of creep compliance (or high values of creep modulus) are indicative of a high resistance to creep, that is, low delayed deformations under sustained loading. As reported in Refs. (Pignatelli et al., 2016; Bauchy et al., 2017), we find that C–S–H exhibits minimum creep compliance at the vicinity of the isostatic threshold (nc ≈ 3). The existence of a minimum in creep compliance around Ca/Si = 1.5 is also supported by available experimental data obtained by micro-indentation (Nguyen et al., 2014) and nano-indentation (Vandamme and Ulm, 2009). This has been explained from the fact that flexible networks exhibit some internal degrees of freedom, which allow the atom to jump over some low energy barriers during sustained loading, which, in turn, facilitates permanent deformations. In contrast, the presence of internal stress in stressed–rigid systems acts as an elastic energy penalty that stimulates the relaxation (i.e., deformation) of the system toward lower states of energy upon creep. In turn, isostatic networks, which are free of both internal stress and modes of deformation, exhibit maximum resistance to creep deformations (Bauchy et al., 2017).
Once again, we find that, rather than being minimum at a fixed threshold composition, the creep compliance exhibits a broad minimum within a range of composition that matches that wherein the fracture toughness/energy and the unrecovered volume are maximum and minimum, respectively. In turn, the creep compliance presents a sudden jump at lower and higher number of constraints per atom. This suggests that the creep compliance acts as another signature of the intermediate phase evidence herein. The fact that the resistance to creep is maximum within the intermediate phase echoes the fact that intermediate phase chalcogenide glasses have been found to exhibit minimum relaxation at the vicinity of the glass transition and minimum aging at room temperature (Boolchand et al., 2001;Chakravarty et al., 2005).
More generally, the fact that stiffness (which essentially depends on the curvature of the local energy landscape) does not present any signature of the intermediate phase suggests that the nature of the intermediate phase is not encoded in the near-equilibrium topography of the energy landscape, but rather in its far-from-equilibrium topography, i.e., that explored upon fracture and plastic non-reversible deformations (i.e., creep) or densification (i.e., unrecovered volume).
Structural Signatures of the Intermediate Phase
We now seek a structural signature of the intermediate phase in C–S–H, as the question as to whether any structural signature of the intermediate phase can be found in isostatic glasses remains unclear (Wang et al., 2017; Zeidler et al., 2017). We first note that we do not observe any obvious anomalous behavior in the short-range order structure of C–S–H (e.g., partial pair distribution function, bond distance, bond angle, coordination number, etc.) (Abdolhosseini Qomi et al., 2014b). As such, we focus our attention on the medium-range order structure—which is encoded in the FSDP of the structure factor (see section Structural Analysis). Figure 4A shows the position of the FSDP of the Si–Si partial structure factor, which captures the existence of some medium-range structural correlations among Si tetrahedra. We observe that the position of the FSDP of the Si–Si partial structure factor shows a maximum at the vicinity of the isostatic threshold (nc ≈ 3). Since the position of the FSDP is inversely related to a typical repetition distance in the medium-range order (see Equation 3), the maximum in the position of the FSDP is associated with a minimum of the Si–Si medium-range order repetition distance (see Figure 4B). Importantly, we note that the compositional window wherein the position of the Si–Si FSDP is maximum (or the Si–Si repetition distance minimum) matches with that of the intermediate phase, wherein several mechanical properties show anomalous behavior (see Figure 3). As shown in Figures 4C,D, similar behavior is observed for the Ca–O FSDP. This suggests that the position of the FSDP of partial structure factors offers a structural signature of the intermediate phase in C–S–H.
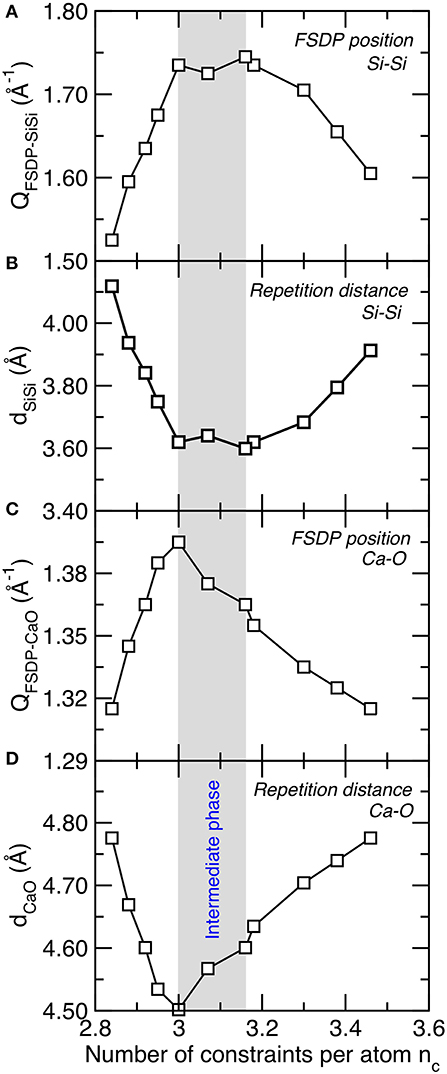
Figure 4. (A) Position of the first sharp diffraction peak (QFSDP) of the Si–Si partial structure factor and (B) corresponding typical repetition distance (D). (C) Position of the first sharp diffraction peak of the Ca–O partial structure factor and (D) corresponding typical repetition distance. The gray area indicates the location of the intermediate phase wherein structural and mechanical properties show some anomalous behaviors.
Interestingly, such behavior was also previously observed in oxide and chalcogenide glasses. First, the positions of the Si–O and O–O FSDP were also found to be maximum in isostatic densified sodium silicate glasses (Micoulaut and Bauchy, 2013). A weakly defined maximum in the position of the As–Se FSDP was also observed in As–Se chalcogenide glasses (Bauchy et al., 2013). Finally, the rigidity of the network was also found to be encoded in the position of FSDP of the structure factor in irradiated silica samples (Wang et al., 2017). All these observations across various families of materials suggest, once again, that this feature might be a generic signature of isostatic disordered networks.
These results suggest that the intermediate phase is encoded in the medium-range (rather than short-range) order structure of C–S–H. The fact that the typical repetition distance is minimum in the intermediate phase can be related to the fact that intermediate-phase glasses have been shown to exhibit an optimal space-filling tendency (for instance, several chalcogenide glasses exhibit a minimum in molar volume in the intermediate phase) (Rompicharla et al., 2008; Boolchand et al., 2018). This can be understood from the fact that, due to their low connectivity, flexible networks tend to present large rings or terminating bonds, which decreases the packing efficiency of the atoms. In turn, since their structure is fully locked by the high number of constraints, stressed–rigid networks are unable to reorganize their structure to achieve more efficiently packed configurations.
Rigidity and Stress Signatures of the Intermediate Phase
Finally, we investigate the nature of the atomic mechanism giving birth to the intermediate phase in C–S–H reported herein. To this end, we first assess the rigidity of the network by subjecting the C–S–H configurations to an energy bump and tracking the resulting atomic motion (see section Computation of the Internal Mobility). The methodology has presently been used to characterize the topography of the energy landscape of disordered networks (Sastry et al., 1998; Krishnan et al., 2017b). Indeed, configurations featuring small energy barriers (i.e., smooth energy landscape) tend to exhibit some large atomic motion following an energy bump, whereas those presenting large energy barriers (i.e., rough energy landscape) tend to show very limited energy atomic motion since the atoms are trapped in their energy basins.
Figure 5A shows the average final MSD of the Ca and Si atoms after an energy bump of 0.1 eV/atom as a function of the number of constraints per atom. We observe that the computed MSD values remain very small (around 0.2 Å2) for nc > 3. This indicates that, in this regime, the system is rigid so that the atoms only vibrate around their average position following the energy bump. In contrast, we observe that the MSD presents a sudden increase for nc < 3. This shows that, at this point, the system becomes flexible and features some internal mobility. Similar behavior was observed in flexible irradiated silica samples (Krishnan et al., 2017b; Wang et al., 2017). This can be understood from the fact that, for nc < 3, the configuration presents more internal degrees of freedom (i.e., initially 3 per atom) than constraints, so that the system comprises some internal floppy modes of deformation (whose number of given by 3 – nc) (Thorpe, 1983; Boolchand et al., 1995). Such floppy modes manifest themselves by the formation of some channels in between the basins of the energy landscape, which enhance the internal mobility of the system.
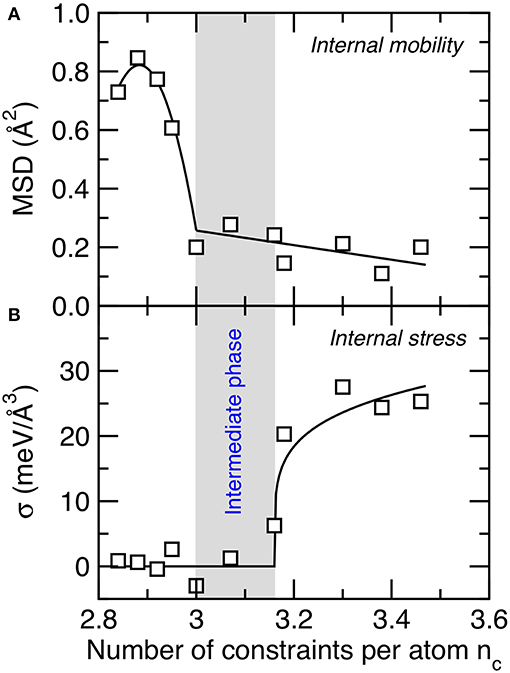
Figure 5. (A) Mean-square displacement of the Ca and Si atoms after an energy bump of 0.1 eV/atom (i.e., a signature of internal mobility within the atomic network) and (B) average atomic-level stress undergone by Si atoms (i.e., a signature of internal stress within the atomic network). The gray area indicates the location of the intermediate phase wherein structural and mechanical properties show some anomalous behaviors.
We now focus on the quantification of the internal stress acting in the network (see section Computation of the Internal Stress). Figure 5B shows the average atomic-level internal stress undergone by Si atoms as a function of the number of constraints per atom. We find that, at low nc, no significant internal stress is observed (Krishnan et al., 2017a). In contrast, we observe a sharp increase in the internal stress at high nc. This indicates that, in this regime, the configuration experiences some local instability wherein some bonds are under tension, whereas some others are under compression (note that the total pressure remains zero in all the C–S–H systems). The existence of some internal stress in highly connected glasses has also been observed in previous experiments (Wang et al., 2005) and simulations (Li et al., 2019). This arises from the fact that, at high nc, the system eventually comprises more constraints than degrees of freedom. In this regime, some constraints become mutually dependent, so that the constraints cannot all be satisfied at the same time (just like the angles of a triangle with three fixed edges cannot present arbitrary values). At this point, the weaker constraints yield to the stiffer ones, which results in the formation of some internal stress (Bauchy et al., 2015b).
Importantly, we observe that the rigid-to-flexible (see Figure 5A) and stressed-to-unstressed (see Figure 5B) transitions do not occur at the same composition. Interestingly, the locations of these two transitions correspond to the beginning and the end of the intermediate phase reported herein (i.e., from nc = 3.00-to-3.16). This signals that the intermediate phase is characterized by an atomic network that is rigid (i.e., with no significant internal flexibility) but also free of internal stress. Although the location of the rigidity transition (at nc = 3.00) is expected from a mean-field enumeration of the constraints (i.e., the point at which the constraints completely exhaust the atomic degrees of freedom), that of the stress transition (at nc = 3.16) cannot be predicted from a mean-field enumeration—which would also predict a stress transition at nc = 3.00, that is, when the number of constraints exceeds the number of atomic degrees of freedom. The fact that the stress occurs at nc > 3 suggests that the system presents some level of self-organization to avoid the formation of any internal stress—since stress otherwise comes with an energy penalty (Bauchy and Micoulaut, 2015; Yan, 2018). These results suggest that the bifurcation between the rigidity (at nc = 3.00) and stress (at nc = 3.16) transitions is at the origin of the intermediate phase reported herein and explain the anomalous behaviors in the mechanical and structural properties of C–S–H in this composition window.
Conclusion
Overall, these results present a large array of mechanical, structural, and dynamical signatures of an intermediate phase in calcium–silicate–hydrate systems. We find that configurations belonging to the intermediate phase exhibit maximum fracture toughness and fracture energy, reversibility under load, and minimum propensity for creep relaxation—which might constitute some generic features of the intermediate phase. These results suggest that the nature of the intermediate phase is not encoded in the near-equilibrium topography of the energy landscape, but rather in its far-from-equilibrium topography. In addition, we report the existence of a structural signature of the intermediate phase, which manifests itself as an optimal space-filling tendency in the medium-range (rather than short-range) order structure of the atomic network. Based on these simulations, we demonstrate that the intermediate phase observed in this system arises from the fact that the flexible-to-rigid and stressed-to-unstressed transitions are decorrelated from each other and do not occur at the same compositional threshold. These results offer a unified picture for the intermediate phase. Further, the observation of an intermediate phase in C–S–H (which, despite being disordered, is not a traditional glass) suggests that the intermediate phase might be generic to disordered materials. However, the formation of an intermediate phase requires some level of structural flexibility (i.e., to enable the network to self-organize to postpone the onset of stress). For instance, although select stoichiometric glasses (e.g., SiO2 and P2O5) present an isostatic network, such monolithic glasses do not appear to have the ability to self-organize to remain isostatic if a small fraction of network modifiers is added (Vaills et al., 2005; Mohanty et al., 2019). Nevertheless, although it has initially been observed in chalcogenide glasses (Boolchand et al., 2001), the intermediate phase has since then been reported to also exist in silicate (Vaills et al., 2005; Bauchy and Micoulaut, 2015; Mantisi et al., 2015) and phosphate glasses (Mohanty et al., 2019)—which suggests that intermediate phases are not restricted to select families of glasses.
Data Availability
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
QZ, MW, and MB conducted the simulations presented herein and analyzed the data. QZ, LG, PB, and MB discussed the results and wrote the manuscript. All the authors contributed to revising the manuscript prior to submission.
Funding
This work was supported by the National Science Foundation under Grant No. 1562066 and by the Beijing General Research Institute of Mining & Metallurgy (BGRIMM) Technology Group.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge fruitful discussion and collaboration with Profs. Gaurav Sant, Matthieu Micoulaut, Mohammad Javad Abdolhosseini Qomi, Roland Pellenq, and Franz-Joseph Ulm.
References
Abdolhosseini Qomi, M. J., Bauchy, M., Pellenq, R. J.-M., and Ulm, F.-J. (2013). “Applying tools from glass science to study calcium-silicate-hydrates” in Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete: A Tribute to Zdenek P. Bazant: Proceedings of the Ninth International Conference on Creep, Shrinkage, and Durability Mechanics (CONCREEP-9), eds U. Franz-Josef, J. M. Hamlin, and R. J.-M Pellenq (Cambridge, MA: ASCE Publications), 78–85. doi: 10.1061/9780784413111.008
Abdolhosseini Qomi, M. J., Bauchy, M., Ulm, F.-J., and Pellenq, R. J.-M. (2014a). Anomalous composition-dependent dynamics of nanoconfined water in the interlayer of disordered calcium-silicates. J. Chem. Phys. 140:054515. doi: 10.1063/1.4864118
Abdolhosseini Qomi, M. J., Krakowiak, K. J., Bauchy, M., Stewart, K. L., Shahsavari, R., Jagannathan, D., et al. (2014b). Combinatorial molecular optimization of cement hydrates. Nat. Commun. 5:4960. doi: 10.1038/ncomms5960
Abdolhosseini Qomi, M. J., Ulm, F.-J., and Pellenq, R. J.-M. (2015). Physical origins of thermal properties of cement paste. Phys. Rev. Appl. 3:064010. doi: 10.1103/PhysRevApplied.3.064010
Bauchy, M. (2012). Structural, vibrational, and thermal properties of densified silicates: Insights from molecular dynamics. J. Chem. Phys. 137:044510. doi: 10.1063/1.4738501
Bauchy, M. (2013). Structure and dynamics of liquid AsSe4 from ab initio molecular dynamics simulation. J. Non-Cryst. Solids 377, 39–42. doi: 10.1016/j.jnoncrysol.2012.12.018
Bauchy, M. (2017). Nanoengineering of concrete via topological constraint theory. MRS Bull. 42, 50–54. doi: 10.1557/mrs.2016.295
Bauchy, M. (2019). Deciphering the atomic genome of glasses by topological constraint theory and molecular dynamics: a review. Comput. Mater. Sci. 159, 95–102. doi: 10.1016/j.commatsci.2018.12.004
Bauchy, M., Abdolhosseini Qomi, M. J., Bichara, C., Ulm, F.-J., and Pellenq, R. J.-M. (2014a). Nanoscale structure of cement: viewpoint of rigidity theory. J. Phys. Chem. C 118, 12485–12493. doi: 10.1021/jp502550z
Bauchy, M., Abdolhosseini Qomi, M. J., Pellenq, R. J. M., and Ulm, F. J. (2014b). Is cement a glassy material? arXiv:1506.06445.
Bauchy, M., Abdolhosseini Qomi, M. J., Ulm, F.-J., and Pellenq, R. J.-M. (2014c). Order and disorder in calcium–silicate–hydrate. J. Chem. Phys. 140:214503. doi: 10.1063/1.4878656
Bauchy, M., Kachmar, A., and Micoulaut, M. (2014d). Structural, dynamic, electronic, and vibrational properties of flexible, intermediate, and stressed rigid As-Se glasses and liquids from first principles molecular dynamics. J. Chem. Phys. 141:194506. doi: 10.1063/1.4901515
Bauchy, M., Laubie, H., Abdolhosseini Qomi, M. J., Hoover, C. G., Ulm, F.-J., and Pellenq, R. J.-M. (2015a). Fracture toughness of calcium–silicate–hydrate from molecular dynamics simulations. J. Non-Cryst. Solids 419, 58–64. doi: 10.1016/j.jnoncrysol.2015.03.031
Bauchy, M., and Micoulaut, M. (2011). Atomic scale foundation of temperature-dependent bonding constraints in network glasses and liquids. J. Non-Cryst. Solids 357, 2530–2537. doi: 10.1016/j.jnoncrysol.2011.03.017
Bauchy, M., and Micoulaut, M. (2013a). Percolative heterogeneous topological constraints and fragility in glass-forming liquids. EPL Europhys. Lett. 104:56002. doi: 10.1209/0295-5075/104/56002
Bauchy, M., and Micoulaut, M. (2013b). Structure of As2Se3 and AsSe network glasses: Evidence for coordination defects and homopolar bonding. J. Non-Cryst. Solids 377, 34–38. doi: 10.1016/j.jnoncrysol.2013.01.019
Bauchy, M., and Micoulaut, M. (2013c). Transport anomalies and adaptative pressure-dependent topological constraints in tetrahedral liquids: evidence for a reversibility window analogue. Phys. Rev. Lett. 110:095501. doi: 10.1103/PhysRevLett.110.095501
Bauchy, M., and Micoulaut, M. (2015). Densified network glasses and liquids with thermodynamically reversible and structurally adaptive behaviour. Nat. Commun. 6:6398. doi: 10.1038/ncomms7398
Bauchy, M., Micoulaut, M., Boero, M., and Massobrio, C. (2013). Compositional thresholds and anomalies in connection with stiffness transitions in network glasses. Phys. Rev. Lett. 110:165501. doi: 10.1103/PhysRevLett.110.165501
Bauchy, M., Micoulaut, M., Celino, M., Le Roux, S., Boero, M., and Massobrio, C. (2011). Angular rigidity in tetrahedral network glasses with changing composition. Phys. Rev. B 84:054201. doi: 10.1103/PhysRevB.84.054201
Bauchy, M., Qomi, M. J. A., Bichara, C., Ulm, F.-J., and Pellenq, R. J.-M. (2015b). Rigidity transition in materials: hardness is driven by weak atomic constraints. Phys. Rev. Lett. 114:125502. doi: 10.1103/PhysRevLett.114.125502
Bauchy, M., Wang, B., Wang, M., Yu, Y., Abdolhosseini Qomi, M. J., Smedskjaer, M. M., et al. (2016a). Fracture toughness anomalies: viewpoint of topological constraint theory. Acta Mater. 121, 234–239. doi: 10.1016/j.actamat.2016.09.004
Bauchy, M., Wang, M., Yu, Y., Wang, B., Krishnan, N. M. A., Masoero, E., et al. (2017). Topological control on the structural relaxation of atomic networks under stress. Phys. Rev. Lett. 119:035502. doi: 10.1103/PhysRevLett.119.035502
Bauchy, M., Wang, M., Yu, Y., Wang, B., Krishnan, N. M. A., Ulm, F.-J., et al. (2016b). Topological control on atomic networks' relaxation under stress. arXiv [Preprint]. arXiv:1605.05043.
Bhosle, S., Gunasekera, K., Boolchand, P., and Micoulaut, M. (2012a). Melt homogenization and self-organization in chalcogenides-part I. Int. J. Appl. Glass Sci. 3, 189–204. doi: 10.1111/j.2041-1294.2012.00093.x
Bhosle, S., Gunasekera, K., Boolchand, P., and Micoulaut, M. (2012b). Melt Homogenization and Self-Organization in Chalcogenides-Part II. Int. J. Appl. Glass Sci. 3, 205–220. doi: 10.1111/j.2041-1294.2012.00092.x
Boolchand, P., Bauchy, M., Micoulaut, M., and Yildirim, C. (2018). Topological phases of chalcogenide glasses encoded in the melt dynamics. Phys. Status Solidi B 255:1800027. doi: 10.1002/pssb.201800027
Boolchand, P., Bhosle, S., Gunasekera, K., Vignarooban, K., and Chakraborty, S. (2011). Glass homogeneity precursive to self-organization. J. Optoelectron. Adv. Mater. 13:1353.
Boolchand, P., Bresser, W., Zhang, M., Wu, Y., Wells, J., and Enzweiler, R. (1995). Lamb-mossbauer factors as a local probe of floppy modes in network glasses. J. Non-Cryst. Solids 182, 143–154. doi: 10.1016/0022-3093(94)00540-0
Boolchand, P., Georgiev, D. G., and Goodman, B. (2001). Discovery of the intermediate phase in chalcogenide glasses. J. Optoelectron. Adv. Mater. 3, 703–720.
Boolchand, P., and Goodman, B. (2017). Glassy materials with enhanced thermal stability. MRS Bull. 42, 23–28. doi: 10.1557/mrs.2016.300
Boutreux, T., and de Geennes, P. G. (1997). Compaction of granular mixtures: a free volume model. Phys. Stat. Mech. Its Appl. 244, 59–67. doi: 10.1016/S0378-4371(97)00236-7
Brochard, L., Hantal, G., Laubie, H., Ulm, F., and Pellenq, R. (2013). Fracture mechanisms in organic-rich shales: role of Kerogen. Poromechanics 2471–2480. doi: 10.1061/9780784412992.288
Chakravarty, S., Georgiev, D. G., Boolchand, P., and Micoulaut, M. (2005). Ageing, fragility and the reversibility window in bulk alloy glasses. J. Phys. Condens. Matter. 17:L1. doi: 10.1088/0953-8984/17/1/L01
Chen, P., Boolchand, P., and Georgiev, D. G. (2010). Long term aging of selenide glasses: evidence of sub-Tg endotherms and pre-Tg exotherms. J. Phys. 22:065104. doi: 10.1088/0953-8984/22/6/065104
Chubynsky, M. V., Brière, M.-A., and Mousseau, N. (2006). Self-organization with equilibration: a model for the intermediate phase in rigidity percolation. Phys. Rev. E 74:016116. doi: 10.1103/PhysRevE.74.016116
Du, J., and Corrales, L. R. (2005). First sharp diffraction peak in silicate glasses: structure and scattering length dependence. Phys. Rev. B 72:092201. doi: 10.1103/PhysRevB.72.092201
Elliott, S. R. (1995). Extended-range order, interstitial voids and the first sharp diffraction peak of network glasses. J. Non-Cryst. Solids 182, 40–48. doi: 10.1016/0022-3093(94)00539-7
Guin, J.-P., Rouxel, T., Sanglebœuf, J.-C., Melscoët, I., and Lucas, J. (2002). Hardness, toughness, and scratchability of germanium–selenium chalcogenide glasses. J. Am. Ceram. Soc. 85, 1545–1552. doi: 10.1111/j.1151-2916.2002.tb00310.x
Hamid, S. (1981). The crystal-structure of the 11-a natural tobermorite. Z. Krist. 154, 189–198. doi: 10.1524/zkri.1981.154.3-4.189
Ioannidou, K., Del Gado, E., Ulm F-J, and Pellenq Roland, J.-M. (2017). Inhomogeneity in cement hydrates: linking local packing to local pressure. J. Nanomech Micromechanics 7:04017003. doi: 10.1061/(ASCE)NM.2153-5477.0000120
Krishnan, N. M. A., Wang, B., Sant, G., Phillips, J. C., and Bauchy, M. (2017a). Revealing the Effect of irradiation on cement hydrates: evidence of a topological self-organization. ACS Appl. Mater. Interfaces 9, 32377–32385. doi: 10.1021/acsami.7b09405
Krishnan, N. M. A., Wang, B., Yu, Y., Le Pape, Y., Sant, G., and Bauchy, M. (2017b). Enthalpy landscape dictates the irradiation-induced disordering of quartz. Phys. Rev. X 7:031019. doi: 10.1103/PhysRevX.7.031019
Li, X., Song, W., Smedskjaer, M. M., Mauro, J. C., and Bauchy, M. (2019). Quantifying the internal stress in over-constrained glasses by molecular dynamics simulations. J. Non-Cryst. Solids X 1:100013. doi: 10.1016/j.nocx.2019.100013
Liu, H., Dong, S., Tang, L., Krishnan, N. M. A., Sant, G., and Bauchy, M. (2019). Effects of polydispersity and disorder on the mechanical properties of hydrated silicate gels. J. Mech. Phys. Solids 122, 555–565. doi: 10.1016/j.jmps.2018.10.003
Liu, H., Du, T., Krishnan, N. M. A., Li, H., and Bauchy, M. (2018). Topological optimization of cementitious binders: advances and challenges. Cem. Concr. Compos 101, 5–14. doi: 10.1016/j.cemconcomp.2018.08.002
Lucas, P., King, E. A., Gulbiten, O., Yarger, J. L., Soignard, E., and Bureau, B. (2009). Bimodal phase percolation model for the structure of Ge-Se glasses and the existence of the intermediate phase. Phys. Rev. B 80:214114. doi: 10.1103/PhysRevB.80.214114
Mantisi, B., Bauchy, M., and Micoulaut, M. (2015). Cycling through the glass transition: evidence for reversibility windows and dynamic anomalies. Phys. Rev. B 92:134201. doi: 10.1103/PhysRevB.92.134201
Manzano, H., Moeini, S., Marinelli, F., van Duin, A. C. T., Ulm, F.-J., and Pellenq, R. J.-M. (2012a). Confined water dissociation in microporous defective silicates: mechanism, dipole distribution, and impact on substrate properties. J. Am. Chem. Soc. 134, 2208–2215. doi: 10.1021/ja209152n
Manzano, H., Pellenq, R. J. M., Ulm, F.-J., Buehler, M. J., and van Duin, A. C. T. (2012b). Hydration of calcium oxide surface predicted by reactive force field molecular dynamics. Langmuir 28, 4187–4197. doi: 10.1021/la204338m
Mauro, J. C., and Varshneya, A. K. (2007). Modeling of rigidity percolation and incipient plasticity in germanium–selenium glasses. J. Am. Ceram. Soc. 90, 192–198. doi: 10.1111/j.1551-2916.2006.01374.x
Maxwell, J. C. (1864). L. On the calculation of the equilibrium and stiffness of frames. Philos. Mag. Ser. 27, 294–299. doi: 10.1080/14786446408643668
Micoulaut, M. (2008). Constrained interactions, rigidity, adaptative networks, and their role for the description of silicates. Am. Mineral. 93, 1732–1748. doi: 10.2138/am.2008.2903
Micoulaut, M., and Bauchy, M. (2013). Anomalies of the first sharp diffraction peak in network glasses: evidence for correlations with dynamic and rigidity properties. Phys. Status Solidi B 250, 976–982. doi: 10.1002/pssb.201248512
Micoulaut, M., Bauchy, M., and Flores-Ruiz, H. (2015). “Topological constraints, rigidity transitions, and anomalies in molecular networks”, in Molecular Dynamics Simulations of Disordered Materials, Vol. 215, eds C. Massobrio, J. Du, M. Bernasconi, and P. Salmon (Cham: Springer), 275–311. doi: 10.1007/978-3-319-15675-0_11
Micoulaut, M., Kachmar, A., Bauchy, M., Le Roux, S., Massobrio, C., and Boero, M. (2013). Structure, topology, rings, and vibrational and electronic properties of GeSe glasses across the rigidity transition: a numerical study. Phys. Rev. B 88:054203. doi: 10.1103/PhysRevB.88.054203
Micoulaut, M., and Phillips, J. C. (2007). Onset of rigidity in glasses: from random to self-organized networks. J. Non-Cryst. Solids 353, 1732–1740. doi: 10.1016/j.jnoncrysol.2007.01.078
Micoulaut, M., and Yue, Y. (2017). Material functionalities from molecular rigidity: maxwell's modern legacy. MRS Bull. 42, 18–22. doi: 10.1557/mrs.2016.298
Mohanty, C., Mandal, A., Gogi, V. K., Chen, P., Novita, D., Chbeir, R., et al. (2019). Linking melt dynamics with topological phases and molecular structure of sodium phosphate glasses from calorimetry, raman scattering, and infrared reflectance. Front. Mater. 6:69. doi: 10.3389/fmats.2019.00069
Nguyen, D.-T., Alizadeh, R., Beaudoin, J. J., Pourbeik, P., and Raki, L. (2014). Microindentation creep of monophasic calcium–silicate–hydrates. Cem. Concr. Compos. 48, 118–126. doi: 10.1016/j.cemconcomp.2013.11.011
Pellenq, R. J.-M., Kushima, A., Shahsavari, R., Vliet, K. J. V., Buehler, M. J., Yip, S., et al. (2009). A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci.U.S.A. 106, 16102–16107. doi: 10.1073/pnas.0902180106
Phillips, J. C. (1979). Topology of covalent non-crystalline solids 1. Short-range order in chalcogenide alloys. J. Non-Cryst. Solids 34, 153–181. doi: 10.1016/0022-3093(79)90033-4
Phillips, J. C. (1981). Topology of covalent non-crystalline solids II: medium-range order in chalcogenide alloys and As-Si-Ge. J. Non-Cryst. Solids 43, 37–77. doi: 10.1016/0022-3093(81)90172-1
Phillips, J. C. (2006). Microscopic reversibility, space-filling, and internal stress in strong glasses. arXiv [preprint] cond-Mat0606418.
Pignatelli, I., Kumar, A., Alizadeh, R., Pape, Y. L., Bauchy, M., and Sant, G. (2016). A dissolution-precipitation mechanism is at the origin of concrete creep in moist environments. J. Chem. Phys. 145:054701. doi: 10.1063/1.4955429
Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19.
Qomi, M. J. A., Bauchy, M., Ulm, F.-J., and Pellenq, R. (2015). “Polymorphism and Its Implications on Structure-Property Correlation in Calcium-Silicate-Hydrates,” in Nanotechnology in Construction, eds K. Sobolev and S. P. Shah (Springer International Publishing), 99–108. Available at: http://link.springer.com/chapter/10.1007/978-3-319-17088-6_12 (accessed May 21, 2015).
Qomi, M. J. A., Masoero, E., Bauchy, M., Ulm, F.-J., Gado, E. D., and Pellenq, R. J.-M. (2019). “C-S-H across Length Scales: From Nano to Micron,” in CONCREEP 10 (American Society of Civil Engineers), 39–48. Available online at: http://ascelibrary.org/doi/abs/10.1061/9780784479346.006 (accessed July 3, 2016).
Richard, P., Nicodemi, M., Delannay, R., Ribière, P., and Bideau, D. (2005). Slow relaxation and compaction of granular systems. Nat. Mater. 4, 121–128. doi: 10.1038/nmat1300
Richardson, I. G. (2013). The importance of proper crystal-chemical and geometrical reasoning demonstrated using layered single and double hydroxides. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 69, 150–162. doi: 10.1107/S205251921300376X
Richardson, I. G. (2014). Model structures for C-(A)-S-H(I). Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 70, 903–923. doi: 10.1107/S2052520614021982
Rompicharla, K., Novita, D. I., Chen, P., Boolchand, P., Micoulaut, M., and Huff, W. (2008). Abrupt boundaries of intermediate phases and space filling in oxide glasses. J. Phys. Condens. Matter Inst. Phys. J. 20:202101. doi: 10.1088/0953-8984/20/20/202101
Sastry, S., Debenedetti, P. G., and Stillinger, F. H. (1998). Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid. Nat. Lond. 393, 554–557. doi: 10.1038/31189
Scrivener, K. L., Juilland, P., and Monteiro, P. J. M. (2015). Advances in understanding hydration of Portland cement. Cem. Concr. Res. 78, 38–56. doi: 10.1016/j.cemconres.2015.05.025
Smedskjaer, M. M., Mauro, J. C., and Yue, Y. (2010). Prediction of glass hardness using temperature-dependent constraint theory. Phys. Rev. Lett. 105:115503. doi: 10.1103/PhysRevLett.105.115503
Thompson, A. P., Plimpton, S. J., and Mattson, W. (2009). General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 131:154107. doi: 10.1063/1.3245303
Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non-Cryst. Solids 57, 355–370. doi: 10.1016/0022-3093(83)90424-6
Thorpe, M. F., Jacobs, D. J., Chubynsky, M. V., and Phillips, J. C. (2000). Self-organization in network glasses. J. Non-Cryst. Solids 266, 859–866. doi: 10.1016/S0022-3093(99)00856-X
Vaills, Y., Qu, T., Micoulaut, M., Chaimbault, F., and Boolchand, P. (2005). Direct evidence of rigidity loss and self-organization in silicate glasses. J. Phys.-Condens. Matter 17, 4889–4896. doi: 10.1088/0953-8984/17/32/003
Vandamme, M., and Ulm, F.-J. (2009). Nanogranular origin of concrete creep. Proc. Natl. Acad. Sci. U.S.A. 106, 10552–10557. doi: 10.1073/pnas.0901033106
Varshneya, A. K., and Mauro, D. J. (2007). Microhardness, indentation toughness, elasticity, plasticity, and brittleness of Ge–Sb–Se chalcogenide glasses. J. Non-Cryst. Solids 353, 1291–1297. doi: 10.1016/j.jnoncrysol.2006.10.072
Vignarooban, K., Boolchand, P., Micoulaut, M., Malki, M., and Bresser, W. J. (2014). Rigidity transitions in glasses driven by changes in network dimensionality and structural groupings. EPL Europhys. Lett. 108:56001. doi: 10.1209/0295-5075/108/56001
Wang, B., Krishnan, N. M. A., Yu, Y., Wang, M., Le Pape, Y., Sant, G., et al. (2017). Irradiation-induced topological transition in SiO2: structural signature of networks' rigidity. J. Non-Cryst. Solids 463, 25–30. doi: 10.1016/j.jnoncrysol.2017.02.017
Wang, B., Yu, Y., Wang, M., Mauro, J. C., and Bauchy, M. (2016). Nanoductility in silicate glasses is driven by topological heterogeneity. Phys. Rev. B 93:064202. doi: 10.1103/PhysRevB.93.064202
Wang, F., Mamedov, S., Boolchand, P., Goodman, B., and Chandrasekhar, M. (2005). Pressure Raman effects and internal stress in network glasses. Phys. Rev. B 71:174201. doi: 10.1103/PhysRevB.71.174201
Wilson, M., and Madden, P. A. (1994). “‘Prepeaks”' and “‘first sharp diffraction peaks”' in computer simulations of strong and fragile ionic liquids. Phys. Rev. Lett. 72, 3033–3036. doi: 10.1103/PhysRevLett.72.3033
Yan, L. (2018). Entropy favors heterogeneous structures of networks near the rigidity threshold. Nat. Commun. 9:1359. doi: 10.1038/s41467-018-03859-9
Yan, L., and Wyart, M. (2014). Evolution of covalent networks under cooling: contrasting the rigidity window and jamming scenarios. Phys. Rev. Lett. 113:215504. doi: 10.1103/PhysRevLett.113.215504
Yang, K., Yang, B., Xu, X., Hoover, C., Smedskjaer, M. M., and Bauchy, M. (2019). Prediction of the Young's modulus of silicate glasses by topological constraint theory. J. Non-Cryst. Solids 514, 15–19. doi: 10.1016/j.jnoncrysol.2019.03.033
Yu, Y., Mauro, J. C., and Bauchy, M. (2017a). Stretched exponential relaxation of glasses: origin of the mixed-alkali effect. Am. Ceram. Soc. Bull. 96, 34–36.
Yu, Y., Wang, M., Anoop Krishnan, N. M., Smedskjaer, M. M., Deenamma Vargheese, K., Mauro, J. C., et al. (2018). Hardness of silicate glasses: Atomic-scale origin of the mixed modifier effect. J. Non-Cryst. Solids 489, 16–21. doi: 10.1016/j.jnoncrysol.2018.03.015
Yu, Y., Wang, M., Smedskjaer, M. M., Mauro, J. C., Sant, G., and Bauchy, M. (2017b). Thermometer effect: origin of the mixed alkali effect in glass relaxation. Phys. Rev. Lett. 119:095501. doi: 10.1103/PhysRevLett.119.095501
Yu, Y., Wang, M., Zhang, D., Wang, B., Sant, G., and Bauchy, M. (2015). Stretched exponential relaxation of glasses at low temperature. Phys. Rev. Lett. 115:165901. doi: 10.1103/PhysRevLett.115.165901
Keywords: intermediate phase, topological constraint theory, rigidity theory, rigidity transition, molecular dynamics, calcium–silicate–hydrate
Citation: Zhou Q, Wang M, Guo L, Boolchand P and Bauchy M (2019) Intermediate Phase in Calcium–Silicate–Hydrates: Mechanical, Structural, Rigidity, and Stress Signatures. Front. Mater. 6:157. doi: 10.3389/fmats.2019.00157
Received: 17 May 2019; Accepted: 19 June 2019;
Published: 09 July 2019.
Edited by:
Limin Wang, Yanshan University, ChinaReviewed by:
Haizheng Tao, Wuhan University of Technology, ChinaQiuju Zheng, Qilu University of Technology, China
Copyright © 2019 Zhou, Wang, Guo, Boolchand and Bauchy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mathieu Bauchy, YmF1Y2h5QHVjbGEuZWR1
 Qi Zhou
Qi Zhou Mengyi Wang
Mengyi Wang Lijie Guo
Lijie Guo Punit Boolchand
Punit Boolchand Mathieu Bauchy
Mathieu Bauchy