- 1Laboratory of Bio-inspired and Graphene Nanomechanics, Department of Civil, Environmental and Mechanical Engineering, University of Trento, Trento, Italy
- 2Center for Micro-BioRobotics, Istituto Italiano di Tecnologia, Pontedera, Italy
- 3Department of Mechanical Engineering, Northwestern University, Evanston, IL, United States
- 4Ket-Lab, Fondazione E. Amaldi, Rome, Italy
- 5School of Engineering and Materials Science, Queen Mary University of London, London, United Kingdom
MEMS-based tensile testing platforms are very powerful tools for the mechanical characterization of nanoscale materials, as they allow for testing of micro/nano-sized components in situ electron microscopes. In a typical configuration, they consist of an actuator, to deliver force/displacement, and a load sensor, which is connected to the sample like springs in series. Such configuration, while providing a high resolution force measurement, can cause the onset of instability phenomena, which can later compromise the test validity. In the present paper such phenomena are quantitatively discussed through the development of an analytical model, which allows to find a relationship between the rise of instability and the sensor stiffness, which is the key parameter to be optimized.
Introduction
Mechanical characterization of materials at the micro/nanoscale has gained increasing attention during the last two decades, as acknowledged by the dramatic increase in number of correlated studies (Pantano et al., 2012). Such trend can be explained by two main reasons. First, the further scaling down of electronic devices, like micro/nanoelectromechanical systems (MEMS/NEMS), is shrinking the size of their structural components to the micro/nanometer scale. Second, experiments carried out on micro/nanostructures, like nanotubes and nanowires, revealed an extraordinary behavior (Wang and Song, 2006; Lee et al., 2008), not known at the macroscale, which can be exploited for a new generation of devices and materials (Ke et al., 2005; Pugno et al., 2005).
For the mechanical characterization of micro/nano-samples, MEMS-based tensile testing devices were shown to be very powerful tools (Zhu and Chang, 2015). In fact, because of their unique compatibility with scanning/transmission electron microscopes (SEM/TEM), they allow tests to be performed under real-time imaging of the sample deformation.
In a typical configuration, the sample to be tested is positioned between an actuator (to apply loads/displacements) and a flexible structure with load sensing function (Haque and Saif, 2002; Espinosa et al., 2007) (i.e., load sensor).
During a test, the actuator pulls the specimen, and this, in turn, transfers part of the delivered displacement to the load sensor, which, as a consequence, undergoes a deformation. This can be measured either electronically (Zhang et al., 2010) or from the analysis of successive pictures taken during the test (Brown et al., 2009), and can then be converted into force if multiplied by the sensor spring constant, known by design.
The choice of the sensor spring constant is not a trivial task. In fact, smaller its value higher the sensitivity of the load measurement. However, if the sensor stiffness is too low compared to that of the specimen, then most of the displacement delivered by the actuator is transferred to the sensor, causing a small deformation of the specimen itself. More critically, a low sensor stiffness may promote the onset of instability phenomena. In fact, when the load sensor moves along with the sample, it accumulates elastic energy. When the force transmitted by the sample to the load sensor decreases after a certain strain has been applied, the elastic energy stored up to that point is released. This means that the load sensor moves back, pulling the end of the specimen attached to it (Agrawal et al., 2009). In such a situation, the displacement-control condition of the sample may no longer be guaranteed, triggering its dynamic failure. Thus, in the case of softening, the testing system may not be able to follow the sample characteristic curve after stress relaxation, even though this could be very interesting to explore.
The influence of the machine stiffness on the mechanical properties and instability phenomena occurring during macroscopic mechanical tests has been pointed out in different studies (Chilver, 1955; Johnston, 1962; Hudson et al., 1972; Han et al., 2009, 2010). In general, it is well-known that a machine with high stiffness should be chosen in order to avoid instability issues in tensile tests. However, while in macroscopic tests, the machine stiffness can be set much bigger than that of the specimen, at the microscale, the metrological strategies adopted for load measurement in MEMS devices make it not possible. The maximum sample deformation which can be achieved before instability occurs can be quantitatively evaluated from the analytical model shown in the following sections.
Analytical Modeling of MEMS-Based Tensile Testing Devices
In most of MEMS tensile testing devices, the load sensor and the sample to be tested are connected like springs in series, as in the lumped parameters model reported in Figure 1A. This is a 2-degrees-of-freedom system, where the sample is represented as a spring with a generic characteristic (its mass is negligible with respect to that of the load sensor), while the load sensor is modeled through a mass (MLS) connected to the substrate through a damper (with damping constant D) and a spring (with spring constant kLS). The sample undergoes a displacement xS, as a consequence of the actuator movement, whereas xLS is the load sensor's displacement.
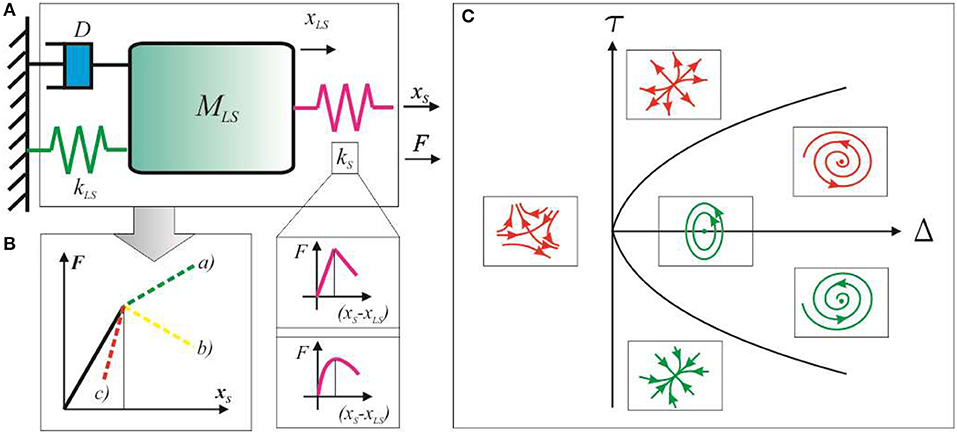
Figure 1. (A) Lumped parameters model of a typical tensile testing device, where the sample can be modeled like a spring whose characteristic shows a softening branch; (B) Global behavior of the system consisting of both the load sensor and the sample, showing the relationship between the force (F) corresponding to the applied displacement (xS). When the sample enters the softening regime, F may increase (line a) or decrease (either line b or c) with xS, depending on the magnitude of the slope of the sample characteristic, ∂F/∂(xS-xLS), compared to the load sensor stiffness, kLS. In particular, line (b) corresponds to ∂F/∂(xS-xLS) <0 and kLS>|∂F/∂(xS-xLS)|, whereas c) to ∂F/∂(xS-xLS) <0 and kLS < |∂F/∂(xS-xLS)|. In order to evaluate the stability of the equilibrium position of the load sensor, its dynamic behavior can be linearized and modeled around such position through a Jacobian matrix. (C) The sign of the trace, τ, and the determinant, Δ, of the Jacobian matrix determine the stability of the equilibrium point.
For simplicity, let us first neglect both the damping and inertial contribution, and let us evaluate the global quasi-static force-displacement relationship characterizing the system comprising the load sensor and sample springs (Figure 1B).
Global System Behavior
The overall deformation undergone by the system is xS = xLS+ (xS-xLS), where (xS-xLS) is the sample elongation. If infinitely small displacements are considered, the overall system elongation becomes:
Since kLS is the load sensor spring constant, then dxLS = dF/kLS. If a general characteristic is assumed for the sample, it follows that d(xS−xLS) = ∂(xS−xLS)/∂FdF, where dF is the force acting on the system, which is the same on both the sample and load sensor (since they are connected in series). Thus, Equation (1) can be rewritten as:
or,
At the beginning, the sample characteristic has a linear increasing trend [e.g., ∂(xS-xLS)/∂F or ∂F/∂(xS-xLS) are constant, and the sample can be modeled like a linear spring], and the slope of the system characteristic (∂F/∂xS) is equal to the equivalent stiffness of the sample and load sensor spring constants. Then, the system characteristic may either increase or decrease with increasing xS, depending on the sample's behavior. In particular, either of the following cases may occur (Figure 1B):
(a) Overall system hardening as a consequence of sample hardening, i.e., if ∂(xS-xLS)/∂F>0;
(b) Overall softening with negative slope, if the sample exhibits softening (i.e., ∂F/∂(xS-xLS) <0) and its slope in modulus is smaller than the load sensor spring constant. In fact, from Equation (3):
which is equivalent to
(c) Overall softening with positive slope, if the sample exhibits softening (e.g., ∂F/∂(xS-xLS) <0) and its slope in modulus is bigger than the load sensor spring constant. In fact, from Equation (3):
which is equivalent to
Thus, in this latter case, the system would tend to come back to smaller values of xS, displaying a snap-back instability with positive slope. However, since in a typical tensile test, xS is progressively increased, the sample is broken without the possibility to follow the snap-back instability and, thus, the corresponding region of the sample characteristic. As a consequence, the optimal design value for the load sensor stiffness depends on the steepest point of interest to be expected during softening regime in the sample characteristic curve. Thus, as a compromise between high resolution during the elastic regime and stability requirement, we can define an optimal load sensor stiffness as
where η is a safety factor for stability, which could be set for example equal to 10%.
Load Sensor Stability
It is now interesting to study what happens to the load sensor when its stiffness is smaller than the sample characteristic slope during softening. To this aim, it is convenient to refer to the model depicted in Figure 1A and write the load sensor's equilibrium equation:
where Fi is the i-th force acting on the load sensor. In this case, three forces have to be considered:
where FS is the force transmitted to the load sensor by the sample and depends on the actual sample elongation (xS-xLS), FLS is the elastic force exerted by the load sensor spring, and FD the damping force. Thus, considering the (9)–(11), Equation (8) can be rewritten as:
In steady-state condition, the equilibrium points of Equation (12) are given by the roots of f(xLS) = −kLSxLS + F(xS − xLS). In order to infer about the stability of a load sensor equilibrium point, (solution of Equation 12), it is convenient to linearize f(xLS) through Taylor expansion as , where (Pelesko and Bernstein, 2003). From this, it follows that the sign of the slope of function f(xLS) depends on the magnitude of the slope of F(xS−xLS) compared to kLS, providing two possible cases:
It is now convenient to rewrite Equation (12) through the following system
that we can linearize near the equilibrium point, , as with
The stability of the solution, , depends on the trace and determinant of the Jacobian matrix (Strogatz, 2000; Pelesko and Bernstein, 2003), τ = tr(J), Δ = det(J), respectively, that on turn depend on f′. In particular, in our system τ = −D/MLS <0, whereas . Therefore, when f′ > 0 (previous case 1) Δ < 0, meaning that the equilibrium point is unstable (saddle point from Figure 1C). On the contrary, when f′ <0 (previous case 2), Δ > 0, always corresponding to stable equilibrium points (Figure 1C). As a conclusion, when the sample characteristic slope is negative (e.g., softening in the sample) and its modulus is smaller than kLS, stable equilibrium points are allowed to the load sensor (case 2); while instead the sample characteristic slope is negative and its modulus is bigger than kLS, no stable equilibrium points are possible (case 1). Indeed, in such case, as shown in the previous section, the system of the sample and load sensor springs show a snap-back instability with a positive slope, which cannot be followed during the tensile test.
In some simple cases, the previous generic (Equation 12) can be solved analytically. As an example, let us consider a piecewise linear expression of F(xS-xLS), which is characterized by an initial region, where the force increases with the deformation, followed by a second region with a decreasing trend (softening region), that can be defined as (Figure 1A):
Its first region defines the sample elastic regime, while the second one corresponds to the softening region. In order to study what happens to the sensor as soon as the sample enters the softening regime, we substitute the second of Equations (13) in Equation (12), which then becomes:
It is convenient to rewrite Equation (14) in dimensionless form. To this aim, we introduce the dimensionless time, t = t', and length, y = xLS/l, being l the sample gage length and k1 ≠ kLS. With these positions, Equation (14) can be rewritten as:
where is a corrected quality factor, which takes into account the presence of the sample through the term k1.
Considering a typical MEMS testing platform, like that one reported in Pantano et al. (2015), the damping contribution can be neglected with respect to the inertial effects (see the Appendix for further details), meaning that α < <1. Thus, in the inertia-dominated regime, Equation (15) simplifies as:
In general, xS = xS(t), but in the hypothesis of a negligible variation of xS with time, Equation (16) can be solved analytically depending on the positive (a) or negative (b) sign of (k1-kLS).
(a) If k1 > kLS, the general solution of Equation (16) is:
(b) If k1 < kLS, the general solution of Equation (16) is instead:
A, B are constants depending on the initial conditions.
In order to infer about the stability of the load sensor equilibrium positions defined by Equations (17) and (18), it is useful to write the second-order differential equation (16) as a non-homogeneous linear system:
This latter can be turned in a homogeneous system, by introducing the translations , χ2 = y2, i.e.,
The above homogeneous linear system has a fixed point, χ*, at χ1 = 0, χ2 = 0, i.e., the origin corresponds to the equilibrium position of the system. Repeating the same logic as before, the trace, τ, and the determinant, Δ, of the Jacobian matrix associated to the linear system provides the stability of the fixed point. In this case, τ = 0, while Δ = -sgn(k1-kLs). Thus, with reference to Figure 1C,
(a) If k1 >kLS, Δ <0, thus the equilibrium point, χ*, is a saddle point, i.e., unstable.
(b) If k1 < kLS, Δ>0, the equilibrium point, χ*, is a center, i.e., neutrally stable.
Since and k1 represents the slope of the decreasing branch of the sample characteristic, the results found now match the conclusions derived previously in case of a sample with a generic characteristic.
Analysis of Results and Discussion
From the analytical models presented above, two main conclusions can be derived. First, the range of possible deformation which can be applied to the specimen is limited by the value of the load sensor spring constant. In particular, higher the sensor spring constant, higher the displacement which can be delivered by the actuator (xS), without compromising the load sensor stability. Second, when the sample characteristic becomes negative and its slope overcomes the load sensor spring constant (in absolute value), the system comprising both the sample and load sensor springs shows a snap-back instability with a positive slope, which cannot be followed during a conventional tensile test, where the end of the sample connected to the actuator is not allowed to come back to decreasing values. From the load sensor's point of view, this translates into unavailability of stable equilibrium positions.
Our result about the occurrence of instability in the case of sample softening with a slope bigger than the sensor stiffness agrees well with similar conclusions drawn in the past, through an energetic approach, from macroscopic compression tests on rocks (Salamon, 1970), as well as with previous hypotheses adduced to explain divergences of the experimental behavior of ZnO nanowires from numerical simulations (Agrawal et al., 2009). As a matter of fact, it is rare to find in the literature experimental stress-strain curves of nanoscale materials showing a steep softening branch. One example can be found in Pantano et al. (2018), where the stress-strain curve of a poly(methyl methacrylate) (PMMA) film with about 100 nm thickness shows a final softening region with negative slope of ~-736 N/m. This value approaches (yet is still below) the limit of the load sensor stability region, whose upper bound corresponds to the load sensor stiffness (831 N/m in this case). Hence, as a design rule, in order to mitigate the instability issues of typical MEMS-based tensile testing configurations, the load sensor stiffness should be chosen according to the optimal value definition reported above. Then, in order to be able to follow the complete stress-strain curve of micro/nano-samples with any kind of softening, alternative designs should be considered. The first solution is to choose a sensor with infinite spring constant. This, in practice, would correspond to fix one end of the specimen, thus preventing any displacement of the sensor itself. In such case, the sensor would lose its sensing function and other metrological strategies than those based on its deformation should be considered for the force measurement. In this regard, a feedback-control strategy could be implemented, as in Pantano et al. (2015). Here, the load sensor is kept fixed at its initial position through the implementation of a position feedback-control, which also provides an electrical load measurement, based on the electrostatic force that has to be applied to keep the sensor at rest (Figure 2).
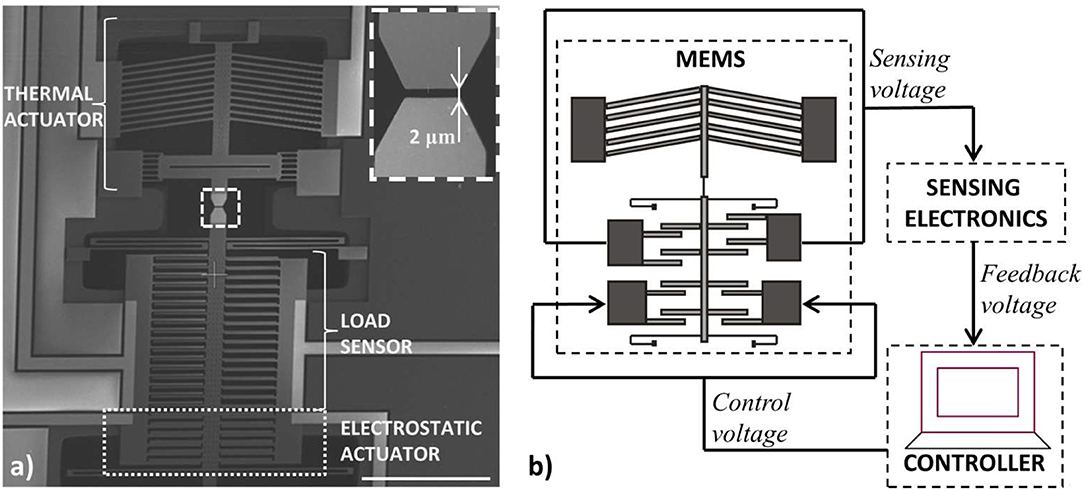
Figure 2. (a) SEM picture of the tensile testing device proposed in Pantano et al. (2015) provided with load sensor feedback control. It consists of a thermal actuator, a capacitive load sensor, and an electrostatic actuator. The thermal actuator and the load sensor are separated by a 2 μm gap for accommodation of the sample to be tested (zoomed view on top); (b) Implementation of the feedback voltage control scheme for keeping the load sensor at rest during test on a sample. Scale bar: 500 μm.
In this case, it is possible to provide the load sensor with a significantly small stiffness (55 N/m by design), which could guarantee high resolution in the displacement measurement. However, in case of softening, if no feedback control is implemented, according to the model presented in the previous section, the maximum slope which can be detected before instability is:
With reference to a typical nanowire with gage length of 4 μm and diameter of about 120 nm, this corresponds to a maximum detectable negative slope in the stress-strain curve of about 20 GPa, which is one fourth of the Young modulus of bulk silver (Wu et al., 2006; Gao et al., 2012) [that represents a lower bound value for the Young modulus of silver nanowires as this increases with size reduction (Sun and Li, 2005)]. This relatively low value would not allow to record the steep load drop at yield of a silver nanowire (118 nm diameter), which can instead be measured if feedback control is implemented in the load sensor operation mode (Figure 3).
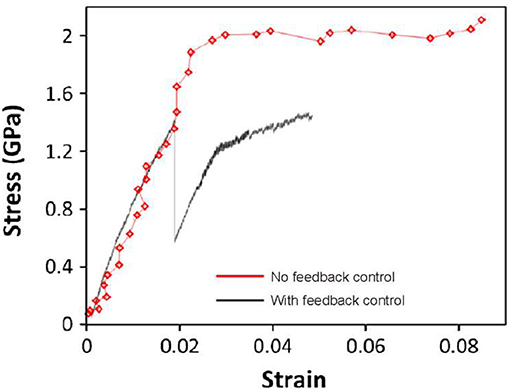
Figure 3. Stress-strain curves derived from tensile tests on silver nanowires of 118 nm diameter. The red curve is referred to a test where the load sensor is allowed to move, while the black curve was derived during a test where a displacement feedback control of the load sensor was implemented. Reprinted with permission from Pantano et al. (2015). Copyright 2015, Springer.
The second possibility for limiting instability issues is a tuning of the load sensor stiffness during the test. In particular, the load sensor stiffness should be relatively low at small sample displacement (in order to guarantee sufficient force resolution) and increase at high sample displacement, when softening is expected. This tunable stiffness ability would be a sort of bio-inspired solution, as examples of stiffness modulation can be found in nature, and, in particular in the behavior of humans, when they have to move in unstable dynamic environments. In fact, in these cases, the central neural system is able to control the muscles stiffness in order to overcome the instability of their movements (Burdet et al., 2001). In the case of MEMS devices, such ability can be readily available if the sensor geometry can change significantly during the tensile test. For example, sensors with a v-shaped geometry, like the amplifier reported in Pantano and Pugno (2014), have a stiffness depending on the length and inclination angle of their chevron beams. In particular, as the test proceeds and this kind of sensor is deformed, both the length and inclination angle of chevron beams change with a consequent stiffness increase. Currently, stiffness tuning finds application in many systems, like atomic force microscopy (AFM) (Mueller-Falcke et al., 2004) and, above all, microresonators (Kozinsky et al., 2006) and the strategies adopted in those cases can be borrowed and transferred to the context of tensile testing devices, too. In particular, among the broad range of available options, solutions based on either an electrostatic or a mechanical working principle are the most interesting, since they allow for the highest stiffness increase (de Laat et al., 2016). In the first case, a voltage is applied between moving and fixed electrodes in order to produce an electrostatic force that causes an increase or reduction of the overall system stiffness, depending on the system design (de Laat et al., 2016). In the second case, the overall system stiffness can be increased by causing the moving shuttle to engage more flexural elements. Such engagement can be induced by applying a critical voltage causing the pull-in of the moving shuttle to the additional springs (de Laat et al., 2016).
Conclusions
The sensor stiffness was shown to play a major role on the efficacy of MEMS tensile testing devices. In fact, if on one hand, it defines the resolution of the force measurement, on the other hand, it can affect the stability of the whole testing system, especially when the sample characteristic starts decreasing after a certain strain has been applied, as a consequence of plasticity or necking, for example.
The development of an analytical model allowed to find a relationship between the sensor stiffness and the rise of instability. In particular, it was shown that instability occurs when the slope of the sample characteristic is negative and its modulus exceeds the sensor stiffness. Thus, in order to prevent load sensor from instability, two possible solutions can be followed with the implementation of either a feedback control to keep the load sensor constantly at rest or a bio-inspired design, where the load sensor's stiffness can be modulated (i.e., increased when instability issues may arise).
Author Contributions
MP conceived the study, developed the analytical models, and wrote the manuscript. BC contributed to the development of the analytical model related to the load sensor. All the authors discussed the results and approved the manuscript.
Funding
NP was supported by the European Commission H2020 under the Graphene Flagship Core 2 No. 785219 (WP14 Composites) and FET Proactive Neurofibres Grant No. 732344 as well as by the Italian Ministry of Education, University and Research (MIUR) under the Departments of Excellence grant L.232/2016 and ARS01-01384-PROSCAN.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors HE.
References
Agrawal, R., Peng, B., and Espinosa, H. D. (2009). Experimental-computational investigation of ZnO nanowires strength and fracture. Nanoletters 9, 4177–4183. doi: 10.1021/nl9023885
Bao, M., and Yang, H. (2007). Squeeze film air damping in MEMS. Sensors Actuators A 137, 3–27. doi: 10.1016/j.sna.2007.01.008
Brown, J. J., Suk, J. W., Singh, G., Baca, A. I., Dikin, D. A., Ruoff, R. S., et al. (2009). Microsystem for nanofiber electromechanical measurements. Sensors Actuators A 155, 1–7. doi: 10.1016/j.sna.2008.11.001
Burdet, E., Osu, R., Franklin, D. W., Milner, T. E., and Kawato, M. (2001). The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature. 414, 446–449. doi: 10.1038/35106566
Chilver, A. H. (1955). The instability of testing machines. Proc. Inst. Mech. Eng. 169, 407–418. doi: 10.1243/PIME_PROC_1955_169_053_02
de Laat, M. L. C., Pérez Garza, H. H., Herder, J. L., and Ghatkesar, M. K. (2016). A review on in situ stiffness adjustment methods in MEMS. J. Micromech. Microeng. 26:063001. doi: 10.1088/0960-1317/26/6/063001
Espinosa, H. D., Zhu, Y., and Moldovan, N. (2007). Design and operation of a MEMS-based material testing system for nanomechanical characterization. J. Microelectromech. Syst. 16, 1219–1231. doi: 10.1109/JMEMS.2007.905739
Gao, Y., Fu, Y., Sun, W., Sun, Y., Wang, H., Wang, F., et al. (2012). Investigation on the mechanical behavior of fivefold twinned silver nanowires. Comput. Mater. Sci. 55, 322–328. doi: 10.1016/j.commatsci.2011.11.005
Han, Z., Li, Y., and Gao, H. J. (2010). Effect of frame stiffness on the deformation behavior of bulk metallic glass. J. Mater. Res. 25, 1958–1962. doi: 10.1557/JMR.2010.0256
Han, Z., Wu, W. F., Li, Y., Wei, Y. J., and Gao, H. J. (2009). An instability index of shear band for plasticity in metallic glasses. Acta Mater. 57, 1367–1372. doi: 10.1016/j.actamat.2008.11.018
Haque, M. A., and Saif, M. T. A. (2002). In-situ tensile testing of nanoscale specimens in SEM and TEM. Exp. Mech. 42, 123–128. doi: 10.1007/BF02411059
Hudson, J. A., Crouch, S. L., and Fairhurst, C. (1972). Soft, stiff and servo-controlled testing machines: a review with reference to rock failure. Eng. Geol. 6, 155–189. doi: 10.1016/0013-7952(72)90001-4
Johnston, W. G. (1962). Yield points and delay times in single crystals. J. Appl. Phys. 33, 2716–2730. doi: 10.1063/1.1702538
Ke, C.-H., Pugno, N., Peng, B., and Espinosa, H. D. (2005). Experiments and modeling of carbon nanotube-based NEMS devices. J. Mech. Phys. Solids 53, 1314–1333. doi: 10.1016/j.jmps.2005.01.007
Kozinsky, I., Postma, H., Bargatin, W. C. I., and Roukes, M. L. (2006). Tuning nonlinearity, dynamic range, and frequency of nanomechanical resonators. Appl. Phys. Lett. 88:253101. doi: 10.1063/1.2209211
Lee, C., Wei, X., Kysar, J. W., and Hone, J. (2008). Measurement of elastic properties and intrinsic strength of monolayer graphene. Science. 321, 385–388. doi: 10.1126/science.1157996
Mueller-Falcke, C., Song, Y. A., and Kim, S. G. (2004). Tunable stiffness scanning microscope probe optomechatronic micro/nano components. devices, and systems. Proc. SPIE. 5604, 31–37. doi: 10.1117/12.571273
Pantano, M. F., Bernal, R. A., Pagnotta, L., and Espinosa, H. D. (2015). Multiphysics design and implementation of a microsystem for displacement-controlled tensile testing of nanomaterials. Meccanica. 50, 549–560. doi: 10.1007/s11012-014-9950-9
Pantano, M. F., Espinosa, H. D., and Pagnotta, L. (2012). Mechanical characterization of materials at small length scales. J. Mech. Sci. Technol. 26, 545–561. doi: 10.1007/s12206-011-1214-1
Pantano, M. F., and Pugno, N. M. (2014). Design of a bent beam electrothermal actuator for in situ tensile testing of ceramic nanostructures. J. Eur. Ceram. Soc. 34, 2767–2773. doi: 10.1016/j.jeurceramsoc.2013.12.001
Pantano, M. F., Speranza, G., Galiotis, C., and Pugno, N. M. (2018). A mechanical system for tensile testing of supported films at the nanoscale. Nanotechnology. 29, 395707. doi: 10.1088/1361-6528/aacf50
Pelesko, J. A., and Bernstein, D. H. (2003). Modeling MEMS and NEMS. Boca Raton, FL: Chapman & Hall/CRC. doi: 10.1201/9781420035292
Pugno, N., Ke, C.-H., and Espinosa, H. D. (2005). Analysis of doubly-clamped nanotube devices in finite deformation regime. J. Appl. Mech. 72, 445–449. doi: 10.1115/1.1875452
Salamon, M. D. G. (1970). Stability, instability and design of pillar workings. Int. J. Rock Mech. Mining Sci. Geomech. Abstracts. 7, 613–631. doi: 10.1016/0148-9062(70)90022-7
Strogatz, S. H. (2000). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Boulder, CO: Westview Press, a member of the Perseus Books Group.
Sun, X., and Li, Y. (2005). Cylindrical silver nanowires: preparation. structure, and optical properties. Adv. Mater. 17, 2626–2630. doi: 10.1002/adma.200500957
Wang, Z. L., and Song, J. (2006). Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 312, 242–246. doi: 10.1126/science.1124005
Wu, B., Heidelberg, A., Boland, J. J., Sader, J. E., Sun, X., and Li, Y. (2006). Microstructure-hardened silver nanowires. Nanoletters 6, 468–472. doi: 10.1021/nl052427f
Zhang, D., Breguet, J. M., Clavel, R., Sivakov, V., Christiansen, S., and Michler, J. (2010). In situ electron microscopy mechanical testing of silicon nanowires using electrostatically actuated tensile stages. J. Microelectromech. Syst. 19, 663–674. doi: 10.1109/JMEMS.2010.2044746
Zhu, Y., and Chang, T. (2015). A review of microelectromechanical systems for nanoscale mechanical characterization. J. Micromech. Microeng. 25:093001. doi: 10.1088/0960-1317/25/9/093001
Appendix
With reference to the MEMS device reported in Pantano et al. (2015), the load sensor mass is about 10–10 kg, kLS=55 N/m, the damping coefficient, D, can be evaluated as due to the squeezing of air trapped between its comb-drive pairs. Considering the classical formula (Bao and Yang, 2007) that describes the squeeze-film air damping between two rectangular plates:
where N is the number of comb-drive finger pairs, μ is the air viscosity, h is the thickness of the air gap, L and w are the larger and the smaller side of the plate, D results to be about 10–4 Ns/m at atmospheric pressure. In this condition, for almost all values of k1, . Furthermore, since these kinds of MEMS devices work in vacuum, D is expected to be much smaller when air is rarefied, causing α to be much smaller than 1 as well, as assumed in section Load Sensor Stability.
Keywords: MEMS, mechanical testing, SEM/TEM, instability, nanomaterials
Citation: Pantano MF, Calusi B, Mazzolai B, Espinosa HD and Pugno NM (2019) Load Sensor Instability and Optimization of MEMS-based Tensile Testing Devices. Front. Mater. 6:161. doi: 10.3389/fmats.2019.00161
Received: 13 January 2019; Accepted: 24 June 2019;
Published: 17 July 2019.
Edited by:
Alberto Corigliano, Politecnico di Milano, ItalyReviewed by:
Shangchao Lin, Florida State University, United StatesDongchan Jang, Korea Advanced Institute of Science & Technology (KAIST), South Korea
Copyright © 2019 Pantano, Calusi, Mazzolai, Espinosa and Pugno. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maria F. Pantano, bWFyaWEucGFudGFub0B1bml0bi5pdA==
 Maria F. Pantano
Maria F. Pantano Benedetta Calusi
Benedetta Calusi Barbara Mazzolai
Barbara Mazzolai Horacio D. Espinosa3
Horacio D. Espinosa3 Nicola M. Pugno
Nicola M. Pugno