Compressive Response of Non-slender Octet Carbon Microlattices

Lattices are periodic three-dimensional architected solids designed at the micro and nano-scale to achieve unique properties not attainable by their constituent materials. The design of lightweight and strong structured solids by additive manufacturing requires the use of high-strength constituent materials and non-slender geometries to prevent strut elastic instabilities. Low slenderness carbon octet microlattices are obtained through pyrolysis of polymeric architectures manufactured with stereolithography technique. Their compressive behavior is numerically and experimentally investigated when the relative density $\bar{\rho }$ ranges between 10 and 50%, with specific stiffness and strength approaching the limit of existing micro and nanoarchitectures. It is shown that additive manufacturing can introduce imperfections such as increased nodal volume, non-cubic unit cell, and orientation-dependent beam slenderness, all of which deeply affect the mechanical response of the lattice material. An accurate numerical modeling of non-slender octet lattices with significant nodal volumes is demonstrated to overcome the limitations of classical analytical methods based on beam theory for the prediction of the lattice stiffness, strength and scaling laws. The presented numerical results and experimental methods provide new insights for the design of structural carbon architected materials toward ultra-strong and lightweight solids.

1. Introduction

Additive manufacturing has become one of the most promising technique to fabricate advanced materials and microstructures that exhibit properties unattained by homogeneous solids or conventionally manufactured architectures. The available 3D printing techniques have recently grown and comprise fused deposition modeling (FDM), direct ink writing (DIW), selective laser sintering (SLS), stereolithography (SLA), etc. Similarly, the selection of materials compatible with these processes has expanded and include thermoelastic polymers (Carneiro et al., 2015), transparent glasses (Nguyen et al., 2017), oxide ceramics (Wilkes et al., 2013), metallic alloys (Schwab et al., 2016), and composites (Spierings et al., 2015; Ni et al., 2018; Quintanilla et al., 2018). The precise micro- and nano-scale topology control achievable through additive manufacturing has allowed the development of unique functionalities to catalysis (Essa et al., 2017), batteries (Xia et al., 2016; Li et al., 2017), scaffolds (Maggi et al., 2017), biomedical implants (Murr et al., 2010), and metamaterials (Hengsbach and Lantada, 2014; Misseroni et al., 2016; Bertoldi et al., 2017; Bilal et al., 2017). In particular, the field of architected material has benefited from the advancement of small-scale manufacturing that enables the design of multistable solids for energy storage (Shan et al., 2015), the evolution of phononic bandgap behavior (Sugino et al., 2015; Amendola et al., 2018) and the exploration of previously inaccessible mechanical property combinations (Bauer et al., 2016). Examples include structural metamaterials designed to achieve extremely lightweight and strong solids through a hierarchical design (Meza et al., 2015) or novel highly deformable and recoverable nanolattices made up of brittle materials (Meza et al., 2014).

Structured solids can be classified as rigid or non-rigid architectures depending on their nodal connectivity, states of self stress, and mechanisms (Pellegrino and Calladine, 1986). The former includes octet lattices and shows a stretching dominated behavior, while the latter mostly presents a bending dominated response as demonstrated by pyramidal lattices. The response of architected materials has been extensively analyzed through the investigation of their constituent unit cells using beam theory to obtain the lattice effective stiffness and strength scaling laws (Gibson and Ashby, 1997; Deshpande et al., 2001). These analytical tools have been proven to well predict the mechanical response of several lattices when the relative density $\bar{\rho }$ is lower than 0.1 and the strut slenderness ratio r/l does not exceed 0.06 (Meza et al., 2017). However, some computational and experimental studies (Schaedler et al., 2011; Meza et al., 2015; Bauer et al., 2016) have recently reported deviations from the classical scaling laws due to non-slender struts and the influence of the node geometry (Portela et al., 2018), thus proposing different scaling laws. The difficult micro- and nano-scale fabrication of slender structured solids that obey to classical scaling laws motivates the investigation of non-slender architectures with pronounced nodal volume caused by an imperfect 3D printing. Therefore, the study of their mechanical properties is fundamental for the design of stronger lattices that do not suffer from strut elastic instabilities.

One of the most promising materials to fabricate extremely lightweight and resistant architected solids is carbon, which has recently become compatible with additive manufacturing processes. Direct ink writing (DIW) with printable inks that contain graphene, carbon nanotube, and graphene oxide (Fu et al., 2017) has been employed for the realization of flexible, conductive, and chemically stable prototypes (Sun et al., 2013; Zhu et al., 2015; Yao et al., 2016; Zhang et al., 2016), while 3D-printed carbon fiber reinforced composites have been manufactured by means of FDM (Lewicki et al., 2017; Anwer and Naguib, 2018). Carbon nano- and micro-lattices are another form of 3D printed carbon which have demonstrated elevated structural performances. Architected carbon materials are obtained by pyrolyzing 3D-printed precursor, especially polymer lattices prepared by photocuring techniques. Carbon nanolattices fabricated through two-photon lithography have shown a strength comparable with the theoretical strength of flaw insensitive glassy carbon (Bauer et al., 2016). This printing technique solidifies the polymeric precursor solution point-by-point at a submicron scale in a prolonged process, thus preventing the production of micro- and nano-architectures at a large scale. Carbon microlattices produced by self-propagating photopolymer waveguides (Jacobsen et al., 2011) and stereolithography (SLA) (Chen et al., 2017) overcome the scalability difficulties toward faster manufacturing of larger scale lattices. However, their mechanical performances are still limited, and the development of enhanced architected solids demands further understanding of the influence of the manufacturing-induced imperfection on the mechanics of 3D-printed carbon lattices.

The aim of this work is to manufacture stiff and strong non-slender octet carbon microlattices through digital light processing stereolithography (DLP-SLA), and to analytically, computationally, and experimentally investigate their compressive mechanical properties and scaling laws. We show that DLP-SLA 3D printing and pyrolysis techniques can affect the designed lattice architecture introducing undesired features as increased nodal volume, non-cubic unit cell and different strut slenderness depending on the beam orientation with respect to the printing direction. We investigate the influence of these factors on the compressive stiffness and strength of non-slender lattices with relative density $\bar{\rho }$ that ranges between 10 and 50%. We prove the inappropriateness of classical analytical tools based on beam theory and the derived expressions for non-slender architectures with negligible effective Poisson's ratio, due to the topological features that are not accounted for in these formulations. We develop computational models that faithfully predicts the experimental lattice response by reproducing the manufactured geometry and we demonstrate that an accurate numerical modeling of non-slender octet lattices with significant nodal volumes allows to identify the deviation from classical scaling laws and enables a proper design of advanced structural DLP-SLA 3D printed carbon architectures.

2. Materials and Methods

2.1. Sample Fabrication

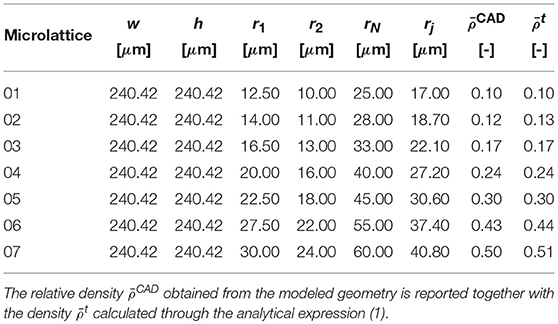
Three sets (A, B, and C) of carbon octet microlattices were manufactured by pyrolyzing polymeric lattices fabricated with a DLP-SLA Autodesk Ember 3D printer that employs a PR-48 transparent photoresist resin. The periodic polymeric 3D printed specimens consisted of a 10 × 3 × 6 (length × width × height) tassellation of 900 μm octet unit cell with three different strut radii of r_A = 52.8 μm, r_B = 71.4 μm, and r_C = 90.0 μm (Figure 1). The microlattices presented a theoretical relative density ${\bar{\rho }}_A=0.16$, ${\bar{\rho }}_B=0.27$, ${\bar{\rho }}_C=0.40$, and a beam slenderness ratio of (r/l)_A = 0.08, (r/l)_B = 0.11, (r/l)_C = 0.14. The DLP-SLA layers were deposited along the height direction and the bottom-most anchoring layer was designed to be thicker in order to sustain the microlattice. Prior to pyrolysis, the anchoring layer of each microstructure was removed using a razor blade to prevent lattice distortion, thus resulting in a 10 × 3 × 5 tassellation. The polymeric lattices were inserted in a fused quartz tube set on a Lindberg tube furnace (model 54357) and pyrolyzed under vacuum. During pyrolysis, the furnace temperature was first raised to 300°C and held constant for 4 h, then increased to 400°C and maintained for 1 h, and finally elevated to 1,000°C and kept constant for 4 h. This procedure, with all heating rates carried out at 10°C/min, led to fully dense microlattices without gasified components and preserved the 3D printed topology.

FIGURE 1

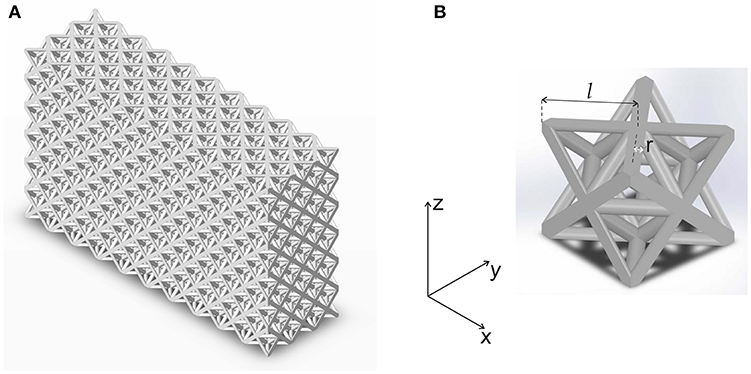
Figure 1. (A) CAD of the microlattice constructed through a three-dimensional tasselation of octet unit cells. (B) A cubic octet unit cell with its geometric parameters l (strut length) and r (strut radius).

2.2. Microstructural Characterization

The polymeric and carbon microlattices obtained after 3D printing and pyrolysis were investigated using a Thermo-Fisher Versa 3D DualBeam Scanning Electron Microscopy (SEM). Specimen sizes, unit cell radii and strut diameters were measured to assess any imperfection and anisotropy introduced during fabrication. The compressive tests on the carbon microlattices were performed using an Instron 5569 electromechanical machine. The load P was applied by imposing a constant displacement rate of 2.5 μm/s on the 5 × 10 unit cells sample surface and was measured with an Instron 2525-804 load cell (R.C. 10 kN). The compressive displacement Δy was evaluated with an LE-01 (Electronic Instrument Research) laser extensometer interfaced with the electromechanical testing frame for data synchronization. Five samples for each set of octet density were characterized and tested along the y-direction. The nominal lattice stress σ was obtained dividing the applied load P by the specimen footprint area, whereas the nominal strain ϵ was calculated from the initial sample height H as ϵ = Δy/H.

2.3. Finite Element Analysis

Full three-dimensional finite element analyses were performed in ABAQUS Standard 2018 in order to simulate the compressive behavior of the microlattices. Numerical simulations were carried out on representative octet unit cells loaded in the y-direction and constrained with boundary conditions that reproduce the response of the unit cell within the lattice. The three-dimensional unit cells were parametrically designed in SolidWorks to reproduce the measured geometrical parameters such as node and beam radii, unit cell height and width, and fillet junction radii between nodes and struts. In addition to the unit cells representative of the fabricated microlattices, other unit cells with different relative density were modeled to investigate the stiffness and strength scaling laws. The microlattices were discretized with linear elastic second-order tetrahedral elements (C3D10) with Young's modulus E = 25.38 GPa (Kudo et.al., in preparation) and Poisson coefficient ν = 0.21 (Price and Kaae, 1969). Compressive forces were applied at the top nodes of the unit cell, with F acting on the central node and F/4 on the lateral nodes shared with four adjacent unit cells. The effective lattice Young's modulus $E_y^{*}=E_x^{*}$ in the y-direction was calculated as the ratio between the average compressive stress on the unit cell ${\sigma }_y^{\mathrm{\text{avg}}}=2F/wh$ and the average compressive strain ${ϵ}_y^{\mathrm{\text{avg}}}={\delta }_y/w$, where δ_y represents the displacement in the y-direction, w and h are the width and height of the unit cell (Figure 2). Similarly, the effective Young's modulus $E_z^{*}$ in the z-direction was obtained as the ratio between the average compressive stress ${\sigma }_z^{\mathrm{\text{avg}}}=2F/w^2$ and the average compressive strain ${ϵ}_z^{\mathrm{\text{avg}}}={\delta }_z/h$, where δ_z represents the displacement in the z-direction. Furthermore, a linear perturbation buckling analysis was conducted on each unit cell to assess the microlattices critical buckling strength.

FIGURE 2

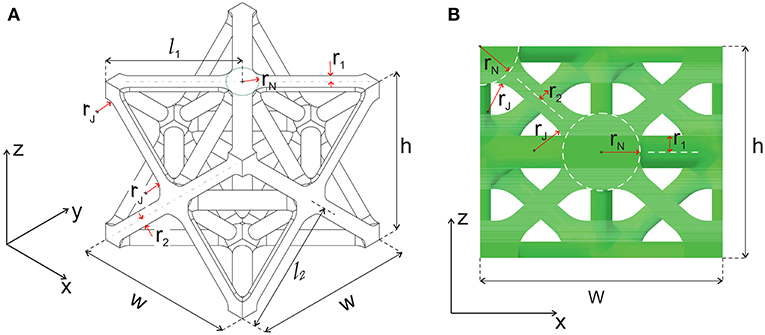
Figure 2. CAD isometric (A) and lateral (B) views of a representative 3D printed and pyrolyzed non-slender octet unit cell as modeled for the finite element analysis. The x-y in-plane beams present radius r₁ and length l₁, while the out-of-plane struts have radius r₂ and length l₂. The struts junction is characterized by the node radius r_N and junction radius r_j.

3. Results and Discussion

3.1. Manufacturing

The geometrical features of the three sets of non-slender 3D-printed polymeric microlattices were investigated by using the SEM. From the images in Figure 3, it was observed that the additive manufacturing technique introduced undesirable lattice imperfections not present in the original computer-aided design (CAD) input files, where the lattices were constituted of cubic octet unit cells with strut radius r and length l. In particular, the height h of the unit cell resulted smaller than the width w, leading to a non-cubic unit cell. Therefore, the length l₁ of the struts deposited along the width direction (x–y plane) was greater than the length l₂ of the inclined struts 3D-printed along the height direction (z-direction). Similarly, the in-plane strut radius r₁ resulted bigger than the out-of-plane beam radius r₂. Moreover, the intersection of twelve struts in a single point produced quasi-spherical nodes with radius r_N and the microlattices presented unsought corrugated surfaces (Figure 3). The deviations from the originally designed lattices were caused by the DLP-SLA 3D printer, whose resolution was limited to 50 μm in the x-y plane and the layer thickness was 25 μm. For these reasons, stereolithography appears inadequate to precisely manufacture features as small as a few tens of microns, which would require other 3D printing techniques as two-photon lithography (Meza et al., 2014; Bauer et al., 2016). The average strut slenderness for the polymeric lattices was ${(r_1/l_1)}_A^{p,xy}=0.10$, ${(r_1/l_1)}_B^{p,xy}=0.12$, and ${(r_1/l_1)}_C^{p,xy}=0.15$ for the struts deposited in x-y plane, and for the inclined struts printed along the z-direction ${(r_2/l_2)}_A^{p,z}=0.07$, ${(r_2/l_2)}_B^{p,z}=0.09$, and ${(r_2/l_2)}_C^{p,z}=0.12$. By comparing the designed struts (from the CAD input files) and the beams of the manufactured lattices, we observed a decrease in the in-plane struts slenderness and an increase in the out-of-plane beam slenderness. This discrepancy is caused by the stereolithography 3D printing.

FIGURE 3

Figure 3. SEM images of the DLP-SLA manufactured polymeric microlattices A (A), B (B), and C (C) observed from the x-z plane. The imperfections introduced by additive manufacturing, visible in all the samples, are orientation dependent strut slenderness, increased nodal volume, and corrugation on the beam surface.

The polymeric lattices were subjected to pyrolysis that led to a ~70% linear shrinkage and produced pyrolytic carbon microlattices (Chen et al., 2017) (Figure 4, left). The three sets of pyrolyzed lattices were examined with SEM and their averaged geometrical parameters were used to define the octet unit cell CAD geometry employed in the numerical simulations (Table 1). Figure 4 shows progressive magnification images which testify that the features present in the original polymeric lattices were preserved throughout the heat treatment for all lattices. It was observed that the strut slenderness after pyrolysis slightly decreased with respect to the polymeric lattices values (maximum deviation was ≈ 10%), hence the heat treatment did not significantly modify the lattice geometry. The average ratio between the unit cell height and width was measured as (h/w)_A = 0.87 and (h/w)_{B, C} = 0.97, thus showing a quasi-cubic architecture for lattices B and C. The ratio between the out-of-plane and in-plane strut radii was r₂/r₁ ≃ 0.8 and the quasi-spherical nodes presented a radius r_N ≃ 2r₁. The highest magnification images report the lateral view of the octet unit cell and are paired with the CAD geometry, showing an excellent agreement between the manufactured and simulated unit cells (Figure 4, right). The only feature not reproduced in the CAD, and therefore not accounted for in the finite element analysis, was the strut corrugation.

FIGURE 4

Figure 4. Optical microscopy (left), SEM characterization (center), and CAD model (right) of the manufactured microlattices A (A), B (B), and C (C) before and after pyrolysis. Progressive magnification images show that pyrolysis preserved the features of the polymeric lattices. The comparison between the fabricated carbon unit cell and the CAD model employed for computational analysis highlights the accuracy of the reproduced architectures.

TABLE 1

Table 1. SEM measured geometrical parameters of the octet unit cell for the manufactured carbon microlattices.

3.2. Relative Density

The relative density of the polymeric lattices was measured before pyrolysis as ${\bar{\rho }}_A^p=0.17$, ${\bar{\rho }}_B^p=0.27$, and ${\bar{\rho }}_C^p=0.39$, thus proving that 3D printing did not alter the desired relative density. After pyrolysis, the density ρ of the carbon microlattices was measured as ρ_A = 0.29 ± 0.02 g/cm³, ρ_B = 0.43 ± 0.02 g/cm³, and ρ_C = 0.62 ± 0.03 g/cm³ for the three sets of manufactured microlattices. Considering the density of pyrolytic carbon ρ_c = 1.85 g/cm³ (Kudo et.al., in preparation), their relative densities were ${\bar{\rho }}_A=0.16\pm 0.01$, ${\bar{\rho }}_B=0.23\pm 0.01$, and ${\bar{\rho }}_C=0.34\pm 0.02$. The relative density of the carbon microlattices slightly decreased with respect to the polymeric lattices, as an effect of the pyrolysis. The theoretical expression for the relative density of a non-cubic octet unit cell in which in-plane cylindrical struts of radius r₁ and length l₁ and out-of-plane cylindrical beams of radius r₂ and length l₂ converge into spherical nodes of radius r_N can be written as

$\begin{array}{ll}{\bar{\rho }}^t=\frac{2\sqrt{2}\pi (r_1^2(l_1-2r_N)+2r_2^2(l_2-2r_N))}{l_1^2{l}_2}+\frac{5\sqrt{2}}{3}\pi \frac{r_N^3}{l_1^2{l}_2},& (1)\end{array}$

where the first term accounts for the struts volume while the second term considers the nodal volume. Although the previous relation neglects the node-strut junctions and the beam corrugations, it well approximates the experimental relative density, with a maximum error of 4% over the three sets of microlattices (Table 1). The same table reports the relative density ${\bar{\rho }}^{\mathrm{\text{CAD}}}$ extrapolated from the unit cell drawing developed with the measured geometrical parameters. The CAD relative density resulted in excellent agreement with the measured relative density even if it does not consider strut corrugation.

3.3. Stiffness

The effective Young's modulus E^* of an ideal octet-truss lattice with beam radius r and length l was first examined by Deshpande et al. (2001) as a stretching dominated solid with pin-jointed struts. Later, several authors investigated the octet lattice as a frame architecture and demonstrated that the assumption of negligible bending effects is valid for a relative density $\bar{\rho }$ lower than 0.1 and strut slenderness r/l lower than 0.06 (Dong et al., 2015; He et al., 2017). From the analysis of the octet unit cell free to deform laterally due to Poisson effect, the lattice stiffness is

$\begin{array}{ll}{E}^{*}=\frac{2\sqrt{2}\pi }{3}E{\left(\frac{r}{l}\right)}^2{K}_b,& (2)\end{array}$

where E is the constituent material Young's modulus, and K_b is a coefficient that accounts for bending effects. In particular, for truss architectures with pin-joined struts K_b = 1, while frame lattices that show bending effects have nodal rigidity K_b > 1, and K_b can be written as

$\begin{array}{ll}{K}_b=\frac{1+15{\left(\frac{r}{l}\right)}^2+36{\left(\frac{r}{l}\right)}^4}{1+7{\left(\frac{r}{l}\right)}^2}.& (3)\end{array}$

These expressions obtained by means of the beam theory predict that the effective Poisson's ratio ν^* is independent of the relative density and equal to 0.33. However, numerical simulations have proven that both rigid (Tancogne-Dejean et al., 2016) and non-rigid (Thiyagasundaram et al., 2010) architectures experience a decrease of ν with an increase of $\bar{\rho }$. Lattices with high relative density behave as bending-dominated structures with irrotational nodes and show limited lateral expansion when compressed. Similarly, the microlattices studied in this work presented a relative density ${\bar{\rho }}_j$ greater than 0.1 and non-slender struts (_ri/li)j > 0.06 for i = 1, 2 and j = A, B, C. These features contribute to limit the lateral displacement of the microlattices, which experimentally showed a negligible effective Poisson's ratio ν^*. Therefore, the effective Young's modulus of non-slender cubic lattices can be obtained by considering the bending effects of a laterally constrained frame unit cell. Through this approximation, equivalent to a null effective Poisson's ratio, the unit cell effective Young's modulus E^* can be written as

$\begin{array}{ll}{E}^{*}=\sqrt{2}\pi E{\left(\frac{r}{l}\right)}^2\left(1+3{\left(\frac{r}{l}\right)}^2\right).& (4)\end{array}$

It should be noticed that the derived formulation (4) predicts the effective stiffness for non-slender lattices with negligible effective Poisson's ratio more accurately than the classical expression (2). However, it can be further improved by considering the manufacturing-induced imperfections as non-cubic unit cells, orientation-dependent beam slenderness, and increased nodal volume, in order to readily provide insights on the influence of each one of these features on the lattice behavior. Therefore, the effective stiffness E^* predicted through Equation (4) is expected to underestimate the experimental microlattice effective Young's modulus as obtained from uniaxial compression tests, testifying the inaccuracy of currently available analytical techniques and justifying the use of numerical tools for the mechanical characterization of the manufactured lattices.

Figure 5 reports the stress-strain curves of the three sets of fabricated carbon microlattices, with five specimens compressed for each relative density considered. It is observed that all samples showed a brittle linear elastic response after an initial toe region. An increase of the relative density yields an higher maximum stress and strain and a lower variability of the results. The effective Young's modulus $E_y^{*}$ resulted $E_{y,A}^{*}$ = 877.90 ± 48.57 MPa for A, $E_{y,B}^{*}$ = 1565.43 ± 66.99 MPa for B, and $E_{y,C}^{*}$ = 2464.81 ± 129.53 MPa for C. Although the achieved stiffnesses do not represent the highest specific stiffness (stiffness to density ratio) ever recorded, they exceed the majority of natural materials and approach the values obtained for nanolattices (Zhang et al., 2019). Figure 6A shows the measured compressive stiffness as a function of the lattice relative density $\bar{\rho }$. The same figure reports the microlattice stiffness obtained from finite element analyses performed on representative octet unit cells with the geometrical parameters measured from SEM (Table 1). The computational effective Young's modulus for the three investigated geometry resulted $E_{y,A}^{*}=1334.74$ MPa, $E_{y,B}^{*}=1876.18$ MPa, and $E_{y,C}^{*}=2849.78$ MPa. The predicted values are in fair agreement with experimental measurements, with 33.5, 16.6, and 13.5% relative errors for the three sets of microlattices A, B, and C. The discrepancy between numerical predictions and measurements decreases with an increase of the sample relative density $\bar{\rho }$. This is primarily attributed to the manufacturing induced corrugation that were not modeled in the computational analysis and were less pronounced as the beam diameter and relative density increase. In particular, the average corrugation amplitude was measured as 18.4% of the off-plane beam diameter for the microlattice A, while it was limited to 11.2 and 8.7% for lattices B and C, respectively. The influence of each one of the manufacturing-induced imperfections on the lattice effective stiffness was not considered because these features are inherently related, however, it is believed that the non-cubic unit cell had the most pronounced effect for the microlattice A, while the nodal geometry had a significant role for microlattices B and C, where the deviation from cubic unit cell is small.

FIGURE 5

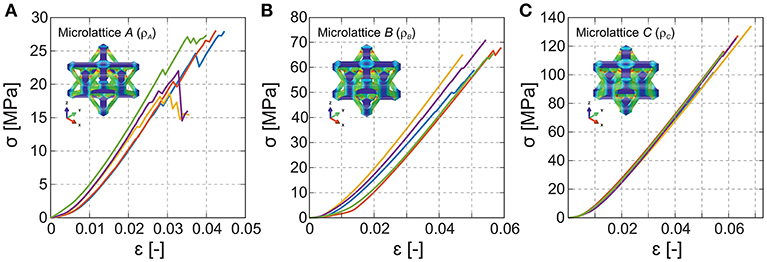
Figure 5. Experimental stress-strain curves for the three sets of microlattices considered: A (A), B (B), and C (C). Five samples were tested for each relative density considered. The insets show the modeled unit cells and their stress distribution during compression.

FIGURE 6

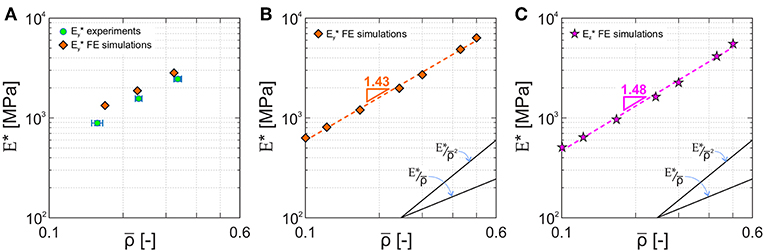
Figure 6. Effective Young's modulus E^* of non-slender carbon microlattices reported as a function of the octet unit cell relative density $\bar{\rho }$. (A) Comparison between the stiffness measured from experiments (green/dot markers) and values predicted from finite element simulations (orange/diamond markers). Effective Young's modulus $E_y^{*}$ (B) and $E_z^{*}$ (C) scaling laws obtained from numerical simulations for relative density that ranges between 10 and 50%.

In order to investigate the effective stiffness scaling law, we performed other numerical simulations on non-slender octet unit cells with relative density $\bar{\rho }$ that varied between 0.10 and 0.50 (Table 2). Similarly to the manufactured microlattices, we modeled cubic unit cells with node radius r_N = 2r₁, junction radius r_j = 1.7r₂, and that contain struts with different in-plane and out-of-plane diameters, with r₂ = 0.8r₁. The obtained stiffness in the y and z directions are reported as a function of the relative density in Figures 6B,C. The effective Young's modulus of the considered non-slender octet lattices scales as $E_y^{*}\propto {\bar{\rho }}^{1.43}$ and $E_z^{*}\propto {\bar{\rho }}^{1.48}$ for the y and z directions respectively, whereas classical scaling law for stretching dominated octet-truss lattices predicts a scaling exponent equal to one (Fleck et al., 2010). Deviations from classical theory were also observed for different rigid architectures when the strut slenderness ratio r/l was larger than 0.07, as a result of nodal contribution on the effective lattice stiffness (Portela et al., 2018). The microlattices manufactured and analyzed in this work present beam slenderness that ranges between 0.065 and 0.17, pronounced nodal volumes and edge effects caused by a limited number of unit cells along the height and width (Christodoulou, 2017). Therefore a scaling exponent m_E > 1 testifies that the lattices experience significant bending during compression.

TABLE 2

Table 2. Geometrical parameters of the octet unit cell employed in the numerical simulations.

3.4. Strength

The compressive strength of an octet-truss lattice material was determined considering the two possible failure mechanisms of elastic buckling or plastic yielding (Deshpande et al., 2001). The analysis of an octet-truss unit cell constituted of cylindrical beams reveals that the strut axial compressive stress σ_a is related to the vertical stress applied to the unit cell σ_v through the relation

$\begin{array}{ll}{\sigma }_v=2\sqrt{2}\pi {\left(\frac{r}{l}\right)}^2{\sigma }_a.& (5)\end{array}$

If the lattice presents a low relative density, elastic buckling will be responsible of the octet-truss structural collapse when the axial stress σ_a reaches the Euler critical value

$\begin{array}{ll}{\sigma }_b=\frac{n^2{\pi }^{2}E}{4}{\left(\frac{r}{l}\right)}^2,& (6)\end{array}$

where n depends on the strut boundary conditions, with n = 1 for a pin-joined strut and n = 2 for a doubly clamped beam. When the strut slenderness increases, buckling is preceded by strut failure (yielding) as the stress reaches the material failure (yield) strength σ_f. Therefore, the compressive strength for an octet-truss material can be expressed as Deshpande et al. (2001)

$\begin{array}{ll}{\sigma }^{*}=\text{min}\left\{\frac{\sqrt{2}{\pi }^3{n}^{2}E}{2}{\left(\frac{r}{l}\right)}^4;2\sqrt{2}\pi {\left(\frac{r}{l}\right)}^2{\sigma }_f\right\}.& (7)\end{array}$

The extension of the expression (7) to non-slender cubic frame lattices was obtained through the analysis of an octet unit cell constrained to deform laterally. Considering bending effects, the relationship (5) between the strut axial stress σ_a and the vertical stress σ_v applied to the unit cell becomes

$\begin{array}{ll}{\sigma }_v=2\sqrt{2}\pi {\left(\frac{r}{l}\right)}^2\left(1+3{\left(\frac{r}{l}\right)}^2\right){\sigma }_a,& (8)\end{array}$

while the dependence of σ_v on the maximum normal stress σ_m at the edges of the strut was obtained considering a combination of the bending moment and axial force effects

$\begin{array}{ll}{\sigma }_z=2\sqrt{2}\pi {\left(\frac{r}{l}\right)}^2\frac{1+3{\left(\frac{r}{l}\right)}^2}{1+6{\left(\frac{r}{l}\right)}^2}{\sigma }_m.& (9)\end{array}$

The octet-frame buckling strength was calculated by inserting Equation (6) into Equation (8), while the lattice failure (yield) strength is achieved when σ_m = σ_f. Hence, the compressive strength for a cubic octet-frame lattice material writes as

$\begin{array}{ll}{\sigma }^{*}=\text{min}\left\{\frac{\sqrt{2}{\pi }^3{n}^{2}E}{2}{\left(\frac{r}{l}\right)}^4\left(1+3{\left(\frac{r}{l}\right)}^2\right);2\sqrt{2}\pi {\left(\frac{r}{l}\right)}^2\frac{1+3{\left(\frac{r}{l}\right)}^2}{1+6{\left(\frac{r}{l}\right)}^2}{\sigma }_f\right\}.& (10)\end{array}$

As observed for the stiffness calculation, simplified analytical expressions fail to capture the complex mechanical response of non-slender architectures as the orientation-dependent slenderness, non cubic unit cell and the nodal contribution are not accounted for Portela et al. (2018). Even though Equation (10) provides an improved strength estimation of octet lattices with negligible effective Poisson's ratio compared to Equation (7), the effects of the manufacturing-induced imperfections are not fully reflected, and they were considered through numerical analyses. Therefore, more comprehensive analytical formulations need to be developed in order to assess the mechanics of imperfect lattices. The experimental strength of the octet microlattices ${\sigma }_y^{*}$ increased with the relative density as shown in Figure 7A, where ${\sigma }_{y,A}^{*}$ = 24.80 ± 4.26 MPa, ${\sigma }_{y,B}^{*}$ = 65.68 ± 4.45 MPa, and ${\sigma }_{y,C}^{*}$ = 122.74 ± 12.28 MPa refer to the three sets of lattices. It should be noticed that the attained specific strengths (strength to density ratio) exceed most of natural materials and approach the values obtained by carbon nanolattices (Bauer et al., 2016; Zhang et al., 2019), which represent the strongest architected materials ever realized. The achievement of strengths comparable to those of nanolattices testifies that through the current manufacturing technique is possible to realize large-scale ultra-strong materials, overcoming the current scalability disadvantages of two-photon lithography nanofabrication.

FIGURE 7

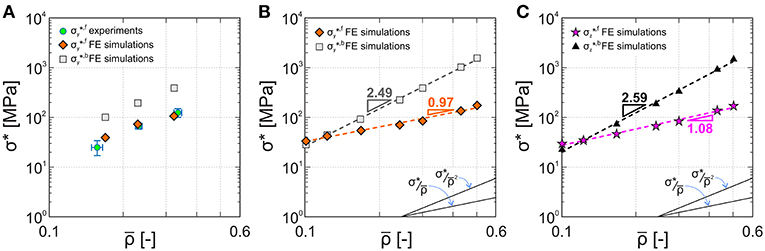
Figure 7. Compressive strength σ^* of non-slender carbon microlattices reported as a function of the octet unit cell relative density $\bar{\rho }$. (A) Comparison between the strength measured from experiments (green/dot markers) and predicted failure ${\sigma }_y^{*,f}$ (orange/diamond markers) and buckling ${\sigma }_y^{*,b}$ (gray/square markers) strengths from finite element simulations. Fracture and buckling strengths scaling laws along the y-direction (B) and z-direction (C) obtained from numerical simulations for a relative density that ranges between 10 and 50%.

Considering the limitations of the analytical formulations, the complex microlattice stress distribution was assessed through numerical simulations, from which the maximum equivalent stress was obtained and was compared with the strength of the constituent material. The bulk strength of pyrolytic carbon has been shown to be dependent on the specimen length-scale (Bullock and Kaae, 1979), with an increase as specimens dimensions decrease. This behavior depends on the probability of finding large critical flaws within the materials, which decreases when the sample dimensions reduce. In brittle materials, the failure strength σ_f is inversely proportional to the square root of the pre-existing flaw size

$\begin{array}{ll}{\sigma }_f=\frac{Y{K}_{Ic}}{\sqrt{\pi a_c}},& (11)\end{array}$

where K_Ic = 0.91 MPa$\sqrt{\mathrm{\text{m}}}$ is the fracture toughness (Zhao et al., 1985; Brezny and Green, 1990), Y = 1 is a non-dimensional geometrical parameter for a semi-elliptical surface flaw loaded in tension or bending (Bauer et al., 2016), and a_c represents the critical flaw size. The strength of glassy carbon fibers of 5 μm diameter made by carbonization of organic polymer reached 2 GPa, corresponding to a flaw size of 66 nm (Kawamura and Jenkins, 1970). Since the strut diameters of the manufactured microlattices range between 20 and 50 μm, we assume that a material strength σ_f = 1.5 GPa can be reached, equivalent to a flaw size of 0.12 μm. From the results of numerical simulations, it is possible to obtain the octet compressive stress along the y-direction that produces a critical equivalent stress within the unit cell. The numerical lattice failure strengths were found ${\sigma }_{y,A}^{*,f}=39.31$ MPa, ${\sigma }_{y,B}^{*,f}=73.17$ MPa, and ${\sigma }_{y,C}^{*,f}=102.83$ MPa for the three sets of carbon microlattices and they are reported in Figure 7A together with the experimental data. Considering the uncertainties in the determination of the material failure strength σ_f and the lack of beam corrugation modeling in the finite element analysis, these results are in fair agreement with the measured values, with a maximum relative error of 36.9%. Furthermore, it should be noted that the numerical simulations were performed on a unit cell level, thus neglecting the edge effects that a finite lattice experience.

Since the struts of the studied microlattices are non-slender, buckling is unlikely to cause failure before the onset of fracture. Numerical buckling analyses on the three octet unit cells confirmed that the fracture strength was achieved before elastic buckling of the out-of-plane beams. The compressive stresses ${\sigma }_y^{*,b}$ that trigger elastic instabilities were numerically found, with ${\sigma }_{y,A}^{*,b}=100.88$ MPa, ${\sigma }_{y,B}^{*,b}=196.07$ MPa and ${\sigma }_{y,C}^{*,b}=389.57$ MPa. It can be seen that the numerical buckling strength ${\sigma }_{y,j}^{*,b}$ is always greater than the fracture strength ${\sigma }_{y,j}^{*,f}$ for the three microlattices j = A, B, C, thus excluding strut instability mechanisms.

The computational analyses on non-slender octet unit cells performed to investigate the effective stiffness scaling laws were employed to calculate the fracture and buckling strengths and their scaling laws. Figures 7B,C shows that for the y loading direction the fracture strength scales as ${\sigma }_y^{*,f}\propto {\bar{\rho }}^{0.97}$, and the buckling strength scales as ${\sigma }_y^{*,b}\propto {\bar{\rho }}^{2.49}$, while in the z-direction ${\sigma }_z^{*,f}\propto {\bar{\rho }}^{1.08}$ and ${\sigma }_z^{*,b}\propto {\bar{\rho }}^{2.59}$. As already noticed for the effective stiffness behavior, the fracture and buckling strengths scaling laws deviate from the classical analysis of octet-truss architectures, where the scaling exponents are m_f = 1 for fracture and m_b = 2 for buckling (Deshpande et al., 2001). The different scaling exponents obtained from the numerical simulations depend on the non-slender architecture and the pronounced nodal volume, and will help the evaluation of the mechanical properties prediction of any lattice with the same ratios between geometrical parameters. Lastly, it should be noted that the results of computational analysis on non-slender cubic octet unit cells with r₂ = 0.8r₁, r_N = 2r₂, and r_j = 1.7r₂ predict that failure due to elastic instability occurs when the relative density $\bar{\rho }$ is lower than 0.12, corresponding to an out-of-plane strut slenderness r₂/l₂ = 0.065.

Similarly to the results reported by Portela et al. (2018), from finite element analyses it was also observed that strain energy concentrates in the nodes and the stress concentration migrates toward the nodes as the relative density increases and beam slenderness decreases. Figure 8, left shows the SEM images of the three sets of manufactured microlattices after catastrophic compression tests, highlighting the failed components and the brittle fracture surfaces. As numerically predicted, the experimental fractographic examination proved that in the lighter microlattice A the nodes remained undamaged and only struts fractured (Figure 8A), while as density increases in lattices B and C node failures were observed (Figures 8B,C). Furthermore, it was commonly noticed among the three sets of samples that fracture within the struts did not follow the stereolithography induced corrugations.

FIGURE 8

Figure 8. SEM fractography of the three sets of manufactures microlattices A (A), B (B), and C (C) after catastrophic mechanical compression tests. Progressive magnification images highlight the brittle fracture surfaces.

4. Conclusion

In the present work, we have investigated the compressive behavior of stiff and strong non-slender octet carbon microlattices obtained by pyrolyzing 3D-printed polymer architectures fabricated through stereolithography. We have shown that additive manufacturing can lead to imperfect lattices with significant nodal volumes and strut slenderness dependent on the beam inclination with respect to the 3D-printing direction. The effects of these features on the lattice structural response have been numerically and experimentally studied considering carbon microlattices with a relative density higher than 10%. The manufactured microarchitectures have achieved superior relative stiffness and strength that approach those of carbon nanolattices. Therefore, we have demonstrated that the employed manufacturing technique can lead a fast realization of large scale strong materials, currently not achievable through nanofabrication. We have extended the classical analytical tools based on beam theory to include non-slender cubic architectures that show a negligible effective Poisson's ratio. These formulations can be adopted for octet lattices constituted of any materials with negligible nonlinearities and viscoelastic effects, independently of the manufacturing process. Although more accurate than classical octet-truss formulations when bending effects are pronounced, the developed analytical construction remains inadequate for the prediction of the effective stiffness and strength of the manufactured non-slender lattices, thus identifying the needs for future analytical investigations of structured solids with orientation dependent geometrical features and pronounced nodal connections, in order to develop optimized materials and assess the influence of these parameters on the lattice mechanical response. To overcome the identified limitations of the analytical tools, we have developed computational models that reproduce the unit cell geometry and capture the mechanical properties of the tested architectures. The numerical investigation has revealed the mechanics of low slenderness microlattices through the prediction of compressive stiffness, failure and buckling strengths, and their scaling laws, which provide a reliable method to estimate the mechanical properties of imperfectly manufactured octet lattices featuring the investigated topology. The presented manufacturing process and numerical methods represent tools to enhance the design of carbon architected materials toward strong and lightweight solids.

Author Contributions

AK, DM, and FB designed the research, discussed the results, and wrote the paper. DM and FB carried out the analytical and numerical analyses. AK manufactured the specimens. AK and YW performed the experiments. All authors reviewed the paper and gave final approval for publication.

Funding

Vannevar-Bush Faculty Fellowship of the US Department of Defense. The Resnick Sustainability Institute Postdoctoral Fellowship of Caltech. Financial support from National Group of Mathematical Physics (GNFM-INdAM).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AK gratefully acknowledges the financial support from the Resnick Sustainability Institute at the California Institute of Technology and from Prof. Julia R. Greer (Caltech) through the Vannevar-Bush Faculty Fellowship of the US Department of Defense. The authors thank Prof. Julia R. Greer's research group (Caltech) and Prof. Sergio Pellegrino (Caltech) for their support in conducting experiments in their laboratories.

References

Amendola, A., Krushynska, A., Daraio, C., Pugno, N., and Fraternali, F. (2018). Tuning frequency band gaps of tensegrity metamaterials with local and global prestress. arXiv preprint arXiv:1803.03472. doi: 10.1016/j.ijsolstr.2018.07.002

CrossRef Full Text | Google Scholar

Anwer, A., and Naguib, H. (2018). Multi-functional flexible carbon fiber composites with controlled fiber alignment using additive manufacturing. Addit. Manuf. 22, 360–367. doi: 10.1016/j.addma.2018.05.013

CrossRef Full Text | Google Scholar

Bauer, J., Schroer, A., Schwaiger, R., and Kraft, O. (2016). Approaching theoretical strength in glassy carbon nanolattices. Nat. Mater. 15, 438–443. doi: 10.1038/nmat4561

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertoldi, K., Vitelli, V., Christensen, J., and van Hecke, M. (2017). Flexible mechanical metamaterials. Nat. Rev. Mat. 2:17066. doi: 10.1038/natrevmats.2017.66

CrossRef Full Text | Google Scholar

Bilal, O. R., Foehr, A., and Daraio, C. (2017). Bistable metamaterial for switching and cascading elastic vibrations. Proc. Natl. Acad. Sci. U.S.A. 114, 4603–4606. doi: 10.1073/pnas.1618314114

PubMed Abstract | CrossRef Full Text | Google Scholar

Brezny, R., and Green, D. (1990). The effect of cell size on the mechanical behavior of cellular materials. Acta Metall. Mater. 38, 2517–2526. doi: 10.1016/0956-7151(90)90263-G

CrossRef Full Text | Google Scholar

Bullock, R., and Kaae, J. (1979). Size effect on the strength of glassy carbon. J. Mater. Sci. 14, 920–930. doi: 10.1007/BF00550723

CrossRef Full Text | Google Scholar

Carneiro, O., Silva, A., and Gomes, R. (2015). Fused deposition modeling with polypropylene. Mater. Des. 83, 768–776. doi: 10.1016/j.matdes.2015.06.053

CrossRef Full Text | Google Scholar

Chen, X., Zhao, G., Wu, Y., Huang, Y., Liu, Y., He, J., et al. (2017). Cellular carbon microstructures developed by using stereolithography. Carbon 123, 34–44. doi: 10.1016/j.carbon.2017.07.043

CrossRef Full Text | Google Scholar

Christodoulou, I. (2017). Mechanical properties of micro-architectured lattices: edge effects, fatigue and fracture (Ph.D. thesis). University College London, London, United Kingdom.

Google Scholar

Deshpande, V., Fleck, N., and Ashby, M. (2001). Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 49, 1747–1769. doi: 10.1016/S0022-5096(01)00010-2

CrossRef Full Text | Google Scholar

Dong, L., Deshpande, V., and Wadley, H. (2015). Mechanical response of t-6al-4v octet-truss lattice structures. Int. J. Solids Struct. 60–61, 107–124. doi: 10.1016/j.ijsolstr.2015.02.020

CrossRef Full Text | Google Scholar

Essa, K., Hassanin, H., Attallah, M., Adkins, N. J., Musker, A., Roberts, G., et al. (2017). Development and testing of an additive manufactured monolithic catalyst bed for htp thruster applications. Appl. Catal. Gen. 542, 125–135. doi: 10.1016/j.apcata.2017.05.019

CrossRef Full Text | Google Scholar

Fleck, N., Deshpande, V., and Ashby, M. (2010). Micro-architectured materials: past, present and future. Proc. R. Soc. Lond. Math. Phys. Eng. Sci. 466, 2495–2516. doi: 10.1098/rspa.2010.0215

CrossRef Full Text | Google Scholar

Fu, K., Yao, Y., Dai, J., and Hu, L. (2017). Progress in 3d printing of carbon materials for energy-related applications. Adv. Mater. 29:1603486. doi: 10.1002/adma.201603486

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibson, L., and Ashby, M. (1997). Cellular Solids: Structures and Properties. Cambridge: Cambridge University Press.

Google Scholar

He, Z., Wang, F., Zhu, Y., Wu, H., and Park, H. (2017). Mechanical properties of copper octet-truss nanolattices. J. Mech. Phys. Solids 101, 133–149. doi: 10.1016/j.jmps.2017.01.019

CrossRef Full Text | Google Scholar

Hengsbach, S., and Lantada, A. (2014). Direct laser writing of auxetic structures: present capabilities and challenges. Smart Mater. Struct. 23.8:085033. doi: 10.1088/0964-1726/23/8/085033

CrossRef Full Text | Google Scholar

Jacobsen, A., Mahoney, S., and Carter, S. N. (2011). Vitreous carbon micro-lattice structures. Carbon 49, 1025–1032. doi: 10.1016/j.carbon.2010.10.059

CrossRef Full Text | Google Scholar

Kawamura, K., and Jenkins, G. (1970). A new glassy carbon fibre. J. Mater. Sci. 5, 262–267. doi: 10.1007/BF00551003

CrossRef Full Text | Google Scholar

Lewicki, J. P., Rodriguez, J. N., Zhu, C., Worsley, M. A., Wu, A. S., Kanarska, Y., et al. (2017). 3d-printing of meso-structurally ordered carbon fiber/polymer composites with unprecedented orthotropic physical properties. Sci. Rep. 7:43401. doi: 10.1038/srep43401

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Leu, M., Panat, R., and Park, J. (2017). A hybrid three-dimensionally structured electrode for lithium-ion batteries via 3D printing. Mater. Des. 119, 417–424. doi: 10.1016/j.matdes.2017.01.088

CrossRef Full Text | Google Scholar

Maggi, A., Li, H., and Greer, J. (2017). Three-dimensional nano-architected scaffolds with tunable stiffness for efficient bone tissue growth. Acta Biomater. 63, 294–305. doi: 10.1016/j.actbio.2017.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Meza, L., Phlipot, G., Portela, C., Maggi, A., Montemayor, L., Comella, A., et al. (2017). Reexamining the mechanical property space of three-dimensional lattice architectures. Acta Mater. 140, 424–432. doi: 10.1016/j.actamat.2017.08.052

CrossRef Full Text | Google Scholar

Meza, L. R., Das, S., and Greer, J. R. (2014). Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 345, 1322–1326. doi: 10.1126/science.1255908

PubMed Abstract | CrossRef Full Text | Google Scholar

Meza, L. R., Zelhofer, A. J., Clarke, N., Mateos, A. J., Kochmann, D. M., and Greer, J. R. (2015). Resilient 3D hierarchical architected metamaterials. Proc. Nat. Acad. Sci. U.S.A. 112, 11502–11507. doi: 10.1073/pnas.1509120112

PubMed Abstract | CrossRef Full Text | Google Scholar

Misseroni, D., Colquitt, D. J., Movchan, A. B., Movchan, N. V., and Jones, I. S. (2016). Cymatics for the cloaking of flexural vibrations in a structured plate. Sci. Rep. 6:23929. doi: 10.1038/srep23929

PubMed Abstract | CrossRef Full Text | Google Scholar

Murr, L. E., Gaytan, S. M., Medina, F., Lopez, H., Martinez, E., Machado, B. I., et al. (2010). Next-generation biomedical implants using additive manufacturing of complex, cellular and functional mesh arrays. Philos. Trans. R. Soc. Lond. Math. Phys. Eng. Sci. 368, 1999–2032. doi: 10.1098/rsta.2010.0010

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, D. T., Meyers, C., Yee, T. D., Dudukovic, N. A., Destino, J. F., Zhu, C., et al. (2017). 3D-printed transparent glass. Adv. Mater. 29. doi: 10.1002/adma.201701181

PubMed Abstract | CrossRef Full Text | Google Scholar

Ni, R., Qian, B., Liu, C., Liu, X., and Qiu, J. (2018). Three-dimensional printing of hybrid organic/inorganic composites with long persistence luminescence. Opt. Mater. Express 8, 2823–2831. doi: 10.1364/OME.8.002823

CrossRef Full Text | Google Scholar

Pellegrino, S., and Calladine, C. (1986). Matrix analysis of statically and kinematically indeterminate frameworks. Int. J. Solids Struct. 22, 409–428. doi: 10.1016/0020-7683(86)90014-4

CrossRef Full Text | Google Scholar

Portela, C., Greer, J., and Kochmann, D. (2018). Impact of node geometry on the effective stiffness of non-slender three-dimensional truss lattice architectures. Extreme Mech. Lett. 22, 138–148. doi: 10.1016/j.eml.2018.06.004

CrossRef Full Text | Google Scholar

Price, R., and Kaae, J. (1969). Poisson's ratio of pyrolytic carbon. Carbon 7, 706–708. doi: 10.1016/0008-6223(69)90529-6

CrossRef Full Text | Google Scholar

Quintanilla, A., Casas, J., Miranzo, P., Osendi, M., and Belmonte, M. (2018). 3D-printed fe-doped silicon carbide monolithic catalysts for wet peroxide oxidation processes. Appl. Catal. B Environ. 235, 246–255. doi: 10.1016/j.apcatb.2018.04.066

CrossRef Full Text | Google Scholar

Schaedler, T. A., Jacobsen, A. J., Torrents, A., Sorensen, A. E., Lian, J., Greer, J. R., et al. (2011). Ultralight metallic microlattices. Science 334, 962–965. doi: 10.1126/science.1211649

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwab, H., Palm, F., Kühn, U., and Eckert, J. (2016). Microstructure and mechanical properties of the near-beta titanium alloy ti-5553 processed by selective laser melting. Mater. Des. 105, 75–80. doi: 10.1016/j.matdes.2016.04.103

CrossRef Full Text | Google Scholar

Shan, S., Kang, S. H., Raney, J. R., Wang, P., Fang, I., candido, F., et al. (2015). Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301. doi: 10.1002/adma.201501708

PubMed Abstract | CrossRef Full Text | Google Scholar

Spierings, A., Wegener, K., Kenel, C., and Leinenbach, C. (2015). Processing of metal-diamond-composites using selective laser melting. Rapid Prototyp. J. 21, 130–136. doi: 10.1108/RPJ-11-2014-0156

CrossRef Full Text | Google Scholar

Sugino, C., Leadenham, S., Ruzzene, M., and Erturk, A. (2015). On the mechanism of bandgap formation in locally resonant finite elastic metamaterials. J. Appl. Phys. 120:134501. doi: 10.1063/1.4963648

CrossRef Full Text | Google Scholar

Sun, K., Wei, T. S., Ahn, B. Y., Seo, J. Y., Dillon, S. G., and Lewis, J. A. (2013). 3D printing of interdigitated Li-ion microbattery architectures. Adv. Mater. 25, 4539–4543. doi: 10.1002/adma.201301036

PubMed Abstract | CrossRef Full Text | Google Scholar

Tancogne-Dejean, T., Spierings, A., and Mohr, D. (2016). Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 116, 14–28. doi: 10.1016/j.actamat.2016.05.054

CrossRef Full Text | Google Scholar

Thiyagasundaram, P., Sankar, B., and Arakere, N. (2010). Elastic properties of open-cell foams with tetrakaidecahedral cells using finite element analysis. AIAA J. 48:818. doi: 10.2514/1.J050022

CrossRef Full Text | Google Scholar

Wilkes, J., Hagedorn, Y., Meiners, W., and Wissenbach, K. (2013). Additive manufacturing of zro2-al2o3ceramic components by selective laser melting. Rapid Prototyp. J. 19, 51–57. doi: 10.1108/13552541311292736

CrossRef Full Text | Google Scholar

Xia, X., Leo, C. D., Gu, X., and Greer, J. (2016). In situ lithiation–delithiation of mechanically robust cu-si core-shell nanolattices in a scanning electron microscope. ACS Energy Lett. 1, 492–499. doi: 10.1021/acsenergylett.6b00256

CrossRef Full Text | Google Scholar

Yao, Y., Fu, K. K., Yan, C., Dai, J., Chen, Y., Wang, Y., et al. (2016). Three-dimensional printable high-temperature and high-rate heaters. ACS Nano 10, 5272–5279. doi: 10.1021/acsnano.6b01059

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Zhang, F., Medarametla, S., Li, H., Zhou, C., and Lin, D. (2016). 3D printing of graphene aerogels. Small 12, 1702–1708. doi: 10.1002/smll.201503524

CrossRef Full Text | Google Scholar

Zhang, X., Vyatskikh, A., Gao, H., Greer, J. R., and Li, X. (2019). Lightweight, flaw-tolerant, and ultrastrong nanoarchitected carbon. Proc. Natl. Acad. Sci. U.S.A. 116, 6665–6672. doi: 10.1073/pnas.1817309116

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, J., Bradt, R., and Walker, P. L. Jr. (1985). The fracture toughness of glassy carbons at elevated temperatures. Carbon 23, 15–18. doi: 10.1016/0008-6223(85)90190-3

CrossRef Full Text | Google Scholar

Zhu, C., Han, T. Y., Duoss, E. B., Golobic, A. M., Kuntz, J. D., Spadaccini, C. M., et al. (2015). Highly compressible 3D periodic graphene aerogel microlattices. Nat. Commun. 6:6962. doi: 10.1038/ncomms7962

PubMed Abstract | CrossRef Full Text | Google Scholar