Properties Tests and Mathematical Modeling of Viscoelastic Damper at Low Temperature With Fractional Order Derivative

Introduction

Viscoelastic materials and dampers are a kind of passive energy dissipation techniques, which are widely used for vibration isolation and suppression in the fields of aerospace, mechanical engineering, precision instruments, and civil engineering. Rao (2003) introduced the noise control and vibration isolation technology with special treated viscoelastic laminates and spray paints and its application in vehicles and commercial airplanes. Rashid and Nicolescu (2008) developed a tuned viscoelastic damper for the unwanted vibration control of a workpiece on a palletized workholding system in milling operations. The tuned viscoelastic damper has high damping performance over a wide range of excitation frequencies, and can effectively reducethe vibration amplitudes during the milling process. Xu Z. D. et al. (2019) utilized a new kind of vibration isolation and mitigation system with high damping viscoelastic materials for reducing dynamic responses of a platform structure. The simulation results show that the system can significantly reduce the dynamic responses of the platform. Xu (2007) and Tsai and Lee (1993) applied the viscoelastic dampers in civil engineering to control the seismic behaviors of the reinforced concrete frame structures and high-rise buildings, respectively. The mathematical models for viscoelastic materials are investigated, and the effectiveness of the viscoelastic dampers are verified with dynamic experiments.

In practical applications, viscoelastic dampers are always added to the building structures or equipment, and work together to reduce the vibration responses. The dynamic properties, structure design and applications of viscoelastic dampers have been extensively studied by scholars. Min et al. (2004) carried out the seismic experiments of a 5-story full-scale steel structure model with added viscoelastic dampers, and presented a design process of the viscoelastic dampers by using the modal strain energy method. Samali and Kwok (1995) summarized the usage of viscoelastic dampers in building structures, and identified the factors affecting the dynamic performance and design procedure of viscoelastic dampers. Matsagar and Jangid (2005) investigated the seismic behaviors of multi-storied base-isolated structures with various types of isolation systems. The structures were also connected to the adjacent base-isolated or base-fixed structures by using viscoelastic dampers. The governing equations of motions for the structures were derived and solved with the Newmark's step-by-step method. The viscoelastic damper connection is found to be effective and useful in upgrading the seismic performance of the combined structures. Xu et al. (2003, 2004) introduced the simplex method to optimize the design parameters and locations of viscoelastic dampers, and conducted shaking table tests about reinforced concrete structures with viscoelastic dampers to validate the efficiency of the simplex method.

Viscoelastic materials are the main components of the viscoelastic damper, and the mechanical properties of the viscoelastic damper are greatly affected by the damping performance of the viscoelastic materials. Therefore, it is necessary to study the dynamic properties of viscoelastic materials. The appropriate selection of mathematical models is the basis for the investigation of energy dissipation and material application of viscoelastic materials. The classical models, such as the Kelvin model, Maxwell model, generalized viscoelastic models et al. (Christensen, 1971), can well describe the dynamic properties of the viscoelastic materials with varying frequencies. Based on classical models, Payne (1963) found that the amplitude of loading displacement had a significant influence on the dynamic properties of viscoelastic materials and proposed the Krous model to capture the displacement effect. Drozdov and Dorfmann (2002) studied the fracture and reformation phenomenon of the polymer molecular chains and formulated the viscoelastic constitutive relations of the rubber polymers considering the temperature influence.

The theory of fractional derivative is a concept from mathematical field, which unifies and generalizes classical calculus for non-integer order of derivation. After the first introduction by Abel in the last decades of nineteenth century, the fractional derivative was successfully applied in many areas such as heat conduction, diffusion, viscoelasticity, and mechanics of solids, control theory, and electricity (Caputo, 1974; Bagley and Torvik, 1983; Koeller, 1984; Rossikhin and Shitikova, 1997). Pritz (2003) and Schiessel et al. (1995) utilized the fractional derivative to study the viscoelastic materials and obtained the five-parameter fractional derivative model and generalized fractional derivative mathematical model. Poojary and Gangadharan (2018) introduced fractional calculation to modify the traditional viscoelastic theories and used the fractional Maxwell model to describe the viscous behavior of magnetorheological elastomers. Liu and Xu (2006) adopt the higher-order fractional derivative model to discuss the rheological properties of human bones, and the test and numerical results show that the higher-order fractional derivative model is successful and efficient in describing the viscoelasticity of human tissues. Xu et al. (2014, 2015, 2016); Xu Y. S. et al. (2019) combined the fractional derivative mathematical models and the temperature-frequency equivalent theory to characterize the effects of ambient temperature and frequency on dynamic performance of viscoelastic dampers.

It can be seen that there are few studies on the dynamic properties of viscoelastic materials and dampers at extreme low temperature with fractional derivative. In the present paper, several dynamic properties tests of the viscoelastic damper at −5°C are conducted under different frequencies and displacements. The seven-parameter fractional derivative model is modified with the temperature-frequency equivalent principle and utilized to describe the dynamic behaviors of the viscoelastic damper. The 9050A and ZN22 viscoelastic materials are used to verify the modified seven-parameter fractional derivative model. The experimental and numerical results show that the viscoelastic damper has perfect energy dissipation at low temperature (−5°C), and the modified seven-parameter fractional derivative model can well capture the dynamic behavior of viscoelastic materials and dampers under different frequencies and temperatures.

Properties Tests

To investigate the mechanical properties of the viscoelastic damper at low temperature, the dynamic properties tests under different excitation frequencies and displacement amplitudes with −5°C are carried out and analyzed. The results show that the viscoelastic damper has perfect energy dissipation capacity, and the dynamic properties are increasing with excitation frequency and reduces when the displacement amplitude increases.

Test Procedure

The viscoelastic damper used in this paper consists of two 10-mm thick parallel viscoelastic layers and three 7-mm thick steel plates, as seen in Figure 1. The viscoelastic material used for the viscoelastic layers is based on the nitrile butadiene rubber, which has been developed and tested in our previous research (Xu et al., 2016), and has high energy dissipation capacity. The viscoelastic layers and the steel plates are connected together by chemical bonding in vulcanization, and deform in the opposite direction. The viscoelastic layer of the viscoelastic damper undergoes almost pure shear deformation and the external energy can be transferred into heat during the loading process.

FIGURE 1

Figure 1. Photo of the viscoelastic damper.

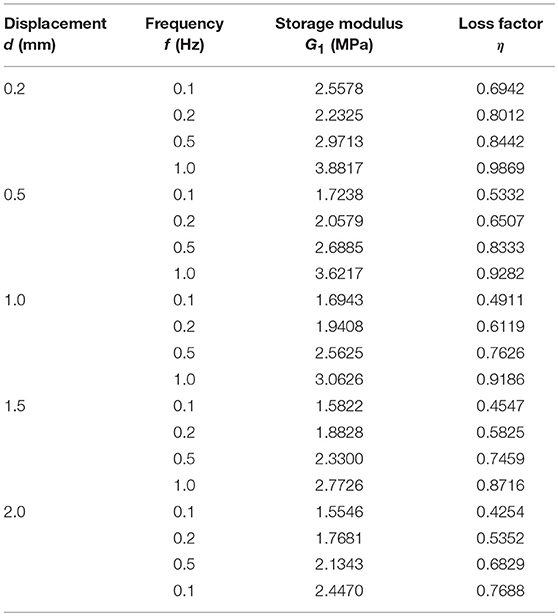
In order to study the influence of excitation frequency and displacement amplitude on mechanic properties of the viscoelastic damper, the performance tests are conducted with a 100 kN servo-hydraulic test machine in RC&PC Key Laboratory of Education Ministry, China, as shown in Figure 2. Each test is conducted with 10 cycles of sinusoidal displacement u_d = u₀sin(2πft), where u₀ is the maximum displacement during one loading circle, and f is the excitation frequency, the loading conditions are listed in Table 1. The environmental temperature of the viscoelastic damper is kept at −5°C with a temperature controlling device during the whole test, as seen in Figure 2.

TABLE 1

Table 1. Loading conditions for properties tests of the viscoelastic damper.

FIGURE 2

Figure 2. Properties tests of the viscoelastic damper.

Test Results and Analysis

To obtain the dynamic properties of the viscoelastic damper, the force-displacement recording of the fifth loading circle at each test condition is picked up and vividly graphed. Additionally, the dynamic properties parameters of the viscoelastic damper at each test condition is obtained and analyzed.

The representative hysteresis curves of the viscoelastic damper are given in Figure 3. It can be seen that the hysteresis curves of the viscoelastic damper are almost full ellipse, which demonstrates that the viscoelastic damper has perfect energy dissipation (Tsai and Lee, 1993; Samali and Kwok, 1995; Min et al., 2004). It can be seen in Figures 3A,B that, the slope and area of the hysteresis curves increase when the frequency increases, meaning that the energy dissipation capacity and stiffness increase with increasing frequency. Figures 3C,D show that the area of the hysteresis curves increases with increasing displacement, while the slope of the hysteresis curves is slightly decreased. As the slope and area of the hysteresis curves are directly related to the energy dissipation and stiffness of the viscoelastic damper, it can be concluded that the energy dissipation increases with increasing displacement and the stiffness decreases.

FIGURE 3

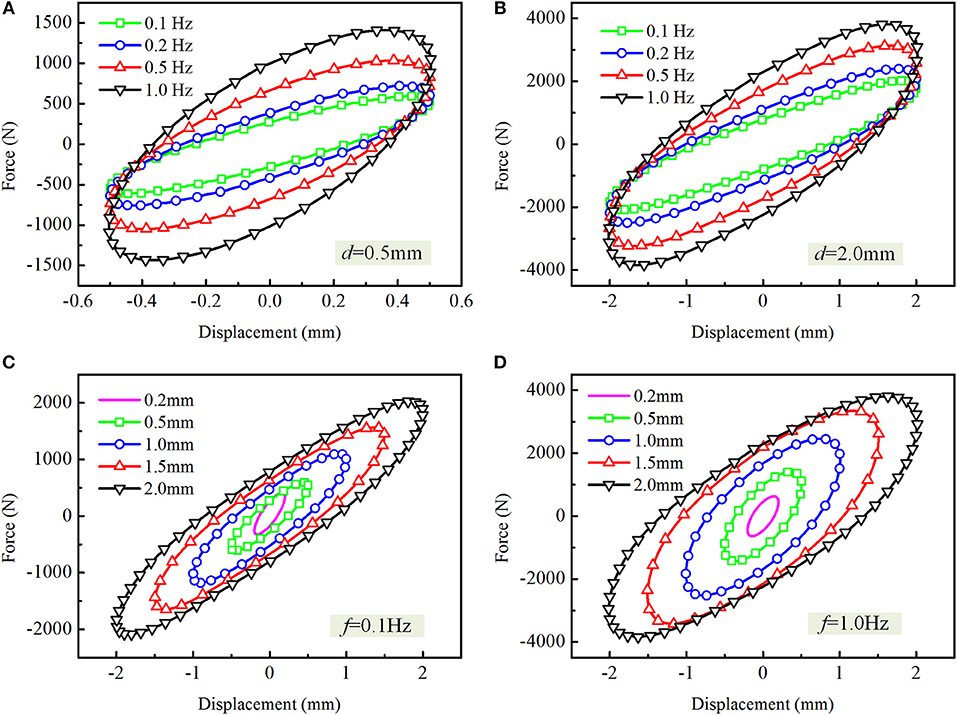
Figure 3. The representative force-displacement hysteresis loops of the viscoelastic damper. (A–D) d = 0.5 mm, d = 2.0 mm, f = 0.1 Hz, and f = 1.0 Hz, respectively.

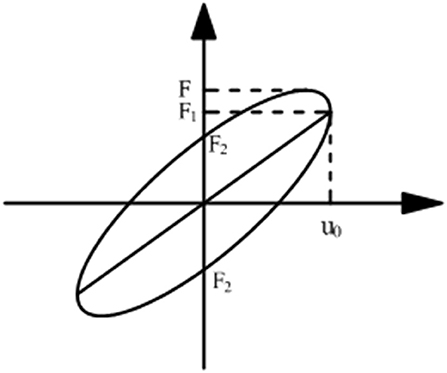
According to the energy dissipation theory of viscoelastic dampers (Tsai and Lee, 1993; Samali and Kwok, 1995; Min et al., 2004), each single hysteresis curve of the viscoelastic damper with the sinusoidal excitation u_d = u₀sin(2πft) can be taken as a full ellipse as shown in Figure 4. The force-displacement relationship has the form

$\begin{array}{ll}{\left(\frac{F_d-K_e{u}_d}{\eta K_e{u}_0}\right)}^2+{\left(\frac{u_d}{u_0}\right)}^2=1& (1)\end{array}$

where F_d and u_d is the damping force and displacement of the viscoelastic damper, respectively; K_e is the equivalent stiffness and $K_e=\frac{F_1}{u_0}$, and u₀ is the displacement amplitude, and F₁ is the damping force at the maximum displacement; F₂ is the corresponding force at the zero displacement, and F is the biggest damping force in the single hysteresis curve.

FIGURE 4

Figure 4. Force-displacement hysteresis curve.

Then, the most important dynamic parameters, the storage modulus G₁ and loss factor η of the viscoelastic damper can be expressed as

$\begin{array}{ll}{G}_1=\frac{F_1{h}_v}{n_v{A}_v{u}_0}& (2)\end{array}$

$\begin{array}{ll}\eta =\frac{F_2}{F_1}& (3)\end{array}$

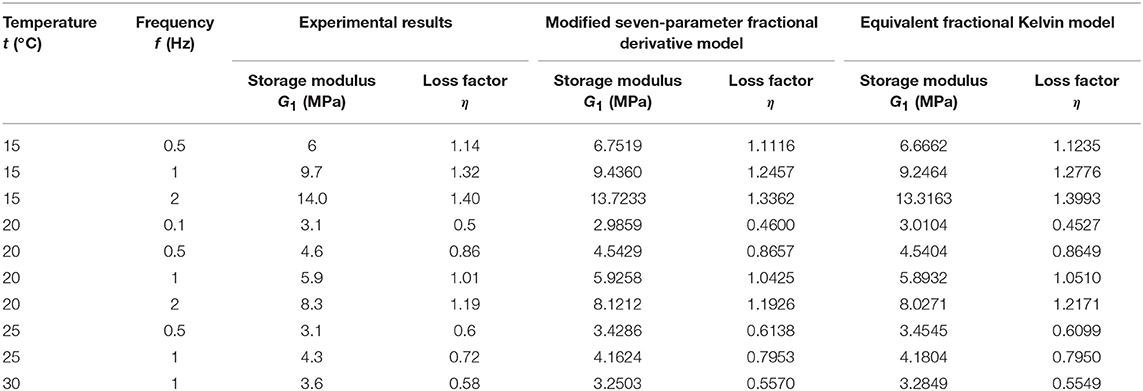
where n_v presents the number of viscoelastic material layers, A_v and h_v is the shear area and thickness of the viscoelastic material layer. For the viscoelastic damper used in this study, n_v = 2, A_v = 3000 mm² and h_v = 10 mm. Then, with Equations (2) and (3), the storage modulus G₁ and loss factor η of the viscoelastic damper at each test condition can be calculated and listed in Table 2.

TABLE 2

Table 2. Characteristic parameters G₁, η of the viscoelastic damper.

To clearly reveal the dynamic properties and energy dissipation of the viscoelastic damper, the storage modulus G₁ and loss factor η at each test condition are pictured in Figure 5.

FIGURE 5

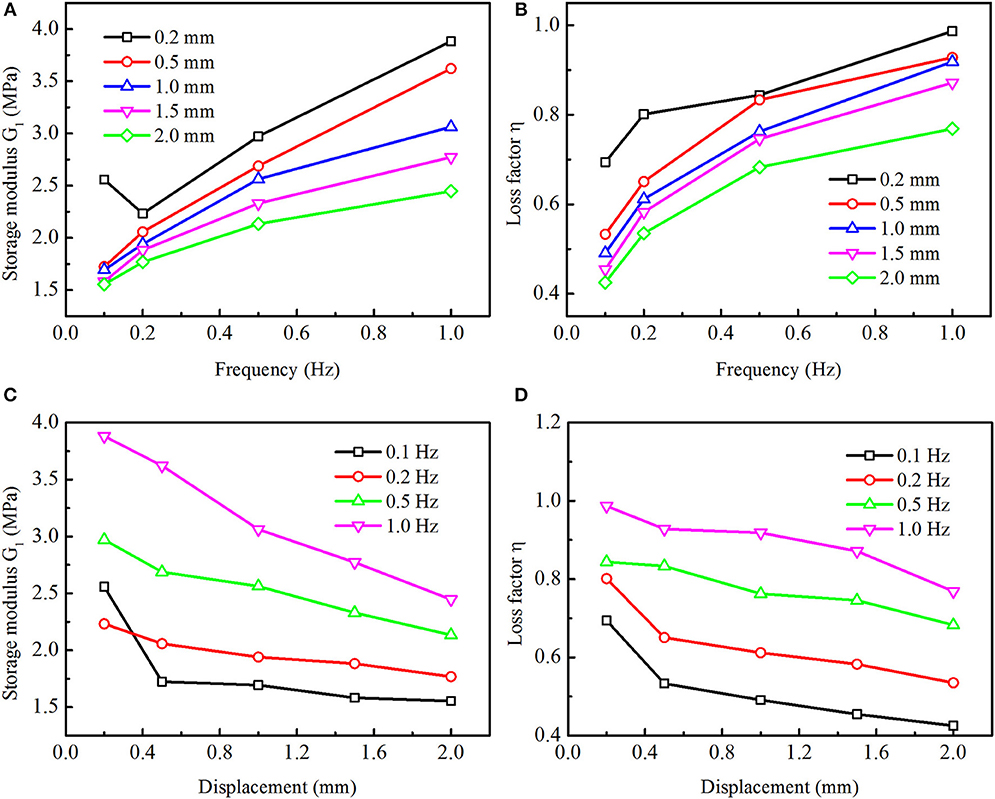
Figure 5. The storage modulus and loss factor of the viscoelastic damper with different test conditions. (A–D) Storage modulus, loss factor, storage modulus, and loss factor, respectively.

Figures 5A,B show the relationship of characteristic parameters and excitation frequency. It can be seen that the storage modulus and loss factor increase rapidly with increasing frequency. Take 1 mm as an example, the storage modulus is increased by 14.59% in the range of 0.1–0.2 Hz, increased by 32.03% in the range of 0.2–0.5 Hz, and increased by 19.52% in the range of 0.5–1.0 Hz. The loss factor is increased by 24.6% in the range of 0.1–0.2 Hz, increased by 24.63% in the range of 0.2–0.5 Hz and increased by 20.46% in the range of 0.5–1.0 Hz. In summary, the storage modulus and loss factor of the viscoelastic damper are greatly influenced by the excitation frequency.

Figures 5C,D give the relationships between the characteristic parameters and displacement amplitude. It can be seen that the storage modulus and loss factor decreases with increasing displacement amplitude. Taking the condition of 0.5 Hz as an example, the storage modulus is decreased by 9.52% in the range of 0.2–0.5 mm, decreased by 4.69% in the range of 0.5–1.0 mm, decreased by 9.07% in the range of 1.0–1.5 mm, and decreased by 8.4% in the range of 1.5–2.0 mm. The loss factor is decreased by 1.29% in the range of 0.2–0.5 mm, decreased by 8.48% in the range of 0.5–1.0 mm, decreased by 2.19% in the range of 1.0–1.5 mm and decreased by 8.45% in the range of 1.5–2.0 mm. It also should be noted that the storage modulus with frequency 0.1 Hz and displacement 0.2 mm are much larger than that with frequency 0.2 Hz and displacement 0.2 mm, this abnormal phenomenon may occur due to the test errors during the experimental process and the properties complexity of viscoelastic materials at low temperature situations. In summary, the displacement amplitude have important influence on the storage modulus and loss factor of the viscoelastic damper.

Modification of the Seven-Parameter Fractional Derivative Model

The seven-parameter fractional derivative model include three parallel elements, one Hook spring element and two fractional Maxwell models (Müller et al., 2011), as shown in Figure 6. The stress-strain relation of the Hook spring can be given as

$\begin{array}{ll}{\mu }_0{\epsilon }_0={\sigma }_0& (4)\end{array}$

where μ₀ presents the modulus of the Hook spring element. For the two fractional Maxwell models

$\begin{array}{ll}{\mu }_i{\epsilon }_{is}={\eta }_i{D}^{{\alpha }_i}{\epsilon }_{id}={\sigma }_i& (5)\end{array}$

$\begin{array}{ll}{\epsilon }_{is}+{\epsilon }_{id}={\epsilon }_i& (6)\end{array}$

where μ_i and η_i present the modulus of the spring and the damping coefficient of the fractional dashpot for the i-th fractional Maxwell model, respectively, i = 1, 2; $D^{{\alpha }_i}$ denotes the α_i-order fractional derivative, and 0 < α_i < 1; σ_i and ε_i denote the stress and strain of i-th fractional Maxwell model, respectively; ε_is andε_id present the strain of the spring and dashpot, respectively. Then we have

$\begin{array}{ll}{\epsilon }_0={\epsilon }_1={\epsilon }_2={\epsilon }_t& (7)\end{array}$

$\begin{array}{ll}{\sigma }_0+{\sigma }_1+{\sigma }_2={\sigma }_t& (8)\end{array}$

where σ_t and ε_t are the stress and strain of the seven-parameter fractional derivative model.

FIGURE 6

Figure 6. The seven-parameter fractional derivative model.

From Equations (5) and (6), we can obtain

$\begin{array}{ll}{\mu }_i{\eta }_i{D}^{{\alpha }_i}{\epsilon }_i=\left({\mu }_i+{\eta }_i{D}^{{\alpha }_i}\right){\sigma }_i& (9)\end{array}$

By performing the Fourier transform on Equation (9), we can get

$\begin{array}{ll}{\mu }_i{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}{\epsilon }_i^{*}=\left({\mu }_i+{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}\right){\sigma }_i^{*}& (10)\end{array}$

where ω is the angular frequency of the loading stress or strain; and j is the unit complex number; and the star symbol denotes that the strain and stress are in complex form. Then the modulus of each fractional Maxwell model in complex form, expressed in the frequency domain, can be obtained as

$\begin{array}{ll}{G}_i^{*}=\frac{{\mu }_i{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}}{{\mu }_i+{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}}& (11)\end{array}$

Together with Equations (4), (7), (8), and (11), we can obtain the complex modulus of the seven-parameter fractional derivative model

$\begin{array}{ll}{G}^{*}={\mu }_0+{\displaystyle \sum _{i=1}^2}\frac{{\mu }_i{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}}{{\mu }_i+{\eta }_i{\left(j\omega \right)}^{{\alpha }_i}}& (12)\end{array}$

By applying the relation $j^{{\alpha }_i}=\mathrm{\text{cos}}\left(\frac{{\alpha }_i\pi }{2}\right)+\mathrm{\text{sin}}\left(\frac{{\alpha }_i\pi }{2}\right)j$ into Equation (12), the complex modulus can be decomposed into two parts, the real part and the imaginary part, which are defined as the storage modulus and loss modulus of viscoelastic materials, and the ratio of the loss modulus to the storage modulus is taken as the loss factor, then

$\begin{array}{ll}{G}_1=\text{Re}\left(G^{*}\right)={\mu }_0+{\displaystyle \sum _{i=1}^2}\frac{{\mu }_i^2{\eta }_i{\omega }^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\mu }_i{\eta }_i^2{\omega }^{2{\alpha }_i}}{{\mu }_i^2+2{\mu }_i{\eta }_i{\omega }^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\eta }_i^2{\omega }^{2{\alpha }_i}}& (13)\end{array}$

$\begin{array}{ll}{G}_2=\text{Im}\left(G^{*}\right)={\displaystyle \sum _{i=1}^2}\frac{{\mu }_i^2{\eta }_i{\omega }^{{\alpha }_i}\text{sin}\left(\frac{{\alpha }_i\pi }{2}\right)}{{\mu }_i^2+2{\mu }_i{\eta }_i{\omega }^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\eta }_i^2{\omega }^{2{\alpha }_i}}& (14)\end{array}$

$\begin{array}{ll}\eta =\frac{G_2}{G_1}& (15)\end{array}$

Where G₁, G₂, and η denote the storage modulus, loss modulus and loss factor of viscoelastic materials.

There is an equivalent relationship between high temperature and low frequency for most viscoelastic materials when the temperature is from the glass transition temperature Tg to Tg⁺ 100°C, which can be described by the temperature-frequency equivalent theory (Xu et al., 2014, 2015, 2016; Xu Y. S. et al., 2019), as shown in Equation (16)

$\begin{array}{l}{G}_1(\omega ,T)=G_1({\alpha }_T\omega ,T_0)\\ \eta (\omega ,T)=\eta ({\alpha }_T\omega ,T_0)& (16)\end{array}$

where T₀ is the reference temperature, and α_T is the function of temperature and has the form

$\begin{array}{ll}{\alpha }_T={10}^{-12(T-T_0)/\left[525+(T-T_0)\right]}& (17)\end{array}$

when this theory is used to describe the dynamic properties of the viscoelastic damper with different temperatures, the dynamic parameters of the viscoelastic damper in Equations (13)–(15) can be changed as

$\begin{array}{ll}{G}_1={\mu }_0+{\displaystyle \sum _{i=1}^2}\frac{{\mu }_i^2{\eta }_i{\left({\alpha }_T\omega \right)}^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\mu }_i{\eta }_i^2{\left({\alpha }_T\omega \right)}^{2{\alpha }_i}}{{\mu }_i^2+2{\mu }_i{\eta }_i{\left({\alpha }_T\omega \right)}^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\eta }_i^2{\left({\alpha }_T\omega \right)}^{2{\alpha }_i}}& (18)\end{array}$

$\begin{array}{ll}{G}_2={\displaystyle \sum _{i=1}^2}\frac{{\mu }_i^2{\eta }_i{\left({\alpha }_T\omega \right)}^{{\alpha }_i}\text{sin}\left(\frac{{\alpha }_i\pi }{2}\right)}{{\mu }_i^2+2{\mu }_i{\eta }_i{\left({\alpha }_T\omega \right)}^{{\alpha }_i}\text{cos}\left(\frac{{\alpha }_i\pi }{2}\right)+{\eta }_i^2{\left({\alpha }_T\omega \right)}^{2{\alpha }_i}}& (19)\end{array}$

$\begin{array}{ll}\eta =\frac{G_2}{G_1}& (20)\end{array}$

Equations (17)–(20) are the formulations of the modified seven-parameter fractional derivative model. The advantage of this modified model is that it is more efficient in describing the nonlinear behavior of viscoelastic materials (Müller et al., 2011), and it can reveal the influence of different temperatures and frequencies on the mechanical properties of viscoelastic materials at the same time.

Model Application for the Viscoelastic Damper

In this section, in order to deeply investigate the influence of frequency on the dynamic properties of the viscoelastic damper at low temperature (−5°C), the abovementioned mathematical model, the modified seven-parameter fractional derivative model, and the equivalent fractional Kelvin model (Xu et al., 2015) are employed to numerically calculate the storage modulus and loss factor of the viscoelastic damper. The expression of the equivalent fractional Kelvin model has the form

$\begin{array}{ll}{G}_1=q_0+q_1{\left({\alpha }_T\omega \right)}^{\gamma }\text{cos}\left(\frac{\gamma \pi }{2}\right)& (21)\end{array}$

$\begin{array}{ll}\eta =\frac{q_1{\left({\alpha }_T\omega \right)}^{\gamma }\text{sin}\left(\frac{\gamma \pi }{2}\right)}{q_0+q_1{\left({\alpha }_T\omega \right)}^{\gamma }\text{cos}\left(\frac{\gamma \pi }{2}\right)}& (22)\end{array}$

where q₀ and q₁ are the coefficients related to the viscoelastic materials, γ is the order of fractional derivative, α_T has been given in Equation (17).

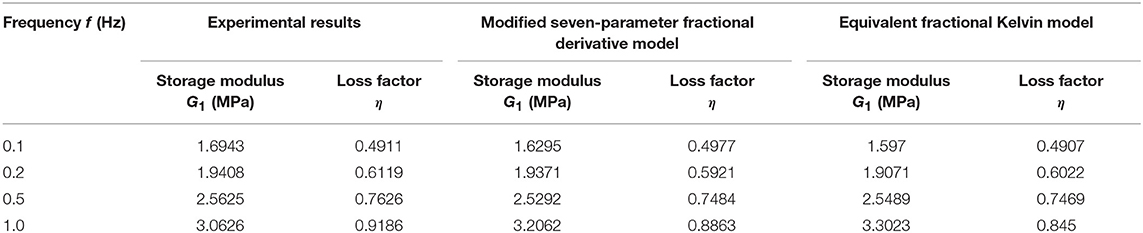
Because Equations (17)–(22) in the two models could not describe the displacement amplitude influence, the impact of displacement amplitude on dynamic properties of viscoelastic dampers is ignored, and only parts of the test data (with displacement 0.2 and 1.5 mm) in Table 2 are used to determine the parameters of the modified seven-parameter fractional derivative model and the equivalent fractional Kelvin model with the least squares method. Then for the modified seven-parameter fractional derivative model, the parameters can be obtained as, ${\mu }_0=2.8954\times {10}^5$, ${\mu }_1=4.4113\times {10}^7$, ${\eta }_1=1.5075\times {10}^6$, α₁ = 0.2054, ${\mu }_2=2.1123\times {10}^8$, ${\eta }_2=1.0714\times {10}^6$, α₂ = 0.7104, and T₀ = −16.89°C. For the equivalent fractional Kelvin model, $q_0=9.3111\times {10}^5$, $q_1=1.831\times {10}^7$, γ = 0.5516, and T₀ = −114.15°C. The test data with the displacement 1.0 mm (which are not used for the parameters determination) are used to verify the numerical results of the proposed model. The experimental and numerical results comparisons of the modified seven-parameter fractional derivative model and the equivalent fractional Kelvin model of the viscoelastic damper are summarized in Table 3 and graphed in Figure 7.

TABLE 3

Table 3. Comparison of experimental and numerical results when d = 1.0 mm.

FIGURE 7

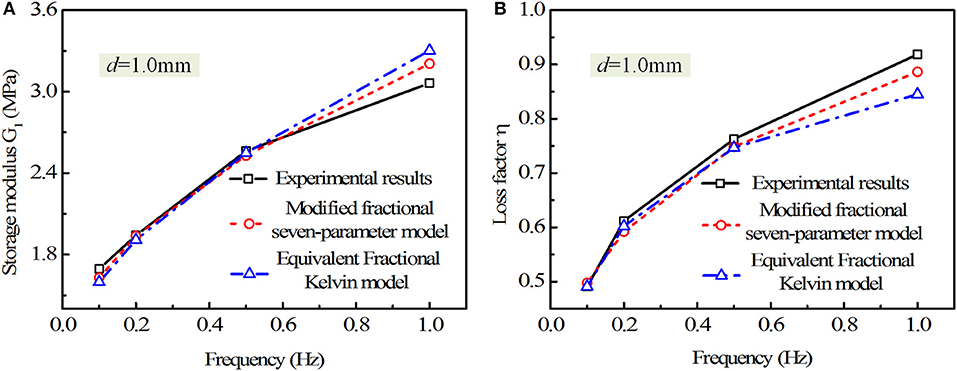
Figure 7. The experimental and numerical results comparison of the viscoelastic damper when d = 1.0 mm. (A,B) Storage modulus, and loss factor, respectively.

It can be obviously seen in Figure 7 that both the modified seven-parameter fractional derivative model and equivalent fractional Kelvin model have perfect accuracy in describing the characteristic parameters of the viscoelastic damper with different frequencies. The errors of both models for storage modulus and loss factor are <10%, but the errors of the modified seven-parameter fractional derivative model always have smaller values. For example, when the frequency is 1 Hz, the storage modulus and loss factor of the viscoelastic damper in test data are 3.0626 MPa and 0.9186; while for the numerical results from the modified seven-parameter fractional derivative model, the storage modulus and loss factor are 3.2062 MPa and 0.8836, and the errors are 4.69 and 3.52%, respectively; for equivalent fractional Kelvin model, the storage modulus and loss factor are 3.3053 MPa and 0.845, the errors are 7.83 and 8.02%, respectively.

Model Verification

To further verify the accuracy of the modified seven-parameter fractional derivative model with different temperatures, the experimental data (Xu et al., 2015) for 9050 A and ZN22 viscoelastic materials under different frequencies and temperatures are compared with the numerical results calculated from the modified seven-parameter fractional derivative model and the equivalent fractional Kelvin model.

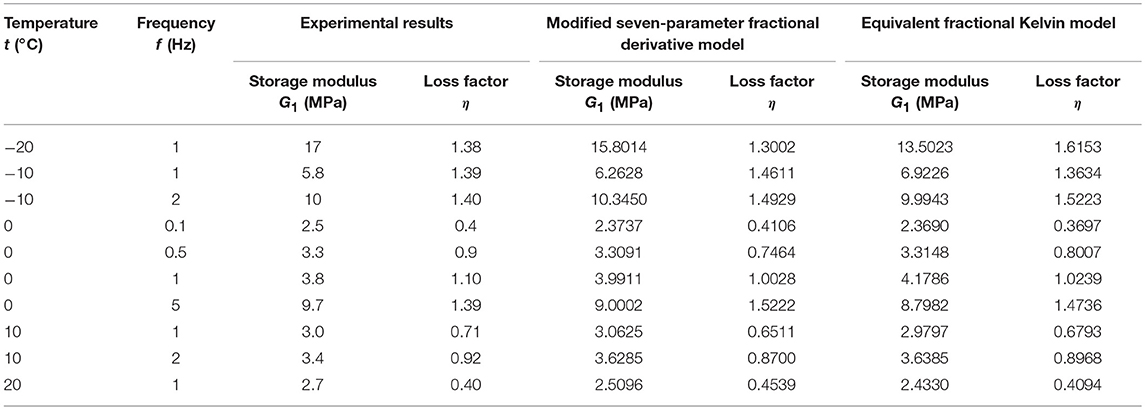
Some parts of the experimental data are used to evaluate the model parameters, and the numerical results are compared with the whole test results. With the least squares method, the model parameters of 9050A materials can be determined as, ${\mu }_0=1.0563\times {10}^6$, ${\mu }_1=4.6305\times {10}^7$, η₁ = 6.1554, α₁ = 0.9741, ${\mu }_2=7.5296\times {10}^8$, ${\eta }_2=4.685\times {10}^4$, α₂ = 0.3144, and T₀ = 153.85°C for the modified seven-parameter fractional derivative model; and $q_0=1.9032\times {10}^6$, q₁ = 229.7502, γ = 0.6888, and T₀ = 164.57°C for the equivalent fractional Kelvin model. The model parameters of ZN22 materials can also be obtained as, ${\mu }_0=2.1575\times {10}^6$, ${\mu }_1=4.6317\times {10}^8$, η₁ = 0.0547, α₁ = 0.6682, ${\mu }_2=3.9676\times {10}^8$, η₂ = 0.0733, α₂ = 0.6326, and T₀ = 272.2°C for the modified seven-parameter fractional derivative model; and $q_0=2.1972\times {10}^6$, q₁ = 0.1322, γ = 0.6575, and T₀ = 270.72°C for the equivalent fractional Kelvin model. The experimental and numerical results comparisons of 9050A and Zn22 viscoelastic materials are given in Tables 4, 5, and vividly graphed in Figures 8, 9. Figure 8 shows the experimental and numerical results comparisons of 9050A material.

TABLE 4

Table 4. Experimental and numerical results comparison for 9050A viscoelastic material.

TABLE 5

Table 5. Experimental and numerical results comparison for Zn22 viscoelastic material.

FIGURE 8

Figure 8. The experimental and numerical results comparison of 9050A viscoelastic material. (A–D) Storage modulus, loss factor, storage modulus, and loss factor, respectively.

FIGURE 9

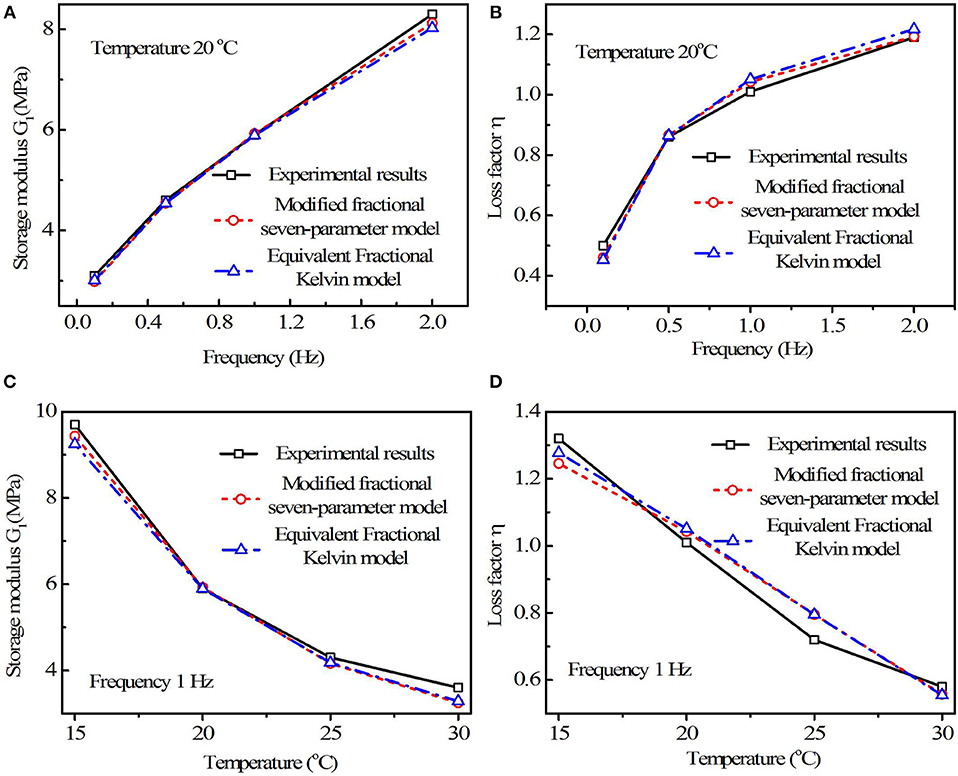
Figure 9. The experimental and numerical results comparison of ZN22 viscoelastic material. (A–D) Storage modulus, loss factor, storage modulus, and loss factor, respectively.

It can be concluded from Figure 8A that the modified seven-parameter fractional derivative model is more accurate than the equivalent fractional Kelvin model when describing the storage modulus with different frequencies. Take 0.1 Hz as an example, the test data for storage modulus is 2.5 MPa; and the numerical results from the modified seven-parameter fractional derivative model is 2.3737 Mpa with error 5.05%; and the numerical results from the equivalent fractional Kelvin model are 2.369 Mpa with error 5.24%. It can be seen in Figure 8B that with the frequencies 0.2–1.0 Hz, the errors of the modified seven-parameter fractional derivative model is a little larger than the equivalent fractional Kelvin model when describing the loss factor with different frequencies, this may due to the complexity of viscoelastic materials at low temperatures, test errors, or the local distortion when determining the model parameters.

It also can be revealed from Figures 8C,D that the modified seven-parameter fractional derivative model is better than the equivalent fractional Kelvin model in capturing the variation trends of storage modulus and loss factor with different temperatures. Take −20°C as an example, the test data for storage modulus and loss factor are 17 MPa and 1.38; and the numerical results from the modified seven-parameter fractional derivative model are 15.8014 Mpa and 1.3002, with errors 7.05 and 5.78%; the numerical results from the equivalent fractional Kelvin model are 13.5023 Mpa and 1.6153, with errors 20.57 and 17.05%. It should be emphasized in Figure 8D that the numerical loss factor curve from the modified seven-parameter fractional derivative model has more consistency with the experimental loss factor curve than that from the equivalent fractional Kelvin model, which proves the advantage of the modified seven-parameter fractional derivative model in describing the nonlinear dynamic behaviors of viscoelastic materials, especially at low temperature. The same conclusion can be obtained from Figure 9 which compares the experimental and numerical results of ZN22 viscoelastic material.

Conclusions

In present paper, the dynamic properties tests of the viscoelastic damper are carried out at low temperature (−5°C). The influence of frequency and displacement on the dynamic properties of the viscoelastic damper are discussed. The seven-parameter fractional derivative model is modified and applied to describe the dynamic behaviors of the viscoelastic damper. The experimental data for 9050 A and ZN22 viscoelastic materials under different frequencies and temperatures are utilized to validate the modified seven-parameter fractional derivative model. Finally, some notable conclusions can be obtained as follows:

(1) The viscoelastic damper has perfect energy dissipation capacity with nearly full ellipse hysteretic curves at low temperature.

(2) The loading frequency and displacement amplitude have important influence on the dynamic properties of the viscoelastic damper. The storage modulus and loss factor increase quickly with increasing frequency, while decrease when the displacement amplitude increases.

(3) The dynamic behavior of the viscoelastic damper and viscoelastic materials (9050A and ZN22) can be precisely depicted by the modified seven-parameter fractional derivative model, which can simulate the nonlinear dynamic properties of viscoelastic materials with varying frequencies and temperatures.

(4) Viscoelastic dampers can serve in a wide temperatures ranges (−20–50°C) with larger displacements. The present work only studies the viscoelastic damper at −5°C with displacements 0.2–2.0 mm. The dynamic properties and mathematical modeling of viscoelastic dampers at extreme temperatures (for example, −20 or 50°C) and large displacement amplitudes still need to be further investigated.

Data Availability

Publicly available datasets were analyzed in this study. This data can be found here: https://journals.sagepub.com/doi/pdf/10.1177/1077546313513604; https://journals.sagepub.com/doi/pdf/10.1177/1077546313513604/a.

Author Contributions

YX and YD carried out the properties tests of the viscoelastic damper. XH formulated the mathematical model. YL and SZ conducted the application and verification of the mathematical model with viscoelastic dampers and materials. YX and YL wrote and checked the manuscript.

Funding

This study was financially supported by the National Key R&D Programs of China with Grant Nos. 2016YFE0200500 and 2016YFE0119700, the Jiangsu Province International Cooperation Project with Grant No. BZ 2018058, the National Science Fund for Distinguished Young Scholars with Grant No. 51625803, the Program of Chang Jiang Scholars of Ministry of Education, National Natural Science Foundation of China with Grant No. 11572088, the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bagley, R. L., and Torvik, P. J. (1983). A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 27, 201–210. doi: 10.1122/1.549724

CrossRef Full Text | Google Scholar

Caputo, M. (1974). Vibrations on an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 56, 897–904. doi: 10.1121/1.1903344

CrossRef Full Text | Google Scholar

Christensen, R. (1971). Theory of Viscoelasticity: An Introduction. New York, NY: Academic Press.

Google Scholar

Drozdov, A. D., and Dorfmann, A. (2002). The effect of temperature on the viscoelastic response of rubbery polymers at finite strains. Acta Mech. 154, 189–214. doi: 10.1007/BF01170707

CrossRef Full Text | Google Scholar

Koeller, R. C. (1984). Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. Trans. ASME, 51, 299–307. doi: 10.1115/1.3167616

CrossRef Full Text | Google Scholar

Liu, J. G., and Xu, M. Y. (2006). Higher-order fractional constitutive equations of viscoelastic materials involving three different parameters and their relaxation and creep functions. Mech. Time Dependent Mater. 10, 263–279. doi: 10.1007/s11043-007-9022-9

CrossRef Full Text | Google Scholar

Matsagar, V. A., and Jangid, R. S. (2005). Viscoelastic damper connected to adjacent structures involving seismic isolation. J. Civil Eng. Manage. 11, 309–322. doi: 10.3846/13923730.2005.9636362

CrossRef Full Text | Google Scholar

Min, K. W., Kim, J., and Lee, S. H. (2004). Vibration tests of 5-storey steel frame with viscoelastic dampers. Eng. Struct. 26, 831–839. doi: 10.1016/j.engstruct.2004.02.004

CrossRef Full Text | Google Scholar

Müller, S., Kästner, M., Brummund, J., and Ulbricht, V. (2011). A nonlinear fractional viscoelastic material model for polymers. Comput. Mater. Sci. 50, 2938–2949. doi: 10.1016/j.commatsci.2011.05.011

CrossRef Full Text | Google Scholar

Payne, A. R. (1963). The dynamic properties of carbon black-loaded natural rubber vulcanizates Part I. J. Appl. Polym. Sci. 6, 57–63. doi: 10.1002/app.1962.070061906

CrossRef Full Text | Google Scholar

Poojary, U. R., and Gangadharan, K. V. (2018). Integer and fractional order-based viscoelastic constitutive modeling to predict the frequency and magnetic field-induced properties of magnetorheological elastomer. J. Vib. Acoust. Trans. ASME 140:041007. doi: 10.1115/1.4039242

CrossRef Full Text | Google Scholar

Pritz, T. (2003). Five-parameter fractional derivative model for polymeric damping materials. J. Sound Vib. 265, 935–952. doi: 10.1016/S0022-460X(02)01530-4

CrossRef Full Text | Google Scholar

Rao, M. D. (2003). Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 262, 457–474. doi: 10.1016/S0022-460X(03)00106-8

CrossRef Full Text | Google Scholar

Rashid, A., and Nicolescu, C. M. (2008). Design and implementation of tuned viscoelastic dampers for vibration control in milling. Int. J. Mach. Tools Manuf. 48, 1036–1053. doi: 10.1016/j.ijmachtools.2007.12.013

CrossRef Full Text | Google Scholar

Rossikhin, Y. A., and Shitikova, M. V. (1997). Applications of fractional calculus to dynamic problems of linear and nonlinear heredity mechanics of solids. Appl. Mech. Rev. Trans. ASME 50, 15–67. doi: 10.1115/1.3101682

CrossRef Full Text | Google Scholar

Samali, B., and Kwok, K. C. S. (1995). Use of viscoelastic dampers in reducing wind-and earthquake-induced motion of building structures. Eng. Struct. 17, 639–654. doi: 10.1016/0141-0296(95)00034-5

CrossRef Full Text | Google Scholar

Schiessel, H., Metzler, R., Blumen, A., and Nonnenmacher, T. F. (1995). Generalized viscoelastic models: their fractional equations with solutions. J. Phys. A Math. Gen. 28, 6567–6584. doi: 10.1088/0305-4470/28/23/012

CrossRef Full Text | Google Scholar

Tsai, C. S., and Lee, H. H. (1993). Applications of viscoelastic dampers to high-rise buildings. J. Struct. Eng. ASCE 120, 1222–1233. doi: 10.1061/(ASCE)0733-9445(1993)119:4(1222)

CrossRef Full Text | Google Scholar

Xu, Y. S., Xu, Z. D., Guo, Y. Q., Ge, T., Xu, C., and Huang, X. H. (2019). A theoretical and experimental study of viscoelastic damper based on fractional derivative approach and micro-molecular structures. J. Vib. Acoust. Trans. ASME 141:031010. doi: 10.1115/1.4042517

CrossRef Full Text | Google Scholar

Xu, Z. D. (2007). Earthquake mitigation study on viscoelastic dampers for reinforced concrete structures. J. Vib. Control 13, 29–45. doi: 10.1177/1077546306068058

CrossRef Full Text | Google Scholar

Xu, Z. D., Huang, X. H., Xu, F. H., and Yuan, J. (2019). Parameters optimization of vibration isolation and mitigation system for precision platforms using non-dominated sorting genetic algorithm. Mech. Syst. Signal Process. 128, 191–201. doi: 10.1016/j.ymssp.2019.03.031

CrossRef Full Text | Google Scholar

Xu, Z. D., Liao, Y. X., Ge, T., and Xu, C. (2016). Experimental and theoretical study on viscoelastic dampers with different matrix rubbers. J. Eng. Mech. ASCE 142:04016051. doi: 10.1061/(ASCE)EM.1943-7889.0001101

CrossRef Full Text | Google Scholar

Xu, Z. D., Shen, Y. P., and Zhao, H. T. (2003). A synthetic optimization analysis method on structures with viscoelastic dampers. Soil Dyn. Earthq. Eng. 23, 683–689. doi: 10.1016/j.soildyn.2003.07.003

CrossRef Full Text | Google Scholar

Xu, Z. D., Wang, S. A., and Xu, C. (2014). Experimental and numerical study on long-span reticulate structure with multidimensional high-damping earthquake isolation devices. J. Sound Vib. 333, 3044–3057. doi: 10.1016/j.jsv.2014.02.013

CrossRef Full Text | Google Scholar

Xu, Z. D., Xu, C., and Hu, J. (2015). Equivalent fractional Kelvin model and experimental study on viscoelastic damper. J. Vib. Control 21, 2536–2552. doi: 10.1177/1077546313513604

CrossRef Full Text | Google Scholar

Xu, Z. D., Zhao, H. T., and Li, A. Q. (2004). Optimal analysis and experimental study on structures with viscoelastic dampers. J. Sound Vib. 273, 607–618. doi: 10.1016/S0022-460X(03)00522-4

CrossRef Full Text | Google Scholar